Все объемные геометрические фигуры и их названия: Основные геометрические фигуры 🟢🟨🔺 и их названия
лучший ответ: Как называются пространственные геометрические фигуры
Пространственные геометрические фигуры называются многогранниками, которые представляют собой объемные геометрические фигуры и имеют ширину, длину и высоту.
Пространственные геометрические фигуры (куб, прямоугольный блок, пирамида, конус, цилиндр и сфера): распознавание, анализ, характеристика и планирование.
Куб, цилиндр, конус, пирамиды и другие являются объектами изучения космической геометрии.
Пространственные геометрические фигуры – это те, которые имеют три измерения: длину, высоту и ширину. Эти фигуры делятся на две группы: круглые тела (ограниченные какой-либо округлой поверхностью) и многогранники (поверхности, ограниченные плоскими геометрическими фигурами).
Плоские фигуры всегда двухмерны. Когда есть трехмерные фигуры, они известны как пространственные. На основных плоских рисунках у каждого из них есть определенная формула для расчета его площади.
Поэтому любая фигура, для построения и определения которой необходимы три измерения, называется пространственной геометрической фигурой. Примеры пространственных фигур: куб, призма, параллелепипед, пирамида, конус, цилиндр, сфера и др.
Примеры пространственных фигур: куб, призма, параллелепипед, пирамида, конус, цилиндр, сфера и др.
На основе примитивных элементов разрабатываются геометрические тела, главными из которых являются многогранники: параллелепипеды, кубы и другие призмы, помимо так называемых платоновских тел; и круглые тела: конус, цилиндр и сфера.
Космические геометрические фигуры, называемые также геометрическими телами, — это те, которые имеют три измерения: длину, ширину и глубину.
Шестиугольная призма: основание образовано шестиугольником. Семиугольная призма: основание образовано семиугольником.
Геометрические тела — это трехмерные объекты, заданные в пространстве. Они делятся на три группы: любые твердые тела, многогранники и круглые тела. Геометрические тела — это трехмерные объекты, заданные в пространстве. Некоторые примеры геометрических тел: кубы, пирамиды, призмы, цилиндры и сферы.
Основными плоскими фигурами являются треугольник, круг, квадрат, прямоугольник, ромб и трапеция, и каждая из них имеет формулу вычисления площади.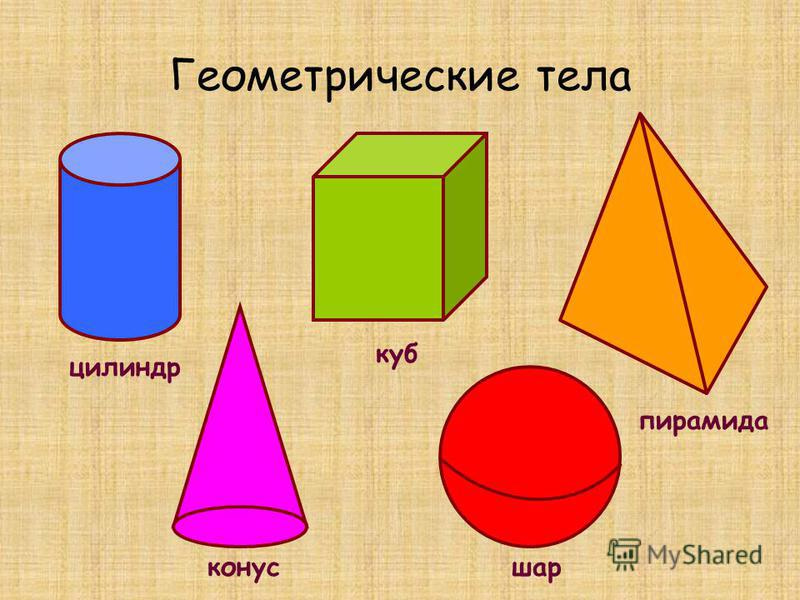 Стоит отметить, что область изучается в планиметрии, геометрии для двухмерных объектов.
Стоит отметить, что область изучается в планиметрии, геометрии для двухмерных объектов.
Определение многогранника следующее: это геометрическое тело, заполненное или незаполненное, с концами, ограниченными отрезками прямых линий, образующих многоугольники. Если вы не помните, многоугольник — это форма, образованная объединением (прямых) линий, пересекающихся в вершинах.
Плоские геометрические фигуры. Плоские фигуры — это поверхности, замкнутые отрезками (минимум три отрезка). Как мы уже видели, все геометрические фигуры, считающиеся плоскими, имеют определенные математические формулы для своего периметра и площади, так как не имеют объема.
Геометрические фигуры — это элементы изучения геометрии, области математики, которая работает с измерениями, расположением и размером фигур в пространстве. Геометрические фигуры присутствуют в нашей повседневной жизни. Геометрические фигуры — это формы окружающих нас предметов.
Планиметрия — это изучение фигур в двух измерениях, таких как квадраты, круги, прямоугольники и треугольники. В то время как пространственная геометрия изучает фигуры в трех измерениях, то есть кубы, сферы, параллелепипеды и пирамиды.
В то время как пространственная геометрия изучает фигуры в трех измерениях, то есть кубы, сферы, параллелепипеды и пирамиды.
ПРОСТРАНСТВЕННЫЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ ИЛИ ГЕОМЕТРИЧЕСКИЕ ТЕЛА ЯВЛЯЮТСЯ ТЕ, КОТОРЫЕ ПРОИСХОДЯТ В ПРОСТРАНСТВЕ, В СВЯЗИ С ИХ ТРЕХМЕРНОСТЬЮ, Т.Е. ИМЕЮТ ТРИ ИЗМЕРЕНИЯ (ВЫСОТУ, ШИРИНУ И ДЛИНУ).
Также известный как шестигранник, куб представляет собой геометрическое тело, все грани которого образованы квадратами. У него 6 граней, 12 ребер и 8 вершин. Куб представляет собой шестигранный многогранник, все грани которого квадратные.
Цилиндр, конус и сфера являются круглыми телами. Мы называем круглыми телами геометрические тела, имеющие криволинейные поверхности. Они также известны как тела вращения, потому что они построены путем вращения плоской фигуры.
Геометрическая форма фигуры представляет собой пирамиду с прямоугольным основанием, имеющую пять граней, пять вершин и восемь ребер.
Многогранники (от лат. poly — много — и edro — грань) — объёмные фигуры, образованные объединением правильных многоугольников, в которых все углы многогранников конгруэнтны. Объединение этих многоугольников образует элементы, составляющие многогранник, это: вершины, ребра и грани.
Объединение этих многоугольников образует элементы, составляющие многогранник, это: вершины, ребра и грани.
Пространственная геометрия — это область математики, изучающая геометрические тела и геометрию в пространстве. Размышление о геометрии с помощью трехмерных объектов означает стремление понять мир, в котором мы живем, поэтому пространственная геометрия направлена на понимание форм объектов в трех измерениях.
Шестиугольник – это многоугольник с шестью параллельными сторонами, образующими равносторонний треугольник. Сумма всех углов равна 360 градусов. Во-первых, когда геометрическая фигура имеет шесть сторон, она называется шестиугольником. Короче говоря, шестиугольники также могут быть правильными, если они имеют одинаковую меру со всех сторон.
Параллелепипед – это геометрическое тело, грани которого образованы параллелограммами.
Куб также является случаем призмы, так как все его квадратные грани конгруэнтны. У призмы все грани образованы многоугольниками, следовательно, это частный случай многогранника.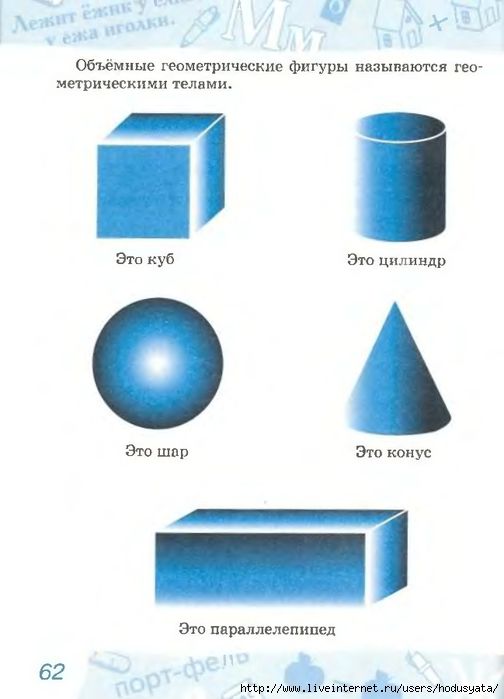
В геометрии трапеция представляет собой четырехугольник с двумя сторонами, параллельными друг другу, которые называются большим основанием и малым основанием.
Основными плоскими фигурами являются треугольник, круг, квадрат, прямоугольник, ромб и трапеция, и каждая из них имеет формулу вычисления площади. Стоит отметить, что область изучается в планиметрии, геометрии для двухмерных объектов.
Поэтому любая фигура, для построения и определения которой необходимы три измерения, называется пространственной геометрической фигурой. Примеры пространственных фигур: куб, призма, параллелепипед, пирамида, конус, цилиндр, сфера и др.
Геометрические фигуры, или С чего начинается геометрия
Многие люди ошибочно полагают, что впервые они встречают геометрические фигуры в средней школе. Там они изучают их названия, свойства и формулы. Но на самом деле с самого детства любой предмет, который видит ребенок, ощущает, чувствует его запах или взаимодействует с ним любым другим образом, представляет собой именно геометрическую фигуру. Кушетка, на которой лежит только что родившая женщина – прямоугольник, лампа, что дает акушерам свет – круглая фигура, форточки в окне – квадраты. Этот список можно продолжать бесконечно.
Кушетка, на которой лежит только что родившая женщина – прямоугольник, лампа, что дает акушерам свет – круглая фигура, форточки в окне – квадраты. Этот список можно продолжать бесконечно.
Геометрические фигуры, непосредственно как элемент науки, впервые встречается школьникам в средних классах. Можно даже сказать, что геометрия начинается именно с них. Однако, как уже говорилось выше, первые взаимодействия с ними происходят задолго до этого. Возьмем, к примеру, точку. Она представляет собой самую маленькую фигуру в геометрии. Кроме того, ее принято считать основой всех остальных (как атомы в химии). Все треугольники, квадраты и прочие фигуры на любом чертеже состоят из множества точек. Они обладают определенными свойствами, каждое из которых присуще только одной фигуре (ни одна другая не может быть ими наделена).
Можно предположить, что все геометрические фигуры состоят непосредственно из линий, но чем является она? Это и есть множество точек, расположенных в ряд. Их можно продолжать бесконечно, поскольку прямая линия не заканчивается.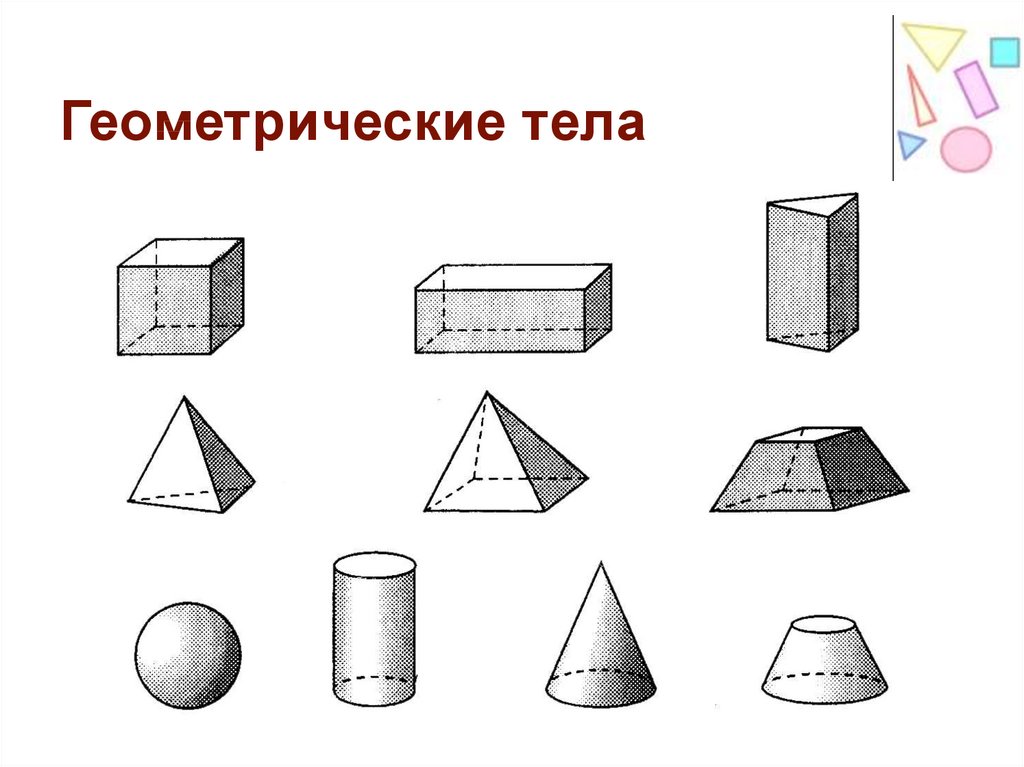 Если же она ограничена с двух сторон, то ее принято называть отрезком. Если имеется только одно ограничение, то перед вами луч. Следовательно, все плоские фигуры в геометрии состоят из отрезков, так как составляющие имеют и конец, и начало. Стоит отметить, что прямая, которая была разделена точкой, является двумя лучами, направленными в противоположные друг другу стороны.
Если же она ограничена с двух сторон, то ее принято называть отрезком. Если имеется только одно ограничение, то перед вами луч. Следовательно, все плоские фигуры в геометрии состоят из отрезков, так как составляющие имеют и конец, и начало. Стоит отметить, что прямая, которая была разделена точкой, является двумя лучами, направленными в противоположные друг другу стороны.
Не только из плоских элементов состоит геометрия, имеются также и объемные геометрические фигуры. К их изучению в школе приступают позже, ближе к окончанию учебы, но сталкивается с ними человек, опять же, гораздо раньше. К примеру, когда ребенок берет в руки кубик, то держит в ладонях куб. Или, если он смотрит на комод, то перед ним прямоугольный параллелепипед. Все объемные фигуры состоят из плоскостей (то есть, она является неопределенным первичным понятием, как и прямая). Тот же самый параллелепипед состоит из шести таких элементов. Наглядно ознакомиться с плоскостью можно, посмотрев на поверхность любого стола. Но это будет только ее часть, поскольку имеются ограничения. Непосредственно плоскость такая же бесконечная, как и прямая линия.
Но это будет только ее часть, поскольку имеются ограничения. Непосредственно плоскость такая же бесконечная, как и прямая линия.
Таким образом, нет сферы, где бы не встречались геометрические фигуры. Названия их различны, они определяют свойства и особенности. К примеру, формула площади треугольника не подойдет для прямоугольника или квадрата.
Желательно приобщать ребенка к геометрическим фигурам еще в дошкольном возрасте. Можно сделать их своими руками, а затем выкладывать ими различные рисунки на бумаге (если это плоские элементы). Однако не стоит отказываться и от объемных фигур. В интернете можно найти множество дидактических игр, связанных с этим. Но нельзя откладывать знакомство с ними, ведь все, что мы видим – геометрические фигуры. Даже человек состоит из них!
Имя трехмерной формы с изображениями
Вы ищете имя трехмерной формы или название трехмерной объемной фигуры с изображениями? Здесь вы найдете список всех распространенных типов названий 3d фигур с картинками.
Трехмерная фигура также называется трехмерной фигурой с определенными свойствами, включая количество ребер, граней и вершин. Все трехмерные объекты представляют собой твердые тела, имеющие некоторые измерения по осям X, Y и Z, называемые длиной, шириной и высотой, которые также называются размерами твердотельного объекта. 3D-формы обычно возникают путем вращения 2D-форм.
Содержание
3D-фигуры Имя
3D-фигуры или тела обладают некоторыми свойствами в зависимости от их форм и размеров
- Вершины: Вершина – это угловая точка, где сходятся ребра.
- Ребра: Ребро – это просто отрезок, проведенный между гранями.
- Грани: Грань — это кривая или плоская поверхность на трехмерной поверхности, покрытая ее краями.
3D-фигуры с названиями и картинками
| Sr No | 3D Shapes Image | 3D Shapes Name | ||||
|---|---|---|---|---|---|---|
1. | Cube | |||||
| 2. | Cuboid | |||||
| 3. | Cylinder | |||||
| 4. | Sphere | |||||
| 5. | Cone | |||||
| 6. | ||||||
| 7. | Pyramid | |||||
| 8. | Prism | |||||
| 9. | Torus | |||||
| 10. | Hemisphere | |||||
| 11. | Tetrahedron | |||||
12 .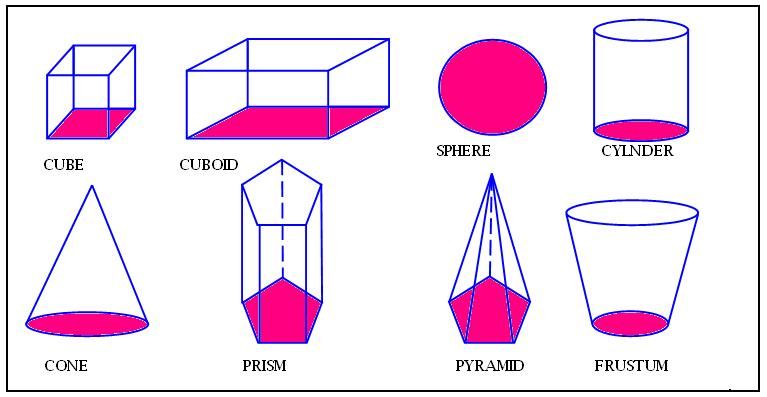 | Пентахедрон | |||||
| 13. | Квадратная пирамида | |||||
| 14. | ||||||
| 15. | ||||||
| 15. | ||||||
| 15.0083 | Triangular prism | |||||
| 16. | Pentagonal prism | |||||
| 17. | Hexagonal prism | |||||
| 18. | Heptagonal Prism | |||||
| 19. | Octagonal prism | |||||
20. | НЕАГОНАЛЬНАЯ ПРИМА | |||||
| 21. | Додекагональная призма | |||||
| 22. | Icosahedron | 900Icosahedron | 92 900..0037 | |||
| 23. | Ellipsoid | |||||
| 24. | Hexahedron | |||||
| 25. | Heptahedron | |||||
| 26. | Octahedron | |||||
| 27. | Nonahedron | |||||
| 28. | Додекаэдр |
Описание трехмерных фигур
1. Куб
Куб
Куб определяется как квадрат с равными трехмерными сторонами. Все грани куба имеют одинаковые размеры. Все углы равны и треугольники прямоугольные.
2. Прямоугольная призма
Прямоугольная призма. Грани кубоида прямоугольные. У него шесть граней, восемь ребер и восемь вершин соответственно.
3. Конус
Конус — это твердый объект с круглым основанием и единственной вершиной. Это геометрическая форма, которая сужается.
4. Цилиндр
Цилиндр – объемная геометрическая фигура, имеющая два параллельных круглых основания, соединенных криволинейной поверхностью. У него нет вершин.
5. Призма
Призма всегда имеет одинаковую форму или грань с обеих сторон.
6. Пирамида
Пирамида со всеми верхними гранями представляет собой равнобедренные треугольники, которые соединяются в одной вершине, а поверхность основания подобна квадрату.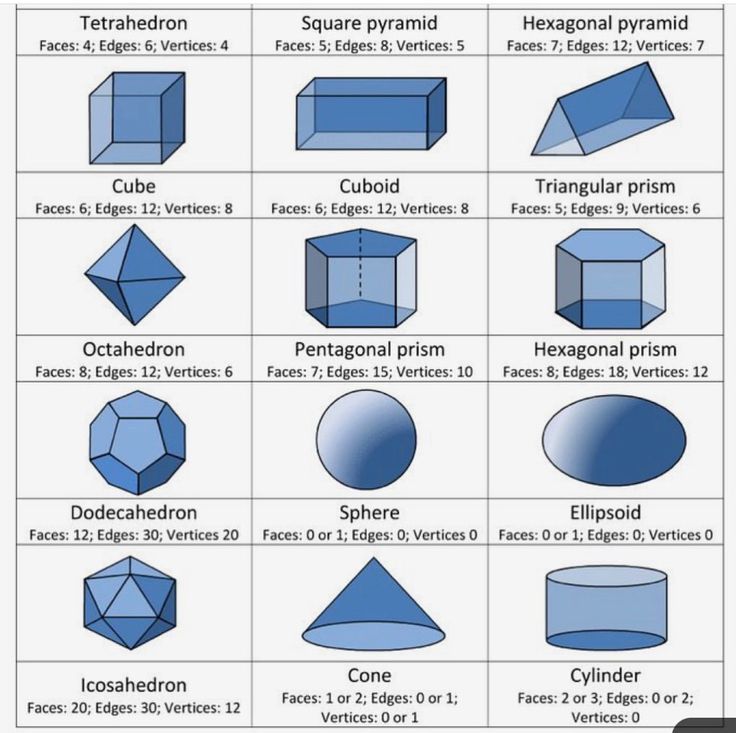
7. Полусфера (полусфера)
Полусфера выглядит как срезанная часть сферы. Поверхность среза выглядит как круг, а другая часть – как сплошной полукруг.
8. Тетраэдр (треугольная пирамида)
Пирамида, все грани которой подобны треугольнику, называется тетраэдром. У него шесть ребер, четыре грани и четыре вершины соответственно.
9. Квадратная пирамида (Пирамида с квадратным основанием)
Квадратная пирамида — это пирамида с квадратным основанием, а остальные грани представляют собой треугольники, соединенные вместе в одной вершине на вершине.
10. Сфера
Сфера – округлый сплошной шар, не содержащий плоской поверхности, ребер и вершин
11. Многогранник
Многогранник представляет собой твердую трехмерную форму, которая содержит плоские поверхности и прямые ребра. Правильный многогранник — это трехмерная фигура, все грани которой имеют одинаковую форму.
12. Додекаэдр
Додекаэдр также называют правильным многогранником, все грани которого имеют одинаковую форму. У него 12 граней, и все они похожи на пятиугольники.
13. Треугольная призма
Треугольная призма – это призма, имеющая две треугольные грани, вершины которых соединены ребром, образующим прямоугольную грань. Он имеет шесть вершин, девять ребер и пять граней.
14. Тор
Тор представляет собой твердое тело в форме пончика с отверстием между ними и образует кольцеобразную структуру.
15. Пятиугольная призма
Пятиугольная призма – это призма, имеющая две пятиугольные грани, соединенные своими вершинами.
Читайте также:
- Цвета радуги
- Водные животные Название
- Животные Имя малыша
- Имя домашних животных
- Имя млекопитающих
- Имя формы
Список геометрических фигур | Определение, примеры, типы, 2D и 3D
Введение Любая структура, открытая или закрытая, с определенной формой и характеристиками, состоящая из линий, кривых и точек, называется геометрической формой. Ниже приведены некоторые примеры хорошо известных геометрических фигур: квадрат, прямоугольник, круг, конус, цилиндр, сфера и т. д. Все эти формы отличаются от других форм и имеют определенные общие характеристики.
Ниже приведены некоторые примеры хорошо известных геометрических фигур: квадрат, прямоугольник, круг, конус, цилиндр, сфера и т. д. Все эти формы отличаются от других форм и имеют определенные общие характеристики.
Геометрические фигуры — это фигуры, используемые в математике для представления форм объектов реального мира. Фигуры — это формы вещей в геометрии, которые имеют поверхности, углы и граничные линии. Существует несколько типов как 2D, так и 3D форм.
Простые геометрические фигуры с определенной границей, площадью внутренней поверхности и площадью внешней поверхности образуют формы. Мы можем узнать о различных формах и их характеристиках с помощью геометрии. Основные формы и термины используются для ознакомления учащихся с геометрией.
Крайне важно, чтобы мы получили необходимое понимание геометрических фигур, прежде чем обращать внимание на более сложные и конкурентоспособные математические идеи геометрии и алгебры. Эта статья расскажет вам об основных геометрических фигурах и их характеристиках.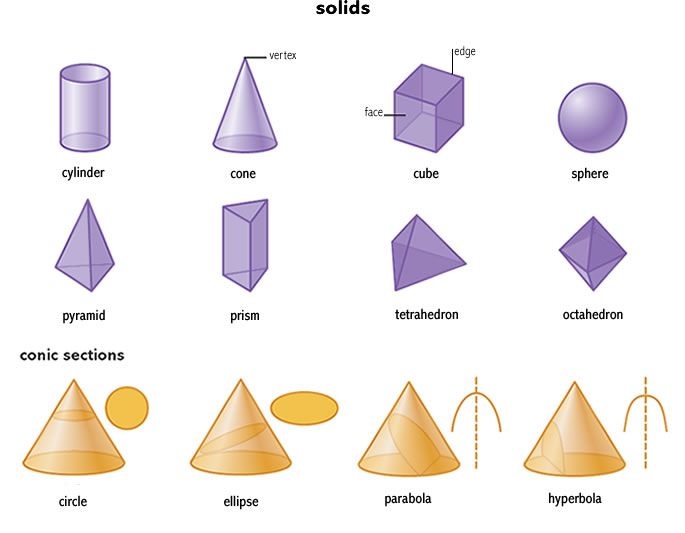
Геометрические фигуры определяются как окруженные границей, состоящей из определенного количества кривых, точек и отрезков. Каждая фигура имеет характерное имя, например, круг, квадрат, треугольник или прямоугольник.
Любой объект с определенной структурой считается геометрической формой. Линии, кривые, углы и поверхности составляют формы на этих рисунках. Квадрат, прямоугольник, круг, цилиндр, цилиндр, куб, сфера и другие знакомые геометрические фигуры — это лишь некоторые из них. Многоугольник – это геометрическая фигура, имеющая три или более сторон. Общие многоугольники включают треугольники, квадраты, ромбы, трапеции и т. д.
В повседневной жизни существуют простые геометрические формы. Например, кусок пиццы имеет форму треугольника, телевизионный экран обычно имеет прямоугольную форму, а шар, среди прочего, имеет форму сферы.
Фигуры, представляющие формы различных объектов, называются геометрическими фигурами. В то время как некоторые фигуры являются трехмерными фигурами, некоторые являются двумерными фигурами. Трехмерные фигуры расположены по осям x, y и z, а двухмерные фигуры существуют только по осям x и y.
В то время как некоторые фигуры являются трехмерными фигурами, некоторые являются двумерными фигурами. Трехмерные фигуры расположены по осям x, y и z, а двухмерные фигуры существуют только по осям x и y.
Начиная с линии, кривой или сегмента линии, вы можете создавать геометрические фигуры. Треугольник – это фигура, в которой соединены трехпрямые отрезки, а пятиугольник и другие формы и фигуры могут быть составлены исходя из количества и расположения этих линий.
Типы геометрических фигурГеометрические фигуры — это фигуры, используемые в математике для представления форм объектов реального мира. Фигуры — это формы вещей в геометрии, которые имеют поверхности, углы и граничные линии. Существует несколько типов как 2D, так и 3D форм.
Двумерные фигуры ( 2D-фигуры ) Двумерные (2D) фигуры — это плоские фигуры, которым не хватает высоты или толщины. Единственными параметрами являются длина и ширина.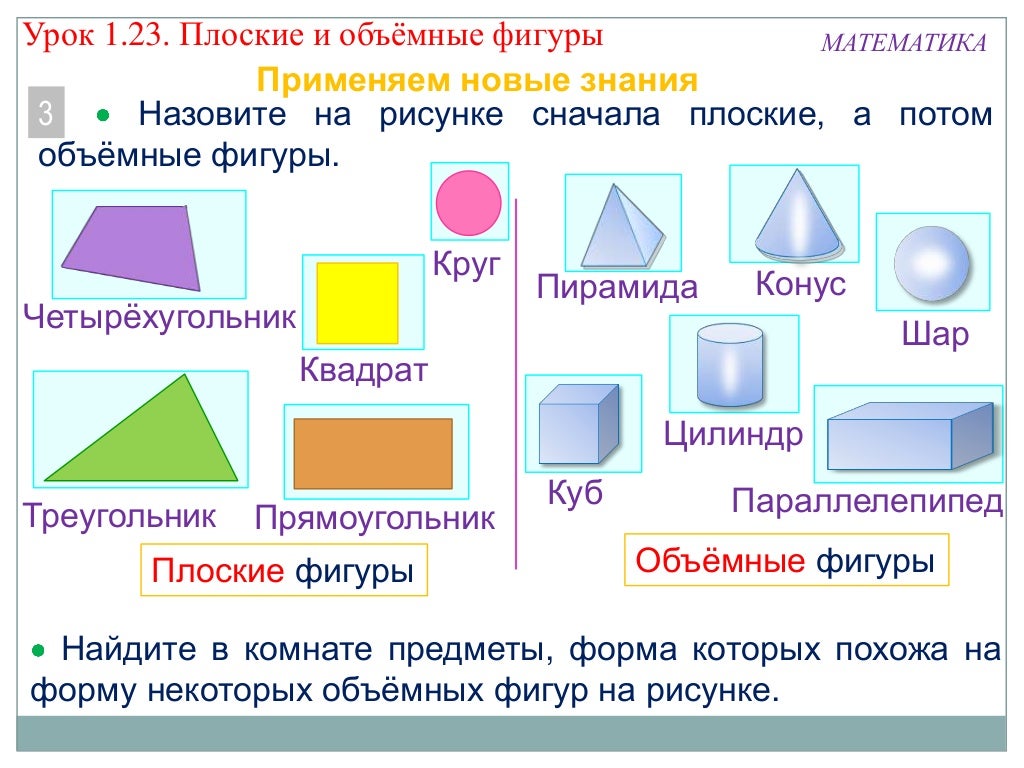 Круги и многоугольники, такие как треугольники, квадраты, прямоугольники и т. д., являются несколькими примерами 2D-фигур.
Круги и многоугольники, такие как треугольники, квадраты, прямоугольники и т. д., являются несколькими примерами 2D-фигур.
Формы обладают характеристиками, которые позволяют нам идентифицировать их как таковые. В зависимости от количества сторон и углов фигуры может существовать несколько фигур. Угол двумерной (2D) формы — это место, где сходятся две стороны. Сторона – это прямая линия. Угол образован, так как вершина – это другое слово для угла. Фигура ниже показывает, что она имеет четыре стороны, четыре угла и четыре угла.
Равная длина сторон фигуры служит описанием. Стороны равной длины обозначаются штриховкой («|»). На рисунке ниже показано, что противоположные стороны равны по длине. Размеры сторон с одной штриховкой и сторон с двумя метками различны.
Типичные 2D-формы и их свойства показаны ниже.
Круг В двух измерениях круг представляет собой изогнутую форму без углов. Радиус, диаметр, длина окружности и другие параметры — вот некоторые из его атрибутов.
- У круга нет ни сторон, ни ребер. Он круглый.
- Расстояние, окружающее окружность, называется его окружностью.
- Радиус — это расстояние от центра окружности до любой точки окружности.
Диаметр — это отрезок с двумя концами на окружности, проходящей через ее центр.
МногоугольникиМногоугольники представляют собой двумерные фигуры с определенным количеством сторон. Треугольники, параллелограммы, квадраты, прямоугольники, ромбы, воздушные змеи и трапеции
s — это несколько многоугольников с равными сторонами и углами.
Многоугольники имеют разные имена в соответствии с определяющими их свойствами, такими как количество сторон, ребер, углов и углов.
Треугольник Треугольники — это трехсторонние многоугольники. Треугольники можно разделить на разносторонние, равнобедренные или равносторонние в зависимости от длины их сторон. Треугольники могут быть острыми, тупоугольными или прямыми, в зависимости от их углов.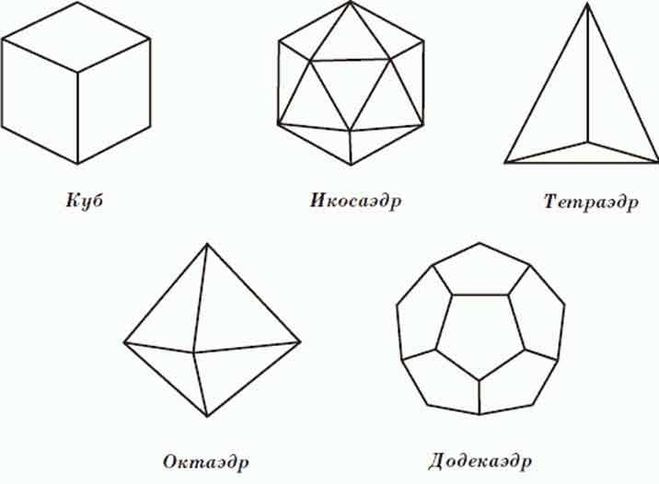
Сумма внутренних углов треугольника равна 180 градусам. У остроугольных треугольников все углы меньше 90 градусов. Одна сторона прямоугольного треугольника составляет угол 90 градусов. Один из углов тупоугольного треугольника больше 90 градусов.
ЧетырехугольникиТермины «четырехугольник» (четыре) и «латеральный» (сторона) произошли от термина «четырехугольник». Семейство четырехугольников состоит из четырех сторон, четырех вершин и четырех углов. Каждая четырехугольная форма немного отличается от других по ряду признаков. В приведенном ниже списке приведены примеры четырехугольников и их свойства:
ПараллелограммЧетыре стороны и четыре угла параллелограмма состоят из параллельных прямых. Параллелограмм имеет параллельные противоположные стороны, но не обязательно равные углы. Различают три вида параллелограммов: квадрат, прямоугольник и ромб.
Сегмент синей линии показывает противоположные стороны параллелограмма.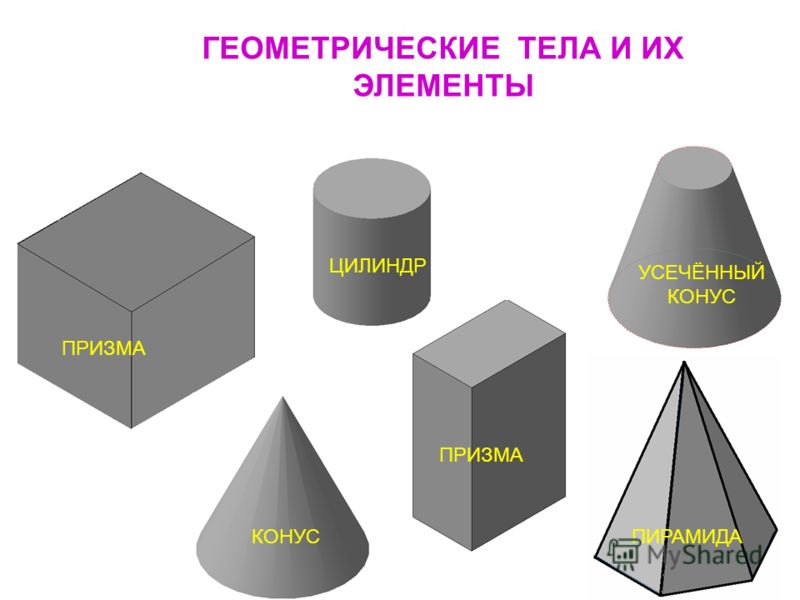
У квадрата четыре стороны и четыре угла. Стороны одинаковой длины составляют квадрат. Квадрат состоит из двух параллельных наборов сторон.
Красные точки обозначают четыре угла квадрата.
Маркировка штриховки указывает на одинаковую длину сторон.
ПрямоугольникУ прямоугольника четыре стороны и четыре угла. Длины двух противоположных пар сторон прямоугольника равны. Два набора сторон прямоугольника параллельны.
Красные точки обозначают четыре угла прямоугольника.
Штриховки указывают на то, что длины противоположных сторон равны.
РомбРомбы — другое название ромбов. Четыре стороны и четыре угла составляют ромб. Ромб похож на наклонный квадрат. Длина сторон одинакова. У ромба противоположные стороны параллельны.
Штриховкой показаны равные по длине стороны ромба.
Красные точки обозначают углы ромба.
Воздушный змей состоит из четырех сторон и четырех углов. Две пары сторон воздушного змея имеют одинаковую длину.
Воздушный змей не может иметь параллельных сторон.
Штриховкой показаны равные по длине стороны ромба.
ТрапецияТрапеция имеет только один набор параллельных сторон. (В Индии и Великобритании используют слово « трапеция” )
Параллельные противоположные стороны показаны отрезками синей линии.
Многоугольники с более чем четырьмя сторонамиВот несколько примеров многоугольников с более чем четырьмя сторонами.
ПятиугольникПятиугольник представляет собой фигуру с пятью сторонами одинаковой длины. Его внутренние углы в сумме эквивалентны 540 градусам — каждый по 108 градусов в углах правильного пятиугольника.
Шестигранник Шестиугольники — это многоугольники с шестью сторонами.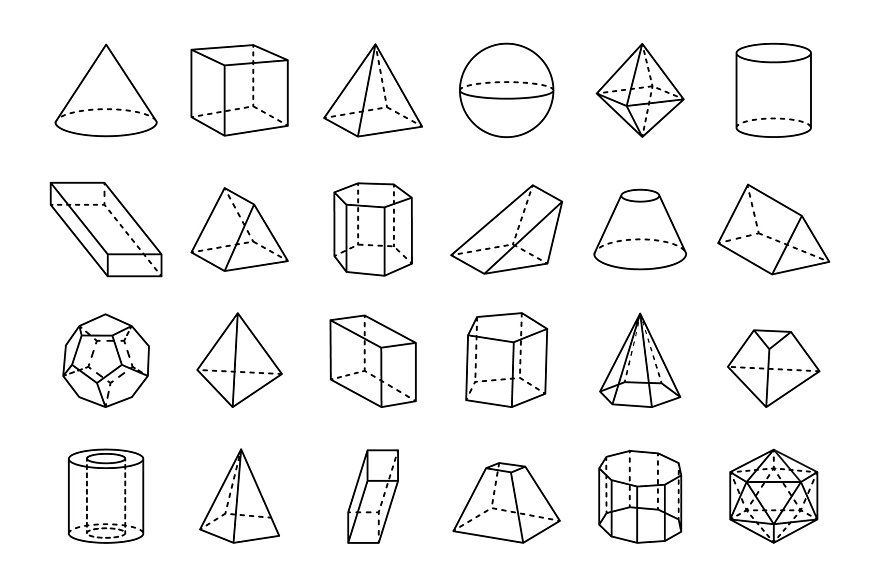 Сумма его внутренних углов равна 720 градусов. В правильном шестиугольнике каждый угол равен 120 градусам.
Сумма его внутренних углов равна 720 градусов. В правильном шестиугольнике каждый угол равен 120 градусам.
Многоугольники, имеющие семь сторон, называются семиугольниками. Внутренние углы семиугольника в сумме составляют 900 градусов. Каждая вершина правильного семиугольника имеет угол 128,57 градуса.
ВосьмиугольникМногоугольник с восемью сторонами называется восьмиугольником. Всего внутренних углов 1080. В правильном восьмиугольнике каждый угол равен 135 градусам.
DecagonДесятиугольники называются «декагонами». Его внутренние углы в сумме составляют 1440 градусов. Каждый угол правильного десятиугольника имеет 144 градуса.
Трехмерные фигуры (3D-фигуры)Трехмерные (3D) фигуры занимают место. Они имеют три измерения: длину, высоту и ширину. Мы можем держать трехмерные объекты, такие как карандаш, телефон, стол и т. д.
Все трехмерные формы имеют общие свойства. Среди этих свойств грани, ребра и углы. Плоская поверхность составляет лицо объемной формы. Лица часто принимают двухмерные формы. Краем поверхности называется линия, разделяющая две ее поверхности
Среди этих свойств грани, ребра и углы. Плоская поверхность составляет лицо объемной формы. Лица часто принимают двухмерные формы. Краем поверхности называется линия, разделяющая две ее поверхности
Угол 3D-фигуры формируется, когда два или более ее ребра встречаются вместе. Вершина — это другое название угла, как и для 2D-объектов.
Вот несколько типичных трехмерных фигур, а также краткое описание каждой из них.
КубУ куба шесть одинаковых граней. Куб имеет квадраты на каждой из его граней. На нем 12 ребер с восемью углами. Грани, ребра и углы имеют одинаковый размер и длину.
Прямоугольная призмаПрямоугольная призма имеет шесть граней. Каждое лицо образует прямоугольник. Размер противоположных граней постоянный. У него 12 ребер и восемь углов.
Треугольная призма Треугольная призма имеет пять граней. Он состоит из трех граней прямоугольной формы и двух граней треугольной формы. Размеры двух треугольных граней одинаковы. У него шесть углов и девять ребер.
Размеры двух треугольных граней одинаковы. У него шесть углов и девять ребер.
Цилиндр имеет трубку посередине и два круга одинакового размера на каждом конце. Он имеет одну изогнутую поверхность и две плоские грани. Цилиндр имеет два ребра и не имеет углов.
КонусВ основании конуса находится круг, а на другом конце – точка. Есть одна плоская грань и одна изогнутая поверхность. Цилиндр имеет одно ребро без углов.
СфераСферическая форма имеет идеальную округлость. Поверхность его изогнута. Сфера не имеет плоских граней, ребер или углов. Расстояние между каждой точкой и центром постоянно на сфере.
Список геометрических фигурВ таблицах ниже показаны геометрические формы, типы и список свойств.
Список двумерных геометрических фигурСписок геометрических фигур (треугольники)
Список геометрических фигур (четырехугольники)
| Name | Illustration | Type | Vertices | Edges |
| Square | | Two-dimensional | 3 | 3 |
| Прямоугольник | | Двумерный | 3 | 3 |
| Ромб | | 2 Двумерный0042 | 3 | 3 |
| Parallelogram | Two-dimensional | 3 | 3 | |
| Trapezoid | Two-dimensional | 3 | 3 | |
| Kite | | Двумерный | 3 | 3 |
Список геометрических фигур (Многоугольники с определенным количеством ребер)
| Name | Illustration | Type | Vertices | Edges |
| Pentagon | | Three-dimensional | 5 | 5 |
| Hexagon | | Трехмерный | 6 | 6 |
| Семиугольник | | Трехмерный | 7 | 7 |
| Octagon | | Three-dimensional | 8 | 8 |
| Decagon | Three-dimensional | 10 | 10 |
Список геометрических фигур (3D)
| Название | Иллюстрация | Type | Vertices | Edges | Faces |
| Cube | Three-dimensional | 8 | 12 | 6 | |
| Cuboid | | Трехмерный | 8 | 12 | 6 |
| Конус | | 1 | 2 | ||
| Cylinder | | Three-dimensional | 0 | 2 | 3 |
| Sphere | | Three-dimensional | 0 | curved | 1 |
Геометрические формы определяются как окруженные границей, состоящей из определенного количества кривых, точек и отрезков.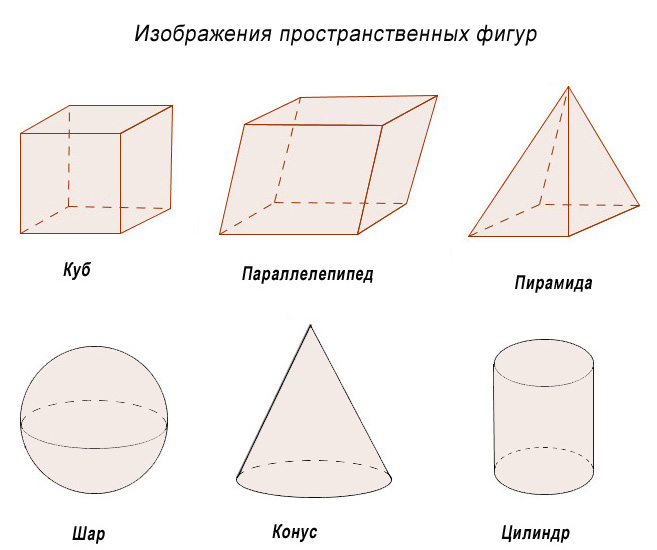 Каждая фигура имеет характерное имя, например, круг, квадрат, треугольник или прямоугольник.
Каждая фигура имеет характерное имя, например, круг, квадрат, треугольник или прямоугольник.
Любой объект с определенной структурой считается геометрической формой. Линии, кривые, углы и поверхности составляют формы на этих рисунках. Квадрат, прямоугольник, круг, цилиндр, цилиндр, куб, сфера и другие знакомые геометрические фигуры — это лишь некоторые из них. Многоугольник – это геометрическая фигура, имеющая три или более сторон. Типичные многоугольники включают треугольники, квадраты, ромбы, трапеции и т. д.
Список геометрических фигур и их свойства
2D-формы
List of Geometric Shapes ( Triangles )
| Name | Type | Vertices | Edges |
| Equilateral Triangle | Two-dimensional | 3 | 3 |
| Равнобедренный треугольник | Двумерный | 3 | 3 |
| Разносторонний треугольник | Двумерный | 3 | 3 |
| Правый треугольник | .3 | 3 |
Список геометрических форм (четырехугольник)
| Имя | |||
| Vertices | Edges | ||
| Square | Two-dimensional | 3 | 3 |
| Rectangle | Two-dimensional | 3 | 3 |
| Rhombus | Двумерный | 3 | 3 |
| Параллелограмм | Двумерный | 3 | 3 |
| Трапециевидный0041 Two-dimensional | 3 | 3 | |
| Kite | Two-dimensional | 3 | 3 |
List of Geometric Shapes ( Polygons with edges greater than 4 )
| Название | Тип | Вершины | КРЕКИ |
| Пентагон | Трехмерный0042 | ||
| Hexagon | Three-dimensional | 6 | 6 |
| Heptagon | Three-dimensional | 7 | 7 |
| Octagon | Three-dimensional | 8 | 8 |
| Десятиугольник | Трехмерный | 10 | 10 |
3D-формы
Список геометрических0003| Name | Type | Vertices | Edges | Faces |
| Cube | Three-dimensional | 8 | 12 | 6 |
| Прямоугольный | Трехмерный | 8 | 12 | 6 |
| Конический | Трехмерный | 2 1 | ||
| 2 | ||||
| Cylinder | Three-dimensional | 0 | 2 | 3 |
| Sphere | Three-dimensional | 0 | curved | 1 |
Двумерные (2D) формы — это плоские формы, которым не хватает высоты или толщины.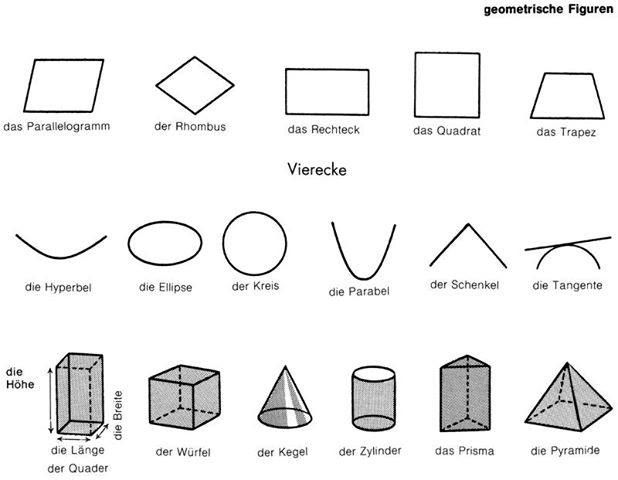 Единственными параметрами являются длина и ширина. Круги и многоугольники, такие как треугольники, квадраты, прямоугольники и т. д., являются несколькими примерами 2D-фигур. Некоторые примеры 2D-фигур включают следующее:
Единственными параметрами являются длина и ширина. Круги и многоугольники, такие как треугольники, квадраты, прямоугольники и т. д., являются несколькими примерами 2D-фигур. Некоторые примеры 2D-фигур включают следующее:
Окружности
Треугольники
Четырехугольники (квадрат, прямоугольник, параллелограмм, ромб, воздушный змей и трапеция)
Многоугольники, такие как пятиугольники, шестиугольники, семиугольники, восьмиугольники, двухугольники и десятиугольники
903D космос. Они имеют три измерения: длину, высоту и ширину. Трехмерные фигуры — это объекты, которые мы можем держать, например карандаш, телефон, стол и т. д. Все трехмерные фигуры имеют общие свойства. Среди этих свойств грани, ребра и углы. Плоская поверхность составляет лицо объемной формы. Лица часто принимают двухмерные формы. Краем поверхности называется линия, разделяющая две ее поверхности. Трехмерная фигура 9Угол 0397 образуется, когда две или более его кромки сходятся вместе. Вершина — это другое название угла, как и для 2D-объектов.
Вершина — это другое название угла, как и для 2D-объектов.
Ниже приведены примеры трехмерных фигур:
Куб, призма, конус, цилиндр и сфера
Чем правильные формы отличаются от неправильных?Правильная форма — это двумерная (2D) форма, у которой (внутренние) углы и стороны имеют одинаковые размеры.
Неправильная форма имеет стороны и углы любой длины и измерения. Количество прямых сторон неправильной формы иногда используется для определения ее названия. Форма неправильная, даже если только одна сторона имеет другое измерение.
Ниже приведены примеры правильных форм.
Ниже приведены примеры неправильных форм.
Каковы примеры геометрических фигур в математике?Существует множество геометрических фигур, основанных на их свойствах. Ниже приведены некоторые примеры основных двухмерных (2D) и трехмерных (3D) фигур:
Примеры двухмерных фигур:
Круг
Треугольник
Квадрат
Прямоугольник
Ромб
Комплект
Пятиугольник
Примеры 3D-форм:
Куб
Куб
Конус
Цилиндр
Сфера403 Что такое основные многоугольники?
Двумерные (2D) формы — это плоские формы, которым не хватает высоты или толщины. Единственными параметрами являются длина и ширина. К основным многоугольникам относятся следующие:
Единственными параметрами являются длина и ширина. К основным многоугольникам относятся следующие:
Треугольник (три стороны)
Четырехугольники (четыре стороны – например, квадрат, прямоугольник, ромб и т. д.)
Пятиугольник (5 ребер)
Шестиугольник (6 ребер)
Семиугольник (7 ребер)
Восьмиугольник (8 ребер)
Десятиугольник (10 ребер)
Является ли круг многоугольником?Многоугольники представляют собой двумерные геометрические фигуры с фиксированным числом сторон. Стороны многоугольников — это соединения отрезков прямых от конца к концу.
Таким образом, круг не является многоугольником, поскольку он создан с использованием кривых.
Какие существуют типы треугольников? Треугольники — это многоугольники с тремя сторонами. Треугольники можно разделить на разносторонние, равнобедренные или равносторонние в зависимости от длины их сторон. Треугольники могут быть острыми, тупоугольными или прямыми, в зависимости от их углов.
Сумма внутренних углов треугольника равна 180 градусам. У остроугольных треугольников все углы меньше 90 градусов. Одна сторона прямоугольного треугольника составляет угол 90 градусов. Один из углов тупоугольного треугольника больше 90 градусов.
Какие примеры изогнутых форм?Изогнутые формы — это геометрические фигуры, состоящие из изогнутых линий и связанных точек. Ниже приведены примеры изогнутых форм.
| Окружность Эта фигура имеет только одну кривую линию и не имеет других связующих или вершинных точек. | Овал/эллипс Хотя он напоминает круг, расстояние между центром и окружностью постоянно меняется. Следовательно, эта форма имеет две оси, большую ось и малую ось, а также удлиненную форму. |
| Линза Эта форма напоминает эллипс, но состоит из двух разных изогнутых линий, которые сходятся на концах.  | Полумесяц Наличие двух изогнутых линий — выпуклой и вогнутой — определяет эту форму. |
Термины «четырехугольник» (четыре) и «латеральный» (сторона) произошли от термина «четырехугольник». Семейство четырехугольников состоит из четырех сторон, четырех вершин и четырех углов. Каждая четырехугольная форма немного отличается от других по ряду признаков. В приведенном ниже списке приведены примеры четырехугольников и их свойства:
| Квадрат У квадрата четыре стороны и четыре угла. Стороны одинаковой длины составляют квадрат. Квадрат состоит из двух параллельных наборов сторон. | Прямоугольник У прямоугольника четыре стороны и четыре угла. Длины двух противоположных пар сторон прямоугольника равны. Два набора сторон прямоугольника параллельны. 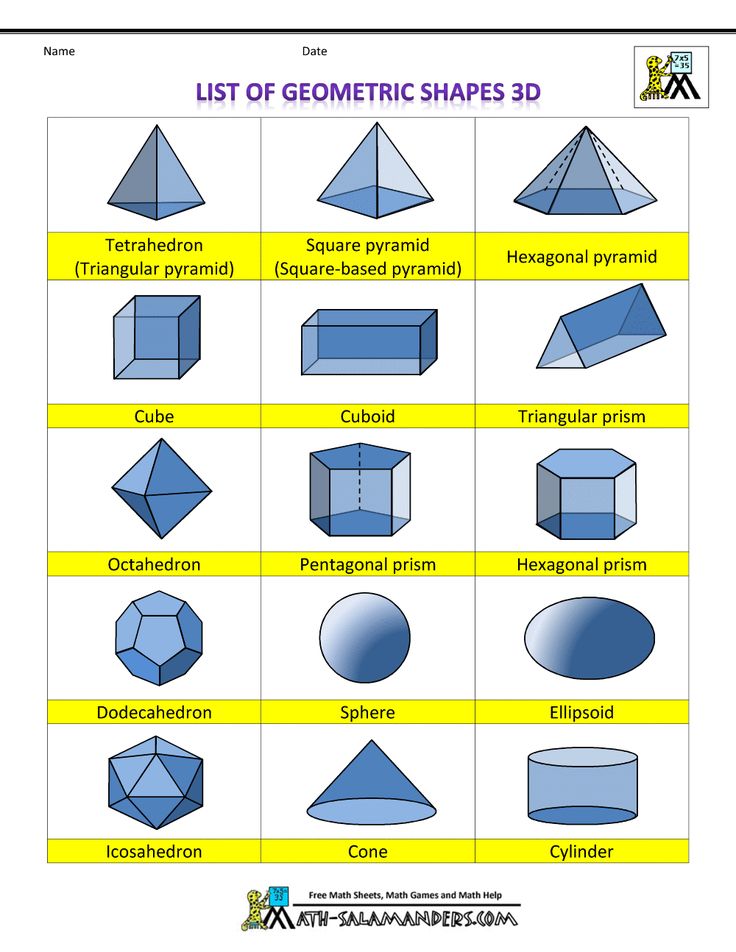 |
| Параллелограмм Параллельные линии образуют четыре стороны и четыре угла параллелограмма. Противоположные стороны параллелограмма параллельны, но углы могут не совпадать. Квадрат, прямоугольник и ромб — это три различных типа параллелограммов. | Ромб Ромб также можно назвать ромбом. У ромба четыре стороны и четыре угла. Ромб напоминает квадрат, наклоненный набок. Стороны одинаковой длины. У ромба противоположные стороны параллельны. |
| Воздушный змей Воздушный змей имеет четыре стороны и четыре угла. Воздушный змей имеет два набора сторон одинаковой длины. Для воздушного змея никогда не бывает параллельных сторон. | Трапеция У трапеции только один набор параллельных сторон. (Говорят « трапеция» в Индии и Великобритании) |
The following are examples of 2D and 3D geometric shapes in real life
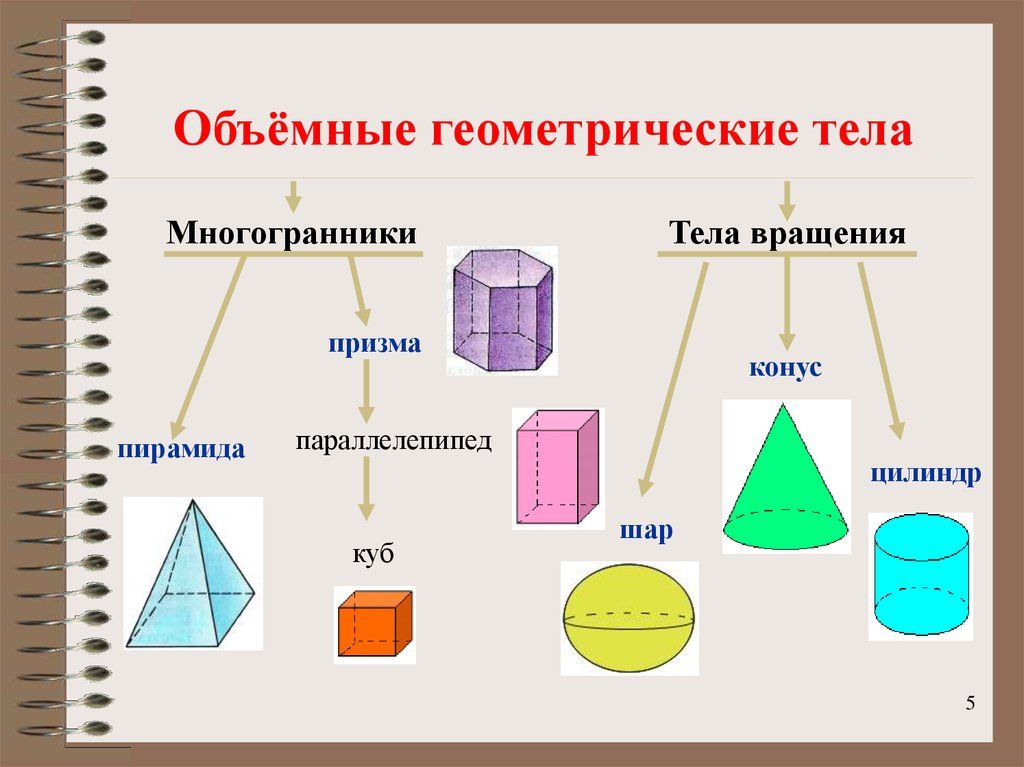 Dimensional
Dimensional