Все геометрические фигуры объемные: Основные геометрические фигуры 🟢🟨🔺 и их названия
«Объемные и плоские геометрические фигуры»
авторы: Оксана Дмитриевна Симонова , работник ДОУ, Белгородская область, Галина Леонидовна Леонова, Белгородская область
Внеурочная деятельность (конкурсные работы)
Внимание! Администрация сайта rosuchebnik.ru не несет ответственности за содержание методических разработок, а также за соответствие разработки ФГОС.
Педагогическое мероприятие соответствовало принципу развивающего образования. Дети увлечённо занимались разной деятельностью. Весь сюжет построен в форме игры, направленной на достижение следующих целевых ориентиров: проявление интереса к математике овладение основными культурными способами деятельности, проявление инициативы и самостоятельности в разных видах деятельности, способность выбирать себе род занятий, способность договариваться и учитывать интересы и чувства других, способность сопереживать неудачам и способность радоваться успехам других.
Тема: «Объемные и плоские геометрические фигуры» (комплексное занятие)
Образовательные области: «Познавательное развитие», «Художественно-эстетическое развитие».
Программные задачи:
- актуализировать знания детей о формах плоских и объемных геометрических фигур, используя проблемную ситуацию;
- развивать мышление, мыслительные операции – анализ, синтез, сравнение, обобщение, связную речь.
- вызвать эмоциональный отклик, воспитывать дружелюбие, уважительное отношение к окружающим, сочувствие, стремление быть полезным окружающим, умение радоваться результатам коллективного труда.
Оборудование и материалы: Персонаж Золушка (роль взрослого), коробка с гелиевым шариком, корзина, объемные фигуры, плоские фигуры среднего размера, «геометрические коврики», 2 листа картона формата Аз, мыльные пузыри.
Предполагаемый результат:
проявление интереса к математике, овладение основными культурными способами деятельности, проявление инициативы и самостоятельности в разных видах деятельности, способность выбирать себе род занятий, участников по совместной деятельности, способность договариваться и учитывать интересы и чувства других, способность сопереживать неудачам и способность радоваться успехам других.
Предварительная работа
Мотивационно-ориентировочный этап
В группу детского сада приходит Золушка, чтобы подружиться с детьми. В это время в группе появляется коробка с воздушным шариком, к которому привязан сверток. Дети и Золушка узнают из свертка задание, которое дала мачеха. Золушка не может справиться с заданием и ищет того, кто может ей помочь.
Проблема: Золушке нужно помочь разобрать содержимое корзины и сделать из этого подарки для принца.
Цель работы детей на занятии:
Организуется обсуждение: чем помочь Золушке? В результате может быть предложен такой план:
- Рассказать Золушке, какие предметы находятся в корзине.
- Объединить данные предметы в группы, чтобы выбрать те, из которых можно сделать подарки по образцу.
- Составить композиции из этих предметов, чтобы подарить их принцу.
Практический этап
Практико-аналитическая работа «Объединим в группы»
– Дети, я рада вас сегодня всех видеть! А вы меня узнали?
– А вы хотите узнать, зачем же я к вам пришла?
– Скажите, пожалуйста, что вы в детском саду любите делать больше всего?
– Я тоже очень люблю играть и сегодня хочу с вами поиграть.
(Незаметно для детей появляется коробка с гелиевым шариком, к которому привязано письмо. Шар замечают дети, воспитатель собирает всех около себя в круг).
– Дети, а кто принес коробку с шаром в группу, кто сделал такой сюрприз для нас, может это ваши родители? Родители наверно хотели, чтобы мы поиграли с ним? (В ходе обсуждения выясняем, что дети и их родители не приносили коробку с шариком в группу. Если дети не замечают, что к шарику привязано письмо, обращаю на него внимание).
– Давайте посмотрим, что это за сверток, может, в нём найдём ответы на наши вопросы.
– А вы хотите узнать, что в этом свертке? Тогда кто хочет, садитесь поудобнее. (Дети садятся за стол по кругу. Воспитатель разворачивает сверток).
– Здесь что – то написано.
(Прошу ребёнка прочитать письмо).
– Кира, помоги мне, прочитай, пожалуйста, письмо.
«Здравствуй, Золушка! Пишет тебе твоя заботливая мачеха.
Я знаю, ты очень хотела поехать на бал, чтобы посмотреть, как будут танцевать твои сестры с принцем. Но прежде тебе необходимо разобрать содержимое коробки и сделать подарки для принца. И если ты успеешь это сделать, то тогда одним глазком посмотришь на бал».
– Ой, что же делать? Я боюсь, что не успею справиться с этим заданием и не попаду на бал. Но самое ужасное – принц останется без подарка.
– Кто же может мне помочь? (Дети решают помочь Золушке).
– Дети, прежде чем разобрать эти предметы на группы, наверно нужно разобраться, что за предметы находятся в коробке? Вы мне поможете?(Дети перечисляют все геометрические фигуры).
– А теперь можно разделить геометрические фигуры на группы?
– А давайте разделимся на две команды и посмотрим, кто справиться быстрее и правильно.
(Дети объединяются в две команды, каждая из которых собирает объемные или плоские геометрические фигуры. Организуется обсуждение, почему дети именно так объединили данные предметы).
– Дети, а из каких геометрических фигур можно сделать подарки по образцу? (показ образцов) (Дети перечисляют все плоские фигуры).
– Спасибо, ребята, вы мне очень помогли, даже быстрее, чем я предполагала. (Смотрит на часы) Мы еще успеваем поиграть.
Экспериментирование
«Объемные и плоские геометрические фигуры»
(На столах у детей находятся мыльные пузыри).
– Посмотрите, что я вам принесла для игры!
(Педагог, предлагает детям окунуть кольцо в мыльный раствор и ответить на вопросы).
– Ой, посмотрите внимательно, а какую форму имеет образовавшаяся внутри круга пленка? (Форму круга).
– Какой – плоской или объемной – геометрической фигурой является круг? (Плоской).
– А как в игре с мыльными пузырями можно плоскую фигуру превратить в объемную?
(Педагог предлагает детям надуть мыльные пузыри и проверить свои догадки, пояснить, какие изменения произошли с плоской фигурой при надувании). – Как называется полученная объемная фигура? (Шар).
– Как называется полученная объемная фигура? (Шар).
– На бал идут нарядными. Что можно надеть? А как еще себя украсить? (бусы)
– Посмотрите, какие бусы мне подарила моя крестная фея! А вы такие хотите сделать?
Практико-аналитическая работа
«Соберем бусы»
(Воспитатель показывает образец с изображением бус и дает задание детям).
– Ребята, есть только одно условие при сборе бус, фигуры одного цвета не должны стоять рядом друг с другом. ( При сборе бус используем набор Фребеля).
Подвижная игра – эстафета «Кто быстрее и правильно»
– Я предлагаю немного отдохнуть и поиграть в игру – эстафету.
(Педагог предлагает детям разделиться на подгруппы. Дети выстраиваются в колонну, по сигналу прыгают на одной ноге по полосе с геометрическими фигурами и называют их. Выигрывает тот, кто выполнит все быстро и правильно).
– Ребята, мы можем уже идти на бал? (Ответы детей).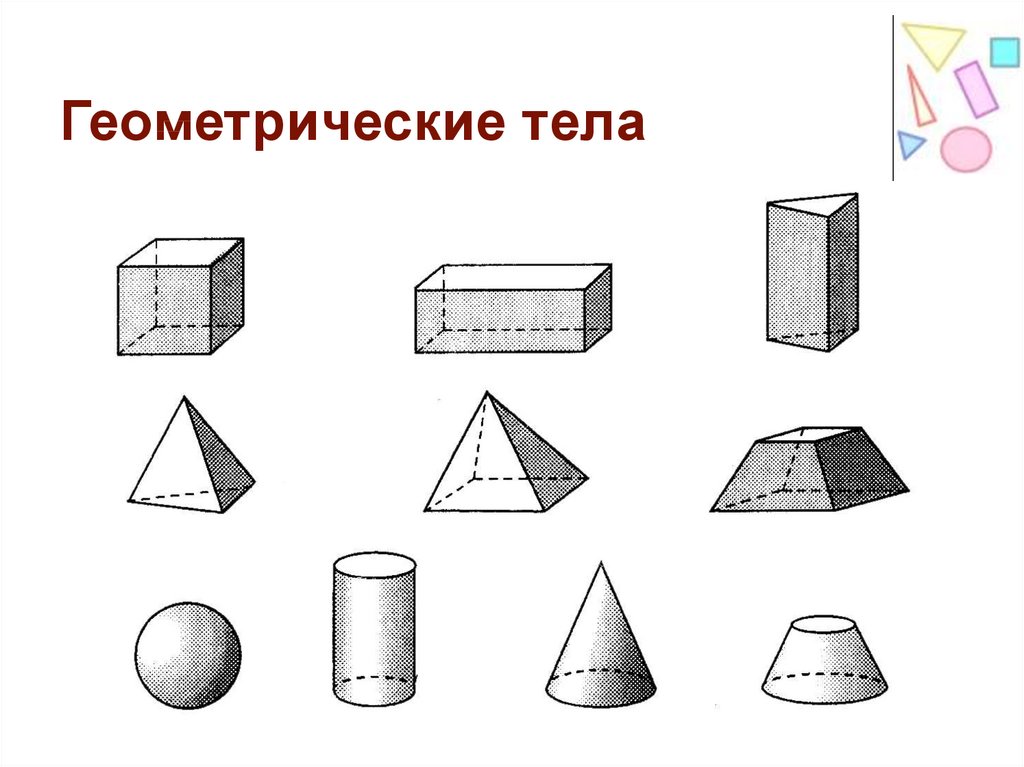
– Давайте изготовим картины по образцу для подарка принцу.
Коллективная аппликация из геометрических фигур
– Дети, теперь мы можем сделать подарки для принца. (Педагог предлагает сложить композиции из геометрических фигур по готовым образцам).
– Для этого мы разделимся на две подгруппы. Каждая подгруппа будет складывать свою композицию. (Используя геометрические шаблоны из наборов Монтессори, дети вырезают нужные фигуры).
(Самостоятельная деятельность детей. По окончании работы – обсуждение полученных продуктов).
Рефлексивно-оценочный этап
Золушка благодарит детей за помощь, отмечает их отдельные достижения, выделяет лучшие качества (готовность помочь, смекалку, доброту и др.).
Педагог организует рефлексию: Что интересного произошло перед занятием? Мы согласились ей помочь? Почему вы так поступили? (Педагог также приводит свои доводы). Как мы помогли Золушке? Какого результата достигли?
– Мы готовы к балу. Как я рада, что мы все сделали вовремя и поездка на бал теперь состоится.
Как я рада, что мы все сделали вовремя и поездка на бал теперь состоится.
Объемные фигуры – Классификации
Объемные фигуры
|
3D-фигуры
Трехмерная (3D) фигура — это фигура или геометрическая фигура, имеющая длину, ширину и высоту.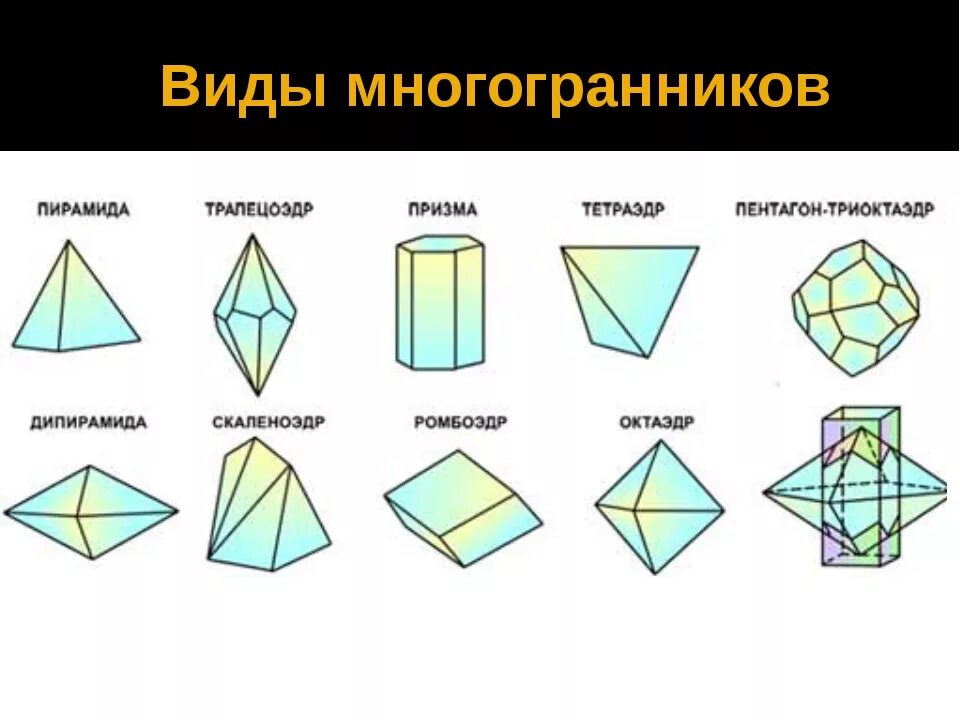 Когда 3D-форма замкнута, можно определить ее объем и площадь поверхности. Ниже приведены несколько примеров трехмерных фигур.
Когда 3D-форма замкнута, можно определить ее объем и площадь поверхности. Ниже приведены несколько примеров трехмерных фигур.
Трехмерные фигуры можно классифицировать по-разному, например, на многогранники (множественное число от «многогранник») и не-многогранники.
Многогранники
Многогранник — это трехмерная фигура, грани которой представляют собой многоугольники. Слово «многогранник» имеет греческое происхождение и означает «многогранный». Призмы и пирамиды — два примера многогранников, которые обычно изучаются в геометрии.
Призма
Призмы — это многогранники с двумя конгруэнтными гранями, называемыми основаниями, которые лежат в параллельных плоскостях. Остальные грани (стороны, не являющиеся основаниями) представляют собой параллелограммы, прямоугольники или квадраты. Призму обычно называют в зависимости от формы ее многоугольных оснований. Ниже приведены три примера.
| Прямоугольная призма | Шестиугольная призма | Треугольная призма |
|---|---|---|
Основания прямоугольники. | Основания шестигранники. | Основания – треугольники. |
Пирамиды
Пирамиды представляют собой многогранники, содержащие только одно многоугольное основание; все остальные грани треугольники. Все треугольные грани (кроме основания треугольной пирамиды) имеют общую вершину, называемую вершиной. Как и призма, пирамида также обычно называется в зависимости от формы ее многоугольного основания. Ниже приведены три примера пирамид с разными основаниями.
| Квадратная пирамида | Треугольная пирамида | Шестиугольная пирамида |
|---|---|---|
| Основание квадратное. | Основание – треугольник. | Основание шестигранник. |
Общие многогранники
Многогранники — это трехмерные фигуры, которые могут принимать множество других форм. Ниже приведены два примера.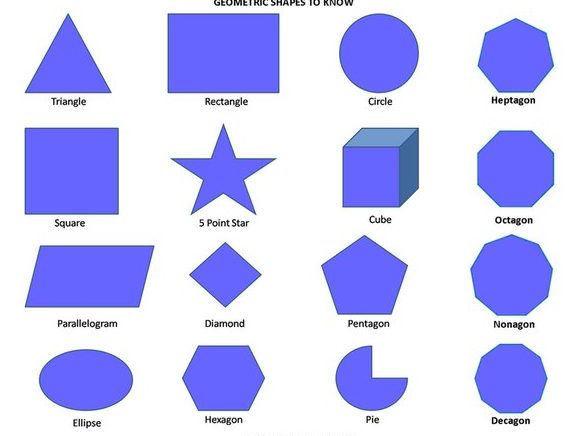
Немногогранники
Немногогранники — это пространственные фигуры, у которых хотя бы одна грань или компонент не являются многоугольниками. В геометрии обычно изучаются три типа не-многогранников: цилиндры, конусы и сферы.
Цилиндр
Цилиндр представляет собой трехмерную фигуру, состоящую из двух плоских круглых оснований и изогнутой поверхности, которая «оборачивает» основания. Ниже приведены два примера.
Конус
Конус представляет собой трехмерную форму, состоящую из круглого основания, сужающегося к острию. Ниже приведены два примера.
Сфера
Сфера — это трехмерная фигура круглой формы. Все точки на поверхности сферы равноудалены от точки, называемой центром.
Знаете ли вы?
Хотя мы можем считать Землю сферической по форме, она не обладает идеальной симметрией. Радиус Земли на экваторе немного больше полярного радиуса с разницей около 22 км (13 миль). Считается, что разница вызвана вращением Земли. Следовательно, Земля имеет форму сплющенной сферы, называемой сплюснутым сфероидом.
Следовательно, Земля имеет форму сплющенной сферы, называемой сплюснутым сфероидом.
Что такое трехмерные фигуры? | Типы, площадь поверхности
Геометрия определяет трехмерную форму как твердую фигуру или объект с тремя измерениями — длиной, шириной и высотой. В отличие от двухмерных фигур трехмерные формы имеют толщину или глубину. Они являются частью трехмерной геометрии. Как мы видим в нашей повседневной жизни, объемная геометрия включает в себя объекты трехмерных форм, таких как цилиндры, кубы, прямоугольные параллелепипеды, конусы, сферы и т. д. Существует так много трехмерных форм, и каждая трехмерная форма занимает некоторое пространство в зависимости от ее размеров. По своей природе трехмерные формы имеют внутреннюю и внешнюю части, разделенные поверхностью. Все физические объекты, к которым можно прикоснуться, трехмерны. Примеры трехмерных фигур, которые можно увидеть в реальной жизни, включают кубик Рубика, глобус, газовый баллон, кубический ящик, прямоугольную доску и т. д.
д.
Реальные примеры Трехмерные фигуры
Ссылка: https://media.nagwa.com/456148939527/en/thumbnail_l.jpeg
В трех измерениях формы определяются вершинами, гранями и ребрами. Грани — это плоские поверхности трехмерных фигур. Ребро — это отрезок, соединяющий две грани. Вершина — это точка, где сходятся три ребра. Кроме того, они имеют глубину, поэтому занимают некоторый объем. Некоторые трехмерные фигуры имеют двухмерные части, например основания и вершины. Одним из примеров является куб, у которого со всех сторон квадратные грани. Формы в 3D можно разделить на несколько категорий. Другие имеют форму пирамид или призм; некоторые имеют изогнутые поверхности.
Faces, Edges and Vertices
Reference: https://dr282zn36sxxg.cloudfront.net/datastreams/f-d%3Acaf8fa01ad1bee390d6f2801f3315e12b52871bc3eceefc8450625ee%2BIMAGE_TINY%2BIMAGE_TINY.1
In mathematics, we explore 3-dimensional objects in the понятия твердых тел и применить их к реальным ситуациям. Футбольные мячи, кубы, ведра и книги — вот несколько примеров трехмерных фигур в реальной жизни.
Футбольные мячи, кубы, ведра и книги — вот несколько примеров трехмерных фигур в реальной жизни.
Трехмерные грани, ребра, вершины
3D-формы и объекты отличаются от 2D-форм и объектов, поскольку они имеют три измерения — длину, ширину и высоту. Это означает, что объекты имеют три измерения, которые переводятся в грани, ребра и вершины. Рассмотрим подробно эти три.
Код:
Лица
- Под гранью понимается любая криволинейная поверхность или отдельная плоскость твердого объекта
- Трехмерные фигуры могут иметь несколько граней
Ребра
- Ребро — это сегмент линии, соединяющий одну вершину (угловую точку) с другой
- Они служат соединением двух граней
Вершины
- Вершина — это точка, в которой встречаются две или более линий.
- Это угол.
- Вершины — это точки пересечения ребер.
Типы трехмерных фигур
Трехмерные фигуры существуют во многих формах, которые имеют разные основания, объемы и площади поверхности. Они:
Они:
- Cube
- Cuboid
- Цилиндр
- Конус
- Sphere
- PRISM
- Pyramid
67. SPEARE
77. SPEARE77. SPEARE
777. SPEARE7. Поверхность этой формы состоит из точек, равноудаленных от ее центра. Земля кажется сферой, но это не так. Планета Земля имеет форму сфероида. Сфероиды напоминают сферы, но их радиус от центра к поверхности не постоянен в каждой точке. Сфера имеет следующие характеристики.
- Он симметричен и имеет форму шара.
- Любой сферический объект имеет радиус, диаметр, длину окружности, объем и площадь поверхности.
- Все точки сферы находятся на одинаковом расстоянии друг от друга.
- У него одна грань, нет ребер и вершин.
- Поскольку у него нет плоских граней, он не является многогранником.
Артикул: https://www.mathlearnit.com/static/images/radius-diameter-sphere.png
Куб и прямоугольный параллелепипед
Куб и прямоугольный параллелепипед — это трехмерные геометрические фигуры с одинаковым количеством граней, вершин и ребер.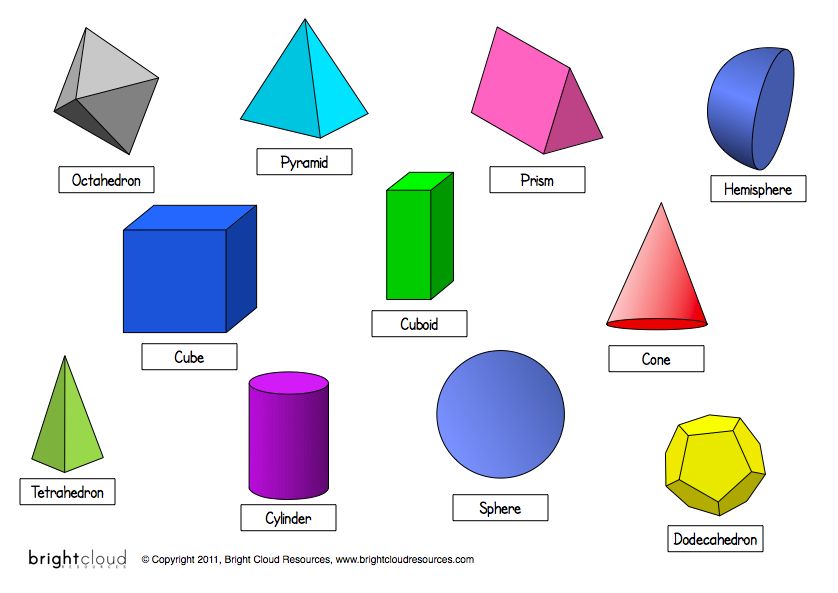 Разница между кубом и прямоугольным параллелепипедом заключается в том, что у куба все шесть граней являются квадратами, а у прямоугольного параллелепипеда все шесть граней являются прямоугольниками. Объем и площадь поверхности куба и прямоугольного параллелепипеда различны. Для куба длина, ширина и высота одинаковы, а для прямоугольного параллелепипеда все они разные.
Разница между кубом и прямоугольным параллелепипедом заключается в том, что у куба все шесть граней являются квадратами, а у прямоугольного параллелепипеда все шесть граней являются прямоугольниками. Объем и площадь поверхности куба и прямоугольного параллелепипеда различны. Для куба длина, ширина и высота одинаковы, а для прямоугольного параллелепипеда все они разные.
Ссылка: https://hi-static.z-dn.net/files/d16/ead1c000ade4760c29cf10c9c514faac.png
Цилиндр
Цилиндры представляют собой трехмерные фигуры с двумя круглыми гранями, одной вверху и одной внизу, и изогнутой поверхностью. Цилиндры имеют высоту и радиус. В цилиндрической форме высота представляет собой перпендикулярное расстояние между верхней и нижней гранями. Ниже приведены некоторые важные характеристики цилиндра.
- Имеет одну изогнутую поверхность.
- От основания до верха форма остается неизменной.
- Трехмерный объект, цилиндры имеют два одинаковых конца, круглые или овальные.

- Круглые основания правых цилиндров лежат на одной линии. Косые цилиндры — это цилиндры, у которых одно основание отделено от другого.
r=радиус, h=высота
Просмотреть все рабочие листы форм
Конус
Конусы также представляют собой трехмерные фигуры с плоским круглым основанием и заостренным концом наверху. Заостренный конец, который находится наверху конуса, называется «Вершина». Конусы также имеют криволинейные поверхности. Как и в случае с цилиндрами, конус также может быть классифицирован как прямой круговой конус и наклонный конус.
- Конусы имеют круглое или овальное основание с вершиной (вершиной).
- Конусы представляют собой повернутые треугольники.
- По совмещению вершины с центром основания образуется прямой конус или косой конус.
- Прямой круговой конус имеет вершину (или заостренный конец), перпендикулярную его основанию. Наклонный конус имеет вершину, расположенную в любом месте, кроме центра основания.

- Конусы имеют высоту и радиус. Конусы также имеют наклонную высоту, которая представляет собой расстояние от точки, в которой вершина встречается с любой точкой на окружности круглого основания конуса.
l= длина, h=высота, r= радиус
Тор
Торы представляют собой трехмерные формы. В трехмерном пространстве он образуется путем вращения меньшего круга радиуса (r) вокруг большего круга радиуса (R).
- Тор представляет собой кольцо, напоминающее шину или бублик.
- У него нет ни ребер, ни вершин.
r= радиус меньшего круга. R= радиус большего круга.
Ссылка: https://math.fel.cvut.cz/mt/mtold/txtd/5/gifc5/pc3dc5ha.gif
Пирамида
Пирамида имеет многоугольное основание и вершину с прямыми ребрами и плоскими гранями. Это многогранник. В зависимости от того, как вершина совмещена с центром основания, можно различить правильные и косые пирамиды. Пирамида состоит из:
- Треугольного основания, известного как Тетраэдр
- Четырехугольного основания, известного как квадратная пирамида
- Пятиугольного основания, известного как пятиугольная пирамида
- Правильного шестиугольного основания, известного как шестиугольная пирамида
а – длина апофемы пирамиды, б – длина основания пирамиды, h – высота пирамиды 04/pyramid-1.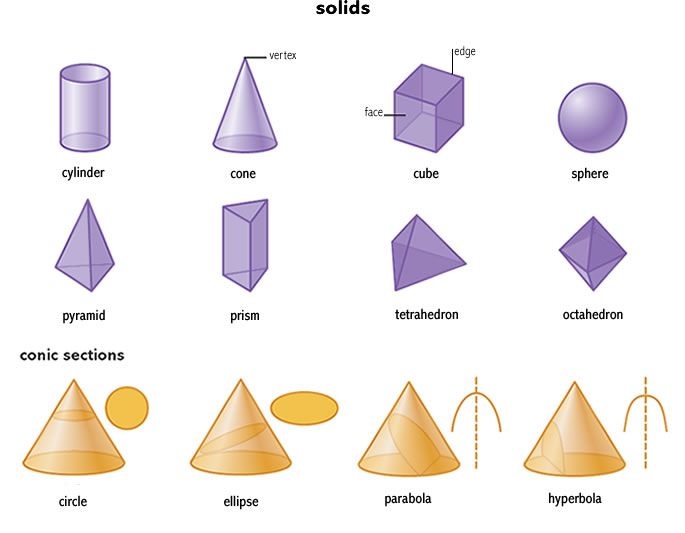 png
png
Призмы
Многоугольные тела с плоскими сторонами в виде параллелограмма являются призмами. Вот некоторые характеристики призм:
- По всей длине имеет одинаковое поперечное сечение.
- Различные типы призм включают треугольные призмы, квадратные призмы, пятиугольные призмы, шестиугольные призмы и т. д.
- Призмы также можно разделить на обычные или наклонные.
Ссылка: https://www.mathlearnit.com/static/images/types-of-polyhedrons-prisms.png
Далее давайте узнаем о трехмерных фигурах с правильными многогранниками (платоническими твердые вещества).
Многогранники
Многогранник представляет собой трехмерную фигуру с многоугольными гранями (треугольник, квадрат, шестиугольник) и прямыми ребрами и вершинами. Многогранник определяется как имеющий:
- Прямые края.
- Грани — это плоские стороны.
- Углы называются вершинами.
Его также называют платоновым телом.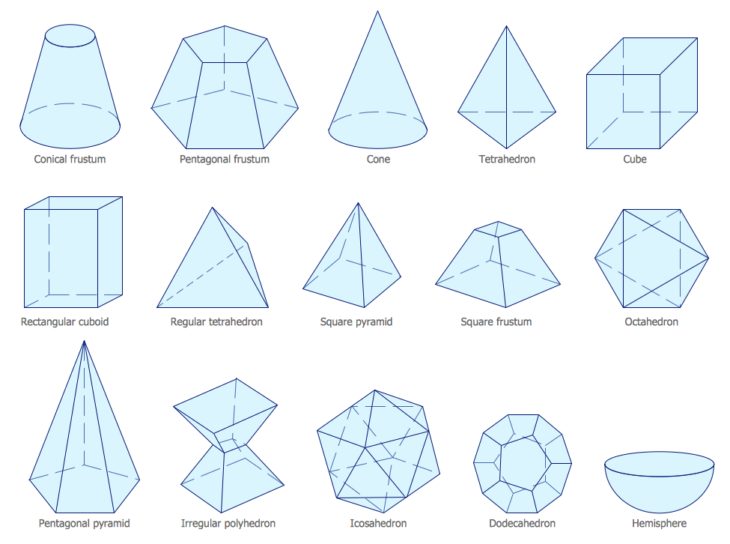 Есть пять правильных многогранников. Все грани правильного многогранника одинаковы. Кубы являются одними из самых основных и знакомых многогранников. Куб представляет собой правильный многогранник с шестью квадратными гранями, двенадцатью ребрами и восемью вершинами.
Есть пять правильных многогранников. Все грани правильного многогранника одинаковы. Кубы являются одними из самых основных и знакомых многогранников. Куб представляет собой правильный многогранник с шестью квадратными гранями, двенадцатью ребрами и восемью вершинами.
Ниже приведены еще несколько примеров правильных многогранников:
- Тетраэдр с four equilateral-triangular faces
- Cube with six square faces also known as a hexahedron
- Octahedron having eight equilateral-triangular faces
- Dodecahedron with twelve regular pentagon faces
- Icosahedron having twenty equilateral -треугольные грани
Ссылка: https://math.andyou.com/content/08/ec/images/mu_pe_08_re_007.png
Трехмерные фигуры с кривыми
Многогранники не включают твердые формы с изогнутыми или закругленными краями.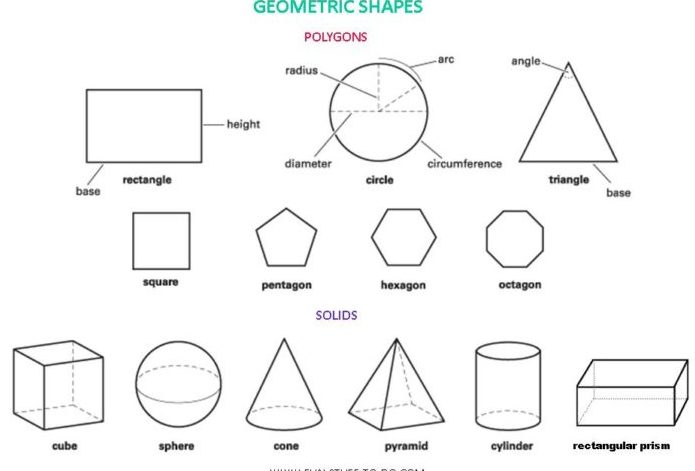 У многогранников можно найти только прямые стороны.
У многогранников можно найти только прямые стороны.
Цилиндр, конус, сфера и тор — четыре самые распространенные кривые в геометрии. Кривые можно найти во многих объектах вокруг нас.
Площадь поверхности и объем трехмерных фигур
Для определения трехмерных фигур используются две различные меры:
- Площадь поверхности
- Объем
Площадь поверхности
Определяется общей площадью поверхности трехмерного объекта. Обычно обозначается как «SA». Площадь поверхности измеряется в квадратных единицах. Ниже приведены три различных классификации площади поверхности. Вы найдете их здесь:
- Площадь всех криволинейных областей называется площадью криволинейной поверхности (CSA). )
- Площадь всех поверхностей, включая основание 3D-объекта, называется общей площадью поверхности (TSA)
Объем
Объем определяется общим пространством, занимаемым твердым объектом или трехмерной формой. Объем обычно обозначается буквой «V». Измеряется в кубических единицах. Все трехмерные фигуры имеют разные площади поверхности и объемы.
Объем обычно обозначается буквой «V». Измеряется в кубических единицах. Все трехмерные фигуры имеют разные площади поверхности и объемы.
Примеры расчета площади поверхности
Куб
Площадь куба можно вычислить, умножив (длина x ширина) на 6, поскольку все шесть граней идентичны.
Поскольку грань куба представляет собой квадрат, вам необходимо провести одно измерение — длина и ширина квадрата по определению одинаковы.
Следовательно, одна грань этого куба равна 10 × 10 см = 100 см 2 . Умножаем на 6 количество граней куба, и получаем, что площадь поверхности этого куба равна 600см 2 .
Другие правильные многогранники
Таким же образом можно вычислить площадь поверхности других правильных многогранников (платоновых тел), найдя площадь одной стороны и затем умножив это число на общее количество сторон – см. Диаграмма основных многогранников выше.
Если площадь одного пятиугольника, составляющего додекаэдр, равна 22 см 2 , умножьте это на количество сторон (12), чтобы получить ответ 264 см 2 .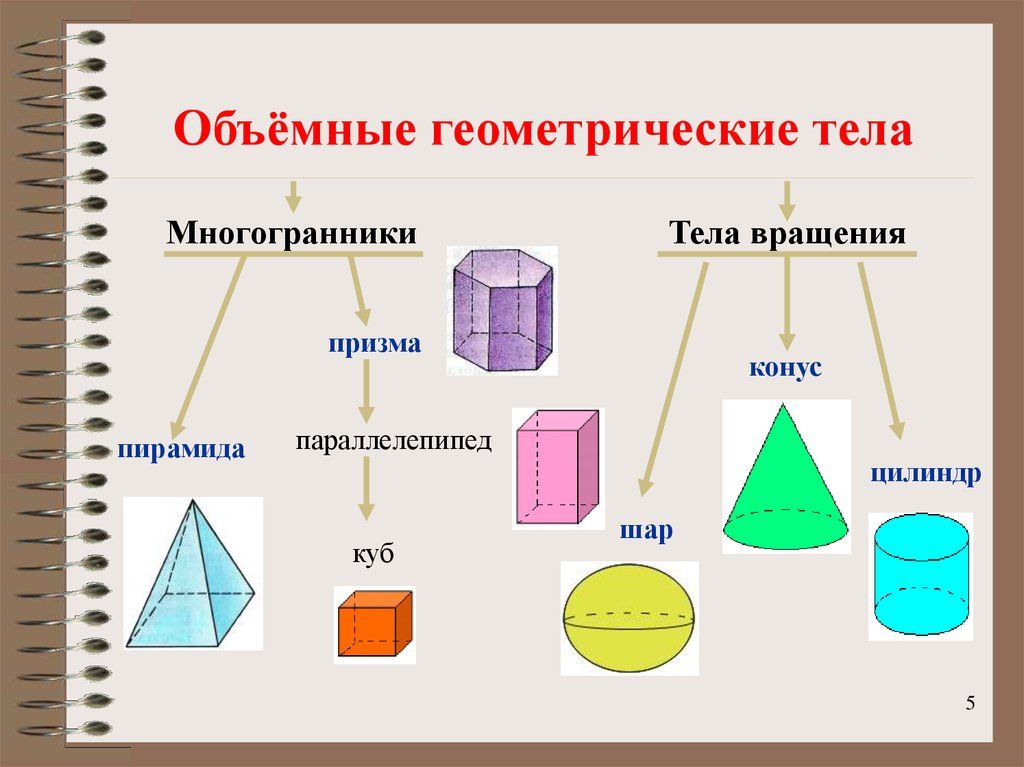
Пирамида
Площадь стандартной пирамиды с четырьмя равными треугольными сторонами и квадратным основанием рассчитывается путем вычисления площади основания (квадрата) длина × ширина.
Далее вычислите площадь одной стороны (треугольника). Затем измерьте ширину вдоль основания и высоту треугольника (также называемую наклонной длиной) от центральной точки основания до вершины.
Разделите ответ на два, чтобы получить площадь поверхности одного треугольника, затем умножьте его на четыре, чтобы получить площадь поверхности всех четырех сторон, или просто умножьте площадь поверхности одного треугольника на два, чтобы получить площадь поверхности всех четырех сторон.
Наконец, просуммируйте площади основания и сторон пирамиды, чтобы найти ее общую площадь.
Чтобы рассчитать площадь поверхности других типов пирамид, сложите основание (площадь основания) и стороны (площадь боковой поверхности). Возможно, вам придется измерить стороны по отдельности.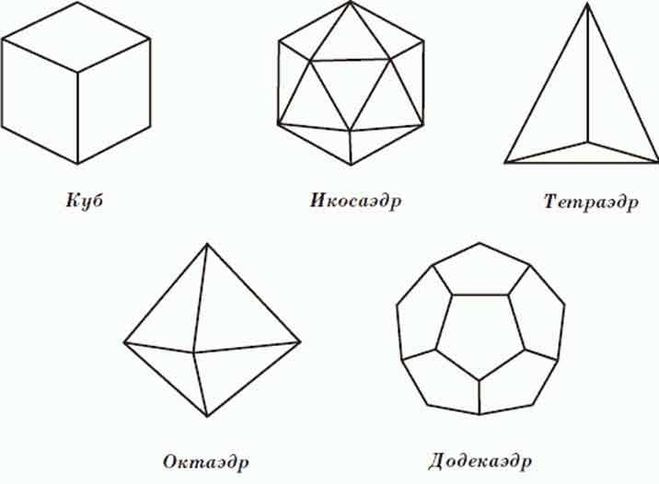
Диаграммы сетей
Геометрическая сеть представляет собой двухмерное представление трехмерного объекта. Площади поверхностей трехмерных объектов могут быть рассчитаны с помощью сетей. На диаграмме ниже вы можете увидеть, как строятся базовые пирамиды, если пирамида развернута, у вас остается сеть.
Правая пирамида Наклонная пирамида
Призма
0003
Призма имеет два одинаковых конца и плоские стороны в виде параллелограмма.
Умножьте площадь одной стороны на 2.
В случае правильной призмы (у которой все стороны одинаковы) умножьте площадь одной стороны на количество сторон.
Если призма имеет неправильные стороны (разной длины), рассчитайте площадь каждой стороны.
Общая площадь призмы равна двум вашим ответам (концы х сторон).
Цилиндр
При расчете площади поверхности цилиндра полезно подумать о составных частях формы.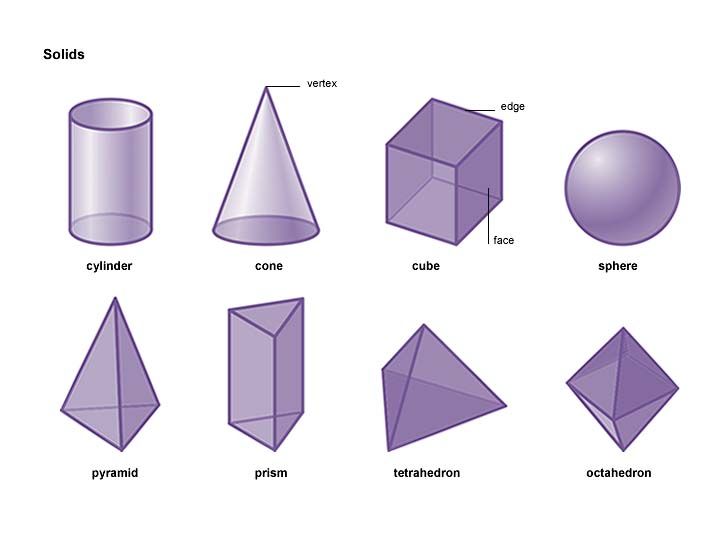 Представьте себе банку сладкой кукурузы, у которой есть верх и низ, оба из которых представляют собой круги. У вас получится прямоугольник, если вы разрежете сторону по длине и сгладите ее. Следовательно, вам нужно найти площади двух кругов и прямоугольника.
Представьте себе банку сладкой кукурузы, у которой есть верх и низ, оба из которых представляют собой круги. У вас получится прямоугольник, если вы разрежете сторону по длине и сгладите ее. Следовательно, вам нужно найти площади двух кругов и прямоугольника.
Сначала определите площадь одного из кругов.
Площадь круга равна π(pi) × радиус 2 .
При радиусе 5 см площадь одного из кругов равна 3,14 × 5 2 = 78,5 см 2 .
Умножьте ответ на 2, так как кругов два 157см 2
Площадь стороны цилиндра равна периметру круга × высоте цилиндра.
Периметр равен π x 2 × радиус. В нашем примере 3,14 × 2 × 5 = 31,4·9.0003
Измерьте высоту цилиндра – в данном примере высота составляет 10 см. Площадь стороны 31,4 × 10 = 314см 2 .
Вы можете вычислить общую площадь поверхности путем сложения площадей кругов и сторон:
157 + 314 = 471см 2
Конус
радиус основания, необходимо учитывать при расчете площади поверхности конуса.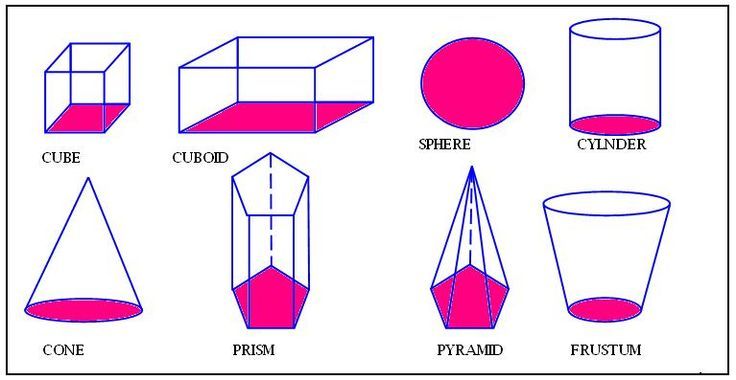
Расчет относительно прост:
Допустим, радиус равен 5 см, а длина наклона 10 см.
Площадь круга в основании конуса равна π(pi) × радиус 2 .
В этом примере сумма равна 3,14 × 52 = 3,14 × 25 = 78,5 см. наклона.
В нашем примере сумма равна 3,14 × 5 × 10 = 157 см 2 .
Наконец, добавьте площадь основания к площади стороны, чтобы получить общую площадь поверхности конуса.
78,5 + 157 = 235,5 см 2
Сфера
Площадь поверхности сферы представляет собой относительно простое расширение формулы для площади круга.
4 × π × радиус 2 .
При определении диаметра сферы часто проще всего измерить расстояние поперек сферы. Вы можете определить радиус, который составляет половину диаметра.
Предположим, что диаметр теннисного мяча равен 2,6 дюйма.
Следовательно, радиус равен 1,3 дюйма.
Для формулы нам нужен квадрат радиуса.
1,3 × 1,3 = 1,69.
Площадь поверхности теннисного мяча, следовательно:
4 × 3,14 × 1,69 = 21,2264 дюйма 2 .
Тор
Чтобы найти площадь тора, необходимо определить два значения радиуса.
Большой радиус (R) — это диаметр от середины отверстия до середины кольца.
Малый или малый радиус (r) рассчитывается путем измерения кольца от центра к внешнему краю.
На диаграмме показаны два вида примера тора и способы измерения его радиусов (или радиусов).
R (большой радиус) = 20 см
r (малый радиус) = 4 см
Площадь поверхности можно рассчитать двумя способами (по одному для каждого радиуса). Для каждой части расчет одинаковый.
Формула: площадь поверхности = (2πR)(2πr)
Для расчета площади поверхности примера тора.
(2 × π × R) = (2 × 3,14 × 20) = 125,6
(2 × π × r) = (2 × 3,14 × 4) = 25,12
Вы можете найти общую площадь поверхности тора из примера, перемножив два ответа.
125,6 × 25,12 = 3155,072см2.
Ссылки
- https://www.mathsisfun.com/geometry/common-3d-shapes.html
- https://www.khanacademy.org/computing/computer-programming/programming-games-visualizations/programming -3d-shapes/a/what-are-3d-shapes
- https://www.open.edu/openlearn/ocw/mod/oucontent/view.php?id=84739§ion=1.3
- https:// Thirdspacelearning.com/blog/what-are-3d-shapes/
- https://www.bbc.co.uk/bitesize/topics/zjv39j6/articles/zgqpk2p
Объем цилиндров, конусов и сферы (спортивная тематика) Рабочие листы по математике
Решение текстовых задач на объем цилиндров, конусов и сфер Рабочие листы по математике для 8-го класса
Словесные задачи на объем твердых фигур (ветеринарная тематика) Рабочие листы
Мы тратим много времени на исследования и компиляцию информация на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника.
7. Поверхность этой формы состоит из точек, равноудаленных от ее центра. Земля кажется сферой, но это не так. Планета Земля имеет форму сфероида. Сфероиды напоминают сферы, но их радиус от центра к поверхности не постоянен в каждой точке. Сфера имеет следующие характеристики.
- Он симметричен и имеет форму шара.
- Любой сферический объект имеет радиус, диаметр, длину окружности, объем и площадь поверхности.
- Все точки сферы находятся на одинаковом расстоянии друг от друга.
- У него одна грань, нет ребер и вершин.
- Поскольку у него нет плоских граней, он не является многогранником.
Артикул: https://www.mathlearnit.com/static/images/radius-diameter-sphere.png
Куб и прямоугольный параллелепипед
Куб и прямоугольный параллелепипед — это трехмерные геометрические фигуры с одинаковым количеством граней, вершин и ребер. Разница между кубом и прямоугольным параллелепипедом заключается в том, что у куба все шесть граней являются квадратами, а у прямоугольного параллелепипеда все шесть граней являются прямоугольниками. Объем и площадь поверхности куба и прямоугольного параллелепипеда различны. Для куба длина, ширина и высота одинаковы, а для прямоугольного параллелепипеда все они разные.
Разница между кубом и прямоугольным параллелепипедом заключается в том, что у куба все шесть граней являются квадратами, а у прямоугольного параллелепипеда все шесть граней являются прямоугольниками. Объем и площадь поверхности куба и прямоугольного параллелепипеда различны. Для куба длина, ширина и высота одинаковы, а для прямоугольного параллелепипеда все они разные.
Ссылка: https://hi-static.z-dn.net/files/d16/ead1c000ade4760c29cf10c9c514faac.png
Цилиндр
Цилиндры представляют собой трехмерные фигуры с двумя круглыми гранями, одной вверху и одной внизу, и изогнутой поверхностью. Цилиндры имеют высоту и радиус. В цилиндрической форме высота представляет собой перпендикулярное расстояние между верхней и нижней гранями. Ниже приведены некоторые важные характеристики цилиндра.
- Имеет одну изогнутую поверхность.
- От основания до верха форма остается неизменной.
- Трехмерный объект, цилиндры имеют два одинаковых конца, круглые или овальные.

- Круглые основания правых цилиндров лежат на одной линии. Косые цилиндры — это цилиндры, у которых одно основание отделено от другого.
r=радиус, h=высота
Просмотреть все рабочие листы форм
Конус
Конусы также представляют собой трехмерные фигуры с плоским круглым основанием и заостренным концом наверху. Заостренный конец, который находится наверху конуса, называется «Вершина». Конусы также имеют криволинейные поверхности. Как и в случае с цилиндрами, конус также может быть классифицирован как прямой круговой конус и наклонный конус.
- Конусы имеют круглое или овальное основание с вершиной (вершиной).
- Конусы представляют собой повернутые треугольники.
- По совмещению вершины с центром основания образуется прямой конус или косой конус.
- Прямой круговой конус имеет вершину (или заостренный конец), перпендикулярную его основанию. Наклонный конус имеет вершину, расположенную в любом месте, кроме центра основания.

- Конусы имеют высоту и радиус. Конусы также имеют наклонную высоту, которая представляет собой расстояние от точки, в которой вершина встречается с любой точкой на окружности круглого основания конуса.
l= длина, h=высота, r= радиус
Тор
Торы представляют собой трехмерные формы. В трехмерном пространстве он образуется путем вращения меньшего круга радиуса (r) вокруг большего круга радиуса (R).
- Тор представляет собой кольцо, напоминающее шину или бублик.
- У него нет ни ребер, ни вершин.
r= радиус меньшего круга. R= радиус большего круга.
Ссылка: https://math.fel.cvut.cz/mt/mtold/txtd/5/gifc5/pc3dc5ha.gif
Пирамида
Пирамида имеет многоугольное основание и вершину с прямыми ребрами и плоскими гранями. Это многогранник. В зависимости от того, как вершина совмещена с центром основания, можно различить правильные и косые пирамиды. Пирамида состоит из:
- Треугольного основания, известного как Тетраэдр
- Четырехугольного основания, известного как квадратная пирамида
- Пятиугольного основания, известного как пятиугольная пирамида
- Правильного шестиугольного основания, известного как шестиугольная пирамида
а – длина апофемы пирамиды, б – длина основания пирамиды, h – высота пирамиды 04/pyramid-1. png
png
Призмы
Многоугольные тела с плоскими сторонами в виде параллелограмма являются призмами. Вот некоторые характеристики призм:
- По всей длине имеет одинаковое поперечное сечение.
- Различные типы призм включают треугольные призмы, квадратные призмы, пятиугольные призмы, шестиугольные призмы и т. д.
- Призмы также можно разделить на обычные или наклонные.
Ссылка: https://www.mathlearnit.com/static/images/types-of-polyhedrons-prisms.png
Далее давайте узнаем о трехмерных фигурах с правильными многогранниками (платоническими твердые вещества).
Многогранники
Многогранник представляет собой трехмерную фигуру с многоугольными гранями (треугольник, квадрат, шестиугольник) и прямыми ребрами и вершинами. Многогранник определяется как имеющий:
- Прямые края.
- Грани — это плоские стороны.
- Углы называются вершинами.
Его также называют платоновым телом. Есть пять правильных многогранников. Все грани правильного многогранника одинаковы. Кубы являются одними из самых основных и знакомых многогранников. Куб представляет собой правильный многогранник с шестью квадратными гранями, двенадцатью ребрами и восемью вершинами.
Есть пять правильных многогранников. Все грани правильного многогранника одинаковы. Кубы являются одними из самых основных и знакомых многогранников. Куб представляет собой правильный многогранник с шестью квадратными гранями, двенадцатью ребрами и восемью вершинами.
Ниже приведены еще несколько примеров правильных многогранников:
- Тетраэдр с four equilateral-triangular faces
- Cube with six square faces also known as a hexahedron
- Octahedron having eight equilateral-triangular faces
- Dodecahedron with twelve regular pentagon faces
- Icosahedron having twenty equilateral -треугольные грани
Ссылка: https://math.andyou.com/content/08/ec/images/mu_pe_08_re_007.png
Трехмерные фигуры с кривыми
Многогранники не включают твердые формы с изогнутыми или закругленными краями. У многогранников можно найти только прямые стороны.
У многогранников можно найти только прямые стороны.
Цилиндр, конус, сфера и тор — четыре самые распространенные кривые в геометрии. Кривые можно найти во многих объектах вокруг нас.
Площадь поверхности и объем трехмерных фигур
Для определения трехмерных фигур используются две различные меры:
- Площадь поверхности
- Объем
Площадь поверхности
Определяется общей площадью поверхности трехмерного объекта. Обычно обозначается как «SA». Площадь поверхности измеряется в квадратных единицах. Ниже приведены три различных классификации площади поверхности. Вы найдете их здесь:
- Площадь всех криволинейных областей называется площадью криволинейной поверхности (CSA). )
- Площадь всех поверхностей, включая основание 3D-объекта, называется общей площадью поверхности (TSA)
Объем
Объем определяется общим пространством, занимаемым твердым объектом или трехмерной формой. Объем обычно обозначается буквой «V». Измеряется в кубических единицах. Все трехмерные фигуры имеют разные площади поверхности и объемы.
Объем обычно обозначается буквой «V». Измеряется в кубических единицах. Все трехмерные фигуры имеют разные площади поверхности и объемы.
Примеры расчета площади поверхности
Куб
Площадь куба можно вычислить, умножив (длина x ширина) на 6, поскольку все шесть граней идентичны.
Поскольку грань куба представляет собой квадрат, вам необходимо провести одно измерение — длина и ширина квадрата по определению одинаковы.
Следовательно, одна грань этого куба равна 10 × 10 см = 100 см 2 . Умножаем на 6 количество граней куба, и получаем, что площадь поверхности этого куба равна 600см 2 .
Другие правильные многогранники
Таким же образом можно вычислить площадь поверхности других правильных многогранников (платоновых тел), найдя площадь одной стороны и затем умножив это число на общее количество сторон – см. Диаграмма основных многогранников выше.
Если площадь одного пятиугольника, составляющего додекаэдр, равна 22 см 2 , умножьте это на количество сторон (12), чтобы получить ответ 264 см 2 .
Пирамида
Площадь стандартной пирамиды с четырьмя равными треугольными сторонами и квадратным основанием рассчитывается путем вычисления площади основания (квадрата) длина × ширина.
Далее вычислите площадь одной стороны (треугольника). Затем измерьте ширину вдоль основания и высоту треугольника (также называемую наклонной длиной) от центральной точки основания до вершины.
Разделите ответ на два, чтобы получить площадь поверхности одного треугольника, затем умножьте его на четыре, чтобы получить площадь поверхности всех четырех сторон, или просто умножьте площадь поверхности одного треугольника на два, чтобы получить площадь поверхности всех четырех сторон.
Наконец, просуммируйте площади основания и сторон пирамиды, чтобы найти ее общую площадь.
Чтобы рассчитать площадь поверхности других типов пирамид, сложите основание (площадь основания) и стороны (площадь боковой поверхности). Возможно, вам придется измерить стороны по отдельности.
Диаграммы сетей
Геометрическая сеть представляет собой двухмерное представление трехмерного объекта. Площади поверхностей трехмерных объектов могут быть рассчитаны с помощью сетей. На диаграмме ниже вы можете увидеть, как строятся базовые пирамиды, если пирамида развернута, у вас остается сеть.
Правая пирамида Наклонная пирамида
Призма
0003
Призма имеет два одинаковых конца и плоские стороны в виде параллелограмма.
Умножьте площадь одной стороны на 2.
В случае правильной призмы (у которой все стороны одинаковы) умножьте площадь одной стороны на количество сторон.
Если призма имеет неправильные стороны (разной длины), рассчитайте площадь каждой стороны.
Общая площадь призмы равна двум вашим ответам (концы х сторон).
Цилиндр
При расчете площади поверхности цилиндра полезно подумать о составных частях формы. Представьте себе банку сладкой кукурузы, у которой есть верх и низ, оба из которых представляют собой круги. У вас получится прямоугольник, если вы разрежете сторону по длине и сгладите ее. Следовательно, вам нужно найти площади двух кругов и прямоугольника.
Представьте себе банку сладкой кукурузы, у которой есть верх и низ, оба из которых представляют собой круги. У вас получится прямоугольник, если вы разрежете сторону по длине и сгладите ее. Следовательно, вам нужно найти площади двух кругов и прямоугольника.
Сначала определите площадь одного из кругов.
Площадь круга равна π(pi) × радиус 2 .
При радиусе 5 см площадь одного из кругов равна 3,14 × 5 2 = 78,5 см 2 .
Умножьте ответ на 2, так как кругов два 157см 2
Площадь стороны цилиндра равна периметру круга × высоте цилиндра.
Периметр равен π x 2 × радиус. В нашем примере 3,14 × 2 × 5 = 31,4·9.0003
Измерьте высоту цилиндра – в данном примере высота составляет 10 см. Площадь стороны 31,4 × 10 = 314см 2 .
Вы можете вычислить общую площадь поверхности путем сложения площадей кругов и сторон:
157 + 314 = 471см 2
Конус
радиус основания, необходимо учитывать при расчете площади поверхности конуса.
Расчет относительно прост:
Допустим, радиус равен 5 см, а длина наклона 10 см.
Площадь круга в основании конуса равна π(pi) × радиус 2 .
В этом примере сумма равна 3,14 × 52 = 3,14 × 25 = 78,5 см. наклона.
В нашем примере сумма равна 3,14 × 5 × 10 = 157 см 2 .
Наконец, добавьте площадь основания к площади стороны, чтобы получить общую площадь поверхности конуса.
78,5 + 157 = 235,5 см 2
Сфера
Площадь поверхности сферы представляет собой относительно простое расширение формулы для площади круга.
4 × π × радиус 2 .
При определении диаметра сферы часто проще всего измерить расстояние поперек сферы. Вы можете определить радиус, который составляет половину диаметра.
Предположим, что диаметр теннисного мяча равен 2,6 дюйма.
Следовательно, радиус равен 1,3 дюйма.
Для формулы нам нужен квадрат радиуса.
1,3 × 1,3 = 1,69.
Площадь поверхности теннисного мяча, следовательно:
4 × 3,14 × 1,69 = 21,2264 дюйма 2 .
Тор
Чтобы найти площадь тора, необходимо определить два значения радиуса.
Большой радиус (R) — это диаметр от середины отверстия до середины кольца.
Малый или малый радиус (r) рассчитывается путем измерения кольца от центра к внешнему краю.
На диаграмме показаны два вида примера тора и способы измерения его радиусов (или радиусов).
R (большой радиус) = 20 см
r (малый радиус) = 4 см
Площадь поверхности можно рассчитать двумя способами (по одному для каждого радиуса). Для каждой части расчет одинаковый.
Формула: площадь поверхности = (2πR)(2πr)
Для расчета площади поверхности примера тора.
(2 × π × R) = (2 × 3,14 × 20) = 125,6
(2 × π × r) = (2 × 3,14 × 4) = 25,12
Вы можете найти общую площадь поверхности тора из примера, перемножив два ответа.
125,6 × 25,12 = 3155,072см2.
Ссылки
- https://www.mathsisfun.com/geometry/common-3d-shapes.html
- https://www.khanacademy.org/computing/computer-programming/programming-games-visualizations/programming -3d-shapes/a/what-are-3d-shapes
- https://www.open.edu/openlearn/ocw/mod/oucontent/view.php?id=84739§ion=1.3
- https:// Thirdspacelearning.com/blog/what-are-3d-shapes/
- https://www.bbc.co.uk/bitesize/topics/zjv39j6/articles/zgqpk2p
Объем цилиндров, конусов и сферы (спортивная тематика) Рабочие листы по математике
Решение текстовых задач на объем цилиндров, конусов и сфер Рабочие листы по математике для 8-го класса
Словесные задачи на объем твердых фигур (ветеринарная тематика) Рабочие листы
Мы тратим много времени на исследования и компиляцию информация на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника.
 Если всё тело окажется по одну сторону этой плоскости, то такое
тело называется выпуклым. Всякая прямая его пересекает не более, чем в двух точках.
Если всё тело окажется по одну сторону этой плоскости, то такое
тело называется выпуклым. Всякая прямая его пересекает не более, чем в двух точках.  Многогранник называется пирамидой (фиг. 3), если одна из его граней многоугольник (основание пирамиды), а
другие грани треугольники, имеющие общую вершину (вершина пирамиды).
Расстояние от вершины до основания наз. высотой пирамиды.
Многогранник называется пирамидой (фиг. 3), если одна из его граней многоугольник (основание пирамиды), а
другие грани треугольники, имеющие общую вершину (вершина пирамиды).
Расстояние от вершины до основания наз. высотой пирамиды.