В л м: Составить слова из слова, слова из букв, анаграммы

л/мин Конвертер единиц расхода объёмного, Метрическая система

л/мин – Литр в минуту. Конвертер величин. / Конвертер единиц расхода объёмного, Метрическая система

EN ES PT RU FR

Ой… Javascript не найден.

Увы, в вашем браузере отключен или не поддерживается JavaScript.

К сожалению, без JavaScript этот сайт работать не сможет. Проверьте настройки браузера, может быть JavaScript выключен случайно?

л/мин – Литр в минуту. Конвертер и таблица перевода величины.

Всё очень просто: Нужна помощь? x Этот конвертер величин очень простой. Правда. 1 Это – страница перевода единицы “литр в минуту (Метрическая система)”. Чтобы выбрать другую единицу, просто найдите её на странице и кликните по ней. Вы также можете перейти на универсальную страницу перевода величин 2 Введите значение единицы (литр в минуту). Щёлкните по кнопке “Посчитать”. Введённое значение мгновенно пересчитывается во все совместимые единицы, представленные на странице. 3 Остаётся только найти на странице нужную единицу и посмотреть результат перевода напротив неё.

Введите значение единицы Нажмите “Посчитать” Получите результат

?Настройки конвертера:

x

Объяснение настроек конвертера

Кстати, пользоваться настройками не обязательно. Вам вполне могут подойти настройки по умолчанию.

Количество значащих цифр

Для бытовых целей обычно не нужна высокая точность, удобнее получить округлённый результат. В таких случаях выберите 3 или 4 значащих цифры. Максимальная точность – 9 значащих цифр. Точность можно изменить в любой момент.

Разделитель групп разрядов

Выберите, в каком виде вам будет удобно получить результат:

1234567.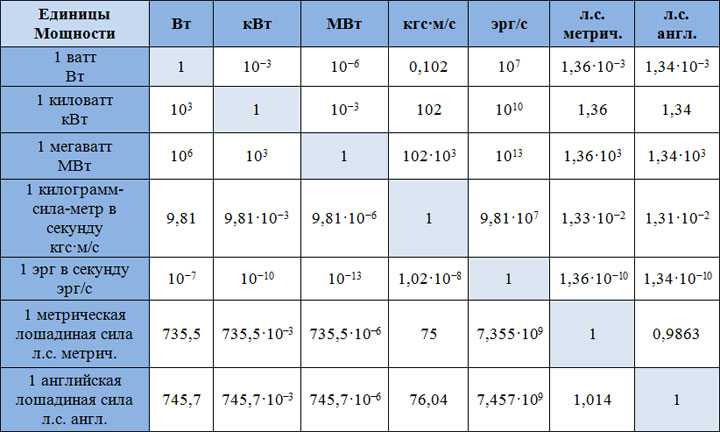 89	нет
1 234 567.89	пробел
1,234,567.89	запятая
1.234.567,89	точка

• Значащих цифр: 1  23456789
• Разделитель разрядов: нет  пробел  запятая  точка  

Укажите значение (литр в минуту, л/мин):

» открыть »

» свернуть »

Метрическая система

литр в минуту → кубический метр в секунду (м³/с)
литр в минуту → кубический метр в минуту (м³/мин)
литр в минуту → кубический метр в час (м³/ч)
литр в минуту → кубический метр в сутки (м³/сутки)
литр в минуту → кубический метр в год (м³/год)
литр в минуту → литр в секунду (л/с)
литр в минуту → литр в час (л/ч)
литр в минуту → литр в сутки (л/сутки)
литр в минуту → литр в год (л/год)
литр в минуту → кубический сантиметр в секунду (см³/с)
литр в минуту → кубический сантиметр в минуту (см³/мин)
литр в минуту → кубический сантиметр в час (см³/час)
литр в минуту → кубический сантиметр в сутки (см³/сутки)
литр в минуту → кубический сантиметр в год (см³/год)

Единицы: кубический метр в секунду (м³/с)  / кубический метр в минуту (м³/мин)  / кубический метр в час (м³/ч)  / кубический метр в сутки (м³/сутки)  / кубический метр в год (м³/год)  / литр в секунду (л/с)  /  / литр в час (л/ч)  / литр в сутки (л/сутки)  / литр в год (л/год)  / кубический сантиметр в секунду (см³/с)  / кубический сантиметр в минуту (см³/мин)  / кубический сантиметр в час (см³/час)  / кубический сантиметр в сутки (см³/сутки)  / кубический сантиметр в год (см³/год)

» открыть »

» свернуть »

Американские и Британские единицы

литр в минуту → акр-фут в секунду
литр в минуту → акр-фут в минуту
литр в минуту → акр-фут в час
литр в минуту → акр-фут в сутки
литр в минуту → акр-фут в год
литр в минуту → баррель (нефтяной) в секунду
литр в минуту → баррель (нефтяной) в минуту
литр в минуту → баррель (нефтяной) в час
литр в минуту → баррель (нефтяной) в сутки
литр в минуту → баррель (нефтяной) в год
литр в минуту → галлон США в секунду (gps)
литр в минуту → галлон США в минуту (gpm)
литр в минуту → галлон США в час (gph)
литр в минуту → галлон США в сутки (gal/day)
литр в минуту → галлон США в год (gal/year)
литр в минуту → брит. галлон в секунду
литр в минуту → брит. галлон в минуту
литр в минуту → брит. галлон в час
литр в минуту → брит. галлон в сутки
литр в минуту → брит. галлон в год
литр в минуту → кубический фут в секунду (ft³/s)
литр в минуту → кубический фут в минуту (ft³/min)
литр в минуту → кубический фут в час (ft³/hour)
литр в минуту → кубический фут в сутки (ft³/day)
литр в минуту → кубический фут в год (ft³/year)
литр в минуту → кубический дюйм в секунду (in³/s)
литр в минуту → кубический дюйм в минуту (in³/min)
литр в минуту → кубический дюйм в час (in³/hour)
литр в минуту → кубический дюйм в сутки (in³/day)
литр в минуту → кубический дюйм в год (in³/year)

Единицы: акр-фут в секунду  / акр-фут в минуту  / акр-фут в час  / акр-фут в сутки  / акр-фут в год  / баррель (нефтяной) в секунду  / баррель (нефтяной) в минуту  / баррель (нефтяной) в час  / баррель (нефтяной) в сутки  / баррель (нефтяной) в год  / галлон США в секунду (gps)  / галлон США в минуту (gpm)  / галлон США в час (gph)  / галлон США в сутки (gal/day)  / галлон США в год (gal/year)  / брит. галлон в секунду  / брит. галлон в минуту  / брит. галлон в час  / брит. галлон в сутки  / брит. галлон в год  / кубический фут в секунду (ft³/s)  / кубический фут в минуту (ft³/min)  / кубический фут в час (ft³/hour)  / кубический фут в сутки (ft³/day)  / кубический фут в год (ft³/year)  / кубический дюйм в секунду (in³/s)  / кубический дюйм в минуту (in³/min)  / кубический дюйм в час (in³/hour)  / кубический дюйм в сутки (in³/day)  / кубический дюйм в год (in³/year)

Не можете найти нужную единицу?

Попробуйте поискать:

Другие варианты:

Посмотрите алфавитный список всех единиц

Задайте вопрос на нашей странице в facebook

< Вернитесь к списку всех конвертеров

Надеемся, Вы смогли перевести все ваши величины, и Вам у нас на Convert-me.Com понравилось. Приходите снова!

 

 

! Значение единицы приблизительное.
Либо точного значения нет,
либо оно неизвестно. ? Пожалуйста, введите число. (?) Простите, неизвестное вещество. Пожалуйста, выберите что-то из списка. *** Нужно выбрать вещество.
От этого зависит результат.

Совет: Не можете найти нужную единицу? Попробуйте поиск по сайту. Поле для поиска в верхней части страницы.

Нашли ошибку? Хотите предложить дополнительные величины? Свяжитесь с нами в Facebook.

Действительно ли наш сайт существует с 1996 года? Да, это так. Первая версия онлайнового конвертера была сделана ещё в 1995, но тогда ещё не было языка JavaScript, поэтому все вычисления делались на сервере – это было медленно. А в 1996г была запущена первая версия сайта с мгновенными вычислениями.

Для экономии места блоки единиц могут отображаться в свёрнутом виде. Кликните по заголовку любого блока, чтобы свернуть или развернуть его.

Слишком много единиц на странице? Сложно ориентироваться? Можно свернуть блок единиц – просто кликните по его заголовку. Второй клик развернёт блок обратно.

Наша цель – сделать перевод величин как можно более простой задачей. Есть идеи, как сделать наш сайт ещё удобнее? Поделитесь!

Минуточку, загружаем коэффициенты…

Дезинфицирующее средство Неодишер ЛМ 2, 1 л (LM 2)

Области применения:

• ручная мойка в иммерсионных и ультразвуковых ваннах лабораторного стекла и хирургических инструментов в больницах, стоматологии, промышленных и биологических лабораториях; 
• мойка клеток подопытных животных; 
• мойка пипеток в специальных моечных машинах.

Состав:
в соответствии с рекомендациями ЕС для моющих и чистящих средств 89/542/EWG

• <5% амфотерные ПАВ, 
• анионогенные ПАВ 
• 15-30% фосфаты.

Свойства:

• содержит слабо пенящиеся поверхностно-активные вещества и различные усилители моющего эффекта. Растворы хорошо смываются и практически не пенятся.
• можно использовать для предварительной мойки, после чего инструменты и принадлежности можно мыть в моечной машине без предварительного ополаскивания. удаляет органические загрязнения, такие как запекшаяся кровь, белок. Неорганические загрязнения, такие как стоматологический цемент, пищевые остатки и остатки жизнедеятельности подопытных животных, также могут быть помыты;
• очень хорошо подходит для мойки хирургических, стоматологических инструментов и особенно микроинструментов в ультразвуковой ванне. Если лабораторное стекло автокпавируется перед машинной мойкой, то мы рекомендуем влажное автоклавирование с добавлением 3% раствором neodisher LM 2;
• не повреждает материалы и используется для мойки всех видов лабораторных принадлежностей из стекла, керамики, легированной стали и пластмасс;
• изделия из легких металлов должны быть протестированы перед мойкой;
• может использоваться в воде любой жесткости.

Применение:

• время воздействия 10-30 мин, раствор может быть нагрет для усиления моющего эффекта.
• 0,5-2,% в иммерсионной или УЗ-ванне.
• 1-3% для мойки пипеток в моечной машине.
• Впоследствии раствор должен быть полностью смыт.
• Не смешивать с другими продуктами.

Определение концентрации:

• фактор титрования 0,19 (в соответствии с методикой неодишер).

Технические данные: 

• Удельная масса (20°С): 1,2 г/см3.
• Уровень pH (0,5-3,0% в деионизированной воде 20°С): 10,3-11,7.
• Вязкость (концентрат 20°С): <10 mPas.

CE стандарт: 

• соответствует закону о медицинских принадлежностях, согласно европейским директивам 93/42/ЕС.

Информация по хранению:

• чувствителен к морозу. 

Срок хранения: 

• 4 года.

Бренд товара:

Неодишер

Обьём:

1 л

Производитель:

Др. Вайгерт ГмбХ, Германия

Неодишер отказное письмо (Neodisher_pismo_otkaz.pdf, 168 Kb) [Скачать]

Неодишер ЛМ 2 свидетельство 2011 (Neodisher_1_sv_2011.pdf, 202 Kb) [Скачать]

Инструкция Неодишер ЛМ 2 (Neodisher_LM_2.pdf, 54 Kb) [Скачать]

Пример линейной регрессии в R с использованием функции lm() — Learn by Marketing

Резюме: линейная регрессия R использует функцию lm () для создания регрессионной модели по некоторой формуле в форме Y~X+X2. Чтобы просмотреть модель, вы используете функцию summary (). Чтобы проанализировать остатки, вы извлекаете переменную $resid из вашей новой модели. Остатки — это различия между прогнозом и фактическими результатами, и вам необходимо проанализировать эти различия, чтобы найти способы улучшить вашу регрессионную модель.

Для выполнения линейной (простой и множественной) регрессии в R вам понадобится встроенная функция lm .

Вот данные, которые мы будем использовать: расходы на маркетинг за год и продажи компании по месяцам. Скачать: CSV

Месяц	Потратить	Продажи
1	1000	9914
2	4000	40487
3	5000	54324
4	4500	50044
5	3000	34719
6	4000	42551
7	9000	94871
8	11000	118914
9	15000	158484
10	12000	131348
11	7000	78504
12	3000	36284

Предполагая, что вы загрузили CSV, мы прочитаем данные в R и назовем их набором данных переменной

#Возможно, вам потребуется использовать команду setwd(directory-name) для
# измените свой рабочий каталог на то место, где вы сохранили csv. 
#Используйте getwd(), чтобы узнать, какой у вас текущий каталог.
набор данных = read.csv("data-marketing-budget-12mo.csv", заголовок = T,
colClasses = c("числовой", "числовой", "числовой"))
 

Простая (одна переменная) и множественная линейная регрессия с использованием lm()

Предикторной (или независимой) переменной для нашей линейной регрессии будет Spend (обратите внимание на заглавную букву S), а зависимой переменной (той, которую мы пытаемся предсказать). ) будет Продажи (опять же, заглавная S).

Для функции lm нужна формула (Y~X), а затем источник данных. Мы будем использовать Продажи ~ Расходы, данные = набор данных и назовем полученную линейную модель «подходящей».

simple.fit = lm (Продажи ~ Расходы, данные = набор данных)
резюме (simple.fit)
multi.fit = lm(Продажи~Затраты+Месяц, данные=набор данных)
резюме (мультифит)
 

Уведомления в строке multi.fit Переменные Spend сопровождаются переменной Month и знаком плюс (+).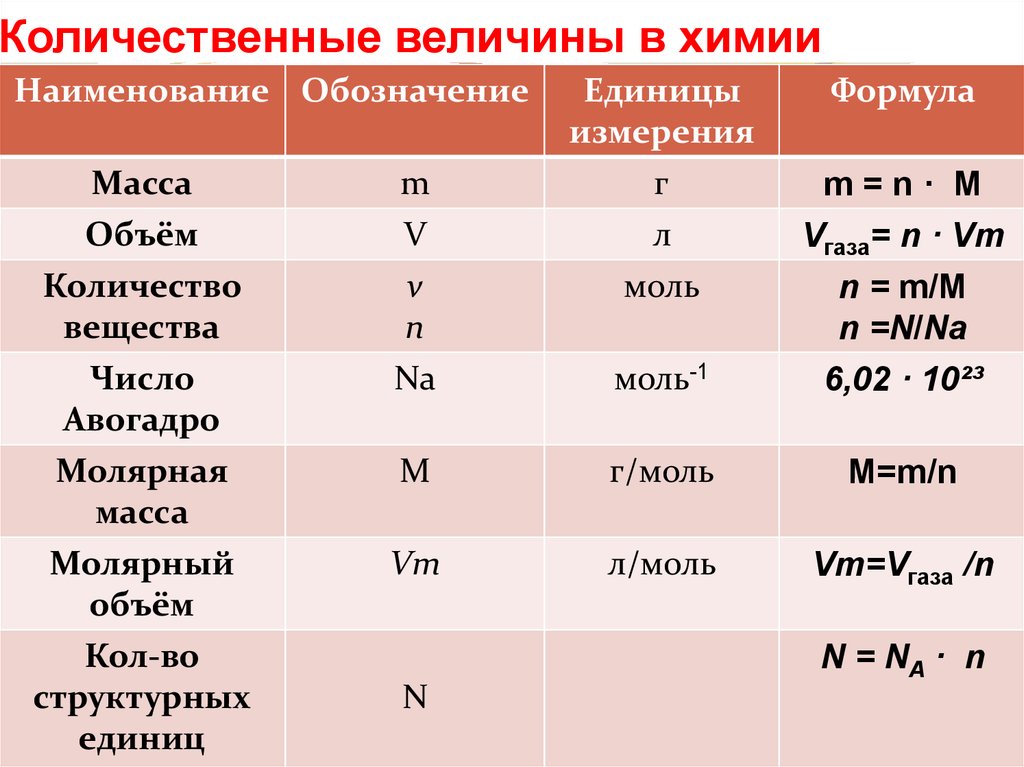 Знак «плюс» включает в модель переменную «Месяц» в качестве предиктора (независимой) переменной.

Функция суммирования выводит результаты модели линейной регрессии.

Выходные данные для R’s lm Функция, показывающая используемую формулу, сводную статистику для остатков, коэффициенты (или веса) переменной-предиктора и, наконец, показатели производительности, включая RMSE, R-квадрат и F-статистику.

Обе модели имеют значимые модели (см. F-статистику для регрессии), а Множественный R-квадрат и Скорректированный R-квадрат исключительно высоки (имейте в виду, это упрощенный пример). Мы также видим, что все переменные являются значимыми (как указано «**»)

Интерпретация результатов регрессии R

• Остатки Результаты. Меньшие остатки лучше.
• Коэффициенты : Для каждой переменной и точки пересечения создается вес, и этот вес имеет другие атрибуты, такие как стандартная ошибка, значение t-критерия и значимость.
  • Оценка : Это вес, присвоенный переменной. В случае простой регрессии (одна переменная плюс точка пересечения) для каждого увеличения расходов на один доллар модель предсказывает увеличение на 10,6222 доллара.
  • Станд. Ошибка : сообщает, насколько точно была измерена оценка. Это действительно полезно только для вычисления t-значения.
  • Значение t и Pr(>[t]) : Значение t рассчитывается путем деления коэффициента на Std. Ошибка. Затем он используется для проверки того, значительно ли коэффициент отличается от нуля. Если он незначителен, то коэффициент действительно ничего не добавляет к модели, и его можно исключить или исследовать дальше. Pr(>|t|) — уровень значимости.

• Показатели производительности : Предоставляются три набора измерений.
  • Стандартная ошибка остатка : это стандартное отклонение остатка. Чем меньше, тем лучше.
  • Множественный / скорректированный R-квадрат : Для одной переменной различие не имеет большого значения. R-квадрат показывает величину дисперсии, объясняемую моделью. Скорректированный R-квадрат учитывает количество переменных и наиболее полезен для множественной регрессии.
  • F-статистика : F-тест проверяет значительно ли вес хотя бы одной переменной отличается от нуля. Это глобальный тест, помогающий оценить модель. Если p-значение незначительно (например, больше 0,05), ваша модель по существу ничего не делает.

Нужны более конкретные пояснения? Я объясняю итоговый вывод на этой странице.

Разобравшись с описаниями, приступим к интерпретации.

Остатки : Мы видим, что модель множественной регрессии имеет меньший диапазон остатков: от -3385 ​​до 3034 по сравнению с -1793 до 1911. Во-вторых, медиана множественной регрессии намного ближе к 0, чем простая регрессионная модель.

• Коэффициенты :
  • (Пересечение): Пересечение — это остаток, когда вы усредняете независимую и зависимую переменные. В простой регрессии мы видим, что точка пересечения намного больше, что означает, что осталось изрядное количество. Множественная регрессия показывает отрицательную точку пересечения, но она ближе к нулю, чем результат простой регрессии.
  • Затраты: как простая, так и множественная регрессия показывают, что на каждый потраченный доллар вы должны получить около 10 долларов продаж.
  • Месяц: когда мы добавляем переменную «Месяц», она умножает эту переменную на числовое (порядковое) значение месяца. Таким образом, за каждый месяц в году вы добавляете к продажам дополнительно 541 ед. Таким образом, февраль добавляет 1082 доллара, а декабрь — 6,49 доллара.2 в продажах.

• Показатели эффективности :
  • Стандартная ошибка невязки : Модель простой регрессии имеет гораздо более высокую стандартную ошибку, что означает, что остатки имеют большую дисперсию. Стандартная ошибка 2313 — это довольно много, учитывая, что средний объем продаж составляет 70 870 долларов.
  • Множественный / скорректированный R-квадрат : R-квадрат очень высок в обоих случаях. Скорректированный R-квадрат учитывает количество переменных, поэтому он более полезен для множественного регрессионного анализа.
  • F-статистика : F-критерий статистически значим. Это означает, что обе модели имеют по крайней мере одну переменную, которая значительно отличается от нуля.

Анализ остатков

Любой может подобрать линейную модель в R. Настоящим испытанием является анализ остатков (ошибка или разница между фактическими и прогнозируемыми результатами).

Есть четыре вещи, на которые мы обращаем внимание при анализе остатков.

• Среднее значение ошибок равно нулю (и сумма ошибок равна нулю)
• Распределение ошибок нормальное.
• Все ошибки независимы.
• Дисперсия ошибок постоянна (гомоскедастическая)

В R вы извлекаете остатки, ссылаясь на модель, а затем на переменную resid внутри модели. Используя простую модель линейной регрессии ( simple.fit ), мы построим несколько графиков, чтобы проиллюстрировать любые проблемы с моделью.

макет (матрица (c (1,1,2,3), 2,2, по ряду = T))
График #Расходы x остатки
график (simple.fit $ resid ~ набор данных $ Spend [порядок (набор данных $ Spend)],
 main="Потратить x остатков\nдля простой регрессии",
 xlab="Маркетинговые расходы", ylab="Остатки")
аблайн (ч = 0, lty = 2)
#Гистограмма остатков
hist(simple.fit$resid, main="Гистограмма остатков",
 ylab="Остатки")
#QQ Сюжет
qqnorm(simple.fit$остаток)
qqline (simple.fit $ resid)
 

 Остатки нормально распределены

Гистограмма и QQ-график позволяют визуально оценить, соответствует ли остаток нормальному распределению.

• Если гистограмма выглядит как гауссовая кривая , она может иметь нормальное распределение.
• Если на графике QQ подавляющее большинство точек находится на линии или очень близко к ней, остатки могут быть распределены нормально.

Графики не кажутся очень близкими к нормальному распределению, но мы также можем использовать статистический тест.

Тест Жарка-Бера (в библиотеке fBasics, который проверяет, подобны ли асимметрия и эксцесс ваших остатков нормальному распределению.

• Нулевая гипотеза теста Джарке-Бера состоит в том, что асимметрия и эксцесс ваши данные равны нулю (так же, как и нормальное распределение).

библиотека (fBasics)
jarqueberaTest(simple.fit$resid) # Проверка остатков на нормальность
#Нулевая гипотеза: асимметрия и эксцесс равны нулю
#Остатки X-квадрат: 0,9575 р Значение: 0,6195
 

При значении p 0,6195 мы не можем отвергнуть нулевую гипотезу о том, что асимметрия и эксцесс остатков статистически равны нулю.

Остатки независимы

Критерий Дарбина-Ватсона используется при анализе временных рядов для проверки наличия тренда в данных, основанных на предыдущих экземплярах – например, при анализе временных рядов. сезонный тренд или тренд каждой второй точки данных.

Используя библиотеку lmtest, мы можем вызвать функцию «dwtest» для модели, чтобы проверить, независимы ли остатки друг от друга.

• Нулевая гипотеза теста Дарбина-Ватсона состоит в том, что ошибки последовательно НЕкоррелированы.

библиотека (lmtest) #dwtest
dwtest(simple.fit) # Тест на независимость остатков
#Null Hypothesis: ошибки последовательно НЕ коррелированы
#Результаты: DW = 1,1347, p-значение = 0,03062.
 

Основываясь на результатах, мы можем отвергнуть нулевую гипотезу о том, что ошибки последовательно некоррелированы. Это означает, что у нас больше работы.

Давайте попробуем выполнить эти движения для модели множественной регрессии.

макет (матрица (c (1,2,3,4), 2,2, по ряду = T))
сюжет (мультифит $ приспособлен, rstudent (мультифит),
 main="Multi Fit Studentized Residuals",
 xlab="Предсказания",ylab="Студенческая резиденция",
 илилим=с(-2. 5,2.5))
аблайн (ч = 0, лти = 2)
график (набор данных $ месяц, multi.fit $ resid,
 main="Остатки по месяцам",
 xlab="Месяц",ylab="Остатки")
аблайн (ч = 0, lty = 2)
hist(multi.fit$resid,main="Гистограмма остатков")
qqnorm(multi.fit$остаток)
qqline(multi.fit$resid)
 

Остатки нормально распределены

• Гистограмма остатков не выглядит нормально распределенной.
• Однако график QQ показывает лишь несколько точек, отклоняющихся от нормальной линии.
• Нам не удалось отвергнуть нулевую гипотезу Харке-Бера (значение p = 0,5059)

библиотека (fBasics)
jarqueberaTest(multi.fit$resid) # Проверка остатков на нормальность
#Нулевая гипотеза: асимметрия и эксцесс равны нулю
#Остатки X-квадрат: 1,3627 p Значение: 0,5059

Остатки независимы

• Мы не можем отвергнуть нулевую гипотезу теста Дарбина-Уотсона (p-значение 0,3133)

библиотека (lmtest) #dwtest
dwtest(multi.fit) # Тест на независимость остатков
#Null Hypothesis: ошибки последовательно НЕ коррелированы
#Результаты: DW = 2,1077, p-значение = 0,3133. 
 

Остатки имеют постоянную дисперсию

Постоянную дисперсию можно проверить, взглянув на “обученные” остатки, нормализованные на основе стандартного отклонения. «Обучение» позволяет сравнивать остатки по моделям.

График Multi Fit Studentized Residuals показывает, что явных выбросов нет. Если точка находится далеко за пределами других точек на графике, вы можете провести расследование. Основываясь на приведенном выше графике, я думаю, что мы можем принять предположение о постоянной дисперсии. Дополнительные данные определенно помогли бы заполнить некоторые пробелы.

Резюме / основные моменты

• Регрессия — это мощный инструмент для прогнозирования числовых значений.
Функция
• R lm создает регрессионную модель.
• Используйте сводную функцию для просмотра весов и показателей производительности.
• Остатки можно проверить, вытащив переменную $resid из вашей модели.
• Вам необходимо проверить остатки по этим четырем предположениям.
  • Среднее значение ошибок равно нулю (и сумма ошибок равна нулю).
  • Распределение ошибок нормальное.
  • Все ошибки независимы.
  • Дисперсия ошибок постоянна (гомоскедастическая)

Вот полный код ниже

набор данных = read.csv("data-marketing-budget-12mo.csv", заголовок = T,
colClasses = c("числовой", "числовой", "числовой"))
голова (набор данных, 5)
#/////Простая регрессия/////
simple.fit = lm (Продажи ~ Расходы, данные = набор данных)
резюме (simple.fit)

#Загружаем необходимые библиотеки
библиотека (lmtest) #dwtest
библиотека (fBasics) #JarqueBeraTest

# Проверка предположений о нормальном распределении и независимости
jarqueberaTest(simple.fit$resid) # Проверка остатков на нормальность
#Нулевая гипотеза: асимметрия и эксцесс равны нулю
dwtest(simple.fit) # Тест на независимость остатков
#Null Hypothesis: ошибки последовательно НЕ коррелированы

#Простые графики остатков регрессии
макет (матрица (c (1,1,2,3), 2,2, по ряду = T))
График #Расходы x остатки
график (simple. fit $ resid ~ набор данных $ Spend [порядок (набор данных $ Spend)],
     main="Потратить x остатков\nдля простой регрессии",
     xlab="Маркетинговые расходы", ylab="Остатки")
аблайн (ч = 0, lty = 2)
#Гистограмма остатков
hist(simple.fit$resid, main="Гистограмма остатков",
     ylab="Остатки")
#QQ Сюжет
qqnorm(simple.fit$остаток)
qqline (simple.fit $ resid)

#///////////Пример множественной регрессии///////////

multi.fit = lm(Продажи~Затраты+Месяц, данные=набор данных)
резюме (мультифит)

# Остаточный анализ для множественной регрессии
dwtest(multi.fit) # Тест на независимость остатков
#Null Hypothesis: ошибки последовательно НЕ коррелированы
jarqueberaTest(multi.fit$resid) # Проверка остатков на нормальность
#Нулевая гипотеза: асимметрия и эксцесс равны нулю

#Графики остатков множественной регрессии
макет (матрица (c (1,2,3,4), 2,2, по ряду = T))
сюжет (мультифит $ приспособлен, rstudent (мультифит),
     main="Multi Fit Studentized Residuals",
     xlab="Предсказания",ylab="Студенческая резиденция",
     илилим=с(-2. 5,2.5))
аблайн (ч = 0, лти = 2)
график (набор данных $ месяц, multi.fit $ resid,
     main="Остатки по месяцам",
     xlab="Месяц",ylab="Остатки")
аблайн (ч = 0, lty = 2)
hist(multi.fit$resid,main="Гистограмма остатков")
qqnorm(multi.fit$остаток)
qqline(multi.fit$resid)
 

Исправления:

• Спасибо Тиаму Хуату за исправление в интерпретации коэффициентов.

статистика – В чем разница между “*” и “+” в lm() в R?

спросил 2 года, 4 месяца назад

Изменено 2 года, 4 месяца назад

Просмотрено 2к раз

Часть R Language Collective Collective

Я хотел бы предварить этот пост тем, что я абсолютный нуб в R и немного разбираюсь в статистике. Я хочу извиниться, если перепутал терминологию (и мне определенно нужно больше читать).

В настоящее время я просматриваю набор данных с 17 переменными, 1 из которых является зависимой переменной, а остальные 16 являются независимыми переменными. Мне нужно выбрать «лучшую» линейную модель из этих переменных.

Вот с чем я работаю:

 MA1 <- step(lm(
  as.formula (вставить (имена столбцов (NLCD) [1], "~",
  вставить (имена столбцов (NLCD) [c (2:17)], свернуть = "*")
  )), данные = NLCD
))
 

Итак, MA1 — это модель, а NLCD — это имя набора данных. Я не понимаю, использовать ли "*" или "+" для ступенчатой ​​регрессии. Когда я запускаю модель с "*" , RStudio на некоторое время зависает, а затем выдает кучу NA с большим количеством имен заголовков и : . Я подумал, что лучше всего использовать "*" , так как это избавляет меня от необходимости писать код вручную, но я действительно не знаю, какова его цель.