Разное

Усложненные задания по математике 2 класс: текстовые, арифметические и нестандартные задачи с ответами для подготовки к олимпиаде

Содержание

текстовые, арифметические и нестандартные задачи с ответами для подготовки к олимпиаде

Математика и логика / 2 класс / Олимпиадные задания

Олимпиадные задачи от ЛогикЛайк помогут второкласснику подготовиться к математическому конкурсу любого уровня сложности.

Выберите возраст ребёнка,

чтобы начать занятия!

1 класс

2 класс

На платформе LogicLike.com 2000 логических и математических заданий с ответами! Типовые и нестандартные задачи, нескучная теория и пояснение способов решения. Все что нужно для подготовки к олимпиаде!

2 формата подготовки к олимпиаде

  • Тесты с прошлых олимпиад. Это хороший формат экспресс-занятий, чтобы проверить уровень подготовки будущего олимпиадника.
  • Регулярные тренировки в решении типовых и нестандартных задач. В блоках с теорией и в комментариях к сложным задачам мы объясняем разные способы решения. 30 минут каждый день – оптимальный режим занятий для детей 8-9 лет.

Задания с прошедших олимпиад

Задача 1

Чтобы решать задачи, нажмите Начать занятия!

Условие: Общая стоимость фруктов по вертикали и горизонтали указана в таблице.

Задание: Найди цену клубники.

Показать решение

Ответ:

1.

Решение
1. Находим строку или столбец с одинаковыми объектами. Проще всего узнать цену персика: 4 ÷ 2 = 2.
2. Таким же образом находим стоимость 1 апельсина: 15 ÷ 3 = 5.
3. Цена клубники: 8-5-2=1.

Задача 2

Чтобы решать задачи, нажмите «Начать занятия»!

Видеоканалы Светы, Карины и Марка называются Фикс, Найс и Атом.
Больше всего подписчиков у канала Найс.
Канал Карины не называется Атом. У канала Карины и канала Марка вместе меньше подписчиков, чем у канала Светы.

Кто назвал свой канал «Атом»?

Показать ответ

Ответ:

Марк.

Рекомендуем тематические курсы

онлайн для 2 класса

Курс логики и мышления Начать

Подготовка к олимпиаде Начать

Задача 3

Условие: Картинки расставили в определённом порядке (в виде закономерности).

Задание: Какой элемент будет следующим в ряду?

Чтобы решать задачи, нажмите «Начать занятия»!

Показать ответ

Ответ:

3-ий.

Пояснение:
Чёрная фигурка внутри цветных фигур перемещается по часовой стрелке.

Самые проблемные задания из ОГЭ по математике и как их решить?

Математика — это один из самых сложных экзаменов для 9 класса. Для его решения нужно владеть программой за 6-9 классы по математике в общем, алгебре и геометрии. И если часть заданий выполняется легко, с другими могут возникнуть серьезные проблемы.

Сколько задач в ОГЭ по математике?

Экзамен состоит из 25 заданий, среди которых 6 требуют развернутого решения, а 19 — краткого ответа.

При этом, максимальный балл можно получить, даже не решив одну из нетипичных задач второй части. А вот тестовые задания придется щелкать как орешки, даже если с ними возникают сложности.

Виды задач

Экзамен по математике делится на две части.

  1. Первая часть — задания с кратким ответом по темам:
    1. Простой счет.
    2. Выражения.
    3. Уравнения и неравенства.
    4. Последовательности чисел.
    5. Функции и графики.
    6. Координаты.
    7. Теория вероятностей.
    8. Геометрия.
  1. Вторая часть — задания с развернутым ответом по темам:
    1. Уравнения и неравенства.
    2. Функции и графики.
    3. Геометрия.

Задача 9 в ОГЭ по математике

Задание №9 — это квадратное уравнение, в ответ к которому надо записать единственный, больший или меньший из корней. Здесь может попасться уравнение двух типов — традиционное или дробно-рациональное.

Первый тип

Традиционное квадратное уравнение может быть двух форматов — приравненное к нулю или числу. Если первое уже готово к решению, то во втором число просто переносится к неизвестным (знак меняется на противоположный). На выходе мы получим уравнение типа: x2+ x -12 = 0.

Оно решается через дискриминант: D = b2– 4ac, где a — число рядом с квадратом, b — рядом с просто неизвестной, c — обычное число.

Здесь D = 1 – 4*1*(-12) = 49 = 72

Дальше находятся корни уравнения, то есть эти самые неизвестные. Формула: -b ± D2a. Здесь x1= -1 — 72= -4, а x2= -1 + 72= 3. Записывается в ответ требуемое число. По заданию — больший из корней.

Ответ: 3.

Второй тип

Уравнение может выглядеть как дробь. В таком случае, перед основным решением придется ввести ОДЗ — область допустимых значений, в которой уравнение под дробью нужно будет сделать неравным нулю.

Здесь ОДЗ будет таким: х+2 ≠ 0, то есть х ≠ -2 (число переносится на другую сторону, знак меняется). Если в корнях уравнения попадется число 2, мы его просто исключим.

D = 16 — 4*1*(-12) = 16 + 48 = 64 = 82

x1= 4 — 82= -2

x2= 4 + 82= 6

Ответ: 6

Задача 10 в ОГЭ по математике

Задачи №10 в математике ОГЭ — это задания на теорию вероятностей. Они также могут быть двух типов — традиционные и усложненные.

Первый тип

Обычные задания на теорию вероятностей состоят из двух-трех объектов (в разном количестве), один из которых гипотетический Вася Пупкин вытягивает. И все, что здесь нужно сделать, — понять, какова вероятность, что он вытащит именно этот объект.

Такие задачи решаются просто — количество вытянутых объектов делится на количество всех объектов. То есть решение этого номера — 34+8+3=315=15=0.2.

Главное в этой задаче — не забыть, что 3 пирожка с яблоками входят в общее число пирожков, то есть делить нужно не на 12, а на 15.

Второй тип

Иногда задание №10 может быть немного сложнее: последовательно вытягивается, например, не один пирожок, а два. Какова вероятность, что оба пирожка будут с яблоком?

В таком случае нужно перемножить обе вероятности — первый пирожок с яблоком ( 15— уже выяснили) и второй пирожок с яблоком (на тарелке осталось 2 яблочных и всего 14 пирожков, потому что один мы уже забрали, то есть вероятность — 214=17). Следовательно, ответ: 1*15*7=135 ≈ 0.03 (округляем до сотых, это обычно сказано в задании).

Задача 17 в ОГЭ по математике

Задание №17 — это номер на поиск площади фигуры. Формулы площади записаны в справочных материалах перед КИМом.

По формуле площади трапеции, ответ к заданию — 7 + 9 + 122*12 = 168.

Задача 18 в ОГЭ по математике

Задачи №18 в математике ОГЭ — это задания на поиск синуса, косинуса или тангенса угла. Это задание можно решить, достроив угол до прямоугольного треугольника.

Удобнее всего построить треугольник, нижняя сторона которого — две клеточки, а боковая — 4 клеточки. Тангенс угла — это отношение противоположного от угла катета (боковой достроенной стороны) к прилежащему (нижней стороне) к противоположному от угла (боковой достроенной стороны). То есть здесь тангенс — 42= 2. Ответ: 2.

Косинус — отношение прилежащего катета (нижней стороны) к гипотенузе, а синус — отношение дальнего (боковой стороны) к гипотенузе.

Таким образом, для решения любого задания достаточно знать программу, уметь использовать справочные материалы и немного логики. И всему этому легко можно научиться!

Макарычев.

Решебник с подробными пояснениями

Готовые домашние задания для 9 класса по алгебре Макарычева

Мало кто из школьников сейчас обходится без помощи решебника. Трудный учебный материал, отвлекающая обстановка на уроке, учитель который рассказывает новую тему быстро и без подробностей – все это становится причиной плохой успеваемости. А если еще пропустить несколько занятий, то без чьей-либо помощи нагнать пропущенное не получится.

В течение всего учебного года ГДЗ от Ответкина становится незаменимым помощником для учащегося и его родителей. Ведь наш сайт это не просто краткие ответы для списывания, но и подробные решения с комментариями, которые помогают восполнить пробелы в знаниях. Все пояснения к каждому номеру написаны понятным языком, содержат только конкретную информацию, которая нужна для усвоения темы. Поэтому школьник может быстро прояснить важные нюансы, с которыми не смог разобраться на уроке.

Почему готовые домашние задания от Ответкина лучше других решебников?

  • Уникальные подсказки с теорией. Наши решения содержат краткий ответ и подробные комментарии – все необходимое для того, чтобы понять алгоритм выполнения задачи. Все материалы перепроверены от опечаток, составлены учителями высшей квалификационной категории.
  • Только актуальные данные. Ответкин строго следит за тем, какие учебники используют сейчас в школах Российской Федерации, и составляет ГДЗ только по актуальным книгам. Поэтому школьникам не придется тратить лишнее время, чтобы найти нужный номер ответа. Нумерация решебника соответствует учебнику.
  • Удобный поиск по сайту. В любой момент, даже сидя на уроке, школьник может подсмотреть ответ на нашем сайте, зайдя в него с мобильного телефона. Для просмотра упражнения нужно всего лишь ввести номер примера в поисковую строку. Чтобы ученик быстро сориентировался в открытых материалах – мы выделили белым цветом короткий ответ, а разноцветным подробный.
  • Несколько вариантов ответа. Разные подходы к решению одной и той же задачи помогают понять сложную тему. Кроме того, имея доступ к нескольким вариантам ответа, школьник может доказать учителю, что понимает алгоритм выполнения задания.

Наше пособие с комментариями лучше не только других решебников, но и видео ответов. Чтобы узнать решение ученику приходится слушать 5-10 минут монотонной речи, в которой еще нужно выделить конкретную информацию под запись. Но поиск ответа на нашем сайте занимает считанные секунды. При этом пользователь получает качественную помощь бесплатно.

Уникальные подробные решения с пояснениями Ответкина

Алгебра – один из непростых школьных предметов и в 9 классе она входит в число экзаменов государственной итоговой аттестации. В течение учебного года школьникам придется освоить разный по содержанию материал. Им предстоит расширить свои знания об уравнениях и неравенствах, свойствах функций, познакомиться с понятием арифметической прогрессии, комбинаторики, теории вероятности.

Чтобы успешно сдать ГИА, девятиклассникам нужно выучить материал текущего учебного года и вспомнить все изученное по программе за 7-8 класс. С этой сложной задачей школьникам поможет справиться Ответкин. Он разрешит затруднения, возникающие при подготовке домашних заданий, подскажет верное решение на уроке. Также учащиеся могут использовать наш сайт для повторения изученного материала, лучшего понимания сложных тем.

Уже не только школьники, но их родители предпочитают Ответкина занятиям с репетитором. Почему так происходит?

  • Это удобно и бесплатно. Дорога к репетитору занимает много времени и сил, его консультация стоит денег. Но наш сайт помогает школьникам подтянуть успеваемость быстро и бесплатно. Кроме того, доступ к подсказкам и готовым ответам круглосуточный, а к репетитору можно обратиться только во время дополнительного занятия, а потом снова ждать 3-5 дней до следующего урока.
  • Появляется свободное время. Как и школьный урок, дополнительные занятия, как правило, длятся 45 минут, а иногда даже целый час. В условиях огромной загруженности в 9 классе это проблематично, но с помощью Ответкина ученик быстро находит нужное решение, проверяет правильность выполнения домашнего задания, проясняет для себя непонятные моменты с помощью чтения комментариев. Остается свободное время, чтобы отдохнуть и расслабиться.
  • Развивается самостоятельность. Как правило, в старших классах детей раздражает чрезмерная опека их родителей, в том числе и стремление окружить отстающего школьника репетиторами. Посредством ГДЗ девятиклассник может сам исправить плохие оценки, подтянуть общую успеваемость, разобраться с темами, пропущенными из-за отсутствия в школе.

Плюс ко всему, далеко не каждый репетитор является профессионалом, умеет простыми словами доносить сложный материал. В создании наших учебных пособий с комментариями принимали участие учителя высшей квалификационной категории. Они подобрали только нужную конкретную информацию по каждой теме, чтобы школьники смогли разобраться в решении задач быстро и без затруднений.

Как пользоваться сайтом и открыть ответы с пояснениями?

Интерфейс Ответкина простой и понятный, чтобы найти нужное решение, достаточно ввести в строку быстрого поиска номер упражнения и пользователю сразу откроется краткий вариант ответа. Чтобы увидеть подробные комментарии с алгоритмом выполнения задачи, потребуется пройти регистрацию. Сделать это можно двумя способами:

Способ 1. Выберите удобную для вас социальную сеть и авторизуйтесь через нее. Для этого нажмите рядом с кнопкой «Войти» значок Вконтакте, гугл аккаунт или любой другой, который вам предложен. Согласитесь с правилами пользования сайтом, подтвердите вход. После этого вы сможете автоматически заходить на Ответкин через выбранную социальную сеть.

Способ 2. Впишите в специально отведенное для этого поле адрес вашей почты. Зайдите в ваш почтовый ящик, откройте письмо со ссылкой активизации аккаунта и пройдите по ссылке.

После регистрации вы получите доступ в личный кабинет. В нем увидите ваши открытые решения, а также количество оставшихся ответов на сегодняшний день. Вы сможете быстро переходить от одного открытого задания к другому, что позволит вам сэкономить время.

В каждые сутки вы можете бесплатно открыть ГДЗ к трем любым заданиям. Их можно просматривать сколько угодно раз в течение 24 часов. Чтобы получить большее количество открываний в день нужно оформить платную подписку за символическую сумму. С подробной информацией по тарифам и срокам действия платной подписки можно ознакомиться в личном кабинете.

Решебник алгебры девятого класса к учебнику алгебры Макарычева, Миндюка, Нешкова и Суворова

Готовые домашние задания с комментариями для 9 класса составлены на основе учебника Макарычева 2014 года. Он рекомендован Министерством образование и науки Российской Федерации для всех общеобразовательных организаций. Номера упражнений в решебнике соответствуют нумерации учебника.

Программа алгебры 9 класса содержит 5 глав, разбитых на 13 параграфов и 36 тем. Задачи, включенные в каждый пункт учебника, расположены по принципу нарастания трудности. В качестве основных и дополнительных упражнений есть усложненные примеры. Для помощи отстающим ученикам в учебнике имеется особый раздел: «Сведения из курса алгебры 7-8 классов». Более подготовленным школьникам предлагаются необязательные задания из рубрики: «Для тех, кто хочет знать больше».

ГДЗ от Ответкина помогает девятиклассникам с освоением следующих тем и понятий:

  1. Понятие квадратичной функции, ее свойства, область определения и значений. Графики квадратичной функции и методы их построения. Квадратичный трехчлен, его корни, разложение его на множители.
  2. Степенная функция, ее корень.
  3. График дробно-линейной функции.
  4. Степень с рациональным показателем.
  5. Уравнения с одной и двумя переменными. Корни целого уравнения и приемы его решения. График уравнения с двумя переменными, его построение. Решение систем уравнений второй степени. Использование систем уравнений второй степени для решения задач.
  6. Неравенства с одной и двумя переменными. Системы неравенств. Решение неравенств методом интервалов. 
  7. Арифметическая прогрессия, ее понятие, формула N-го члена арифметической прогрессии. Формулы суммы первых членов арифметической прогрессии. Метод математической индукции.
  8. Геометрическая прогрессия, ее понятие, формула N-го члена геометрической прогрессии. Формулы суммы первых членов геометрической прогрессии.
  9. Элементы комбинаторики. Параметры комбинаторных задач. Размещения, сочетания, перестановки.
  10. Первое знакомство с теорией вероятности. Ее понятие. Сложение и умножение вероятностей. Вероятность разных событий с равной долей возможности. Относительная частота случайного события.

Кроме того, для успешной сдачи итогового экзамена по алгебре, девятиклассникам предстоит повторить упражнения за 7-8 класс. В этом непростом деле им опять же поможет Ответкин, где есть не только решения задач, но и подробные к ним объяснения.

Мы надеемся, что наш сайт поможет вам не только повысить успеваемость и восполнить пробелы в знаниях по алгебре, но и полюбить этот сложный предмет. Не забудьте просмотреть наши готовые домашние задания и по другим школьным предметам, например, физике и русскому языку.

Популярные решебники

ГДЗ по Алгебре 9 класс: Макарычев Ю.Н.

Издатель: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2014-2022г.

ГДЗ по Алгебре 9 класс: Мордкович А.Г.

Издатель: А.Г. Мордкович, Л.А. Александрова, Т.Н. Мишустина – 2010-2017г.

ГДЗ по Алгебре 9 класс: Мерзляк А.Г.

Издатель: А.Г. Мерзляк. Вентана-Граф, 2014-2021г.

Департамент начального и среднего образования штата Миссури

 

 

Новости математики!

  • Информацию, возможности для работы по оценке, ресурсы, материалы и записи презентаций с собраний по математическому содержанию можно найти в Math Content Hub.
  • Обновлена ​​информация о калькуляторе для оценок MAP для учащихся с 6 по алгебру 2
    • Математические блоки
  • MO LEAP предоставляют мини-прогрессии, сложные задачи и ресурсы для открытия модулей, которые можно использовать с любой учебной программой округа.
  • В сотрудничестве с педагогами штата Миссури DESE выпустил приоритетные стандарты и ресурсы для поддержки обучения и ускоренного обучения учащихся.
  • Преподаватели математики штата Миссури будут собираться для проведения контентных занятий в течение 2022–2023 учебного года. Пожалуйста, ознакомьтесь с календарем учебных программ, чтобы зарегистрироваться на летние и учебные собрания по содержанию
  • Мы ищем учителей #STEM для 6-12 классов, которые демонстрируют глубокие знания предмета и способность мотивировать учащихся на успех. Если вы знаете учителя, который подходит под это описание, назовите его сегодня. Подробности можно найти в информации о наградах.
  • Обновление интерфейса! Следующая конференция по интерфейсу вернется к очной форме. Мы планируем провести собрание в конце сентября/начале октября в 2023 году. У нас не будет конференции в 2022-23 учебном году из-за нехватки времени и наличия помещений. Переход к проведению конференции осенью позволит сделать содержание более полезным для учителей.

Набор для разработки оценок

В рамках цикла разработки оценок DESE Assessment приглашает преподавателей штата Миссури принять участие в этом процессе, чтобы помочь поделиться опытом. Миссури всегда ищет педагогов для участия в этих встречах. Если вы хотите, чтобы вас рассматривали для участия в каких-либо будущих встречах по вопросам развития, пожалуйста, заполните онлайн-форму подачи заявок по адресу https://dese.mo.gov/form/assessment-meetings-interest. После завершения вы получите электронное письмо на личный адрес электронной почты, указанный для подтверждения отправки.

Основные ресурсы

Основные ресурсы

Спецификации предмета математики

В 2014 году законодатели штата Миссури приняли законопроект 1490 Палаты представителей, предписывающий разработку требований к обучению штата Миссури. В апреле 2016 года эти требования к обучению в штате Миссури были приняты Советом по образованию штата. Группы преподавателей штата Миссури со всего штата объединились для создания документов, необходимых для реализации этих ожиданий.

Одним из разработанных документов является документ со спецификацией предметов, который включает в себя все ожидаемые уровни/курсы штата Миссури, сгруппированные по областям/направлениям. Он определяет, что может быть измерено с помощью различных оценок. Документ служит основой процесса разработки оценки.

Хотя учителя могут использовать этот документ для уточнения ожиданий, эти спецификации предназначены для целей суммирования, сравнительного анализа и крупномасштабного оценивания.

Компоненты спецификации изделия включают:

  • Expectation Unwrapped раскрывает список четко очерченного содержания и навыков, которые учащиеся должны знать и уметь выполнять после освоения Expectation.
  • Потолок глубины знаний (DOK) указывает на самый высокий уровень когнитивной сложности, который обычно оценивается при крупномасштабном оценивании. Потолок DOK не предназначен для ограничения сложности обучения в классе.
  • Формат элемента указывает типы элементов, используемых в крупномасштабной оценке. Для каждого ожидания формат элемента указывает тип, который лучше всего подходит для этого конкретного ожидания.
  • Ограничения содержания/границы оценки — это параметры, которые составители заданий должны учитывать при разработке крупномасштабной оценки. Например, некоторые ожидания не должны оцениваться в рамках крупномасштабной оценки, а лучше подходят для локальной оценки.
  • Образцы стеблей — это примеры, которые относятся к конкретным элементам каждого ожидания и относятся к различным уровням DOK. Образцы основ, представленные в этом документе, никоим образом не предназначены для ограничения глубины и широты возможных основ элементов. Ожидание следует оценивать по-разному.
  • Калькулятор Обозначение указывает, будет ли доступен калькулятор для тестовых вопросов, составленных в соответствии с конкретными ожиданиями по крупномасштабному оцениванию.
    Детский сад 6 класс
    Класс 1 7 класс
    2 класс 8 класс
    3 класс Алгебра I
    4 класс Алгебра II
    5 класс Геометрия

Расширенная версия требований по математике для классов и курсов

Следующие документы, ссылки на которые приведены ниже, были созданы преподавателями штата Миссури, чтобы предоставить классным руководителям более описательную версию ожиданий по математике для классов и курсов (GLE и CLE). Большая часть этой работы исходила от комитетов, которые разработали новые ожидания; однако многие другие педагоги прочитали их и внесли свой вклад в них. Пожалуйста, помните, что это документы по разработке учебного плана, а не ресурс для оценивания. Кроме того, приведенные примеры и списки не являются исчерпывающими и не предназначены для ограничения работы, выполняемой в классах штата Миссури, или разработки оценивания.

Несмотря на то, что комитеты приложили все усилия, чтобы дать четкое представление о том, чего учащиеся ожидают от обучения, иногда может быть трудно установить, что именно имел в виду комитет. Эти документы снимут некоторые вопросы, неизбежно возникающие при обнародовании новых ожиданий.

В приведенном ниже примере, который иллюстрирует организацию документов, в левой части перечислены официальные GLE или CLE по порядку. Правая сторона — расширенное ожидание.

Код MLS

Формулировка фактического ожидания

Расширенное ожидание

5. NF.A.3

Сравните и упорядочите дроби и/или десятичные знаки до тысячных, используя символы >, = или <, и обоснуйте решение.

Студент должен сравнивать и упорядочивать дроби или десятичные числа с точностью до тысячных, рассуждая об их размере. Запишите результаты сравнений символами >, = или < и обоснуйте выводы. ( например, с использованием эталонов, числовых линий, манипуляций или рисунков)

Читатель найдет примеры, когда исходная и расширенная версии совпадают. В этих случаях было установлено, что ожидания были ясными, и любое дополнительное описание могло нанести ущерб или ограничить первоначальные намерения комитета.

Это рабочие документы, и авторы призывают читателей разработать свои собственные примеры и списки, чтобы воплотить эти математические ожидания в жизнь в своих классах. Также обратите внимание, что эти документы по разработке учебных программ могут быть обновлены в будущем, чтобы включить более подробную информацию или уточнения предполагаемого обучения учащихся.

ОЖИДАНИЯ ОТ УРОВНЯ
  • Детский сад – Расширенные ожидания PDF | Слово
  • Класс 1 – Расширенные ожидания PDF | Ворд
  •  2 класс – Расширенные ожидания PDF | Ворд
  •  3 класс – Расширенные ожидания PDF | Ворд
  • Класс 4 – Расширенные ожидания PDF | Ворд
  •  5 класс – Расширенные ожидания PDF | Ворд
  •  6 класс – Расширенные ожидания PDF | Ворд
  •  7 класс – Расширенные ожидания PDF | Ворд
  •  8 класс – Расширенные ожидания PDF | Слово
ОЖИДАНИЯ ОТ УРОВНЯ КУРСА
  • Алгебра 1 – Расширенные ожидания PDF | Ворд
  • Геометрия – Расширенные ожидания PDF | Ворд
  • Алгебра 2 – Расширенные ожидания PDF | Ворд

 

Дескрипторы уровня производительности (PLD)

КАРТА PLD УРОВНЯ СОСТОЯНИЯ
  • Детский сад
  • Класс 1
  • 2 класс
  • Класс 3
  • Класс 4
  • 5 класс
  • 6 класс
  • 7 класс
  • 8 класс
КОНЕЦ КУРСОВ PLD
  • Алгебра 1
  • Алгебра 2
  • Геометрия
Дополнительные ресурсы

Оцененные стандарты

Пересмотренные стандарты, утвержденные 19 апреля 2016 года, подлежат внедрению с 2016-2017 учебного года. Они будут оцениваться с 2017-2018 учебного года.

Математика – К-5: К-5 PDF | K-5 Word
Математика – 6-12: 6-12 PDF | 6-12 Word
Математика – K-12: K-12 Excel 

Дополнительные ресурсы

  • Математические пешеходные переходы: K | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Алгебра 1 | Алгебра 2 | Геометрия
  • 2020–2021 Схемы оценивания на уровне классов 
  • 2020-2021 Чертежи EOC

Математические ресурсы MLS

  • Справочник по математике в конце курса 
  • Справочник по математике 3-5
  • Справочник по математике 6-8 

Математические практические формы

3 класс
  • Математическая бумага/карандаш
  • Математика Крупный шрифт
  • Руководство по подсчету очков по математике
Класс 4
  • Математическая бумага/карандаш
  • Математика Крупный шрифт
  • Руководство по подсчету очков по математике
Класс 5
  • Математическая бумага/карандаш
  • Математика Крупный шрифт
  • Руководство по подсчету очков по математике
Класс 6
  • Математическая бумага/карандаш
  • Математика Крупный шрифт
  • Руководство по подсчету очков по математике
Класс 7
  • Математическая бумага/карандаш
  • Математика Крупный шрифт
  • Руководство по подсчету очков по математике
8 класс
  • Математическая бумага/карандаш
  • Математика Крупный шрифт
  • Руководство по подсчету баллов по математике 
Формы практики EOC
  • Алгебра I
  • Геометрия
  • Алгебра II
Презентации

Презентации

Математические материалы собраний и записи в Math Hub

Обновления о внедрении стандартов обучения математике штата Миссури

  • Обновление учебного плана и оценки, январь 2019 г.
  • Обновление оценки 20 сентября 2018 г.
Профессиональное обучение

Профессиональное обучение

собрания по математическому содержанию на 2021–2022 годы пройдут в сентябре, ноябре, январе и марте. В этом году мы планируем виртуальные сессии. Вот ссылка на календарь учебной программы: https://dese.mo.gov/college-career-readiness/curriculum#Calendar, чтобы зарегистрироваться на эти встречи. В каждом из этих месяцев будет K-5, 6-12 и сессия обновления оценки.

Математические материалы собраний и записи в Math Hub.

Пожалуйста, свяжитесь с Chip Sharp по адресу [email protected], если у вас возникнут вопросы или для получения более подробной информации.

Карты расширенного обучения (ELM)

Воспользуйтесь возможностью бесплатного профессионального развития! Департамент начального и среднего образования штата Миссури набирает заинтересованных учителей для участия в проекте Enhanced Learning Maps (ELM) — инновационной программе, направленной на разработку и внедрение основанных на исследованиях учебных ресурсов по английскому языку и математике, преподаваемых во 2–8 классах. Для получения дополнительной информации позвоните в Управление подготовки к колледжу и карьере/учебной программе и оценке по телефону 573-751-3545 или перейдите по этой ссылке: https://bit.ly/2q6Jy47  

Интерфейс 2022 – изменение истории

Вот уже более тридцати лет конференция Interface является местом, где педагоги сотрудничают, чтобы улучшить преподавание математики и естественных наук для детей Миссури. Пожалуйста, подумайте о том, чтобы выступить на одном из главных профессиональных учебных мероприятий в Миссури. Не стесняйтесь пересылать это сообщение другим преподавателям, которые, по вашему мнению, также заинтересованы в предоставлении высококачественных презентаций.

Даты интерфейса 2022:
  • Вторник, 22 февраля – Четверг, 24 февраля 2022 г.
    * Интерфейсы A и B будут проводиться одновременно из-за виртуального характера этой конференции.
  • Информация о регистрации интерфейса 2022 г. — доступна осенью 2021 г.

При поддержке Департамента начального и среднего образования штата Миссури в сотрудничестве с Конференц-офисом MU

  • Контактный чип Sharp
Национальный совет учителей математики
Организации

Профессиональные математические организации

Преподавателям математики в штате Миссури жизненно важно быть активными учениками на протяжении всей жизни в области улучшения преподавания математики. Две характеристики того, кто учится на протяжении всей жизни, — это активное участие в профессиональных организациях и общение с другими профессионалами в своей области. Следующие организации, перечисленные ниже, могут оказать поддержку преподавателям математики. Пожалуйста, подумайте о том, чтобы стать активным участником одной или нескольких из этих групп. Если у вас есть вопросы, посетите их веб-сайты или свяжитесь с лицом, указанным для каждой группы.

Национальные математические организации
Национальный совет учителей математики (NCTM)
  • Веб-сайт: http://www. nctm.org/
Национальный совет наблюдателей математики (NCSM)
  • Членство: https://www.matedleadership.org/join/index.html
  • Миссури Руководитель группы: Мэрилин Кэннон [email protected]

Государственные математические организации
Совет учителей математики штата Миссури (MCTM)
  • Веб-сайт: https://www.moctm.org/
  • Контактное лицо: Синди Брайант, [email protected]

Совет по надзору за математикой штата Миссури (MoCSM)

Математическая лига американских регионов (ARML)
  • Веб-сайт: https://mathleague.org/arml/armlinvt.htm
  • Контактное лицо: Соня Лэнд, [email protected]

Математическая ассоциация штата Миссури по повышению квалификации учителей (MAT)2
  • Веб-сайт: https://sites.google. com/site/missourimatsquared/
  • Контактное лицо: Энн Маккой, [email protected]

Региональные математические организации

Преподаватели математики в Центральном Миссури (CM2E)

  • Веб-сайт: http://www.ucmo.edu/math-cs/undergrad/mathed/educators.cfm
  • Контактное лицо: Энн Маккой, [email protected]
Учителя математики округа Канзас-Сити (KCATM)
  • Веб-сайт: www.kcatm.net/
  • Контактное лицо: Рита Баргер, [email protected]
Преподаватели математики Большого Сент-Луиса (MEGSL)
  • Веб-сайт: http://www.megsl.org/
  • Контактное лицо: Патрик Муни, [email protected]
Преподаватели математики Южно-Центрального Миссури (MESCM)
Ассоциация учителей математики округа Юго-Западный Миссури (SWMDAMT)
  • Веб-сайт: https://associations. missouristate.edu/SWMDAMT/
  • Контактное лицо: Джесси Хиетт, [email protected]
Дополнительные элементы образца

Дополнительные элементы образца

Класс 1
  • Смысл числа и операции с основанием 10
    • 1.NBT.A.4 Пример 1
    • 1.NBT.B.5 Пример 1
    • 1.NBT.B.6 Примеры 1 и 2
    • 1.NBT.B.7 Примеры 1 и 2
  • Числовой смысл и операции
    • 1.NS.A.2 Пример 1
  • Отношения и алгебраическое мышление
    • 1.RA.A.1 Пример 1
    • 1.RA.A.1 Примеры 2 и 3
3 класс
  • Данные и статистика
    • 3.DS.A.2 Пример 1 
    • 3.DS.A.4 Пример 1
  • Геометрия и измерения
    • 3.GM.A.2 Пример 1 
    • 3.GM.A.3 Пример 1
    • 3.GM.B.4 Пример 1
    • 3.GM.B.4 Пример 2 
    • 3.GM.B.5 Пример 1 
    • 3. GM.B.6 Пример 1 
    • 3.GM.B.6 Пример 2 
    • 3.GM.B.8 Пример 1
    • 3.GM.C.9 Пример 1 
    • 3.GM.C.10 Пример 1
    • 3.GM.C.11 Пример 1
    • 3.GM.C.11 Пример 2
    • 3.GM.C.12 Примеры 1, 2 и 3
    • 3.GM.C.12 Пример 4 
    • 3.GM.C.13 Примеры 1 и 2
    • 3.GM.C.14 Пример 1
  • Смысл чисел и операции с дробями
    • 3.NF.A.3 Пример 1
    • 3.NF.A.3 Пример 2
    • 3.NF.A.3 Пример 3
    • 3.NF.A.6 Пример 1
    • 3.NF.A.6 Пример 2
    • 3.NF.A.6 Пример 3
    • 3.NF.A.7 Пример 1
    • 3.NF.A.7 Пример 2
    • 3.NF.A.7 Пример 3
    • 3.NF.A.7 Пример 4
  • Отношения и алгебраическое мышление
    • 3.RA.D.10 Примеры 1 и 2
4 класс
  • Данные и статистика
    • 4.DS.A.1 Пример 1
    • 4.DS.A.2 Пример 1
  • Геометрия и измерения
    • 4. G.A.1 Пример 1
    • 4.GM.A.2 Пример 1
    • 4.GM.A.3 Пример 1
    • 4.GM.B.4 Пример 1
    • 4.GM.C.7 Пример 1
    • 4.GM.C.8 Пример 1
  • Смысл числа и операции с основанием 10
    • 4.NBT.A.1 Пример 1
    • 4.NBT.A.1 Пример 2
    • 4.NBT.A.2 Пример 1
    • 4.NBT.A.2 Пример 2
    • 4.NBT.A.3 Пример 1
    • 4.NBT.A.5 Пример 1
    • 4.NBT.A.5 Пример 2
    • 4.NBT.A.6 Пример 1
    • 4.NBT.A.6 Пример 2
    • 4.NBT.A.7 Примеры 1 и 2
  • Смысл чисел и операции с дробями
    • 4.NF.A.1 Пример 1
    • 4.NF.A.1 Пример 2
    • 4.NF.A.1 Пример 3
    • 4.NF.A.1 Примеры 4 и 5
    • 4.NF.A.1 Пример 6
    • 4.NF.A.1 Примеры 7 и 8
    • 4.NF.A.2 Пример 1
    • 4.NF.A.2 Пример 2
    • 4.NF.A.2 Примеры 3 и 4
    • 4.NF.A.2 Пример 5
    • 4.NF.A.2 Пример 6
    • 4.NF.A.3 Пример 1
    • 4.NF.A.3 Пример 2
    • 4. NF.B.5 Пример 1
    • 4.NF.B.5 Пример 2
    • 4.NF.B.6 Пример 1
    • 4.NF.B.6 Пример 2
    • 4.NF.B.7 Примеры 1 и 2
    • 4.NF.B.8 Пример 1
    • 4.N.C.9 Пример 1
    • 4.NF.C.9 Пример 2
    • 4.NF.C.10 Пример 1
    • 4.NF.C.10 Пример 2
    • 4.N.C.10 Пример 3
    • 4.N.C.11 Пример 1
    • 4.NF.C.11 Пример 2
    • 4.NF.C.11 Пример 3
    • 4.N.C.11 Пример 4
    • 4.NF.C.12 Пример 1
    • 4.N.C.12 Пример 2
    • 4.NF.C.12 Пример 3
    • 4.N.C.12 Пример 4
    • 4.NF.C.12 Пример 5
  • Отношения и алгебраическое мышление
    • 4.RA.B.4 Пример 1
    • 4.RA.C.6 Пример 1
    • 4.RA.C.7 Пример 1 
5 класс
  • Геометрия и измерения
    • 5.G.A.3 Пример 1
  • Смысл числа и операции с основанием 10
    • 5.NBT.A.1 Примеры 1 и 2
    • 5.NBT.A.3 Пример 1
    • 5. NBT.A.3 Пример 2
    • 5.NBT.A.4 Примеры 1 и 2
    • 5.NBT.A.7 Пример 1
    • 5.NBT.A.8 Пример 1
    • 5.NBT.A.8 Пример 2
  • Смысл чисел и операции с дробями
    • 5.NF.A.2 Пример 1
    • 5.NF.A.2 Пример 2
    • 5.NF.A.2 Пример 3
    • 5.NF.A.3 Примеры 1 и 2
    • 5.NF.A.3 Пример 3
    • 5.NF.A.3 Примеры 4 и 5
    • 5.NF.A.3 Пример 6
    • 5.NF.B.4 Примеры 1 и 2
    • 5.NF.B.4 Примеры 3, 4 и 5
    • 5.NF.B.4 Пример 6
    • 5.NF.B.5a Пример 1
    • 5.NF.B.5b Примеры 1 и 2
    • 5.NF.B.5b Пример 3
    • 5.NF.B.5b Пример 4
    • 5.NF.B.5c Пример 1
    • 5.NF.B.5c Пример 2
    • 5.NF.B.5c Примеры 3 и 4
    • 5.NF.B.5c Пример 5
    • 5.NF.B.5d Примеры 1 и 2
    • 5.NF.B.5d Примеры 3 и 4
    • 5.NF.B.5d Пример 5
    • 5.NF.B.5d Пример 6
    • 5.NF.B.6 Пример 1
    • 5.NF.B.6 Пример 2
    • 5.NF.B.7b Примеры 1 и 2
  • Отношения и алгебраическое мышление
    • 5. RA.A.1 Пример 1
    • 5.RA.C.5 Примеры 1, 2 и 3
6 класс
  • Анализ данных, статистика и вероятность
    • 6.DSP.A.1 Пример 1
  • Выражения, уравнения и неравенства
    • 6.EEI.A.1 Пример 1
    • 6.EEI.A.1 Пример 2
    • 6.EEI.A.2a Пример 1
    • 6.EEI.A.2a Пример 2
    • 6.EEI.A.2b Пример 1
    • 6.EEI.A.2b Пример 2
    • 6.EEI.A.2c Пример 1
    • 6.EEI.A.2c Пример 2
    • 6.EEI.A.2c Пример 3
    • 6.EEI.A.2e Пример 1
    • 6.EEI.A.3 Пример 1
    • 6.EEI.A.3 Пример 2
    • 6.EEI.A.3 Пример 3
    • 6.EEI.B.4 Примеры 1, 2 и 3
    • 6.EEI.B.4 Пример 4
    • 6.EEI.B.4 Пример 5
    • 6.EEI.B.4 Пример 6
    • 6.EEI.B.4 Пример 7
    • 6.EEI.B.5 Примеры 1 и 2
    • 6.EEI.B.5 Пример 3
    • 6.EEI.B.5 Пример 4
    • 6.EEI.B.5 Пример 5
    • 6.EEI.B.6 Пример 1
    • 6.EEI.B.6 Пример 2
    • 6. EEI.B.7 Пример 1
    • 6.EEI.B.7 Пример 2
    • 6.EEI.B.8a Пример 1
    • 6.EEI.B.8b Пример 1
    • 6.EEI.C.9a Пример 1
    • 6.EEI.C.9a Пример 2
    • 6.EEI.C.9a Пример 3
    • 6.EEI.C.9b Пример 1
    • 6.EEI.C.9b Пример 2
  • Геометрия и измерения
    • 6.G.A.1 Пример 1
    • 6.GM.A.2a Пример 1
    • 6.GM.A.3c Пример 1
    • 6.GM.A.4b Примеры 1 и 2
  • Числовой смысл и операции
    • 6.NS.C.6c Примеры 1, 2 и 3
  • Соотношения и отношения пропорциональности
    • 6.RP.A.1 Пример 1
    • 6.RP.A.2 Пример 2
    • 6.RP.A.3a Пример 1
    • 6.RP.A.3a Пример 2
    • 6.RP.A.3c Пример 1
    • 6.RP.A.3d Пример 1
7 класс
  • Анализ данных, статистика и вероятность
    • 7.DSP.C.5b Пример 1
    • 7.DSP.C.8a Пример 1
    • 7.DSP.C.8b Пример 1
  • Выражения, уравнения и неравенства
    • 7. EEI.A.1 Пример 1
    • 7.EEI.A.2 Пример 1
    • 7.EEI.B.4b Пример 1
    • 7.EEI.B.4c Пример 1
  • Геометрия и измерения
    • 7.GM.A.1 Пример 1
    • 7.GM.A.2a Примеры 1 и 2
    • 7.GM.A.2b Примеры 1 и 2
    • 7.GM.A.3 Пример 1
    • 7.GM.A.4a Пример 1
  • Числовой смысл и операции
    • 7.NS.A.2f Пример 1
    • 7.NS.A.2f Примеры 2, 3 и 4
    • 7.NS.A.3 Пример 1
  • Соотношения и отношения пропорциональности
    • 7.RP.A.1 Пример 1 
    • 7.RP.A.1 Пример 2
    • 7.RP.A.1 Пример 3
    • 7.RP.A.2c Пример 1
    • 7.RP.A.2d Пример 1
    • 7.RP.A.3 Пример 1
8 класс
  • Анализ данных, статистика и вероятность
    • 8.DSP.A.1 Пример 1
    • 8.DSP.A.2 Пример 1
  • Выражения, уравнения и неравенства
    • 8.EEI.A.1 Пример 1
    • 8. EEI.A.1 Пример 2
    • 8.EEI.A.2a Пример 1
    • 8.EEI.A.2b Пример 1
    • 8.EEI.A.2c Пример 1
    • 8.EEI.A.4b Пример 1
    • 8.EEI.B.5a Пример 1
    • 8.EEI.B.5a Пример 2
    • 8.EEI.B.5a Пример 3
    • 8.EEI.B.5b Пример 1
    • 8.EEI.B.5b Пример 2
    • 8.EEI.C.7a Примеры 1 и 2
    • 8.EEI.C.7b Примеры 1, 2 и 3
    • 8.EEI.C.8c Пример 1
    • 8.EEI.C.8d Пример 1
  • Функции
    • 8.F.B.4a Пример 1
    • 8.F.B.4b Пример 1
    • 8.F.B.4c Пример 1
  • Геометрия и измерения
    • 8.GM.A.1b Пример 1
    • 8.GM.A.3 Пример 1
    • 8.GM.A.4a Пример 1
    • 8.GM.B.6 Пример 1
    • 8.GM.B.7 Пример 1
    • 8.GM.B.8 Пример 1
  • Числовой смысл и операции
    • 8.NS.A.1a Пример 1
    • 8.NS.A.1b Пример 1
    • 8.NS.A.1c Пример 1
    • 8.NS.A.1d Пример 1
    • 8.NS.A.2 Пример 1
Алгебра 1
  • Строительные функции
    • A1. BF.A.1 Пример 1
    • A1.BF.A.1 Пример 2
    • A1.BF.A.1 Примеры 3 и 4
  • Создание уравнений и неравенств
    • A1.CED.A.1 Пример 1
    • A1.CED.A.1 Пример 2
    • A1.CED.A.2 Пример 1
    • A1.CED.A.2 Пример 2
    • A1.CED.A.3 Пример 1
    • A1.CED.A.3 Пример 2
    • A1.CED.A.3 Пример 3
    • A1.CED.A.3 Пример 4
    • A1.CED.A.4 Примеры 1 и 2
    • A1.CED.A.4 Пример 3
    • A1.CED.A.4 Пример 4
    • A1.CED.A.4 Пример 5
    • A1.CED.A.4 Пример 6
  • Данные и статистика
    • A1.DS.A.1 Примеры 1 и 2
    • A1.DS.A.2 Пример 1
    • A1.DS.A.3 Пример 1
    • A1.DS.A.5b Пример 1
    • A1.DS.A.6 Пример 1
  • Функции интерпретации
    • A1.IF.C.7 Пример 1
  • Линейные, квадратичные и экспоненциальные модели
    • A1.LQE.A.1a Пример 1
    • A1.LQE.A.1a Пример 2
    • A1. LQE.A.2 Пример 1
    • A1.LQE.A.2 Пример 2
    • A1.LQE.A.3 Пример 1
    • A1.LQE.B.4 Пример 1
    • A1.LQE.B.6 Пример 1
  • Номер и количество
    • A1.NQ.A.1 Пример 1
    • A1.NQ.B.3a Пример 1
    • A1.NQ.B.3d Пример 1
    • A1.NQ.B.4 Пример 1
    • A1.NQ.B.5 Пример 1
  • Видение структуры в выражениях
    • A1.SSE.A.1 Пример 1
    • A1.SSE.A.3a Пример 1
    • A1.SSE.A.3b Пример 1
    • A1.SSE.A.3b Пример 2
    • A1.SSE.A.3b Пример 3
Геометрия
  • Конгруэнтность
    • G.CO.A.1 Пример 1
    • G.CO.A.2 Пример 1
    • G.CO.C.8 Пример 1
    • G.CO.C.9 Пример 1
    • G.CO.C.9 Пример 2
    • G.CO.C.9 Пример 3
    • G.CO.C.10 Пример 1
  • Подобие, прямоугольные треугольники и тригонометрия

    • G.SRT.A.3 Пример 1

Алгебра 2
  • Арифметика с полиномами и рациональными выражениями
    • A2. 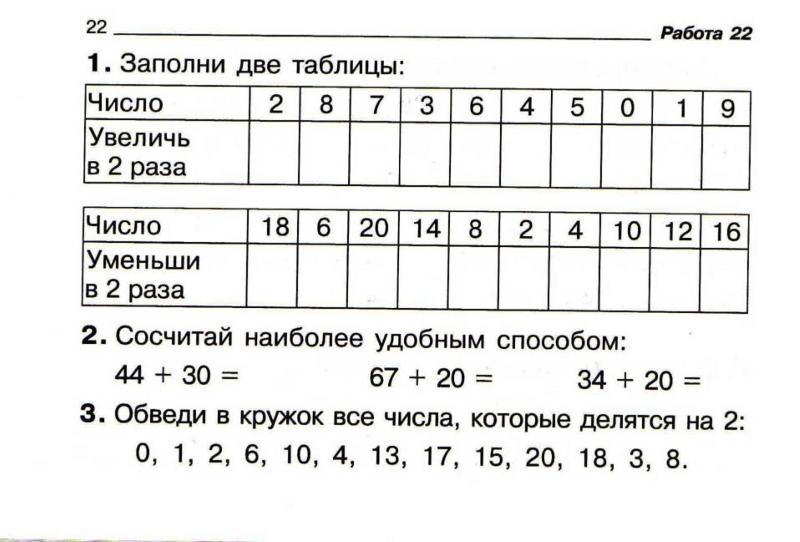APR.A.2 Пример 1
    • A2.APR.A.2 Пример 2
    • A2.APR.A.3 Пример 1
    • A2.APR.A.4 Пример 1
  • Строительные функции
    • A2.BF.A.1 Пример 1
    • A2.BF.A.1 Пример 2
    • А2.БФ.А.2. Пример 1
    • A2.BF.A.2 Пример 2
  • Моделирование с помощью функций или функций и моделирования
    • A2.FM.A.1 Пример 1
    • A2.FM.A.1 Пример 2
  • Функции интерпретации
    • A2.IF.A.2 Пример 1
  • Номер и количество
    • A2.NQ.B.5 Пример 1
    • A2.NQ.B.6 Пример 1
  • Рассуждения с уравнениями и неравенствами
    • A2.REI.A.2 Пример 1
    • A2.REI.A.2 Пример 2
    • A2.REI.B.3 Пример 1
  • Просмотр структуры в функциях выражений
    • A2.SSE.A.3 Пример 1
    • A2.SSE.A.3 Пример 2
    • A2.SSE.A.4 Пример 1
Опубликованы оцениваемые события производительности

Опубликованы оцениваемые события производительности

3 класс 4 класс
5 класс 6 класс
7 класс 8 класс

 

Способ удовлетворения потребностей ряда способностей в одном классе – обучение сейчас

 

Дифференцированная задача – это вопрос или действие, которое допускает несколько точек входа, а также несколько способов решения. Одной из целей использования дифференцированных задач является удовлетворение потребностей учащихся с разным уровнем способностей, которые мы часто встречаем на одном математическом уроке. Традиционные рабочие листы часто требуют, чтобы учащиеся сосредоточились на решении процедур, и вопросы обычно имеют одинаковый уровень сложности. См. пример ниже:

В этом примере у нас есть рабочий лист для сложения двузначных чисел. Если учащийся еще не понимает эту концепцию, он даже не сможет начать работу с рабочим листом, а те, кто знает, как складывать двузначные числа, будут работать на процедурном уровне для всего рабочего листа (и в в этом случае, поскольку они сложены, скорее всего, будет выполняться только сложение цифр, а не сложение чисел).

Кроме того, у вас, вероятно, будут студенты, которые очень быстро выполняют процедуру, и поэтому они будут выполнены до того, как вы даже успеете помочь тем, кто не имеет понятия, как начать (и этим студентам может даже не понадобиться это дополнительная практика того, что они уже умеют делать хорошо). Я уверен, что многие учителя могут относиться к этому сценарию; мы часто спешим помочь тем, кто не может даже начать, и пытаемся помочь случайному студенту, который «застревает» на определенном вопросе, и прежде чем мы успеваем даже пройти через всех студентов, которым нужна помощь, есть много которые закончили рабочий лист и нуждаются в указании, что делать дальше.

Почему следует использовать дифференцированные задачи?

Когда я использую дифференцированные задачи, многие из упомянутых выше проблем исчезают. Дополнительным преимуществом использования дифференцированных заданий является то, что учащиеся работают не только над своей процедурной беглостью, но и развивают более глубокое концептуальное понимание математических понятий. Кроме того, они на самом деле складывают числа, а не просто складывают цифры, и поэтому у них развивается более сильное чувство числа. Эти задачи достаточно открыты, чтобы даже учащийся, который не занимается математикой на уровне своего класса, все же мог получить доступ к вопросу и развить свои математические навыки.

Например, если мы посмотрим на дифференцированную задачу «два числа имеют сумму 82, какими могут быть эти два числа?» возможным решением может быть 81+1 = 82. Учащиеся, которые еще не понимают, как складывать двузначные числа, могут решить эту задачу, прибавив двузначное число к однозначному числу. Хотя мы еще не работаем над навыком (сложение двузначных чисел), к которому стремимся, я бы предпочел, чтобы мои ученики были заняты решением задачи и развитием своих математических навыков, а не просто сидели с поднятыми руками в ожидании помощи. Поскольку мы работаем над навыком сложения двузначных чисел, я бы посоветовал своим ученикам попытаться найти как можно больше решений, используя двузначные числа.

Те учащиеся, которые уже имеют четкое представление о том, как складывать двузначные числа, могут искать закономерности или решать параллельную задачу, например, «сложить два двузначных числа, сумма которых равна 82 и одна числа имеет семерку вместо единицы». Использование этого типа заданий вовлекает всех учащихся в вашем классе, независимо от их текущего уровня способностей или набора навыков, и предназначено для того, чтобы бросить им вызов на их уровне.

Мне также нравится использовать эти типы заданий, потому что учащиеся должны думать о размерах чисел, которые они будут использовать, а не просто следовать процедуре (кстати, многие даже не понимают, почему она работает). . При работе с дифференцированной задачей, подобной этой, учащиеся также могут работать в своем собственном темпе; те, кто думает глубоко, или обрабатывает медленнее, или пишет медленнее, все еще учатся, и их не наказывают за то, что они не так быстры, и тех, кто работает быстрее.

Цель состоит в том, чтобы учащиеся поняли и смогли применить концепцию сложения двузначных чисел, и это понимание не происходит с одинаковой скоростью или одинаковым образом для каждого учащегося, поэтому имеет смысл разрешить разные подходы и разное количество практических вопросов.

Могу ли я потратить целый урок на один вопрос?

Может показаться странным тратить 40 минут на работу над одним вопросом, но я считаю, что мои ученики много думают, учатся и практикуются, пока ищут решения. Я также замечаю, что мои ученики лучше понимают концепцию, когда я выполняю дифференцированное задание, а не рабочий лист в традиционном стиле. Важно обсудить, как учащиеся решают задачу, поскольку они, как правило, придумывают множество творческих стратегий для решения проблемы, а их сверстникам может быть полезно изучить несколько подходов к одной и той же проблеме.

Ко мне часто приходят ученики и записывают свои решения на доске. Затем мы проверяем решения и проверяем их правильность. Это очень расширяет возможности учащихся, особенно тех, кто традиционно плохо успевал по математике. Студентам нравится иметь уникальные решения, и это положительный опыт обучения, когда есть много правильных ответов. Для учащихся также ценно увидеть и услышать различные подходы, которые использовали их сверстники при решении проблемы. Эти типы вопросов требуют больше размышлений, а не просто действий, и, как мы знаем, математика должна быть комбинацией того и другого.

Дифференцированные задачи, которые вы можете использовать в классе

Ниже вы найдете несколько примеров дифференцированных задач для некоторых из наиболее основных операций с целыми числами. Со временем и практикой вы сможете создавать свои собственные дифференцированные задачи, основанные на математической концепции, над которой вы работаете. Несколько советов, которые могут помочь вам начать работу:

1. Дайте учащимся ответ и операцию и попросите их составить вопросы

2. Укажите диапазон чисел, которые можно использовать в вопросе о сальсе (это способ, которым учащиеся могут легче выбирать более сложные числа в зависимости от их текущего уровня навыков)

3. Создайте рабочий лист, опустив часть вопроса и дав ответ. (См. примеры вопросов ниже – обратите внимание, что вопросы, отмеченные звездочкой, имеют более одного возможного решения)

Сложение целых чисел

Дифференцированная задача: сумма двух чисел равна 873. Какими могут быть эти два числа?

В этом задании так много разных ответов, и для некоторых учеников оно может быть слишком простым, потому что 872+ 1 будет достаточно. Если вы хотите, чтобы они отработали навык сложения многозначных чисел, вы можете попробовать выполнить такие задания:

1. ) Дифференцированное задание: Сложите 2 трехзначных числа, сумма которых равна 873. Какими могут быть эти два числа? Найдите как можно больше решений.

2.) Дифференцированное задание: Сложите 2 многозначных числа, сумма которых равна 873. Какими могут быть эти два числа? Найдите как можно больше решений.

3.) Параллельная задача: сложите 2 трехзначных числа, сумма которых равна 873 и в одном из чисел вместо единицы стоит девятка. Какими могут быть эти два числа? Найдите столько, сколько сможете. Вы видите закономерность?

4.) Параллельная задача: сложите 2 трехзначных числа, сумма которых равна 873 и одно из которых примерно в два раза больше другого. Какими могут быть эти два числа? Как вы решили это?

Подсказка: Использование блоков с основанием 10 значительно упрощает эту работу для большинства учащихся. Однако, если учащийся решает решать задачи символически, но затем застревает, вы можете попросить его использовать блоки Base 10 в качестве инструмента решения проблем или как способ «выйти из затруднительного положения».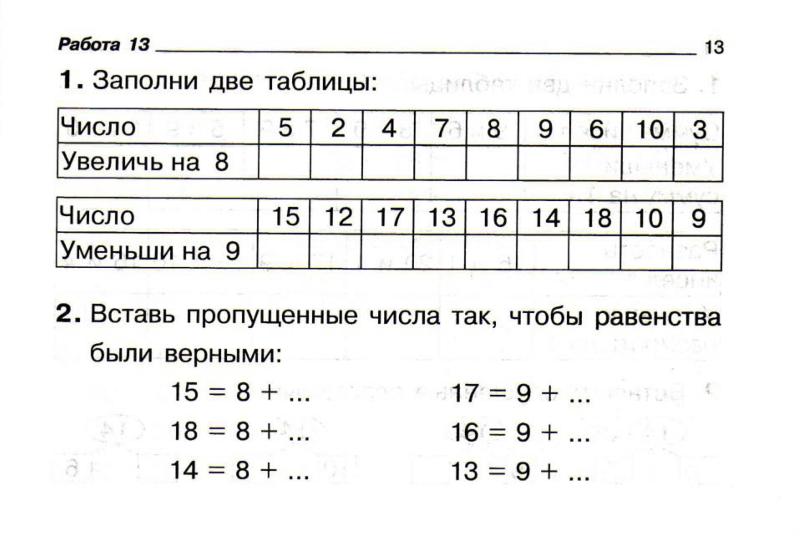

Задание, которое показывает, понимают ли ваши учащиеся контексты, в которых добавление является необходимой операцией для решения: Создайте задачу, которая будет решена путем вычисления 345 + 143.

Вычитание целых чисел

1.) Дифференцированное задание: вычитали 2 трехзначных числа, разница между которыми составляет 163. Какими могут быть эти два числа?

2.) Дифференцированное задание: вычитаются 2 многозначных числа, разница между которыми составляет 163. Какими могут быть эти два числа?

3.) Параллельная задача: вычтены 2 трехзначных числа, разница между которыми равна 163, но в одном из чисел вместо единицы стоит девятка. Какими могут быть эти два числа? Найдите не менее пяти различных решений. Видите ли вы закономерность среди решений?

4.) Дифференцированное задание: вычитаются 2 трехзначных числа, разница между которыми составляет 27. Какими могут быть эти два числа? Какую стратегию или стратегии вы использовали для решения этой проблемы? Найдите не менее пяти различных решений.

Задание, которое покажет вам, понимают ли ваши ученики контексты, в которых вычитание является необходимой операцией для решения: Создайте задачу, которая будет решена путем вычисления 817-286.

Умножение целых чисел

1.) Дифференцированная задача: Два числа имеют произведение 24, какими могут быть эти два числа? Найдите все возможные решения, используя целые числа.

2.) Дифференциальное задание: Площадь прямоугольника 36, какие могут быть размеры? Найдите как можно больше решений.

3.) Дифференцированные задачи: произведение двух чисел равно 196, какими могут быть эти два числа? Найдите как можно больше решений. Как вы решили это?

4.) Дифференцированное задание: Два двузначных числа имеют произведение от 400 до 600, какими могут быть числа? Найдите как можно больше решений. Какова была ваша стратегия поиска решений?

5.) Параллельная задача: Два числа имеют произведение от 400 до 600, какими могут быть числа? Найдите как можно больше решений. Какова была ваша стратегия поиска решений?

6.) Дифференцированное задание: несколько друзей скинулись равными суммами денег, чтобы купить подарок для своего учителя. Подарок стоит от 60 до 70 долларов. Сколько друзей внесли свой вклад и сколько денег вложил каждый? Найдите как можно больше разных решений — какие решения найти проще всего? Какую стратегию вы использовали?

Задание, которое покажет вам, понимают ли ваши ученики контексты, в которых умножение является необходимой операцией для решения: Создайте сюжетную задачу, которая будет решена путем решения 4×6.

Целое деление:

1.) Дифференцированное задание: у Дэвида есть от 400 до 600 долларов, он собирается разделить их поровну между своими детьми, сколько получит каждый ребенок и сколько детей у него может быть? Какие числа вы выбрали для облегчения работы? Какие числа вы бы выбрали для большей сложности?

2.) Параллельная задача: У Дэвида есть от 400 до 600 долларов, и он собирается разделить их поровну между тремя своими детьми.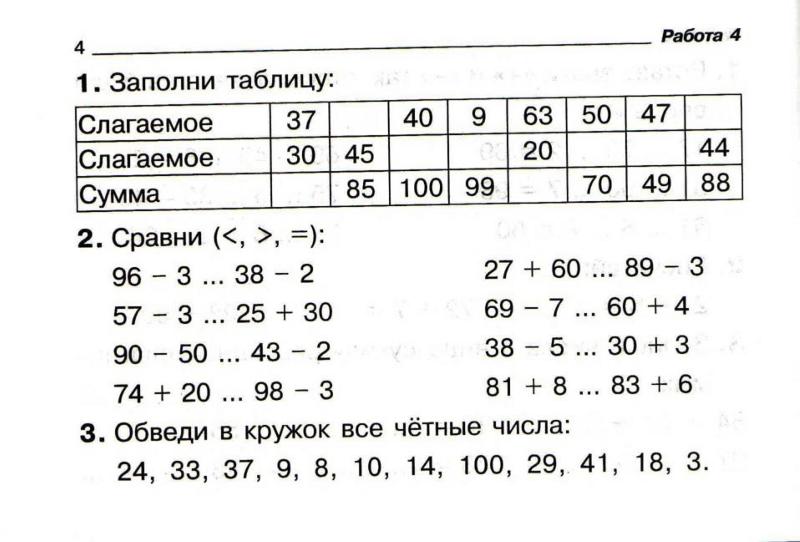 Сколько мог получить каждый ребенок? Какие числа вы выбрали для облегчения работы? Какие числа вы бы выбрали для большей сложности?

3.) Параллельная задача: у Дэвида есть 460 долларов, и он собирается разделить их поровну между тремя своими детьми. Покажите не менее двух различных способов выполнения этого деления. (Подсказка: попробуйте разбить 460 долларов разными способами, чтобы упростить деление на 3).

4.) Дифференцированное задание: У Джейми 75 игрушек, и он должен разделить их поровну с 6 детьми. Сколько игрушек получит каждый ребенок? Останутся ли игрушки?

Задание, которое покажет вам, понимают ли ваши ученики контексты, в которых деление является необходимой операцией для решения: Придумайте рассказ, который будет решаться с помощью 45 ÷ 6, и включите в свой рассказ, что означают все остатки.

Попробуйте!

Я призываю вас попробовать использовать некоторые дифференцированные задания и увидеть, услышать и почувствовать, чем они отличаются от традиционных рабочих листов и учебников. Не забудьте сказать своим ученикам, что цель состоит в том, чтобы углубить понимание, изучить закономерности и стратегии и проявить творческий подход! Пожалуйста, пишите и делитесь своим опытом (хорошим и плохим), чтобы мы все могли учиться друг у друга. Веселитесь с ним и посмотрите, куда он идет!

Educating Now был создан по просьбе учителей, чтобы Никки была их ежедневным тренером по математике. На сайте есть урок за уроком видеоуроки для учителей, которые помогут им подготовиться к следующему уроку математики и включить в свой класс манипуляции, дифференцированные задачи, игры и особый язык. Учителя, использующие сайт, могут улучшить вовлеченность и понимание учащихся, а также сэкономить время на подготовку, посмотрев 10-минутный видеоурок и загрузив подробный план урока.

Никки Лайнхэм

Моя миссия состоит в том, чтобы учителя были довольны своим влиянием на обучение учащихся. Я упрощаю для учителей подготовку и проведение уроков, которые изменят жизнь.

Математика в фокусе | K-8 Singapore Math Curriculum

Математики в первую очередь решают задачи. Когда дети не могут найти значение цифр и символов, решение проблем становится проблемой. Math in Focus ® : Singapore Math ® Маршалл Кавендиш ® помогает учащимся выучить язык математики. Благодаря практическому обучению, визуализации и графическим изображениям их понимание, уверенность и любовь к математике растут.

Math in Focus © 2020, американское издание высокоэффективной учебной программы Singapore Math ® , в которой представлены самые обширные изменения программы с момента ее первоначального выпуска 2009 года. Приведенный в соответствие с изменениями в учебной программе Сингапура и предлагающий учителям и учащимся беспрецедентный цифровой опыт, новый Math in Focus © 2020 en español обеспечивает полностью равноправный печатный и цифровой опыт на испанском языке.

Развивает понимание с помощью последовательного обучения с использованием конкретных изображений и абстрактных изображений.

Предоставляет учителям надежную, экономящую время и персонализированную цифровую среду.

Преподносит педагогику, лежащую в основе высоких достижений Сингапурской математики ® , американским учащимся.

Обзор

Обеспечение способности каждого учащегося осваивать концепции и применять математику

Использование передового мирового опыта и исследований для создания уникального подхода, основанного на мощных визуальных моделях, увлекательных практических занятиях и последовательном педагогическом подходе K–8, это решение позволяет учащимся развивать навыки критического мышления, позитивного отношения и уверенности в себе, необходимые для подготовки к достижениям.

  • Концептуализация
    Упор на конкретно-графический-абстрактный подход позволяет учащимся получить более глубокое концептуальное понимание с помощью практических манипуляций, диаграмм и моделей, а также абстрактных символов.

  • Постепенный выпуск
    Фокусные циклы «Занимайся-Узнай-Попробуй» в последней учебной программе Singapore Math ® представляют концепцию шаг за шагом, чтобы учащиеся могли легко ее усвоить.

  • Решение проблем
    Решение проблем занимает центральное место в обучении. Учащиеся ориентируются в приобретении и применении концепций и навыков для решения нестандартных, открытых и реальных проблем.

  • На конкретном этапе учащиеся используют практические манипуляции для изучения новых концепций.

  • Оттуда учащиеся переходят к этапу рисования, чтобы увидеть эти идеи, представленные в виде диаграмм, и узнать, как модели помогают продемонстрировать отношения между числами.

  • Наконец, учащиеся связывают свой конкретный опыт и графические представления с абстрактными символами, такими как числа.

Студенческий опыт

Математика в фокусе помогает обучающимся удовлетворять потребности отдельных учащихся с практическим обучением и визуальными моделями, которые поддерживают и оптимизируют обучение.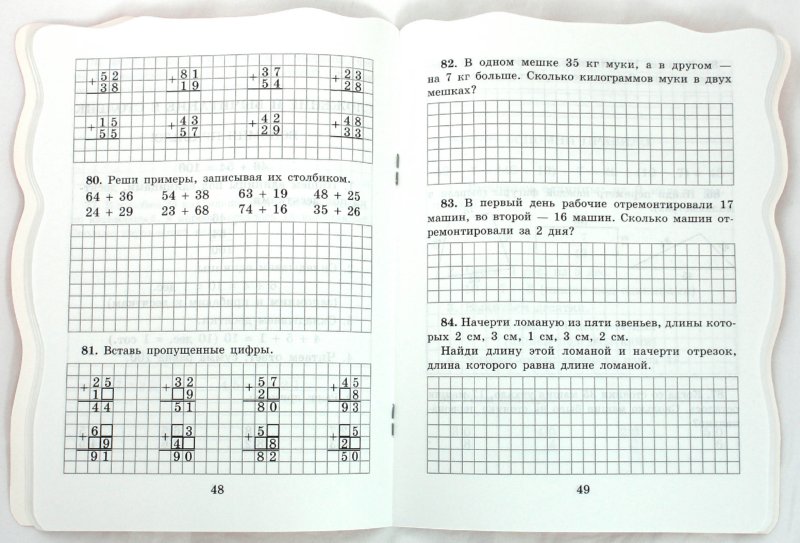

  • Визуальные модели, в том числе линейчатые модели, помогают учащимся развивать способность визуализировать математические ситуации, что является ключом к успешному решению задач.

  • Практические занятия и манипулятивные упражнения вовлекают учащихся и позволяют им конкретизировать концепции.

  • Ed , учебная платформа HMH предоставляет учащимся привлекательный интерфейс для прохождения тестов и взаимодействия с электронными книгами, обучающими видео, мини-играми и виртуальными манипуляциями.

Преподавательский опыт

Благодаря исчерпывающим и простым в использовании ресурсам, Math in Focus предоставляет учителям все необходимое для поддержки учащихся в развитии базовых знаний. Последовательный, четкий путь обучения способствует сосредоточению внимания на новом содержании и поощряет математическое мышление.

  • На каждом уроке предоставляется пошаговое планирование и поддержка обучения, а также встроенное профессиональное развитие.

  • Ресурсы для дифференциации для стремящихся, продолжающих и продвинутых учащихся, а также изучающих английский язык изложены в Изданиях для учителей и доступны для печати в Интернете.

  • Ряд формативных и итоговых оценок предлагает инструменты для измерения прогресса учащихся и оценки истинного мастерства, а также выявления пробелов в обучении и оказания дополнительной поддержки.

  • Math Solutions предоставляет встроенное обучение по запросу для поддержки в любое время для успешного первого года обучения, а также руководство по профессиональному обучению, доступное по номеру Ed .

  • НОВЫЙ «Уголок учителя» ™ обеспечивает дополнительный встроенный доступ к профессиональному обучению по запросу и поддержке преподавателей в любое время и в любом месте, включая советы коллег-учителей и живые мероприятия.

  • Math Solutions может предоставить поддержку, необходимую для развития вашей практики, с онлайн-коучингом, курсами и профессиональными обучающими сообществами.

Цифровой опыт

После более чем десятилетия оглушительного успеха в классах США, Math in Focus теперь является частью объединенного опыта преподавания и обучения HMH.

  • Connected Teaching and Learning
    С Ed , учебной платформой HMH, у вас будет доступ к аутентичным инструкциям Math in Focus , дополнительной поддержке, профессиональному обучению и оценке — все в одном месте с одним входом в систему .

  • Мониторинг успеваемости
    Постоянный доступ к данным, позволяющим действовать, автоматизированные инструменты группировки и составления отчетов обеспечивают мощный обзор успеваемости учащихся на основе показателей роста HMH.

  • Доступ: онлайн, оффлайн и на ходу
    HMH Go     ™ — это бесплатное обучающее приложение, которое соединяет учащихся и преподавателей с Math in Focus Контент и учебные ресурсы онлайн, офлайн или в пути.

Family Experience

Math in Focus предоставляет семьям и опекунам ресурсы, необходимые им для поддержки обучения учащихся, независимо от того, происходит ли оно дома или в школе.

  • Семейная комната

    , через вход учащегося в систему Ed, поддерживает разнообразные учебные среды и делает домашнее обучение более управляемым для семей и опекунов, предоставляя равные ресурсы по запросу для помощи учащимся.

  • Связи между школой и домом предусмотрены для каждой главы Math in Focus Classes K–5. В этом письме описаны мероприятия, которые учащиеся могут выполнять вне класса, которые соответствуют учебной программе, и определены основные цели обучения. Они доступны в дополнительных практических и домашних рабочих тетрадях, а также в виде цифровых ресурсов для печати.

  • Справочные листы для учащихся и родителей предназначены для помощи при входе в систему и навигации по ресурсам и заданиям Ed Math in Focus .

РЕЗУЛЬТАТЫ

Благодаря подходу CPA и визуализации учащиеся получают конкретное представление о математических концепциях, получая практический опыт, который создает истинное фундаментальное понимание.

Упражнения, в которых учащимся предлагается по-разному применять математические концепции и создавать альтернативные решения проблемы, поощряют критическое и творческое мышление и повышают мастерство.

Решение задач является неотъемлемой частью всех инструкций и обсуждений в Math in Focus . Учащиеся учатся применять различные стратегии, и им предлагается рассмотреть наилучшие стратегии для решения рутинных и нестандартных задач, чтобы развить сильные навыки решения проблем.

Программа Singapore Math ® признает роль, которую отношение играет в изучении математики, и помогает учащимся подходить к решению задач с интересом и энтузиазмом, укрепляя их уверенность в своих силах.

Ed, Учебная платформа HMH предоставляет учителям непрерывный доступ к действенным данным и инструментам отчетности, обеспечивая мощный взгляд на успеваемость учащихся.

Изучите инструкции в Математика в фокусе .

Предварительный просмотр онлайн

Исследования и результаты

Максимальная эффективность благодаря педагогике

Принципы, лежащие в основе подхода Singapore Math ® , основаны на фундаментальных исследованиях, в ходе которых были определены наиболее эффективные методы обучения математике. Результаты неоспоримы.

Сильный рейтинг ESSA

Math in Focus Школа получила рейтинг Strong ESSA на основе особого объема и качества профессионального обучения, которое учителя получают в рамках программы Math in Focus .

Критерии доказательств ESSA для Математика в фокусе K – 5

Читать сейчас

Основные исследования

Узнайте больше о развитии Math In Focus и педагогика, которая постоянно удерживает Сингапур на вершине международных исследований математических достижений.

Math in Focus ® : Singapore Math ® by Marshall Cavendish ® : База данных исследований

Демонстрирует обоснование

  • Тип отчета: База научных данных
  • Уровень оценки: Начальный, Средний

Математика в фокусе : Исследование эффективности, классы 3, 4 и 5

Демонстрирует обоснование

  • Тип отчета: Исследование эффективности, исследование, проведенное третьей стороной
  • Уровень оценки: элементарный
  • Область, край: Средний Запад, Северо-Восток
  • Район Урбанизация: Городской, Пригородный, Сельский

Математика в фокусе : Рандомизированное контрольное исследование (РКИ), классы 3–5

Веские доказательства

  • Тип отчета: Исследование эффективности, исследование, проведенное третьей стороной
  • Уровень оценки: элементарный
  • Область, край: Запад
  • Район Урбанизация: Городской, Пригородный, Сельский
  • Размер района: Большой

Математика в центре внимания : Сингапурское исследование эффективности математики в средних классах

Демонстрирует обоснование

  • Тип отчета: Исследование эффективности, исследование, проведенное третьей стороной
  • Уровень оценки: Середина
  • Область, край: Северо-восток, запад
  • Район Урбанизация: Пригородный, Сельский
  • Размер района: Большой маленький

ресурсы

pdf

Решение задач в Сингапуре по математике ®

Взгляд на сингапурский подход к обучению решению задач и причины его успеха.

pdf

История успеха

Сила учебной программы Singapore Math ® основана на постоянных пересмотрах, основанных на текущих исследованиях и передовом опыте. Узнайте, как он изменился за эти годы.

Справедливость и доступность в каждом классе

Узнайте, как программа «Математика в центре внимания» обеспечивает равноправие для каждого учащегося — от уникального пути обучения до беспрецедентной цифровой поддержки.

Узнайте, как Math in Focus может работать в вашем классе.

ПРЕДПРОСМОТР ОНЛАЙН

Авторы и консультанты

Лидеры, внедряющие учебную программу по математике мирового класса в классы США

На основе педагогических принципов успешной школы Singapore Math ® , учебная программа Math in Focus была разработана международной командой опытных преподавателей математики. Их работа дает американским студентам возможность извлечь выгоду из пути обучения, который, как доказано, повышает успеваемость и уверенность в математике.

АВТОРЫ

Доктор Фонг Хо Хеонг

Математика в фокусе Классы K–5 и курс 3 Автор и консультант

Мишель Чу

Автор

Математика в фокусе 9 классы K–35

Челви Рамакришнан

Математика в фокусе классы 1–5 автора

Gan Kee Soy

Math In Focus 4–5 и курс 100003

Dr. NG Wee Leng

    929 и Math в фокусе

    Dr. NG Wee Leng

      92 889 в фокусе

      Dr. NG Wee Leng

        889 в фокусе

        Dr. NG Wee Leng

        9000 889 в фокусе

                            Автор курса 1

                            Д-р Лай Чи Чонг

                            Math in Focus Автор курса 2

                            Low Wai Cheng

                            Math in Focus Курс 2 и курс 2 ускоренный автор

                            May Kuen
                              Леонг0003

                              Math In Focus Курс 2 и курс 2 Ускоренный автор

                              YAP Shin Tze

                              Math в фокусе Курс 2 Ускоренные и курс 3 Автор

                              US Consultants

                              Kimberly Mickle

                                889. Math Math in Mocide

                                  . Рецензент из США

                                  Элизабет Арделл

                                  Math in Focus 1-й класс Писатель из США и 2-й класс Рецензент из США

                                  Энди Кларк

                                  Math in Focus Писатель 3-й курс 9-го курса и 3-й курс США0003

                                  Сьюзен Resnick

                                  Math In Focus 1-го консультанта по США 3-й курс.

                                  Math in Focus Писатель 3-го класса США и рецензент 4-го класса США

                                  Susan D’Souza

                                  Math in Focus Писатель 4-го класса США и рецензент 5-го класса США

                                  3 900 Cordes0003

                                  Math In Focus 5 класс США писателя и 3 -го класса. Рецензент США

                                  Шелли Дубоз

                                  Математика в фокусе Курс 1 США писатель и курс 2 и курс 2 Удвоил рецензент

                                  Связанные растворы

                                  Мы знаем успех. не из одного решения, а из сети поддержки. Когда вы выбираете решение из HMH ® , это является началом отношений, которые помогут вам внедрить и повысить успеваемость таким образом, который лучше всего подходит для вашего округа, школы или класса.

                                   

                                   

                                   

                                  Math Solutions

                                  Math Solutions насчитывает более 250 высококвалифицированных специалистов по математике, готовых предоставить каждому учителю профессиональное обучение, которое формирует классы учащихся, уверенных в математике.

                                  Учить больше

                                  HMH Into AGA

                                  Комплексная учебная программа по алгебре 1, геометрии и алгебре 2, обеспечивающая глубину знаний, сложность понимания и беглость процедур, необходимые учащимся для успеха.

                                  Waggle

                                  Waggle ® для классов K–8 предлагает дополнительную практику и обучение, которые погружают учащихся в индивидуальное обучение и максимально экономят время учителей.

                                  МАТЕМАТИКА 180

                                  МАТЕМАТИКА 180 ® обеспечивает интенсивную помощь учащимся 5–12 классов, отстающим по математике на один или два года.

                                  Новости и события

                                  Следите за Math in Focus сообщество

                                  Будьте в курсе последних новостей и событий от Math in Focus идейные лидеры и эксперты по математике HMH, а также присоединяйтесь к нашему Math in Focus Hub Club для получения дополнительных ресурсов.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *