Условие задачи по математике 2 класс: Задачи по математике 2 класс
Страница 33 – ГДЗ Математика 2 класс. Моро, Бантова. Учебник часть 1
- Главная
- ГДЗ
- 2 класс
- Математика
- Моро, Бантова. Учебник
- Длина ломаной
- Страница 33. Часть 1
Вернуться к содержанию учебника
Длина ломаной
Вопрос
4. Дополни условие задачи и поставь вопрос так, чтобы она решалась вычитанием. Реши её устно.
1) Высота берёзы 15 м, а клёна на 5 м … .
2) Масса арбуза кг, а тыквы 10 кг.
3) На двух веточках смородины 15 ягод. На одной из них ягод.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
5.
За день мимо станции прошло 2 скорых поезда и 6 товарных. Только 3 поезда на этой станции остановилось. Сколько поездов прошло мимо станции без остановки?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
6. До остановки автобуса папа идёт 10 мин, а на автобусе едет на работу на 20 мин больше, чем идёт до остановки. Сколько всего времени он тратит на дорогу?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
7. Реши примеры. Покажи, что они круговые.
| 6 + 6 | 14 – 5 | 8 + 6 | 11 – 3 |
| 7 + 4 | 13 – 7 | 9 + 4 | 12 – 5 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
8.
Используя два или три числа на стене домика, набери число, записанное в окошке под крышей (12). Например, 8 и 4 или 4, 6, 2.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Рассмотри рисунок. От дома проложены дорожки к колодцу и к беседке. Какая дорожка длиннее?
Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника
ГДЗ по математике, 2 класс, Моро М.И. Дополни задачи и реши их. – Рамблер/класс
ГДЗ по математике, 2 класс, Моро М.И. Дополни задачи и реши их. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания “Останкино”?Дополни задачи и реши их.
1) Вася делал зарядку 12 мин, а его сестра — на 5 мин меньше.
2) Кате 10 лет. На сколько лет Катя старше
своего братишки?
3) Дима собрал 6 стаканов малины, а бабушка — □ стаканов. На варенье бабушка взяла
□ стаканов малины.
ответы
1) Задачу нужно дополнить вопросом: «Сколько минут
делала зарядку сестра Васи?».
12 – 5 = 7 (мин). Ответ: 7 мин.
2) Условие задачи нужно дополнить возрастом братишки,
например числом 4.
Условие: «Кате 10 лет, а её братишке 4 года.»
10 – 4 = 6 (лет). Ответ: на 6 лет.
3) Условие задачи надо дополнить числами и сформулировать вопрос задачи.
Дима собрал 6 стаканов малины, а бабушка — 10 стаканов. На варенье бабушка взяла 9 стаканов малины. Сколько стаканов малины осталось?
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
3 класс
5 класс
Репетитор
Химия
похожие вопросы 5
Запиши С 14.
№ 2 ГДЗ Математика 2 класс Моро М.И.
1) Запиши 3 любых двузначных числа. Умень-
ши каждое из них на 10.
2) Запиши 3 любых однозначных числа. Уве- (Подробнее…)
ГДЗМатематика2 классМоро М.И.
Реши задачу С 17.№ 4 ГДЗ Математика 2 класс Моро М.И.
Оля перепрыгнула через верёвочку 18 раз, а
Света — только 10 раз.
Поставь вопрос и реши задачу.
ГДЗМатематика2 классМоро М.И.
Выполните деление. ГДЗ Математика 6 класс Чесноков. Дидактические материалы по математике для 6 класса. Вар.1 Вопр.161
Кто сможет? Выполните деление:
(Подробнее…)
ГДЗМатематика6 классЧесноков А.С.
№ 77. ГДЗ Физика 10 класс Рымкевич. Какую скорость приобрел троллейбус?
Троллейбус за время t прошел путь s. Какую скорость v приобрел он в конце пути и с каким ускорением а двигался, если начальная скорость (Подробнее…)
ГДЗФизика10 классРымкевич А.
П.
Употребите глаголы 1A № 6 ГДЗ Spotlight Английский 7 класс Ваулина Ю. Е.
Put the verbs in brackets in the present simple or the present continuous. Give reasons.
1 A: Why ………………. (Подробнее…)
ГДЗSpotlightАнглийский язык7 классВаулина Ю.Е.
Общие базовые государственные стандарты по математике для второго класса: обзор
- Выберите класс
- Детский сад
- Первый класс
- Второй класс
- Третий класс
- Четвертый класс
- Пятый класс
- Шестой класс
- Седьмой класс
- Восьмой класс
- Выберите тему
- Математика
Прыгать на:
Операции и алгебраическое мышление | Числа и операции с основанием десять | Измерения и данные | Геометрия
Операции и алгебраическое мышление
Представлять и решать задачи на сложение и вычитание.
2.OA.A.1
Используйте сложение и вычитание в пределах 100 для решения одно- и двухшаговых задач со словами, включающих ситуации сложения, отнимания, сложения, разъединения и сравнения с неизвестными во всех позициях , например, используя рисунки и уравнения с символом неизвестного числа для представления проблемы.
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков
Складывать и вычитать в пределах 20.
2.OA.B.2
Свободно складывать и вычитать в пределах 20, используя умственные стратегии. К концу 2 класса знать наизусть все суммы двух однозначных чисел.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
Работайте с равными группами предметов, чтобы получить основы для умножения.
2.OA.C.3
Определить, имеет ли группа объектов (до 20) нечетное или четное число элементов, например, путем объединения объектов в пары или подсчета их по 2; Напишите уравнение, выражающее четное число в виде суммы двух равных слагаемых.
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков
2.OA.C.4
Используйте сложение, чтобы найти общее количество объектов, расположенных в прямоугольных массивах до 5 строк и до 5 столбцов; напишите уравнение, выражающее сумму в виде суммы равных слагаемых.
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков.
Числа и операции с основанием 10.
2.NBT.A.1
Поймите, что три цифры трехзначного числа представляют количество сотен, десятков и единиц; например, 706 равно 7 сотням, 0 десяткам и 6 единицам. Понимайте следующее как частные случаи:
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков
2.NBT.A.2
Сосчитайте в пределах 1000; пропуск счета на 5, 10 и 100 секунд.
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков.
См. соответствующие рабочие листы, рабочие тетради, планы уроков.
См.
соответствующие рабочие листы, рабочие тетради, игры, планы уроков
Используйте понимание разрядности и свойства операций сложения и вычитания.
2.NBT.B.5
Свободно складывать и вычитать в пределах 100, используя стратегии, основанные на позиционном значении, свойствах операций и/или отношениях между сложением и вычитанием.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков.
См. соответствующие рабочие листы, рабочие тетради, планы уроков
2.NBT.B.7
Сложение и вычитание в пределах 1000 с использованием конкретных моделей или рисунков и стратегий, основанных на позиционном значении, свойствах операций и/или отношениях между сложением и вычитание; связать стратегию с письменным методом. Поймите, что при сложении или вычитании трехзначных чисел добавляются или вычитаются сотни и сотни, десятки и десятки, единицы и единицы; а иногда надо составить или разложить десятки или сотни.
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков
2.
NBT.B.8
Мысленно прибавьте 10 или 100 к заданному числу 100–900 и мысленно вычтите 10 или 100 из заданного числа 100–900.
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков
2.NBT.B.9
Объясните, почему работают стратегии сложения и вычитания, используя разрядность и свойства операций.
См. соответствующие рабочие листы, рабочие тетради, планы уроков
Измерения и данные
Измерение и оценка длины в стандартных единицах.
2.MD.A.1
Измерьте длину объекта, выбрав и используя соответствующие инструменты, такие как линейки, линейки, измерительные рейки и рулетки.
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков. опишите, как два измерения соотносятся с размером выбранной единицы измерения.
См. соответствующие рабочие листы, рабочие тетради
2.MD.A.3
Расчет длины в дюймах, футах, сантиметрах и метрах.
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков
2.
MD.A.4
Измерьте, чтобы определить, насколько длиннее один объект, чем другой, выражая разницу в длине в единицах стандартной длины.
Смотрите похожие игры
Свяжите сложение и вычитание с длиной.
2.MD.B.5
Используйте сложение и вычитание в пределах 100 для решения текстовых задач с длинами, заданными в одних и тех же единицах, например, используя рисунки (например, рисунки линеек) и уравнения с символом неизвестного числа для представления задачи.
См. соответствующие рабочие листы, рабочие тетради, планы уроков
2.MD.B.6
Представлять целые числа в виде длин от 0 на диаграмме числовых линий с равноотстоящими точками, соответствующими числам 0, 1, 2,… , и представляют суммы и разности целых чисел в пределах 100 на диаграмме числовых линий.
Смотрите похожие игры
Работа с деньгами и временем.
2.MD.C.7
Скажите и запишите время по аналоговым и цифровым часам с точностью до ближайших пяти минут, используя время до и после полудня.
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков
2.MD.C.8
Решите текстовые задачи с участием долларовых купюр, четвертаков, десятицентовиков, пятаков и пенни, используя соответствующие символы $ и ¢.
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков
Представление и интерпретация данных.
2.MD.D.9
Генерация данных измерений путем измерения длины нескольких объектов с точностью до целой единицы или выполнения повторных измерений одного и того же объекта. Покажите измерения, построив линейный график, где горизонтальная шкала отмечена в целых числах.
См. соответствующие рабочие листы, рабочие тетради, планы уроков
2.MD.D.10
Нарисуйте графическое изображение и столбчатую диаграмму (с единичным масштабом), чтобы представить набор данных с четырьмя категориями. Решайте простые задачи по сборке и разборке и сравнивайте их, используя информацию, представленную в виде гистограммы.
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков.
2.G.A.1
Распознавать и рисовать фигуры с заданными атрибутами, такими как заданное количество углов или заданное количество равных граней. Определите треугольники, четырехугольники, пятиугольники, шестиугольники и кубы.
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков
2.G.A.2
Разбейте прямоугольник на строки и столбцы квадратов одинакового размера и посчитайте, чтобы найти их общее количество.
См. соответствующие планы уроков. целое как две половины, три трети, четыре четверти. Признайте, что равные части одинаковых целых не обязательно должны иметь одинаковую форму.
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков
Как учить задачи на сложение и вычитание
Мои ученики мучились с , как решать задачи на сложение и вычитание , казалось, целую вечность. Они могли подчеркнуть вопрос и найти числа.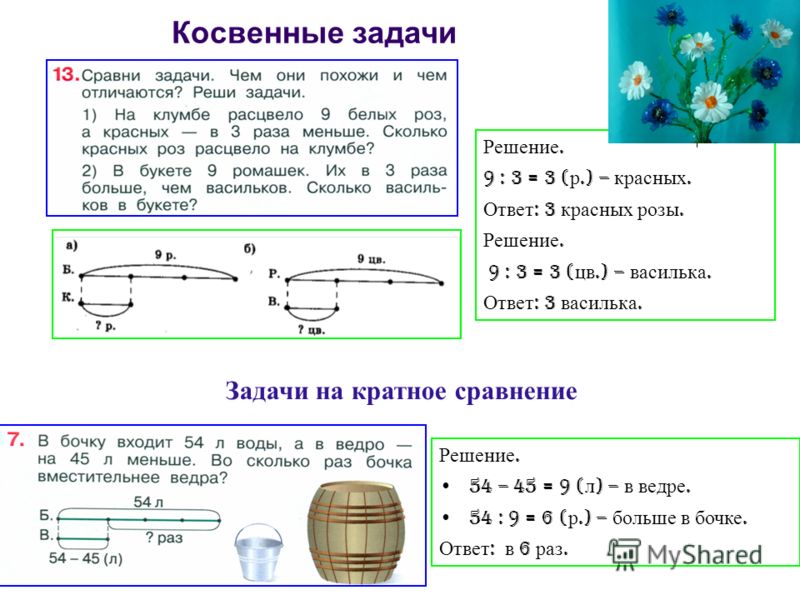
В большинстве случаев мои ученики просто складывали два числа вместе, не понимая смысла задачи.
Тьфу.
Вы можете рассказать?
Ниже приведены пять стратегий решения математических задач, которые можно использовать при обучении словесным задачам на сложение и вычитание с использованием любого ресурса.
Итак, как учить текстовые задачи? Это довольно сложно, но так весело, как только вы войдете в него.
Как обучать задачам на сложение и вычитание
Основные компоненты обучения задачам на сложение и вычитание включают:
- Обучение соотношению чисел s – Как учитель, знайте тип задач и помогайте учащимся решать действие в задаче
- Дифференцируйте числа – Дайте учащимся только правильные числа, чтобы они могли прочитать задачу, не увязая в вычислениях
- Используйте академический словарь – и будьте последовательны в том, что вы используете.
- Остановить поиск «Ответа» — дело не в ответе; речь идет о процессе
- Различие между моделями и стратегиями – одна связана с отношениями между числами, а другая связана с тем, как учащиеся «решают» или вычисляют задачу.
Я большой сторонник НЕ преподавания списков ключевых слов. Это просто не работает последовательно во всех проблемах. Это короткий путь, ведущий к сбоям в математическом мышлении. Вы также не должны просто давать учащимся рабочие листы с текстовыми задачами и заставлять их искать ключевые слова для текстовых задач. Я более подробно рассказываю о том, почему это не работает, в статье «Проблема с использованием ключевых слов для решения текстовых задач».
Научите соотношению чисел в математических задачах со словами
Один из способов помочь вашим ученикам решать задачи со словами — научить их отношениям между числами. Другими словами, помогите им понять, что числа в задаче каким-то образом связаны друг с другом.
Я учу текстовые задачи, убирая числа. Звучит странно, верно?
Устранение отвлекающих факторов на числа помогает учащимся сосредоточиться на проблемной ситуации и понять действие или взаимосвязь чисел. Это также удерживает учащихся от решения задачи до того, как мы поговорим о взаимосвязи чисел.
Когда я преподаю текстовые задачи, я даю ученикам задачи с пробелами и без чисел. Сначала поговорим о действии в задаче. Мы определяем, добавляется ли что-то к чему-то другому или отнимается от чего-то другого. Это становится нашим уравнением. Мы определяем, что нам нужно решить, и составляем уравнение с пробелами и квадратом для неизвестного числа.
___ + ___ = неизвестно
Хотите бесплатный образец текстовых задач, которые я использую в своем классе? Щелкните ссылку или изображение ниже. БЕСПЛАТНЫЙ образец текстовых задач по типу задачи
Различие чисел в задачах Word
Только после того, как мы обсудим задачу, я даю ученикам числа. Я различаю числа в зависимости от потребностей учащихся. В начале года мы все делаем одни и те же числа, чтобы я мог убедиться, что ученики понимают процесс.
После того, как учащиеся ознакомятся с процессом, я начинаю давать разным учащимся разные числа в зависимости от их уровня математического мышления.
Я также меняю номера в течение года с однозначных на двузначные. Прелесть пустых мест в том, что я могу вставить в задачу любые числа, которые захочу, чтобы попрактиковаться в стратегиях, над которыми мы работали в классе.
В какой-то момент мы создаем список слов, но не список ключевых слов. Мы создаем список действий или глаголов и определяем, соединяют ли эти действия что-то или разделяют. Сколько вы можете придумать?
Вот несколько идей:
Присоединяйтесь: положил, получил, взял, купил, сделал
Разделить: съел, потерял, положил, уронил, использовал
Не бойтесь использовать академическую лексику при обучении словесным задачам
Я учу своих учеников определять начало задачи, изменение в задаче и результат задачи. Я учу их искать неизвестных .
Все эти слова мы используем при решении задач, и мы изучаем структуру словесной задачи через словарный запас и взаимосвязь чисел.
На самом деле, использование одного и того же словаря для разных типов задач помогает учащимся увидеть взаимосвязь чисел на более глубоком уровне.
Возьмите эти примеры, можете ли вы определить запустить, изменить и результат в каждой проблеме? Подсказка: посмотрите на код, используемый для типа проблемы, в правом нижнем углу.
Для сравнения задач мы используем термины больше , меньше , больше и меньше . Попробуйте решить эти задачи и посмотрите, сможете ли вы определить компоненты словесных задач.
Прекратите искать «ответ» при решении текстовых задач
Это заблуждение труднее всего разрушить.
Учащиеся не решают словесную задачу, чтобы найти «ответ». Хотя ответ помогает мне, учителю, понять, понял ли ученик взаимосвязь чисел, я хочу, чтобы ученики могли объяснить свой процесс и понять глубину словесных задач.
Ладно, это первоклассники и второклассники. Я знаю.
Мои ученики все еще могут объяснить после обучения, что они начинают и с одного числа. Проблема результат ed в другом другом номере. Затем учащиеся узнают, что они ищут замену на между этими двумя числами.
Все дело в отношениях.
Различие между моделями и стратегиями
Пару лет назад я наткнулся на эту статью о необходимости помочь учащимся разработать адекватные модели для понимания связи чисел в задаче.
У меня в голове взорвалась лампочка. Мне нужно было провести различие между модели учащиеся используют, чтобы понять взаимосвязь чисел в задаче и стратегии для решения вычислений в задаче. Модели и стратегии работают в тандеме, но очень разные.
Модели — это визуальные способы представления проблем. Стратегии — это способы, которыми учащийся решает задачу, складывая и разбирая числа.
Самое главное в моделях – отойти от них. Я знаю, это звучит странно.
Вы так долго обучаете студентов пользоваться моделями, а потом не хотите, чтобы они использовали модели. Ну, на самом деле, вы хотите, чтобы студенты двигались к эффективности.
Младшие школьники разыгрывают задачи, рисуют задачи с изображениями и рисуют задачи с кругами или линиями. Направьте учащихся к эффективности. По мере того, как числа становятся больше, модель должна представлять отношение чисел
Это яркий пример перехода от модели с перевернутой буквой v к модели с стержнями.
Ученик переходит от рисования кругов к использованию перевернутой буквы v.
Учащиеся должны полностью использовать одну модель, прежде чем переходить на другую. Они могут даже использовать два одновременно, пока выясняют сходство между моделями.
Учащиеся также должны уметь создавать свои собственные модели. Вы увидите, как я иногда давал студентам копии модели, которые они могли вклеить в свои тетради, а иногда студенты рисовали свою собственную модель. Они должны нести ответственность за выбор того, что лучше всего подходит для них. Начните обучение с конкретных моделей, а затем позвольте учащимся выбрать одну из них для использования. Всегда подталкивайте учащихся к более эффективным моделям.
То же самое касается стратегий для вычислений. Сначала обучайте стратегиям с помощью математических фактов, а затем применяйте их к текстовым задачам, чтобы учащиеся понимали стратегии и могли быстро выбрать одну из них для использования. При обучении сосредоточьтесь на одной или двух стратегиях. Как только учащиеся овладеют некоторыми стратегиями, попросите их выбрать стратегии, которые работают для решения различных задач.
Какие числа вы вставляете в пробелы?
Будьте целеустремленны в числах, которые вы выбираете для своих текстовых задач. Разные наборы чисел подходят для разных стратегий и разных моделей. Используйте числовые наборы, которые учащиеся уже использовали в вычислениях.
Если вас научили составлять 10, используйте числа, которые составляют 10.