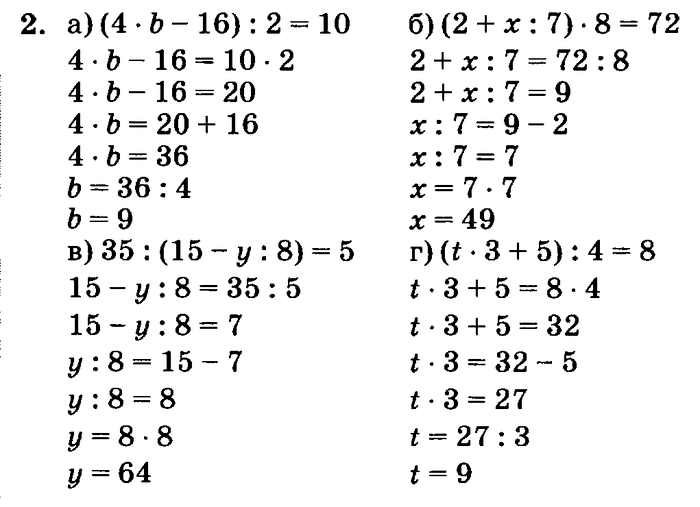Уравнения и примеры для 3 класса: Реши уравнения 3 класс

Думаю, это поможет прояснить некоторые вещи, которые я путал в голове. Когда люди говорят о том, что детям необходимо хорошо понимать эквивалентность, они на самом деле имеют в виду несколько разных вещей. Вот два, которые появились выше:

• Особое значение знака равенства (из этого следует, что уравнение может быть написано как слева направо, так и справа налево, т.е. оно симметрично)
• Обычные способы написания уравнений (например, без повторений, может включать несколько операций и терминов с каждой стороны)

Но это только начало, потому что часто люди говорят о множестве других вещей, когда говорят об «эквивалентности». Вот лишь некоторые из них:

• Вы можете выполнять одинаковые операции с каждой стороной  (известно полезно для решения уравнений)
• Вы можете манипулировать одинаковыми элементами на одной стороне уравнения, чтобы создать истинное уравнение (10 + 5 можно превратить в 9 + 6 можно превратить в 8 + 7; 8 x 7 можно превратить в 4 x 14; 3 (x + 4) можно превратить в 3x + 12 и т. д.)

Когда ребенок не может решить 5 + 10 = ___ + 9 правильно или легко, используя «реляционное понимание», это часто винят в понимании ребенком знака равенства, эквивалентности или конкретных способов соотнесения 5 + 10 с __ + 9. Но теперь я ясно вижу, что это разные вещи, и одни даются детям легче, чем другие.

Итак, мы подошли к следующему уроку с моими 3-классниками.

Я начал, как обычно в этой ситуации, с избегая знака равенства . Я обнаружил, что двойная стрелка хорошо служит для этой цели, поэтому я изобразил на доске соотношение стрелок:

2 x 6 <–> 8 + 4

Я указал, что 2 x 6 дает 12, а также 8 + 4.

Да. Я не сделал фото, но я был благодарен, что все подошло. Дети прекрасно смешивали операции, например, 12 – 2 <–> 5 + 5, в целом казалось, что это не сложно, дети точно знали, что я имею в виду, и могли генерировать множество идей.

Следующим моим шагом было сделать паузу и ввести в этот разговор знак равенства. Кто-нибудь будет возражать, если я заменю эту двойную стрелку знаком равенства? Во всяком случае, именно это и означает знак равенства. Ничего страшного, тоже все прошло нормально.

Дети даже показывали замечательные примеры, такие как 1 x 2 = 2 x 1 или 12 = 12. Замечательно.

Затем я представил задачу дня в стиле Open Middle (R) (TM) (C):

Да, я быстро написал ее от руки маркером. Это был именно такой день.

Я подробно объяснил ограничения. 10 – 2 + 7 + 1 было правильным уравнением, но для этой головоломки не годилось. Как и 15 – 5 = 6 + 4. А потом я дал детям время на поиск решений, сколько они смогли найти.

Бла-бла-бла, большинство детей добились успеха, другим было трудно начать, но все в конце концов добились определенного успеха. Вот несколько фотографий учеников, которые меня украшают:

Вот фотография ученика, который боролся, но в конце концов нашел решение:

Вот фотография ученика из класса, в котором я учился больше всего волнует. Вы можете видеть отметки вдоль его страницы, когда он пытается обрабатывать такие вещи, как 12 – 9, когда он пытается вычитать разные числа из 12. Я думаю, что с правой стороны могло происходить какое-то умножение, не знаю почему. В любом случае:

Дело в том, что накануне этот последний студент чуть не сломался от разочарования из-за своей неспособности разобраться в этих «нетрадиционных» уравнениях. Так что это заставляет меня выглядеть отлично — я сделал это! Я научил его эквивалентности примерно за день. Тада.

Но я не думаю, что это то, что происходит. Понятие о равенстве двух разных вещей не было для него трудным. На самом деле, я не думаю, что это понятие вообще сложно для очень многих учеников — дети знают, что различные сложения равны 10. И для этого ребенка не было особенно сложно объединить это понятие эквивалентности со знаком равенства. Мол, нет, он не думал, что именно это означает знак равенства, но что бы там ни было, это было просто на основании того, что он думал раньше. Это просто условность. Я сказал ему, что знак равенства означает что-то еще, хорошо, конечно. Не так уж и плохо.

Однако для этого студента было очень трудно вычитать из 12. Это правда — мне бы очень хотелось, чтобы этот студент знал, что 10 + 2 <–>

В завершение несколько вопросов и несколько предварительных ответов:

В: Сложно ли преподавать или изучать концепцию эквивалентности.

A: №

Q: Трудно ли выучить знак равенства и его значение?

A: Это сложнее , но это все условно. Если вы введете новый символ, такой как «<–>», я не думаю, что дети так сильно спотыкаются. Иногда им приходится забыть о том, что они сделали из предыдущего опыта, который был слишком ограничен (т. е. всегда ставить результат на правильную сторону). Таким образом, вы не делаете детям никаких одолжений, делая это, хорошо представлять уравнения в разных формах, как только дети впервые видят уравнения в K или 1-м классе. Я имею в виду, почему бы и нет?

В: Если дети не узнают, как обычно работают уравнения, не споткнется ли это позже в алгебре?

О: Да. Но всем моим детям складывать и вычитать сложнее, чем понимать эти условности. Я считаю, что вам не нужно года , чтобы привыкнуть к тому, как работают уравнения. Тебе нужен час или два, чтобы представить его.

В: Нужно ли обучать этому материалу заранее? Не слишком ли поздно изучать алгебру, как работают уравнения?

A: Я думаю, что дети должны учиться этому рано, но ВООБЩЕ не поздно, если они этого не сделают.

Я вел занятия по алгебре в 8-м и 9-м классах, где ученики не понимали, как работают уравнения. По моим воспоминаниям, это раздражало, потому что я слишком поздно понял, что происходит, и мне пришлось отступить. Но, основываясь на том, что я обучаю этому младших детей, я не могу себе представить, что уже слишком поздно учить этому старшеклассников.

Я думаю, вполне возможно, что с годами становится все труднее вытрясти учеников из их более ограниченного понимания уравнений, потому что они укрепляют их теорию об уравнениях и символе равенства. Я не знаю.

Я не вижу причин не учить этому раньше, но я думаю, важно помнить, что в средней школе мы говорим детям, что иногда вычитание числа делает его больше и что существуют отрицательные показатели степени. Дети могут узнать что-то новое и в более поздние годы.

В: Так что же мешает маленьким детям решать уравнения вроде 5 + 10 = 6 + __?

A: Совершенно верно, что дети, которые не понимают, как читать такого рода уравнения, вообще не смогут участвовать. Но самому относительному мышлению, как мне кажется, труднее всего научить и чему научиться.

Вот мысленный эксперимент. Что, если бы у вас была школа или учебная программа, в которой только использовали знаки равенства и уравнения скучным, ограниченным способом «5 + 10 = »? и «6 х ? = 12” на протяжении всей школы, но в то же время глубоко и эффективно обучали реляционному мышлению с использованием <–> и другой терминологии? А затем в 8-м классе у них есть несколько уроков, обучающих «новому» способу понимания знака равенства? Будет ли это иметь большое значение? Я не знаю, я так не думаю.

В: Есть данные, свидетельствующие о том, что изучение вышеперечисленных вещей помогает детям добиться большего успеха в алгебре на более позднем этапе. Твои мысли?

О: Не знаю! Мне кажется, что если что-то и имеет значение для более поздней алгебры, то это должна быть либо концепция эквивалентности, либо условность уравнений, либо реляционное мышление.

Я думаю, что понятие эквивалентности знакомо каждому ребенку. Я думаю, что правила уравнений не так уж трудно выучить, но они действительно имеют смысл только в том случае, если вы свяжете уравнения с концепцией эквивалентности. Концепция эквивалентности объясняет почему уравнения имеют определенные соглашения. Так что я понимаю, почему эти двое идут вместе. Но может ли этого быть достаточно, чтобы помочь студентам с более поздним опытом алгебры? Может быть. Это потому, что учителя алгебры не учат правилам уравнений на своих занятиях? Будет ли преимуществом ранний опыт работы с уравнениями, если его будут преподавать учителя алгебры?

В конце концов, это не имеет большого значения, потому что маленькие дети могут этому научиться, так почему бы не научить их этому? Не повредит, только стоит вам час или два.

Но еще одна важная вещь — это реляционное мышление. Теперь я не думаю, почему реляционное мышление имеет место в контексте уравнений. Вы МОЖЕТЕ использовать другие символы, такие как двойные стрелки или что-то еще. Но в математике уже есть этот символ эквивалентности, так что вы можете также учить реляционному мышлению о сложении/вычитании/умножении/делении в контексте уравнений. И это действительно сложная, очень важная математика для изучения. Важно, чтобы ребенок понял, что 2 х 14 равно 4 х 7.

По очень многим причинам, практически по всем причинам важно, что арифметика является основой алгебры. Я не могу перечислить их сейчас, но я хочу сказать, что это выходит за рамки уравнений. Реляционное мышление (например, как различные дополнения соотносятся друг с другом) огромно и чрезвычайно важно.

Изменится ли понимание условностей знаков равенства и уравнений при отсутствии опыта, который поможет детям понять отношения? Начинают ли некоторые дети самостоятельно устанавливать связи, когда учатся писать уравнения? Неужели обучение реляционному пониманию проваливается просто потому, что дети не понимают, что означают уравнения, которые используют их учителя?

Не знаю.

Нравится:

Нравится Загрузка. ..

Что такое уравнение в математике? Определение, типы, примеры, факты

Существует множество способов, которыми можно определить уравнение. В своей простейшей форме в алгебре определение уравнения представляет собой математическое утверждение, показывающее, что два математических выражения равны. Например, 3x + 5 = 14 — это уравнение, в котором 3x + 5 и 14 — это два выражения, разделенные знаком «равно». Самые основные и простые алгебраические уравнения состоят из одной или нескольких переменных в математике. 9{3}$ + 5x

9t

Различные типы уравнений:

Некоторые математические уравнения, используемые в алгебре:

1. Линейное уравнение

Линейное уравнение может иметь более одной переменной. Линейное уравнение — это уравнение, в котором наивысшая степень переменной всегда равна 1. Оно также известно как уравнение одной степени.

2. Квадратное уравнение

Это уравнение второго порядка. В квадратных уравнениях хотя бы одна из переменных должна быть возведена в степень 2. 9{3}$ – 27 = 0

4. Рациональное уравнение

Рациональное уравнение — это уравнение, содержащее дроби с переменной в числителе, знаменателе или в обоих случаях.

Пример:  $\frac{x}{2} = \frac{x + c}{4}$.

Математическое выражение отличается от математического уравнения. Уравнение всегда будет использовать оператор равенства (=) между двумя математическими выражениями.

Например,

Что такое решение уравнения?

Значение переменной, которая делает уравнение истинным утверждением, является решением уравнения.

Пример 1:

Проверить, что x = 3 является решением уравнения 4x − 8 = − 5 + 3x

Подставить x = 3 в данное уравнение

LHS

4x − 8 = 4(3) − 8 = 12 − 8 = 4

RHS

−5 + 3x = −5 + 3(3) = −5 + 9 = 4

LHS = RHS

Таким образом, x = 3 является решением уравнения 4x − 8 = −5 + 3x.

Пример 2:

Убедитесь, что y = −2 является решением уравнения 2m – 4 = 1

Подставьте y = −2 в данное уравнение.

левый

2m – 4 = 2(−2) – 4 = – 4 – 4 = – 8 не решение данного уравнения 2m – 4 = 1.

Как решать линейные уравнения с одной переменной?

• Упростите выражения внутри круглых и фигурных скобок, фигурных скобок и дробей.
• Одно и то же количество можно складывать, вычитать, умножать или делить из обеих частей уравнения без изменения равенства.

Или

Любой член уравнения можно перевести из одной части в другую с изменением его знака. Этот процесс называется транспозицией.

Пример:

4a – 9 = 13 – 7a

4a + 7a = 13 + 9 [транспонировать −7a в левое положение и −9 в правое]

11a = 22 [добавить похожие термины]

a = $\ frac{22}{11}$ [транспонировать 11 в RHS]

a = 2

Пример:

$\frac{1}{5} + 3w = \frac{2}{5}$

3w = $\frac{2}{5} – \frac{1 }{5}$ [транспонировать 15 в RHS]

3w = $\frac{1}{5}$

w = $\frac{1}{5\times 3}$ [транспонировать 3 в RHS]

w = $\frac{1}{15}$

Решенные примеры:

Пример 1: Решите для x .

x + 8 = 12

Решение:

Вот уравнение, которое нужно решить: x + 8 = 12

Нам нужно оставить x в одной части уравнения. Для этого мы должны отнять по 8 с обеих сторон.

Итак, x + 8 – 8 = 12 – 8

или x = 4

Пример 2: Определите, является ли значение 3 решением уравнения:

4x – 3 = 3 1

Решение:

Подставим в это уравнение значение 3 и проверим, равно ли левое уравнение правой части.

Итак,

4(3) – 2 = 3(3) + 1

или 12 – 2 = 9 + 1

или 10 = 10

Да, 3 является решением данного уравнения.

Пример 3: Решите уравнение: 6(2x + 3) + x – 7 = 3(5x + 7) + 2x

Решение:

6(2x + 3) + x – 7 = 3 (5x + 7) + 2x

Раскрывая полученные члены,

12x + 18 + x – 7 = 15x + 21 + 2x

или, 13x + 11 = 17x + 21

При дальнейшем упрощении,

13x – 17x = 21 – 11

−4x = 10

x = -$\frac{10}{4}$

x = -$\frac{5}{2}$

Практические задачи

1

Что из этого является уравнением?

7x + 5y = 19

5 – 2

$\frac{4}{7} – \frac{2}{7}$

3a + 9b

Правильный ответ: 7x + 5y = 19
Поскольку вариант a имеет знак равенства (=) между двумя математическими выражениями, это уравнение. Другие параметры являются выражениями.

2

Определите уравнение, для которого 7 не является решением.

n + 2 = 9

7 – g = 0

x – 4 = 3

h$\times$ 1 = 8

Правильный ответ: h$\times$ 1 = 8
7$\times $ 1 = 7 и 7 ≠ 8. Таким образом, 7 не является решением данного уравнения.

3

Решите 9k = −27

3

2

−3

−1

= Правильный ответ: −3
9k = −9 k29} {frac 9043} $
k = -3

Заключение

Таким образом, мы узнали определение уравнения и его различные типы. Кроме того, здесь также было решено несколько вопросов, чтобы дать учащимся четкое представление о решении уравнения. Учащийся может хорошо усвоить эту концепцию, решая такие задачи. Преподавание математических понятий может быть сложной задачей, особенно когда ученики маленькие дети. Итак, чтобы облегчить жизнь родителей и учителей, SplashLearn предлагает несколько курсов, специально разработанных для учащихся K-8.