Уравнения 3 класс на умножение и деление: Урок математики 3 класс “Решение уравнений на основе знания связи между компонентами и результатами умножения и деления”
Решение сложных уравнений: советы профессионала
4.9
(62)
Овладение детьми способом решения уравнений в начальной школе создает прочную основу для дальнейшего обучения алгебры, химии, физики и других предметов.
Начиная с 3-го класса, ученикам встречаются сложные уравнения, но справиться с ними очень просто.
Дети уже умеют решать простые уравнения, читай об этом здесь.
А эта статья будет посвящена решению сложных уравнений в 2-3 действия.
Очень часто родители, желая помочь, объясняют так: вот смотри, сейчас вот это число перенести в другую часть от знака равенства, надо поменять знак на противоположный: было умножение, меняем на деление; было сложение меняем на вычитание.
В начальной школе это объяснение не срабатывает, т.к. ребенок не знаком с законами алгебры.
Как сложное уравнение привести к тому, которые мы уже умеем решать, а именно к уравнению в 1 действие?
Рассмотрим уравнение в 2 действия:
х + 56 = 98 — 2 — оно достаточно легкое.
Здесь особого труда не будет в решении, потому что ребенок сразу догадается, что сначала надо 98-2.
х + 56 = 98 — 2
х + 56 = 96 – это простое уравнение. А его решаем очень быстро!
Сейчас мы рассмотрим уравнение:
2• (х + 5) = 30.
Такое уравнение можно решить несколькими способами.
- У нас здесь неизвестное число х. Мы не знаем, что спрятано за этим числом.
А когда к х + 5 – это число тоже известно.
Закроем его и пусть это будет другое число, например b .
Мы видим, что у нас получилось самое простое уравнение в 1 действие.
2 • b = 30
А чтобы найти а, нам нужно 30 : на 2.
А b не что иное, как х + 5.
х + 5 = 30 : 2
х + 5 = 15
х = 15 – 5
х = 10
Проверку делаем как обычно: переписываем первое уравнение: 2 • (10 + 5) = 30.
30 – переписываем, а левую часть считаем — будет 30.
30 = 30, значит, уравнение решили правильно.
При решении таких сложных уравнений самое главное – понять, что заменить на другое неизвестное число. Когда в уравнении всего 2 действия – это очень просто.
- Более удобно и понятно, как показывает практика, если использовать решение сложных уравнений на основе зависимости между компонентами действий.
Наше уравнение 2 • (х + 5) = 30 читаем так: число 2 умножить на сумму х и пяти, получится 30. В данном случае – нам неизвестна сумма, чтобы ее найти, надо 30:2.
Рассмотрим уравнение:
48 : (16 – а) = 4.
Если опять заменять часть уравнения другим неизвестным числом, можно запутаться. Поэтому легче использовать взаимосвязи компонентов и результата действия: число 48 разделить на разность.
Нам неизвестна разность, поэтому сначала нужно узнать чему она равна. Надо 48 : 4.
16 — а = 48 : 4
16 — а = 12 – это простое уравнение.
а = 16 — 12
а = 4
Проверка: 48 : (16 — 4) = 4
Давайте посмотрим еще одно:
96 – (с – 14) = 94.
Из 96 надо вычесть разность с и 16. Чтобы найти разность, надо 96-94.
С — 14 = 96 — 94
С — 14 = 2
С = 14 + 2
С = 16
Проверка: 96 — (16 — 14) = 94
А сейчас мы переходим к тем уравнениям, у которых не 2, а 3 действия. Как же нам поступать в этом случае? При решении таких сложных уравнения используем знания порядка выполнения действий в выражениях со скобками и без них.
Рассмотрим уравнение: 36 – (8 • у + 5) = 7
Прежде всего, нужно внимательно оценить левую часть уравнения: ту, которая с неизвестным числом. Вы должны четко себе представить какое вы будете делать действие первым, какое – вторым, какое – третьим: сначала делается умножение, потом сложение и последним – вычитание.
И вот то, которое вы будете делать третьим, с него и начнем, т.
е. начинаем упрощать уравнение с последнего действия. Последнее действие – вычитание. С него и начнем: из числа 36 вычесть то, что в скобках и получим 7.
Значит, то что в скобках – вычитаемое, чтобы его найти, надо 36 — 7.
(8 • у + 5) = 36 — 7
По правилам математики в данной записи скобки – не ставим.
8 • у + 5 = 36 — 7
8 • у + 5 = 29 – уравнение сложное. Нужно его упростить. Данное уравнение читаем так: к произведению 8 и у прибавили 5 и получилось 29. Нам неизвестно произведение, чтобы его найти, надо 29-5.
Получится:
8 • у = 29 – 5
8 • у = 24 – это уравнение простое.
у = 24 : 8
у = 3
Проверка: 36 — (8 • у + 5) = 7 . Правую часть – 7 — переписываем, а левую считаем.
Итак: 7 = 7. Значит, уравнение решили правильно.
(36 + d) : 4 + 8 = 18. Определяем порядок действий: первое – сложение в скобках, второе – деление, третье сложение вне скобок. Значит, все, что до 8 – это первое слагаемое, чтобы его найти, надо 18 — 8
(36 + d) : 4 = 18 — 8
(36 + d) : 4 = 10 – уравнение сложное, теперь последнее действие — :, значит
36 + d = 10 • 4
36 + d = 40 – уравнение простое и его мы решаем легко!
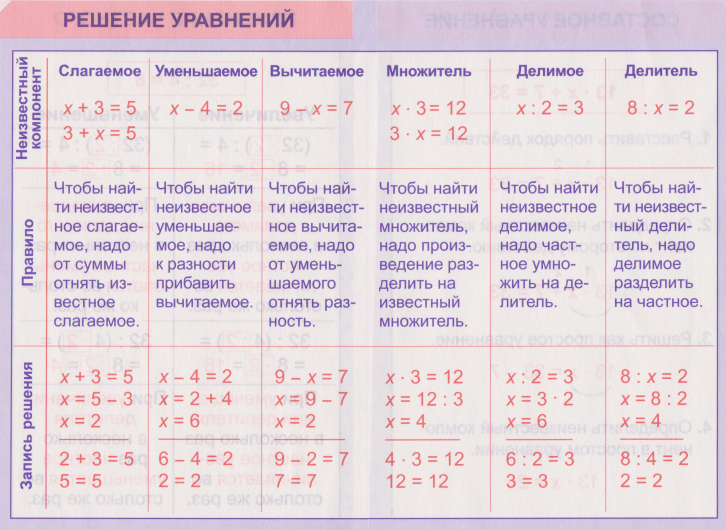
Для удобства и быстроты решения сложных уравнений можете пользоваться данной памяткой
Дело в том, что при кажущейся сложности, если внимательно изучить все приемы, которые я вам сегодня показала, эти уравнения дети будете щелкать как семечки.
Обязательно напишите в комментариях, какой способ вам более удобен.
Скачать
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.9 / 5. Количество оценок: 62
Оценок пока нет. Поставьте оценку первым.
Похожие статьи
Уравнения. Внетабличное деление и умножение (3 класс)
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Математика
3 класс
Закрепление по теме «Уравнения».
Проверочная работа «Уравнение.
Внетабличное деление и умножение». Решение
задач изученных видов (закрепление).
Математический диктант «Умножение и
деление»
8 февраля
Классная работа
Семья
Родина
Найдите в
этих словах
спрятанные
числа.
Запишите эти цифры в
тетрадь
71
Запишите только ответы:
6 x 1=
2х9=
4 х 9=
32 : 4 =
18 : 6=
8х5=
7х7=
1 x7=
0 x 9=
42 : 6 =
81 : 9=
64 : 8 =
6 x 7=
4х0=
48 : 6 =
8х9=
6 x 1= 6
4 х 9 = 36
18 : 6= 3
7 х 7 = 49
0 x 9= 0
81 : 9= 9
6 x 7 = 42
48 : 6 = 8
2 х 9 =18
32 : 4 =8
8 х 5 =40
1 x7=7
42 : 6 =7
64 : 8 = 8
4 х 0 =0
8 х 9 =72
Работа по учебнику:
Стр.24, № 1, 2 – самостоятельно. Устно
объяснить решение.
Решить задачу № 6.
На спектакле в школьном зале дети
сидели в 6 рядах по 15 человек и ещё в
одном ряду 10 человек.
Сколькодетей смотрело спектакль?
Решение текстовой задачи
Краткая запись:
I – ? 6 р. по 15 ч.
?
II – 10 ч.
Схематический чертёж.
? 6 р. по 15 ч.
10 ч.
?
Решение текстовой задачи
Решение:
1)15 х 6 =90 (ч.) – сидели в шести рядах
2)90 + 10 = 100 (ч.)
15 х 6 +10 = 100 (ч.)
Ответ: 100 человек смотрели спектакль.
Вид оценки: взаимопроверка групп (группы
обмениваются работами )
Форма оценки: эталон.
Решите уравнения:
18 ∙ х = 54
78 : х = 13
х : 6 = 16
Проверка:
18 ∙ х = 54
х = 54 : 18
х =3
18 ∙ 3 = 54
54 = 54
78 : х = 13
х = 78 : 13
х =6
78 : 6 = 13
13 = 13
х : 6 = 16
х = 16 ∙ 6
х = 96
96 : 6 = 16
16 = 16
Математический диктант.
1. Найдите произведение чисел 14 и 3.
2. Делимое 60, делитель 4, найдите частное.
3. Увеличьте 25 в 3 раза.
4. Какое число надо уменьшить на 9, чтобы получилось
34?
5. Чему равна сумма чисел 28 и 17?
6.
найдите второй множитель.
7. Уменьшите 45 в 3 раза.
8. Самое большое двузначное число разделите на 3.
9. Сумму чисел 50 и 25 разделите на 5.
10. Разность чисел 80 и 16 разделите на 4.
Проверочная работа.
1. Решите примеры.
7 · 12 =
96 : 3 =
25 · 3 =
76 : 2 =
18 · 5 =
70 : 14 =
4 · 21 =
84 : 28 =
14 · 7 =
90 : 15 =
3 · 26 =
46 : 2 =
2. Решите задачу.
Школьники посадили 4 ряда яблонь по 15 деревьев
в каждом ряду и 3 ряда слив по 10 деревьев в каждом ряду.
Сколько всего деревьев посадили школьники?
3. Решите уравнения.
х · 14 = 84
96 : х = 24
80: x =16
23 · х = 69
Домашнее задание:
с.25 №8, №11
English Русский Правила
NC.3.OA.3 – Математические задачи на умножение/деление в 3-м классе Северной Каролины
Проблемы со словами на умножение/деление
3.OA.3 – North Carolina Grade-3 Math Multiplication/Division Word Problems | EGVideos” src=”https://www.youtube.com/embed/7wv-T7h9rnk?rel=0″ allowfullscreen=”” mozallowfullscreen=”” webkitallowfullscreen=”” oallowfullscreen=”” msallowfullscreen=”” scrolling=”no” allow=”accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture”> Описание
Представляйте, интерпретируйте и решайте одношаговые задачи на умножение и деление. • Решайте задачи на умножение слов с коэффициентами до 10 включительно. Представьте задачу, используя массивы, картинки и/или уравнения с символом неизвестного числа для представления задачи. • Решайте задачи на деление слов с делителем и частным до 10 включительно. Представьте задачу, используя массивы, картинки, многократное вычитание и/или уравнения с символом неизвестного числа для представления задачи.
Дополнительная информация
Ключевые слова
Больше тем о Северной Каролине
- NC.
3.OA.7
3.OA.7Демонстрировать свободное владение умножением и делением с использованием множителей, частных и делителей до 10 включительно. • Знать наизусть все продукты с коэффициентами до 10 включительно. • Проиллюстрируйте и объясните, используя взаимосвязь между умножением и делением. • Определить неизвестное целое число в умножении или уравнении деления, связывающем три целых числа.
- NC.3.OA.1
Для произведений целых чисел с двумя множителями до 10 включительно: • Интерпретируйте множители как представляющие количество равных групп и количество объектов в каждой группе. • Проиллюстрировать и объяснить стратегии, включая массивы, многократное сложение, разложение фактора и применение коммутативных и ассоциативных свойств.
- НК.3.МД.8
Решайте задачи, связанные с периметрами многоугольников, в том числе нахождение периметра по длинам сторон и нахождение неизвестной длины стороны.
- NC.3.OA.7
Демонстрировать свободное владение умножением и делением с использованием множителей, частных и делителей до 10 включительно. • Знать наизусть все продукты с коэффициентами до 10 включительно. • Проиллюстрируйте и объясните, используя взаимосвязь между умножением и делением. • Определить неизвестное целое число в умножении или уравнении деления, связывающем три целых числа.
- NC.3.NF.2
несвязанный
Вот навык, которым Северная Каролина требует от вас овладеть
- Уровень образования
- Государственный тест Тест в конце класса
- ГОСТы Стандартный курс обучения в Северной Каролине
- Предмет Математика
- Название темы Словесные задачи на умножение/деление
- Стандартный идентификатор NC.3.OA. 3
- Описание
Представлять, интерпретировать и решать одноэтапные задачи на умножение и деление. • Решайте задачи на умножение слов с коэффициентами до 10 включительно. Представьте задачу, используя массивы, картинки и/или уравнения с символом неизвестного числа для представления задачи. • Решайте задачи на деление слов с делителем и частным до 10 включительно. Представьте задачу, используя массивы, картинки, многократное вычитание и/или уравнения с символом неизвестного числа для представления задачи.
3 Определение темы
Умножение – это многократное добавление одного числа к самому себе столько раз, сколько второе число. Например, 3 × 5 представляет собой 3 набора по 5 и может быть получено путем прибавления 5 к самому себе 3 раза: 5 + 5 + 5. Изучение фактов умножения — это более быстрый способ найти это повторяющееся значение сложения.
Умножение – это действие, при котором одно число прибавляется к самому себе столько раз, сколько второе число, что быстрее, чем многократное прибавление после того, как факты умножения изучены.
Продукт это ответ, полученный при перемножении двух или более чисел.
Раздел это процесс равного распределения или равного распределения .
Разделение – это разделение на равные группы или части.
Частное – это ответ на задачу на деление. Число, которое делится, называется делимым , а число, на которое делится делимое, называется делителем .
Разделение — это разделение числа, набора или формы на более мелкие единицы, группы или части.
Прямоугольный массив – это набор объектов, расположенных в строках и столбцах, образующих прямоугольник.
Модель площадей представляет собой прямоугольную диаграмму, которую можно использовать для задач на умножение и деление. При умножении множители определяют длину и ширину прямоугольника, а площадь представляет произведение.
измерение – это число, показывающее длину, количество, вес или другой количественный атрибут чего-либо.
Рисунки – визуальные модели , которые можно использовать для иллюстрации или демонстрации проблемы, концепции, процесса или навыка.
Уравнение – это математическое выражение или числовое выражение, включающее знак равенства между двумя выражениями.
Символ — это символ или изображение, используемое для представления слова или значения.
Education Galaxy помогает учащимся освоить стандартный курс обучения в Северной Каролине
Education Galaxy помогает учащимся освоить стандартный курс обучения в Северной Каролине, чтобы подготовить их к выпускному тесту, проводимому школами Северной Каролины. Программа подготовки Education Galaxy обеспечивает онлайн-оценку и практику для учащихся классов K-6, чтобы помочь им освоить стандартный курс обучения в Северной Каролине. Наша уникальная онлайн-программа проста в использовании и доставляет удовольствие как учителям, так и ученикам. Учащиеся работают над своими учебными планами, практикуя важные концепции, в то время как учителя составляют отчеты о формативной оценке, чтобы определить сильные и слабые стороны своего класса и отдельных учащихся.
Общие базовые стандарты — умножение
Многие штаты перешли к группе единых ключевых стандартов для каждого уровня обучения. Они известны как общие основные стандарты. Ниже приведены общие основные стандарты, касающиеся базового умножения. Наш сайт работает над созданием ресурсов для ВСЕХ общих основных стандартов, касающихся умножения. Выделены стандарты, на которые мы сейчас ориентируемся.
OA.2 
OA.6 