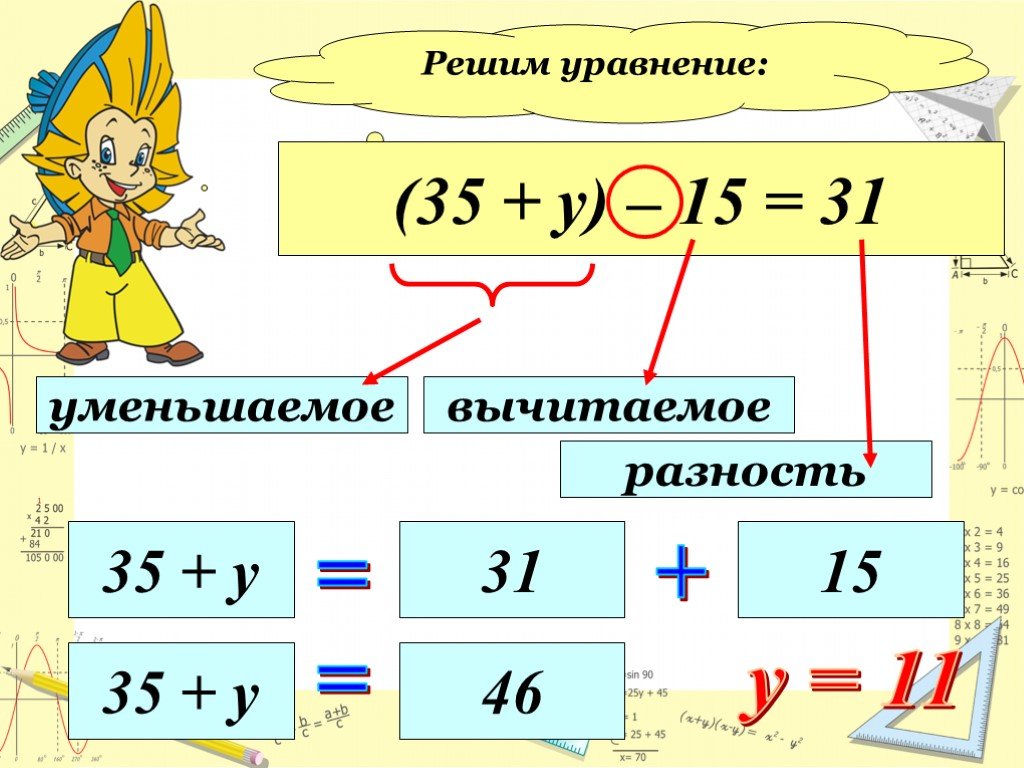
Уравнения 3 класс: Контрольная работа по математике на тему “Решение уравнений” (3 класс) – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Решаем примеры и уравнения. 3 класс (Елизавета Коротяева)

180 ₽

+ до 27 баллов

Бонусная программа

Итоговая сумма бонусов может отличаться от указанной, если к заказу будут применены скидки.

Офлайн

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

В наличии в 19 магазинах. Смотреть на карте

Пособие «Решаем примеры и уравнения. 3 класс» предназначено для самостоятельной работы учащихся. Каждый раздел четко структурирован: он содержит правила, образцы выполненных заданий различных типов, предусмотренных программой по математике для начальной школы, и упражнения для отработки практических навыков. В книге размещены ключи ко всем заданиям. . .Издание предназначено для учеников младших классов, их родителей и учителей.

Описание

Характеристики

Феникс

На товар пока нет отзывов

Поделитесь своим мнением раньше всех

Как получить бонусы за отзыв о товаре

Сделайте заказ в интернет-магазине

Напишите развёрнутый отзыв от 300 символов только на то, что вы купили

Дождитесь, пока отзыв опубликуют.

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Книга «Решаем примеры и уравнения. 3 класс» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене. Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом другом регионе России, вы можете оформить заказ на книгу Елизавета Коротяева «Решаем примеры и уравнения.

3 класс» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.

Урок математики 3 класс. Составные уравнения

Конспект урока математики

Учитель: Разинкова Екатерина Станиславовна

УМК: Школа 2100

Предметная область: Математика (Т.Е.Демидова, С.А.Козлова, А.П.Тонких) 3 кл

Тема: Составные уравнения.

Тип урока: урок открытия нового знания

Цель: научиться решать составные уравнения, получить возможность научиться решать задачи с помощью составных уравнений.

Задачи урока:

Сформировать умение решать составные уравнения.
Отрабатывать навыки решения уравнений на нахождение компонентов арифметических действий.
Тренировать вычислительный навык, умение анализировать уравнения.
Составить алгоритм решения составных уравнений.

Планируемые результаты:

Личностные УУД:

1.Создание условий для проявления познавательной инициативы в оказании помощи одноклассникам.

2. Способность к самооценке на основе критерия успешности учебной деятельности.

3.Формирование толерантности (уважительного отношения к мнению одноклассников).

Регулятивные УУД:

1.Уметь определять и формулировать цель на уроке с помощью учителя.

2.Проговаривать последовательность действий на уроке.

3.Планировать своё действие в соответствии с поставленной задачей.

4.Работать по коллективно составленному плану.

5.Оценивать правильность выполнения действия.

6.Высказывать своё предположение.

Познавательные УУД:

1.Уметь ориентироваться в своей системе знаний (отличать новое от уже известного с помощью учителя).

2.Добывать новые знания (находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке).

3.Создавать алгоритм деятельности, использовать знаково-символические средства.

4.Строить логическую цепочку рассуждений.

Коммуникативные УУД:

1.Уметь оформлять свои мысли в устной форме.

2.Слушать и понимать речь других.

3.Совместно договариваться о правилах поведения и общения и следовать им.

4.Уметь выражать свои мысли с достаточной полнотой и точностью.

Используемые технологии: технология развития критического мышления.

Оборудование: компьютер, мультимедийный проектор, презентация к уроку, учебник «Математика» (2 часть), памятки, карточки с заданиями, алгоритм.

Ход урока

1.Организация урока.

-Друзья мои, добрый день. У нас сегодня необычный урок, присутствуют гости, повернитесь, поприветствуйте гостей, садитесь.

Все за парты дружно сели,

Друг на друга посмотрели,

Улыбнулись, пожелали друг другу удачи.

И вперед за новыми знаниями.

-Что прежде всего на до сделать?

– Откройте тетради и запишите число, классная работа.

2.Математическая разминка.

Сначала мы должны понять, чему научились на предыдущих уроках?

13	310

680	50	180	720	12	310

В 780:60= И 6*120=

М 250:5= А 910:7=

Н 360:2= Ы 930:3=

У 170*4= Ц 72:6=

-ВЫ УМНИЦЫ

Все знания, которые у вас есть, вам сегодня очень пригодятся.

Ребята, сегодня на уроке постарайтесь показать свои умения

– вычислять

– доказывать

– рассуждать

3. Актуализация знаний. «Загадка».

Послушайте загадку и скажите отгадку.

Он есть у слова и цветка,
Он есть у уравнений,
Заданий многих он итог,
И с этим мы не спорим.
Надеемся, что каждый смог
Ответить: это ……(корень).

– Где мы встречаемся с корнем на уроках математики? (в уравнении)

– Что вы знаете об уравнении?

(Уравнения – это равенства с переменной, которую нужно найти.

Решить уравнение, значит найти корень уравнения.

– Какие мы решаем уравнения

(Есть уравнения, в которых нужно найти неизвестные слагаемое, множитель, уменьшаемое, вычитаемое, делимое, делитель.)

4. Постановка проблемы.

Рассмотрите записи

На какие 2 группы можно разбить данные записи?

Прочитайте числовые выражения

Чем являются остальные записи

-Возьмите карандаш и отметьте уравнения

505 +25 48 : Х = 8

694 – 94 40 – Х = 12

808 : 8 140+Х= 200

150 * 3 Х:5 = 6+ 9

Числовые Уравнения

выражения–

Докажите, что во 2 столбике – уравнения (это равенства, содержащие переменную)

– Чем мы пользуемся, когда решаем уравнения? (алгоритмом)

– Давайте вспомним его.

Восстановите последовательность алгоритма решения уравнения(На листах )

Алгоритм решения простого уравнения.

1. Выделяем неизвестный компонент.

2. Применяем правило нахождения неизвестного компонента.

3. Выполняем действие и получаем ответ.

4. Делаем проверку

– Решите уравнения.

– Какое уравнение не смогли решить? Прочитайте его, используя математ. язык

-Почему не смогли решить? ( 2действия)

-А интересно ли узнать как решаются эти уравнения

-Давайте вспомним наш девиз:

Все то, что неизвестно –

Ужасно интересно!

– Как бы вы назвали это уравнение?(СОСТАВНОЕ)

– Сформулируйте тему урока (Решение уравнений нового вида)

– Какую же цель мы для себя определим на этом уроке?

(Научиться решать уравнения нового вида)

-Что мы хотим узнать?

(Как решать уравнения нового вида. Какой алгоритм для этого нужен?)

– Подходит ли наш алгоритм для решения этого уравнения?

5. Постановка проблемы.

Откроем учебник . Познакомимся с основным вопросом урока

Парно-групповая работа. Задание № 1, с. 88

– Прочитайте задание.

– Рассмотрите рисунок.

– Обсудите в парах уравнение Вити.

Текст со знаком ?!.

– Подходит ли наш алгоритм для решения этого уравнения?

– Предложите способы его решения

6.Открытие нового (узнаём новое).

1. Задание № 2, с. 88

Цель работы:

– на основе наблюдений над представленным способом действий сформулировать правило поиска решения уравнений нового вида, сводимого к способу решения уравнений, изученных во 2-м классе.

– Прочитайте задание.

– Рассмотрите схему.

– Обсудите в парах, как найти значение а.

– Предложите ход решения полученного уравнения.

2. Работа с текстом в оранжевой рамке.

– Какой алгоритм действий вы предложите?

(Сначала найти значение правой части уравнения, затем решать уравнение как обычно).

7. Первичное закрепление (применяем новые знания).

Работа в парах.1. Задание № 3, с. 88

– Обсудите в парах и придумайте задачу по рисунку.

– Пользуясь предложенным алгоритмом решения, найдите

значение х.

8.ФИЗМИНУТКА

9. Задание № 4, с. 89

– Прочитайте и обсудите задание.

– Внимательно рассмотрите уравнения.

– Можно ли выбрать пары уравнений, не решая их? (Да)

Назовите уравнения парами.

Решите уравнения нового вида, используя и новый алгоритм.

10.Тренинг (выбираем задания и тренируемся).

Решение задач.1. Задача № 5а, с. 89

– Прочитайте задачу.

– Выделите необходимую информацию в условии.

– Предложите модель для записи условия. (Схема).

– Как в схеме изобразить рисунки Майи? (Одна часть).

– А Лики? (В 3 раза больше – 3 такие части).

– Сколько всего рисунков за лето сделали девочки?

– Расскажите задачу по схеме.

– На какой вопрос надо ответить?

– Составьте план решения задачи.

– Решите задачу.

( 1). 1 + 3 = 4 (части) – всего; 2). 120 : 4 = 30 (рис.) – сделала Майя;

3). 30 ∙ 3 = 90 (рис.) – сделала Лика; или 3). 120 – 30 = 90(рис.)

Проверка решения индивидуальная либо у доски по алгоритму самооценки.

Вопросы к ученикам, выполнявшим работу:

– Что вам нужно было сделать в задании?

– Удалось ли правильно решить поставленные задачи?

– Вы сделали всё правильно или были ошибки, недочёты?

– Вы решили всё сами или с чьей-то помощью?

— Какого уровня сложности было задание? — Оцените свою работу.

– Есть ли у ребят какие-либо дополнения, замечания? Согласны ли вы с такой самооценкой?

11. Рефлексия учебной деятельности на уроке. Подведение итогов урока.

Какие равенства мы сегодня решали? – Уравнения.

Что содержит уравнение?- Переменную.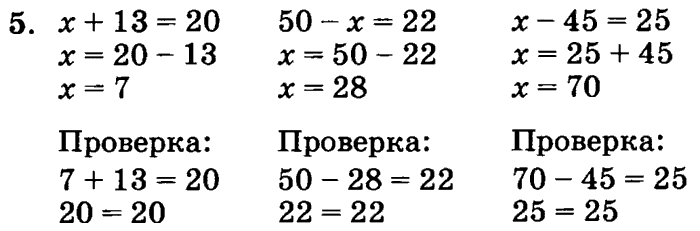

Что значит решить уравнение?- Найти его корень.

– Что нового вы узнали сегодня на уроке? – Чему научились?

– Какие задачи решали?- Всё ли получалось?

– Над чем ещё надо поработать?

Кто может сказать, уходя с урока, что он научился решать составные уравнения?

Посмотрите на свои листы самооценки и оцените свою работу на уроке.
-Кто уверенно сказал себе: “Я добился цели!”
– Кто сегодня все задания выполнил без ошибок?
– У кого одна ошибка? У кого больше? Значит, на следующих уроках нам надо над этим поработать.

12. домашнее задание. Задания № 5б, 6, с. 89

Переменные в уравнениях сложения и вычитания — Математика 3-го класса

На прошлом уроке вы узнали, что переменные — это буквы, которые заменяют неизвестные вам числа.

Давайте перепишем задачи выше 👆, используя переменные.

Мы можем заменить каждую коробку буквой!

Совет: Удобно использовать переменные вместо просто вопросительных знаков?, потому что иногда может быть больше одного неизвестного! Поэтому им нужны собственные имена.

😺 Итак, переменная — это просто короткое имя, например y, которое вы выбираете для чего-то неизвестного.

Решение для значения из переменной просто означает нахождение того числа, которое входит в поле, чтобы сделать уравнение верным.

Как решить для переменной

x + 6 = 9

Как мы можем найти значение из x , при котором уравнение остается верным?

Давайте подумаем. 🤓 Знак равенства говорит нам, что значение слева такое же, как справа.

Вы можете думать об этом как о сбалансированных весах.

Мы хотим знать, какое значение из x будет поддерживать баланс уравнения .

👉 Итак, мы хотим, чтобы получило x на одной стороне шкалы только , чтобы мы могли видеть его общее значение!

Как?

👉 Мы должны отменить то, что было сделано с x.

Что сделано с переменной x? 🤔

👉 6 было добавлено к переменной x.

Как это отменить?

👉 Мы вычитаем 6.

Совет: Сложение есть противоположное вычитания. Чтобы отменить сложение, вы должны вычесть.

🤔 Но как мы можем сохранить уравнение сбалансированным , если мы вычтем 6 из левой части уравнения?

Правильно!

Чтобы сохранить уравнение сбалансированным , что бы мы ни делали с одной стороны, мы должны делать и с другой стороны.

Итак, если мы вычтем 6 из левой части, мы должны вычесть 6 из правой части тоже.

Давайте попробуем.

x + 6 = 9

x + 6 – 6 = 9 – 6

x = 3

с другой стороны, уравнение остается сбалансированным !

Взгляните:

Совет : Думайте об этом, как о взятии одинакового количества шариков из двух чаш.

🤓 Как только мы получим что-то вроде « переменная = некоторое число », это значение переменной, которая делает уравнение верным!

Значение переменной , которое делает уравнение истинным , называется решением для уравнения .

Это означает, что x = 3 — это решение в уравнение ! 🎉

Решение для переменной Пример

10 – y = 2

Наша цель — получить только y с одной стороны.

Что сделано с переменной y? 🤔

👉 Переменная y была вычтена из 10.

Как это отменить?

👉 Поскольку y было вычтено из 10, давайте попробуем прибавить y и посмотреть, что получится.

Только не забудьте сделать то же самое с обеих сторон.

10 – у + у = 2 + y

10 = 2 + y

Подсказка: -y + y = 0, потому что все минус само равно 0.

Теперь у нас более простая задача.

Итак, какова наша цель?

👉 Наша цель — получить переменную y только в одной части уравнения. Вот как мы решаем уравнение .

Итак, давайте попробуем вычесть 2 из обеих частей, чтобы получить только y:

10 = 2 + y

10 – 2 = 2 + y – 2

8 = Y + 2 – 2
Совет: Мы Просто поменял заказ y и 2 правой стороны. . Мы также упростили левую сторону.

8 = y

Это означает, что y = 8 есть решение к уравнение !

Чтобы решить уравнение с одной переменной, возьмите одну переменную с одной стороны уравнения и упростите остальные.

Давайте посмотрим на последний пример.

Найти z :
15 + 5 = z – 3

Что было сделано с переменной z?

👉 3 было вычтено из переменной z.

Как это отменить?

👉 Добавив 3 к обеим частям уравнения, чтобы сохранить его баланс.

15 + 5 + 3 = z – 3 + 3

Теперь мы упростить все что можно.

23 = z

Это означает, что значение z равно 23, а z = 23 – это решение к уравнение !

Чтобы проверить правильность ответа, замените переменную в исходном уравнении найденным числом.

Проверяем, имеем:

15 + 5 = z – 3

15 + 5 = 23 – 3

20 = 20 ✅

Так как левая часть равна правой. Это означает, что мы нашли правильное значение z.

Отлично научился решать уравнения! Сначала это может быть сложно, но вы быстро справитесь! 💪

Завершите практику, чтобы узнать больше и дольше помнить.

Уравнения и эквивалентность в 3-м классе

Итак, я тупо болтал в Интернете с некоторыми невероятно серьезными исследователями об эквивалентности и знаке равенства и о том, что это не такая сложная тема для преподавания, когда — ОЙ! — мое фактическое преподавание мешало.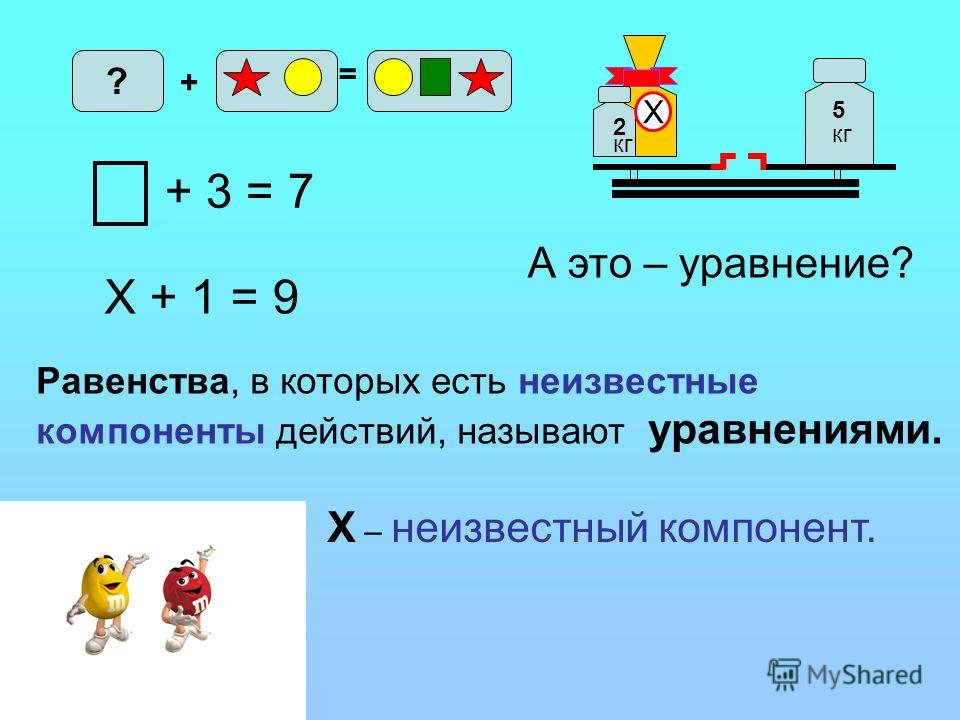

Я поступил правильно. В моем 3-м классе я хотел ввести «?» как символ неизвестного, поэтому я написал на доске несколько уравнений:

15 = ? х 5

3 + ? = 10

10 + 3 = 11 + ?

И я не был ни шокирован, ни моргнул, когда ребенок сказал мне, что последнее уравнение не имеет никакого смысла. Ах, подумал я, пора пресечь это в зародыше.

Я выслушал ребенка и сказал, что понял, но хотел бы поделиться, как это все-таки имеет смысл. Я спросил, знает ли кто-нибудь, что означает знак равенства, и один ребенок сказал «делает», а другой сказал «такой же, как». Замечательно, сказал я, потому что последнее уравнение просто говорит, что левая часть равна правой. Итак, какое число сделает их одинаковыми? 2? Фантастика, идем дальше.

Затем, на следующий день, я поставил задачу на доске:

5+ 10 = ___ + 5

И вы знаете, что будет дальше, верно? Все согласны с тем, что пробел равен 15. «Но разве мы не говорили вчера, что знак равенства означает «такой же, как»?» Я спросил.

Ребенок поднял руку и объяснил, что это действительно означает это, но ответ все равно должен быть 15. Вот как она хотела, чтобы мы прочитали уравнение в виде прогона:

(5 + 10 = 15 ) + 5

Два теперь мне все стало ясно. Во-первых, моя гордость тем, что я четко и решительно занялся этим вопросом, была ошибочной. Мне нужно было сделать больше и глубже вникнуть в это.

Во-вторых, разве это не интересно? Вы можете иметь совершенно правильное понимание знака равенства и по-прежнему совершать те же «классические» ошибки, интерпретируя реальное уравнение.

Думаю, это поможет прояснить некоторые вещи, которые я путал в голове. Когда люди говорят о том, что детям необходимо хорошо понимать эквивалентность, они на самом деле имеют в виду несколько разных вещей. Вот два, которые появились выше:

Особое значение знака равенства (из этого следует, что уравнение может быть написано как слева направо, так и справа налево, т.е. оно симметрично)

Обычные способы написания уравнений (например, без последовательностей, может включать несколько операций и условий с каждой стороны)

Но это только начало, потому что часто люди говорят о множестве других вещей, когда говорят об «эквивалентности». Вот лишь некоторые из них:

Вы можете выполнять одинаковые операции с каждой стороной (известно полезно для решения уравнений)
Вы можете манипулировать одинаковыми элементами на одной стороне уравнения, чтобы создать истинное уравнение (10 + 5 можно превратить в 9 + 6 можно превратить в 8 + 7; 8 x 7 можно превратить в 4 x 14; 3 (x + 4) можно превратить в 3x + 12 и т. д.)

Когда ребенок не может решить 5 + 10 = ___ + 9 правильно или легко, используя «реляционное понимание», это часто винят в понимании ребенком знака равенства, эквивалентности или конкретных способов соотнесения 5 + 10 с __ + 9. Но теперь я ясно вижу, что это разные вещи, и одни даются детям легче, чем другие.

Итак, мы подошли к следующему уроку с моими 3-классниками.

Я начал, как обычно в этой ситуации, с избегая знака равенства . Я обнаружил, что двойная стрелка хорошо служит для этой цели, поэтому я изобразил на доске соотношение стрелок:

2 x 6 <–> 8 + 4

Я указал, что 2 x 6 дает 12, а также 8 + 4. Я спросил, могут ли дети придумать что-нибудь еще подобное?

Да. Я не сделал фото, но я был благодарен, что все подошло. Дети прекрасно смешивали операции, например, 12 – 2 <–> 5 + 5, в целом казалось, что это не сложно, дети точно знали, что я имею в виду, и могли генерировать множество идей.

Следующим моим шагом было сделать паузу и ввести в этот разговор знак равенства. Кто-нибудь будет возражать, если я заменю эту двойную стрелку знаком равенства? Во всяком случае, именно это и означает знак равенства. Ничего страшного, тоже все прошло нормально.

Дети даже представляли замечательные примеры, такие как 1 x 2 = 2 x 1 или 12 = 12. Замечательно.

Затем я представил задачу дня в стиле Open Middle (R) (TM) (C):

Да, я быстро написал ее от руки маркером. Это был именно такой день.

Я подробно объяснил ограничения. 10 – 2 + 7 + 1 было правильным уравнением, но для этой головоломки не годилось. Как и 15 – 5 = 6 + 4. А потом я дал детям время на поиск решений, сколько они смогли найти.

Бла-бла-бла, большинство детей добились успеха, другим было трудно начать, но все в конце концов добились определенного успеха. Вот несколько фотографий учеников, которые меня украшают:

Вот фотография ученика, который боролся, но в конце концов нашел решение:

Вот фотография ученика из класса, в котором я учился больше всего волнует. Вы можете видеть отметки вдоль его страницы, когда он пытается обрабатывать такие вещи, как 12 – 9, когда он пытается вычитать разные числа из 12. Я думаю, что с правой стороны могло происходить какое-то умножение, не знаю почему. В любом случае:

Дело в том, что накануне этот последний студент чуть не сломался от разочарования из-за своей неспособности разобраться в этих «нетрадиционных» уравнениях. Так что это заставляет меня выглядеть отлично — я сделал это! Я научил его эквивалентности примерно за день. Тада.

Но я не думаю, что это то, что происходит. Понятие равенства двух различных вещей не было для него трудным.

На самом деле, я не думаю, что это понятие вообще сложно для очень многих учеников — дети знают, что различные сложения равны 10. И для этого ребенка не было особенно сложно объединить это понятие эквивалентности со знаком равенства. Мол, нет, он не думал, что именно это означает знак равенства, но что бы там ни было, это было просто на основании того, что он думал раньше. Это просто условность. Я сказал ему, что знак равенства означает что-то еще, хорошо, конечно. Не так уж и плохо.
Однако для этого студента было очень сложно вычитать из 12. Это правда — мне бы очень хотелось, чтобы этот студент знал, что 10 + 2 <–> 9 + 3, и поэтому, когда он увидел 12, он мог связать это с 10 + 2 и, следовательно, быстро перейти к 9 + 3 и понять, что 12 — 3 = 9 Я имею в виду, что это то, что делают многие мои третьеклассники, не так много слов. Это очень полезно.
В завершение несколько вопросов и несколько предварительных ответов:

В: Сложно ли преподавать или изучать концепцию эквивалентности.
A: №
Q: Трудно ли выучить знак равенства и его значение?
А: Это сложнее , но это все условно. Если вы введете новый символ, такой как «<–>», я не думаю, что дети так сильно спотыкаются. Иногда им приходится забыть о том, что они сделали из предыдущего опыта, который был слишком ограничен (т. е. всегда ставить результат на правильную сторону). Таким образом, вы не делаете детям никаких одолжений, делая это, хорошо представлять уравнения в самых разных формах, как только дети впервые видят уравнения в K или 1-м классе. Я имею в виду, почему бы и нет?
В: Если дети не узнают, как обычно работают уравнения, не запутаются ли они позже в алгебре?
О: Да. Но всем моим детям складывать и вычитать сложнее, чем понимать эти условности. Я считаю, что вам не нужно года , чтобы привыкнуть к тому, как работают уравнения. Тебе нужен час или два, чтобы представить его.
В: Нужно ли учить этому заранее? Не слишком ли поздно изучать алгебру, как работают уравнения?
A: Я думаю, что дети должны учиться этому рано, но ВООБЩЕ не поздно, если они этого не сделают.
Я вел занятия по алгебре в 8-м и 9-м классах, где ученики не понимали, как работают уравнения. По моим воспоминаниям, это раздражало, потому что я слишком поздно понял, что происходит, и мне пришлось отступить. Но, основываясь на том, что я обучаю этому младших детей, я не могу себе представить, что уже слишком поздно учить этому старшеклассников.
Я думаю, возможно, что с годами становится все труднее вытряхнуть учащихся из их более ограниченного понимания уравнений, потому что они укрепляют их теорию об уравнениях и символе равенства. Я не знаю.
Я не вижу причин не учить этому раньше, но я думаю, важно помнить, что в средней школе мы говорим детям, что иногда вычитание числа делает его больше и что существуют отрицательные показатели степени. Дети могут узнать что-то новое и в более поздние годы.
В: Так что же мешает маленьким детям решать уравнения вроде 5 + 10 = 6 + __?
О: Совершенно верно, что дети, которые не понимают, как читать такого рода уравнения, вообще не смогут участвовать. Но самому относительному мышлению, как мне кажется, труднее всего научить и чему научиться.
Вот мысленный эксперимент. Что, если бы у вас была школа или учебная программа, в которой только использовали знаки равенства и уравнения скучным, ограниченным способом «5 + 10 = »? и «6 х ? = 12” на протяжении всей школы, но в то же время глубоко и эффективно обучали реляционному мышлению с использованием <–> и другой терминологии? А затем в 8-м классе у них есть несколько уроков, обучающих «новому» способу понимания знака равенства? Будет ли это иметь большое значение? Я не знаю, я так не думаю.
В: Есть данные, свидетельствующие о том, что изучение вышеперечисленных вещей помогает детям добиться большего успеха в алгебре на более позднем этапе. Твои мысли?
А: Не знаю! Мне кажется, что если что-то и имеет значение для более поздней алгебры, то это должна быть либо концепция эквивалентности, либо условность уравнений, либо реляционное мышление.
Я думаю, что понятие эквивалентности знакомо каждому ребенку. Я думаю, что правила уравнений не так уж трудно выучить, но они действительно имеют смысл только в том случае, если вы свяжете уравнения с концепцией эквивалентности. Концепция эквивалентности объясняет почему уравнения имеют определенные соглашения. Так что я понимаю, почему эти двое идут вместе. Но может ли этого быть достаточно, чтобы помочь студентам с более поздним опытом алгебры? Может быть. Это потому, что учителя алгебры не учат правилам уравнений на своих занятиях? Будет ли преимуществом ранний опыт работы с уравнениями, если его будут преподавать учителя алгебры?
В конце концов, это не имеет большого значения, потому что маленькие дети могут этому научиться, так почему бы не научить их этому? Не повредит, только стоит вам час или два.
Еще одна важная вещь — это реляционное мышление. Теперь я не думаю, почему реляционное мышление имеет место в контексте уравнений. Вы МОЖЕТЕ использовать другие символы, такие как двойные стрелки или что-то еще.