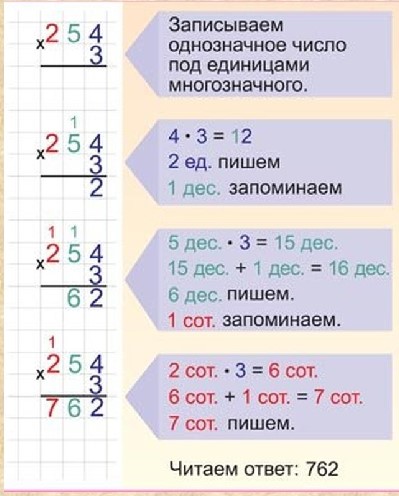
Умножение столбиком 3 класс примеры тренажер: Тренажер на умножение столбиком

Тренажер: умножение в столбик – intmag24.ru

60,00 ₽

Примеры в столбик на умножение. Выбор первого и второго множителей: однозначные, двузначные и трехзначные.  С ответами. Для решения  на компьютере (в Excel без печати).

Артикул: i-13739 Категория: Для учебы Метки: 3 класс, 4 класс, 5-8 класс, Примеры в столбик

• Описание
• Детали
• Отзывы (0)

Описание

Тренажер на умножение в столбик – программа, которая формирует примеры на умножение в столбик, чтобы решать их на компьютере (не распечатывая).

Программа написана в Excel с помощью макросов. С помощью генератора примеров можно создать неограниченное число примеров. Можно выбрать уровень сложности: задать отдельно первый и второй множители — однозначные, двузначные или трехзначные числа.

• При нажатии кнопки «Начать» запускается счетчик (обнуляется), который подсчитывает количество решенных примеров, в том числе  правильных и решенных с ошибкой.
• При нажатии кнопки «Новый пример» формируется новый пример на умножение в столбик. При этом статистика правильных и неправильных примеров сохраняется.
  При нажатии кнопки «Проверить» программа проверяет правильность решения примеров.

Записывать ответ можно с помощью клавиатуры или кнопок (для удобства в карточке есть кнопки с цифрами, которые можно использовать при выборе ответа).

Тренажер примеров на умножение в столбик по математике удобен, так как не нужно заранее покупать задачники и пособия по математике с примерами. Можно скачать файл и решать примеры в любое время независимо от подключения к интернету.

Если Вы хотите посмотреть принцип работы программы, можете скачать программу «Тренажер счета в пределах 10» бесплатно.

Карточки для печати в формате А4 можно получить в программе «Умножение в столбик» или «Умножение в столбик 2 (с клеткой)«.

• Другие программы, которые помогут закрепить навыки счета:
  • • Деление в столбик, Деление в столбик 2 (с клеткой)
    • Умножение и деление в столбик
    • Сложение и вычитание в столбик, Сложение и вычитание в столбик 2 (с клеткой)
    • Примеры в столбик на сложение, вычитание и умножение: заполнить пропуски
    • Умножение и деление по типам (табличное, внетабличное, круглых чисел)
    • Деление с остатком на число (с выбором уровня сложности)

На сайте представлен

каталог программ, в котором все программы распределены по группам. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.

Вам также будет интересно…

• Задачи на движение (разные виды)

  80,00 ₽В корзину

• Сложение и вычитание в столбик 2 (с клеткой)

  75,00 ₽В корзину

• Умножение в столбик 2 (с клеткой)

  75,00 ₽В корзину

• Умножение в столбик

  60,00 ₽В корзину

• Сложные примеры на порядок действий

  100,00 ₽В корзину

• Тренажер: сложение и вычитание в столбик

  60,00 ₽В корзину

• Сложение и вычитание в столбик

  Оценка 5. 00 из 5

  60,00 ₽В корзину

• Деление в столбик

  60,00 ₽В корзину

• Умножение и деление в столбик

  Оценка 4.50 из 5

  80,00 ₽В корзину

• Порядок действий в пределах 1000 (все действия)

  80,00 ₽В корзину
• Деление в столбик 2 (с клеткой)

  75,00 ₽В корзину

• Примеры в столбик на сложение, вычитание и умножение: заполнить пропуски

  80,00 ₽В корзину

Тренажер сложения, вычитания, умножения и деления столбиком

Skip Navigation Links

Тренажер сложения, вычитания, умножения и деления столбиком оснащен функцией автоматической проверки решения, индикатором времени и статистикой правильных и неправильных ответов. Тренажер будет полезен детям учащимся во 2, 3 и 4 классе.

 Тип примера
  СложениеВычитаниеУмножениеДелениеЛюбой типСложение и вычитаниеСложение и умножениеСложение и делениеВычитание и умножениеВычитание и делениеУмножение и деление

 Уровень сложности
 

1

2

3

4

Правильно:&nbsp&nbsp 0

Ошибок:&nbsp&nbsp 0

00:00:00

+	−
×	÷

Тренажер по математике Тренажер по математике предназначен для развития навыков устного счета, таких математических операций как: сложение, вычитание, умножение и деление. Для начала работы выберите тип примера и уровень сложности. Тренажер оснащен функцией автоматической проверки решения, индикатором времени и статистикой правильных и неправильных ответов.

49	17
25	12

Тренажер решения примеров. Найди правильный ответ. Тренажер решения примеров позволит улучшить навыки сложения, вычитания, умножения и деления. Для того чтобы начать тренировку, выберете математическую операцию и уровень сложности, далее необходимо выбрать правильный ответ из трех предложенных вариантов. Тренажер отображает время прошедшее от начала тренировки, а также количество верных ответов и ошибок. Данный тренажер будет полезен детям с 1 по 5 класс, а также всем, кто хочет улучшить навыки быстрого счета в уме.

5 × 5 = 25

Тренажер таблицы умножения Тренажер таблицы умножения отображает количество правильных и неправильных ответов. Тренажер будет полезен детям от 8 лет 2 класс, а также всем, кто хочет улучшить знание таблицы умножения.

45
_________
15

Тренажер сложения, вычитания, умножения и деления столбиком Тренажер сложения, вычитания, умножения и деления столбиком оснащен функцией автоматической проверки решения, индикатором времени и статистикой правильных и неправильных ответов. Тренажер будет полезен детям учащимся во 2, 3 и 4 классе.

Тренажер счета для дошкольников Данный тренажер поможет выучить цифры от 0 до 10 детям дошкольного возраста. В процессе занятия ребенку необходимо сосчитать количество предметов и выбрать правильный ответ из двух предложенных вариантов. Данный тренажер послужит хорошей альтернативой счету на палочках и закрепит знание цифр у детей.

Тренажер счета на внимательность для дошкольников Данный тренажер поможет выучить цифры от 0 до 10 и повысит внимательность у детей дошкольного возраста. В процессе занятия ребенку необходимо сосчитать количество предметов среди других и выбрать правильный ответ из двух предложенных вариантов. Данный тренажер послужит хорошей альтернативой счету на палочках и закрепит знание цифр у детей.

Тренажер решения примеров с разными действиями Данный тренажер предназначен для тренировки решения примеров на различные действия как со скобками, так и без скобок. Вы быстро научитесь правильно расставлять действия в выражении. Для записи промежуточных решений воспользуйтесь окном в самом низу тренажера.

Объяснение урока: Умножение матриц | Nagwa

В этом объяснителе мы узнаем, как определять условия для матрицы умножение и вычисление произведения двух матриц, если это возможно.

Начнем с того, что вспомним скалярное умножение, которое намного проще, чем умножение матриц. Скалярное умножение включает в себя умножение матрицы скаляром (или числом). Например, рассмотрим матрицу 𝐴=2132.

Если бы мы хотели умножить эту матрицу на скаляр 2, мы бы умножили каждое из компоненты матрицы на 2: 2×𝐴=2×22×12×32×2=4264.

Мы видим, что умножить матрицу на скаляр очень просто. Однако это намного сложнее умножить матрицу на другую матрицу. Прежде чем мы сможем обсуждать, как умножить матрицу на другую матрицу, нам нужно понять когда можно перемножить пару матриц.

Напомним, что порядок матрицы определяется выражением ()×().numberofrowsnumberofcolumns

Например, матрица с 𝑚 строк и 𝑛 столбцов называется матрица 𝑚×𝑛. Чтобы перемножить пару матриц, их порядки должны быть совместимы.

Правило: критерий умножения матриц

Пусть 𝐴 и 𝐵 — матрицы. Чтобы вычислить матрицу умножение 𝐴×𝐵, количество столбцов в 𝐴 должно равняться количеству строк в 𝐵. Если 𝐴 — матрица 𝑚×𝑛 для некоторого положительного целые числа 𝑚 и 𝑛, 𝐵 обязательно быть матрицей 𝑛×𝑝 для некоторого положительного целого числа 𝑝. В этом случае 𝐴×𝐵 является 𝑚×𝑝 матрица.

Из этого критерия умножения матриц видно, что 𝐴×𝐵 не то же самое, что 𝐵×𝐴 для матриц 𝐴 и 𝐵. На самом деле, возможно, что один из них может быть определен, а другой не является.

Например, скажем, что матрицы 𝐴 и 𝐵 в порядке 1×2 и 2×3 соответственно. Тогда количество столбцов 𝐴 равно количеству строк 𝐵, который означает, что умножение матриц 𝐴×𝐵 определено. С другой стороны, количество столбцов 𝐵 не равно к количеству рядов 𝐴. Это означает, что матрица умножение 𝐵×𝐴 не определено. Это говорит нам о том, что матрица умножение некоммутативно, а это означает, что порядок матриц в умножении матриц изменить нельзя.

В первом примере мы найдем порядок матрицы, полученной из умножение матриц.

Пример 1. Порядок матриц при умножении матриц

Заполните пропуск: Если 𝐴 — матрица порядка 2×3 и 𝐵 — матрица порядка 1×3, то матрица 𝐴𝐵 имеет порядок .

1. 3×1
2. 2×1
3. 1×2
4. 3×2

Ответ

Напомним, что количество столбцов в матрице 𝐴 должно быть равным количеству строк в матрице 𝐵 для вычисления умножение матриц 𝐴×𝐵. Мы также вспоминаем что порядок матрицы определяется выражением ()×().

количество строкколичество столбцов

Поскольку порядок матрицы 𝐴 равен 2×3, это говорит нам о том, что количество столбцов в матрице 𝐴 равен 3. Порядок 𝐵 равно 1×3, что означает эта матрица 𝐵 имеет 1 строку и 3 столбца. 𝐵 является транспонированием 𝐵, и мы знаем, что транспонирование матрицы меняет строки матрицы на столбцы его транспонировать. Поскольку транспонирование 𝐵 имеет 1 строку и 3 столбца, матрица 𝐵 должно быть 3 строки и 1 столбец. Это говорит нам что количество столбцов в матрице 𝐴 и количество строк в матрице 𝐵 равно 3, что означает, что умножение матриц допустимо.

Напомним, что умножение матрицы порядка 𝑚×𝑛 матрицей порядка 𝑛×𝑝 приводит к матрице порядка 𝑚×𝑝. В этом примере мы умножение матрицы 2×3 на Матрица 3×1. Это означает 𝑚×𝑛=2×3,𝑛×𝑝=3×1.

Следовательно, 𝑚=2, 𝑛=3 и 𝑝=1. Порядок матрицы 𝐴𝐵 равен 𝑚×𝑝=2×1. Это вариант B.

В следующем примере мы найдем порядок матрицы умножается на основе порядка матрицы произведения, а также порядка другой матрицы.

Пример 2: Порядок матриц при умножении матриц

Заполните пропуск: Если матрица 𝐴 имеет порядок 2×3 и матрица 𝐴𝐵 имеет порядок 2×1, тогда матрица 𝐵 по порядку.

1. 1×3
2. 2×1
3. 1×2
4. 3×1

Ответ

Напомним, что количество столбцов в матрице 𝐴 должно быть равным количеству строк в матрице 𝐵 до вычислить умножение матриц 𝐴×𝐵. Напомним также, что порядок матрицы определяется выражением ()×().количество строкколичество столбцов

Поскольку порядок матрицы 𝐴 равен 2×3, это говорит нам о том, что количество столбцов в матрице 𝐴 равно 3. Это число должно равняться количество строк в матрице 𝐵. Следовательно, количество строк в матрице 𝐵 должно быть равно 3.

Напомним также, что количество строк в матрице 𝐴𝐵 равно количеству строк в матрице 𝐴, а также количество столбцов в 𝐴𝐵 равно количеству столбцов в матрице 𝐵. Нам дано, что матрица 𝐴 есть порядка 2×3 и матрица 𝐴𝐵 имеет порядок 2×1, и мы видим, что количество строк в матрицах 𝐴 и 𝐴𝐵 одинаковы. Поскольку матрица 𝐴𝐵 имеет 1 столбец, это говорит нам о том, что число столбцов в 𝐵 должно быть равно 1,

Следовательно, матрица 𝐵 имеет порядок 3×1. Это вариант D.

В следующем примере мы проверим критерий умножения матриц на определить, корректно ли определено данное матричное умножение.

Пример 3. Нахождение произведения двух заданных матриц

Учитывая, что 𝐴=512−3−4−3,𝐵=1−25−4, определить 𝐴𝐵, если это возможно.

Ответ

Напомним, что количество столбцов в матрице 𝐴 должно равно количеству строк в матрице 𝐵 для вычисления умножение матриц 𝐴×𝐵. Мы также вспоминаем что порядок матрицы определяется выражением ()×().количество строкколичество столбцов

Мы видим, что матрица 𝐴 имеет 2 строки и 3 столбца. а матрица 𝐵 имеет 2 строки и 2 столбца. Поскольку количество столбцов в 𝐴 не равно количеству строк в матрице 𝐵, умножение матриц 𝐴𝐵 не определено.

В предыдущих примерах мы рассмотрели свойство порядка матриц при умножении матриц. Теперь, когда мы знаем, когда пара матриц может быть умножаются, рассмотрим, как перемножать матрицы. Простейший умножение матриц – это умножение матрицы-строки на столбец матрица.

Практическое руководство. Умножение матриц-строк на матрицы-столбцы

Пусть 𝐴 и 𝐵 будут матрицами-строками и матрицами-столбцами соответственно. Тогда матрица 𝐴𝐵 корректно определена и имеет порядок 1×1. Запись этой матрицы получается умножение каждой записи в матрице-строке на соответствующую запись в матрице матрица столбцов, а затем суммирование всех продуктов.

Мы продемонстрируем этот процесс в следующем примере.

Пример 4. Нахождение произведения двух заданных матриц

Рассмотрим матрицы 𝐴=(12−7),𝐵=−46−2.

Найдите 𝐴𝐵, если возможно.

Ответ

Мы знаем, что умножение матриц возможно, только если число столбцов первой матрицы совпадает с количеством строк вторая матрица. Заметим, что количество столбцов первого матрица 𝐴 и количество строк второго обе матрицы 𝐵 равны 3, поэтому возможно вычислить умножение матриц 𝐴𝐵.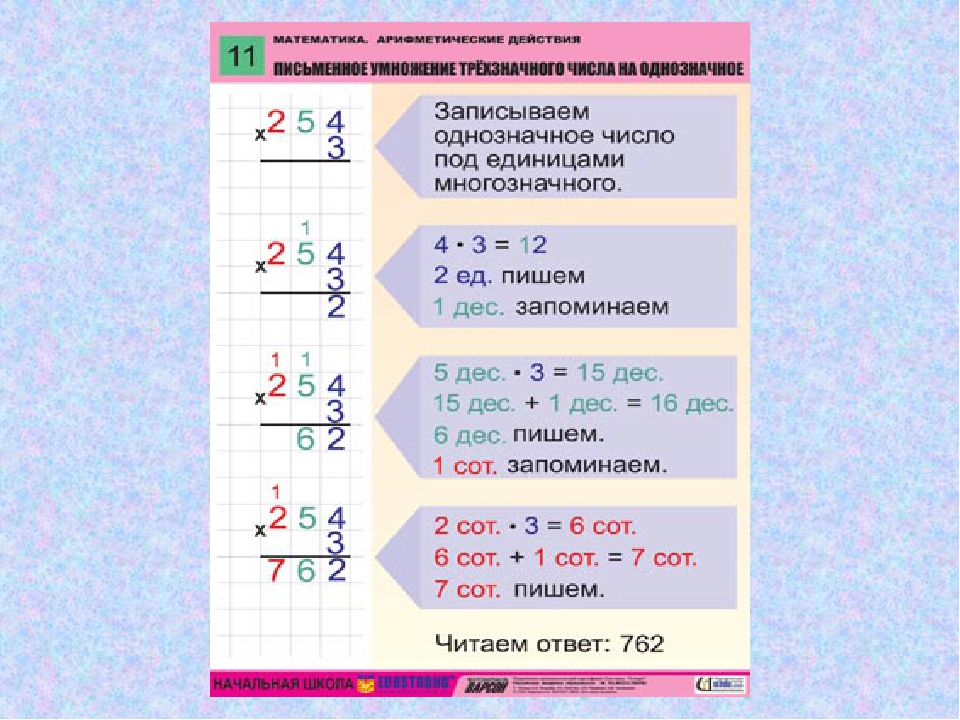

Мы также знаем, что умножение матрица 𝑚×𝑛 на матрица 𝑛×𝑝 дает 𝑚×𝑝 матрица. Мы видим, что заказы матрицы 𝐴 и 𝐵 являются 1×3 и 3×1 соответственно. Следовательно, 𝑚=1, 𝑛=3 и 𝑝=1. Это говорит нам о том, что матрица 𝐴𝐵 имеет порядок 𝑚×𝑝=1×1.

Так как матрица 𝐴 имеет только одну строку, это строка матрица. Точно так же матрица 𝐵 является матрицей-столбцом. Напомним, что мы можем умножить матрицу-строку на матрицу-столбец на умножая каждую запись в матрице 𝐴 на соответствующая запись в столбце 𝐵 и суммирование все продукты. В следующем расчете мы выделили соответствующие записи в каждой матрице одного цвета: 𝐴𝐵=(12−7)−46−2=(1×(−4)+2×6+(−7)×(−2))=(−4+12+14)=[22].

Мы видим, что порядок 𝐴𝐵 равен 1×1, как и ожидалось.

Следовательно, 𝐴𝐵=[22].

В предыдущем примере мы умножили матрицу строк на матрицу столбцов, что в результате получилась матрица с одной записью путем умножения 𝑗-й записи матрицу-строку по 𝑗-му элементу матрицы-столбца и суммируя все продукты. В результирующей матрице была только одна запись, потому что первая матрица в умножении матриц была одна строка, а во второй матрице – один столбец.

Этот процесс можно обобщить для умножения любой пары матриц на совместимые заказы, где результирующая матрица может иметь несколько записей. Чтобы умножить матрица с несколькими строками на матрицу с несколькими столбцами, нам нужно выбрать одна строка из первой матрицы и один столбец из второй матрицы. Рассматривая выбранную строку и столбец как матрицы строк и столбцов соответственно, мы можем умножить матрицу строк и матрицу столбцов, используя метод введены ранее. Продолжаем этот процесс до тех пор, пока каждый из рядов первая матрица умножается на каждый из столбцов второй матрица.

Практическое руководство. Перемножение матриц

Пусть 𝐴 и 𝐵 — матрицы порядков 𝑚×𝑛 и 𝑛×𝑝 соответственно. Для каждого 𝑖=1,2,…,𝑚 и 𝑗=1,2,…,𝑝, мы можем вычислить запись в 𝑖-й строке и 𝑗-м столбце матрицы 𝐴𝐵 путем умножения 𝑖-й строки 𝐴 по 𝑗й столбец 𝐵.

Мы знаем, что если умножить матрицу порядка 𝑚×𝑛 на матрицу порядка 𝑛×𝑝, мы получаем матрицу порядка 𝑚×𝑝. Это означает, что нам необходимо вычислить это 𝑚×𝑝 раз, чтобы заполнить матрицу умножение.

Продемонстрируем этот процесс графически, умножив Матрица 3×2 на матрицу 2×3. Мы знаем, что полученная матрица будет порядка 3×3, а это значит, что нам нужно умножить строку столбиком 9 раз. Рассмотрим следующие матрицы: 𝐴=2−42−144,𝐵=5−1−2316.

Мы видим, что матрица 𝐴 имеет 2 столбца и матрицу 𝐵 имеет 2 ряда. Следовательно, мы можем вычислить произведение 𝐴𝐵. Мы также знаем, что товар будет в порядке 3×3. Во-первых, мы можем умножить первую строку на первую столбец, чтобы найти запись в первой строке и первом столбце матрицы 𝐴𝐵:

Далее умножаем первую строку 𝐴 на вторую колонку 𝐵 для получения

Этот процесс продолжается до тех пор, пока мы не закончим умножение матриц:

Пример 5: Нахождение произведения двух заданных матриц

Учитывая, что 𝐴=−3−7−1341,𝐵=6−43, найти 𝐴𝐵 если возможно.

Ответ

Мы знаем, что умножение матриц возможно, только если число столбцов первой матрицы совпадает с количеством строк второй матрица. Заметим, что количество столбцов первой матрицы 𝐴 и количество строк второй матрицы 𝐵 оба равны 3, поэтому можно вычислить умножение матриц 𝐴𝐵.

Мы также знаем, что умножение матрица 𝑚×𝑛 на матрица 𝑛×𝑝 дает 𝑚×𝑝 матрица. Мы видим, что заказы матрицы 𝐴 и 𝐵 являются 2×3 и 3×1 соответственно. Следовательно, 𝑚=2, 𝑛=3, и 𝑝=1. Это говорит нам о том, что матрица 𝐴𝐵 в порядке 𝑚×𝑝=2×1. Нам нужно вычислить элементов этой матрицы.

Напомним, что запись в 𝑖-й строке и 𝑗й столбец матрицы 𝐴𝐵 равен получается умножением 𝑖-й строки 𝐴 по 𝑗й колонке 𝐵. Начнем с того, что возьмем первый ряд 𝐴, которую можно записать в виде матрицы-столбца (−3−7−1). Так же берем первую (и единственную) столбец 𝐵, который можно записать как столбец матрица 6−43. Умножение каждой записи в матрице строк на соответствующую запись в матрице столбцов, а затем суммируя все продукты, (−3−7−1)6−43=[−3×6+(−7)×(−4)+(−1)×3]=[7].

Так как это произведение первой строки 𝐴 и первый столбец 𝐵, это говорит нам о том, что 7 — это запись в первой строке и первом столбце матрицы 𝐴𝐵.

Далее умножаем вторую строку 𝐴, (341), по первому столбцу 𝐵, 6−43, что приводит к (341)6−43=[3×6+4×(−4)+1×3]=[5].

Следовательно, 5 — это запись во второй строке и первом столбце матрицы 𝐴𝐵. Это ведет к 𝐴𝐵=75.

В предыдущем примере мы перемножили пару матриц, у которых были совместимые заказы. Мы сделали это, взяв подматрицы-строки первой матрицы и подматрицы столбцов второй матрицы, а затем их умножение вместе. Хотя это правильный процесс для умножения двух матриц, неэффективно каждый раз записывать матрицы строк и столбцов. Вместо этого мы можем сократить эти вычисления, написав произведение соответствующие матрицы строк и столбцов в каждой записи результирующего матрица, как видно из следующей формулы.

Определение: умножение матриц

Пусть 𝐴 и 𝐵 — матрицы порядков 𝑚×𝑛 и 𝑛×𝑝, соответственно, заданный 𝐴 = ⎛⎜⎜⎝𝑎𝑎 ⋯ ⋯ 𝑎 ⋮⋮ ⋱ ⋮ 𝑎𝑎 ⋯ 𝑎⎞⎟⎟⎠, 𝐵 = ⎛⎜⎜⎜⎝𝑏𝑏 𝑏𝑏𝑏 ⋯ 𝑏 ⋮⋮ ⋱ ⋮ 𝑏𝑏… 𝑏⎞⎟⎟⎟⎠.  

Тогда матрица произведения имеет порядок 𝑚×𝑝 и определяется как 𝐴𝐵=⎛⎜⎜⎝𝑐𝑐⋯𝑐𝑐𝑐⋯𝑐⋮⋮⋱⋮𝑐𝑐⋯𝑐⎞⎟⎟⎠, куда 𝑐=𝑎𝑏=𝑎𝑏+⋯+𝑎𝑏.

В следующем примере мы умножим пару матриц по этой формуле.

Пример 6. Нахождение произведения двух заданных матриц

Рассмотрим матрицы 𝐴=11−2−4477,𝐵=−8−96−489.

Найдите 𝐴𝐵, если возможно.

Ответ

Мы знаем, что умножение матриц возможно, только если число столбцов первой матрицы совпадает с количеством строк второй матрица. Заметим, что количество столбцов первой матрицы 𝐴 и количество строк второй матрицы 𝐵 оба равны 2, поэтому можно вычислить умножение матриц 𝐴𝐵.

Мы также знаем, что умножение матрица 𝑚×𝑛 на матрица 𝑛×𝑝 дает 𝑚×𝑝 матрица. Мы видим, что заказы матрицы 𝐴 и 𝐵 являются 3×2 и 2×3 соответственно. Следовательно, 𝑚=3, 𝑛=2, и 𝑝=3. Это говорит нам о том, что матрица 𝐴𝐵 в порядке 𝑚×𝑝=3×3. Нам нужно вычислить 9 элементов этой матрицы.

Напомним, что запись в 𝑖-й строке и 𝑗й столбец матрицы 𝐴𝐵 равен получается путем умножения каждой записи 𝑖th строку 𝐴 соответствующей записью 𝑗-й столбец 𝐵, а затем суммируя все произведения.

Например, чтобы получить запись в первой строке и первом столбце матрицы 𝐴𝐵 нам нужно умножить первую строку матрица 𝐴, (11−2), на матрица первого столбца 𝐵, −8−4. Это означает, что мы умножаем каждую запись в матрице строк на соответствующую запись в матрице столбцов, а затем просуммировать все продукты. Это дает 11×(−8)+(−2)×(−4)=−80.

Следовательно, запись в первой строке и первом столбце матрицы 𝐴𝐵 равно −80. Мы можем продолжить в таким же образом, пока мы не заполним матрицу 3 × 3: 11−2−4477−8−96−489=11×(−8)+(−2)×(−4)11×(−9)+(−2)×811×6+(−2)×9(−4)×( −8)+4×(−4)(−4)×(−9)+4×8(−4)×6+4×97×(−8)+7×(−4)7×(−9 )+7×87×6+7×9=−80−11548166812−84−7105.

В этом объяснении мы обсудили, как умножить две матрицы совместимых заказы. Заметим, что матричное умножение сильно отличается от умножение двух действительных чисел, так как оно имеет более сложную структуру. Хотя трудно понять, почему нам нужно определить матричное умножение в этом образом, есть веская причина для этого. Эта причина станет яснее по мере того, как мы узнаем о более сложных темах по матрицам. Тем не менее, мы можем видеть проблеск этой причины, когда мы рассматриваем реальный пример, который может быть решен с помощью умножения матриц.

В нашем последнем примере мы рассмотрим реальное применение матрицы умножение.

Пример 7. Решение задач Word путем применения операций над матрицами

В таблице ниже показано количество номеров различных типов в трех гостиницах, принадлежащих Компания. Если одноместный номер стоит 160 LE за ночь, двухместный номер стоит 430 египетских фунтов за ночь, а люкс стоит 740 LE за ночь, определите ежедневный доход компании, когда все помещения заняты.

Hotel	Single Room	Double Room	Suite
First Hotel	45	74	15
Second Hotel	48	74	19
Третий отель	49	94	10

Ответ

В этом примере нам нужно определить ежедневный доход компании, когда все комнаты заняты. Эта компания владеет тремя гостиницами, а количество номеров каждого типа указано в данной таблице. Если мы взять только числа в таблице, мы можем составить Матрица 3 × 3, которую мы можем записать как 457415487419499410.

Первый столбец этой матрицы представляет количество одиночных номера в каждом отеле. Чтобы рассчитать доход компании от этих номера, нам нужно умножить эти цифры на 160 LE, что является стоимость одноместного номера. Точно так же нам нужно умножить второе колонка на 430 ЛЭ, это стоимость двухместного номера. Таким же образом записи в третьем столбце следует умножить на 740 LE, что составляет стоимость люкса. В итоге мы можем получить суммарный дневной дохода путем суммирования всех элементов полученной матрицы: 45×16074×43015×74048×16074×43019×74049×16094×43010×740.

Если мы суммируем записи в каждой строке, мы получим

45×160+74×430+15×74048×160+74×430+19×74049×160+94×430+10×740.

(1)

Запись в каждой строке приведенной выше матрицы показывает нам ежедневный доход от каждый отель. Мы можем закончить вычисление, найдя каждую запись выше и суммирование записей. Но давайте остановимся здесь на секунду, чтобы отметить, что приведенная выше матрица также может быть получена, когда мы умножаем наш исходный матрица 3×3 на матрицу-столбец, содержащую стоимость каждого типа номера: 457415487419499410160430740.

Рассмотрим это умножение. Мы знаем эту матрицу умножение возможно только в том случае, если число столбцов первая матрица совпадает с количеством строк второй матрицы. Мы обратите внимание, что количество столбцов первой матрицы и число строк второй матрицы равны 3, поэтому возможно чтобы вычислить это матричное умножение.

Мы также знаем, что можно умножить пару матриц путем умножения каждой строке первой матрицы по каждому столбцу второй матрицы. Умножим первую строку 3×3 матрица, (457415), по столбцу второй матрицы, 160430740. Это означает, что мы умножаем каждую запись в матрице строк на соответствующую запись в матрице столбцов, а затем просуммируйте все продукты. Это дает 45×160+74×430+15×740, что совпадает с первой строкой матрицы, приведенной в (1). Точно так же мы можем видеть, что умножение вторая и третья строки матрицы 3×3 по матрице столбцов приводит к элементам во втором и третьем строки матрицы в (1). Вычисление каждого запись в (1) дает нам 457415487419499410160430740=501205356055660.

Суммируя все записи, мы имеем 50120+53560+55660=159340.

Следовательно, когда все помещения заняты, компания Ежедневный доход составляет 159‎ ‎340 LE.

Давайте закончим повторением нескольких важных понятий из этого объяснения.

Ключевые точки

• Пусть 𝐴 и 𝐵 — матрицы. К вычислить умножение матриц 𝐴×𝐵, число столбцов в 𝐴 должно быть равно количеству строк в 𝐵. Если 𝐴 является матрица 𝑚×𝑛 для некоторых натуральных чисел 𝑚 и 𝑛, 𝐵 должны быть матрица 𝑛×𝑝 для некоторого положительного целого числа 𝑝. В этом случае 𝐴×𝐵 является 𝑚×𝑝 матрица:
• Пусть 𝐴 и 𝐵 будут строкой и столбцом матрицы соответственно. Тогда матрица 𝐴𝐵 равна определена и имеет порядок 1×1. Вход этой матрицы получается путем умножения каждой записи в строке матрица соответствующей записью в матрице-столбце, а затем суммируя все произведения.
• Пусть 𝐴 и 𝐵 — матрицы заказы 𝑚×𝑛 и 𝑛×𝑝, соответственно, определяется как 𝐴 = ⎛⎜⎜⎝𝑎𝑎 ⋯ ⋯ 𝑎 ⋮⋮ ⋱ ⋮ 𝑎𝑎 ⋯ 𝑎⎞⎟⎟⎠, 𝐵 = ⎛⎜⎜⎜⎝𝑏𝑏 𝑏𝑏𝑏 ⋯ 𝑏 ⋮⋮ ⋱ ⋮ 𝑏𝑏… 𝑏⎞⎟⎟⎟⎠.  Тогда матрица произведения 𝐴𝐵 имеет порядок 𝑚×𝑝 и определяется как 𝐴𝐵=⎛⎜⎜⎝𝑐𝑐⋯𝑐𝑐𝑐⋯𝑐⋮⋮⋱⋮𝑐𝑐⋯𝑐⎞⎟⎟⎠, куда 100028

Умножение матриц

Вы можете умножить только два матрицы если их Габаритные размеры находятся совместимый , что означает, что количество столбцов в первой матрице совпадает с количеством строк во второй матрице.

Если А знак равно [ а я Дж ] является м × н матрица и Б знак равно [ б я Дж ] является н × п матрица, продукт А Б является м × п матрица.

А Б знак равно [ с я Дж ] , куда с я Дж знак равно а я 1 б 1 Дж + а я 2 б 2 Дж + … + а я н б н Дж .

(Запись в я й ряд и Дж й столбец обозначается двойным нижним индексом а я Дж , б я Дж , а также с я Дж . Например, запись а 23 это запись во второй строке и третьем столбце.)

Определение матричного умножения указывает на умножение строк за столбцами, где элементы в я й ряд А умножаются на соответствующие записи в Дж й столбец из Б а затем добавить результаты.

Умножение матриц НЕ является коммутативным. Если ни А ни Б является единичной матрицей, А Б ≠ Б А .

Умножение строки на столбец

Мы начнем с того, что покажем вам, как умножить 1 × н матрица н × 1 матрица. Первый — это всего лишь одна строка, а второй — один столбец. По вышеприведенному правилу продукт является 1 × 1 матрица; другими словами, одно число.

Во-первых, давайте назовем записи в строке р 1 , р 2 , … , р н , а записи в столбце с 1 , с 2 , … , с н . Тогда произведение строки и столбца равно 1 × 1 матрица

[ р 1 с 1 + р 2 с 2 + . .. + р н с н ] .

Пример:

Найдите продукт.

[ 1 4 0 ] ⋅ [ 2 − 1 5 ]

Мы должны умножить 1 × 3 матрица 1 × 3 матрица. Количество столбцов в первом равно количеству строк во втором, поэтому они совместимы.

Продукт:

[ ( 1 ) ( 2 ) + ( 4 ) ( − 1 ) + ( 0 ) ( 5 ) ] знак равно [ 2 + ( − 4 ) + 0 ] знак равно [ − 2 ]

Умножение больших матриц

Теперь, когда вы знаете, как умножать строку на столбец, умножать большие матрицы несложно. Для вступления в я й ряд и Дж й столбец матрицы продуктов, умножьте каждую запись в я й строку первой матрицы соответствующей записью в Дж й столбец второй матрицы и сложения результатов.

Возьмем следующую задачу на умножение 2 × 3 матрица с 3 × 2 матрица, чтобы получить 2 × 2 матрица как произведение. Элементы матрицы произведения называются е я Дж когда они в я й ряд и Дж й столбец.

[ 1 0 1 0 1 2 ] ⋅ [ 3 5 − 1 0 2 − 1 ] знак равно [ е 11 е 12 е 21 е 22 ]

Получить е 11 , умножить ряд 1 первой матрицы по столбцу 1 второй.

е 11 знак равно [ 1 0 1 ] ⋅ [ 3 − 1 2 ] знак равно 1 ( 3 ) + 0 ( − 1 ) + 1 ( 2 ) знак равно 5

Получить е 12 , умножить ряд 1 первой матрицы по столбцу 2 второй.

е 12 знак равно [ 1 0 1 ] ⋅ [ 5 0 − 1 ] знак равно 1 ( 5 ) + 0 ( 0 ) + 1 ( − 1 ) знак равно 4

Получить е 21 , умножить ряд 2 первой матрицы по столбцу 1 второй.