Умножение и деление онлайн столбиком: Онлайн калькулятор. Сложение, вычитание, умножение и деление столбиком

Деление столбиком

Паскалина – школьный онлайн калькулятор

1. Калькуляторы
2. Вычисления в столбик
3. Деление столбиком

:

С остатком

{{_dividend}} : {{_divisor}} = {{response.dividend}} : {{response.divisor}} ={{response.result}}{{_dividend}} : {{_divisor}} = {{response.result}} (остаток {{response.remainder}})Проверка умножением
{{response.resultNormal}} × {{_divisor}} = {{_dividend}}

Проверка делением
{{_dividend}} : {{response.resultNormal}} = {{_divisor}}

Проверка умножением
{{response.resultNormal}} × {{_divisor}} + {{response.remainder}} = {{response.resultNormal.mul(_divisor)}} + {{response.remainder}}= {{_dividend}}

ОПИСАНИЕ

Калькулятор деление столбиком онлайн поможет Вам быстро и правильно поделить натуральные числа. Калькулятор поделит число как нацело, так и выполнит деление с остатком. Кроме того, результаты деления будут проверены умножением.

РУКОВОДСТВО

Введите в соответствующие поля натуральные числа и нажмите кнопку “Рассчитать”

ТЕОРИЯ

ДЕЛЕНИЕ

Действие деление определяют с помощью действия умножения. Например, разделить число 54 на 18 – значит найти такое число, которое при умножении на 18 дает число 54. Имеем: 18 * 3 = 54, поэтому 54 : 18 = 3.

Вообще, для натуральных чисел a, b и c равенство a : b = c верно, если верно равенство b * c = a.

Рассмотрим еще несколько примеров:

156 : 12 = 13, так как 12 * 13 = 156;

345 : 15 = 23, так как 15 * 23 = 345.

В равенство a : b = c число a называют делимым, число b – делителем, число c и запись a : b – частным.

Частное a : b показывает, во сколько раз число a больше числа b или во сколько раз число b меньше числа a.

Можно ли например, вычислить частное 12 : 0? Если предположить, что такое частное существует и равно некоторому числу c, то должно выполнять равенство 0 * c = 12, но на самом деле 0 * c = 0. Следовательно, вычислить частное 12 : 0 нельзя.

А можно ли вычислить частное 0 : 0? Пусть 0 : 0 = c. Тогда 0 * c = 0. Такое равенство справедливо при любом c. А это означает, что значением числового выражения 0 : 0 может быть любое число, то есть такое частное вычислить нельзя.

Вывод: на нуль делить нельзя.

Вместе с тем, поскольку a * 0 = 0, то для любого натурального числа a верно равенство:

0 : a = 0

Также для любого натурального числа a верны равенства:

a : a = 1

a : 1 = a

Эти равенства легко проверить с помощью умножения.

АЛГОРИТМ ДЕЛЕНИЯ СТОЛБИКОМ

Рассмотрим алгоритм деления столбиком на примере:

18231 : 3, где:

18231 – делимое;

3 – делитель.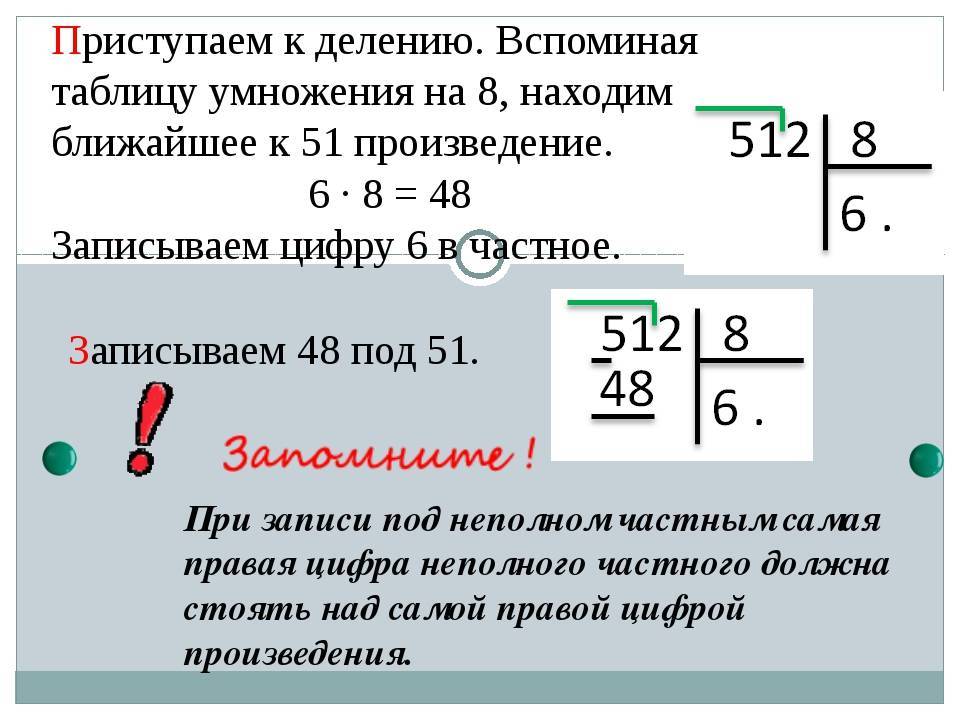

1. Запишем делимое и делитель с помощью уголка следующим образом:

2. Определим первое неполное делимое. Для этого будем сравнивать слева направо цифры делимого с делителем, до тех пор, пока неполное делимое не станет больше делителя.

Первая цифра слева у делимого это 1. Сравним ее с делителем:

1 < 3 – цифра делимого меньше делителя, поэтому 1 не может быть первым неполным делимым. В этом случае добавим к первой цифре делимого следующую за ней, получим 18. Сравним ее с делителем:

18 > 3 – значит 18 – первое неполное делимое.

3. Разделим первое неполное делимое на делитель:

18 : 3 = 6 (остаток 0), запишем найденное частное 6 под делителем (под линией), получим:

4. Проверяем деление умножением, для этого умножаем найденную цифру частного на делитель:

6 * 3 = 18, записываем произведение под первым неполным делимым и находим их разность, получаем:

5. Сравниваем разность с делителем:

0 < 3, значит, деление первого неполного делимого мы выполнили правильно и первая цифра частного верна.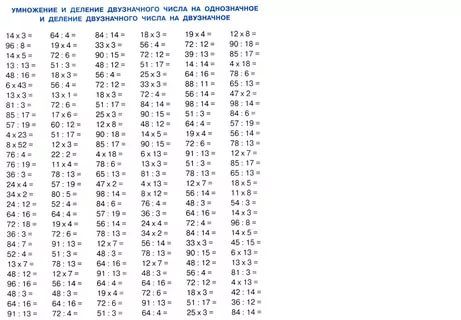 Важно! Если бы разность оказалась больше делимого, то это бы означало, что первое неполное делимое мы поделили неверно.

6. Определим второе неполное делимое. Для этого снесем следующую, нами не использованную цифру делимого, вниз к найденной разности, получим:

Сравним полученное число с делителем:

2 < 3, значит 2, не может быть неполным делимым. Снесем вниз следующую цифру, но при этом запишем в частное 0, так как мы сносим уже вторую цифру. Важно! Если при нахождении неполного делимого мы сносим вниз более одной цифры, то при сносе каждой цифры после первой в частное необходимо записать 0. Получаем:

Сравним полученное число с делителем:

23 > 3, значит 23 – второе неполное делимое.

7. Разделим второе неполное делимое на делитель:

23 : 3 = 7 (остаток 2), запишем найденное неполное частное 7 под делителем (под линией), получим:

8. Проверяем деление умножением, для этого умножаем найденную цифру частного на делитель:

7 * 3 = 21, записываем произведение под вторым неполным делимым и находим их разность, получаем:

9. Сравниваем разность с делителем:

2 < 3, значит, деление второго неполного делимого мы выполнили правильно и первая цифра частного верна. Важно! Если бы разность оказалась больше делимого, то это бы означало, что второе неполное делимое мы поделили неверно.

10. Определим третье неполное делимое. Для этого снесем следующую, нами не использованную цифру делимого, вниз к найденной разности, получим:

Сравним полученное число с делителем:

21 > 3, значит 21 – третье неполное делимое.

11. Разделим третье неполное делимое на делитель:

21 : 3 = 7 (остаток 0), запишем найденное частное 7 под делителем (под линией), получим:

12. Проверяем деление умножением, для этого умножаем найденную цифру частного на делитель:

7 * 3 = 21, записываем произведение под третьим неполным делимым и находим их разность, получаем:

13. Сравниваем разность с делителем:

0 < 3, значит, деление третьего неполного делимого мы выполнили правильно и первая цифра частного верна. Важно! Если бы разность оказалась больше делимого, то это бы означало, что третье неполное делимое мы поделили неверно.

14. Так как, мы использовали все цифры делимого (сносить вниз больше нечего), значит деление завершено. Получаем:

Таким образом, итоговый результат будет выглядеть следующим образом:

18231 : 3 = 6077

Мы рассмотрели пример деления столбиком на однозначное число. Аналогично выполняется деление на многозначное число.

Проверка деления

Проверить деление можно следующими способами:

1) Умножением, для этого необходимо частное умножить на делитель. Если в результате получится делимое, значит, деление было выполнено верно.

6077 * 3 = 18231

2) Делением, для этого необходимо делимое разделить на частное. Если в результате получится делитель, значит, деление было выполнено верно.

18231 : 6077 = 3

ДЕЛЕНИЕ С ОСТАТКОМ

Как разделить число 20 на число 6? Ответ на этот вопрос можно получить, решив следующую задачу. Как разделить поровну 20 конфет между шестерыми друзьями?

Скорее всего, каждому достанется по 3 конфеты, но при этом 2 конфеты останутся.

Такое распределение конфет иллюстрирует следующее равенство:

20 = 6 * 3 + 2.

Заметим, что 3 – это наибольшее число, произведение которого на делитель 6 меньше делимого 20. В записи 20 = 6 * 3 + 2 число 3 называют неполным частным, а число 2 – остатком. Также говорят, что при делении числа 20 на число 6 получили неполное частное, равное 3, и остаток – 2. Заметит, что остаток 2 меньше делителя 6.

Конфеты можно было разделить и другим способом, например, дать каждому по 2 конфеты и оставить 8. Ведь 20 = 6 * 2 + 8. Но здесь число 2 не является неполным частным, а число 8 – остатком.

Остаток всегда меньше делителя.

Разделим число 189 на число 13:

Поскольку 7 < 13, то мы вынуждены прекратить процесс деления. Это означает, что при делении числа 189 на число 13 получили неполное частное, равное 14, и остаток – 7. Имеем: 189 = 13 * 14 + 7.

Этот пример иллюстрирует такое правило.

Чтобы найти делимое, надо делитель умножить на неполное частное и прибавить остаток.

В буквенном виде это правило записывают так:

a = bq + r, где:

a – делимое, 

b – делитель,

q – неполное частное,

r – остаток, r < b.

Рассмотрим равенство 21 = 7 * 3. Его можно переписать так: 21 = 7 * 3 + 0. Говорят, что при делении числа 21 на число 7 остаток равен нулю. Также можно сказать, что число 21 делится нацело на число 7.

Проверка деления с остатком:

Чтобы проверить деление с остатком, нужно неполное частное умножить на делитель и к произведению прибавить остаток. Если в результате получится делимое, значит, деление с остатком было выполнено верно.

13 * 14 + 7 = 182 + 7 = 189

Стр. 35 – ГДЗ Математика 4 класс Учебник Моро Часть 2

org/BreadcrumbList”>
1. Главная
2. ГДЗ
3. 4 класс
4. Математика
5. Моро учебник
6. Что узнали. Чему научились
7. Страница 35. Часть 2

Вернуться к содержанию учебника

Что узнали. Чему научились

Вопрос

1.

84 • 10 – 40	10 • (920 – 20)	184 • 100 – 300
78 • 10 – 700	8 • (720 – 700)	100 • 391 – 3000

Ответ

Вопрос

2.

50 : 50 • 100	15 • 2 • 100	25 • 4 • 100	180 : 2 + 210 • 4
24 • 10 : 8	48 : 3 • 10	100 : 2 : 10	150 : 3 + 250 • 4

Вопрос

3.

107 • 7	250 • 4	320 • 3	125 • 4	182 • 2
206 • 4	105 • 8	430 • 2	125 • 8	316 • 3

Ответ

Вопрос

4. Выполни деление с остатком.

327 : 10	1684 : 100	15928 : 100	135628 : 10
358 : 10	1605 : 10	15862 : 10	36704 : 10
615 : 100	1730 : 100	34518 : 100	52080 : 100

Вопрос

5. Вычисли удобным способом.

45 • (2 • 7)

720 : (9 • 2)

67 • (4 • 25)

17 • 2 • 8 • 125

Ответ

Вопрос

6.

213 • 90	1872 • 60	529 • 800	905 • 200
487 • 40	6097 • 70	674 • 500	708 • 600

Ответ

Вопрос

7.

3800 • 40	1090 • 700	600 • 580	3070 • 80
4200 • 60	2900 • 300	700 • 402	40300 • 20

Ответ

Вопрос

8.

6510 : 30	46800 : 600	38960 : 80	34500 : 300
2280 : 50	395000 : 500	81720 : 90	52200 : 600

Вопрос

9.

100520 – 470 • 50 + 13980	400000 – 867 • 400
14110 + 801000 : 900 – 7604	9805 + 146510 : 70
734600 : 50 + 454 • 40	8213 • 30 – 12240 : 30
(560 – 12240 : 30) + 145	11140 : (2076 – 2056)

Вопрос

10.

463700 : 50 + 546 • 40	8130 : 30 – 2640 : 10
55440 : 90 – 10460 : 20	900100 – (735 – 184) • 80
41090 : 70 + 11950 : 50	60997 + (6012 + 6228) : 30

Вопрос

11. Какими могут быть длины сторон прямоугольника, периметр которого равен 26 см, а площадь  – 40 см²?

Ответ

Вопрос

12. Вычислительная машина работает так:

Какой ответ будет получаться на выходе из машины, если на входе будет число 47; 53; 28; 94?

Ответ

Вопрос

Сравни площади фигур

Ответ

Вернуться к содержанию учебника

---

Умножение, деление — математические визуальные эффекты

Сколько СЕЙЧАС?

Крисси Ньюэлл отлично работает с точками, чтобы осветить умножение в разговоре о числах. Проверьте ее оригинальный пост здесь.

Удвоение с числами, кратными 4, 6 и 8

Удвоение, одинаковые/различные

Умножение

Как использовать What you do Ask What do Ask What you note:

Как использовать? Что вам интересно? Как это может выглядеть для других проблем?

Коэффициенты умножения

Как использовать: Спросите: Что вы заметили? Что вам интересно? Какие уравнения будут соответствовать каждому массиву? Что такое шаблон?

Коммутативное умножение

Как использовать: Посмотрите и спросите: Что вы заметили? Что вам интересно? Что такое же? Какая разница? Это работает с другими номерами? Как это может облегчить решение других задач?

Связанное умножение и деление

Еще одна строка или столбец, одинаковые/другие

Способы видеть 6×5

Как использовать: Посмотрите и спросите: Что вы заметили? Что вам интересно? Что еще вы можете придумать? Как это помогает вам думать о 6×5?

Схема соединения сотен умножения

Как использовать: Посмотрите и спросите: Что вы заметили? Что вам интересно? Можете ли вы предсказать, как она упадет и/или расколется? Можете ли вы предсказать, каким будет следующее число, используя то, что вы знаете о таблице сотен? (Прочитайте пост Грэма Флетчера о «перевернутой» диаграмме сотен, использованной в этом видео, здесь)

Умножение на 10

Соединение повторений с 5×18

Способы решения 18×5

Как использовать: Попросите учащихся решить 18×5 и покажите это наглядно. Посмотрите на это изображение и спросите: какой из них был больше всего похож на ваш и почему? Выберите одну из этих стратегий и объясните, как она работает.

Этот рисунок вдохновлен Джо Боалер и сайтом www.youcubed.org, отличным местом, где можно узнать о продуктивном математическом мышлении, исследованиях и занятиях.

Столкновение массивов

Атомные точки

Типы деления

Как использовать: Посмотрите и спросите: Что вы заметили? Что вам интересно? Что такое же? Какая разница? Какой рассказ может сравниться с первым? Чем история должна отличаться, чтобы соответствовать второй?

Разделение на группы или массив

Как использовать: Посмотрите и спросите: Что вы заметили? Что вам интересно? Что такое же? Какая разница? Какая история могла бы соответствовать этим? Какие уравнения могут совпадать?

Распечатка умножения

Перейдите на страницу распечаток для загрузки.

Нравится:

Нравится Загрузка…

Сложение, вычитание, умножение и деление

Может быть полезно понять, как использовать различных математических операций , поскольку их можно использовать каждый день во многих различных ситуациях, точно так же, как вычисление того, как пакет конфет можно разделить поровну между группа людей.

Сложение, вычитание, умножение и деление определение

Сложение, вычитание, умножение и деление — все виды операций, используемых в математике.

Сложение

Сложение — это тип операции, результатом которой является сумма двух или более чисел. Существует знак, обозначающий операцию сложения, называемый знаком плюс, то есть +.

Вычитание

Вычитание — это тип операции, результатом которой является нахождение разницы между двумя числами. Знак, обозначающий операцию вычитания, называется знаком минус и выглядит он так: -.

Умножение

Умножение — это тип операции, который требует сложения равными группами, в результате умножения получается произведение. Знак, обозначающий операцию умножения, можно назвать знаком умножения, и он выглядит так: ×.

Деление

Деление — операция, обратная умножению, заключается в разбиении числа на равные части. Знак, обозначающий операцию деления, называется просто знаком деления и выглядит так: ÷.

Правила сложения, вычитания, умножения и деления

Существуют различные правила и методы, которые могут быть полезны при использовании каждой из этих операций.

Сложение

При сложении двух или более чисел можно использовать метод сложения столбцов. Это включает в себя размещение чисел одно над другим в столбце, затем вы работаете справа налево, добавляя числа, которые находятся в одном столбце.

Рассчитать 122+552

Решение:

Для начала вы можете расположить числа друг над другом:

122+552

Теперь, работая справа налево, сложите два горизонтальных числа вместе, начиная с 2 и 2:

122 +5524

Теперь переходим к 2 и 5:

122+55274

И, наконец, 5 и 1:

122+552672

Следовательно, 122+552=672

5 900 больше 10, вы можете перенести число.

Вычитание

При вычитании двух чисел можно также использовать метод столбца; метод вычитания столбцов. Это работает так же, как метод сложения столбцов, однако вы вычитаете числа, а не добавляете их.

Вычислить 538-214

Решение:

Для начала вы можете расположить числа друг над другом, поместив число, от которого вы вычитаете, сверху:

538-214

Теперь работаем справа влево отнять одно число от другого, начиная с 8 и 4:

538-2144

теперь переходит на 3 и 1:

538-21424

и, наконец, 5 и 2:

538-214324

Следовательно, 538-214 = 324

Если номер, вы подтекаете. выше числа, из которого вычитается, нужно будет взять цифру из столбца слева.

Умножение

При умножении двух чисел можно использовать различные методы, включая метод сетки. Это включает в себя разбиение двух чисел и размещение их в сетке. Затем вы выполняете отдельные умножения, а затем складываете их все вместе.

Вычислить 23×42

Решение:

Для начала начертите сетку, разбейте числа и поместите их в сетку следующим образом:

8 20	9
40
2

, чтобы заполнить сетку.0208 3 40 800 120 2 40 6

Now you can add all of the values ​​together to find the answer to the question, может быть проще сделать это пошагово:

800+120=920

40+6=46

920+46=966

Таким образом, 23×42=966

Деление

При делении числа на другой вы можете использовать метод, называемый коротким делением, этот метод лучше всего работает, когда вы делите число на 10 или меньше. Короткое деление предполагает мысленное деление числа на более мелкие этапы.

Вычислить 306÷9

Решение:

Для начала вы можете нарисовать свой расчет, записав число, на которое вы делите, слева, а число, которое вы делите, запишите справа, как показано ниже:

9306

Теперь вам нужно проработать число, которое вы делите по одной единице за раз, начните с выяснения, сколько раз 9 может перейти в 3. Поскольку это невозможно, вам нужно перенести 3 к следующему блоку:

93306

Теперь вы можете подумать о том, сколько раз 9 может перейти в 30. 9 входит в 30 три раза с остатком три:

9×3=27

Затем это можно записать в ваше деление, как показано ниже, с помощью делимое число записывается над вычислением, а остаток 3 переносится на 6:

9333036

Наконец, вы можете вычислить, сколько раз 9 входит в число 36:

9×4=36

93433036

Следовательно, 306÷9=34

Взаимосвязи сложения, вычитания, умножения и деления

Операции могут иметь взаимосвязи друг с другом. Существует связь между сложением и вычитанием, а также связь между умножением и делением.

Сложение и вычитание

Сложение и вычитание можно считать обратными друг другу. Это просто означает, что операции противоположны, вы можете отменить сложение, вычитая то же число, и наоборот!

Умножение и деление

Умножение и деление также считаются обратными друг другу, если вы хотите отменить умножение, вы можете просто разделить число.

Примеры сложения, вычитания, умножения и деления

Вычислить 647+278

Решение:

Для начала вы можете расположить числа друг над другом:

647+278

5 9 Теперь работаем справа слева, сложите два горизонтальных числа вместе. Начиная с 7 и 8, так как они равны 15, вам нужно перенести 1 на:

647+27815

Теперь вам нужно сложить вместе 4, 7 и 1, опять же, поскольку это больше 10, вам нужно перенести единицу:

647+2781125

Наконец, вы можете сложить вместе 6, 2 и 1:

647+27811925

Вычислить 732-426

Решение:

Для начала вы можете поместить числа друг над другом, поместив число, из которого вы вычитаете:

7 900 -426

Теперь, работая справа налево, вычтите одно число из другого, начиная с 2 и 6. Поскольку 6 больше двух, вам нужно позаимствовать цифру из столбца слева:

72312-4266

Now you can subtract 2 from 2:

72312-42606

Finally, you can subtract the 4 from 7:

72312-426306

Calculate 53×35

Solution:

To begin with, draw out a grid, break down your numbers, and place them into the grid-like so:

	50	3
30
5

To fill out the grid you simply multiply each number in the columns:

	50	3
30	1500	90
5	250	15

Теперь вы можете сложить все значения вместе, чтобы найти ответ на вопрос, может быть проще сделать это пошагово:

1500+90=1590

250+15 = 265

1590+265 = 1855

Расчет 434 ÷ 7

Решение:

Давайте начнем с написания суммы, используя метод короткого дивизиона:

7434

Сейчас начнутся с суммы подсчитав, сколько раз 7 входит в 4, это невозможно, поэтому вы можете перенести 4 в 3:

74434

Затем вы можете посмотреть, сколько раз 7 может войти в 43:

7×6= 42

Это оставляет нам остаток от 1, который можно перенести на 4:

7644314

Наконец, подсчитайте, сколько раз 7 может входить в число 14:

7×2=14

76244314

Следовательно, 434÷7=62

Деление 90 и вычитание 4 операции часто используются в повседневной жизни, давайте рассмотрим несколько примеров:

У Эми 326 наклеек в коллекции наклеек, у Клэр 213 наклеек. Сколько наклеек у них было бы, если бы они объединили свои коллекции?

Решение:

Начните с размещения двух чисел друг над другом:

326+213

Теперь вы можете сложить их вместе, работая справа налево, начиная с 6 и 3:

326+2139

Проработайте числа:

326+213539

Следовательно, если бы Эми и Клэр объединили свои коллекции, в их коллекции было бы

539 наклеек .

У Сэма 142 конфеты, он отдает своему другу 54, сколько конфет осталось у Сэма?

Решение:

Чтобы узнать, сколько конфет у Сэма, мы можем вычесть 54 из 142. Начните с размещения двух чисел друг над другом:

142-54

Теперь действуем справа налево, вычесть одно число из другого. Не забывайте, так как 2 меньше 4, вам нужно взять единицу из столбца слева:

13412-548

Теперь вы можете двигаться дальше, опять же, поскольку 3 меньше 5, вам нужно будет взять единица из столбца слева:

113412-5488

Следовательно, у Сэма осталось 88 конфет .

Дейв готовит на 12 человек, но по его рецепту он рассчитан только на 4. Если по рецепту требуется 72 грамма пасты, сколько пасты понадобится Дейву?

Решение:

Чтобы узнать, сколько макаронных изделий потребуется Дейву для его рецепта, мы можем использовать операцию умножения. Поскольку 4 входит в 12, 3 раза, Дейву понадобится в три раза больше, чем указано в рецепте. Для этого мы можем использовать метод сетки:

	70	2
3	210	6

. 216 грамм пасты на 12 персон.

Барбара обедает с тремя друзьями, счет составляет 188 фунтов стерлингов, и они решают разделить его поровну. Сколько платит каждый человек?

Решение:

Для начала запишите задачу, используя метод короткого деления. Счет составил 188 фунтов стерлингов, и его делят между 4 людьми, поэтому его можно записать следующим образом:

4188

Теперь сделайте первый шаг и посмотрите, сколько раз 4 может войти в первое число слева.