Таблица соответствия роста веса и возраста: 7 таблиц правильного соотношения веса роста и возраста человека
Таблица Соответствия Рост Вес Возраст Женщины. Формула брока
Анжела Курпатова 0 Комментариев как определить тип телосложения, определение по таблице, формула брока, формула кетле, формула маккалума, формула наглера
Семь таблиц правильного соотношения веса, роста и возраста человека
Индекс Кетле неплохо показывает количество жира в организме, но не указывает, как распределяется жир, иначе говоря, не дает зрительной- эстетической картины.
- астенический – женщинам данного типа присущи длинные и достаточно тонкие кости, хрупкие руки и ноги, высокий рост, небольшой обхват груди, плеч и бедер, а также сравнительно малый вес;
- нормостенический – к данному типу относятся женщины с пропорциональными частями тела, у них кости имеют нормальную толщину, бедра и плечи достаточно широкие, а талия узкая, вес средний;
- гиперстенический – у девушек и женщин данного типа широкие бедра, плечи, большой обхват груди, кроткую шею, отличаются большим весом.

С целью определения типа телосложения, женщине придется измерить обхват запястья в наиболее тонком месте (где выступает косточка). Результат до 16 см устанавливается астениками, от 16 до 18 см – нормостениками, более 18 см – гиперстениками.
Таблица правильного соотношения веса и роста у взрослых девушек и женщин с учетом типа фигуры
Кроме того, для уточнения соотношения веса и роста учитывается возраст. Женщина, которая старше, имеет большую массу тела, чем девушка младше, если другие параметры равны. Это связано с обменом веществ, который замедляется с возрастом.
Соотношение роста и веса у женщин – таблица
Поэтому, избыток жира в организме оценивается не только по приведенным формулам, но и по толщине кожных складок и просто по внешнему виду.
Формула Брока
Так, к форме гиперстеники добавляют 10%, а астеники – вычитают 10%. Что касается роста, то теперь расчет предлагают вести следующим образом (Х – это рост в сантиметрах): менее 165 см: Х — 100 165-175 см: Х — 105 более 175 см: Х — 110.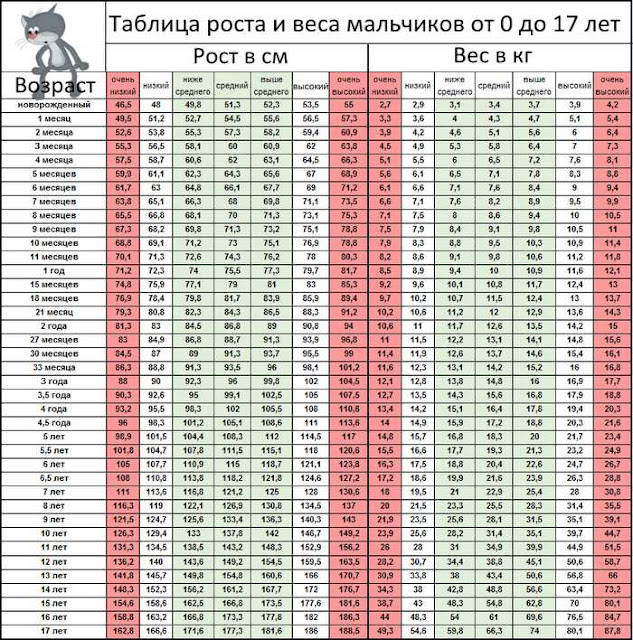
Уже в таком виде результат получается более оптимальным. Так, девушка с нормостеническим телосложением и ростом 168 см должна весить: 168-105 = 63 кг.
Мнение эксперта
Знайка, главный эксперт в Цветочном городе
Если у вас возникли сложности, обращайтесь ко мне, и я помогу разобраться 🦉
Задать вопрос эксперту
Таблица роста и веса, соотношение у женщин и мужчин с учетом возраста Первой 30 лет, при этом она имеет нормальный тип телосложения. А если у Вас остались вопросы, задайте их мне!
- наследственность (не стоит ожидать у невысоких родителей сына-баскетболиста)
- питание (ни для кого не секрет, что при дефиците питательных веществ, витаминов и минералов замедляется рост и развитие ребенка)
- физические нагрузки (например занятия теннисом, волейболом, баскетболом способствуют увеличению роста)
- здоровье ребенка (дети, имеющие хронические заболевания зачастую отстают в физическом развитии от своих сверстников)
- психологическая ситуация в семье, в школе, недостаток сна и т.
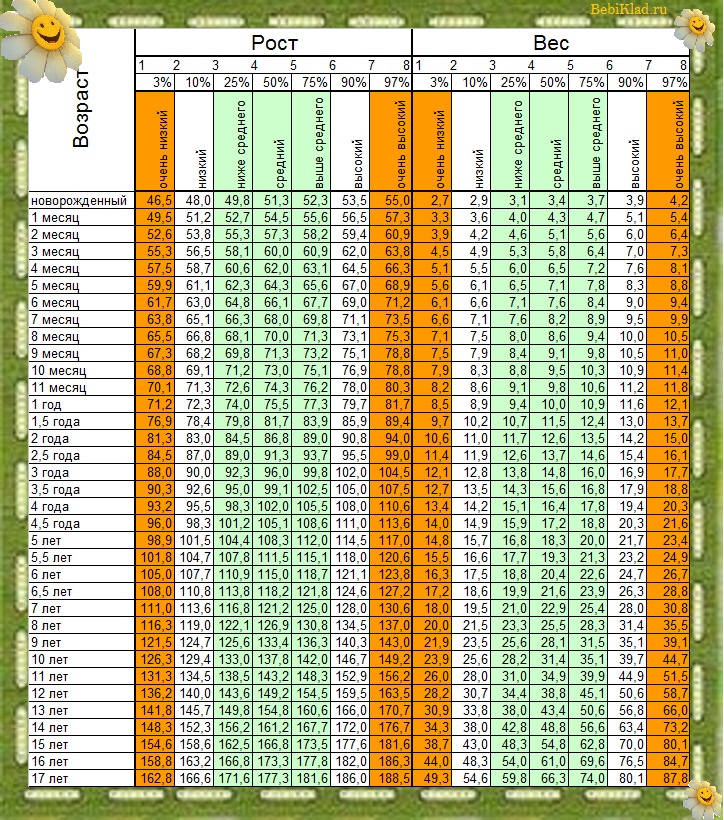
Как рассчитать женщине свой идеальный вес с учетом возраста?
| Астеническое сложение | Нормастеническое сложение | Гиперстенический сложение | |
| 155 | 50 | 56 | 62 |
| 160 | 54 | 60 | 66 |
| 165 | 57 | 64 | 70 |
| 170 | 61 | 68 | 74 |
| 175 | 65 | 72 | 78 |
| 180 | 69 | 75 | 81 |
| 185 | 74 | 79 | 85 |
Таблица правильного соотношения веса и роста у взрослых девушек и женщин с учетом типа фигуры.
Мечта Лоренца
Многие родители совершают ошибку, сравнивая состояние своих разнополых детей. Существуют таблицы, позволяющие определить возможные отклонения.
Мнение эксперта
Знайка, главный эксперт в Цветочном городе
Если у вас возникли сложности, обращайтесь ко мне, и я помогу разобраться 🦉
Задать вопрос экспертуСоответствие роста, веса, параметров фигуры для мужчин и женщин в таблице: как рассчитать индекс массы тела в зависимости от возраста? Какой идеальный вес для девушки, таблица идеального роста и веса для девушек.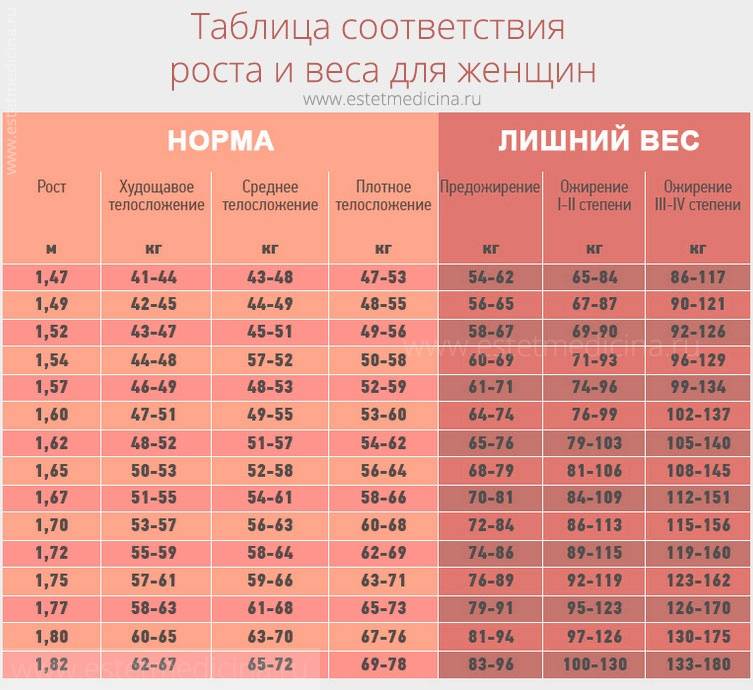 А если у Вас остались вопросы, задайте их мне!
А если у Вас остались вопросы, задайте их мне!
- Телосложение считается идеальным, если обхват талии на 25 см меньше обхвата бедер, а обхват бедер примерно равен обхвату груди.
- Обхват талии должен быть равен «рост в сантиметрах — 100″. То есть женщина ростом 172 см будет сложена пропорционально, если обхват талии будет 72 см, обхват бедер и талии — около 97 см, то есть если она носит размер одежды 48.
- Если обхват бедер меньше обхвата груди, а обхват талии меньше обхвата бедер на 20 см, то такая фигура называется «яблоко». Если обхват груди меньше обхвата бедер, а обхват талии меньше обхвата бедер на 30 см и более – это фигура типа «груша».
- Для женщин и девушек среднего роста — от 165 до 175 см — такое наблюдение оказалось справедливым. Обхват их талии в сантиметрах приблизительно равен весу в килограммах. Один килограмм похудения дает убавление в талии на один сантиметр.
Влияние возраста на телосложение
Подсчёты по этой формуле уже включают в себя тип телосложения и возраст человека, поэтому результаты считаются наиболее приближенными к реальности.
Как определить свой тип телосложения?
Одна из лучших формул, создана экспертом-методистом Джоном Маккаллумом. Формула Маккаллума основывается на измерении обхвата запястья.
Но не у всех физические данные будут точно соответствовать данным соотношениям, цифры имеют усреднённое, среднестатистическое значение.
Содержание:
- 0.1 Семь таблиц правильного соотношения веса, роста и возраста человека
- 1 Соотношение роста и веса у женщин
- 1.0.1 Таблица правильного соотношения веса и роста у взрослых девушек и женщин с учетом типа фигуры
- 1.1 Соотношение роста и веса у женщин – таблица
- 1.2 Формула Брока
- 1.3 Как рассчитать женщине свой идеальный вес с учетом возраста?
- 1.4 Мечта Лоренца
- 1.5 Влияние возраста на телосложение
- 1.5.1 Как определить свой тип телосложения?
Соответствие роста и веса тела полу и возрасту :: SYL.ru
Когда встречаются овощи, фрукты и мясо: тыква, начиненная сосиской и яблоками
Мера молочки — 2 больших пальца: как подсчитать оптимальную порцию пищи
Пальто дафлкот: с чем и как сочетать модные модели осени-зимы 2022-2023
Тыква и сливочный сыр. Готовим сезонный чизкейк
Готовим сезонный чизкейк
Почему надо включить йогурт в домашний уход, и каких проблем он поможет избежать
Какие тренды осенней моды 2022 подходят для женщин размера плюс-сайз
Как вписать маленькое черное платье в повседневный осенний лук: стильные фишки
Десерт осени. Готовим яблочный чизкейк для семьи
Полоска и вырез в виде сердечка. Трендовое дополнение к простым джинсам
Как поддерживать чистоту напольного покрытия из разных материалов на кухне
Автор Татьяна Рудакова
Давно стало известно, что соответствие роста и веса тела человека установленным стандартам является одним из самых важных показателей здоровья. Если не брать для рассмотрения людей с генетическими отклонениями в развитии, а также профессиональных спортсменов, то в большинстве случаев данный показатель организма выражает содержание жировой ткани. Естественно, что человек, обладающий избытком последней, всегда будет находиться в определенной зоне риска. Ведь повышенный уровень жира в организме приводит к развитию серьезных заболеваний, например, таких как инфаркт, инсульт и т. п. По этой причине любой человек должен знать, каким должно быть соответствие роста и веса. Во многом на данный показатель вляют возраст, пол, генетическая предрасположенность, костная структура и т. п.
Если не брать для рассмотрения людей с генетическими отклонениями в развитии, а также профессиональных спортсменов, то в большинстве случаев данный показатель организма выражает содержание жировой ткани. Естественно, что человек, обладающий избытком последней, всегда будет находиться в определенной зоне риска. Ведь повышенный уровень жира в организме приводит к развитию серьезных заболеваний, например, таких как инфаркт, инсульт и т. п. По этой причине любой человек должен знать, каким должно быть соответствие роста и веса. Во многом на данный показатель вляют возраст, пол, генетическая предрасположенность, костная структура и т. п.
Как правильно рассчитать соотношение роста и веса тела?
Каждый человек имеет свою индивидуальную структуру. Поэтому, несмотря на то что в норме все люди должны подходить под определенные стандарты, согласно которым уровень жира в организме находится в оптимальной концентрации, далеко не всегда можно установить истинное положение дел с помощью такого параметра тела человека, как соотношение роста и веса. У женщин, к примеру, при одинаковом значении данного показателя может наблюдаться совершенно различное содержание тканей. Кто-то из них может иметь подтянутую спортивную фигуру с большой долей активной мышечной массы, а кто-то, наоборот, достаточно «рыхлое» телосложение с превышающим пределы нормы уровнем жира. Специалистами в области здоровья и решения данной проблемы была разработана и внедрена в практику специальная таблица соответствия роста и веса, согласно которой каждый человек может рассчитать свой индекс массы тела, опираясь на индивидуальные показатели (возраст, пол и т. п.).
У женщин, к примеру, при одинаковом значении данного показателя может наблюдаться совершенно различное содержание тканей. Кто-то из них может иметь подтянутую спортивную фигуру с большой долей активной мышечной массы, а кто-то, наоборот, достаточно «рыхлое» телосложение с превышающим пределы нормы уровнем жира. Специалистами в области здоровья и решения данной проблемы была разработана и внедрена в практику специальная таблица соответствия роста и веса, согласно которой каждый человек может рассчитать свой индекс массы тела, опираясь на индивидуальные показатели (возраст, пол и т. п.).
Что может означать подсчитанный индекс массы тела?
Исходя из утверждения, приведенного выше, дать точную оценку состоянию тела можно не только на основании такого показателя, как соответствие роста и веса полу и возрасту, но и общего внешнего вида, а также путем специальных методов, позволяющих определять процентное соотношение какой-либо ткани организма к его общей массе. Только путем подобных сложных процедур выясняется истинная картина состояния здоровья человека.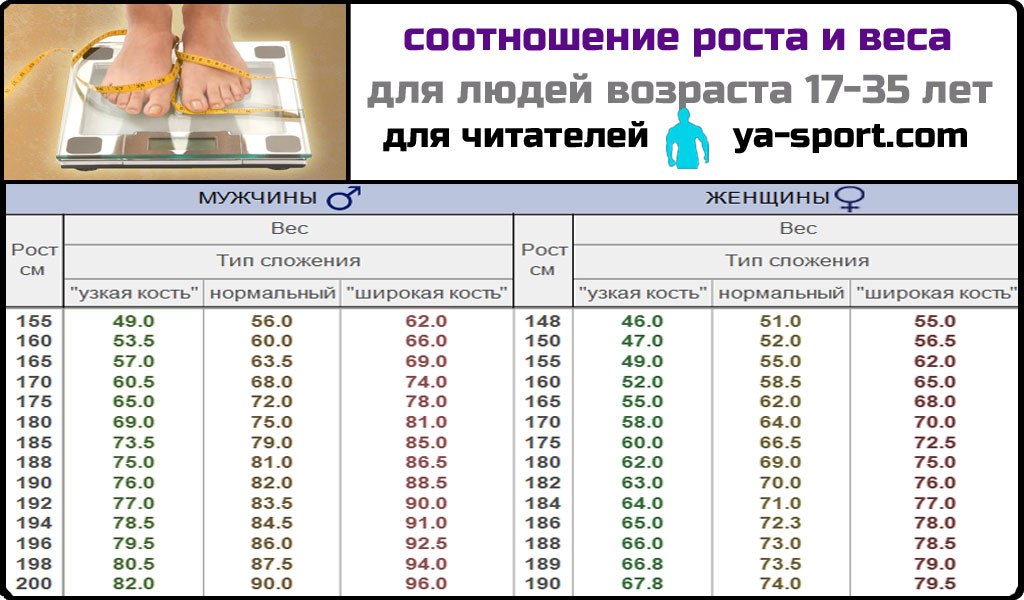 Однако в большинстве случаев отправной точкой в принятии или непринятии каких-либо мер в этом направлении все же служит измерение индекса массы тела.
Однако в большинстве случаев отправной точкой в принятии или непринятии каких-либо мер в этом направлении все же служит измерение индекса массы тела.
Формула для расчета индекса массы тела
В наши дни существует множество формул для подсчета основного показателя организма, характеризующего соответствие роста и веса тела другим его особенностям. Наиболее простую с точки зрения вычислений формулу придумал Брок. Она разделяет всех людей по возрасту на две категории – до 40 лет и после, по типу сложения на три типа – тонкокостный, нормальный и ширококостный. Для того чтобы рассчитать идеальный вес тела, необходимо от своего роста в сантиметрах отнять 110 или 100, в зависимости от категории по первой классификации. Кроме того, людям с тонкой структурой кости нужно отнять от полученного значения 10 %, а ширококостным, наоборот, прибавить эти 10 %. Например, человеку с нормальным строением скелета в возрасте 35 лет при росте в 180 см необходимо весить в среднем 70 кг.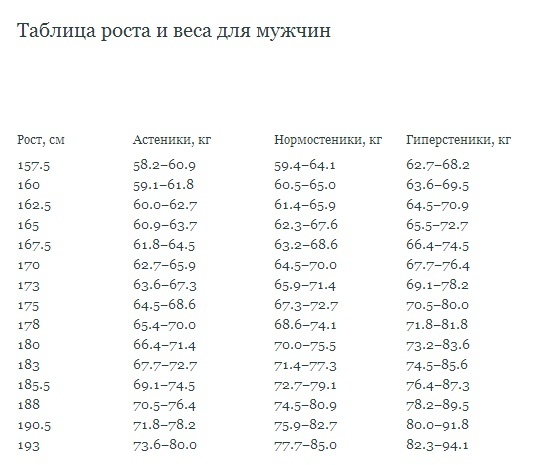
Похожие статьи
- Соотношение роста и веса у детей. Полезная таблица: возраст, рост, вес
- Правильное соотношение веса и роста у девушек
- Вес и рост: норма, основные показатели и особенности
- ИМТ: расчет с учетом возраста. Индекс массы тела: таблица
- Как рассчитать ИМТ с учетом возраста и пола
- Таблица роста и веса для женщин и мужчин
- Сколько должен весить ребенок в 4 месяца? Таблица веса и роста
Также читайте
Используйте пакет анализа для выполнения сложного анализа данных
Если вам необходимо разработать сложный статистический или инженерный анализ, вы можете сэкономить шаги и время, используя пакет анализа. Вы предоставляете данные и параметры для каждого анализа, а инструмент использует соответствующие статистические или инженерные макрофункции для расчета и отображения результатов в выходной таблице. Некоторые инструменты создают диаграммы в дополнение к выходным таблицам.
Вы предоставляете данные и параметры для каждого анализа, а инструмент использует соответствующие статистические или инженерные макрофункции для расчета и отображения результатов в выходной таблице. Некоторые инструменты создают диаграммы в дополнение к выходным таблицам.
Функции анализа данных можно использовать одновременно только на одном рабочем листе. При выполнении анализа данных на сгруппированных рабочих листах результаты появятся на первом рабочем листе, а пустые отформатированные таблицы появятся на остальных рабочих листах. Чтобы выполнить анализ данных на остальных листах, пересчитайте инструмент анализа для каждого листа.
Пакет инструментов анализа включает инструменты, описанные в следующих разделах. Чтобы получить доступ к этим инструментам, щелкните Анализ данных в группе Анализ на вкладке Данные . Если команда Data Analysis недоступна, необходимо загрузить надстройку Analysis ToolPak.
- org/ItemList”>
Щелкните вкладку Файл , щелкните Параметры , а затем щелкните значок Надстройки категории.
В поле Управление выберите Надстройки Excel и нажмите Перейти .
Если вы используете Excel для Mac, в меню файлов выберите Инструменты > Надстройки Excel.
В поле Add-Ins установите флажок Analysis ToolPak и нажмите 9.0007 ОК .
Если Analysis ToolPak не указан в списке Доступные надстройки , нажмите Browse , чтобы найти его.
Если вам будет предложено, что пакет инструментов анализа в настоящее время не установлен на вашем компьютере, нажмите Да , чтобы установить его.
Примечание. Чтобы включить функции Visual Basic для приложений (VBA) в пакет анализа, вы можете загрузить надстройку Analysis ToolPak — VBA так же, как вы загружаете пакет анализа. В поле Доступные надстройки установите флажок Analysis ToolPak — VBA .
Инструменты анализа Anova обеспечивают различные типы дисперсионного анализа. Инструмент, который вы должны использовать, зависит от количества факторов и количества образцов, которые у вас есть из популяций, которые вы хотите протестировать.
Anova: один фактор
Этот инструмент выполняет простой дисперсионный анализ данных для двух или более выборок. Анализ обеспечивает проверку гипотезы о том, что каждая выборка взята из одного и того же основного распределения вероятностей, в сравнении с альтернативной гипотезой о том, что основные распределения вероятностей не одинаковы для всех выборок. Если есть только два образца, вы можете использовать функцию рабочего листа T . ТЕСТ . При наличии более двух выборок нет удобного обобщения T . TEST , и вместо этого можно вызвать модель Single Factor Anova.
Анализ обеспечивает проверку гипотезы о том, что каждая выборка взята из одного и того же основного распределения вероятностей, в сравнении с альтернативной гипотезой о том, что основные распределения вероятностей не одинаковы для всех выборок. Если есть только два образца, вы можете использовать функцию рабочего листа T . ТЕСТ . При наличии более двух выборок нет удобного обобщения T . TEST , и вместо этого можно вызвать модель Single Factor Anova.
Anova: двухфакторный анализ с репликацией
Этот инструмент анализа полезен, когда данные можно классифицировать по двум различным параметрам. Например, в эксперименте по измерению высоты растений растениям можно давать удобрения разных марок (например, А, В, С), а также можно хранить при разных температурах (например, низкой, высокой). Для каждой из шести возможных пар {удобрение, температура} у нас есть равное количество наблюдений за высотой растений. Используя этот инструмент Anova, мы можем протестировать:
Используя этот инструмент Anova, мы можем протестировать:
Получена ли высота растений для различных марок удобрений из одной и той же основной популяции. Температуры игнорируются для этого анализа.
Берется ли высота растений для разных температурных уровней из одной и той же основной популяции. Марки удобрений в этом анализе не учитываются.
Независимо от того, учитывались ли различия между марками удобрений, указанными в первом маркированном пункте, и различиями в температурах, указанными во втором маркированном пункте, шесть образцов, представляющих все пары значений {удобрение, температура}, взяты из одной и той же совокупности. Альтернативная гипотеза состоит в том, что существуют эффекты, обусловленные конкретными парами {удобрение, температура}, помимо различий, основанных только на удобрении или только на температуре.
Anova: двухфакторный без репликации
Этот инструмент анализа полезен, когда данные классифицируются по двум разным измерениям, как в случае двухфакторного анализа с репликацией. Однако для этого инструмента предполагается, что существует только одно наблюдение для каждой пары (например, для каждой пары {удобрение, температура} в предыдущем примере).
КОРРЕЛ и Функции рабочего листа PEARSON вычисляют коэффициент корреляции между двумя измеряемыми переменными, когда измерения по каждой переменной наблюдаются для каждого из N субъектов. (Любое отсутствующее наблюдение для любого субъекта приводит к тому, что этот субъект игнорируется при анализе.) Инструмент корреляционного анализа особенно полезен, когда имеется более двух переменных измерения для каждого из N субъектов. Он предоставляет выходную таблицу, корреляционную матрицу, которая показывает значение CORREL 9.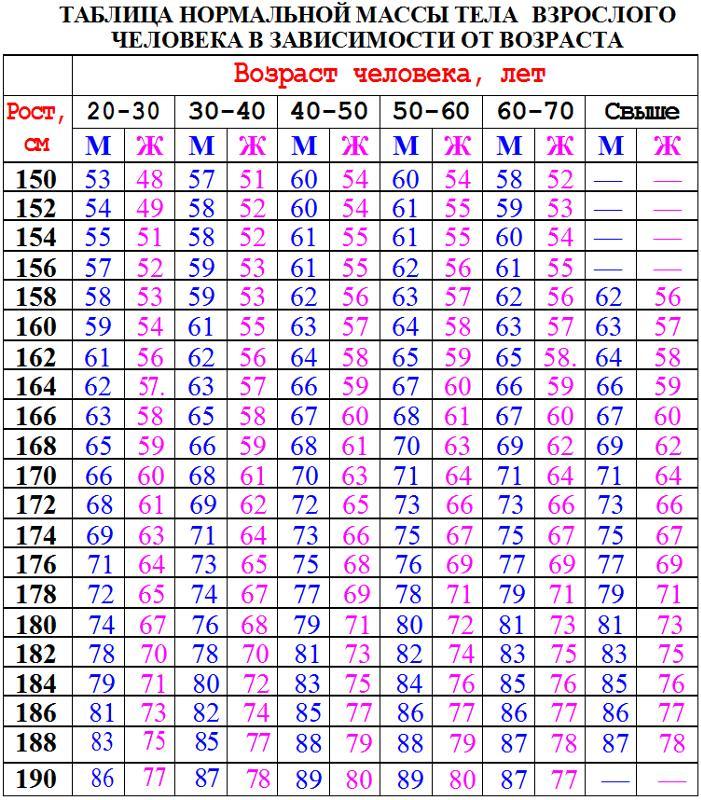 0008 (или PEARSON ) применяется к каждой возможной паре измеряемых переменных.
0008 (или PEARSON ) применяется к каждой возможной паре измеряемых переменных.
Коэффициент корреляции, как и ковариация, является мерой степени, в которой две измеряемые переменные «изменяются вместе». В отличие от ковариации, коэффициент корреляции масштабируется таким образом, что его значение не зависит от единиц, в которых выражаются две переменные измерения. (Например, если двумя измеряемыми переменными являются вес и рост, значение коэффициента корреляции не изменится при переводе веса из фунтов в килограммы.) Значение любого коэффициента корреляции должно находиться в диапазоне от -1 до +1 включительно.
Вы можете использовать инструмент корреляционного анализа, чтобы проверить каждую пару переменных измерения, чтобы определить, имеют ли две переменные измерения тенденцию двигаться вместе — то есть, связаны ли большие значения одной переменной с большими значениями другой (положительная корреляция ), связаны ли малые значения одной переменной с большими значениями другой (отрицательная корреляция) или значения обеих переменных не связаны между собой (корреляция близка к 0 (нулю)).
Инструменты корреляции и ковариации можно использовать в одних и тех же условиях, когда у вас есть N различных измеряемых переменных, наблюдаемых на наборе людей. Инструменты Correlation и Covariance дают выходную таблицу, матрицу, которая показывает коэффициент корреляции или ковариацию, соответственно, между каждой парой измеряемых переменных. Разница в том, что коэффициенты корреляции масштабируются так, чтобы лежать в диапазоне от -1 до +1 включительно. Соответствующие ковариации не масштабируются. И коэффициент корреляции, и ковариация являются мерами степени, в которой две переменные «изменяются вместе».
Инструмент Covariance вычисляет значение функции рабочего листа COVARIANCE.P для каждой пары измеряемых переменных. (Прямое использование COVARIANCE.P вместо инструмента Covariance является разумной альтернативой, когда есть только две измеряемые переменные, то есть N = 2.) Запись на диагонали выходной таблицы инструмента Covariance в строке i, столбце i: ковариация i-й переменной измерения с самой собой. Это всего лишь дисперсия совокупности для этой переменной, рассчитанная с помощью функции рабочего листа 9.0007 ВАР . Р .
Это всего лишь дисперсия совокупности для этой переменной, рассчитанная с помощью функции рабочего листа 9.0007 ВАР . Р .
Инструмент “Ковариация” можно использовать для проверки каждой пары переменных измерения, чтобы определить, имеют ли две измеряемые переменные тенденцию двигаться вместе — то есть, связаны ли большие значения одной переменной с большими значениями другой (положительная ковариация). , имеют ли малые значения одной переменной тенденцию быть связанными с большими значениями другой (отрицательная ковариация) или имеют ли значения обеих переменных тенденцию быть несвязанными (ковариация около 0 (нуля)).
Инструмент анализа описательной статистики создает отчет одномерной статистики для данных во входном диапазоне, предоставляя информацию о центральной тенденции и изменчивости ваших данных.
Инструмент анализа «Экспоненциальное сглаживание» прогнозирует значение, основанное на прогнозе за предыдущий период с поправкой на ошибку в этом предыдущем прогнозе.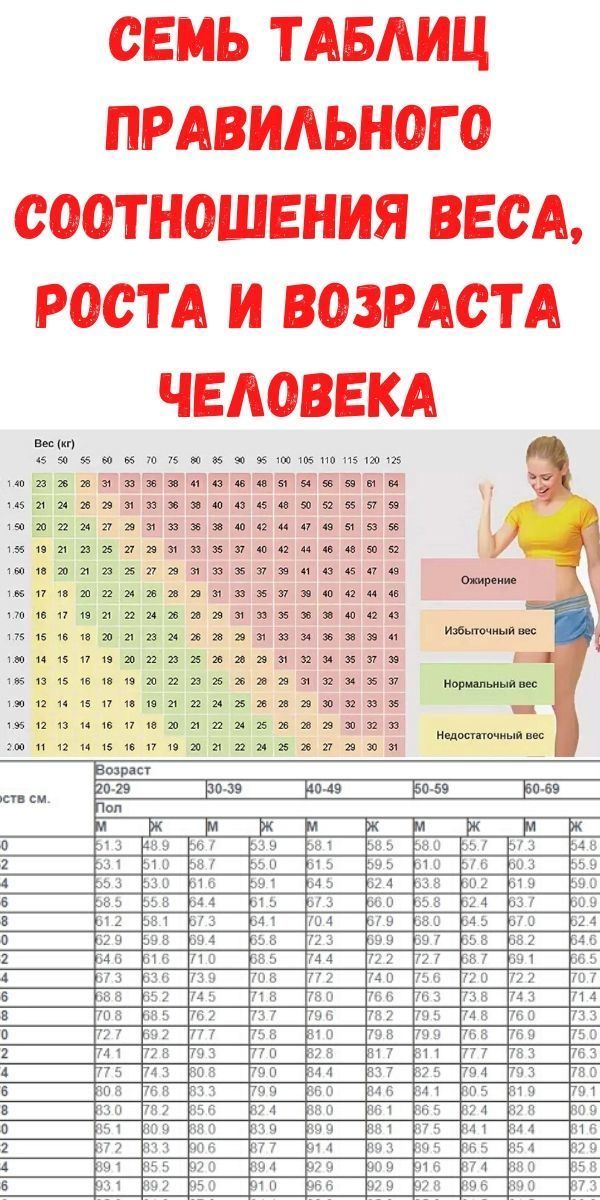 Инструмент использует константу сглаживания a , величина которой определяет, насколько сильно прогнозы реагируют на ошибки в предыдущем прогнозе.
Инструмент использует константу сглаживания a , величина которой определяет, насколько сильно прогнозы реагируют на ошибки в предыдущем прогнозе.
Примечание. Значения от 0,2 до 0,3 являются приемлемыми константами сглаживания. Эти значения указывают на то, что текущий прогноз должен быть скорректирован на 20–30 % из-за ошибки в предыдущем прогнозе. Большие константы дают более быстрый отклик, но могут давать неустойчивые прогнозы. Меньшие константы могут привести к большим задержкам для прогнозируемых значений.
Инструмент анализа двухвыборочных F-тестов для дисперсии выполняет двухвыборочный F-критерий для сравнения двух дисперсий генеральной совокупности.
Например, вы можете использовать инструмент F-Test для образцов времени в соревнованиях по плаванию для каждой из двух команд. Инструмент предоставляет результат проверки нулевой гипотезы о том, что эти две выборки взяты из распределений с одинаковой дисперсией, в отличие от альтернативы, согласно которой дисперсии не равны в базовых распределениях.
Инструмент вычисляет значение f F-статистики (или F-коэффициента). Значение f, близкое к 1, свидетельствует о том, что базовые дисперсии генеральной совокупности равны. В выходной таблице, если f < 1, «P (F <= f) односторонний» дает вероятность наблюдения значения F-статистики меньше, чем f, когда дисперсии генеральной совокупности равны, и «F Критический односторонний» дает критическое значение меньше 1 для выбранного уровня значимости Alpha. Если f > 1, «P(F <= f) односторонний» дает вероятность наблюдения значения F-статистики, превышающего f, когда дисперсии генеральной совокупности равны, а «F Критический односторонний» дает критическое значение больше 1 для Альфы.
Инструмент анализа Фурье решает проблемы в линейных системах и анализирует периодические данные, используя метод быстрого преобразования Фурье (БПФ) для преобразования данных. Этот инструмент также поддерживает обратные преобразования, при которых обратные преобразованные данные возвращают исходные данные.
Инструмент анализа гистограмм вычисляет индивидуальные и совокупные частоты для диапазона ячеек данных и ячеек данных. Этот инструмент генерирует данные о количестве вхождений значения в набор данных.
Например, в классе из 20 учеников можно определить распределение баллов по буквенным категориям. В таблице гистограмм представлены границы буквенных оценок и количество баллов между самой низкой границей и текущей границей. Единственная наиболее частая оценка – это режим данных.
Совет: В Excel 2016 теперь можно создавать гистограммы или диаграммы Парето.
Инструмент анализа скользящего среднего проецирует значения в прогнозный период на основе среднего значения переменной за определенное количество предшествующих периодов. Скользящее среднее предоставляет информацию о тренде, которую замаскирует простое среднее всех исторических данных. Используйте этот инструмент для прогнозирования продаж, запасов или других тенденций. Каждое значение прогноза основано на следующей формуле.
Каждое значение прогноза основано на следующей формуле.
где:
N количество предыдущих периодов для включения в скользящее среднее
А j фактическое значение на момент времени j
Ф j прогнозируемое значение на момент времени j
Инструмент анализа Генерация случайных чисел заполняет диапазон независимыми случайными числами, взятыми из одного из нескольких распределений. Вы можете охарактеризовать субъектов в популяции с помощью распределения вероятностей. Например, вы можете использовать нормальное распределение, чтобы охарактеризовать совокупность роста людей, или вы можете использовать распределение Бернулли двух возможных результатов, чтобы охарактеризовать совокупность результатов подбрасывания монеты.
Вы можете охарактеризовать субъектов в популяции с помощью распределения вероятностей. Например, вы можете использовать нормальное распределение, чтобы охарактеризовать совокупность роста людей, или вы можете использовать распределение Бернулли двух возможных результатов, чтобы охарактеризовать совокупность результатов подбрасывания монеты.
Инструмент анализа рангов и процентилей создает таблицу, содержащую порядковый и процентный ранги каждого значения в наборе данных. Вы можете анализировать относительное положение значений в наборе данных. Этот инструмент использует функции рабочего листа RANK.EQ и PERCENTRANK.INC . Если вы хотите учитывать связанные значения, используйте функцию RANK.EQ , которая обрабатывает связанные значения как имеющие одинаковый ранг, или используйте RANK. СРЕДНИЙ , которая возвращает средний ранг связанных значений.
Инструмент регрессионного анализа выполняет линейный регрессионный анализ, используя метод наименьших квадратов, чтобы провести линию через набор наблюдений. Вы можете проанализировать, как на одну зависимую переменную влияют значения одной или нескольких независимых переменных. Например, вы можете проанализировать, как на результат спортсмена влияют такие факторы, как возраст, рост и вес. Вы можете распределить доли в показателе производительности для каждого из этих трех факторов на основе набора данных о производительности, а затем использовать результаты для прогнозирования производительности нового, непроверенного спортсмена.
Вы можете проанализировать, как на одну зависимую переменную влияют значения одной или нескольких независимых переменных. Например, вы можете проанализировать, как на результат спортсмена влияют такие факторы, как возраст, рост и вес. Вы можете распределить доли в показателе производительности для каждого из этих трех факторов на основе набора данных о производительности, а затем использовать результаты для прогнозирования производительности нового, непроверенного спортсмена.
Инструмент регрессии использует функцию рабочего листа ЛИНЕЙН .
Инструмент анализа выборки создает выборку из совокупности, рассматривая входной диапазон как совокупность. Когда генеральная совокупность слишком велика для обработки или построения диаграммы, можно использовать репрезентативную выборку. Вы также можете создать выборку, содержащую только значения из определенной части цикла, если считаете, что входные данные являются периодическими. Например, если входной диапазон содержит квартальные данные о продажах, выборка с периодичностью четыре помещает значения из того же квартала в выходной диапазон.
Инструменты анализа Two-Sample t-Test проверяют равенство совокупностей, лежащих в основе каждой выборки. В трех инструментах используются разные предположения: дисперсии популяции равны, дисперсии популяции не равны и что две выборки представляют собой наблюдения до и после лечения одних и тех же субъектов.
Для всех трех инструментов ниже вычисляется значение t-Statistic, t, которое отображается как «t Stat» в выходных таблицах. В зависимости от данных это значение t может быть отрицательным или неотрицательным. В предположении равной базовой совокупности означает, что если t < 0, «P (T <= t) односторонний» дает вероятность того, что будет наблюдаться значение t-статистики, которое будет более отрицательным, чем t. Если t >=0, “P(T <= t) one-tail" дает вероятность того, что будет наблюдаться значение t-статистики, которое будет более положительным, чем t. «t Critical one-tail» дает значение отсечки, так что вероятность наблюдения значения t-Statistic, большего или равного «t Critical one-tail», равна Alpha.
“P(T <= t) two-tail" дает вероятность того, что будет наблюдаться значение t-статистики, которое по абсолютной величине больше, чем t. «P Критический двухсторонний» дает пороговое значение, так что вероятность того, что наблюдаемая t-статистика больше по абсолютному значению, чем «P Критический двухсторонний», равна Альфа.
t-тест: два образца в паре для средних значений
Вы можете использовать парный тест, когда в выборках есть естественное спаривание наблюдений, например, когда группа выборок тестируется дважды — до и после эксперимента. Этот инструмент анализа и его формула выполняют парный t-критерий Стьюдента для двух выборок, чтобы определить, вероятно ли, что наблюдения, полученные до обработки, и наблюдения, полученные после обработки, получены из распределений с равными средними значениями совокупности. Эта форма t-критерия не предполагает, что дисперсии обеих совокупностей равны.
Примечание. Среди результатов, генерируемых этим инструментом, есть объединенная дисперсия, накопленная мера разброса данных о среднем значении, полученная по следующей формуле.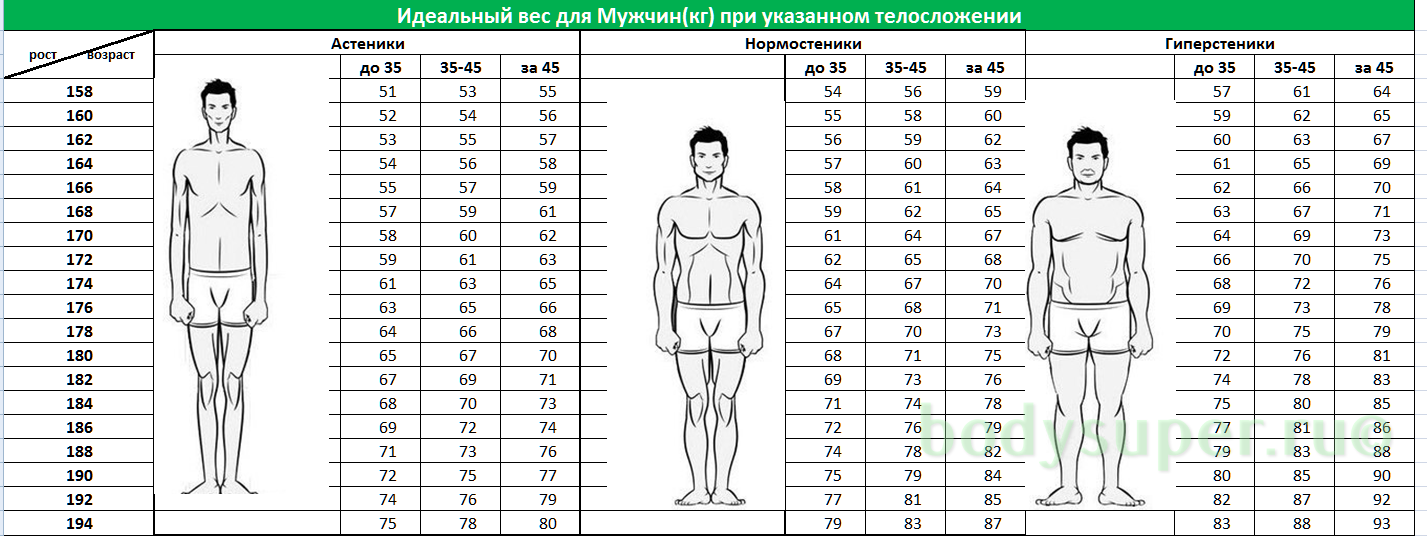
t-критерий: две выборки при условии равенства дисперсий
Этот инструмент анализа выполняет t-критерий Стьюдента для двух выборок. Эта форма t-теста предполагает, что два набора данных получены из распределений с одинаковыми дисперсиями. Он называется гомоскедастическим t-критерием. Вы можете использовать этот t-критерий, чтобы определить, вероятно ли, что две выборки получены из распределений с равными средними значениями генеральной совокупности.
t-критерий: две выборки, предполагающие неравные дисперсии
Этот инструмент анализа выполняет t-критерий Стьюдента для двух выборок. Эта форма t-теста предполагает, что два набора данных получены из распределений с неравной дисперсией. Он называется гетероскедастическим t-критерием. Как и в предыдущем случае с равными отклонениями, вы можете использовать этот t-критерий, чтобы определить, вероятно ли, что две выборки получены из распределений с равными средними значениями генеральной совокупности.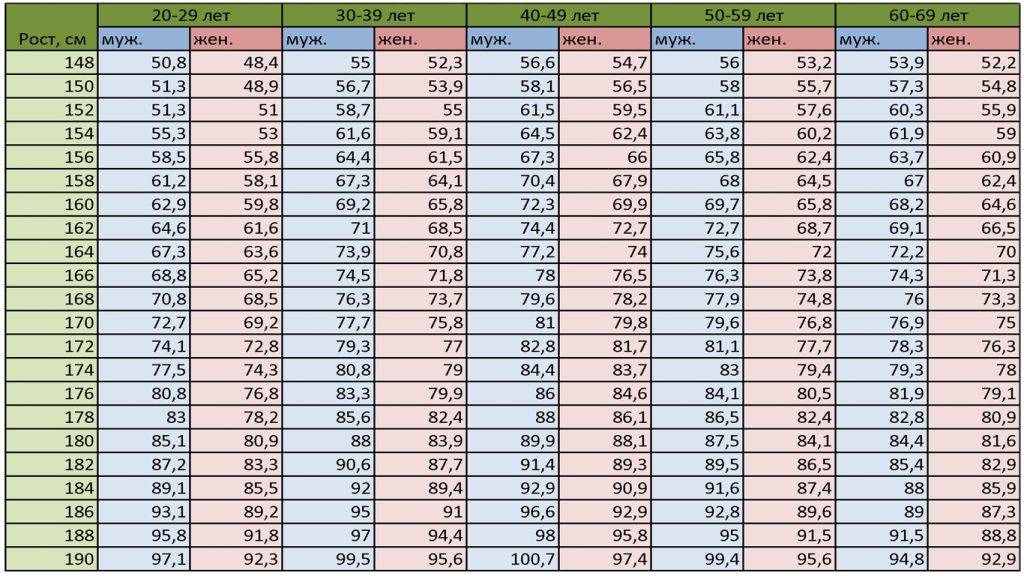 Используйте этот тест, когда в двух выборках есть разные предметы. Используйте парный тест, описанный в следующем примере, когда есть один набор субъектов, и две выборки представляют измерения для каждого субъекта до и после лечения.
Используйте этот тест, когда в двух выборках есть разные предметы. Используйте парный тест, описанный в следующем примере, когда есть один набор субъектов, и две выборки представляют измерения для каждого субъекта до и после лечения.
Следующая формула используется для определения статистического значения t .
Следующая формула используется для расчета степеней свободы, df. Поскольку результат вычисления обычно не является целым числом, значение df округляется до ближайшего целого числа, чтобы получить критическое значение из таблицы t. Функция листа Excel T . ТЕСТ использует рассчитанное значение df без округления, так как можно вычислить значение для Т . TEST с нецелым df. Из-за этих разных подходов к определению степеней свободы результаты T . TEST и этот инструмент t-Test будут отличаться в случае неравных отклонений.
Z-тест: инструмент анализа двух выборок для средних значений выполняет z-тест с двумя выборками для средних с известной дисперсией.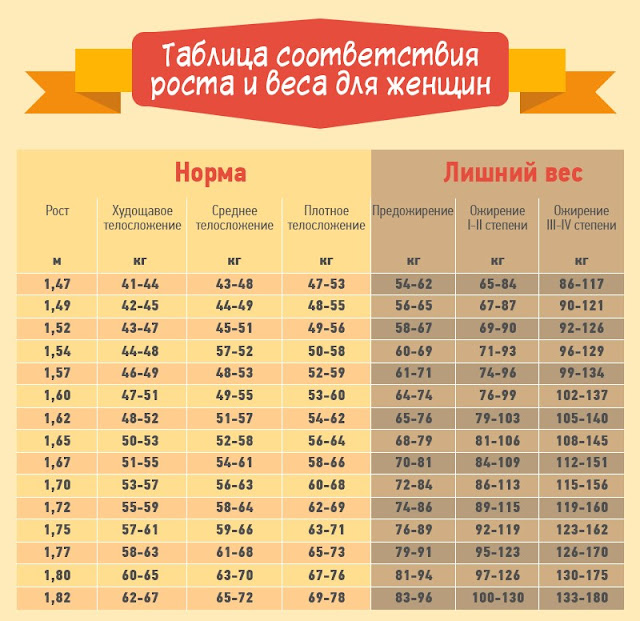 Этот инструмент используется для проверки нулевой гипотезы об отсутствии различий между двумя средними значениями генеральной совокупности по сравнению с односторонней или двусторонней альтернативной гипотезой. Если отклонения неизвестны, функция рабочего листа З . Вместо этого следует использовать TEST .
Этот инструмент используется для проверки нулевой гипотезы об отсутствии различий между двумя средними значениями генеральной совокупности по сравнению с односторонней или двусторонней альтернативной гипотезой. Если отклонения неизвестны, функция рабочего листа З . Вместо этого следует использовать TEST .
При использовании инструмента z-Test внимательно следите за выводом. «P(Z <= z) с одним хвостом» на самом деле является P(Z >= ABS(z)), вероятностью значения z дальше от 0 в том же направлении, что и наблюдаемое значение z, когда нет разницы между значит население. «P(Z <= z) двусторонний» на самом деле P(Z >= ABS(z) или Z <= -ABS(z)), вероятность того, что значение z дальше от 0 в любом направлении, чем наблюдаемое z-значение, когда нет разницы между средними значениями населения. Двусторонний результат — это просто односторонний результат, умноженный на 2. Инструмент z-Test также можно использовать в случае, когда нулевая гипотеза состоит в том, что существует конкретное ненулевое значение для разницы между двумя средними значениями генеральной совокупности. Например, вы можете использовать этот тест для определения различий между характеристиками двух моделей автомобилей.
Например, вы можете использовать этот тест для определения различий между характеристиками двух моделей автомобилей.
Нужна дополнительная помощь?
Вы всегда можете обратиться к эксперту в техническом сообществе Excel или получить поддержку в сообществе ответов.
См. также
Создайте гистограмму в Excel 2016
Создайте диаграмму Парето в Excel 2016
Загрузите пакет инструментов анализа в Excel
ИНЖЕНЕРНЫЕ функции (ссылка)
Обзор формул в Excel
Как избежать неработающих формул
Найдите и исправьте ошибки в формулах
Сочетания клавиш и функциональные клавиши Excel
9{2}\) значений и, следовательно, потенциально разные выводы.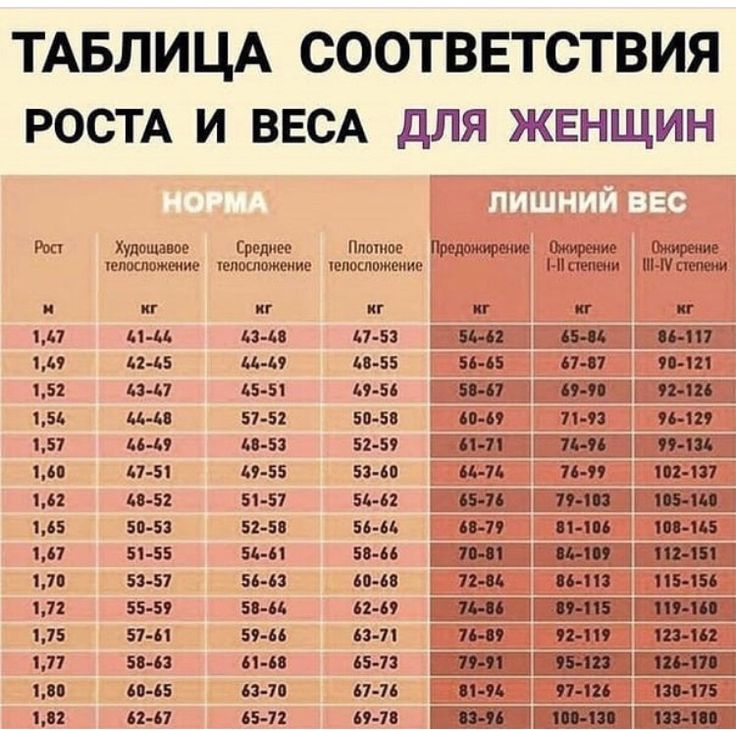 Как всегда, мы хотим сделать выводы о популяциях , а не только о выборках. Для этого нам нужно либо провести проверку гипотезы, либо рассчитать доверительный интервал. В этом разделе мы узнаем, как провести проверку гипотезы для коэффициента корреляции населения \(\rho\) (греческая буква «ро»).
Как всегда, мы хотим сделать выводы о популяциях , а не только о выборках. Для этого нам нужно либо провести проверку гипотезы, либо рассчитать доверительный интервал. В этом разделе мы узнаем, как провести проверку гипотезы для коэффициента корреляции населения \(\rho\) (греческая буква «ро»).Как правило, исследователь должен использовать проверку гипотезы о корреляции генеральной совокупности \(\rho\), чтобы узнать о линейной связи между двумя переменными, когда не очевидно, какую переменную следует рассматривать как отклик. Давайте проясним этот момент на примерах двух разных исследовательских вопросов.
Подумайте о том, существует ли линейная зависимость между смертностью от рака кожи и широтой. В Уроке 2 мы увидим, что можем выполнить любой из следующих тестов:
- t -тест для тестирования \(H_{0} \colon \beta_{1}= 0\)
- ANOVA F – тест для тестирования \(H_{0} \colon \beta_{1}= 0\)
Для этого примера совершенно очевидно, что широту следует рассматривать как предикторную переменную, а смертность от рака кожи как отклик.
Напротив, предположим, что мы хотим оценить, существует ли линейная зависимость между возрастом мужа и возрастом его жены (данные о муже и жене). В этом случае можно рассматривать возраст мужа как ответ:
Корреляция Пирсона HAge и WAge = 0,939…или можно рассматривать возраст жены как ответ:
Корреляция Пирсона WAge и HAge = 0,939В случаях таких как они, мы отвечаем на наш исследовательский вопрос о существовании линейной зависимости, используя t – тест для проверки коэффициента корреляции совокупности \(H_{0}\colon \rho = 0\).
Давайте сразу к делу! Мы следуем стандартным процедурам проверки гипотез при проведении проверки гипотезы для коэффициента корреляции населения \(\rho\).
Этапы проверки гипотезы для \(\boldsymbol{\rho}\) Раздел
- Шаг 1: Гипотезы
Сначала указываем нулевую и альтернативную гипотезы: 92}}\)
- Шаг 3: P-значение
В-третьих, мы используем полученную тестовую статистику для вычисления значения P .
 Как всегда, P -значение является ответом на вопрос: «Насколько вероятно, что мы получили бы тестовую статистику t* столь же экстремальную, как если бы нулевая гипотеза была верна?» Значение P определяется обращением к распределению t- с n -2 степенями свободы.
Как всегда, P -значение является ответом на вопрос: «Насколько вероятно, что мы получили бы тестовую статистику t* столь же экстремальную, как если бы нулевая гипотеза была верна?» Значение P определяется обращением к распределению t- с n -2 степенями свободы. - Шаг 4: Решение
Наконец, мы принимаем решение:
- Если P -значение меньше уровня значимости \(\alpha\), мы отклоняем нулевую гипотезу в пользу альтернативы. Мы заключаем, что «имеется достаточно доказательств на \(\альфа\) уровне, чтобы заключить, что существует линейная зависимость в популяции между предиктором x и ответом y».
- Если P -значение больше, чем уровень значимости \(\alpha\), мы не можем отклонить нулевую гипотезу. Мы заключаем, что «на уровне \(\альфа\) недостаточно доказательств, чтобы заключить, что существует линейная зависимость в популяции между предиктором x и ответ y .
 ”
”
Пример 1-5: Данные о муже и жене Раздел
Проведем проверку гипотезы на данных о возрасте мужа и жены, в которой выборочная корреляция, основанная на n = 170 пар, составляет r = 0,939. Чтобы проверить \(H_{0} \colon \rho = 0\) против альтернативы \(H_{A} \colon \rho ≠ 0\), мы получаем следующую тестовую статистику:
92}}\\ &=35.39\end{align}Чтобы получить P -значение, нам нужно сравнить тестовую статистику с t -распределением со 168 степенями свободы (поскольку 170 – 2 = 168 ). В частности, нам нужно найти вероятность того, что статистика теста окажется более экстремальной, чем 35,39, а затем, поскольку мы проводим двусторонний тест, умножим эту вероятность на 2. Здесь нам поможет Minitab:
Распределение Стьюдента с 168 DF
| х | Р(Х<= х) |
|---|---|
| 35,3900 | 1. 0000 0000 |
Вывод говорит нам, что вероятность получения тестовой статистики меньше 35,39 больше 0,999. Следовательно, вероятность получить тестовую статистику выше 35,39 меньше 0,001. Как показано в следующем видео, мы умножаем на 2 и определяем, что значение P меньше 0,002.
С P -значение мало — скажем, меньше 0,05 — мы можем отклонить нулевую гипотезу. Существует достаточно статистических данных на уровне \(\альфа = 0,05\), чтобы сделать вывод о наличии значительной линейной зависимости между возрастом мужа и возрастом его жены.
Между прочим, мы можем позволить статистическим программам вроде Minitab делать за нас всю грязную работу. При этом Minitab сообщает:
Корреляция: WAge, HAge
Корреляция Пирсона WAge и HAge = 0,939
P-Value = 0.
