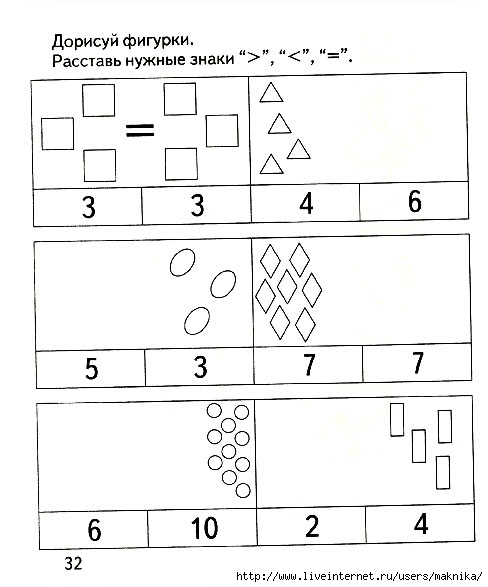
Сравнение чисел задания для дошкольников: Задания на сравнение для детей – скачать бесплатно – Практические задания – Развитие ребенка – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Циклы в программировании. Цикл while. Урок 10 курса “Python. Введение в программирование”

Циклы являются такой же важной частью структурного программирования, как условные операторы. С помощью циклов можно организовать повторение выполнения участков кода. Потребность в этом возникает довольно часто. Например, пользователь последовательно вводит числа, и каждое из них требуется добавлять к общей сумме. Или нужно вывести на экран квадраты ряда натуральных чисел и тому подобные задачи.

Цикл while

“While” переводится с английского как “пока”. Но не в смысле “до свидания”, а в смысле “пока имеем это, делаем то”.

Можно сказать, while является универсальным циклом. Он присутствует во всех языках, поддерживающих структурное программирование, в том числе в Python. Его синтаксис обобщенно для всех языков можно выразить так:

while логическое_выражение {
    выражение 1;
    …
    выражение n;
}

Это похоже на условный оператор if. Однако в случае циклических операторов их тела могут выполняться далеко не один раз. В случае

if, если логическое выражение в заголовке возвращает истину, то тело выполняется единожды. После этого поток выполнения программы возвращается в основную ветку и выполняет следующие выражения, расположенные ниже всей конструкции условного оператора.

В случае while, после того как его тело выполнено, поток возвращается к заголовку цикла и снова проверяет условие. Если логическое выражение возвращает истину, то тело снова выполняется. Потом снова возвращаемся к заголовку и так далее.

Цикл завершает свою работу только тогда, когда логическое выражение в заголовке возвращает ложь, то есть условие выполнения цикла больше не соблюдается. После этого поток выполнения перемещается к выражениям, расположенным ниже всего цикла. Говорят, “происходит выход из цикла”.

Рассмотрите блок-схему цикла while.

На ней ярко-голубыми прямоугольниками обозначена основная ветка программы, ромбом – заголовок цикла с логическим выражением, бирюзовым прямоугольником – тело цикла.

С циклом while возможны две исключительные ситуации:

Если при первом заходе в цикл логическое выражение возвращает False, то тело цикла не выполняется ни разу. Эту ситуацию можно считать нормальной, так как при определенных условиях логика программы может предполагать отсутствие необходимости в выполнении выражений тела цикла.
Если логическое выражение в заголовке while никогда не возвращает False, а всегда остается равным True, то цикл никогда не завершится, если только в его теле нет оператора принудительного выхода из цикла (break) или вызовов функций выхода из программы – quit()
, exit() в случае Python. Если цикл повторяется и повторяется бесконечное количество раз, то в программе происходит зацикливание. В это время она зависает и самостоятельно завершиться не может.

Вспомним наш пример из урока про исключения. Пользователь должен ввести целое число. Поскольку функция input() возвращает строку, то программный код должен преобразовать введенное к целочисленному типу с помощью функции int(). Однако, если были введены символы, не являющиеся цифрами, то возникает исключение ValueError, которое обрабатывается веткой except. На этом программа завершается.

Другими словами, если бы программа предполагала дальнейшие действия с числом (например, проверку на четность), а она его не получила, то единственное, что программа могла сделать, это закончить свою работу досрочно.

Но ведь можно просить и просить пользователя корректно вести число, пока он его не введет. Вот как может выглядеть реализующий это код:

n = input("Введите целое число: ")
 
while type(n) != int:
    try:
        n = int(n)
    except ValueError:
        print("Неправильно ввели!")
        n = input("Введите целое число: ")
 
if n % 2 == 0:
    print("Четное")
else:
    print("Нечетное")

Примечание 1. Не забываем, в языке программирования Python в конце заголовков сложных инструкций ставится двоеточие.

Примечание 2. В выражении type(n) != int с помощью функции type() проверяется тип переменной n. Если он не равен int, то есть значение n не является целым числом, а является в данном случае строкой, то выражение возвращает истину. Если же тип

n равен int, то данное логическое выражение возвращает ложь.

Примечание 3. Оператор % в языке Python используется для нахождения остатка от деления. Так, если число четное, то оно без остатка делится на 2, то есть остаток будет равен нулю. Если число нечетное, то остаток будет равен единице.

Проследим алгоритм выполнения этого кода. Пользователь вводит данные, они имеют строковый тип и присваиваются переменной n. В заголовке while проверяется тип n. При первом входе в цикл тип n всегда строковый, то есть он не равен int. Следовательно, логическое выражение возвращает истину, что позволяет зайти в тело цикла.

Здесь в ветке try совершается попытка преобразования строки к целочисленному типу. Если она была удачной, то ветка

except пропускается, и поток выполнения снова возвращается к заголовку while.

Теперь n связана с целым числом, следовательно, ее тип int, который не может быть не равен int. Он ему равен. Таким образом логическое выражение type(n) != int возвращает False, и весь цикл завершает свою работу. Далее поток выполнения переходит к оператору if-else, находящемуся в основной ветке программы. Здесь могло бы находиться что угодно, не обязательно условный оператор.

Вернемся назад. Если в теле try попытка преобразования к числу была неудачной, и было выброшено исключение ValueError, то поток выполнения программы отправляется в ветку except и выполняет находящиеся здесь выражения, последнее из которых просит пользователя снова ввести данные.

Переменная n теперь имеет новое значение.

После завершения except снова проверяется логическое выражение в заголовке цикла. Оно даст True, так как значение n по-прежнему строка.

Выход из цикла возможен только тогда, когда значение n будет успешно конвертировано в число.

Рассмотрим следующий пример:

total = 100
 
i = 0
while i < 5:
    n = int(input())
    total = total - n
    i = i + 1
 
print("Осталось", total)

Сколько раз “прокрутится” цикл в этой программе, то есть сколько итераций он сделает? Ответ: 5.

Сначала переменная i равна 0. В заголовке цикла проверяется условие i < 5, и оно истинно. Тело цикла выполняется. В нем меняется значение i, путем добавления к нему единицы.
Теперь переменная i равна 1. Это меньше пяти, и тело цикла выполняется второй раз.
В нем i меняется, ее новое значение 2.
Два меньше пяти. Тело цикла выполняется третий раз. Значение i становится равным трем.
Три меньше пяти. На этой итерации i присваивается 4.
Четыре по прежнему меньше пяти. К i добавляется единица, и теперь ее значение равно пяти.

Далее начинается шестая итерация цикла. Происходит проверка условия i < 5. Но поскольку теперь оно возвращает ложь, то выполнение цикла прерывается, и его тело не выполняется.

“Смысловая нагрузка” данного цикла – это последовательное вычитание из переменной total вводимых чисел. Переменная i в данном случае играет только роль счетчика итераций цикла. В других языках программирования для таких случаев предусмотрен цикл

for, который так и называется: “цикл со счетчиком”.

Его преимущество заключается в том, что в теле цикла не надо изменять переменную-счетчик, ее значение меняется автоматически в заголовке for.

В языке Python тоже есть цикл for. Но это не цикл со счетчиком. В Питоне он предназначен для перебора элементов последовательностей и других сложных объектов. Данный цикл и последовательности будут изучены в последующих уроках.

Для while наличие счетчика не обязательно. Представим, что надо вводить числа, пока переменная total больше нуля. Тогда код будет выглядеть так:

total = 100
 
while total > 0:
    n = int(input())
    total = total - n
 
print("Ресурс исчерпан")

Сколько раз здесь выполнится цикл? Неизвестно, все зависит от вводимых значений. Поэтому у цикла со счетчиком известно количество итераций, а у цикла без счетчика – нет.

Самое главное для цикла while – чтобы в его теле происходили изменения значений переменных, которые проверяются в его заголовке, и чтобы хоть когда-нибудь наступил случай, когда логическое выражение в заголовке возвращает False. Иначе произойдет зацикливание.

Примечание 1. Не обязательно в выражениях

total = total - n и i = i + 1 повторять одну и ту же переменную. В Python допустим сокращенный способ записи подобных выражений: total -= n и i += 1.

Примечание 2. При использовании счетчика он не обязательно должен увеличиваться на единицу, а может изменяться в любую сторону на любое значение. Например, если надо вывести числа кратные пяти от 100 до 0, то изменение счетчика будет таким i = i - 5, или i -= 5.

Примечание 3. Для счетчика не обязательно использовать переменную с идентификатором i. Можно назвать переменную-счетчик как угодно. Однако так принято в программировании, что счетчики обозначают именами i и j (иногда одновременно требуются два счетчика).

Практическая работа

Измените последний код из урока так, чтобы переменная total не могла уйти в минус. Например, после предыдущих вычитаний ее значение стало равным 25. Пользователь вводит число 30. Однако программа не выполняет вычитание, а выводит сообщение о недопустимости операции, после чего осуществляет выход из цикла.
Используя цикл while, выведите на экран для числа 2 его степени от 0 до 20. Возведение в степень в Python обозначается как **. Фрагмент вывода:
```
...
  32
  64
 128
 256
 512
1024
...
```

Примеры решения и дополнительные уроки в pdf-версии и android-приложении курса

Калькулятор округления числа

0
AC		+/-	÷
7	8	9	×
4	5	6	–
1	2	3	+
0	00	,	=

Калькулятор округления чисел, округлит числа, до целого (до единиц), десятых, сотых, тысячных, десятитысячных представленные: обыкновенной либо десятичной дробью и экспоненциальной записью и отобразит подробное решение.

Вы можете выбрать тип округления, а так же указать количество чисел после запятой. Примеры записи числа, которое необходимо округлить: 5765, -1652, 1/3, -3/6, -5/-7, 34.012, 56,23, 2.3e+5, 5.8e-123 и т.д.

Число
Тип округления До целого (до единиц)До десятыхДо сотыхДо тысячныхДо десятитысячныхУказать количество чисел после запятой

Пожалуйста, опишите возникшую ошибку.

Подтвердите, что вы не робот

Правила округления целых чисел

Правило 1. Если справа от цифры до которой необходимо округлить число, стоит цифра:
0, 1, 2, 3, 4,
то тогда необходимо просто заменить нулями все цифры до цифры до которой необходимо округлить число.

Примеры:
Красной чертой отделим округляемый разряд, а зеленым выделим цифру, которая стоит справа.

Округлим число 423012324 до десятых

42301232|4 ≈ 423012320

Округлим число 423012324 до сотых

4230123|24 ≈ 423012300

Округлим число 423012324 до тысячных

423012|324 ≈ 423012000

Округлим число 423012324 до десятитысячных

42301|2324 ≈ 423010000

Округлим число 4.230123243 до семи знаков после запятой

42|3012324 ≈ 420000000

Правило 2. Если справа от цифры до которой необходимо округлить число, стоит цифра:
5, 6, 7, 8, 9,
то тогда необходимо к цифре до которой необходимо округлить число прибавить 1.

Примеры:
Красной чертой отделим округляемый разряд, а зеленым выделим цифру, которая стоит справа.

Округлим число 94856757 до тысячных
Необходимо округлить до тысячных, значит после красной черты мы оставляем 3 цифры.
Красной чертой отделим округляемый разряд, а зеленым выделим цифру, которая стоит справа.

94856|757

Если справа от красной черты, стоит цифра: 0, 1, 2, 3, 4 то тогда необходимо заменить нулями все цифры стоящие после красной черты, а если стоит цифра: 5, 6, 7, 8, 9 то тогда необходимо тоже заменить нулями все цифры стоящие после красной черты и к цифре стоящей слева от красной черты прибавить число 1.

После красной черты у нас стоит цифра 7, значит мы должны заменить нулями все цифры стоящие после красной черты и прибавить 1 к цифре слева от красной черты.

94856 + 1 = 94857

94856757 ≈ 94857000

Правила округления десятичных чисел

Правило 1. Если справа от цифры до которой необходимо округлить число, стоит цифра:
0, 1, 2, 3, 4,
то тогда необходимо просто отбросить все цифры до цифры до которой необходимо округлить число.

Примеры:
Красной чертой отделим округляемый разряд, а зеленым выделим цифру, которая стоит справа.

Округлим число 4.23012324 до целого (до единиц)

4.|23012324 ≈ 4

Округлим число 4.23012324 до десятых

4.2|3012324 ≈ 4.2

Округлим число 4.23012324 до сотых

4.23|012324 ≈ 4.23

Округлим число 4.23012324 до тысячных

4.230|12324 ≈ 4.230

Округлим число 4.23012324 до десятитысячных

4.2301|2324 ≈ 4.2301

Округлим число 4.230123243 до семи знаков после запятой

4.2301232|43 ≈ 4.2301232

Примеры:
Красной чертой отделим округляемый разряд, а зеленым выделим цифру, которая стоит справа.

Округлим число 12.56843 до целого (до единиц)
Необходимо округлить до целого (до единиц), значит после точки мы оставляем 0 цифры.

12.|56843

Если справа от красной черты, стоит цифра: 0, 1, 2, 3, 4 то тогда необходимо просто отбросить все цифры стоящие после красной черты, а если стоит цифра: 5, 6, 7, 8, 9 то тогда необходимо тоже отбросить все цифры стоящие после красной черты и к цифре стоящей слева от красной черты прибавить число 1.

После красной черты у нас стоит цифра 5, значит мы должны отбросить все цифры стоящие после красной черты и прибавить 1 к цифре слева от красной черты.

12 + 1 = 13

12.56843 ≈ 13

Округлим число 985.0029 до тысячных
Необходимо округлить до тысячных, значит после точки мы оставляем 3 цифры.

985.002|9

После красной черты у нас стоит цифра 9, значит мы должны отбросить все цифры стоящие после красной черты и прибавить 1 к цифре слева от красной черты.

2 + 1 = 3

985.0029 ≈ 985.003

Вам могут также быть полезны следующие сервисы

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор упрощения выражений

Калькулятор со скобками

Калькулятор уравнений

Калькулятор суммы

Калькулятор пределов функций

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Калькулятор делителей числа

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Калькулятор свойств корней и степеней

Калькулятор комплексных чисел

Калькулятор среднего арифметического

Калькулятор арифметической прогрессии

Калькулятор геометрической прогрессии

Калькулятор модуля числа

Калькулятор абсолютной погрешности приближения

Калькулятор абсолютной погрешности

Калькулятор относительной погрешности

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькулятор нахождения наименьшего угла

Калькулятор определения вида угла

Калькулятор смежных углов

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N₂ | Двоичная система счисления

N₃ | Троичная система счисления

N₄ | Четырехичная система счисления

N₅ | Пятеричная система счисления

N₆ | Шестеричная система счисления

N₇ | Семеричная система счисления

N₈ | Восьмеричная система счисления

N₉ | Девятеричная система счисления

N₁₁ | Одиннадцатиричная система счисления

N₁₂ | Двенадцатеричная система счисления

N₁₃ | Тринадцатеричная система счисления

N₁₄ | Четырнадцатеричная система счисления

N₁₅ | Пятнадцатеричная система счисления

N₁₆ | Шестнадцатеричная система счисления

N₁₇ | Семнадцатеричная система счисления

N₁₈ | Восемнадцатеричная система счисления

N₁₉ | Девятнадцатеричная система счисления

N₂₀ | Двадцатеричная система счисления

N₂₁ | Двадцатиодноричная система счисления

N₂₂ | Двадцатидвухричная система счисления

N₂₃ | Двадцатитрехричная система счисления

N₂₄ | Двадцатичетырехричная система счисления

N₂₅ | Двадцатипятеричная система счисления

N₂₆ | Двадцатишестеричная система счисления

N₂₇ | Двадцатисемеричная система счисления

N₂₈ | Двадцативосьмеричная система счисления

N₂₉ | Двадцатидевятиричная система счисления

N₃₀ | Тридцатиричная система счисления

N₃₁ | Тридцатиодноричная система счисления

N₃₂ | Тридцатидвухричная система счисления

N₃₃ | Тридцатитрехричная система счисления

N₃₄ | Тридцатичетырехричная система счисления

N₃₅ | Тридцатипятиричная система счисления

N₃₆ | Тридцатишестиричная система счисления

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка.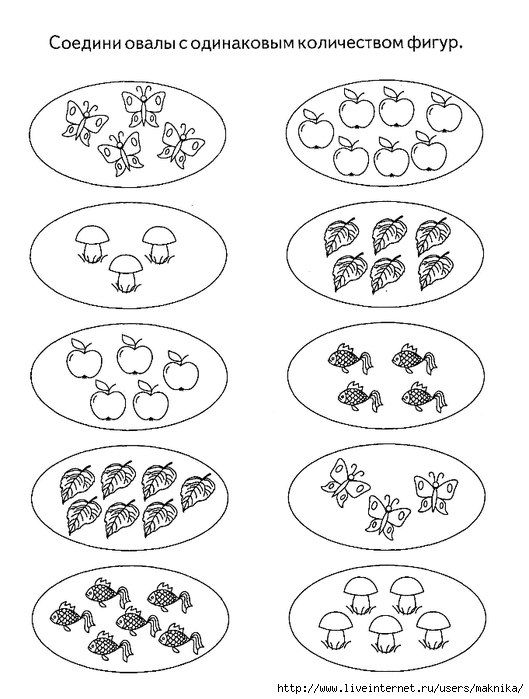

Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Генератор Pdf с примерами

Тренажёры решения примеров

Тренажёр таблицы умножения

Тренажер счета для дошкольников

Тренажер счета на внимательность для дошкольников

Тренажер решения примеров на сложение, вычитание, умножение, деление.

Найди правильный ответ.

Тренажер решения примеров с разными действиями

Тренажёры решения столбиком

Тренажёр сложения столбиком

Тренажёр вычитания столбиком

Тренажёр умножения столбиком

Тренажёр деления столбиком с остатком

Калькуляторы решения столбиком

Калькулятор сложения, вычитания, умножения и деления столбиком

Калькулятор деления столбиком с остатком

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Цифры в текст

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона.

Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора.

Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

Сравнение чисел (объектов)

Уроки
Детский сад
Математика
Подсчет, чтобы сказать, сколько

Мероприятие 1 / Соответствие: классификация игрушек по размеру.
Рабочий лист
Этот рабочий лист требует, чтобы ваш ребенок настроился на свои навыки наблюдения и счета. Текст требует, чтобы ваш малыш внимательно просматривал изображения и считал предметы. Далее они должны обвести тарелки, содержащие наименьшее, наибольшее или равное количество узоров. Не уделяя должного внимания или не имея хороших способностей к счету, ваш ребенок, скорее всего, сочтет это задание достаточно легким
Заполнить онлайн
Отметить как выполненное
Добавить в избранное
Мероприятие 2 / Более или менее рабочий лист
В Интернете нет недостатка в бесплатных печатных рабочих листах для детского сада. В Kids Academy мы считаем, что дети должны учиться разными способами, чтобы концепции «прилипли». Этот более или менее рабочий лист использует базовую концепцию из Сингапурской математики, чтобы помочь вашему маленькому ученику понять количество.
Заполнение этого рабочего листа поможет вашему ребенку:
• Визуально распознавать группы чисел
• Отрабатывать навыки счета.
• Понимать количество.
• Сравнивать группы чисел. анализ числовых групп. Этот рабочий лист поможет вашему ребенку быстро распознавать числовые группы при сравнении количества.
Заполнить онлайн
Отметить как выполненное
Добавить в избранное
Мероприятие 3 / Давайте сравним числа!

Попробуйте Детскую Академию БЕСПЛАТНО!

Посмотреть полную программу обучения

Да, я хочу добавить Электронный блок – совместимый с кирпичом конструктор для построения 3D схем с подсветкой, звуками, движением и т. д.

19,99 $

Подарочная карта Введите код купона

Примечание. Вам не будет выставлен счет, пока не закончится бесплатная пробная версия. и может отменить в любой момент. Безвоздмездно.

Отличное приложение

Вау! Это приложение действительно отличное. Впервые моим детям действительно нравится изучать математику и читать. Игры в Kids Academy образовательные и очень веселые.

Кимберлихо

Отличное приложение!

Это был действительно интересный способ заставить моих детей попрактиковаться в математике. Я обычно изо всех сил пытаюсь вовлечь их в это, и Kids Academy делает это легко.

Фернанндас Стоун

Отличное приложение!

Это замечательное приложение для моего 7-летнего сына! 🙂 Он фокусируется на базовых навыках чтения, письма и математики. Система вознаграждений отличная и последовательная!

Лилбиттигарза

Так увлекательно

Нам нравится, как мы можем сосредоточиться на математике с помощью этого приложения. Это увлекательно, и нам нравится, как мы можем настраивать и адаптировать уровни в соответствии со знаниями и навыками нашего сына!

Мама Анна

Отлично подходит для детей

Наша 7-летняя дочь любит чтение и все офлайн-игры, которые предлагает Kids Academy. Это очень хорошее приложение, я очень рекомендую его!

ТониТан

Любимец дочери

По-прежнему самый любимый для нашего 7-летнего ребенка. Ей нравится зарабатывать звезды, когда она учится выводить буквы и цифры. Окраска и звуки привлекают внимание и соответствуют возрастной группе ребенка и 9-летнему возрасту.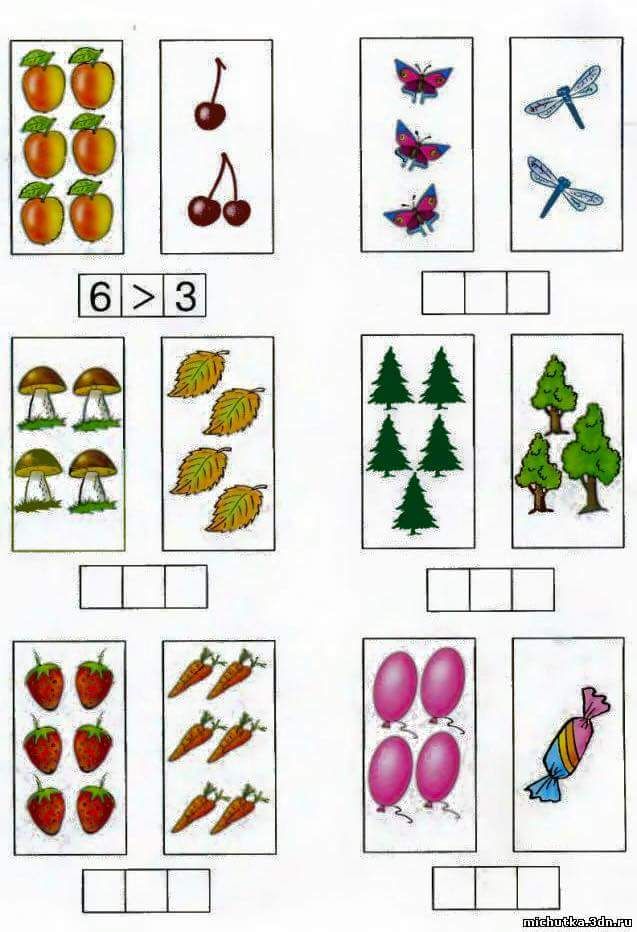 0017

Выживание5Дети

Карточки с математическими заданиями для сравнения трехзначных чисел

1,50 $

Всего страниц: 15
Размер файла: 12 МБ

ПРЕДПРОСМОТР

Количество карточек с задачами по математике «Сравнение трехзначных чисел»

Добавить в список желаний

Категория: Снова в школу Ресурсы Теги: 1-й, 2-й, 3-й, Деятельность, Основные операции, Домашнее обучение, Математика, Математические центры, Числа, Карточки с заданиями

Описание
Отзывы (0)
Вопросы и Ответы

Это 12 карточек сравнение трехзначных чисел карточная игра с математическими задачами с 4 разными листами для записей! Развлекайте своих учеников веселыми и интерактивными карточными играми каждый месяц! Эти карточные игры с заданиями можно использовать как занятие для всей группы, занятие в малых группах, центр математики или грамотности, независимую работу или как развлечение для мозга.

Посмотрите ПРОСМОТР, чтобы увидеть, как работают эти карты!

☆ НРАВИТСЯ? Ознакомьтесь с моим НАБОРОМ Карточек с заданиями на месяц для второго класса

☆ ХОТИТЕ ВСЕ мои карточки с заданиями для второго класса БЕСПЛАТНО?! ВСЕ они БЕСПЛАТНО включены в мой НАБОР Субпланов второго класса!

– Каждую карточную игру можно использовать с карандашом/мелком и бумагой ИЛИ поместить в защитный лист и использовать с маркером для сухого стирания!

-Легко отличить! Эта карточная игра включает в себя ЧЕТЫРЕ различных листа для записей!

При сравнении трехзначных чисел учащимся будет предложено:
– найти буквы A-L (карточка с заданиями на листе записи)
– ОПРЕДЕЛИТЬ и ЗАПИСАТЬ большее и меньшее число на
-ЦВЕТ знак (<,>,=), который описывает связь между каждым набором чисел
-ЦВЕТ фразу (больше, меньше, равно), которая описывает связь между каждым набором чисел

*ЭТА КАРТОЧКА-ЗАДАНИЕ ТАКЖЕ ВКЛЮЧЕНА В МОИ ДОПОЛНИТЕЛЬНЫЕ ПЛАНЫ ДОБРО ПОЖАЛОВАТЬ ДЛЯ Второго класса на декабрь
И ВСЕ ЕЖЕМЕСЯЧНЫЕ КАРТОЧКИ С ЗАДАЧАМИ ДЛЯ ВТОРОГО КЛАПАНА БУДУТ ВКЛЮЧЕНЫ В ПОДПЛАНЫ ДЛЯ ВТОРОГО КЛАДА НА КРУГЛЫЙ ГОД + редактируемая дополнительная информация

Если вы приобрели этот ежемесячный подплан или набор, вы ПОЛУЧИТЕ ВСЕ мои игры с карточками-заданиями!

★ Хотите получить мои новые продукты со скидкой 60%?! Все новинки продаются со скидкой первые 48 часов!

★ СЛЕДУЙТЕ ЗА МНОЙ:
Instagram: @thekinderlife
Блог: thekinderlifeblog.

Циклы в программировании. Цикл while. Урок 10 курса “Python. Введение в программирование”

Цикл while

Практическая работа

Калькулятор округления числа

Правила округления целых чисел

Правила округления десятичных чисел

Сравнение чисел (объектов)

Мероприятие 1 / Соответствие: классификация игрушек по размеру.

Мероприятие 2 / Более или менее рабочий лист

Мероприятие 3 / Давайте сравним числа!

Карточки с математическими заданиями для сравнения трехзначных чисел

Добавить комментарий Отменить ответ