Составить задачу на умножение 3 класс: Текстовые задачи на умножение и деление, 3 класс | Картотека по математике (3 класс):
Задачи на умножение для 3 класса
Математика / 3 класс
Предлагаем решить 10 задач для тренировки навыков умножения и улучшения успеваемости по математике.
Занятия на платформе ЛогикЛайк помогают развить мышление и кругозор.
В буфете на витрине 9 тарелок. На каждой тарелке лежит 5 пирожных. Сколько всего пирожных на витрине?
Показать ответ
9 × 5 = 45 пирожных.
В парке 4 ряда по 12 деревьев в каждом. Сколько всего деревьев в парке?
Показать ответ
4 × 12 = 48 деревьев.
У Наташи в аквариуме 11 рыбок. У Маши в 5 раз больше рыбок, чем у Наташи.
Сколько рыбок у Маши?
11 × 5 = 55 рыбок.
В спортзале было 6 корзин по 12 мячей в каждой. Сколько всего мячей?
Показать ответ
6 × 12 = 72 мячей.
В детском саду 5 младших групп. В каждой группе по 14 детей.
Сколько детей в детском саду?
Показать ответ
5 × 14 = 70 детей.
У Светы 3 машинки. У Димы в 20 раз больше машинок, чем у Светы.
Сколько машинок у Димы?
Показать ответ
3 × 20 = 60 машинок.
На кондитерской фабрике в каждый новогодний подарок складывают 18 конфет.
Сколько конфет потребуется, чтобы сложить 6 таких подарков?
Показать ответ
18 × 6 = 108 конфет.
Шеф-повар ресторана готовит омлет из 3 яиц.
Если повару нужно приготовить 72 омлета, то сколько яиц ему понадобится?
Показать ответ
3 × 72 = 216 яиц.
В школу купили 35 коробок с пазлами. В каждой коробке по 60 деталей.
Сколько всего деталей во всех коробках?
Показать ответ
35 × 60 = 2100 деталей.
Предприятие по производству петард за 1 час делает 5 коробок петард.
В каждой коробке по 24 петарды.
Сколько петард производит завод за час?
Показать ответ
24 × 5 = 120 петард.
Подключайтесь к ЛогикЛайк!
Более 2 000 000 ребят
со всего мира уже занимаются на LogicLike.
com.
Начать занятия
3 класс. Моро. Учебник №1. Ответы к стр. 18
Вспомни и объясни, что означает каждое число в записи двух чисел со знаком умножения: 3 • 4, 6 • 3.
Эти числа — множители: первое число (3 и 6) — число, которое повторяется, второе число (4 и 3) — сколько раз повторяется первое число.
1. Рассмотри суммы и скажи, чем они похожи.
2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 2 • 8 = 16
7 + 7 + 7 + 7 + 7 + 7 7 • 6 = 42
25 + 25 + 25 + 25 25 • 4 = 100
13 + 13 + 13 13 • 3 = 39
Одно и тоже одинаковое слагаемое повторяется несколько раз.
2.
4 + 4 + 4 < 4 • 5 16 + 16 + 16 = 16 • 3
8 + 8 + 8 > 8 • 2 32 + 32 < 32 • 3
9 + 9 + 9 = 9 • 3 48 + 48 = 48 • 2
3. Рассмотри чертёж и объясни, почему верны равенства.
4 • 2 = 2 • 4 6 • 3 = 3 • 6 8 • 3 = 3 • 8
Данные равенства выражают площади прямоугольников на чертеже.
4. Составь по рисунку задачу на умножение и две обратные ей задачи.
На дереве было 4 гнезда, а в каждом гнезде сидело по две птички. Сколько всего птичек было на дереве?
О т в е т: всего на дереве было 8 птичек.
На дереве в гнёздах сидело 8 птичек. В каждом гнезде была пара птичек. Сколько было гнёзд на дереве?
8 : 2 = 4 (г.) — было на дереве.
О т в е т: на дереве было 4 гнезда.
На дереве 8 птичек сидели в четырёх гнёздах поровну. По скольку птичек было в каждом гнезде?
8 : 4 = 2 (п.) — было в каждом гнезде.
О т в е т: в каждом гнезде было по две птички.
5. Легковое такси может взять 4 пассажиров. Сколько пассажиров могут взять 3 такие машины?
Составь две задачи, обратные данной, и реши их.
3 • 4 = 12 (п.
) — могут взять.
О т в е т: 3 такси могут взять 12 пассажиров.
В трёх такси разместилось 12 пассажиров поровну. Сколько пассажиров было в одном такси?
12 : 3 = 4 (п.) — в одной машине.
Пассажиры сели в такси по 4 человека. Всего пассажиров было 12. Сколько такси им понадобилось?
12 : 4 = 3 (т.) — им понадобилось.
О т в е т: пассажирам понадобилось 3 такси.
6. Составь задачи по кратким записям и реши их.
| Было — 50 р. Истратили — 14 р. и 6 р. Осталось — ? | Было — 30 р. и 15 р. Истратили — ? Осталось — 20 р. |
У Васи было 50 р. Он купил краски за 14 р. и кисточку за 6 р. Сколько денег у него осталось?
1) 14 + 6 = 20 (р.) — потратил Вася.
2) 50 — 20 = 30 (р.) — осталось у Васи.
О т в е т: у Васи осталось 30 р.
Ваня принёс в школу 30 р., а Петя — 15 р. После столовой у них осталось 20 р. Сколько денег ребята истратили в столовой?
2) 45 — 20 = 25 (р.) — истратили ребята.
О т в е т: Ребята истратили в столовой 25 р.
Сколько лап у восьми цыплят?
2 • 8 = 16
Ответы по математике. Учебник. 3 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Математика. 3 класс
Zam@dminТипы задач на умножение и деление
Проблемы со словами могут быть такой проблемой. Особенно в 3-х классах и выше, когда учащимся приходится решать все операции и многошаговые словесные задачи. Студенты часто пытаются определить представленную операцию или пропускают часть шагов, необходимых для решения. Явное преподавание типов словесных задач может помочь нашим ученикам распознавать операции в контексте.
Стандарты Common Core State излагают различные типы задач на умножение и деление, которые должны знать учащиеся. Обучая их явно, мы помогаем учащимся понять умножение и деление в контексте, чтобы помочь им по-настоящему понять операции. Мы связываем то, как математика, которую они изучают, имеет отношение к их реальной жизни. Сосредоточив внимание на текстовых задачах и их типах, мы сосредоточимся на том, что делает умножение и деление тем, чем они являются.
В этом посте подробно рассматриваются все типы задач на умножение и деление слов. Я также даю несколько полезных ссылок внизу, в которых обсуждаются когнитивно-управляемые инструкции или типы задач CGI. Они используют несколько иную лексику, чем CCSS, но имеют тот же набор навыков. Важное примечание: когда я говорю об обучении типам задач на умножение и деление слов в явном виде, я не имею в виду, что они практикуются только во время определенного раздела или что мы обучаем определенным ключевым словам для каждого типа задач.
Учащиеся должны прочитать задачу и понимать контекст. Распознавание типа проблемы может поддержать эту работу, но оно не сосредоточено на ключевых словах. Кроме того, я ежедневно решаю задачи со словами вне нашей основной работы. Я твердо верю в спираль стандартов в текстовых задачах, чтобы учащиеся должны были сосредоточиться на контексте для решения. Для получения дополнительной помощи в решении проблем ознакомьтесь с моей публикацией «Почему ваши учащиеся борются с задачами в Word и что вы можете с этим поделать».
Важное замечание, прежде чем мы начнем: на протяжении всего нашего исследования обеих операций мы часто возвращаемся к всего . На первом уроке мы определили, что умножение позволяет нам найти общее количество предметов, расположенных в равных группах. Когда мы начинаем исследовать деление, мы знаем общее количество объектов, которые у нас есть, и должны найти неизвестное в связи с группами. На протяжении всей нашей работы с массивами, площадями и равными группами мы продолжаем возвращаться к понятию в сумме , чтобы помочь учащимся определить необходимую операцию.
Именно путем определения суммы как известной или неизвестной учащиеся по-настоящему поймут операции умножения и деления. Как вы увидите, это основное внимание в каждом из типов задач на умножение и деление.
Равные группы как умножение и деление
В своих постах «Введение в умножение и работу с делением» я прохожу практические, увлекательные уроки, которые я использую для ознакомления с каждой операцией. При введении обеих операций мы ориентируемся на равные групповые договоренности. Для учащихся крайне важно понять, что умножение и деление работают с равными группами, поэтому имеет смысл начать здесь. Когда мы впервые начинаем работать со словесными задачами на умножение и деление, я прошу учащихся определить элементы, которые расположены в группах, и определить, на что похожа эта группа. Например, группа может быть коробкой или сумкой. Эти объекты также могут быть просто объектами в других сценариях. Таким образом, определение того, что объект сгруппирован внутри чего-либо, помогает учащимся понять проблему слова и то, что присутствует сценарий равной группы.
| УМНОЖЕНИЕ | КОЛИЧЕСТВЕННЫЙ ПОДРАЗДЕЛ | ЧАСТНОЕ ПОДРАЗДЕЛЕНИЕ | |
| ВСЕГО НЕИЗВЕСТНО | # из ГРУППЫ НЕИЗВЕСТНО | # в каждом | |
4 х 6 = ? ? ÷ 4 = 6 | ? Х 6 = 24 24 ÷ ? = 6 | 4 х ? = 24 24 ÷ 4 = ? | |
| Равные группы | На прилавке было 4 сумки. В каждом пакете было по 6 яблок. Сколько яблок было всего? | В мешках поровну разложено 24 яблока. В каждом пакете по 6 яблок. Сколько мешков с яблоками? | 24 яблока поровну разделены на 4 мешка. Сколько яблок в каждом мешке? |
Это задачи со словами, которые мы обычно думаем с умножением.
Это расположение элементов в равные группы, чтобы найти общее количество элементов. Определение того, что количество групп и количество элементов в каждой группе известно, а общее количество неизвестно, помогает учащимся решать эти словесные задачи.
Когда количество групп неизвестно, это проблема квотного деления. Поясню, я не учу своих студентов термину кавычка . Скорее, я учу их тому, что есть два типа разделения. Когда учащиеся могут определить, что общее количество объектов известно, но количество групп неизвестно, они знают, что они делятся. Важно, чтобы студенты имели много практики с обоими типами разделения.
ЧАСТИЧНОЕ ДЕЛЕНИЕ – # в каждой группе Неизвестно Если в текстовой задаче указано общее количество элементов и их расположение, но не указано число в каждой группе, это деление на части. Думайте об этом как разделение . Количество групп известно, поэтому известны и разделы.
Опять же, я не учу этому термину своих студентов, но важно, чтобы студенты знали, что деление представлено двумя способами.
После того, как обе операции будут представлены и отработаны по отдельности, мне нравится использовать мои карточки с заданиями по умножению и делению, чтобы практиковаться в написании уравнений и понимании группового расположения в контексте. Я считаю, что удаление всех компонентов словесной задачи и работа только с общей и групповой информацией помогает учащимся по-настоящему понять операции, связанные с равными группами. Это помогает им затем применить свои знания в текстовых задачах. Студенты получают практику с различными способами группировки элементов, что помогает им искать и определять отношения группировки в текстовых задачах позже.
Массивы как умножение и деление
В связи с обучением равным групповым расположениям, описанным выше, также должны быть включены массивы. Массивы – это то, как учащиеся впервые знакомятся с умножением во 2-м классе.
Учащиеся должны иметь базовые знания с строк и столбцов словарного запаса. Массивы — это то, как я связываю то, что мы изучаем сейчас, с тем, что они узнали раньше. Поэтому я преподаю массивы в то же время, что и равные групповые аранжировки. Соотношу ряды и количество групп. Я всегда подчеркиваю, что столбцы совпадают с числом в каждой строке (или группе).
| УМНОЖЕНИЕ | КОЛИЧЕСТВЕННЫЙ ПОДРАЗДЕЛ | ЧАСТНОЕ ПОДРАЗДЕЛЕНИЕ | |
| ВСЕГО НЕИЗВЕСТНО | # из ГРУППЫ НЕИЗВЕСТНО | # в каждом ГРУППА НЕИЗВЕСТНО | |
| 4 х 6 = ? ? ÷ 4 = 6 | ? Х 6 = 24 24 ÷ ? = 6 | 4 х ? = 24 24 ÷ 4 = ? | |
| Массивы | Есть 4 ряда мешков по 6 мешков в каждом ряду. Сумки расположены в 4 ряда и 6 столбцов. Сколько сумок? | 24 мешка расположены рядами по 6 штук. Сколько рядов мешков? 24 мешка расположены в 6 колонках. Сколько рядов мешков? | 24 мешка расположены равномерно в 4 ряда. Сколько мешков в каждом ряду? 24 мешка расположены равномерно в 4 ряда. Сколько столбцов мешков есть? |
Важно отметить, что CCSS предлагает две строгости задач с массивами слов: те, в которых представлены элементы в строках, и те, которые дают задачи со словами в строках и столбцах. Благодаря постоянному воздействию и практике студенты понимают, что они взаимозаменяемы. Задачи со словами-массивами не очень распространены, но определенно являются тем типом задач, с которым учащиеся должны ознакомиться и попрактиковаться. Они также закладывают основу для работы учащихся с нашим следующим типом словесных задач: область 9.0003
Площадь как умножение и деление
Площадь является важным компонентом нашей работы по умножению и делению.
Это основная часть обучения математике в 3-м классе, и важно, чтобы учащиеся работали со многими текстовыми задачами, где они должны распознавать область в контексте и решать. Это особенно важно, чтобы научиться различать площадь и периметр, устанавливая связи между массивами и тем, что известно об умножении и делении. Площадь должна быть представлена массивами и связана с моделью площади. Этот конкретный наглядный пример помогает учащимся связать то, что они уже знают (массивы), со своим новым обучением (областью). Единичные квадраты написаны в стандартах, чтобы быть этим мостом. Модели площадей продолжаются по мере того, как вы работаете с более сложными прямолинейными фигурами, и помогают учащимся понять распределительное свойство умножения. CCSS не перечисляет проблемы области как отдельную строку, а включает их в массивы. Хотя это, безусловно, имеет смысл, поскольку массивы могут быть созданы внутри прямоугольника, и именно так следует вводить площадь, в большинстве задач со словами с площадями не используются строки или столбцы при задании длин сторон.
Я думаю, что важно рассматривать задачи со словами отдельно от массивов.
| ДЛИНА СТОРОНЫ НЕИЗВЕСТНА | ДЛИНА СТОРОНЫ НЕИЗВЕСТНА | ||
| Зона | У прямоугольника одна сторона равна 6 футам, а другая — 4 футам. Чему равна площадь прямоугольника? | Прямоугольник имеет площадь 24 квадратных фута. Если одна сторона имеет длину 6 футов, какой длины должна быть перпендикулярная сторона? | Прямоугольник имеет площадь 24 квадратных фута. Если одна сторона имеет длину 6 футов, какой длины должна быть перпендикулярная сторона? |
Решение проблем области снова соединяется с общим числом и известными/неизвестными значениями. Когда учащиеся пытаются определить общую площадь фигуры и им даны длины обеих сторон, учащиеся должны умножить, чтобы найти площадь.
ДЕЛЕНИЕ Когда учащимся дается общая площадь фигуры , но им нужно найти недостающую длину стороны, они должны разделить.
В конечном счете, если учащиеся хорошо понимают задачи на умножение и деление и их связь с всего , они, скорее всего, успешно справятся с задачами на площадь.
Задания на сравнение
На мой взгляд, самыми сложными задачами на умножение и деление являются задачи на сравнение. Подобно тому, как они связаны со сложением и вычитанием, структура этих задач делает их более сложными, чем другие. Для них важно рассмотреть каждый из различных типов проблем и переварить то, что дается. Я использую процедуру «3 чтения» при работе с текстовыми задачами, и эти задачи всегда вызывают наибольшее обсуждение, поскольку учащиеся борются с представленной информацией.
| СРАВНЕНИЕ НЕИЗВЕСТНО | ПОСТОЯННАЯ НЕИЗВЕСТНАЯ | ||
| Сравнить | Небольшой пакет яблок стоит 4 доллара. Ящик яблок стоит в 6 раз дороже. Сколько стоит коробка яблок? | Небольшой пакет яблок стоит 4 доллара. Ящик яблок стоит 24 доллара. Во сколько раз коробка дороже мешка с яблоками? | Ящик яблок стоит 24 доллара, что в 6 раз больше, чем стоимость маленького мешка яблок. Сколько стоит маленькая сумка? |
Примеры умножения и деления на части (постоянная неизвестная) имеют очень похожие формулировки, поскольку они оба имеют оператор сравнения: «в 6 раз больше». Это описание отношений между двумя группами – общей и группой сравнения. Пример с кавычками (сравнение) формулируется по-другому, поскольку неизвестное представляет собой отношение сравнения: «Во сколько раз больше, чем больше»
Ключ к пониманию задач мультипликативного сравнения заключается в том, что сравнение представляет собой повторяющиеся группы, тогда как константа — это размер группы. .
В словесной задаче на умножение вам сообщается сумма в группе сравнения, 6, и константа, 4. Каждый мешок яблок стоит 4 доллара, поэтому, если это в 6 раз больше, это то же самое, что иметь 6 мешков.
Таким образом, 4 x 6.
В делении ( долей) словесная задача вам дано общее число (стоимость ящика яблок). Как только вы разделите или разделите эту стоимость на 6 равных групп, вы сможете определить стоимость одной из этих групп, которая равна стоимости маленького мешка яблок, и это то же самое, что и количество утки.
В ( в кавычках) делении словесной задачи вам дана константа, стоимость маленького мешка, а также стоимость ящика яблок. Неизвестно, каковы отношения между ними. В этих текстовых задачах формулировка вопроса часто может сбить учащихся с толку.
Как только учащиеся смогут разложить задачу на слова, чтобы определить сумму и сравнение, они смогут связать это с тем, что они уже знают об умножении и делении, чтобы помочь им при решении. Ключевым моментом является обучение студентов внимательному чтению слова «проблема». Чтобы узнать больше о моей рутине 3 чтения, вы можете щелкнуть изображение ниже.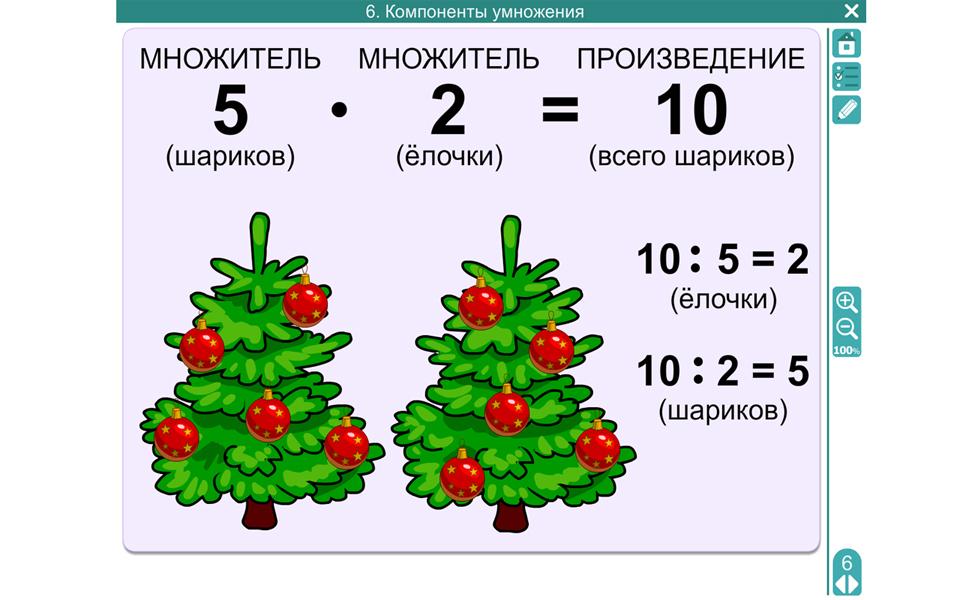
Ищете дополнительные ресурсы? Вы можете скачать мой справочный лист «Типы задач на умножение и деление» и использовать его, чтобы определить и написать различные типы задач на слова для занятий в классе.
Хотите попрактиковаться в задачах на умножение и деление? У меня есть набор БЕСПЛАТНЫХ карточек с задачами на умножение и деление слов. Каждый из типов задач на умножение и деление слов, обсуждаемых здесь, отрабатывается в наборе из 24 карточек с заданиями. Это отличная практика для более поздних лет, чтобы учащиеся имели достаточную практику с каждым типом. Это даже было бы отличным инструментом, чтобы помочь учащимся обсудить различные типы проблем и то, как они представлены. Чтобы загрузить карточки с задачами на умножение и деление слов, просто заполните форму ниже, и они будут отправлены прямо на вашу электронную почту.
Информационный бюллетень
Подпишитесь, чтобы получать бесплатные карточки с задачами на умножение и деление! После подтверждения электронной почты вы получите файл и будете подписаны на мою еженедельную рассылку.
Загрузка…
Вам также могут быть полезны следующие ссылки.
Деление на части и цитаты из SFUSD
Ресурсы CGI из LAUSD
Задачи на умножение и деление из ND Counts
Два способа мышления о делении из Langford Math
Как решать задачи на умножение
Вы хорошо решаете задачи со словами? Решение текстовых задач является очень важной частью математики, потому что с ними вы понимаете и практикуете то, чему научились (сложение, вычитание, умножение…)
Сегодня мы рассмотрим задачи на умножение : как мы их распознаем, что делать, чтобы их решить… все это мы рассмотрим в этом посте.
Проблемы со словами на умножение: повторение
Это первый тип задачи на умножение слов, которую учатся решать. Например:
У Анны 5 коробок для яиц. В каждой упаковке 12 яиц. Сколько яиц у нее всего?
Находим:
- Количество наборов: У Анны 5 коробок для яиц.
- Количество предметов в каждом наборе: В каждой коробке 12 яиц.
- Вопрос об общем количестве вещей: Сколько всего яиц у нее?
Чтобы решить эту задачу со словами, мы должны подумать: если в каждой коробке 12 яиц, а у Анны 5 коробок, чтобы узнать, сколько всего яиц, мы прибавим 12 + 12 + 12+ 12+ 12, или, что в итоге получается одинаково: умножим 5 х 12 : Всего у Анны 60 яиц.
Проблемы со словами на умножение: сравнение в один шаг
В задаче на умножение этого типа одна величина сравнивается с другой величиной, которая больше или меньше:
Чтобы купить подарок отца, Джон вложил 10 долларов, а Патриция вложила в 3 раза больше денег, чем Джон. Сколько денег вложила Патрисия?
Находим:
- Число, выражающее одно количество: Джон вложил 10 долларов.
- Число, выражающее сравнение второй величины с первой: Патриция вложила в 3 раза больше денег, чем Джон.
- Вопрос о второй сумме: Сколько денег вложила Патрисия?
Чтобы решить эту задачу со словами, мы должны подумать: если Патриция вложила в 3 раза больше денег, чем Хуан, то она вложила в три раза больше денег, мы умножим на 10 x 3 . Патрисия вложила 30 долларов.
Задачи на умножение слов: одношаговые формулы
В этом типе задач на умножение слов нам предстанут формул, например, формула скорости:
Джастин – водитель автобуса. Он сказал мне, что если он не будет делать остановок и всегда будет поддерживать одну и ту же скорость 80 миль в час, то завершит свой маршрут ровно за 2 часа. Сколько миль составляет его маршрут?
Находим:
- Скорость: Если бы он поддерживал скорость 80 миль в час…
- Время: Он прибудет через 2 часа.
- Вопрос о расстоянии: Сколько миль его маршрут?
Чтобы решить эту словесную задачу, мы должны подумать: если он поддерживает скорость 80 миль в час, это будет означать, что каждый час, за который он едет, он преодолевает 80 миль.
Мы также знаем, что он едет с этой скоростью 2 часа. Следовательно, чтобы узнать общее количество миль, которые он преодолел, нам придется умножить 80 x 2 : Его путь составляет 160 миль.
Задачи на умножение слов: комбинация или декартово произведение
В задаче на умножение этого типа мы найдем два или более набора предметов или людей. Эти наборы нужно комбинировать между собой, образуя все возможные пары:
Сегодня мы зашли покушать в итальянский ресторан, который специализируется на пасте. Мне было сложно решить, какое блюдо заказать, так как в меню было 9 видов пасты и 11 видов соуса, а любую пасту можно было сочетать с любым соусом. Сколько различных комбинаций пасты и соуса вы могли бы выбрать?
Находим:
- Количество элементов, которое имеет первый набор: 9 видов макарон.
- Количество элементов, которые есть во втором наборе: 11 видов соуса.
- Вопрос, относящийся к количеству возможных комбинаций между наборами: Из скольких различных комбинаций пасты и соуса вы можете выбрать?
Чтобы решить задачу со словами, мы должны подумать: мы можем объединить каждый вид пасты с 11 доступными видами соуса. Таким образом, только из макарон первого типа мы можем получить 11 разных блюд. Сочетая второй вид пасты с каждым из 11 соусов, мы могли бы получить еще 11 блюд. То есть для каждого из 9видов пасты мы получим 11 различных сочетаний соусов. Таким образом, чтобы узнать количество возможных блюд, мы умножим 9 х 11 : Вы можете выбрать из 99 различных блюд из пасты.
Это 4 основные модели задач на умножение слов. В Smartick у нас есть много таких типов текстовых задач и многое другое. Если вы хотите практиковать их, зарегистрируйтесь сейчас!
На сегодня все. Что вы думаете об этом посте? Помогло ли это вам лучше понять задачи на умножение слов? Если вам это нравится, поделитесь им с друзьями, чтобы они тоже могли учиться.