Состав числа это что такое: Объясняем ребёнку состав числа: инструкция для родителей

Объясняем ребёнку состав числа: инструкция для родителей

• Text Link

Алёна Хромова

Учитель начальных классов, дефектолог

‍

Состав числа — это сумма чисел, которая равна изначальному числу. Например, состав числа 5 — это 5 и 0, 1 и 4, 2 и 3.

Наиболее подходящий возраст для изучения состава числа — 6–7 лет. Важно, чтобы ребёнок умел считать в прямом и обратном порядке в пределах десяти.

Вариант 1. Счётные палочки и пальцы

Проще всего начинать с пяти. На руке пять пальцев, нужно загибать 1, 2, 3, 4 и считать, сколько остаётся. Постепенно счёт можно увеличивать до 10.

С палочками можно начинать с единицы. Например, брать шесть палочек, одну убирать и считать, сколько осталось.

Вариант 2. Примеры

Когда ребёнок закрепил зрительное восприятие чисел, то есть точно знает, как они пишутся, можно изучать состав с помощью тетради и ручки или доски и мела. Здесь может быть два варианта:

• Подбор. 3 + ? = 5. Необходимо выяснить, что спрятано за вопросительным знаком.
• Выбор. Нужно подобрать пары чисел, которые в сумме дают 5.

<<Форма демодоступа>>

Вариант 3. Дома

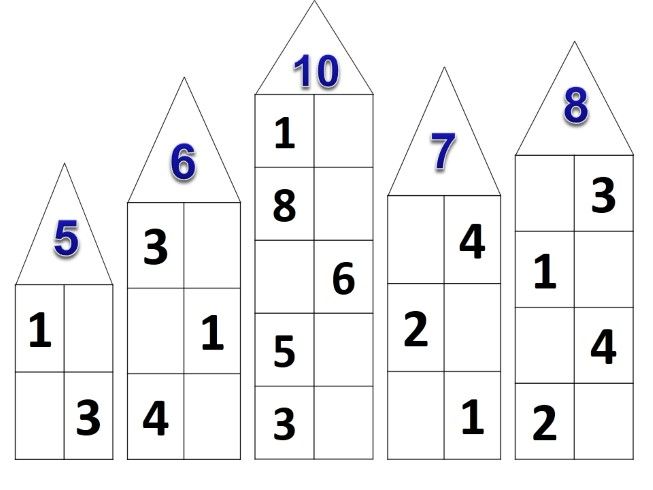
Самый популярный пример в садике и школе. Под крышей пишется число, а в параллельных окошках — его состав. Иногда числа раскладывают на повторяющиеся составы, например, 5 — это 2 и 3, 3 и 2. От перемены мест слагаемых сумма не меняется, поэтому это повтор. Но повторы часто встречаются в оформлении дома, чтобы можно было закрывать любой ряд и по памяти восстанавливать второй.

Вариант 4. Карточки 

Формат, который придётся создавать самостоятельно. Одна карточка соответствует одному составу. Например, 5 — это 0 и 5. Каждое число из состава можно закрыть окошком, чтобы восстанавливать по памяти.

<<Форма аттестации>>

Вариант 5. Счёты

Формат сложный для современных детей, но так как учиться на счётах необязательно, можно запомнить составы чисел.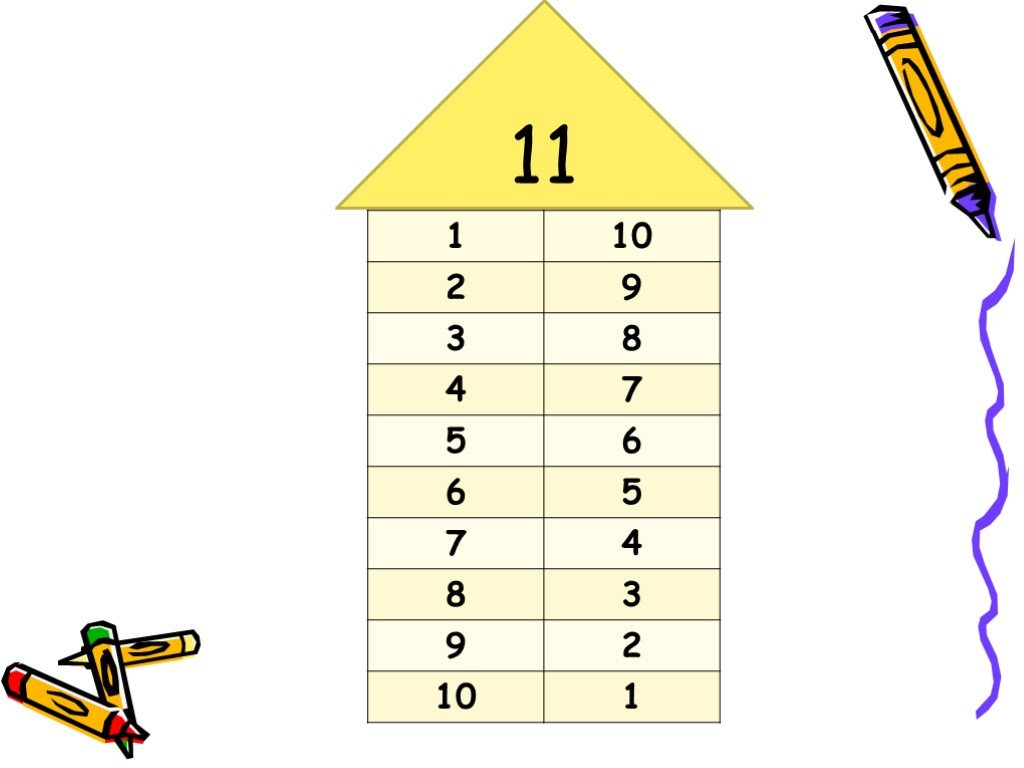 На одной прямой 10 колец, соответственно, ребёнку нужно выяснить, сколько останется, если какое-то количество отодвинуть.

Вариант 6. Домино

Наиболее знакомый ребёнку вариант. В домино есть возможность играть задолго до освоения чисел, а расположение точек малыш будет запоминать как рисунок. Позже можно складывать количество точек на гранях и получать состав числа.

Иллюстрация: Maryna Kizilova / Dribbble

Узнайте больше о реальном опыте семейного обучения!

Если у вас остались вопросы о домашнем образовании и вы хотите получить советы опытных хоумскулеров, оставьте заявку. Наши специалисты свяжутся с вами для бесплатной консультации.

Принимаю условия соглашения и политики конфиденциальности

Записали!
Скоро с вами свяжется консультант, расскажет об обучении в нашей онлайн-школе.
Проверьте вашу электронную почту — там письмо о том, что стоит сделать перед консультацией.

Упс 🙁 Что-то пошло не так. Попробуйте позвонить нам по телефону +7 (800) 500-17-81 либо написать на почту [email protected].

Как объяснить ребенку состав числа?

Современная программа обучения в школе задает для будущих первоклассников достаточно высокую планку. Придя в школу, ребенок уже должен иметь определенный багаж знаний и навыков, одним из которых является понимание состава числа.

Состав числа – это возможность раскладывать числа от 1 до 10 на два меньших числа. Этот навык заложит фундамент, благодаря которому ребенку в будущем будет легче осваивать математику, например, сложение и вычитание. Если уделять время занятиям и постепенно осваивать эту тему, то результат не заставит себя ждать. А математические тренажеры помогут в усвоении новых знаний.

Чтобы ребенок мог успешно освоить эту тему, он уже должен узнавать графические образы цифр, уметь считать от 1 до 10 и, желательно, от 10 до 1 в обратном порядке. Также плюсом будет возможность самостоятельной записи ребенком цифр.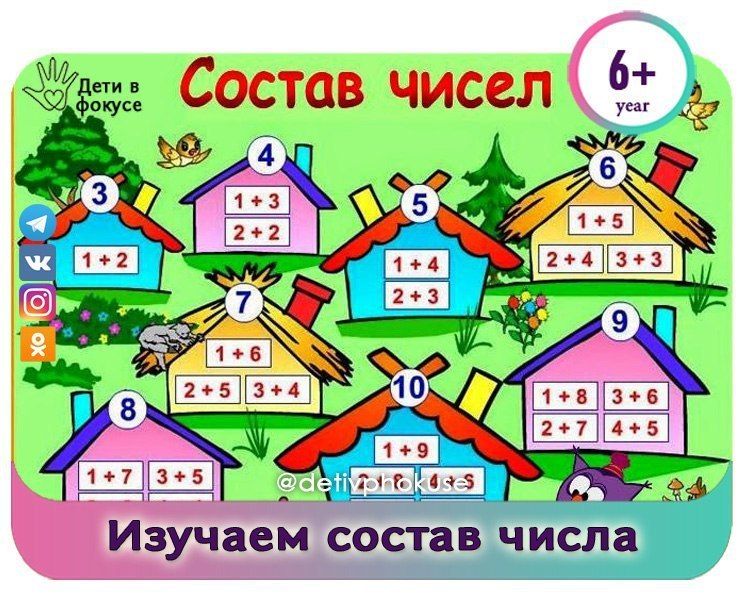 Подходящий возраст для занятий по составу числа – от 6 лет, но иногда можно начинать изучать состав небольших чисел и раньше. Все зависит от индивидуальных особенностей и базы знаний, которыми он владеет.

Состав числа в пределах 10

Засели домик цифрами

Состав числа в пределах 20

Для чтобы осваивать состав числа ребенку было интересно и увлекательно, можно воспользоваться проверенными методами и упражнениями.  Например, числовые карточки. На них изображено число и предметы, количество которых ему соответствует. Они наглядно иллюстрируют состав чисел, поэтому рекомендуем начать знакомство с темой с них.

Объяснять ребенку основы сложения можно помощью подручных предметов – пуговиц, камушков, конфет и т.д. Пригодятся здесь и числовые карточки: например, на одной из них изображено 1 яблоко, а на другой – 2 апельсина. Если сложить их вместе, то сколько фруктов получится? Ребенок посчитает все фрукты и назовет сумму, постепенно запоминая результаты сложения разных чисел.

Когда ребенок начнет понимать, как складывать предметы, можно перейти к разбору состава числа. Родитель говорит, сколько предметов должно получиться в итоге, начиная с маленьких чисел,  а потом помогает ребенку собрать необходимое количество. Например, нужно собрать 4 банана. Берем карточку с изображением одного банана и спрашиваем, сколько еще нужно собрать. Затем добавляем карточку с двумя бананами и повторяем вопрос. Так вместе с ребенком вы переберете разные комбинации и освоите базовые составы числа.

Постепенно переходите к большим числам, где вариативность комбинаций увеличивается. Многократное проведение такого упражнения поможет закрепить в памяти состав числа и ребенок сможет легко его воспроизводить. Потом можно поупражняться таким же методом в вычитании. Взять несколько карточек например, 1 яблоко, 3 яблока и 4 яблока. Спросить у ребенка, сколько яблок на всех этих карточках. И спросить, какую карточку нужно убрать, чтобы получилось 7  яблок.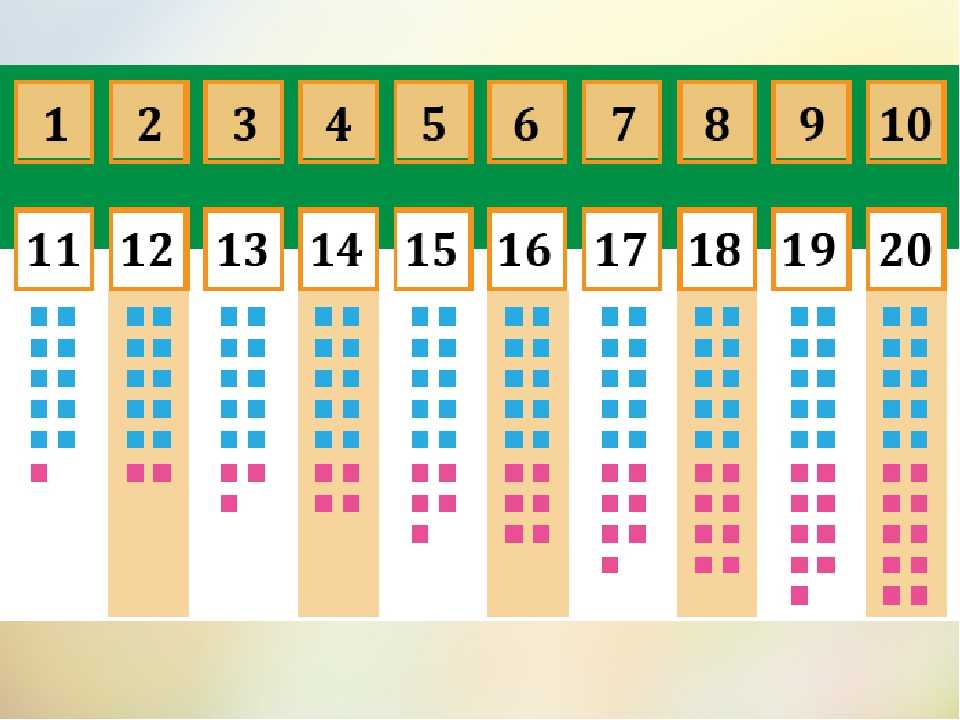

Для закрепления темы хорошо подойдут числовые домики – это следующий этап освоения состава чисел. Домик, где живут цифры, имеет несколько этажей с двумя окошками на каждом. На крыше находится число, которое разбивается на два числа-соседа на каждом этаже. Количество этажей зависит от количества возможных комбинаций, на которые можно разложить требуемое число.

Можно нарисовать такой домик самостоятельно. Например, для числа 4 будет 2 этажа: на одном числа-соседи – 2 и 2, на втором – 1 и 3. А можно воспользоваться готовыми числовыми домиками, где ребенку нужно будет только найти подходящие цифры соседи.

Начинать можно с первого или последнего этажа. Если у ребенка поначалу задание вызовет трудности, можно помочь ему, заполнив некоторые этажи. Позже можно объяснить секрет домика: переходя на этаж число становится на 1 больше или меньше.

После усвоения состава чисел до 10, можно переходить ко второму десятку, если ребенок уже его знает. Тренажер состав чисел в пределах 20 поможет ему поупражняться.

При занятиях с ребенком важно помнить, что успех складывается из регулярности и поддержки. Хвалите его за успешные решения, это отлично мотивирует! Поддерживайте в трудных моментах и относитесь с пониманием к ошибкам. Так, небольшими шажочками и с вашей поддержкой, тема «Состав числа» будет успешно освоена ребенком.

Изучение состава числа

Когда ребенок понимает состав числа, он понимает, что числа состоят из других чисел. Они «видят числа внутри» других чисел: во-первых, что все числа состоят из единиц, а затем, что их можно составить из пар больших чисел.

Так, например, 5 состоит из «пяти единиц», или из «1 и 4», или из «2 и 3».

Символы CBeebies Numberblocks демонстрируют это своей способностью разделяться на другие символы, как показано в этом клипе:

Понимание состава числа имеет основополагающее значение для понимания структуры отношений часть-часть-целое, которые могут быть представлены с помощью модели часть-часть-целое, как показано ниже:

Если 5 разделить на 3 и 2, то 3 будет частью, 2 будет частью, а 5 будет целым.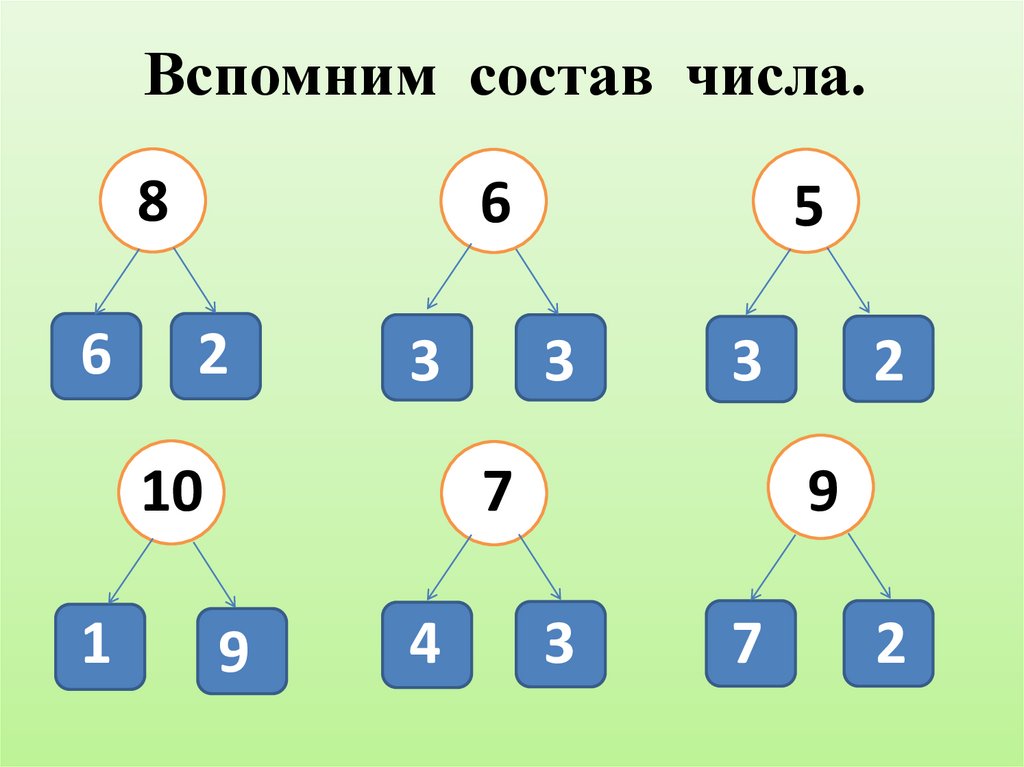

Концепция композиции позволяет детям развивать беглость с числовыми связями — не только числовыми связями 10, но и все число облигаций внутри числа. Итак, вернемся к примеру с числом 5: числовые связи числа 5: 0 и 5, 1 и 4, 2 и 3.

Понимание состава также поддерживает понимание коммутативности: если вы узнали, что 2+3=5, то вы также знаете, что 3+2=5 без необходимости заучивать это как новый факт.

Композиция также имеет решающее значение для понимания сложения и вычитания и их обратных отношений. Для тех, кто понимает состав числа, помните, что 2 + 3 = 5 и 5-2 = 3, и то, как соотносятся эти два факта, — это не столько повторение и запоминание, сколько применение структурного понимания. Когда мы складываем, мы составляем: когда мы вычитаем, мы разлагаем.

В рамках программы NCETM/Maths Hubs Mastering Number, занятия предназначены для понимания состава числа для детей в приемной, 1-го и 2-го классов. рекомендуется «субитизировать» (см. без подсчета) меньшие числа «внутри» больших чисел.

Что ты видишь? Может 4 в квадрате, а нечетная 1?

Что вы видите, если они окрашены в такой цвет? Вероятно, 2 и 3.

Детей можно попросить сказать: «Я знаю, что это 5, потому что я вижу 3 красные точки и 2 черные точки».

Различное расположение цветных точек в венгерских числовых рамках помогает развивать распознавание различных конфигураций 3 и 2 и, следовательно, 5.

Перемещение птиц между разными проводами позволяет детям увидеть, что разные пары чисел составляют 5.

Для чисел от 5 до 10 детям предлагается, опять же с помощью используемых представлений, увидеть структуру «5 с небольшим». Понимание чисел по отношению к 5 и 10 важно для разработки эффективных стратегий расчета. Так что увидеть 5 (и немного) в 6, 7, 8 и 9 особенно полезно.

Помимо определения того, что 5 является частью чисел 6,7,8 и 9, другие связи этих чисел также исследуются отдельно.

Различные представления 6 используются для демонстрации различных композиций 6: «5 и немного», а также «3 и 3» или «2 и 2 и 2».

Рисунок кубика подчеркивает «3 и 3»:

Сетка из 9 позволяет переместить одиночные фишки из знакомой схемы игры в кости, чтобы увидеть, что у нас все еще есть 6. Исследуются различные способы деления чисел в пределах 6 для составления 6.

Использование ящика для яиц позволяет разделить яйца на коричневые и белые и использовать истории о яйцекладке, чтобы увидеть разные числа в пределах 6.

Более подробная информация о композиции, в том числе идеи для занятий, графики прогресса, типичные ошибки и то, на что следует обращать внимание при работе с маленькими детьми, содержится на странице «Композиция для детей младшего возраста». Вас также могут заинтересовать другие статьи из этого набора: «Количественность и числовой смысл» и «Обучение порядкового порядка — больше, чем просто первая, вторая и третья».

NCETM и Maths Hubs рассматривают программу освоения чисел на 2022/23 год. Если вы заинтересованы в участии, пожалуйста, заполните Форму выражения заинтересованности.

Композиция функций

«Композиция функций» — это применение одной функции к результатам другой:

Результат f() передается через g()

Записывается: (g º f)(x)

Что означает: g(f(x))

 

Пример:

f(x) = 2x+3 и g(x) = x ²

“x” просто заполнитель . Чтобы избежать путаницы, давайте просто назовем это «ввод»:

f(ввод) = 2(ввод)+3

g(ввод) = (ввод) ²

Начнем:

(g8) º f)(x) = g(f(x))

Сначала мы применяем f, затем применяем g к этому результату:

(g º f)(x) = (2x+3) ²

 

Что, если мы обратный порядок f и g?

(f º g)(x) = f(g(x))

Сначала мы применяем g, затем применяем f к этому результату:

(f º g)(x) = 2x ² + 3

 

Получаем другой результат!

Когда мы меняем порядок, результат редко бывает таким же.

Будьте осторожны, какая функция стоит первой.

Символ

Символ композиции — маленький кружок:

(g º f)(x)

Это , а не закрашенная точка: (g · f)(x), так как это означает, что умножается на .

Составлено с самим собой

Мы можем даже составить функцию с самим собой!

Пример:

f(x) = 2x+3

 

(f º f)(x) = f(f(x))

Сначала мы применяем f, затем применяем f к этому результату:

(f º f)(x) = 2(2x+3)+3 = 4x + 9

Мы должны сделать это без красивой диаграммы:

(f º f)(x)= f( е (х))

 = f(2x+3)

 = 2(2x+3)+3

 = 4x + 9

Доменов

До сих пор это было легко, но теперь мы должны рассмотреть Доменов функций .

Домен — это набор всех значений , которые входят в функцию.

Функция должна работать для всех значений, которые мы ей даем, поэтому зависит от нас, , чтобы убедиться, что мы правильно определили домен!

Пример: домен для √x (квадратный корень из x)

Мы не можем получить квадратный корень из отрицательного числа (если только мы не используем мнимые числа, а это не так), поэтому мы должны исключить отрицательных чисел:

Домен √x неотрицательный Действительный Числа

На числовой строке это выглядит так:

Используя нотацию конструктора множеств, записывается:

{ x | x ≥ 0}

Или, используя интервальную запись, это:

[0,+∞)

Важно правильно указать Домен, иначе мы получим плохие результаты!

Домен составной функции

Мы должны получить оба домена правильно (композитная функция и первая используемая функция).

При выполнении, например, (g º f)(x) = g(f(x)):

• Убедитесь, что мы правильно получили домен для f(x) ,
• Затем также убедитесь, что g(x) получает правильный домен

Пример:

f(x) = √x и g(x) = x ²

Домен f(x) = √x — все неотрицательные действительные числа

Домен g(x) = x ² — все действительные числа

Составная функция:

(g º f)(x) = g(f(x))

 = (√x) ²

 = x

Теперь “x” обычно имеет домен всех действительных чисел …

… но поскольку это составная функция , мы должны также учитывать f(x) ,

Таким образом, домен состоит из неотрицательных действительных чисел

Почему оба домена?

Ну представь функции машины… первая проплавляет отверстие пламенем (только для металла), вторая просверливает отверстие побольше (работает по дереву или металлу):

То, что мы видим в конце, это просверленное отверстие, и мы можем подумать, что “это должно подойти для дерева или металла “. Но если мы подложим дрова в g º f, то первая функция f разожжет огонь и все сожжет!

Так что то, что происходит “внутри машины”, очень важно.

 

Функция декомпозиции

Мы можем пойти другим путем и разбить функцию на композицию других функций.

Пример:

(x+1/x) ²

Эту функцию можно составить из следующих двух функций:

f(x) = x + 1/x

g(x) = x ²

И получаем:

(g º f)(x) = g(f(x))

 = g(x + 1/x)

 = (x + 1/x) ²

Это может быть полезно, если исходная функция слишком сложна для работы.

Резюме

• «Композиция функций» — это применение одной функции к результатам другой.
• (g º f)(x) = g(f(x)) , сначала применить f(), затем применить g()
• Мы также должны учитывать домен первой функции
• Некоторые функции можно разложить на две (или более) более простые функции.