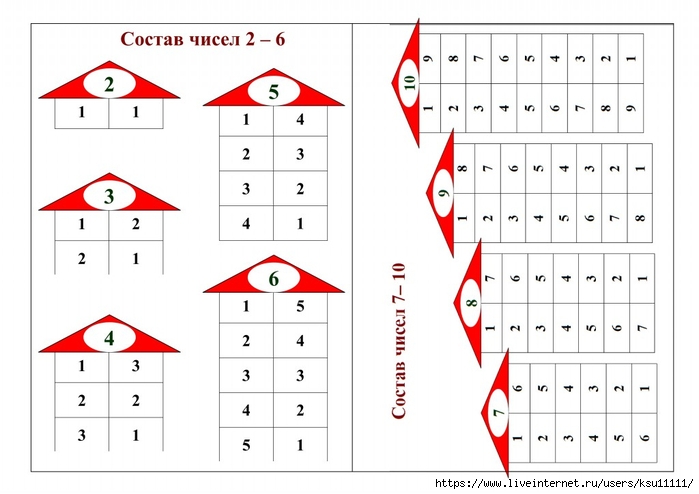
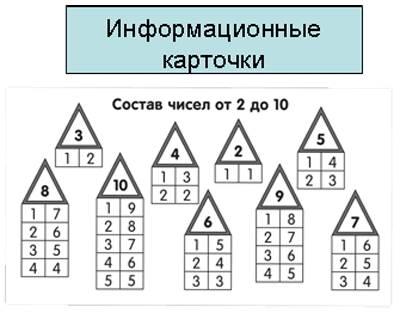
Состав числа 5 карточки: Индивидуальные карточки состава числа 5. Учим состав чисел первой “пятерки”

Набор карточек Логико-малыш Математика Состав числа от 5 до 10

0 отзывов

Прошлая цена: 250 руб

Нет в наличии

Сообщить о поступлении

• Описание
• Характеристики

      Набор карточек Логико-малыш Математика “Состав числа от 5 до 10” – способствуют формированию у детей основных математических представлений. В этом сборнике предлагается поработать над составом чисел в пределах первого десятка. Ребенок узнает, к примеру, что одно число может состоять как из двух одинаковых (6=3+3), так и из разных (6=2+4). Казалось бы, знания о составе числа элементарны, но без их своевременного усвоения невозможно впоследствии успешное решение задач. В этом же комплекте карточек ребенок познакомится с простейшими задачками на сложение, вычитание и нахождение неизвестного слагаемого.

В комплекте 8 двусторонних карточек с разнообразными заданиями. Комплект сопровождается методическими рекомендациями для родителей и педагогов.

Как заниматься?

      Карточки предназначены для работы со специальным планшетом. Он позволяет детям выполнять задания и самостоятельно проверять ответы.
      Перед началом игры необходимо передвинуть фишки вниз планшета. Далее ребенок должен выбрать одну из восьми карточек  и вставить ее в планшет так, чтобы вверху листа находилась зеленая вопросная полоска.  Затем нужно изучить карточку. На ней шесть основных изображений (рядом с ними находятся кружки того же цвета, что и фишки) и шесть картинок в правом ряду. Задача ребенка – установить между ними логическую связь. Выбрав рисунок с основного поля, нужно найти фишку того же цвета и переместить ее к верному ответу. Таким же способом выполняются и все остальные упражнения.
      Чтобы проверить, верно ли выполнено задание, переверните карточку. Цвета фишек  и кружков должны совпасть.

Если ребенок ошибся, предложите ему вернуть фишку вниз и попробовать найти  правильный ответ еще раз.
      Занимаясь с набором карточек Логико-малыш Математика “Состав числа от 5 до 10”, ваш ребенок освоит состав чисел от 5 до 10, научится мыслить логически. Комплект поможет ему в легкой игровой форме усвоить те знания, которые пригодятся на первых школьных уроках математики.

Рекомендуемый возраст: от 4 лет.

 

Издательство: Издательский дом “Зимородок”Упаковка картонная коробка: 22,5х16,5 см.

 

       Купить набор карточек Логико-малыш Математика “Состав числа от 5 до 10” в Новосибирске Вы можете в магазине развивающих и настольных игр “Игры Почемучек”.

Артикул:	490050
Возраст:	до года от 1 до 3 лет
Пол:	Мальчик Девочка

Правила оформления отзывов

1. Оставлять отзывы могут только зарегистрированные и авторизованные пользователи.
2. Пользователи, оставляющие отзывы, несут полную правовую ответственность за их содержание.
3. В отзывах сохраняется авторская орфография и пунктуация.
4. В отзывах запрещено:
   • Использовать нецензурные выражения, оскорбления и угрозы
   • Публиковать адреса, телефоны и ссылки содержащие прямую рекламу
   • Писать просьбы найти какой-либо товар или любые другие посторонние тексты
   • Писать отвлеченные от темы и бессмысленные комментарии

УЧИМ СОСТАВ ЧИСЛА — 1 ответов

Вам понадобится

– карточки на состав числа;
– много одинаковых игрушек и других мелких предметов;
– шашки или пуговицы одинаковой формы, но разного цвета.

Инструкция

1. / На первом занятии используйте игрушки или предметы домашнего обихода. Это могут быть кубики, карандаши, чашки, ложки. Вид и размер роли не играют, предметы должны быть просто одинаковыми.
Начните с числа 2. Попросите ребенка положить на стол 1 ложку и спросите, что нужно сделать, чтобы ложек стало 2.
Старший дошкольник обычно знает ответ, более младшему ребенку можно подсказать. Из каких чисел можно сложить число 2?
Если ребенок сразу не сообразит, задайте наводящий вопрос.

2. / Повторите задание с другими предметами.
Ребенок должен понять, что число 2 в любом случае состоит из двух единиц, вне зависимости от того, выкладывает он на стол ложки, камешки или кубики.

3./ Когда ребенок станет отвечать уверенно, переходите к изучению числа 3. Его состав можно представить в трех вариантах.
Можно выложить 3 ложки по одной, к двум прибавить одну или к одной – две. Раскладывать предметы можно по-разному.
Если вы представляете число 3 состоящим из трех единиц, то камешки или ложки можно положить на разном расстоянии друг от друга и даже один камешек на другой. Представляя это же число как состоящие из пары предметов и одного, два положите вместе, а один – на некотором расстоянии.

4./ Используйте для занятий шашки. Предложите своему ученику поставить на доску 4 одинаковых шашки. А если поставить 3 красных и 1 черную? Тоже получится 4 шашки. И если взять по две разного цвета, то их все равно будет четыре. То есть это число можно представить несколькими способами.

5./ Обзаведитесь карточками на состав числа. Их можно купить или сделать. Они бывают нескольких типов, и лучше, чтобы они были двух видов. Разрезная карточка состоит из двух половинок. На одной изображен 1 предмет, на другой – 1, 2, 3 и больше точно таких же предметов. Половинки могут быть соединены знаком «+», но «плюс» можно сделать и отдельно. Второй комплект представляет собой набор картинок, на которых изображены эти же предметы одним множеством, без всякого разделения.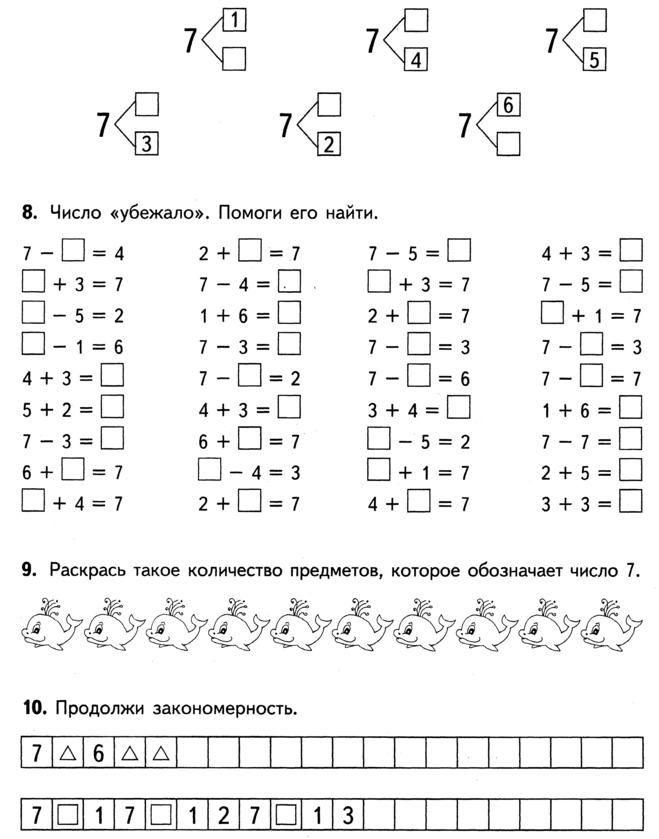 Когда ребенок хорошо научится сопоставлять число и цифру, можно сделать такие же карточки с цифрами. Их может быть несколько комплектов, чтобы представлять каждое число в разных вариантах.

6./ Проводите занятия регулярно. Покажите ребенку карточку, на которой изображено, скажем, 5 предметов. Предложите подобрать картинки так, чтобы на всех вместе тоже было столько же яблок или кружочков. Периодически меняйтесь ролями. Пусть ребенок тоже дает вам задания, а вы его старательно выполняйте. Иногда делайте ошибки, ваш ученик должен научиться контролировать ваши действия.

7./ Аналогичные задания поводите и с цифрами. Покажите, например, число 9 и точно так же, как в предыдущем случае, предложите найти несколько вариантов его состава. Объясните ребенку, что чем больше число – тем больше возможностей его составить.

Из стандартной 52-карточной колоды сколько 5-карточных комбинаций полностью состоят из красных карт?

В математике под перестановкой понимается процесс упорядочивания набора, в котором все элементы набора располагаются в некотором ряду или порядке. Процесс перестановки известен как перестановка его компонентов, если набор уже упорядочен. Перестановки происходят более или менее важным образом почти во всех областях математики. Они часто появляются, когда рассматриваются разные команды на определенных конечных множествах.

Что такое комбинация?

Комбинация — это действие по выбору элементов из группы, при котором (в отличие от перестановки) порядок выбора не имеет значения. В меньших случаях можно подсчитать количество комбинаций. Под комбинацией понимается объединение n вещей, взятых по k за раз, без повторения. В комбинации вы можете выбирать элементы в любом порядке. К тем комбинациям, в которых допускается повторение, часто применяют термины k-отбор или k-комбинация с репликацией.

Формула перестановки

При перестановке r вещей выбираются из набора n вещей без замены. В этом порядок выбора материи.

ⁿ P _r = (n!) / (n-r)!

Здесь

n = размер набора, общее количество предметов в наборе

r = размер подмножества, количество предметов, которые нужно выбрать из набора выбираются из множества n вещей, причем порядок выбора не имеет значения.

ⁿ C _r = n!/(n−r)!r!

Здесь

n = количество элементов в наборе

r = количество элементов, выбранных из набора

Сколько из стандартной колоды из 52 карт состоит из пяти карт, полностью состоящих из красных карт?

Решение:

Всего красных карточек 26, т.е. 13 червей и 13 ромбов.

Из 26 красных карточек выберите 5.

Ответ: биномиальный коэффициент

( ²⁶ C ₅ ) и вы можете прочитать это как 26 выбрать 5.

Итак, есть

( ²⁶ C ₅ ) = 26! ⁄ 5!(26−5)!

= 26! ⁄ 5!21!

= 26×25×24×23×22×21! ⁄ 5×4×3×2×1×21!

= 26×25×24×23×22 ⁄ 5×4×3×2

= 26⁄2×25⁄5×24⁄12×23×22

= 13×5×2×23×22

= 13×10×23×22  

= 130×506 = 65 780

Возможные 5-карточные комбинации, состоящие только из красных карт.

Похожие вопросы

Вопрос 1: Сколько 6-карточных комбинаций из стандартной колоды из 52 карт полностью состоят из черных карт?

Решение:

Всего черных карт 26, т. е. 13 треф и 13 пик.

Из 26 черных карт выберите 6.

Ответом является биномиальный коэффициент

( ²⁶ C ₆ ) и вы можете прочитать это как 26 выберите 6.

Итак, есть

( ²⁶ С ₆ ) = 26! ⁄ 6!(26−6)!

= 26! ⁄ 6!20!

= 26×25×24×23×22×21×20! ⁄ 6×5×4×3×2×1×20!

= 26×25×24×23×22×21 ⁄ 6×5×4×3×2  

= 26⁄2×25⁄5×24/24×23×22×21⁄3

= 13 ×5×23×22×7=13×115×154

= 1495×154 = 230 230

Возможные 6-карточные комбинации, состоящие только из черных карт.

Вопрос 2: Сколько двухкарточных комбинаций из стандартной 52-карточной колоды полностью состоят из черных карт?

Решение:

Всего черных карт 26, т.е. 13 треф и 13 пик.

Из 26 черных карт, выберите 2.

Ответ – биномиальный коэффициент

²⁶ C ₂ , и вы можете прочитать это как 26 Выберите 2.

, так что есть

²⁶ C ₂

, так что есть

²⁶ C ₂ = 26! ⁄ 2!(26−2)!

= 26! ⁄ 2!24!

= 26×25×24! ⁄ 2×1×24!

= 26×25 ⁄ 2  

= 26/2×25  

= 13×25=13×25  

= 325

Возможные 2-карточные комбинации, состоящие только из черных карт.

NAMBARZ® Игра с числами

Айхам Алата

I. СОСТАВ ПАЛУБЫ

II. ЦЕЛЬ ИГРЫ

III. МЕТОДЫ ИГРЫ

1. Подбирая пары

2. Математическими операциями

IV. ИСПОЛЬЗОВАНИЕ ПОДСТАВНЫХ КАРТИН

V. НАКАЗАНИЯ

VI. ВАРИАНТЫ ИГРЫ

VII. КОЛИЧЕСТВО И ВОЗРАСТ ИГРОКОВ

VIII. ЗАВЕРШЕНИЕ РАУНДА ИГРЫ

IX. ИГРА ОТДЕЛЬНО ИЛИ В КОМАНДАХ

X. ПОДСЧЕТ РЕЗУЛЬТАТОВ

XI. ВАРИАНТЫ ИГРЫ

I. СОСТАВ КОЛОДЫ

Игра состоит из колоды из 9 карт.2 игральные карты (рисунок 1) :

A. 40 карт, помеченных только цифрами. B. 40 карточек с цифрами и картинками. C. 3 подстановочных знака, которые позволяют изменить номер. D. 3 подстановочных знака, позволяющие сменить картинку. E. 3 подстановочных знака, которые позволяют изменить номер или изображение. F. 3 подстановочных знака, разрешающих повтор

Рисунок 1

II. ЦЕЛЬ ИГРЫ

После тщательной перетасовки карт выпадает 7 карт. раздается каждому игроку. Остальные карты остаются в стопке. Чтобы начать игру, дилер переворачивает верхнюю карту в оставшейся стопке лицевой стороной вверх, и эта карта не должна быть подстановочным знаком. Игрок, сидящий слева от дилера, делает первый ход. Цель каждого игрока — стать первым игроком или командой, которые сбросят все свои или ее карты.

Если у игрока нет обычных карт или подходящих подстановочных карт, позволяющих играть, игрок должен взять карту из центральной стопки. Если эта карта игровая, ее можно разыграть напрямую или в сочетании с другими картами или добавить в руку игрока. В этом случае игрок говорит: «Я пасую», и ход переходит к следующему игроку. Если центральная стопка карт исчерпана, все сброшенные карты образуют новую стопку.

III. МЕТОДЫ ИГРЫ

Есть два альтернативных способа сброса карт: парами совпадающих карт или с помощью математических операций.

1. Сопоставлением пар

Перевернутая верхняя карта в центральной стопке карт может быть покрыта картой игрока с соответствующим номером или картой с совпадающая картинка.

Например, карта «3 пчелы» может быть покрыта любым из следующих типов карт (рисунок 2) :

• идентичная карта «3 пчелы»
• другая карта с номером 3, например обычная карточка с цифрой 3 или «3 бегемота»
• или другая карточка с таким же изображением, но другим номером, например «8 пчел»

Рисунок 2

С другой стороны, карта с простой картой 3 может быть закрыта только любым из следующих типов карт (рисунок 3) :

• идентичная простая карта 3
• другая карта с таким же числа, такие как «3 гиппопотама» или «3 пчелы»

Рисунок 3

Карточки с числами и картинками предлагают больше вариантов сопоставления, чем карточки с одними числами.

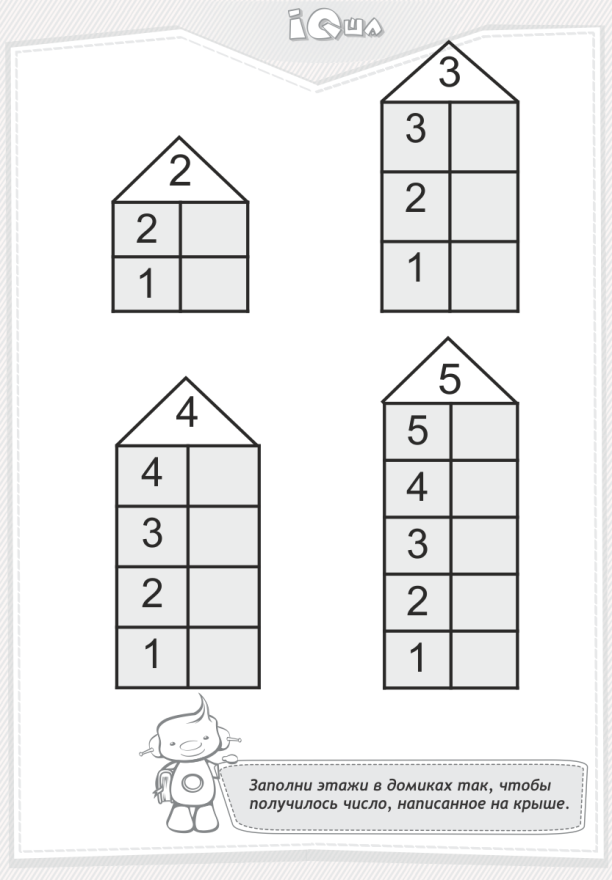
2. С помощью математических операций

Также можно исключить два или более карты сразу, выполняя математические расчеты, которые приводят к ответу что соответствует числу, требуемому во время этого хода. Все карты которые участвуют в операции, должны быть отброшены в том порядке, в котором они использовались при выполнении математики.

Можно включить несколько расчетов за один ход, используя сложение, вычитание, умножение и/или деление, используя любой порядок и количество карт, необходимых для получения желаемого результат.

Всегда разрешено и желательно использовать математику, даже если у игрока есть требуемая совпадающая карта в его или ее руке, пока эта совпадающая карта не используется в расчетах, как будет объяснено позже.

Правила использования математики просты:

• Заказ математические операции решает игрок. Поэтому ответ на первая операция с картами один и два затем может использоваться в комбинации с третьей картой, чтобы вычислить новый ответ, и этот ответ затем можно объединить с четвертой картой в новой операции и так далее, насколько это возможно.
• Карточки используемые в математических операциях, должны быть одного типа: либо все простые карточки с числами или все карточки с числами и картинками. Впрочем, неважно, какой тип карты, какая карта должна быть покрыта и какая окончательная расчет должен совпадать.

Например: карта «3 пчелы» или одна карта 3 может быть покрыта несколькими различными комбинациями карт:

A. комбинация с использованием карт с простыми номерами (рисунок 4) может использовать: карты с номерами 1 и 2 по формуле 1+2 или карты 10, 4 и 2 с использованием (10 – 4)/2. (В последнем примере игрок кладет карту с 10, затем 4 и затем 2.) Затем следующий игрок должен закрыть карту 2.

B. Комбинация с использованием карточек с числами и картинками (рисунок 5)  можно использовать: карты «7 рыб» и «4 курицы» по формуле 7-4 или карты «10 медведей», «1 стрекоза», «1 черепаха» и «9 уток» по формуле: 10 +1+1-9.

Рисунок 4 Рисунок 5

Игрок всегда должен быть уверен, что математический результат получается при использовании минимального количества карточек.

Например, чтобы закрыть карту «3 пчелы» или карту 3 в одиночку, игроку не разрешается выкладывать простые карты 6, 5, 2 и 10 по математической формуле: 6+5+2-10= 3, потому что тот же результат может быть достигнут с картой 6 и 2 картой, вычисляя 6/2=3 (рисунок 6) . Таким образом, игрок должен разыграть карты 6 и 2 и оставить карты 5 и 10.

Рисунок 6

Кроме того, карта, соответствующая карте не может быть использован в математической операции, потому что он предназначен для играл сам по себе.

Например, чтобы закрыть карту «3 пчелы», игрок не может положить простую карту 9 и простую карту 3, используя 9/3, потому что обычная карта 3 уже имеет тот же номер, что и карта, которую нужно сопоставить. Также невозможно использовать карту «8 пчел» и карту «5 кошек» с использованием 8-5, так как карта «8 пчел» уже соответствует дизайну карты, которую нужно закрыть. В этих двух примерах игрок должен разыграть совпадающую карту саму по себе и удерживать остальные карты 9.0005 (рисунок 7) .

Рисунок 7

IV. ИСПОЛЬЗОВАНИЕ ПОДСТАВНЫХ КАРТ

• Подстановочный знак, позволяющий изменить число (рис. 1-C), может охватывать только карту, отображающую только число. Он не может покрывать номер плюс карточку с изображением. При использовании этого подстановочного знака игрок имеет право выбрать и разыграть другую карту, если это карта с числом (рисунок 8) .
• Подстановочный знак, разрешающий изменение изображения (рис. 1-D), может охватывать только карту, на которой отображается число плюс изображение. Он не может покрывать карту с одним номером. Разыгрывая эту карту, игрок имеет право выбрать и переиграть другую карту, если это число плюс карта с изображением 9.0005 (рисунок 8) .
• Подстановочный знак, разрешающий изменение числа ИЛИ изображения (рис. 1-E), может охватывать любой тип карты (только число или число плюс изображение). Затем игрок имеет право выбрать и разыграть еще одну карту любого типа (рисунок 8) .

Рисунок 8

Также можно разыграть один из трех типов подстановочных знаков без повторного розыгрыша другой карты (например, при использовании подстановочного знака в качестве последней карты, сброшенной из руки, или при разрешении товарищу по команде выбрать и разыграть карту ). В этой ситуации следующий игрок кладет карту с простым числом или карту с числом и изображением, в зависимости от типа только что использованного подстановочного знака.

Правило о том, что результат должен быть получен при использовании минимального количества карт, также относится к использованию подстановочных знаков. Следовательно, игрок не должен разыгрывать совпадающую карту после использования подстановочного знака, поскольку совпадающая карта должна разыгрываться отдельно. Кроме того, нельзя разыгрывать два подстановочных знака подряд, правило, которое применяется только к первым 3 типам подстановочных знаков.

• Сделав ход, игрок может бросить повтор wildcard (рисунок 1-F), если в его руке есть другая карта или другие карты, которые можно сбросить. По сути, этот подстановочный знак позволяет игроку сделать дополнительный ход и исключить одну новую совпадающую карту или несколько карт, используя математические вычисления. В любом случае, этот дополнительный ход должен соответствовать последней карте, выложенной перед розыгрышем подстановочного знака. Этот подстановочный знак также можно разыграть, даже если у игрока нет подходящих карт для повтора (или если это единственная оставшаяся карта игрока). Если это происходит, игрок берет карту из центральной стопки и разыгрывает ее отдельно или в сочетании с другими картами, если это возможно, а если нет, то оставляет ее у себя в руке. Кроме того, разрешается разыгрывать эту подстановочную карту, даже не сыграв первую часть этого хода (из-за отсутствия подходящих карт), так как это позволит игроку выбрать карту из стопки в надежде, что она улучшить свою руку.

Этот подстановочный знак очень важен, потому что он дает возможность исключить несколько карт за один ход (6 или более, если игрок выполняет мастерский ход). Например, чтобы закрыть карту с номером 1, игрок может написать: «9 кур», «6 стрекоз» и «3 гиппопотама», используя математическую формулу (9-6)/3, затем положить подстановочный знак повтора и наконец, используя другие карты, которые могут покрыть карту, которая предшествовала подстановочному знаку, в данном случае « 3 гиппопотама. » Чтобы покрыть эту карту, игрок может использовать карту только с 10 номерами, карту только с 6 номерами и карту только с 1 номером, рассчитав: 10-6-1 (рисунок 9) .

Рисунок 9

V. ШТРАФЫ

Игрок наказывается и должен взять 3 карты из центральной стопки в следующих случаях: ).

Если карта, которая соответствует карте, которую нужно закрыть, используется в математической операции (также, как уже было показано).

Если разные типы карт (только цифры и карты с цифрами и картинками) используются за один ход, связанный с математикой. В этом случае игрок должен забрать только что сыгранные карты, и ход переходит к следующему игроку.

Если результат математических операций выполнен неправильно, в том смысле, что он не соответствует номеру на стопке карт, которую необходимо закрыть. Если игрок может изменить математику, чтобы получить правильный ответ, используя все те же карты, что и в первой попытке (то есть, не меняя используемые карты), он или она может сыграть эти карты. Если нет, игрок должен сохранить эти карты, и ход переходит к следующему игроку.

Когда игрок неправильно использует подстановочный знак.

Как только карта покидает руку игрока, она считается сыгранной. Игрок не может забрать ее обратно и попытаться разыграть другую карту.

VI. ВАРИАНТЫ ИГРЫ

Игроки могут выбирать между:

• короткая игра: если все игроки будут играть по одному раунду,
• стандартная продолжительная игра: играя в 3 раунда,
• или более длинная игра: на продление игры до 5 раундов.

Один раунд игры обычно начинается с 15 до 30 минут, когда в игру играют 6 человек.

VII. КОЛИЧЕСТВО И ВОЗРАСТ ИГРОКОВ

В NAMBARZ могут играть от 2 до 12 игроков одновременно, индивидуально или в командах. Он подходит для детей, начиная с 8 лет, в возрасте, когда усваиваются простые арифметические операции (сложение, вычитание, умножение и деление).

В нее могут играть даже совсем маленькие дети, если используемые математические операции ограничены теми, которые ребенок освоил. Например, играя в игру с ребенком, сначала ограничьте использование математики сложением и вычитанием, а позже расширите ее, включив в нее умножение и деление.

VIII. ЗАВЕРШЕНИЕ РАУНДА ИГРЫ

Раунд заканчивается, когда определенное количество игроков израсходовали все свои карты, в зависимости от общего количества игроков участие в игре.

• От 2 до 5 игроков: когда все, кроме одного оставшегося игрока, использовали все свои карты.
• От 6 до 12 человек игроков: когда 5 игроков использовали все свои карты.

Игрок, набравший наибольшее количество очков в одном раунде, начинает игру в следующем раунде.

IX. ИГРА ОТДЕЛЬНО ИЛИ В КОМАНДАХ

В NAMBARZ® можно играть индивидуально игроков, и в этом случае каждый игрок получает свои собственные очки независимо. Однако игроки также могут участвовать в качестве команды из 2-х или 3-х и более игроков в команде. Тогда у каждого игрока есть рука из 7 карты, и каждый игрок делает свой ход. Единственным ограничением является то, что члены одной команды ходят по очереди, один за другим, до того, как игра перейдет к членам следующей команды, и так далее. Это позволяет команде участникам разыгрывать одну карту или несколько карт таким образом, чтобы что это осуществимо, максимизирует шансы следующего члена той же команды играть хорошо. Товарищи по команде могут консультироваться друг с другом, чтобы решить, как каждая команда участник должен разыграть свой ход с максимальной выгодой. Цель каждой команды – получить хорошие рейтинги для своих членов, заработав как можно больше баллов, независимо от того, кто из членов команды закончит раздачу первым. В конце раунда, все очки, полученные каждым членом одной команды, суммируются получить общий балл команды.

Если единственные игроки, которые все еще держат карты в руках, принадлежат к одной команде, раунд заканчивается, и члены команды получают свои очки в зависимости от их ситуации на момент окончания раунда.

X. ПОДСЧЕТ РЕЗУЛЬТАТОВ

В конце каждого раунда игроки получают очков в соответствии со своим рейтингом: тот, кто первым закончит раунд, получает 40 очков, второй получает 32 очка, третьему дается 25 очков, четвертому получает 19 очков, а пятый – 14 очков. Кроме того, любой Полученные баллы за «мастерский ход» затем добавляются к окончательным оценкам.

Когда в игре участвуют от 2 до 5 игроков, очки начисляются каждому игроку (включая того, кто не сбросил всю свою руку) в соответствии с рейтингом каждого игрока. С другой стороны, если играют от 6 до 12 человек, очки распределяются только между 5 игроками, которые использовали все свои карты (поскольку раунд заканчивается, когда 5 игроков завершили свои руки).

МАСТЕРСКИЙ ХОД: Игрок делает «Мастерский удар» и получает 7 дополнительных очков, если он или она использует 4 карты в одной математической игре (например: 10+1+1-9=3, как на фиг.5). Если кто-то удаляет сразу 5 карт (например: 8+8-1-1-9=5), это будет считаться «супермастерским ходом» и будет вознаграждено 14 дополнительными очками. Помимо 5 карт, за каждую дополнительную карту, использованную в одной игре, связанной с математикой, начисляется еще 7 бонусных очков. (Например: если используется 6 карт, вы получаете 21 бонусное очко.) Предупреждение: Такие дополнительные очки начисляются только при соблюдении правил, связанных с использованием математики.

В конце игры общее количество игроков баллы суммируются. Если в игру играли команды участников, каждый очки участника команды учитываются при подсчете общего балла команды. игрок или команда, набравшая наибольшее количество очков, побеждает в игре, а остальные занимают место по их окончательным результатам.