Сложные уравнение 3 класс по математике: Решение сложных уравнений: советы профессионала

Решение сложных уравнений: советы профессионала

4.9

(60)

Овладение детьми способом решения уравнений в начальной школе создает прочную основу для дальнейшего обучения алгебры, химии, физики и других предметов.

Начиная с 3-го класса, ученикам встречаются сложные уравнения, но справиться с ними очень просто.

Дети уже умеют решать простые уравнения, читай об этом здесь.

А эта статья будет посвящена решению сложных уравнений в 2-3 действия.

Очень часто родители, желая помочь, объясняют так: вот смотри, сейчас вот это число перенести в другую часть от знака равенства, надо поменять знак на противоположный: было умножение, меняем на деление; было сложение меняем на вычитание.

В начальной школе это объяснение не срабатывает, т.к. ребенок не знаком с законами алгебры.

Как сложное уравнение привести к тому, которые мы уже умеем решать, а именно к уравнению в 1 действие?

Рассмотрим  уравнение в 2 действия:

х + 56 = 98 — 2  — оно достаточно легкое.

Здесь особого труда не будет в решении, потому что ребенок сразу догадается, что сначала надо 98-2.

х + 56 = 98 — 2

х + 56 = 96 – это простое уравнение. А его решаем очень быстро!

Сейчас мы рассмотрим уравнение:

2• (х + 5) = 30.

Такое уравнение можно решить несколькими способами.

1.  У нас здесь неизвестное число х. Мы не знаем, что спрятано за этим числом.

А когда к х + 5 – это число тоже известно.

Закроем его и пусть это будет другое число, например b .

Мы видим, что у нас получилось самое простое уравнение в 1 действие.

2 • b = 30

А чтобы найти а, нам нужно 30 : на 2.

А b не что иное, как х + 5.

х + 5 = 30 : 2

х + 5 = 15

х = 15 – 5

х = 10

Проверку делаем как обычно: переписываем первое уравнение: 2 • (10 + 5) = 30.

30 – переписываем, а левую часть считаем  — будет  30.

30 = 30, значит, уравнение решили правильно.

При решении таких сложных уравнений самое главное – понять, что заменить на другое неизвестное число. Когда в уравнении всего 2 действия – это очень просто.

1. Более удобно и понятно, как показывает практика, если использовать решение сложных уравнений на основе зависимости между компонентами действий.

Наше уравнение  2 • (х + 5) = 30 читаем так: число 2 умножить на сумму х и пяти, получится 30. В данном случае – нам неизвестна сумма, чтобы ее найти, надо 30:2.

Рассмотрим уравнение:

48 : (16 – а) = 4.

Если опять заменять часть уравнения другим неизвестным числом, можно запутаться. Поэтому легче использовать взаимосвязи компонентов и результата действия: число 48 разделить на разность.

Нам неизвестна разность, поэтому сначала нужно узнать чему она равна. Надо 48 : 4.

16 — а = 48 : 4

16 — а = 12 – это простое уравнение.

а = 16 — 12

а = 4

Проверка: 48 : (16 — 4) = 4

Давайте посмотрим еще одно:

96 – (с – 14) = 94.

Из 96 надо вычесть разность с и 16. Чтобы найти разность, надо 96-94.

С — 14 = 96 — 94

С — 14 = 2

С = 14 + 2

С = 16

Проверка: 96 — (16 — 14) = 94

А сейчас мы переходим к тем уравнениям, у которых не 2, а 3 действия. Как же нам поступать в этом случае? При решении таких сложных уравнения используем знания порядка выполнения действий в выражениях со скобками и без них.

Рассмотрим уравнение: 36 – (8 • у + 5) = 7

Прежде всего, нужно внимательно оценить левую часть уравнения: ту, которая с неизвестным числом. Вы должны четко себе представить какое вы будете делать действие первым, какое – вторым, какое – третьим: сначала делается умножение, потом сложение и последним – вычитание.

И вот то, которое вы будете делать третьим, с него и начнем, т. е. начинаем упрощать уравнение с последнего действия. Последнее действие – вычитание. С него и начнем: из числа 36 вычесть то, что в скобках и получим 7.

Значит, то что в скобках – вычитаемое, чтобы его найти, надо 36 — 7.

(8 • у + 5) = 36 — 7

По правилам математики в данной записи скобки – не ставим.

8 • у + 5 = 36 — 7

8 • у + 5 = 29 – уравнение сложное. Нужно его упростить. Данное уравнение читаем так: к произведению 8 и у прибавили 5 и получилось 29. Нам неизвестно произведение, чтобы его найти, надо 29-5.

Получится:

8 • у = 29 – 5

8 • у = 24 – это уравнение простое.

у = 24 : 8

у = 3

Проверка: 36 — (8 • у + 5) = 7 .  Правую часть – 7 —  переписываем, а левую считаем.

 Итак: 7 = 7. Значит, уравнение решили правильно.

(36 + d) : 4 + 8 = 18. Определяем порядок действий: первое – сложение в скобках, второе – деление, третье сложение вне скобок. Значит, все, что до 8 – это первое слагаемое, чтобы его найти, надо 18 — 8

(36 + d) : 4 = 18 — 8

(36 + d) : 4 = 10 – уравнение сложное, теперь последнее действие — :, значит

36 + d = 10 • 4

36 + d = 40 – уравнение простое и его мы решаем легко!

Для удобства и быстроты решения сложных уравнений можете пользоваться  данной памяткой

Дело в том, что при кажущейся сложности, если внимательно изучить все приемы, которые я вам сегодня показала, эти уравнения дети будете щелкать как семечки.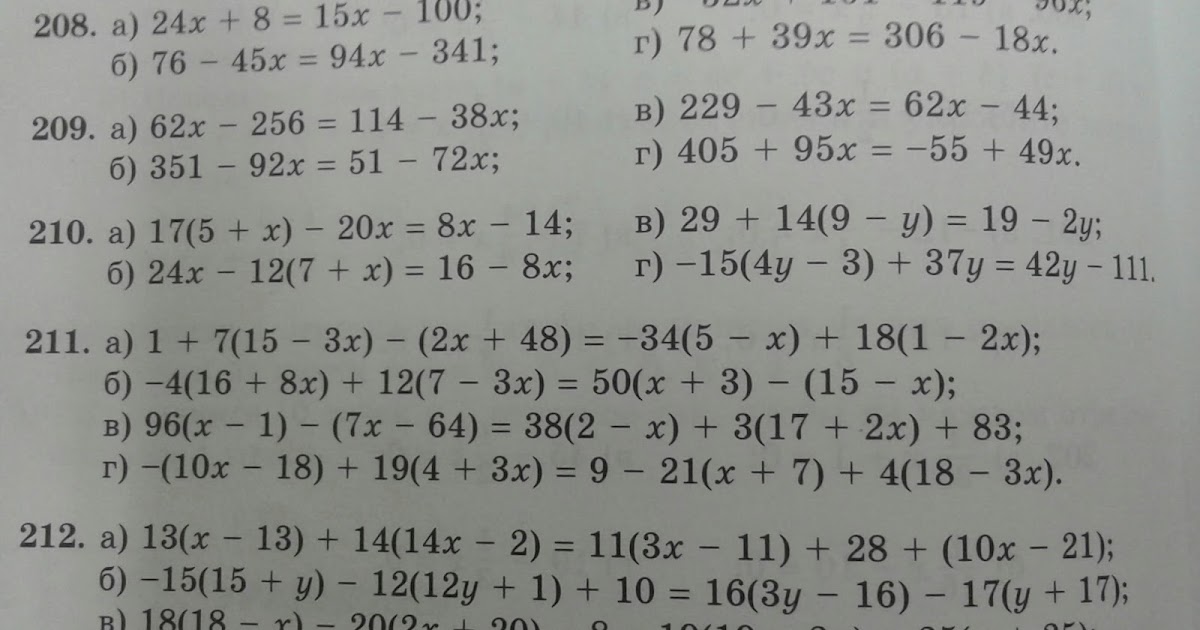 Обязательно напишите в комментариях, какой способ вам более удобен.

Скачать

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.9 / 5. Количество оценок: 60

Оценок пока нет. Поставьте оценку первым.

Похожие статьи

Урок математики в 3 классе Уравнения сложной структуры

Предлагает выполнить задание №1, в котором нужно

выполнить вычисления и узнать, кто из детей сколько

раз посещал библиотеку.

Задание аналогичное предыдущему уроку: «Найди

лишнее слово».

Постановка цели (проблемная ситуация).

Для того чтобы создать проблемную ситуацию

необходимо повторить смысл слов: «уравнение» и

«выражение». Работу с данными математическими

понятиями можно провести так: педагог делит доску

пополам и выполняет с детьми сначала задания, в

которых надо составить уравнения, затем на другой

половине – записывают выражения по заданию

педагога.

Задания, в которых надо записать уравнение:

Составьте уравнение, решите его и узнайте, какое число

задумал Андрей.

а) Я задумал число, увеличил его в 20 раз, и получил

220. Какое число я задумал?

б) Я задумал число, увеличил его в 20 раз, прибавил 100

и получил 220. Какое число я задумал?

Задания, в которых надо записать выражение:

Запишите выражения, и найдите их значения:

а) Число 11 увеличить в 20 раз.

б) Произведение чисел 11 и 20 увеличить на 100.

После того, как появились записи этих заданий,

педагог спрашивает, как называются записи справа и

слева.

– Чем они похожи и чем различны?

Таким образом, дети дают определение терминам:

«выражение» и «уравнение».

Можно построить беседу по вопросам:

– Какую из записей можно назвать уравнением?

– Что такое уравнение?

– Что значит решить уравнение?

– Что такое корень уравнения?

Дети решали подобные усложненные уравнения с

действиями сложения и вычитания, то уравнения

усложненной структуры с действиями умножения и

деления не вызовут затруднения. Урок можно

построить так, чтобы дети увидели сходства в структуре

таких уравнений и вспомнили уже известный алгоритм

решения таких уравнений.

Открытие нового.

Знакомство с новым материалом можно провести на

материале учебника или на доске написать аналогичные

уравнения (задание №2).

Педагог вводит термин «упростить уравнение».

Первичное закрепление с проговариванием

Задание №2 проговаривают в сравнении два алгоритма.

Самостоятельная работа

Реши. Проверь.

х · (250:50)=75 k +160 : 4 = 452

Я могу:

 упростить сложное уравнение;

 найти корень уравнения;

 выполнить вычисления;

 выполнить проверку

Применение нового.

Предлагает выполнить задание №3 на решение

уравнений.

Работа над ранее изученным.

Предлагает выполнить задания №4-7.

Задание №4 содержит творческую часть.

Придумай задание с сундучком на 6 примеров

с умножением и делением. Для тех детей, которые

быстро справляются с вычислениями, предлагает

создание своих сундучков ответов. Эти, созданные

детьми задания, раздает тем, кто плохо справляется

с быстротой вычислений. Проверку также возлагает на

учащихся, кто составил примеры и сундучок ответов.

Задания №5-7 по своему усмотрению в зависимости от

необходимости конкретному учащемуся.

Составь вопросы по теме урока.

В каждом уроке нового или закрепления учащиеся

составляют вопросы. Это позволит помочь провести

рефлексию усвоения темы. Со словами, приведенными

в учебнике надо составить вопросы.

Можно использовать прием: ромашка или кубик Блума

Решенные уравнения со сложными решениями

BY: Мэри Джейн Стерлинг и

Обновлены: 07-13-2021

Из книги: Algebra II Рабочая тетрадь для Dummies

Algebra II Рабочая книга Dummies.

Купить книгу на Amazon

В алгебре вы часто сталкиваетесь с уравнениями, не имеющими реальных решений, или с уравнениями, у которых есть потенциал для гораздо большего количества реальных решений, чем есть на самом деле. Например, уравнение x ² + 1 = 0 не имеет действительных решений. Если вы запишете это как x ² = –1 и попытаетесь извлечь квадратный корень из каждой стороны, у вас возникнут проблемы.

Пока у вас нет мнимых чисел, вы не можете написать, что решение этого уравнения равно x = +/– i . Уравнение имеет два комплексных решения.

Пример уравнения без достаточного количества действительных решений: x ⁴ – 81 = 0. Факторы этого уравнения в ( x ² – 9)( x ² + 9) = 0. Двумя действительными решениями этого уравнения являются 3 и –3. Два комплексных решения: 3

i и –3 i .

Чтобы найти сложные решения уравнения, вы используете факторинг, свойство квадратного корня для решения квадратного уравнения и формулу квадратного уравнения.

Примеры вопросов

1. Найдите все действительные и комплексные корни уравнения x ³ – 2 х ² + 25 х – 50 = 0,

   x = 2, 5 i , -5 i . Сначала разложите уравнение на множители, чтобы получить x ² ( x – 2) + 25( x – 2) = ( x – 2)( x ² Используя свойство умножения нуля, вы определяете, что x – 2 = 0 и x = 2. Вы также получаете x ² + 25 = 0 и x . ² = –25. Возьмите квадратный корень из каждой стороны и

   Упростите радикал, используя эквивалентность для i , и комплексные решения равны

   Действительный корень равен 2, а мнимые корни равны 5 i и –5 i .

2. Найдите все корни, действительные и мнимые, уравнения

   х = 0,4 + 0,6 и , 0,4 – 0,6 и . Квадратное число не учитывается, поэтому вы используете квадратичную формулу:

   Комплексными являются только два решения: 0,4 + 0,6 i и 0,4 – 0,6 i .

Практические вопросы

1. Найдите все корни, действительные и мнимые, x ² + 9 = 0.

2. Найдите все корни, действительные и мнимые, x ² + 4 x + 7 = 0,

3. Найдите все корни, действительные и мнимые, из 5 x ² + 6 x + 3 = 0.

4. Найдите все корни, действительные и мнимые, числа

   x ⁴ + 12 x ² – 64 = 0,

Ниже приведены ответы на практические вопросы:

1. Ответ: x = 3 i , -3 i .

   Добавьте -9 к каждой стороне, чтобы получить х ² = –9. Извлеките квадратный корень из каждой стороны. Затем упростите выражение, используя i для отрицательного числа под радикалом:

2. Ответ

   Используйте квадратичную формулу, чтобы найти x . Упростите выражение, используя i для отрицания под корнем:

3. Ответ

   Используйте квадратичную формулу, чтобы найти x . Упростите выражение, используя i для минуса под корнем:

4. Ответ: x = 2, –2, 4 i , –4 i .

   Фактор левой стороны: ( x ²

   + 16)( x ² – 4) = ( x ² + 16)( x 2 9019 – 0 ) = 0. Получите два действительных корня, установив x – 2 и x + 2 равными 0. Когда x ² + 16 = 0, вы обнаружите, что х ² = –16. Взяв квадратный корень из каждой стороны и используя i вместо -1 под корнем, вы получите два мнимых корня.

Об этой статье

Эта статья взята из книги:

• Рабочая тетрадь по алгебре II для чайников,

Об авторе книги:

Мэри Джейн Стерлинг преподавала математику в средней и старшей школе, прежде чем начать свою карьеру в качестве преподаватель Университета Брэдли, где она преподавала более 35 лет.

Эту статью можно найти в категории:

• Алгебра,

Комплексные числа

Комплексный номер

Комплексное число представляет собой комбинацию
Действительного числа и Воображаемого числа

 

Реальные числа — это такие числа, как:

1

12,38

−0,8625

3/4

√2

1998

Практически любое число, которое вы можете придумать, является действительным числом!

Мнимые числа, когда в квадрате дают отрицательный результат .

Обычно этого не происходит, потому что:

• когда мы возводим в квадрат положительное число, мы получаем положительный результат, а
• когда мы возводим в квадрат отрицательное число, мы также получаем положительный результат (поскольку отрицательное число, умноженное на отрицательное, дает положительный результат), например −2 × −2 = +4

Но представьте, что такие числа существуют, потому что они нам нужны.

Поговорим еще о мнимых числах…

«Единица» мнимого числа (например, 1 для действительных чисел) — это i, которое является квадратным корнем из −1

Потому что, возведя i в квадрат, мы получим −1

i ² = −1

Примеры мнимых чисел Номера:

3i

1.04i

−2,8i

3i/4

(√2)я

1998i

И мы держим здесь маленькую букву «i», чтобы напомнить себе, что нам нужно умножить на √−1

Комплексные числа

Когда мы объединяем действительное число и мнимое число, мы получаем комплексное число :

.

Примеры:

1 + я

39 + 3i

0,8 − 2,2i

−2 + πi

√2 + i/2

 

Может ли число быть комбинацией двух чисел?

Можем ли мы составить число из двух других чисел? Мы можем точно!

Мы постоянно делаем это с дробями. Дробь ³ / ₈ — это число, состоящее из 3 и 8. Мы знаем, что это означает «3 из 8 равных частей».

Комплексное число — это всего лишь два числа, сложенные вместе (действительное и мнимое число).

Любая часть может быть равна нулю

Итак, у комплексного числа есть действительная и мнимая части.

Но любая часть может быть

0 , поэтому все действительные числа и мнимые числа также являются комплексными числами.

Комплексный номер	Реальная часть	Воображаемая часть
3 + 2i	3	2
5	5	0	Чисто настоящий
−6i	0	−6	Чисто воображаемый

Сложно?

Комплекс , а не означает сложный.

Это означает, что два типа чисел, действительные и мнимые, вместе образуют комплекс , как строительный комплекс (здания соединены вместе).

Визуальное объяснение

Вы знаете, как идет числовая линия влево-вправо ?

Хорошо, пусть мнимые числа идут вверх-вниз :

И получаем Сложный Самолет

Комплексное число теперь может отображаться в виде точки:

Комплекс № 3+4 и

Добавление

Чтобы сложить два комплексных числа, складываем каждую часть отдельно:

(a+b i ) + (c+d i ) = (a+c) + (b+d) i

Пример: добавьте комплексные числа

3 + 2 i и 1 + 7 i

• добавьте действительные числа и
• добавить мнимые числа:

(3 + 2i) + (1 + 7i)
= 3 + 1 + (2 + 7) i
= 4 + 9i

Попробуем еще:

Пример: добавьте комплексные числа

3 + 5 I и 4 – 3 I

(3 + 5 I ) + (4 – 3 I )
= 3 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 (5 + 4 + 4 (5 + 4 + 4 (5 + 4 + 4 (5 .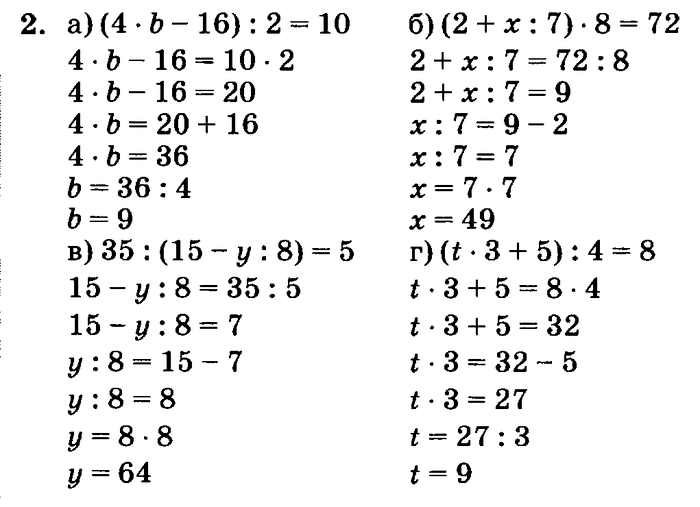 ) i

= 7 + 2 i

На комплексной плоскости это:

Умножение

Чтобы умножить комплексные числа:

Каждая часть первого комплексного числа умножается на
каждая часть второго комплексного числа

Просто используйте «ФОЛЬГА», что означает « F первых, O маточных, I внутренних, L астровых» (подробнее см. Биномиальное умножение):

	Первые: a × c Внешний: a × d i Внутренние: b i × c Колодки: b i × d i
(a+b i )(c+d i ) = ac + ad i + bc i + bd i 2

Вот так:

Пример: (3 + 2i)(1 + 7i)

(3 + 2i)(1 + 7i) = 3×1 + 3×7i + 2i×1+ 2i×7i

 = 3 + 21i + 2i + 14i ²

= 3 + 21i + 2i − 14 (поскольку i ² = −1)

 = −11 + 23i

А это:

Пример: (1 + i)

²

(1 + i)(1 + i)= 1×1 + 1×i + 1×i + i ²

 = 1 + 2i − 1  (потому что i ² = −1)

 = 0 + 2i

Но есть более быстрый способ!

Используйте это правило:

(a+b i )(c+d i ) = (ac−bd) + (ad+bc) i

Пример: (3 + 2i)(1 + 7i) = (3×1 − 2×7) + (3×7 + 2×1)i = −11 + 23i

Почему это правило работает?

Это просто метод “ФОЛЬГА” после небольшой работы:

(a+b i )(c+d i ) =ac + ad i + bc i + bd i ²  метод ФОЛЬГИ 9007 b07 b0ac +

0 i − bd   (потому что i ² = −1)

 = (ac − bd) + (ad + bc) i   (собирая подобные термины)

И у нас есть (ac − bd) + (ad + bc) и узор.

Это правило, безусловно, быстрее, но если вы его забудете, просто запомните метод FOIL.

Давайте попробуем i

²

Ради интереса воспользуемся методом вычисления i ²

Пример: i

²

Мы можем записать i с действительной и мнимой частями как 0 + i

i ² = (0 + i) ²

 = (0 + i)(0 + i )

 = (0×0 − 1×1) + (0×1 + 1×0) i

= −1 + 0 i

= −1

И это хорошо согласуется с определением i ² = −1

Так все замечательно работает!

Дополнительные сведения см. в разделе Умножение комплексных чисел.

Конъюгаты

Через минуту нам нужно будет узнать о конъюгатах!

В сопряжении мы меняем знак в середине следующим образом:

Спряжение часто пишется с чертой над ним:

Пример:

5 − 3 i   =   5 + 3 i

Разделение

Конъюгат используется для облегчения сложного деления.

Хитрость заключается в том, чтобы умножить верхнее и нижнее на сопряженное нижнее .

Пример: выполните следующее деление:

2 + 3 i 4 − 5 i

Умножьте верхнее и нижнее число на сопряженное число 4 − 5 2 6 : 60835 2 + 3 I 4 – 5 I × 4 + 5 I 4 + 5 I = 8 + 10 I + 12 I I + + + + + + + I . ² 16 + 20 I – 20 I – 25 I ²

Теперь I ² = −1, SO:

= 83535 83535 83535353535353 8 8. 10. 100066. + 12 и − 15 16 + 20 и − 20 и + 25

Добавить Нравится Термины (и обратите внимание, как внизу 20 i − 20 i отменяется!):

=   −7 + 22 i

41

Последний ответ 9 обратно в a + b i форма:

=   −7 41 + 22 41 i

ГОТОВО!

Да, нужно немного посчитать. Но это можно сделать.

Умножение на конъюгат

Однако есть более быстрый способ.

В предыдущем примере интересно то, что произошло внизу:

(4 – 5 i )(4 + 5 i ) = 16 + 20 i – 20 i – 25 i ²

Средние члены (20 i − 20 i ) сокращаются:

(4 – 5 i )(4 + 5 i ) = 16 – 25 i ²

Также i ² = −1 :

(4 – 5 i )(4 + 5 i ) = 16 + 25

А 16 и 25 (магически) являются квадратами 4 и 5:

(4 – 5 i )(4 + 5 i ) = 4 ² + 5 ²

Довольно простой результат. Общее правило:

(a + b i ) (a − b i ) = a ² + b ²

Это может сэкономить нам время при делении, например:

Пример: попробуем еще раз

2 + 3 I 4 – 5 I

Умножение верхнего и дна на конъюгат 4 – 5 I :

2 + 3 I 3838383838383838383838383838383838383838383838383838383838. – . i × 4 + 5 i 4 + 5 i   =   8 + 10 i + 12 i + 15 i ² 16 + 25

= −7 + 22 i 41

А затем обратно в форму a + b i :

=   −7 41 + 22 41 i

ГОТОВО!

 

Обозначение

Мы часто используем z для комплексного числа. И Re() для действительной части и Im() для мнимой части, например:

Что выглядит на комплексной плоскости так:

 

Набор Мандельброта

Прекрасное множество Мандельброта (на фото) основано на комплексных числах. Это график того, что происходит, когда мы берем простое уравнение z 2 + c (оба комплексных числа) и возвращаем результат обратно в z снова и снова. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Имя * Email * Сайт Комментарий *