Скорость счета: скорость счета | это… Что такое скорость счета?

скорость счета | это… Что такое скорость счета?

2.6 скорость счета (counting rate): Увеличение показаний прибора в единицу времени.

Источник: СТО НП АВОК 4.3-2007: Распределители стоимости потребленной теплоты от комнатных отопительных приборов. Распределители с электрическим питанием

Смотри также родственные термины:

2.14 скорость счета акустической эмиссии [ N] (count rate, acoustic emission): Число зарегистрированных выбросов сигнала АЭ в единицу времени.

Определения термина из разных документов: скорость счета акустической эмиссии

Источник: ГОСТ Р ИСО 12716-2009: Контроль неразрушающий. Акустическая эмиссия. Словарь оригинал документа

15н. Скорость счета импульсов на аналитической линии на контрольном образце

Скорость счета импульсов на выходе электронно-регистрирующего устройства спектрометра или спектрометрического канала, настроенного на аналитическую линию данного элемента в измеряемом контрольном образце

Определения термина из разных документов: Скорость счета импульсов на аналитической линии на контрольном образце

Источник: ГОСТ 16865-79: Аппаратура для рентгеноструктурного и рентгеноспектрального анализов. Термины и определения оригинал документа

3.12 скорость счета импульсов от счетного образца n₀ , с^-1: Разность скоростей счета импульсов с источником и фоновых импульсов

n₀ = n – f.                                                                     (6)

Определения термина из разных документов: скорость счета импульсов от счетного образца n₀

Источник: ГОСТ Р 51730-2001: Вода питьевая. Метод определения суммарной удельной альфа-активности радионуклидов оригинал документа

Скорость счета импульсов радиометрической установки

Отношение числа статистически распределенных импульсов, зарегистрированных за некоторый интервал времени, к этому интервалу

Определения термина из разных документов: Скорость счета импульсов радиометрической установки

Источник: ГОСТ 26412-85: Материалы защитные радиохимических производств и ядерных энергетических установок. Метод определения изолирующих свойств по отношению к загрязнению бета-радионуклидами оригинал документа

3. 11 скорость счета импульсов с источником n, с^-1: Отношение количества импульсов, зарегистрированных радиометром с размещенным в нем источником N_n, за время регистрации t, к этому интервалу времени

n = N_n/t.                                                                       (5)

Определения термина из разных документов: скорость счета импульсов с источником n, с^-1

Источник: ГОСТ Р 51730-2001: Вода питьевая. Метод определения суммарной удельной альфа-активности радионуклидов оригинал документа

17.

Скорость счета счетного прибора

Число перемещений разряда от одного разрядного промежутка газоразрядного прибора к другому в секунду

Определения термина из разных документов: Скорость счета счетного прибора

Источник: ГОСТ 20724-83: Приборы газоразрядные. Термины и определения оригинал документа

3.10 скорость счета фоновых импульсов f, с^-1: Отношение количества зарегистрированных радиометром импульсов N_f, не связанных с альфа-частицами, от находящихся в измеряемом счетном образце радионуклидов за время регистрации t, к этому интервалу времени

f = N_f/t.                                                                          (4)

Определения термина из разных документов: скорость счета фоновых импульсов f, с^-1

Источник: ГОСТ Р 51730-2001: Вода питьевая. Метод определения суммарной удельной альфа-активности радионуклидов оригинал документа

Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.

Скорость счета в ментальной арифметике: в чем секрет?

04

Март

Автор: Евгения Климкович

Рубрика: Ментальная арифметика

Здравствуйте, друзья! На связи Евгения Климкович.

Сегодня пополню рубрику ментальная арифметика новенькой статьей. Речь в ней пойдет о том, как же достигается такая высокая скорость счета в ментальной арифметике. Для начала давайте посмотрим видео.

Круто, не правда ли? Но как это? В чем секрет? Сейчас попробую объяснить.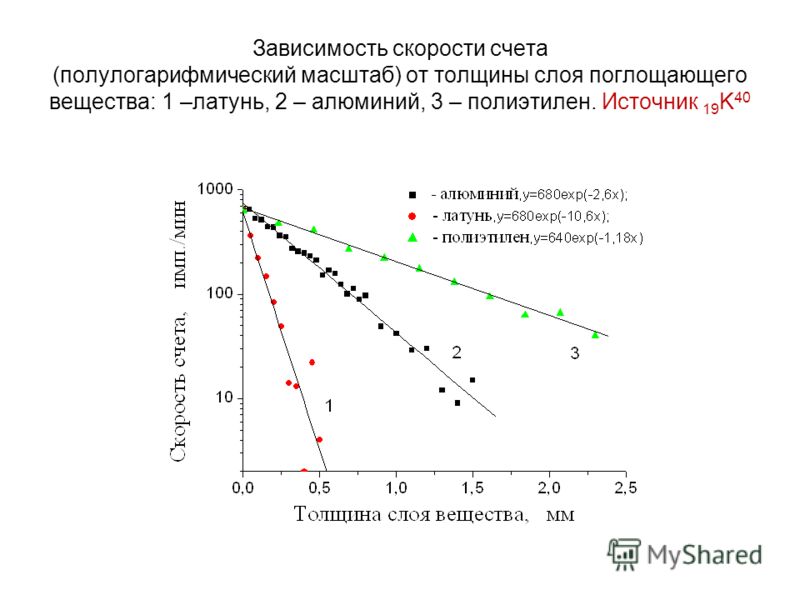

Давайте на примерах. Попробуйте сосчитать)

5 + 3 – 2 + 1 – 3

Сколько получилось? 4? Правильно! А как вы это посчитали? Вы посчитали это в уме. То есть, сначала к 5 прибавили 3, получили 8. Потом из 8 вычли 2, равно 6. Затем к 6 прибавили 1, равно 7. И, в конце концов, вычли еще 3 и получили ответ 4. То есть, для того, чтобы дойти до окончательного ответа 4, вам пришлось сначала получить три промежуточных результата 8, 6 и 7.

А если бы вы считали не в уме, а ментально, то на окончательный ответ 4, вы бы вышли без подсчета результатов промежуточных. И это прибавило бы вам скорости. Причем, это касается не только таких простейших примеров, который мы с вами рассмотрели.

А как понять, что такое ментальный счет? Как вы уже догадались, к расчетам в уме (в обычном понимании) это не имеет никакого отношения. Что происходит в голове у человека считающего таким способом?  А в голове у него возникает образ соробана, основного инструмента на занятиях. И человек силой своего воображения передвигает косточки на этом воображаемом соробане.

На уроках детей учат считать на соробане, и учат делать это очень быстро. А затем с помощью специальных упражнений переводят это умение на ментальный уровень. Это когда абакуса под руками нет, а ты все равно на нем считаешь, представляя его и мысленно передвигая косточки.

Если сравнить скорость вычислений непосредственно на абакусе и вычислений ментальных, то последний вариант выиграет. Потому что в воображении косточки передвигаются намного быстрее, чем пальчиками.

Вот и весь секрет. Конечно, чтобы добиться таких сногсшибательных результатов, как эта супер-девочка на видео, потребуется время, желание и много-много тренировок. Но скоростное решение примеров – это не главное в менталке. Это всего лишь 30% того, что она может дать вашему ребенку. В качестве дополнительного бонуса вы получаете разностороннее развитие и оказываете благоприятное воздействие:

• на мелкую моторику;
• скорость мышления;
• концентрацию внимания;
• межполушарные связи;
• зрительную, слуховую, мышечную и фотографическую память.

Подробнее об этом можно почитать вот здесь.

Так что занимайтесь, друзья, поражайте нас своими успехами и развивайтесь!

Удачи вам!

Ваша Евгения Климкович.

Понравилась статья? Поделись с друзьями:

Будь в курсе школьных событий!

Подпишись на новости блога!
Раз в неделю получай анонсы свежих статей на почту!

Нажимая на кнопку я даю согласие на обработку персональных данных и принимаю политику конфиденциальности.

Производная скорость счета – что это такое?

При динамическом рассеянии света (DLS) нас обычно больше всего интересует уровень флуктуаций интенсивности, тем не менее нам необходимо увидеть хороший сигнал, прежде чем мы сможем его проанализировать. Сила сигнала — это интенсивность рассеяния, и она измеряется в фотонах в секунду или, чаще всего, как в Zetasizer, в килоимпульсах в секунду, для краткости kcps. Фактическое среднее количество фотонов в секунду, поступающих на детектор, также называется средней скоростью счета, фактической скоростью счета или просто интенсивностью рассеяния.

Какова средняя скорость счета?

Если детектор Zetasizer собирает 1 000 000 фотонов в течение 100 секунд, то средняя скорость счета во время этого измерения составляет 1 000 000 фотонов/100 с = 10 000 фотонов/с = 10 килогерц в секунду. Это число представляет среднюю интенсивность рассеяния во время измерения с , конкретного образца в этом конкретном приборе при определенных оптических настройках эксперимента. В реальных образцах средняя скорость счета, вероятно, намного выше, обычно 200–500 кпс. Zetasizer имеет очень большой динамический диапазон, что означает, что он может обнаруживать рассеяние как от образцов с очень низкой концентрацией, так и от образцов с очень высокой концентрацией. Одна хитрость, которая используется внутри системы, заключается в том, что часть сигнала может быть заблокирована аттенюатором, поэтому, даже если для чувствительного детектора фотонов будет слишком много света, можно измерить его часть с помощью аттенюатора. .

Какова производная скорость счета?

Если во время измерения используется аттенюатор, который пропускает только 0,3 % света, то измеренная средняя скорость счета будет составлять только 0,3 % сигнала, который можно было бы получить, если бы аттенюатор отсутствовал. В Zetasizer можно использовать ряд различных аттенюаторов, и в автоматическом режиме система выберет уровень аттенюации для достижения средней скорости счета в оптимальном диапазоне 200-500 тыс. импульсов в секунду. В Zetasizer microV и APS доступны еще более точные настройки, поскольку интенсивность лазера также может регулироваться независимо. Как мы можем сравнить уровень сигнала двух разных образцов, которые были измерены с разными уровнями затухания? Мы можем просто использовать теоретическую скорость счета можно было бы получить при 100% мощности лазера с нулевым затуханием. Это называется производной скоростью счета (DCR) и может быть полезной мерой для сравнения силы сигнала от разных образцов: более высокая производная скорость счета обычно указывает на более высокую концентрацию, более крупные частицы или более высокую концентрацию и более крупные частицы. В таблице справа перечислены различные положения аттенюаторов и соответствующие им уровни затухания или передачи. Существует также более старый FAQ-что-есть-производный-счетчик? Чтобы отобразить производную скорость счета в вашем программном обеспечении, ознакомьтесь с часто задаваемыми вопросами, упомянутыми в разделе «Как отобразить пользовательский параметр».

Пример 1: если образец имеет среднюю скорость счета 200 тыс. импульсов в секунду, а Zetasizer использует аттенюатор с ослаблением 0,3%, тогда полученная скорость счета будет равна 100 тыс. импульсов в секунду / 0,3% = 100 тыс. импульсов в секунду / 0,003 = 33 333 кГц.

Пример 2: если образец имеет среднюю скорость счета 150 тыс. импульсов в секунду, а в Zetasizer microV используется аттенюатор 0,1% и мощность лазера 10%, тогда полученная скорость счета составит 150 тыс. импульсов в секунду / 0,1% / 10% = 150 kcps / 0,001 / 0,1 = 1 500 000 kcps

Как это связано с SLS?

В принципе, в идеальном образце полученная скорость счета может использоваться для статического светорассеяния (SLS), где рассеяние как функция концентрации образца приводит к молекулярной массе и второму коэффициенту Вириала (A2 или B22). В реальных экспериментальных ситуациях статическое рассеяние света обычно выполняется путем фиксирования всех параметров затухания, чтобы избежать какой-либо неопределенности в коэффициентах затухания. Кроме того, поскольку в SLS мы часто ищем самые маленькие рассеиватели в выборке, обычно усредняют интенсивность по многим коротким подвыборкам (~ 20 мс, затем берут среднее значение после исключения выбросов) вместо более длительных периодов корреляции, используемых в DLS (~ 10 с). , где все способствует).

Как отобразить производную скорость счета?

Выберите рабочую область, например, рабочую область размера, а затем отредактируйте ее — Параметры просмотра записи — Измерение — Размер — Производная скорость счета и переместите ее в рабочую область с помощью стрелки вправо. Полученная скорость счета для каждой записи размера будет отображаться в рабочей области размера.

Раньше

• Как получить последнюю версию программного обеспечения для DLS и дзета-потенциала? (бесплатная загрузка)
• Комплексное титрование – переменная дозировка (дзета и размер)
• Советы и рекомендации по характеристике наночастиц (44 вопроса и ответа)
• Полидисперсность по нескольким пикам в DLS
• Какой размер правильный: распределение интенсивности по объему (вероятно, проблема № 1)

Если у вас есть какие-либо вопросы, пожалуйста, напишите мне по адресу ulf.

[email protected]. Спасибо! Хотя высказанные мнения, как правило, принадлежат автору, некоторые части могут быть изменены нашей редакцией.

Экспериментальная физика – Какая связь между интенсивностью излучения и скоростью счета?

спросил 8 лет, 4 месяца назад

Изменено 6 лет, 2 месяца назад

Просмотрено 10 тысяч раз

$\begingroup$

Если известно, что радиоактивным источником является, например, цезий-137, можно ли экстраполировать зависимость между скоростью счета и интенсивностью излучения? Если это невозможно, какова минимальная информация, необходимая для определения этого, например. активность? 99 Бк$.

Энергия излучения зависит от схемы распада. Например, для Cs-137 вы найдете (источник: http://upload.

wikimedia.org/wikipedia/commons/6/66/Caesium-137_Decay_Scheme-de.svg)

Здесь вы видите, что есть два разных путей распада Cs-137: один дает Ba-137 с испусканием $\beta-$ (электрона) с энергией до 1,17 МэВ, а другой проходит через промежуточный (метастабильный) 137-Ba, который впоследствии распадается до стабильного 137-Ba с испусканием гамма-излучения с энергией 662 кэВ. 92$.

Когда вы смотрите на радиационные повреждения, вы действительно используете меру энергии. Грей — это единица СИ, выраженная в $Дж/кг$ — другими словами, количество энергии, выделяемой на кг поглощающего материала. Это зависит не только от испускаемого излучения, но и от получаемого материала. Материалы с более высоким Z обычно останавливают больше энергии на единицу массы и, следовательно, имеют более высокие значения дозы облучения. Обратите внимание, что серый используется для

неживых материалов . Для биологических материалов предпочтительнее Зиверт (Зв), поскольку он представляет собой «повреждение», а не просто «поглощенную энергию». Для более полного объяснения см., например, http://en.wikipedia.org/wiki/Gray_(unit)

$\endgroup$

2

$\begingroup$

Как отмечено в комментариях, скорость счета (в первом порядке) пропорциональна активности: $$ \text{ставка} = k \cdot \text{активность} \,.$$

Константа пропорциональности равна

$$ k = \text{принятие} \times \text{эффективность} \times \text {дробное время жизни} \,$$

, где приемлемость — геометрический фактор, квантовая эффективность — свойство детектора, а время жизни связано как с детектором, так и с фактической скоростью поступления счетчиков (т. е. $\text{активность } \times \text{принятие} \times \text{эффективность}$).

Это означает, что время жизни может фактически привнести некоторую степень нелинейности, но пока вы держите время жизни около 1,0 (полностью живое), уровень нелинейности, как правило, незначителен. 2} \,. $$ Аппроксимация очень хороша, когда $r$ много больше как линейного размера источника, так и линейного размера активной области детектора.

Эффективность. Как правило, вы должны доверять производителю в этом вопросе, и вам, возможно, придется перемножить несколько коэффициентов полезного действия подкомпонентов или выполнить некоторые расчеты ожидаемого количества фотонов, попадающих на поверхность ФЭУ, и т.п. Немного искусства.

Живое время. Определим дробное время жизни как $$\ell = \frac{\text{время, когда детектор был доступен для записи события}}{\text{длина всего периода сбора данных}} \,.$$ дробное мертвое время $d = 1 – \ell$ намного меньше единицы, фактическое мертвое время можно оценить как $D = N \tau$, где $N$ — общее количество зарегистрированных отсчетов, а $\tau$ — время детектор проводит в активном состоянии в результате однократного подсчета. Получить поправку в реальном времени для более сложной ситуации может быть действительно очень сложно.