Сходство подобных предметов: Сходство предметов, 8 (восемь) букв

4 базовых закона восприятия в дизайне и инфографике

• Инфографика
• 4 мин на чтение
• 7442

Теории Гештальта более сотни лет, но она не теряет актуальности и применяется в новых и новых сферах. Она основана на теории того, что взгляд (и разум) воспринимает объект как целостную структуру до того, как начинает различать отдельные компоненты. То есть, целостный образ — это не просто сумма отдельных частей, а самостоятельный объект.

Теория работает, благодаря устройству нашего мозга, который по природе склонен создавать порядок из хаоса. Законы работают в 99,9% случаев, потому что являются врожденными для каждого человека. Их знание полезно дизайнеру, т.к. помогает организовать визуальные объекты эффективно для восприятия.

1. Сходство

Создать сходство (или контраст) в инфографике можно с помощью цвета, размера или формы

В процессе познания люди склонны к группировке объектов, имеющих сходные черты. Причем, эта привычка лежит глубоко на подсознательном уровне, т.к. является одной из базовых функций мозга. Психолог Пол Блум говорит: «Чтобы выжить, любому существу необходимо умение учиться. А часть успешного обучения — это умение делать статистические обобщения на основе ограниченного опыта. Вы съели яблоко, второе, третье, — они были хорошими на вкус, — и вы делаете вывод, что можете есть яблоки, что все яблоки вкусные. И когда вы голодны, вы ищете яблоки, это адаптация, это рационально, это целесообразно».

Самый маленький ребенок умеет обобщать все, что видит вокруг — съедобные и несъедобные предметы, своих и чужих людей, со временем обобщение усложняется до категоризации людей по признаку пола, возраста, расе, профессии и т.д. [1]. Причем предметам, которые внешне похожи, подсознательно приписываются и сходные функции (внутреннее сходство). Так, подобные элементы образуют группы, то есть два чем-то похожих друг на друга предмета (человека) даже вне нашего желания будут восприниматься как группа, как общее целое.

Создать сходство (или контраст) в инфографике можно с помощью цвета, размера или формы. Дизайнеры также используют одинаковый фон для того, что хотят объединить, контрасты для выделения главных элементов из группы. Но хорошие дизайнеры при этом помнят, что на одном экране не должно быть слишком много контрастов, т.к. это будет отвлекать и усложнять восприятие.

2. Близость

Группировать только то, что поддерживает общую логику инфографики

Подсознание группирует элементы, находящиеся близко друг к другу. Согласно этому принципу, объекты, расположенные ближе в пространстве, связаны. И наоборот — «разбросанные» в пространстве объекты воспринимаются разными. Это объясняется природной «ленью» мозга, а точнее нежеланием тратить лишнюю энергию. Серому веществу легче обработать одну порцию информации — один визуальный стимул, чем несколько (пусть и малых) стимулов, поэтому он избегает когнитивных перегрузок и объединяет близкие элементы друг с другом.
Пример из области манипуляций сознанием — фото политика размещают в журнале или на новостном сайте в окружении положительных фото (природа, дети, счастливые люди) и его рейтинг растет, т.к. зрители приписывают ему положительные качества, сами того не осознавая [2].

Это правило реализуется и в композиции — изображения должны гармонично вписываться в фон, оставляя свободное место вокруг. Связанные элементы нужно держать вместе и наоборот. Это не только уменьшает риск того, что зритель не поймет связи между общими компонентами, но и заставляет мозг сравнивать, искать сходства и связи между нужными автору предметами. Главное для дизайнера соотносить действие этой закономерности с приоритетами информации на каждом отдельном экране инфографики, то есть группировать только то, что поддерживает общую логику инфографики.

3. Простота

И отсечь все, что усложняет композицию и отвлекает от созерцания гармонии

Мозг воспринимает и анализирует необычные или сложные изображения с помощью максимально простых и ровных фигур.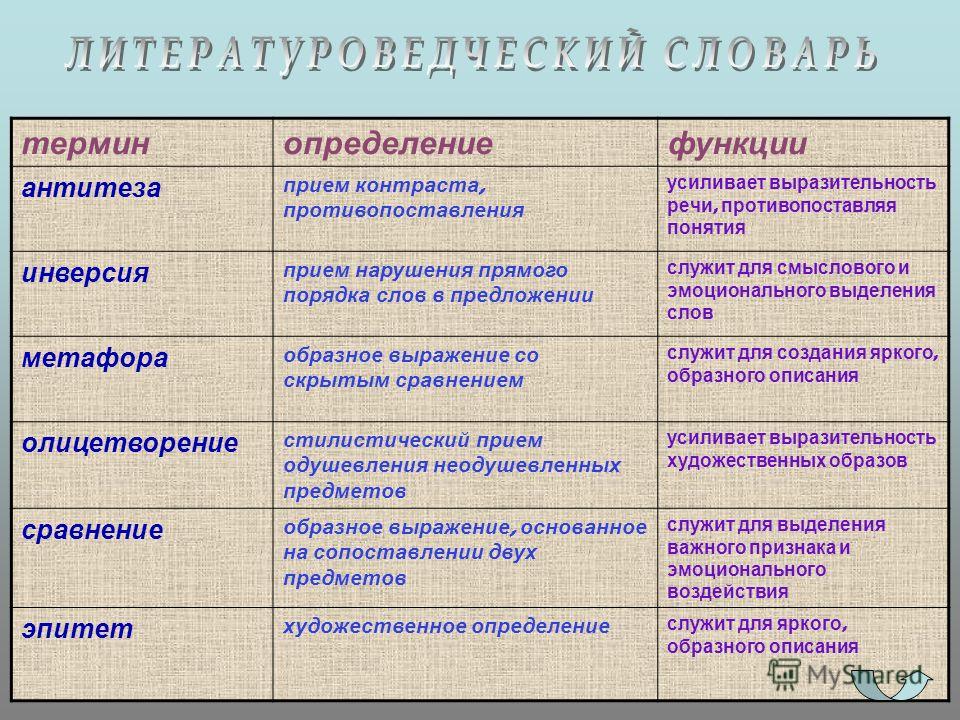 Психологи утверждают, что большинство людей считает наиболее привлекательным среднестатистическое лицо. Именно так — мы от природы любим лица, не содержащие в себе необычных черт [1].

Закон простоты также называют законом «хорошей» формы — подсознательное предпочтение человек отдает наиболее простым и устойчивым фигурам. Они архетипически ассоциируются со стабильным положением в пространстве. От простых, понятных, симметричных фигур подсознание не ожидает никаких опасностей или неожиданностей, поэтому может спокойно сосредоточиться на содержании этих фигур. Кстати, времени на простые фигуры у мозга уходит меньше, значит и нужная информация доходит до сознания быстрее.

В инфографике это означает, что экран воспринимается полностью и вся композиция должна вписываться в простые формы — квадрат, круг или треугольник. Эффект достигается и следующим образом: максимально упростить графическую форму при первом восприятии. И только потом усложнять ее, постепенно добавляя новые и новые элементы, если это действительно необходимо. Создав инфографику, нужно проанализировать ее с позиции данного принципа. И отсечь все, что усложняет композицию и отвлекает от созерцания гармонии.

4. Завершенность

Особенности восприятия «автоматически» дополнят картину

Как и все перечисленные законы восприятия, этот связан с тем, что наш внутренний процессор быстрее и охотнее «считывает» все простое. Только в данном случае быстрее срабатывает опыт. Ведь в первую очередь, при восприятии сигнал посылается в тот отдел мозга, где хранится информация о прошлом опыте взаимодействия человека с тем или иным объектом. То есть происходит узнавание (если возможно).

И стоит отдельным частям «зацепить» в подсознании знакомый предмет, как недостающая информация дополняет образ. Так, например, в бесформенном пятне ребенок видит медведя или утку. Или вспомним детское упражнение, где дано множество точек и нужно их соединить, чтобы увидеть целый образ.

И в инфографике зритель подсознательно ищет знакомые образы, дополняя или исключая элементы, которые этому мешают.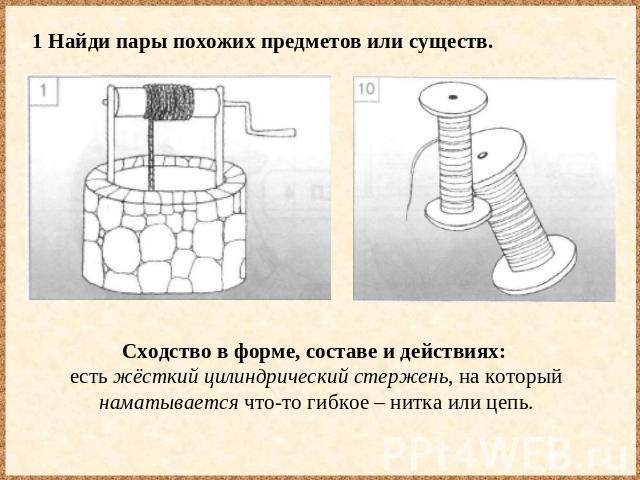

Закон можно использовать так — обозначить границы или «намекнуть» отдельными частями на хорошо знакомый людям объект — а особенности восприятия «автоматически» дополнят картину. Ключевым моментом здесь будет опора на тот образ, который обязательно знаком зрителю, ведь то, что ранее не воспринималось, не будет узнано и дополнено.

Источник: infographer.ru

• #дизайн
• #законы
• #инфографика
• #советы
• #статья

• 1

Категория “сходство до степени смешения” в авторском праве

 

Казалось бы, здесь и обсуждать нечего. Уже в нескольких судебных актах прозвучал недвусмысленный ответ на этот вопрос:

“институт авторского права не оперирует категорией сходства до степени смешения”.

Постановление Суда по интеллектуальным правам от 14.05.2015 № С01-332/2015 по делу № А19-2243/2014

Но не всё так просто – важно сначала понять, почему категория “сходство до степени смешения” так часто упоминается в делах о защите авторских прав, несмотря на то, что авторское право такой категорией не оперирует. Неужели все сплошь и рядом такие уж непрофессионалы? Думаю, что дело не в этом.

Обращение истцов и судов к категории “сходство до степени смешения”, наоборот, кажется вполне понятным, не случайным и даже естественным. В каких случаях истцам может прийти в голову заявить о сходстве до степени смешения? Очевидно, тогда, когда имеет место использование ответчиком какого-либо товара / произведения, которое не тождественно произведению истца, но при этом сильно на него похоже.

Такие случаи авторским правом квалифицируются не как вопроизведение произведения, а могут квалифицироваться как его переработка (создание производного произведения). При этом в 4-й части ГК РФ вообще не прописаны какие бы то ни было критерии, по которым можно было бы установить факт переработки. Вот суды вместе с истцами и обращаются к уже достаточно хорошо знакомой категории из смежной области правового регулирования – сходство до степени смешения.

Действительно, коль скоро произведения сходны до степени смешения, то можно смело утверждать, что произведение, использованное ответчиком, было создано на основе произведения истца. Иначе откуда бы взяться такому сходству? И ведь этого действительного может быть достаточно, особенно тогда, когда имеет место сходство, скажем, на 95% (изменены несколько незначительных деталей). Зачем устанавливать какие-то ещё обстоятельства для подтверждения факта переработки?

Может, и не нужен тогда весь этот формализм – мол, нет в разделе об авторском праве слов “сходство до степени смешения”, а потому и нельзя применять его ни в коем случае? Если сходства до степени смешения самого по себе недосататочно, так почему бы не использовать его как один из критериев, которые могли бы свидетельствовать о переработке, хотя бы в определённых случаях, например, при крайне высокой степени сходства (те же условные 95%)?

Вот и СИП высказал похожую мысль, правда, не развив её до конца:

“Коллегия судей принимает во внимание, что наличие внешнего сходства между персонажем и используемым ответчиком образом является лишь одним из обстоятельств, учитываемых для установления факта воспроизведения или переработки используемого произведения (его персонажа). Основное значение имеют характерные отличительные признаки, легко узнаваемые всеми: имя, внешний вид и иные символы, позволяющие узнавать героя аудио-визуального произведения, формирующие его образ”.

Постановление Суда по интеллектуальным правам от 14.05.2015 № С01-332/2015 по делу № А19-2243/2014

Или вот это:

“При этом суд кассационной инстанции отмечает, что использование апелляционным судом при установлении обстоятельств использования произведения подходов, применяемых при проведении анализа тождества (сходства) обозначений (средств индивидуализации), не могло, применительно к обстоятельствам настоящего спора, привести к неправильному выводу,

поскольку объектом сравнительного анализа являлись изображения, в отношении которых такой анализ допустим“.

Постановление Суда по интеллектуальным правам от 01.04.2015 № С01-206/2015 по делу № А19-1320/2014

НО. Есть дела, где вся эта логика точно не будет работать. Те дела, где прослеживается принципиальная разница между охраной объектов авторских прав и охраной товарных знаков.

Во-первых, авторское право теоретически допускает так называемое паралелльное творчество, то есть создание разными авторами независимо друг друга похожих произведений. Вполне допустима ситуация, когда сходные до степени смешения произведения будут охраняться независимо, и произведение, созданное позднее, не будет нарушать авторские права на произведение, созданное ранее. Подробнее о параллельном творчестве я писал здесь.

В таких делах нужно было бы выяснять, действительно ли автор более позднего произведения создал его самостоятильным творческим трудом, а не скопировал с более ранего произведения. Тут может много сложностей и аспектов. Очень подброно вопросы копирования чужого произведения разработаны в американской доктрине.

Во-вторых, в некоторых спорах в принципе нельзя ставить вопрос о сходстве до степени смешения. Например, нельзя сравнить таким образом набор слов, описывающих персонажа литературного произведения, и куклу в виде этого же персонажа. Суды должны будут установить, использованы ли в кукле характерные черты персонажа, тем или иным образом описанные в первоначальном литературном произведении.

В-третьих, можно представить ситуацию, когда сходства до степени смешения между произведениями не будет, но при этом будет иметь место нарушение авторских прав. Ярким примером тому может служить недавно описанное мной дело о защите прав на Бэтмобиль. Там Бэтмобили истца и машины-бэтмобили ответчика достаточно сильно различались визуально, но американсие суды сочли, что в бэтмобилях ответчика использован персонаж Бэтмобиль истца.

Глубокой проработки этих аспектов в нашей практике я пока не обнаружил. Думаю, это вопрос времени. Рано или поздно от выявления критериев переработки будет зависеть какой-то очень важный вопрос, и высшие суды их-таки разработают. Мне, по крайней мере, кажется это логичным развитием практики в делах о защите авторских прав.

А пока несколько примеров того, как суды устанавливают факт переработки.

Внешний вид торта “Ягодка. Ассорти” создан на основе уже существующего внешнего вида торта “Малика – классика”, с сохранением в переработке всех основных элементов формы первоначального произведения (внешний вид в виде стилизованного сердца с отделкой боковой поверхности кремом с крошкой, использованием для украшения верхней поверхности методом сплошного заполнения срезов фруктов, расположенных под желе, в сочетании с выступающими из него мелкими круглыми ягодами, применением в отделке верхней поверхности краевого бордюра из крема, выполненного в виде гофрированной полосы), а потому не является творчески самостоятельным произведением.

Постановление Девятого арбитражного апелляционного суда от 08.09.2009 N 09АП-13024/2009 по делу N А40-7200/09-110-86

Суд исходил из неких ключевых внешних признаков, характеризующих первоначальный торт, а не просто говорил о визуальном сходстве. Иными словами суд привёл аргументы, свидетельствующие о том, что торт ответчика был явно скопирован (заимствован) с торта истца, а не создан самостоятельным творческим трудом.

Может быть, в таком направлении практика и будет двигаться.

Вдругих делах суды как бы устранялись от принятия собственного решения и опирались на мнение экспертов.

“Устанавливая факт нарушения ответчиком исключительных прав истца на произведение путем переработки дизайна обручального кольца, суды правомерно приняли в качестве доказательства факта переработки оригинального произведения заключение специалиста N 003406/3/77001/442013/И-1533 от 09.12.2013. Несмотря на то, что указанное заключение по смыслу статьи 86 Арбитражного процессуального кодекса Российской Федерации заключением эксперта не является, оно правомерно принято судами в качестве письменного доказательства, которое содержит мнение специалиста в области искусствоведения. Компетентность специалиста, проводившего исследование, подтверждена копией диплома ВСВ N 0497467.

Ответчик, считая заключение специалиста ненадлежащим доказательством, заявление о его фальсификации в порядке, предусмотренном статьей 161 Арбитражного процессуального кодекса Российской Федерации, не подавал, о назначении судебной экспертизы на предмет установления наличия или отсутствия факта переработки дизайна обручального кольца истца не ходатайствовал”.

Постановление Суда по интеллектуальным правам от 20.11.2014 № С01-1128/2014 по делу N А40-13480/2014

В этом же акте СИП сделал интересную оговорку:

“Доказательств, опровергающих выводы, содержащиеся в заключении специалиста, а также подтверждающих оригинальность дизайна обручального кольца ответчика, последним в материалы дела не представлено”

Стало быть, представь ответчик такие доказательства, например заключение с противположным выводом, то суд бы отказал в иске?

В другом деле суд, опять же опираясь на заключение, установил, что переработки не было:

“Вывод суда апелляционной инстанции о том, что гобеленовые картины является переработкой произведения, поскольку создана иным, отличным от написания картины способом не может быть признан обоснованным, так как согласно заключению специалиста N 01-001\4 от 19.01.2012 г. композиция изображения в раме и произведении “OLD MILL COTTAGE” построена по одинаковой схеме, тождественна, имеет идентичный сюжет. В процессе исследования выявлены отличия от произведения в цветовом строе, однако подобные изменения не является признаками творческого переосмысления. И не влияют на общее художественное решение, и таким образом является полном воспроизведением произведения” “OLD MILL COTTAGE”

Постановление ФАС Московского округа от 03.06.2013 по делу N А40-88686/12-19-686

Не уверен, что судам стоит отдавать вопрос о наличии переработки на откуп специалистам, экспертам. Не думаю, что вопрос о переработке принципильно сложнее вопроса о сходстве до степени смешения. А ведь ещё в 2007 году ВАС РФ сказал, что вопрос о сходстве до степени смешения – вопрос факта и может быть разрешён судом самостоятельно.

Пока что мне ясно одно – судам нужны какие-то аргументы, позволяющие как-то увязать производное произведение с первоначальным, чтобы сделать вывод о переработке. Как именно это делать, решать нужно, видимо, отдельно в каждом конкретном случае.  И сходство до степени смешения сравниваемых произведений, на мой взгляд, должно учитываться судами как одно из обстоятельств, свидетельствующих о переработке.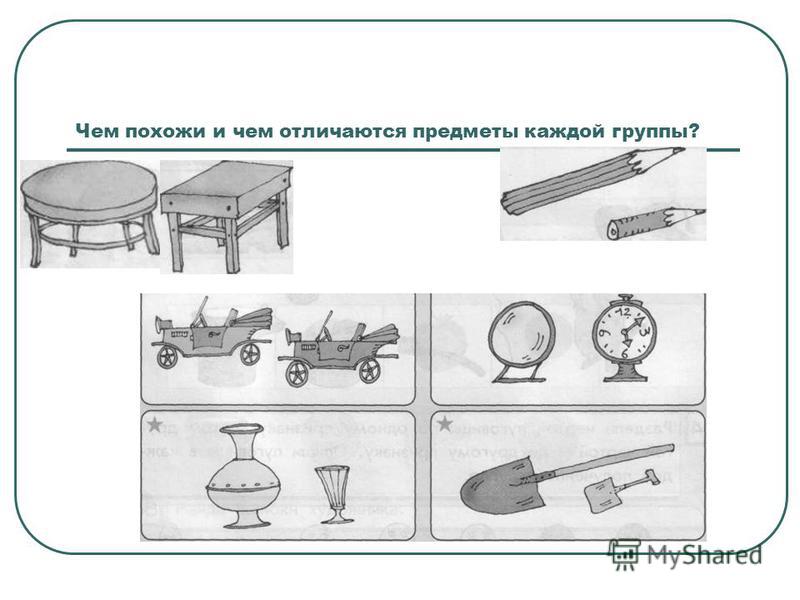

What, Definition, Examples, Techniques & Tips

Сходство/подобие — это жанр, изучаемый в математике, который очень хорошо известен. Это часто изображается как проблема в цифрах. В задачах подобия есть задачи доказательства и задачи вычисления. Поэтому важно, чтобы младшие школьники понимали условия, при которых фигуры подобны. Кроме того, они должны уметь вычислять длины сторон подобных фигур. В этом случае используются пропорциональные выражения.

Что такое сходство?

Когда две или более фигур или объектов кажутся одинаковыми или равными по форме, это называется сходством (похожестью). Сходство – это увеличение или уменьшение объектов. Например, изображение можно увеличить или уменьшить двумя способами. Один способ — растянуть/сжать его пропорционально, а другой — растянуть/сжать по горизонтали или вертикали. Пропорциональное увеличение/уменьшение означает, что если мы хотим увеличить/уменьшить длину на определенный процент, мы также должны увеличить/уменьшить ширину на тот же процент.

Одинаковые фигуры всегда накладываются друг на друга при увеличении или уменьшении. Точнее, одно можно получить из другого путем равномерного масштабирования (увеличения или уменьшения), возможно, с дополнительным переносом, поворотом и отражением. В результате любое изображение можно изменить в размере, переместить и отразить так, чтобы оно идеально совпадало с другим изображением. Подобные объекты конгруэнтны друг другу, если применяется единообразное масштабирование. Например, все круги подобны друг другу, все квадраты подобны друг другу и все равносторонние треугольники подобны друг другу. Точно так же не все эллипсы одинаковы, прямоугольники не все одинаковы, а равнобедренные треугольники не все одинаковы.

Все геометрические фигуры, имеющие одинаковую форму, но разные размеры, называются подобными фигурами. В общем, любые два отрезка всегда будут похожи, но они не обязательно должны быть конгруэнтными. Если их длины равны, то они конгруэнтны.

Математически две фигуры подобны, если их соответствующие углы конгруэнтны (конгруэнтные углы имеют одинаковую меру) и отношения длин их соответствующих сторон равны. Мы называем это общее отношение масштабным коэффициентом. Символ ∼ используется для обозначения подобия.

Какие фигуры похожи?

Евклидова геометрия определяет сходные объекты как те, которые имеют одинаковую форму, или как те, зеркальное отражение которых похоже. Точнее говоря, с помощью равномерного масштабирования (увеличения или уменьшения) и, возможно, поворота, переноса и отражения одно можно получить из другого. Это означает, что любой объект можно масштабировать, позиционировать и отражать так, чтобы он точно пересекался с другим. Подобные объекты конгруэнтны, когда результаты равномерного масштабирования одинаковы.

• Если одна фигура является увеличением другой, то математически они подобны
• Эквивалентные углы в двух фигурах будут равны
• Эквивалентные длины в двух фигурах будут в одинаковом соотношении и связаны масштабным коэффициентом ( которые вам обычно придется вычислять).

Работа с похожими формами

• Определить эквивалентные известные длины
• Установить направление (больше или меньше?)
• Найти масштабный коэффициент = вторая длина ÷ первая длина
• (Проверьте, что SF < 1 становится меньше, а SF > 1 увеличивается)
• Масштабный коэффициент используется для определения длины

Пример

На рисунке ниже пятиугольник ABCDE ~ пятиугольник VWXYZ

3 Двумерные фигуры подобны, если вторая может быть получена из первой посредством поворотов, отражений, переносов и расширений.

На приведенном выше рисунке

• Шестигранник A ₁ B ₁ C ₁ D ₁ E ₁ F ₁ is horizontally flipped to get A ₂ B ₂ C ₂ D ₂ E ₂ F ₂

• Then the hexagon A ₂ B ₂ C ₂ D ₂ E ₂ F ₂   is translated to get A ₃ B ₃ C ₃ D ₃ E ₃ F ₃

• Наконец, шестигранник A ₃ B ₃ C ₃ D ₃ E ₃ F ₃ is dilated by a scale factor of ½ to get A ₄ B ₄ C ₄ D ₄ E ₄ F ₄

Вот. 2 D ₂ E ₂ F ₂ ∼ A ₃ B ₃ C ₃ D ₃ E ₃ F ₃   ∼ A ₄ B ₄ C ₄ D ₄ E ₄ F ₄

That is, all four hexagons похожи. На самом деле, судя по рисунку, первые три конгруэнтны.

Правила подобия

Когда две линейные фигуры подобны, это означает:

• Все соответствующие пары углов равны.
• Все соответствующие стороны пропорциональны.

Подобные многоугольники

В математике подобными называются два многоугольника с одинаковым числом сторон. Это происходит, если:

1. Соответствующие углы равны, и

2. Длины их соответствующих сторон пропорциональны

Если два многоугольника ABCDE и PQRST подобны, их можно записать как ABCDE~PQRST, где символ означает «похож на»

Из приведенного выше определения следует, что:

• Угол при А = Угол при Р
• Угол при B = Угол при Q,
• Угол при C = Угол при R,
• Угол при D = Угол при S,
• Угол при E = Угол при T.

Следовательно, мы можем заключить, что AB/PQ = BC/QR = CD/RS = DE/ST = EA/TP

Когда речь идет о многоугольниках с более чем тремя сторонами, два условия, данные в определении, не являются независимыми от каждого из них. другое, т. е. любое из двух условий без другого недостаточно для того, чтобы многоугольники с более чем тремя сторонами были похожими. Другими словами, два многоугольника не обязательно должны быть похожими, если углы соответствующих сторон обоих многоугольников одинаковы, но их длины не пропорциональны. Тот же аргумент применим, если соответствующие углы двух многоугольников не совпадают, но их стороны пропорциональны.

Можно сказать, что треугольник — это особый тип многоугольника. Если выполняется одно из двух условий, приведенных выше, то в треугольниках автоматически выполняется другое.

Подобные треугольники

Здесь перечислены некоторые свойства подобных треугольников

• Оба имеют одинаковую форму, но размеры могут различаться
• Каждая пара соответствующих углов равна
• Отношение между соответствующими сторонами одинаково

Использование правил треугольника необходимо, когда мы не знаем всех углов и сторон двух треугольников.

Есть несколько способов доказать сходство. Методы аналогичны тем, которые используются для доказательства конгруэнтности: они доказывают, что все соответствующие углы равны, а все соответствующие стороны пропорциональны, без необходимости знать размеры всех шести частей каждого треугольника.

Критерий подобия AA

Треугольник подобен, если его углы равны углам другого треугольника. Согласно критерию сходства треугольников АА, два треугольника подобны, если их углы одинаковы. Следовательно, равнобедренные треугольники имеют подобные углы.

Теоретически этот критерий должен называться критерием AAA (Angle-Angle-Angle), но мы называем его AA, так как два угла должны быть равны, чтобы третья пара также была равна из-за свойства суммы углов треугольников.

Вот пример, в котором ΔKLM и ΔXYZ равноугольны, т.е. only-math.com/images/side-angle-side-congruency.png

Эти треугольники называются подобными на основании критерия AA.

Критерий подобия SSS

Критерий подобия SSS утверждает, что два треугольника подобны, если их три стороны пропорциональны друг другу.

Другими словами, треугольники в таких парах будут одинаковыми (каждая соответствующая пара углов одинакова).

Вот пример, где два треугольника пропорциональны друг другу (ΔKLM и ΔXYZ):

Ссылка: https://www.math-only-math.com/images/side-side-side-congruency.png

KL = XY, LM = YZ и KM = XZ.

Следовательно, ∆KLM ≅ ∆XYZ.

Критерий подобия SAS

Критерий подобия SAS утверждает, что если две стороны одного треугольника пропорциональны двум сторонам другого и если углы между ними равны, то два треугольника подобны.

Большое ударение на слове «включено». Тогда два треугольника не могут быть подобны, если равный угол является не включенным углом.

Рассмотрим следующую цифру:

Ссылка: https://www.math-only-math.com/images/side-angle-side-congruency. png

Здесь в ∆KLM и ∆XYZ,

KL = XY, LM = YZ и ∠L = ∠Y

Следовательно, ∆KLM ≅ ∆XYZ.

Правый критерий подобия

Два треугольника подобны, если отношение гипотенузы к одной стороне прямоугольного треугольника равно отношению гипотенузы к одной стороне другого прямоугольного треугольника.

На рисунке ∠L = ∠Y = 90°, KM = XZ и KL = XY.

Следовательно, ∆KLM ≅ ∆XYZ

В евклидовой геометрии есть несколько элементарных результатов, касающихся подобных треугольников:

• Любые два равносторонних треугольника подобны.
• Два треугольника подобны друг другу (транзитивность подобия треугольников) и оба подобны третьему треугольнику.
• В подобных треугольниках соответствующие высоты имеют то же отношение, что и соответствующие стороны.
• Два прямоугольных треугольника подобны, если их гипотенуза и другая сторона имеют одинаковое отношение длин. В этом случае существует несколько эквивалентных условий, таких как прямоугольные треугольники, имеющие острый угол одинаковой меры или длины сторон, находящиеся в одинаковой пропорции.

Примеры подобия/сходства

Q1: Рассмотрим следующий рисунок:

Найдите значение ∠E.

Решение

Убедитесь, что самая длинная сторона соответствует самой длинной стороне, а самая короткая сторона соответствует самой короткой стороне, и сравните все три соотношения.

Три стороны каждого из двух треугольников пропорциональны:

DE/AB = 4,2/6  = 0,7

DF/AC = 2,8/4 = 0,7

EF/BC = 3,5/5 = 0,7

DE/AB = DF/AC = EF/BC

Таким образом, по критерию подобия SAS ΔABC∼ΔDEF. Это означает, что они также равноугольны.

Внимательно отметьте, что равные углы будут: + 82,820) ⇒ тий = 41,410

ome = Ϫb = 180 – (55,770 + 82,820)

⇒me = 41,410

Следовательно, ad = 8 см

Q2: Рассмотрите два аналогичных TRIANGLE, ΔBC.ABC и ΔBCC и ΔBC. . AP и DQ являются медианами в двух треугольниках соответственно. Покажите, что AP/BC=DQ/EF

Решение

Поскольку два треугольника подобны, они равноугольны.

Это означает, что ∠B=∠E

Кроме того, AB/DE = BC/EF ⇒ AB/DE = (BC/2) / (EF/2) = BP/EQ

Следовательно, по подобию SAS критерий,

ΔABP∼ΔDEQ

Таким образом, стороны этих двух треугольников будут соответственно пропорциональны, и поэтому:

AB/DE = AP/DQ ⇒ AP/DQ = BC/EF ⇒ AP/BC = DQ/EF

Q3: В ΔABC длины сторон даны как AP = 5 см, PB = 10 см и BC = 20 см. Также PQ||BC. Найдите ПК.

Решение

В ΔABC и ΔAPQ ∠PAQ является общим и ∠APQ = ∠ABC (соответствующие углы)

⇒ ΔABC ~ ΔAPQ (критерий АА для подобных треугольников) 5/15 = PQ/20

⇒ PQ = 20/3 см

Q4: Проверьте, подобны ли два треугольника.

Решение

В треугольнике PQR по свойству суммы углов;

∠P + ∠Q + ∠R = 180°

60° + 70° + ∠R = 180°

130° + ∠R = 180°

Вычесть обе стороны на 130°.

∠ R= 50°

Снова в треугольнике XYZ, по свойству суммы углов;

∠X + ∠Y + ∠Z = 180°

∠60° + ∠Y + ∠50°= 180°

∠ 110° + ∠Y = 180°

2° ∠0 0 0 1 Y = 70°

Так как ∠Q = ∠ Y = 70° и ∠Z = ∠ R= 50°

Следовательно, согласно правилу угла-угла (AA), Конгруэнтность?

Пара одинаковых фигур конгруэнтна, если они имеют одинаковый размер и форму.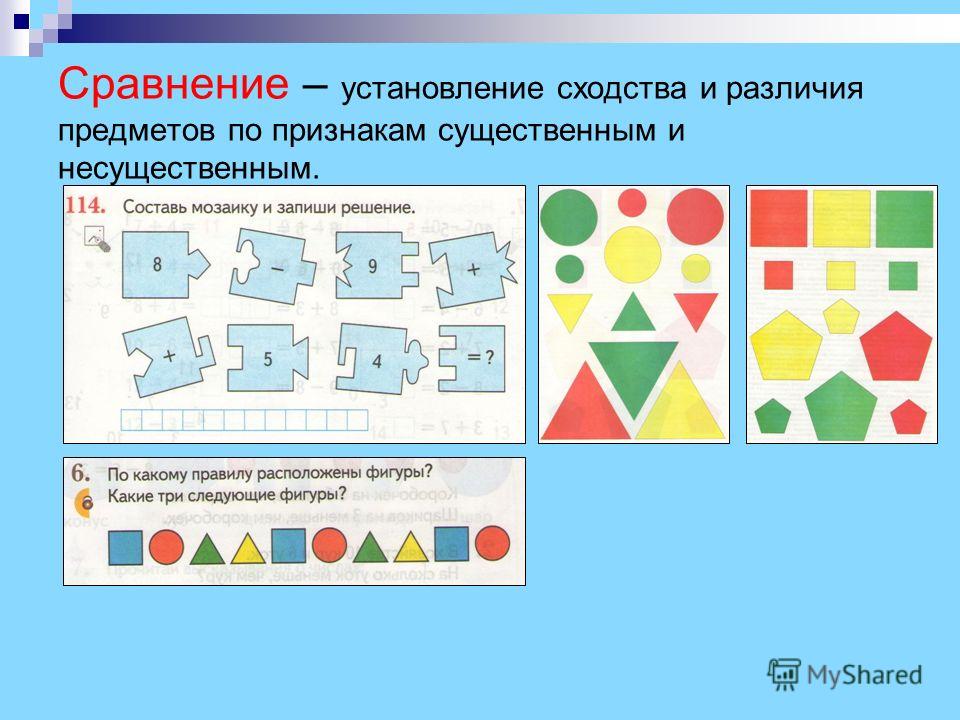 Они подобны, если имеют одинаковую форму, но не одинаковый размер.

Конгруэнтная фигура равна во всех аспектах, что означает, что ее периметр, длина и площадь равны.

Ключевое отличие состоит в том, что все конгруэнтные фигуры подобны, но подобные фигуры не конгруэнтны.

Подобные треугольники и конгруэнтные треугольники

В таблице ниже мы приводим несколько сравнений между подобными треугольниками и конгруэнтными треугольниками

Подобные треугольники

Одинаковая форма и размер Отношение всех соответствующих сторон одинаково.

Отношение соответствующих сторон равно постоянной величине

Подобие как преобразование размера

Как уже упоминалось ранее, если две фигуры имеют одинаковую форму, но различаются по размеру, то они называются подобными. Жесткое движение в сочетании с масштабированием известно как преобразование подобия. Другой взгляд на это заключается в том, что преобразование подобия может изменить местоположение и размер при сохранении формы.

Чертеж в масштабе

Чертеж в масштабе объекта имеет ту же форму, что и объект, но отличается по размеру.

Масштаб чертежа определяется соотношением длины чертежа и реальной вещи.

Существует два способа записи масштаба: отношение размера или отношение числа к длине.

Представьте себе следующие масштабы: 1:400 и 11 сантиметров: 4 метра

Масштаб равен отношению совпадающих длин, а совпадающие углы равны.

Типы преобразования подобия

Существует четыре основных типа преобразования подобия. Они описаны ниже.

• Отражение. Зеркальные изображения можно создавать, переворачивая фигуры через воображаемую линию.
• Вращение — для вращения или поворота фигур используется ось.
• Трансляция – Перемещение фигур по плоскости
• Расширение – Увеличение или уменьшение размеров объекта или формы для увеличения или уменьшения

Отражение

В геометрии флип представляет собой отражение. Зеркальные изображения фигур известны как отражения. Линия отражения представляет собой отражение самого себя. Когда фигура описывается как зеркальное отражение другой фигуры, то каждая точка на первой фигуре равноудалена от соответствующей точки на второй фигуре. Отраженные изображения должны иметь тот же размер и форму, что и оригинал, но должны быть обращены в противоположную сторону.

Вращение

Чтобы определить, идентичны ли треугольники, мы должны расположить их в одинаковой ориентации. Для этого одну фигуру нужно повернуть так, чтобы она совпадала с другой. Вращение является термином для такого преобразования.

Перевод

Увидев многоугольник и его перевод, вы можете подумать, что один и тот же многоугольник показан дважды. Мы перемещаем фигуры, перемещая их по плоскости, в которой они существуют, не меняя их ориентации (мы не вращаем их).

Расширение или изменение размера

Расширение — это преобразование, которое используется для изменения размера объекта. Расширение заставляет предметы казаться больше или меньше. Это преобразование создает то же изображение, что и исходное. Однако есть разница в размерах формы. Расширение можно использовать для расширения или уменьшения исходной формы. Термин «коэффициент масштабирования» определяет это преобразование.

Сходство в многоугольниках

Понятие подобия применимо к многоугольникам с более чем тремя сторонами. Пара подобных многоугольников эквивалентна, если соответствующие стороны взяты в одной и той же последовательности (даже если последовательность против часовой стрелки для одного многоугольника и по часовой стрелке для другого). Тем не менее, одна только пропорциональность соответствующих сторон не доказывает подобия для многоугольников вне треугольников (иначе все ромбические многоугольники были бы подобны). Точно так же равенство всех углов в последовательности не гарантирует подобия (иначе все прямоугольники были бы одинаковыми). Чтобы многоугольники были похожи, их соответствующие стороны и диагонали должны быть пропорциональны.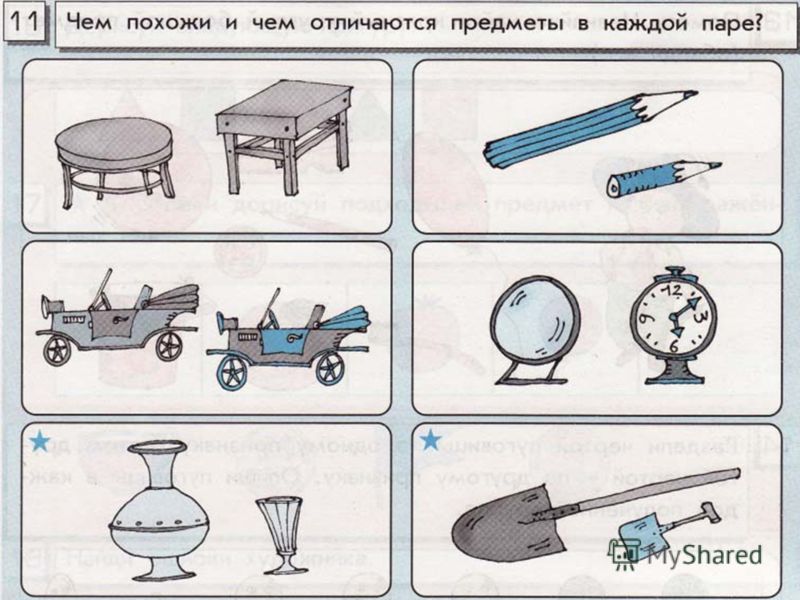

Применение подобия?

Вот несколько примеров того, как можно применять сходство.

• Понятие подобия широко используется в архитектуре.
• Проблемы решаются с помощью высоты и расстояния.
• Использование треугольников для решения математических задач.

Заключение

В заключение несколько замечаний. Отделите общую формулу от частных экземпляров формы. Все круги похожи, но больший круг лучше маленького.

Аналогии помогают нам помнить. Сходство выходит за рамки геометрии — речь идет об идентификации классов предметов с одинаковыми внутренними свойствами.

Реальное определение сходства гораздо более тонкое: можно сказать, что они подобны, если формулы, основанные на их расстоянии, всегда одни и те же (например, они должны быть равномерно масштабированы или расширены).

Ссылка:

1. https://www.math-only-math.com/criteria-for-congruency.html
2. https://byjus.com/maths/similar-triangles/
3. http://www. differencebetween.net/language/difference-between-congruent-and-similarity/
4. https://www.toppr.com/guides/maths/triangles/similarity-of-triangles/

Понимание конгруэнтности и подобия 2D-фигур Рабочие листы по математике для 8-го класса
Рабочие листы по треугольникам (модная тематика)
Определение треугольников, четырехугольников, пятиугольников, шестиугольников и кубов Рабочие листы по математике для 2-го класса

Мы тратим много времени на изучение и сбор информации по этому предмету сайт. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать или указать Helping with Math в качестве источника. Мы ценим вашу поддержку!

Подобные фигуры – подобие треугольников, определение, примеры

Подобные фигуры означают, что две фигуры имеют одинаковую форму, но разные размеры. Другими словами, две фигуры называются подобными, когда они обе имеют много одинаковых свойств, но все же могут не быть идентичными. Например, солнце и луна могут казаться одинакового размера, но на самом деле они разные. Тем не менее, мы похожи, поскольку обе фигуры имеют круглую форму. Это явление рассматривается как свойство сходства с учетом формы и расстояния. Давайте узнаем больше об этом интересном понятии, определив подобные фигуры, их роль в геометрии и решив несколько примеров.

1.	Определение похожих фигур
2.	Применение подобных фигурок
3.	Подобие треугольников
4.	Подобие полигонов
5.	Разница между сходством и соответствием
6.	Часто задаваемые вопросы по подобным фигуркам

Определение похожих фигур

Когда два или более объектов или фигур кажутся одинаковыми или равными из-за их формы, это свойство известно как подобие или похожие фигуры. Когда мы увеличиваем или уменьшаем эти фигуры, они всегда накладываются друг на друга. В геометрии, когда две формы, такие как треугольники, многоугольники, четырехугольники и т. д., имеют одинаковую размерность или общее соотношение, но разные размеры или длину, они считаются похожими фигурами. Например, два круга (любого радиуса) имеют одинаковую форму, но разные размеры, потому что они подобны. Посмотрите на изображение ниже.

Символ для обозначения сходных фигур — это тот же символ конгруэнтности, т. е. «∼», но похожие не означают одинаковые по размеру. Формы также считаются подобными, когда отношения соответствующих сторон эквивалентны, т. Е. При делении каждого набора соответствующих длин сторон полученное число является масштабным коэффициентом. Это число помогает увеличивать или уменьшать фигуры по размеру, но не по форме, делая их похожими на фигуры. Например, прямоугольник имеет длину 5 единиц и ширину 2 единицы. Теперь, если мы увеличим размер этого прямоугольника с коэффициентом масштабирования 2, стороны станут равными 10 единицам и 4 единицам соответственно. Следовательно, мы можем использовать масштабный коэффициент, чтобы получить размеры измененных фигур.

Применение подобных фигурок

Ниже перечислены некоторые приложения с похожими или похожими цифрами.

• Подобие широко используется в архитектуре.
• Решение задач связано с высотой и расстоянием.
• Решение математических задач на треугольники.

Подобие треугольников

Два треугольника будут подобны, если углы равны (соответствующие углы) и стороны находятся в одинаковом соотношении или пропорции (соответствующие стороны). Подобные треугольники могут иметь разные индивидуальные длины сторон треугольников, но их углы должны быть равны, и их соответствующее отношение длин сторон или масштабный коэффициент должны быть одинаковыми. Если два треугольника подобны, значит,

• Все соответствующие пары углов треугольников равны.
• Все соответствующие стороны треугольников пропорциональны.

Поймем сходство треугольников с тремя теоремами по их углам и сторонам.

Критерий подобия AA

Критерий подобия треугольников AA утверждает, что если три угла одного треугольника соответственно равны трем углам другого, то два треугольника будут подобны. Короче говоря, равноугольные треугольники подобны. В идеале имя этого критерия должно быть критерием AAA (угол-угол-угол), но мы называем его критерием AA, потому что нам нужно, чтобы только две пары углов были равными – тогда третья пара автоматически будет равна критерию Свойство суммы углов треугольников.

Рассмотрим следующий рисунок, на котором ΔABC и ΔDEF равноугольны, т. е.

• ∠A = ∠D
• ∠В = ∠Е
• ∠С = ∠Ф

Используя критерий АА, мы можем сказать, что эти треугольники подобны.

Критерий подобия SSS

Критерий подобия SSS утверждает, что если три стороны одного треугольника соответственно пропорциональны трем сторонам другого, то два треугольника подобны. По сути, это означает, что любая такая пара треугольников также будет равноугольной (все соответствующие пары углов равны). Рассмотрим следующий рисунок, на котором стороны двух треугольников ΔABC и ΔDEF соответственно пропорциональны:

То есть дано, что:

\[\frac{{AB}}{{DE}} = \frac{{BC}}{{EF}} = \frac{{AC}}{ {DF}}\]

Критерий подобия SAS

Критерий подобия SAS утверждает, что если две стороны одного треугольника соответственно пропорциональны двум соответствующим сторонам другого и если углы между ними равны, то два треугольника подобны. Обратите внимание на ударение на слове «включено». Если равный угол является невключенным углом, то два треугольника могут быть не подобны. Рассмотрим следующий рисунок:

Дано, что

\[\begin{align}& \frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} \end{align}\]

∠A = ∠D

Критерий SAS говорит нам, что ΔABC ~ ΔDEF

Сходство полигонов

Подобные многоугольники имеют одинаковую форму, но разные размеры. В подобных полигонах должны быть определенные одинаковые соотношения. Другими словами, соответствующие углы равны, но соответствующие стороны пропорциональны. Многоугольники — это двумерные фигуры, состоящие из прямых линий. Говорят, что они имеют замкнутую форму, так как все линии соединены. Есть два важных свойства подобных многоугольников:

• Соответствующие углы равны. (Внутренний и внешний углы одинаковые)
• Соотношение соответствующих сторон одинаково для всех сторон. Следовательно, периметры разные.

Четырехугольники — это многоугольники с четырьмя сторонами. Сумма внутренних углов четырехугольника равна 360 градусов. Два четырехугольника являются подобными четырехугольниками, когда три соответствующих угла одинаковы (четвертые углы автоматически становятся равными, поскольку сумма внутренних углов равна 360 градусам), и две смежные стороны имеют равные отношения.

Разница между сходством и соответствием

Слова сходство и конгруэнтность связаны с формой и размером в геометрии. Конгруэнтность означает одинаковую структуру, размер и форму, тогда как подобные фигуры означают одинаковую форму, но разный размер. Давайте посмотрим на разницу между обоими терминами.

Конгруэнтность	Подобие
Конгруэнтностью или конгруэнтностью называют фигуры одинаковой формы и размера.	Под подобными или подобными фигурами понимаются фигуры одинаковой формы, но разных размеров.
Конгруэнтные фигуры равны по размеру и накладываются друг на друга.	Похожие фигуры идентичны, но не могут накладываться друг на друга.
Конгруэнтность следует из теорем подобия.	Подобие не следует никаким теоремам.
Конгруэнтность может быть выражена как наложение и совпадение.	Сходство может быть выражено цифрами, сходными по своей природе.

Важные примечания

• Если два угла двух треугольников равны, то их третий угол всегда равен. 2}\)

Связанные темы

Ниже перечислены несколько тем, связанных с похожими цифрами, взгляните.

• Геометрия расширения
• Теорема о сходстве треугольников
• ЦПКТС
• Внутренние углы с одной стороны

Часто задаваемые вопросы по подобным фигуркам

Как сходство используется в реальной жизни?

Подобие используется при проектировании, решении задач на высоту и расстояние и т. д.

Что такое правила сходства?

Три правила сходства: сходство SSS, сходство SAS и сходство AA или AAA.

Является ли SSA теоремой подобия?

Нет, SSA не является теоремой подобия.

Что такое заявление о сходстве?

Когда два или более объектов или фигур кажутся одинаковыми или равными из-за их формы, это свойство называется сходством.

Что такое теорема подобия SSS?

Критерий подобия SSS утверждает, что если три стороны одного треугольника соответственно пропорциональны трем сторонам другого, то эти два треугольника подобны.