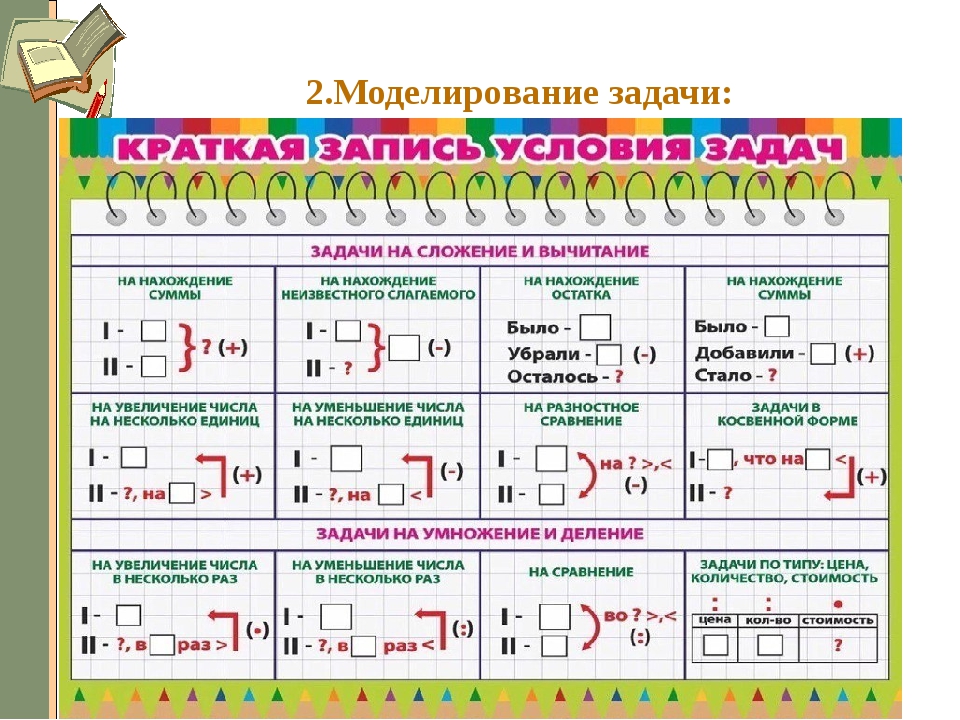
Схемы решения задач по математике 3 класс: Схематический рисунок к задаче 3 класс по математике
схемы к решению задач по математике 2-3 класс | Материал (2 класс) на тему:
Опубликовано 16.11.2015 – 13:50 – Оводова Светлана Борисовна
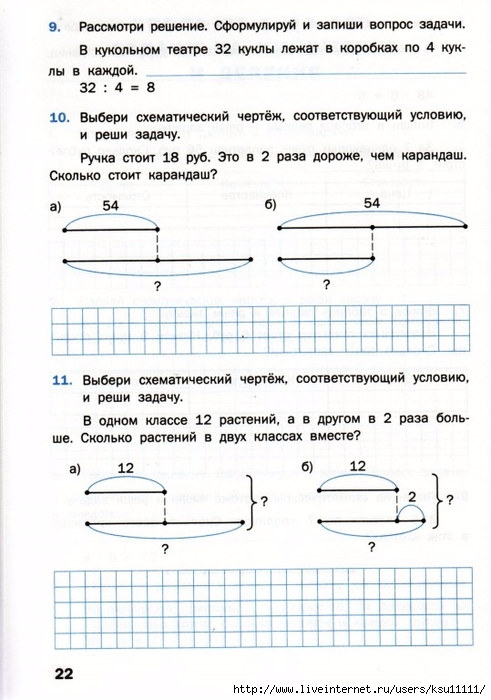
схемы используем для записи при решении задач , на нахождение целого по его частям , частей от целого.
Скачать:
Предварительный просмотр:
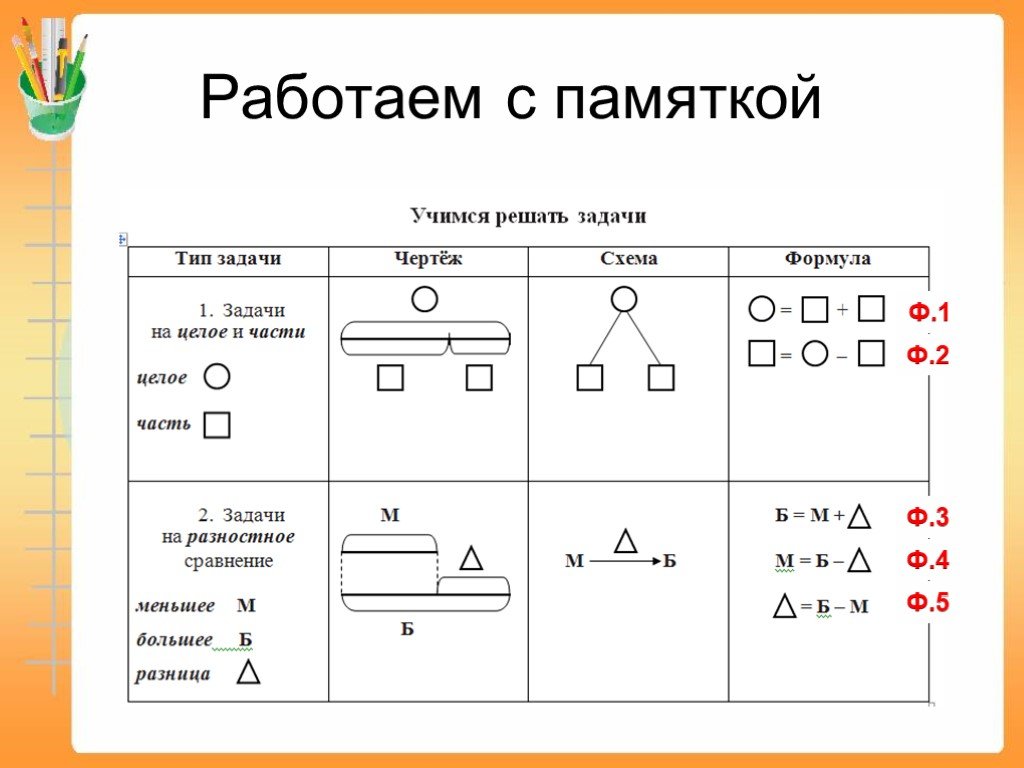
Памятка по решению задач
1.Чтобы найти целое, надо сложить части.
?
б в б + в = А
2.Чтобы найти часть, надо из целого вычесть известную часть.
А
? в А – в = б
3.Чтобы найти большее число, надо к меньшему числу прибавить разницу. ?
Б В + Б = А
В
4. Чтобы найти меньшее число, надо из большего вычесть разницу.
Чтобы найти меньшее число, надо из большего вычесть разницу.
А
Б А – Б = В
?
5. Чтобы найти разницу, надо из большего числа вычесть меньшее число.
А
В
Предварительный просмотр:
1.Глагол – это …, которая обозначает …. и отвечает на вопросы….. |
2.Глаголы в неопределённой форме отвечают на вопросы …. и имеют суффиксы…. |
3.Глаголы имеют форму времени и бывают …. |
4.Глаголы прошедшего времени отвечают на вопросы…. изменяются по …., а …. числе по …. |
5.Глаголы настоящего времени отвечают на вопросы… |
6.Глаголы будущего времени отвечают на вопросы… |
7.Глаголы настоящего и будущего времени изменяются по …. и ….. |
8.Изменение глаголов по лицам и числам называется …. |
9.Глаголы бывают … и …. спряжения |
10.К глаголам II спряжения относятся ….. |
11.К глаголам I спряжения относятся |
12.Глаголы I спряжения во 2 лице и в 3 лице ед.числа пишутся с буквой …., а глаголы II спряжения с буквой … |
13.В 3 лице мн.числа у глаголов I спряжения окончания….., а у глаголов II спряжения …. |
14.В окончаниях глаголов 2 лица ед. числа пишется ….. |
15.Глаголы, оканчивающиеся на –СЯ называются …. |
16.ТЬСЯ пишется с мягким знаком, если это глагол ……, и без мягкого знака если это глагол …лица |
17. Частица НЕ с глаголами пишется … , кроме глаголов которые …. |
1.Глагол – это …, которая обозначает …. и отвечает на вопросы….. |
2.Глаголы в неопределённой форме отвечают на вопросы …. и имеют суффиксы…. |
3.Глаголы имеют форму времени и бывают …. |
4.Глаголы прошедшего времени отвечают на вопросы…. изменяются по …., а …. числе по …. |
5. |
6.Глаголы будущего времени отвечают на вопросы… |
7.Глаголы настоящего и будущего времени изменяются по …. и ….. |
8.Изменение глаголов по лицам и числам называется …. |
9.Глаголы бывают … и …. спряжения |
10.К глаголам II спряжения относятся ….. |
11.К глаголам I спряжения относятся |
12.Глаголы I спряжения во 2 лице и в 3 лице ед.числа пишутся с буквой …., а глаголы II спряжения с буквой … |
13.В 3 лице мн.числа у глаголов I спряжения окончания….., а у глаголов II спряжения …. |
14.В окончаниях глаголов 2 лица ед. числа пишется …. |
15.Глаголы, оканчивающиеся на –СЯ называются …. |
16.ТЬСЯ пишется с мягким знаком, если это глагол ……, и без мягкого знака если это глагол …лица |
17. Частица НЕ с глаголами пишется … , кроме глаголов которые …. |
По теме: методические разработки, презентации и конспекты
Презентация и конспект урока математики по теме “Решение задач с избыточными данными”, 3 класс, ПНШ
Материал содержит разработку урока математики “Решение задач с избыточными данными” по учебнику Чекина 3 класс, презентацию к уроку для интерактивной доски….
Конспект урока по математике на тему “Решение задач на разностное сравнение.”, 1 класс.
Дети осваивают новый способ решения задач….
“Связь вычитания со сложением. Подготовка к решению задач” – урок математики в 1 классе
Урок по теме “Связь вычитания со сложением. Подготовка к решению задач” преследует следующие цели:: дать понятие связи между конкретными операциями, используя демонстрацию шкалы линейки; формиро…
Подготовка к решению задач” преследует следующие цели:: дать понятие связи между конкретными операциями, используя демонстрацию шкалы линейки; формиро…
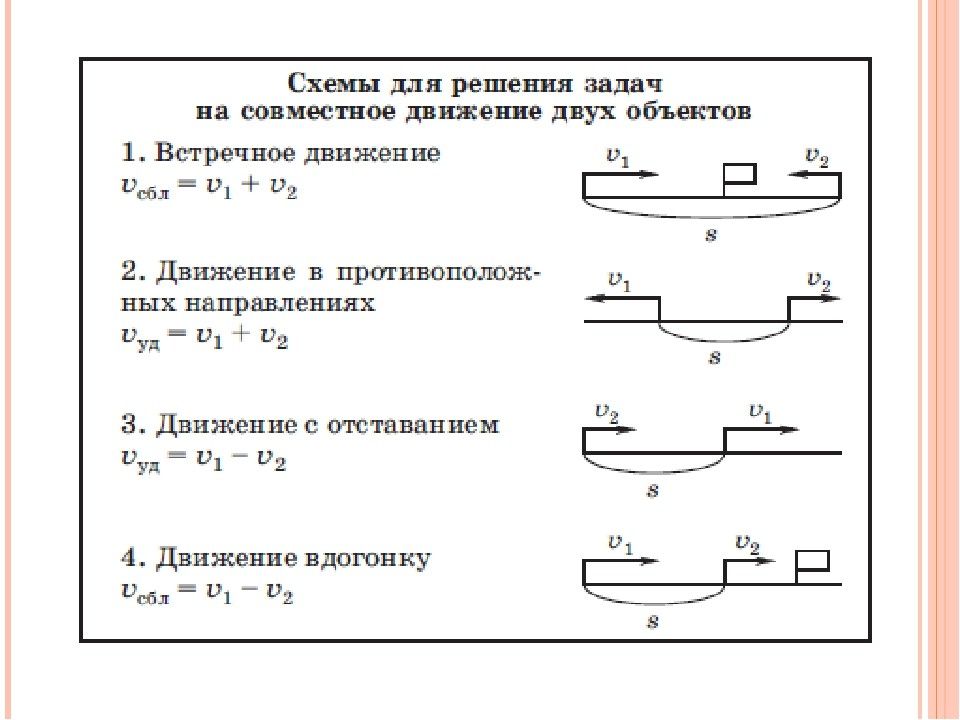
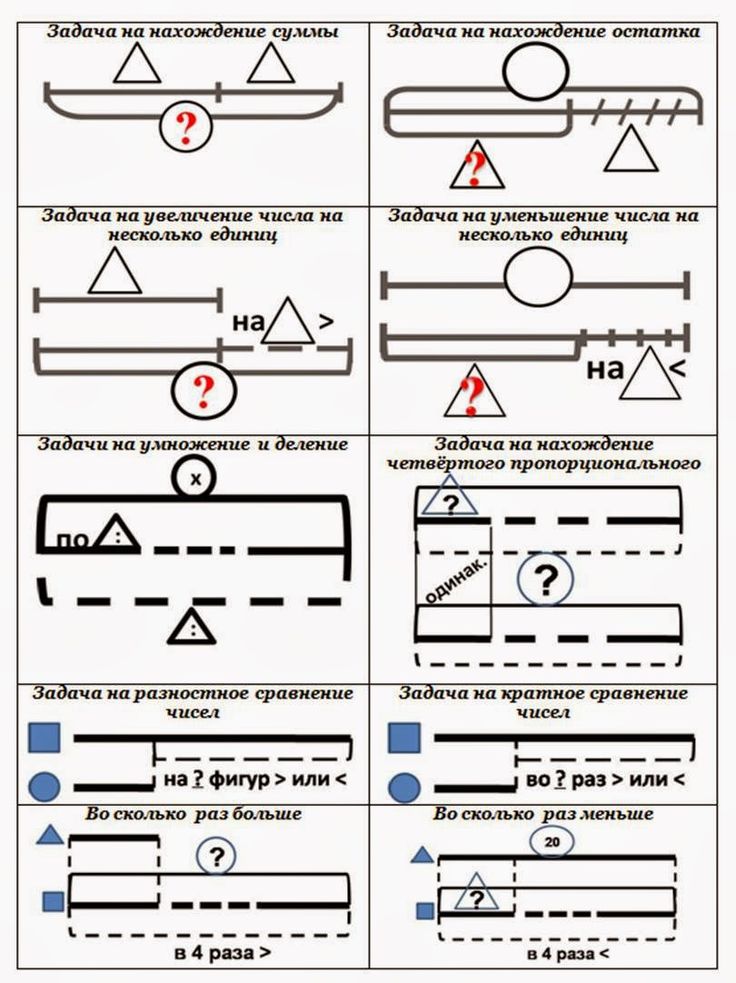
Методическая разработка: схема анализа и решения задач по математике
Данная схема помогает учащимся при анализе и выборе решения задач, при составлении опорных сигналов….
Опорные схемы для решения задач (3 класс)
Схемы помогут ученикам выполнить краткую запись задач….
Готовые схемы для решения задач
. Человек в течении своей жизни сталкивается с задачами различной степени сложности. Умение решать разнообразные задачи, в том числе текстовые, является одним из важнейших умений. В…
Опорные схемы для решения задач
Все виды опорных схем для решения задач по математике в начальной школе….
Поделиться:
Математика 3 класс. Школьная программа. Учитель Ульянова Надежда Николаевна – Урок №2.
 Письменные приемы сложения и вычитания. Задачи в два действияКомментарии преподавателяНа данном уроке рассмотрены отличия простой задачи от составной. Также более подробно разобраны способы решения задач в два действия. В качестве повторения объяснены письменные приемы сложения и вычитания двузначных чисел.
Письменные приемы сложения и вычитания. Задачи в два действияКомментарии преподавателяНа данном уроке рассмотрены отличия простой задачи от составной. Также более подробно разобраны способы решения задач в два действия. В качестве повторения объяснены письменные приемы сложения и вычитания двузначных чисел.Источник : http://interneturok.ru/ru/school/matematika/3-klass/undefined/pismennye-priemy-slozheniya-i-vychitan…
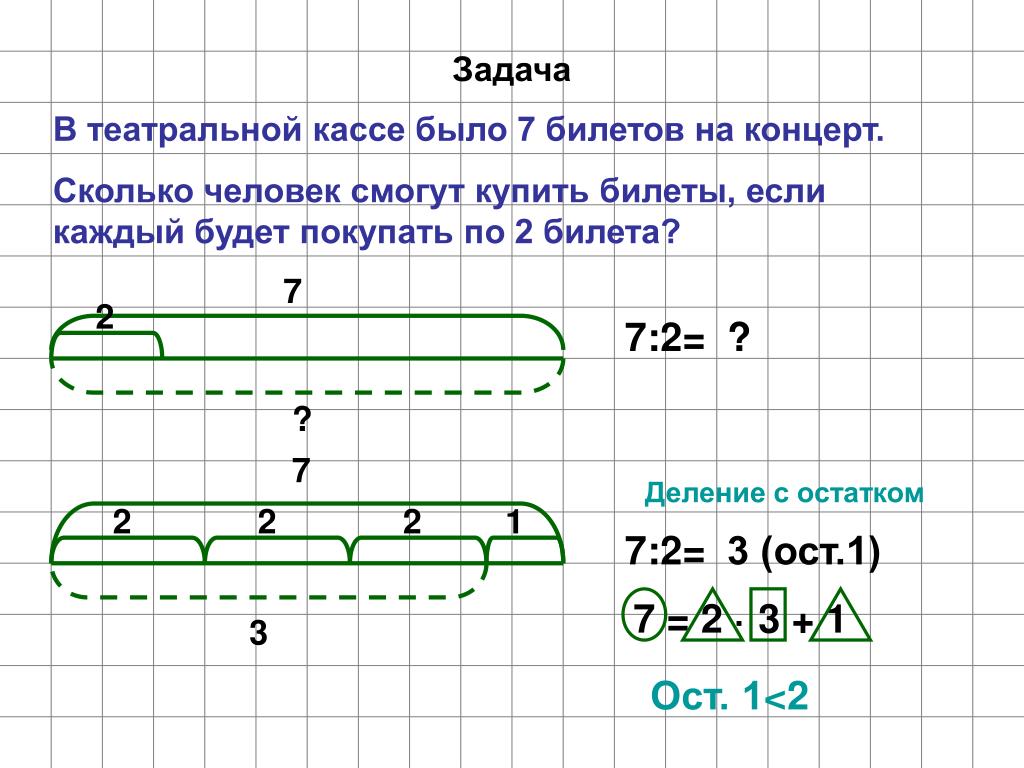
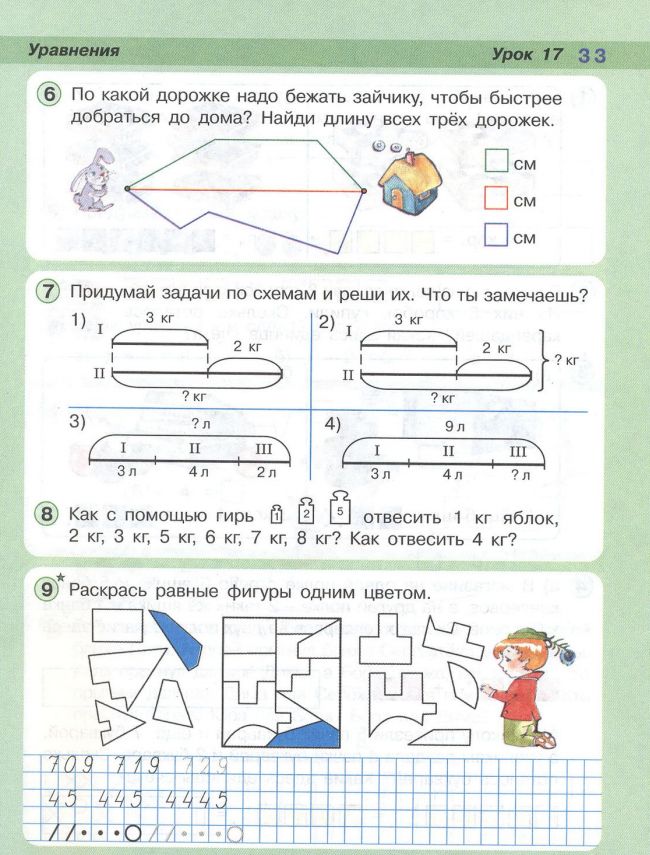
Выполним первое задание (рис. 1).
Рис. 1. Задача
Прочитаем условие задачи. Рассмотрим предложенные схемы.
Как правильно выбрать схему задачи к первому вопросу?
Прочитаем условие задачи: длина кита от хвоста до головы – 16 м, а длина головы – на 12 м меньше. Чтобы ответить на первый вопрос задачи и узнать, какова длина головы кита, выберем схему. Рассуждаем так: больший отрезок на каждой схеме соответствует длине кита от хвоста до головы – 16 м. Меньший отрезок обозначает длину головы. По условию задачи она на 12 м меньше. Это обозначено на схеме 1 и схеме 3. Схема 2 и схема 4 не подходят для решения задачи. Значит, нам подходит схема 1, так как вопрос обозначен под коротким отрезком.
По условию задачи она на 12 м меньше. Это обозначено на схеме 1 и схеме 3. Схема 2 и схема 4 не подходят для решения задачи. Значит, нам подходит схема 1, так как вопрос обозначен под коротким отрезком.
Как правильно выбрать решение задачи при ответе на первый вопрос?
Рассуждаем так: мы знаем, что длина головы на 12 м меньше, значит нужно из большего числа вычесть меньшее. Из 16 вычтем 12. Решение № 1 подходит для ответа на первый вопрос.
Правильный ответ: 16-12=4. Длина головы кита – 4 м.
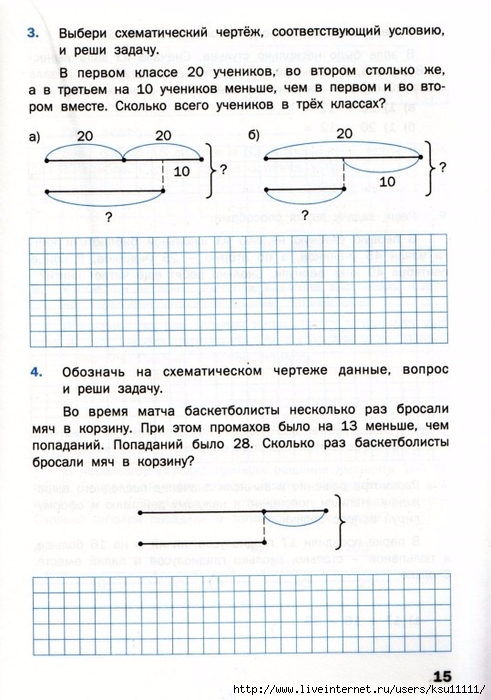
Как правильно выбрать схему и решение задачи ко второму вопросу?
Чтобы ответить на второй вопрос задачи и узнать, какова общая длина кита, выберем схему. Рассуждаем так: для того чтобы узнать общую длину кита, необходимо выполнить два действия, так как сначала нужно узнать длину головы кита. Условию и вопросу задачи соответствует схема 3. Теперь выберем решение. В решении № 2 сначала предлагается узнать длину головы кита: 16-12, а затем прибавить длину кита от хвоста до головы: 16+(16-12).
Правильный ответ: 16+(16-12)=16+4=20. Общая длина кита – 20 м.
Как правильно выбрать схему и решение задачи к третьему вопросу?
Прочитаем третий вопрос: на сколько метров длиннее тело кита, чем голова? Выясним, что этот вопрос не соответствует условию задачи, так как уже из условия известно, что голова кита на 12 м меньше, чем длина туловища кита.
Сделаем вывод.
Если на схеме или краткой записи два вопроса, это составная задача, ее необходимо решать в несколько действий.
Вспомним приемы письменных вычислений сложения и вычитания.
Найдем значения данных выражений
43+12 35-21
57+23 95-65
24+67 83-26
Применим способ вычисления в столбик.
43+12
Запишем второе слагаемое под первым, начнем складывать с разряда единиц. К 3 прибавить 2 получим 5. Запишем под единицами. Затем складываем десятки. К 4 прибавить 1 получится 5. Записываем под десятками. Ответ: 55.
57+23
Записываем второе слагаемое под первым: единицы – под единицами, десятки – под десятками. Начинаем складывать с единиц. К 7 прибавить 3 получится 10. 10 – это один десяток. Цифру 0 пишем под единицами, а один десяток запоминаем. Складываем десятки. К 5 прибавить 2 получится 7 десятков, и еще прибавить один, который мы запомнили, получится 8 десятков. Записываем под десятками. Ответ: 80.
Начинаем складывать с единиц. К 7 прибавить 3 получится 10. 10 – это один десяток. Цифру 0 пишем под единицами, а один десяток запоминаем. Складываем десятки. К 5 прибавить 2 получится 7 десятков, и еще прибавить один, который мы запомнили, получится 8 десятков. Записываем под десятками. Ответ: 80.
24+67
Записываем второе слагаемое под первым: единицы – под единицами, десятки – под десятками. Начинаем складывать с единиц. К 4 прибавить 7 получится 11. 11 – это один десяток и одна единица. Одну единицу пишем под единицами, а один десяток запоминаем. Складываем десятки. К 2 прибавить 6 получится 8 десятков, да еще прибавить один, который мы запомнили, получится 9 десятков. Записываем под десятками. Ответ: 91.
35-21
Записываем пример в столбик: единицы пишем под единицами, десятки – под десятками. Вычитаем с разряда единиц. Из 5 вычитаем 1, получаем 4. Пишем в разряде единиц. Из 3 десятков вычитаем 2 десятка, получаем 1 десяток. Записываем под десятками. Ответ: 14.
95-65
Записываем пример в столбик: единицы пишем под единицами, десятки – под десятками. Вычитаем с разряда единиц. Из 5 вычитаем 5, получаем 0. Пишем в разряде единиц. Из 9 десятков вычитаем 6 десятков, получаем 3 десятка. Записываем под десятками. Ответ: 30.
83-26
Записываем пример в столбик: единицы пишем под единицами, десятки – под десятками. Вычитаем с разряда единиц. Из 3 вычесть 6 нельзя. Занимаем из разряда десятков один десяток и ставим точку. Один десяток и три единицы – это 13. Из 13 вычесть 6, получится 7. Пишем под единицами. У нас осталось 7 десятков. Из 7 вычесть 2 получится 5 десятков. Записываем под десятками. Ответ: 57.
Выполним следующее задание.
Выпишем уравнения, которые решаются вычитанием, и решим их.
х – 24 = 46
72 – х = 40
с + 35 = 60
с – 35 = 60
Рассуждаем так: в первом уравнении х-24=46 неизвестно уменьшаемое. Чтобы найти уменьшаемое, нужно к значению разности прибавить вычитаемое. Значит, данное уравнение нм не подходит.
Во втором уравнении 72-х=40 неизвестно вычитаемое. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть значение разности. Значит, это уравнение решается вычитанием.
Решим его.
72 – х = 40
х = 72 – 40 = 70 + 2 – 40 = 30 + 2 = 32
х = 32
Во третьем уравнении с + 35 = 60 неизвестно слагаемое. Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое. Значит, это уравнение решается вычитанием.
Решим его.
с + 35 = 60
Выполним вычитание в столбик. Запишем единицы под единицами, десятки под десятками. Вычитаем с разряда единиц. От 0 5 нельзя отнять. Занимаем один десяток и ставим точку. Из 10 вычесть 5 получится 5. Записываем под единицами. Вычитаем десятки. Осталось 5 десятков. Из 5 вычесть 3 получится 2. Ответ: 25.
В последнем уравнении с – 35 = 60 неизвестно уменьшаемое. Чтобы найти уменьшаемое, нужно к значению разности прибавить вычитаемое. Данное уравнение решается сложением и нам не подходит.
Потренируемся в нахождении значений выражений.
Выберем выражение, в котором сложение будет первым действием, и найдем значение этого выражения, выполняя вычисления столбиком.
70 – 56 + 16
86 – (28 + 14)
Рассуждаем так: в первом выражении, соблюдая порядок выполнения действий, необходимо выполнить сначала вычитание, потом сложение. Во втором выражении сначала выполняем действие в скобках, сложение, а затем из 86 вычтем полученный результат. Складываем числа в столбик. Записываем единицы под единицами, десятки под десятками. Вычисляем, складываем единицы: 8+4=12, 2 единицы записываем под единицами, 1 десяток запоминаем. Складываем десятки: 2+1=3, и еще один десяток получится 4 десятка, получаем 42. Теперь из 86 вычтем 42. Запишем пример в столбик: единицы под единицами, десятки под десятками. Выполним вычитание: из 6 единиц вычтем 2 единицы, получим 4 единицы, из 8 десятков вычтем 4 десятка, получим 4 десятка, ответ: 44.
Сегодня на уроке мы повторили отличия простой и составной задачи, вспомнили, как складывать и вычитать двузначные числа столбиком.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Nsportal.ru (Источник).
- Prosv.ru (Источник).
- Do.gendocs.ru (Источник).
Нет дополнительных материалов для этого занятия.
Элементарная математическая задача Ключевые слова и их ограничения — классная комната без помех
Когда вы говорите своим ученикам, что будете работать над задачами, вы слышите хор стонов? Если так, то ты не одинок! Обучение учащихся тому, как решать математические задачи со словами, как правило, не является самым захватывающим математическим упражнением в начальной математической программе (особенно если не изучать ключевые слова задач со словами и то, как их можно использовать для решения задач). Они также, как правило, очень сложны для студентов. Неудивительно, что многие студенты не любят их!
Однако для того, чтобы учащиеся овладели математикой, им необходимо применить свои математические знания в реальных жизненных ситуациях, чего можно достичь с помощью текстовых задач. Этот опыт не должен заключаться в следовании механическим процедурам и вычислению правильных ответов. При решении задач такого типа важно, чтобы учащиеся применяли несколько стратегий, чтобы разобраться в проблеме и решить ее. Этот опыт должен основываться на применении стратегии и решении проблем, а не просто на вычислениях.
Этот опыт должен основываться на применении стратегии и решении проблем, а не просто на вычислениях.
Выявление ключевых слов словесных задач — одна из многих стратегий, которые учащиеся начальной школы могут использовать для решения одноэтапных и многоэтапных текстовых задач. Кроме того, учащимся необходим доступ к якорным диаграммам, инструментам и манипуляторам, которые снабдят их ресурсами, необходимыми для решения этих проблем. Использование ключевых слов для задач по математике — это только одна часть головоломки!
Этот пост в блоге ответит на следующие вопросы:
- Что такое ключевые слова для задач со словами?
- Какие есть примеры ключевых слов для задач на сложение слов?
- Можете ли вы поделиться некоторыми примерами ключевых слов для задач на вычитание?
- Какие есть примеры ключевых слов для задач на умножение?
- Можете ли вы поделиться некоторыми примерами ключевых слов для задач на деление слов?
- Каковы ограничения использования ключевых слов для решения текстовых задач?
- Является ли использование ключевых слов для решения задач эффективной стратегией?
Что такое ключевые слова задач Word?
Ключевые слова словесной задачи — это слова или фразы, указывающие, какие операции (сложение, вычитание, умножение или деление) необходимы для решения математической текстовой задачи.
Использование ключевых слов для решения математических задач (часто называемых словами-подсказками и фразами) — это стратегия, позволяющая разобраться в задачах и решить их. Идея состоит в том, чтобы научить мозг искать определенные слова и фразы, чтобы определить, какие математические операции необходимы. Вот пример этой стратегии на практике:
Эрин читает задачу: У Пэт 3 красные рубашки. У него 2 синие рубашки. Сколько всего у него красных и синих рубашек? Прочитав задачу один раз, Эрин перечитывает задачу, но на этот раз она ищет ключевые слова и фразы, которые она выучила. Она выделяет или подчеркивает фразу «во всем». В классе она узнала, что «во всем» сигнализирует читателю, что им нужно добавить. Эта стратегия помогла ей разобраться в задаче (что в данном случае означает необходимость операции сложения), составить уравнение (3 + 2 = ?) и найти ответ (5 рубашек).
Общие математические задачи Ключевые слова и фразы
Ниже приведен список ключевых слов и фраз, которые учащиеся могут использовать для решения задач на сложение, вычитание, умножение и деление. Если вы учите младшие классы, вам будет полезен список ключевых слов сложения и вычитания. Если вы учите старшие классы, вам пригодятся эти слова, а также ключевые слова умножения и деления.
Если вы учите младшие классы, вам будет полезен список ключевых слов сложения и вычитания. Если вы учите старшие классы, вам пригодятся эти слова, а также ключевые слова умножения и деления.
Дополнительные ключевые слова
Вот несколько примеров addition key words :
- add
- altogether
- both
- combine
- in all
- increase
- increased by
- larger
- larger than
- longer
- longer than
- more
- more than
- периметр
- плюс
- сумма
- вместе
- всего
ключевые слова вычитания
Вот несколько примеров ключевых слов вычитания :
- изменить
- уменьшить
- разницу
- меньше
- отдать
- Сколько еще…?
- На сколько меньше…?
- Слева
- Осталось более
- Меньше
- Менее
- Минус
- Осталось
- Шортер, чем
- Меньше, чем
- , выберите
Ключевые слова
9001 9001 2Ключевые слова
9001 9002СЛЕДУЕТСЯ КЛЮЧЕСКИЕ СЛОВА
9001СЛЕДУЮЩИЕ СЛОВА.
 :
:- Область
- Cubed
- Double
- Каждая
- Группы
- на
- Продукт
- . деление ключевые слова :
- среднее
- разделить
- каждый
- равная группа
- четвертый
- половина
- четверть
- частное
- отношение
- доля
- отдельно
- разделить
- треть
, непосредственное обучение и практика с ключевыми словами (также иногда записываются как ключевые слова для задач со словами или ключевые слова для задач по математике). Однако учащиеся должны понимать, что проблемы можно решать разными способами. Это всего лишь один из инструментов в их арсенале. Это не всегда самая эффективная стратегия для решения данной проблемы со словами. Например, учащихся не следует приучать всегда вычитать, когда они видят слово меньше, потому что они могут использовать отсутствующее сложение в сложении для решения.
 Эту стратегию следует использовать вместе с другими стратегиями (например, визуализацией). По мере того как учащиеся продвигаются по математическому образованию и сталкиваются с более сложными текстовыми задачами, эта стратегия становится менее эффективной. В результате ваши ученики должны быть оснащены множеством разнообразных стратегий.
Эту стратегию следует использовать вместе с другими стратегиями (например, визуализацией). По мере того как учащиеся продвигаются по математическому образованию и сталкиваются с более сложными текстовыми задачами, эта стратегия становится менее эффективной. В результате ваши ученики должны быть оснащены множеством разнообразных стратегий.Математические ресурсы для учителей 1-5 классов
Если вам нужны печатные и цифровые математические ресурсы для вашего класса, ознакомьтесь с моими математическими коллекциями, которые помогут вам сэкономить время и деньги!
Бесплатные ресурсы по элементарной математике
Мы будем рады, если вы попробуете эти ресурсы для решения текстовых задач со своими учениками. Он предлагает им возможность попрактиковаться в применении стратегий ключевых слов для текстовых задач, а также других стратегий решения проблем. Вы можете загрузить рабочие листы с текстовыми задачами для своего уровня (наряду с множеством других бесплатных материалов по математике) в нашем наборе бесплатных математических ресурсов для печати по этой ссылке: бесплатные математические задания для учителей начальных классов.
Посмотрите мои ежемесячные ресурсы по решению текстовых задач!
- 1-й класс. Проблемы с словом
- 2-й класс. Проблемы с слов
- 3-й класс. Проблемы слов
- 4-й класс. Hervey, Generation Ready
К тому времени, когда маленькие дети поступают в школу, они уже находятся на пути к тому, чтобы стать способными решать проблемы. С самого рождения дети учатся учиться: они реагируют на свое окружение и реакцию окружающих. Это осмысление опыта является непрерывным, рекурсивным процессом. Мы давно знаем, что чтение — это сложная деятельность по решению проблем. Совсем недавно учителя пришли к пониманию того, что повышение математической грамотности — это также сложная деятельность по решению проблем, которая становится более мощной и гибкой, если практиковаться чаще. Проблема в математике — это любая ситуация, которая должна быть решена с помощью математических инструментов, но для которой нет очевидной стратегии. Если путь вперед очевиден, это не проблема — это простое приложение.
Математики всегда понимали, что решение задач занимает центральное место в их дисциплине, потому что без задачи нет математики. Решение проблем играет центральную роль в мышлении педагогов-теоретиков с момента публикации книги Полиа «Как это решить» в 1945 году. Национальный совет учителей математики (NCTM) последовательно выступает за решение проблем для почти 40 лет, в то время как международные тенденции в преподавании математики показали повышенное внимание к решению задач и математическому моделированию, начиная с начала 19 века.90-е. По мере того, как педагоги во всем мире все больше осознавали, что предоставление опыта решения задач имеет решающее значение для того, чтобы учащиеся могли осмысленно использовать и применять математические знания (Wu and Zhang, 2006), мало что изменилось на школьном уровне в Соединенных Штатах.
«Решение задач — это не только цель изучения математики, но и основное средство для этого».
(NCTM, 2000, стр. 52)
В 2011 году Стандарты Common Core State включили Стандарты процессов NCTM по решению задач, рассуждению и доказательству, общению, представлению и связям в Стандарты математической практики.
 Для многих учителей математики это был первый раз, когда они должны были объединить сотрудничество учащихся и обсуждение с решением проблем. Эта практика требует обучения совершенно по-другому, поскольку школы перешли от ориентированного на учителя к более диалогическому подходу к преподаванию и обучению. Задача учителей состоит в том, чтобы научить учащихся не только решать задачи, но и изучать математику посредством решения задач. Хотя многие учащиеся могут развить беглость процедур, им часто не хватает глубокого концептуального понимания, необходимого для решения новых задач или установления связей между математическими идеями.
Для многих учителей математики это был первый раз, когда они должны были объединить сотрудничество учащихся и обсуждение с решением проблем. Эта практика требует обучения совершенно по-другому, поскольку школы перешли от ориентированного на учителя к более диалогическому подходу к преподаванию и обучению. Задача учителей состоит в том, чтобы научить учащихся не только решать задачи, но и изучать математику посредством решения задач. Хотя многие учащиеся могут развить беглость процедур, им часто не хватает глубокого концептуального понимания, необходимого для решения новых задач или установления связей между математическими идеями.«Однако учебная программа по решению задач требует от учителя другой роли. Вместо того, чтобы руководить уроком, учитель должен предоставить ученикам время для решения проблем, самостоятельного поиска стратегий и решений и научиться оценивать свои собственные результаты. Несмотря на то, что учитель должен присутствовать очень активно, главное внимание в классе должно быть сосредоточено на мыслительных процессах учащихся».
(Burns, 2000, стр. 29)
Обучение решению проблем
Чтобы понять, как учащиеся становятся способными решать задачи, нам нужно взглянуть на теории, лежащие в основе обучения математике. К ним относятся признание аспектов обучения, связанных с развитием, и тот важный факт, что учащиеся активно участвуют в изучении математики посредством «действий, разговоров, размышлений, обсуждений, наблюдений, исследований, слушания и рассуждений» (Copley, 2000, стр. 29). . Концепция совместного конструирования обучения является основой теории. Более того, мы знаем, что каждый студент находится на своем уникальном пути развития.
Убеждения, лежащие в основе эффективного преподавания математики
- Самобытность, язык и культура каждого учащегося должны уважаться и цениться.
- Каждый учащийся имеет право на доступ к эффективному математическому образованию.
- Каждый ученик может стать успешным учеником по математике.
Дети приходят в школу с интуитивным пониманием математики.
 Учителю необходимо установить связь и опираться на это понимание через опыт, который позволяет учащимся изучать математику и делиться своими идеями в содержательном диалоге с учителем и своими сверстниками.
Учителю необходимо установить связь и опираться на это понимание через опыт, который позволяет учащимся изучать математику и делиться своими идеями в содержательном диалоге с учителем и своими сверстниками.Обучение происходит в социальных условиях (Выготский, 1978). Учащиеся строят понимание посредством участия в решении проблем и взаимодействия с другими в этих действиях. Благодаря этим социальным взаимодействиям учащиеся чувствуют, что они могут рисковать, пробовать новые стратегии, а также давать и получать обратную связь. Они учатся совместно, когда делятся разными точками зрения или обсуждают способы решения проблемы. Именно через разговоры о проблемах и обсуждение своих идей дети строят знания и осваивают язык, чтобы осмысливать опыт.
Учащиеся приобретают понимание математики и развивают навыки решения задач в результате решения задач, а не непосредственного обучения (Hiebert1997). Роль учителя состоит в том, чтобы создавать проблемы и представлять ситуации, которые обеспечивают форум, на котором может происходить решение проблем.

Почему важно решать проблемы?
Наши учащиеся живут в обществе, основанном на информации и технологиях, где им необходимо уметь критически мыслить о сложных вопросах, а также «анализировать и логически мыслить о новых ситуациях, разрабатывать неопределенные процедуры решения и ясно и убедительно сообщать свое решение другим». (Баруди, 1998). Математическое образование важно не только из-за «роли контролера, которую математика играет в доступе учащихся к образовательным и экономическим возможностям», но и потому, что процессы решения задач и приобретение стратегий решения задач готовят учащихся к жизни после школы (Кобб). и Ходж, 2002).Важность решения задач при изучении математики исходит из убеждения, что математика в первую очередь связана с рассуждениями, а не с запоминанием. Решение проблем позволяет учащимся развивать понимание и объяснять процессы, используемые для достижения решений, а не запоминать и применять набор процедур. Именно благодаря решению задач учащиеся развивают более глубокое понимание математических концепций, становятся более вовлеченными и ценят актуальность и полезность математики (Wu and Zhang, 2006).

- Способность мыслить творчески, критически и логически
- Способность структурировать и организовывать
- Способность обрабатывать информацию
- Удовольствие от интеллектуальной задачи
- Навыки решения проблем, которые помогают им исследовать и понимать мир
Решение задач должно лежать в основе всех аспектов преподавания математики, чтобы учащиеся могли ощутить силу математики в окружающем их мире. Этот метод позволяет учащимся рассматривать решение задач как средство построения, оценки и уточнения своих математических теорий и теорий других.
«Проблемные» проблемы
Требования учителя к ученикам очень важны. Учащиеся учатся справляться со сложными проблемами, только столкнувшись с ними. Учащиеся должны иметь возможность работать над сложными задачами, а не над серией простых задач, вытекающих из сложной задачи. Это важно для стимулирования математических рассуждений учащихся и создания прочных математических знаний (Энтони и Уолшоу, 2007).
 Задача учителей заключается в обеспечении того, чтобы задачи, которые они ставят, были разработаны для поддержки обучения математике и были подходящими и сложными для всех учащихся. Задачи должны быть достаточно сложными, чтобы вызвать затруднения , но не настолько сложными, чтобы учащиеся не смогли добиться успеха. Учителя, которые понимают это правильно, создают устойчивых решателей проблем, которые знают, что при настойчивости они могут добиться успеха. Задачи должны находиться в «зоне ближайшего развития» учащихся (Выготский 19).68). Эти типы сложных проблем предоставят возможности для обсуждения и обучения.
Задача учителей заключается в обеспечении того, чтобы задачи, которые они ставят, были разработаны для поддержки обучения математике и были подходящими и сложными для всех учащихся. Задачи должны быть достаточно сложными, чтобы вызвать затруднения , но не настолько сложными, чтобы учащиеся не смогли добиться успеха. Учителя, которые понимают это правильно, создают устойчивых решателей проблем, которые знают, что при настойчивости они могут добиться успеха. Задачи должны находиться в «зоне ближайшего развития» учащихся (Выготский 19).68). Эти типы сложных проблем предоставят возможности для обсуждения и обучения.Учащиеся будут иметь возможность объяснить свои идеи, ответить на идеи других и бросить вызов своему мышлению. Те ученики, которые думают, что математика — это все о «правильном» ответе, нуждаются в поддержке и поощрении, чтобы пойти на риск. Терпимость к трудностям необходима для решения проблем, потому что «застревание» — это неизбежный этап решения практически любой проблемы.
 Выход из тупика обычно требует времени и включает в себя использование различных подходов. Студенты должны научиться этому на опыте. Эффективных задач:
Выход из тупика обычно требует времени и включает в себя использование различных подходов. Студенты должны научиться этому на опыте. Эффективных задач:- Доступны и расширяемы
- Разрешить отдельным лицам принимать решения
- Способствовать обсуждению и общению
- Поощряйте оригинальность и изобретательность
- Поощряйте «а что, если?» и «а что, если нет?» вопросы
- Содержит элемент неожиданности (адаптировано из Ahmed, 1987)
«Студенты учатся решать задачи по математике в первую очередь посредством «действия, разговора, размышления, обсуждения, наблюдения, исследования, слушания и рассуждений».
(Copley, 2000, стр. 29)
«…когда учащиеся исследуют вместе. Оно становится мини-обществом – сообществом учащихся, занятых математической деятельностью, дискурсом и размышлениями. Учащимся должна быть предоставлена возможность действовать как математики, позволяя, поддерживая и бросая вызов их «математизации» конкретных ситуаций.
 Сообщество обеспечивает среду, в которой отдельные математические идеи могут быть выражены и проверены на соответствие идеям других… Это позволяет учащимся стать более ясными и уверенными в том, что они знают и понимают».
Сообщество обеспечивает среду, в которой отдельные математические идеи могут быть выражены и проверены на соответствие идеям других… Это позволяет учащимся стать более ясными и уверенными в том, что они знают и понимают». (Fosnot, 2005, стр. 10)
Исследования показывают, что
Эффективные учителя формируют у своих учеников хорошие привычки решать проблемы. Их вопросы разработаны, чтобы помочь детям использовать различные стратегии и материалы для решения проблем. Студенты часто хотят начать без плана в виду. Посредством соответствующих вопросов учитель дает учащимся некоторую структуру для начала решения проблемы, не говоря им, что именно делать. В 1945 Полиа опубликовал следующие четыре принципа решения проблем, чтобы помочь учителям помочь своим ученикам.
- Понять и изучить проблему
- Найдите стратегию
- Используйте стратегию для решения проблемы
- Оглянитесь назад и подумайте над решением
Решение проблем — это не линейный, а сложный интерактивный процесс. Учащиеся перемещаются вперед и назад между фазами Pólya и между ними. Стандарты Common Core State описывают этот процесс следующим образом:
«Подкованные в математике учащиеся начинают с того, что объясняют себе смысл задачи и ищут точки входа в ее решение. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто пытаются найти решение. Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной задачи, чтобы получить представление о ее решении. Они отслеживают и оценивают свой прогресс и при необходимости меняют курс». (Стандарты обучения математике нового поколения штата Нью-Йорк, 2017 г.

Принципы решения проблем Полиа
- Понять и изучить проблему
- Найдите стратегию
- Используйте стратегию для решения проблемы
- Оглянитесь назад и подумайте над решением
Учащиеся перемещаются вперед и назад по ходу решения задач.
Цель состоит в том, чтобы учащиеся имели ряд стратегий, которые они используют для решения проблем, и понимали, что может быть более одного решения. Важно понимать, что процесс столь же важен, если не более важен, чем получение решения, поскольку именно в процессе решения учащиеся раскрывают математику. Получение ответа — это не конец процесса. Размышление о стратегиях, используемых для решения проблемы, дает дополнительный опыт обучения. Изучение подхода, используемого для решения одной проблемы, помогает учащимся более комфортно использовать эту стратегию в различных других ситуациях.
При осмыслении идей учащиеся должны иметь возможность работать как самостоятельно, так и совместно.
Будут времена, когда учащиеся должны иметь возможность работать самостоятельно, а в других случаях им нужно будет иметь возможность работать в небольших группах, чтобы они могли делиться идеями и учиться с другими и у них.
Реальность
Эффективные учителя математики создают для учащихся целенаправленный учебный опыт, решая задачи в релевантных и осмысленных контекстах. Хотя текстовые задачи — это способ поместить математику в контекст, он не делает ее автоматически реальной. Задача учителей состоит в том, чтобы давать учащимся задачи, основанные на их опыте реальности, а не просить их приостановить его. Реалистичность не означает, что задачи обязательно связаны с реальным контекстом, скорее они заставляют учащихся думать «настоящим» образом.
Планирование беседы
Планируя и продвигая беседу, учителя могут активно вовлекать учащихся в математическое мышление. На уроках математики, насыщенных дискурсом, учащиеся объясняют и обсуждают стратегии и процессы, которые они используют при решении математических задач, тем самым связывая свой повседневный язык со специальной лексикой математики.

Учащиеся должны понимать, как общаться математически, давать разумные математические объяснения и обосновывать свои решения. Эффективные учителя поощряют своих учеников сообщать свои идеи устно, письменно и с использованием различных представлений. Слушая учеников, учителя могут лучше понять, что знают их ученики, и неправильные представления, которые у них могут быть. Именно заблуждения открывают окно в процесс обучения студентов. Эффективные учителя рассматривают мышление как «процесс понимания», они могут использовать мышление своих учеников как ресурс для дальнейшего обучения. Такие учителя отзывчивы как к своим ученикам, так и к дисциплине математики.
«Сегодня математика требует не только вычислительных навыков, но и способности мыслить и рассуждать математически, чтобы решать новые задачи и изучать новые идеи, с которыми учащиеся столкнутся в будущем. Обучение улучшается в классах, где учащиеся должны оценивать свои собственные идеи и идеи других, им предлагается делать математические предположения и проверять их, а также им помогают развивать свои навыки рассуждения».
(Джон Ван де Валле)
«Капитал. Превосходство в математическом образовании требует справедливости — высоких ожиданий и сильной поддержки для всех учащихся».
(NTCM)
Заключение
То, как учителя организуют обучение в классе, во многом зависит от того, что они знают и думают о математике, а также от того, что они понимают в преподавании и изучении математики. Учителя должны признать, что процессы решения проблем развиваются с течением времени и значительно улучшаются за счет эффективных методов обучения. Роль учителя начинается с выбора подробных задач по решению задач, которые сосредоточены на математике, которую учитель хочет, чтобы их ученики изучали. Подход к решению проблем – это не только способ развития мышления учащихся, но и создание контекста для изучения математических понятий. Решение проблем позволяет учащимся перенести то, что они уже узнали, в незнакомые ситуации. Подход к решению проблем позволяет учащимся активно формировать свои представления о математике и брать на себя ответственность за свое обучение.

 Глаголы настоящего времени отвечают на вопросы…
Глаголы настоящего времени отвечают на вопросы… .
.