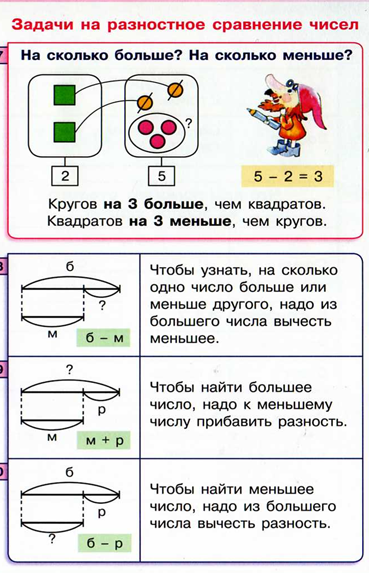
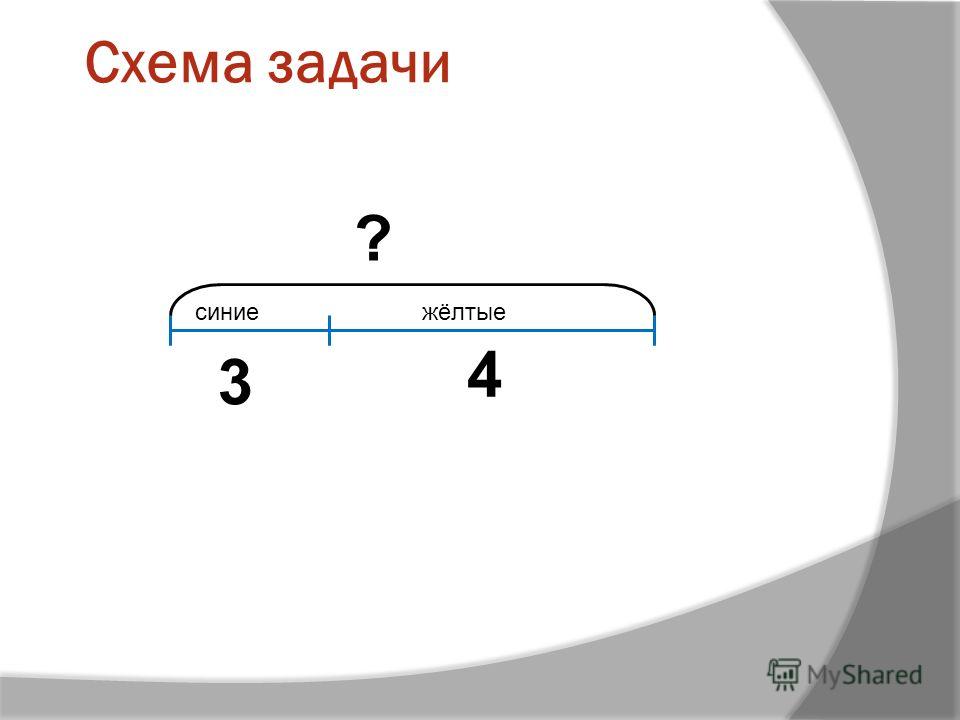
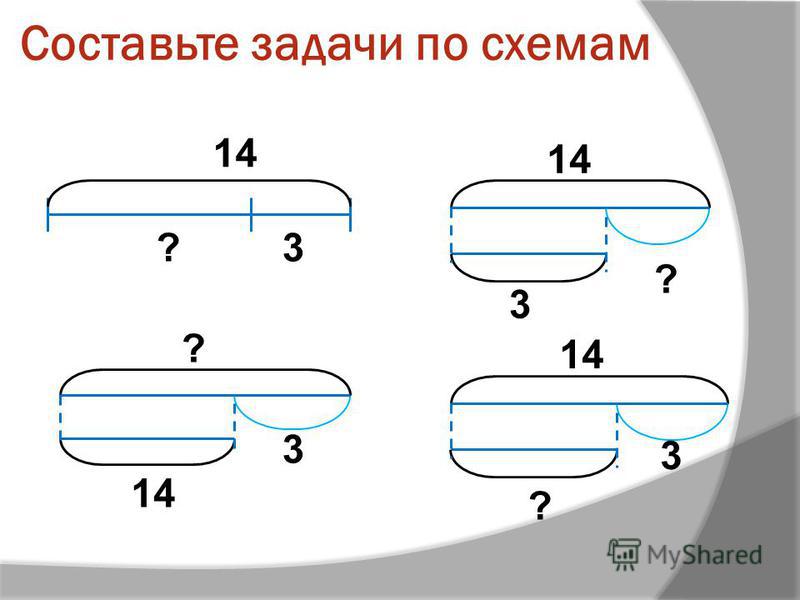
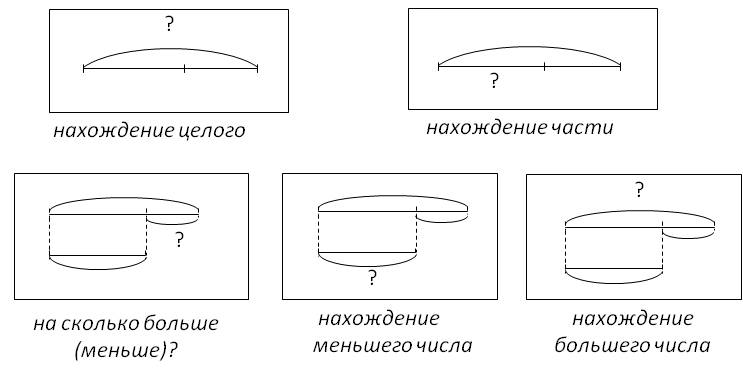
Схемы к задачам 4 класс: Опорные схемы к задачам 1-4 класс | Учебно-методический материал по математике на тему:
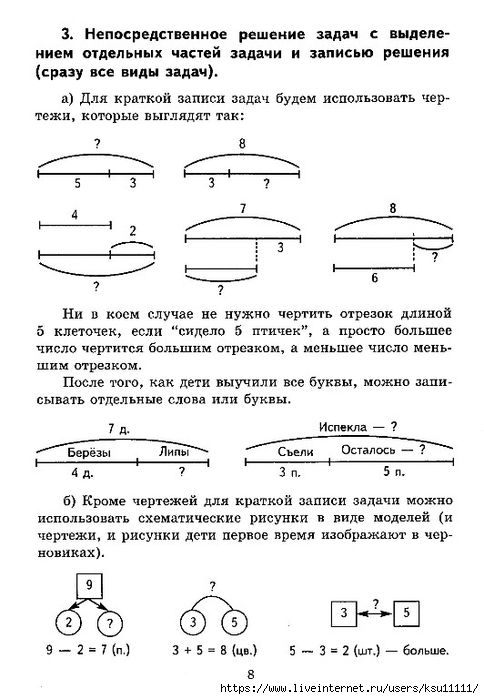
4. Обучение детей использованию схемы в виде отрезков при решении задач
При обучении учащихся построению вспомогательных графических моделей при решении задач важно обеспечить постепенный, но своевременный переход от использования одних видов моделей к другим: от более конкретных к менее конкретным. К концу 1 класса или во 2 классе имеет смысл постепенно перевести детей на использование схемы в отрезках. Время этого «перевода» учитель определяет, ориентируясь на конкретную ситуацию в классе, поскольку схема в отрезках становится необходимостью только при знакомстве с задачами на деление. Все задачи, содержащиеся в учебниках до этого времени позволяют использование рассмотренной ранее рисованной схемы.
Проиллюстрируем на примере одной и той же задачи различные способы ее моделирования.
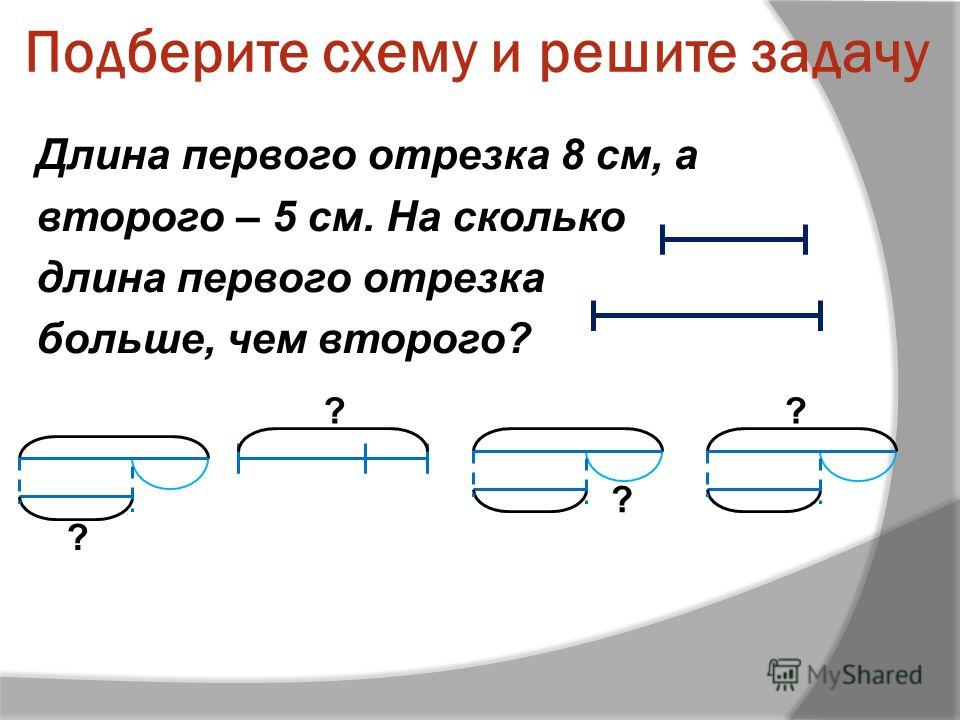
У Кати 7 книг на полке, а в портфеле на 5 книг меньше. Сколько всего книг у Кати?
Решая
задачу, ученики могут воспользоваться
условным рисунком: на одной строке
рисуют 7 кружочков, на другой — столько
же, затем, руководствуясь текстом
условия, 5 из них зачеркивают.
Использование такого рисунка фактически является дублированием соответствующих предметных действий. Такая модель наиболее близка к конкретной наглядности.
Другой вариант использования приема моделирования — это изображение ситуации задачи с помощью схемы:
Данная схема отражает отношения между данными и искомым, которые описаны в задаче, но не дает возможности найти ответ пересчетом. Чтобы ответить на вопрос задачи, необходимо выполнить действие. Такая модель является более абстрактной.
Еще один вариант схематического изображения отношений между данными и искомым — это чертеж «в отрезках». Такой чертеж может быть двух видов:
1) длина отрезка «в клеточках» соответствует данным задачи, в этом случае ответ задачи можно получить пересчетом;
2)
длины отрезков условны и отражают только
отношения между данными и искомым, а
численное их значение записывается с
помощью цифр: найти искомое в этом случае
становится возможным лишь выполнив те
или иные арифметические действия над
указанными на чертеже числами.
К приведенной выше задаче этот чертеж в виде отрезков выглядел бы соответственно так:
Очевидно, что графическая модель в виде отрезков является моделью более высокого уровня абстрактности, чем схематический рисунок. Такая модель требует сформированное™ определенного уровня умения читать схематические изображения ситуаций, и еще более сложного умения составлять такие графические изображения ситуаций.
В связи с высоким уровнем абстрактности схема в отрезках обладает большим количеством «степеней свободы», т. е. при использовании одного и того же чертежа в отрезках можно решать задачу несколькими способами, и не нужно каждый раз рисовать новую схему, как в случае со схемами предыдущего вида, рассмотренными выше.
На
этапе усвоения учеником смысла понятия
«разные способы решения одной задачи»
такая работа была полезна. Рисуя схему
каждый раз заново, ученик отражает в
рисунке разный ход мысли при решении
одной и той же задачи, что является
главным для усвоения понятия «разные
способы решения».
Когда это умение
сформировано на определенном уровне,
полезно перейти к использованию менее
наглядной, но более универсальной модели
задачи, чтобы дать больше свободы
мышлению, т. е. перейти к схеме в отрезках.
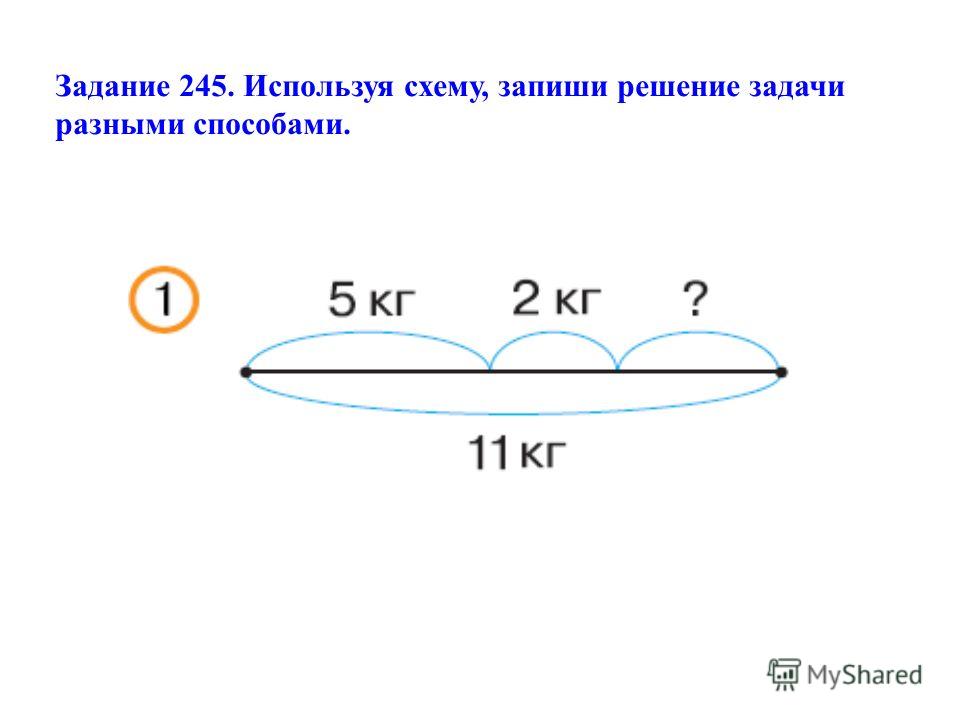
Знакомство с моделированием задач схемами в виде отрезков целесообразно начать с таких задач, данные которых выражены в мерах длины. В этом случае изображение данных и искомого в виде отрезков будет понятнее детям.
Приведем пример такого моделирования.
В куске было 15 м ткани. Одному покупателю продали 5 м, а другому 4 м. Сколько метров ткани осталось в куске?
Рассмотрим процесс построения схемы к этой задаче:
— Сколько ткани было в куске? (15 м.) Изобразим с помощью произвольного отрезка длину всего куска ткани, надпишем над ним, что он изображает 15 м:
— Что еще известно в задаче? (Одному покупателю продали 5 м.) Давайте отметим эту часть отрезка и подпишем под ним, что он изображает 5 м:
— Что
известно о ткани, проданной второму
покупателю? (Ее
было 4 м.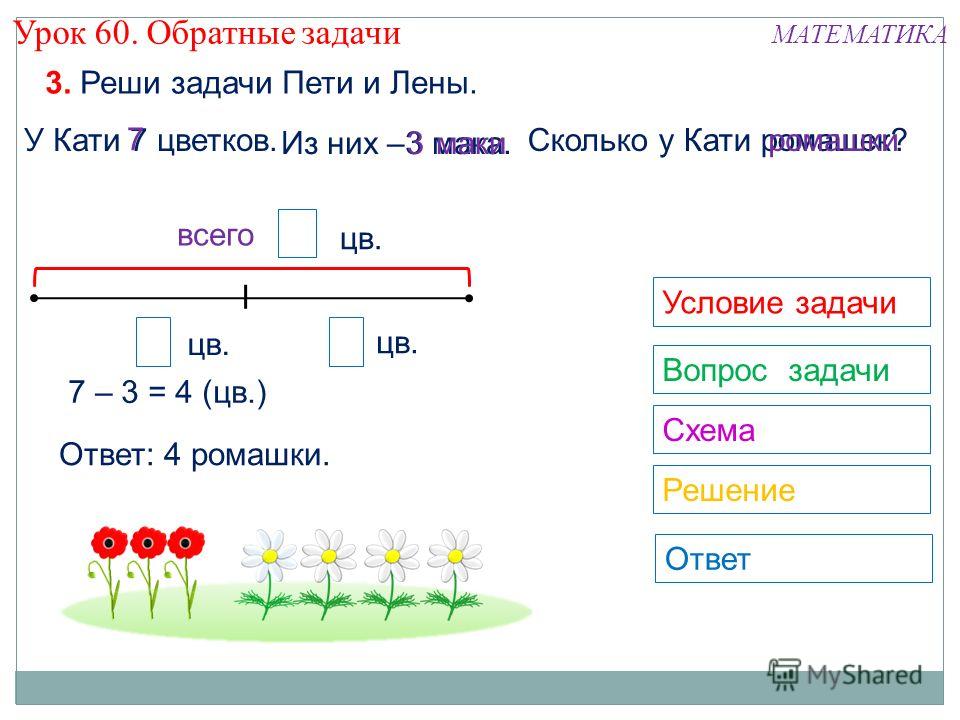
) Обозначим
это отрезком и подпишем:
— Что надо найти? (Сколько ткани осталось в куске.)
— Покажите на чертеже отрезок, который обозначает оставшуюся ткань.
Ученик показывает и вслед за движением руки рисует скобку, над которой ставит знак вопроса:
Если первоначально отрезок, изображающий 15 м ткани, отложить размером 15 клеточек, то ответ задачи можно найти пересчетом, т. е. задача будет решена графически и другого решения она не требует.
Если длина отрезка была условной, то анализ задачи проводится по чертежу. Лучше выбрать вариант анализа «от данных».
— Что можно узнать, если известно, что продано одному покупателю 4 м, а другому 5 м? (Сколько им продано обоим.)
— Какое действие нужно выполнить? (Сложение.)
Знак действия ставится на чертеже и обозначается скобкой, какие числа будут складывать.
— Как
узнать, сколько ткани осталось в куске? (От
всей ткани отнять то, что продано.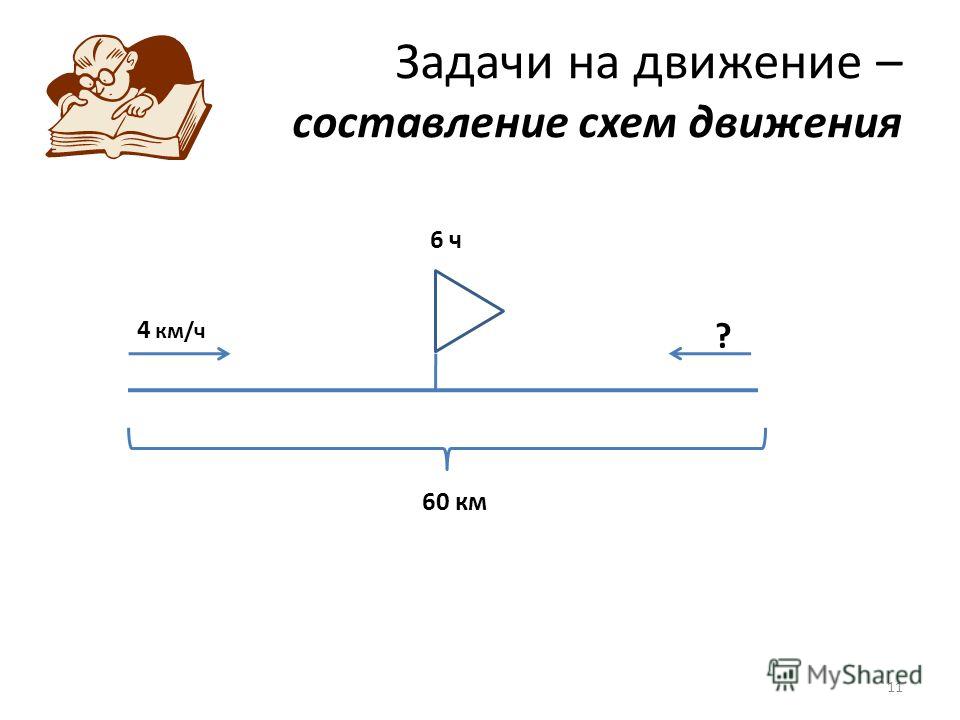
)
В таком виде чертеж играет роль также и плана решения. Модель такого вида вызывает в сознании ученика совершенно конкретное представление о ситуации, структуру связей между данными и искомыми отражает в явном виде, т. е. прогнозирует ход решения. Причем одна и та же модель допускает разные способы решения, а также явно подводит ученика к способу записи решения выражением: 15 – (4 + 5) или (15 – 4) – 5.
Выполненная средствами языка графики, такая модель позволяет ученику подняться на достаточно высокую ступеньку абстрактности — никаких соотношений, кроме количественных, эта схема не отражает, все второстепенные детали опущены, выбор действия производится без учета «главного» слова, а только исходя из логики происходящих изменений.
Знакомить
учащихся с таким способом моделирования
задачи полезно уже в первом классе, хотя
бы при решении задач, в которых данные
и искомые выражены в единицах длины.
Постепенно учащиеся знакомятся с другими
задачами, которые удобно моделировать
в «отрезках».
Такая работа является
подготовительной к постепенному переходу
от схематического моделирования (в 1
классе) к графическому (во 2 и 3 классах,).
Понимать чертеж «в отрезках» учащиеся
должны к тому времени, как начинают
решать простые задачи на деление,
поскольку задачи на деление нельзя
моделировать схематическим рисунком,
рассмотренным ранее, эти задачи требуют
рисунка «в отрезках».
Рассмотрим задачу:
Из 12 м ткани в мастерской сшили несколько платьев, расходуя на каждое по 3 м. Сколько платьев получилось из этого куска ткани?
Моделировать такую задачу с помощью схемы со стрелками неудобно — прежде чем ее нарисовать, фактически приходится задачу решить, поскольку иначе неизвестно, сколько стрелок изобразить.
Такая задача является очень удобной для перехода к рисунку «в отрезках»: дети чертят отрезок длиной 12 клеточек, а затем откладывают по 3 м (3 клетки), отделяя их черточкой. В результате получаем графическое решение задачи. Ответ можно найти пересчетом маленьких отрезков:
Опыт
показывает, что такой переход для детей,
имеющих опыт моделирования задач схемами
со стрелками, не представляет никакой
трудности, поскольку умение моделировать
словесно заданную ситуацию средствами
графики является общим умением, опыт
применения которого дети уже имеют.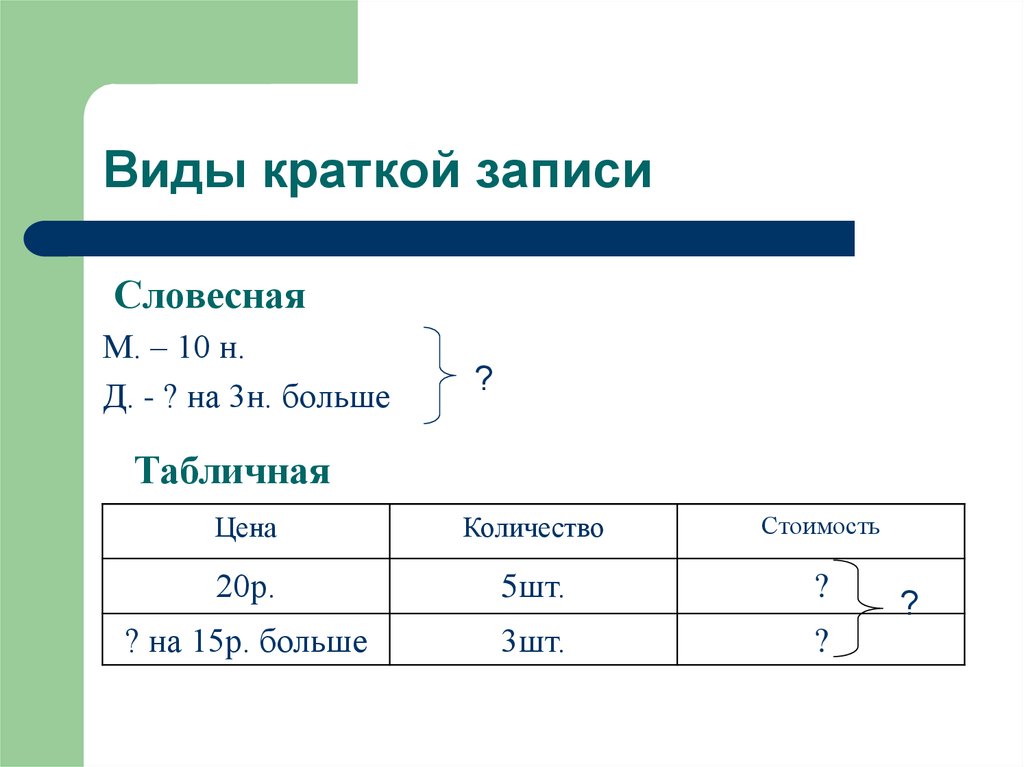
Другой вид рисунка поначалу затрудняет
только немногих детей, причем чаще это
обусловлено только характером ребенка,
а не трудностью восприятия схемы нового
вида — есть дети (как и взрослые), трудно
привыкающие к новому во всем (даже в
одежде!). Эти дети обычно еще долго
пользуются старым «проверенным» способом
моделирования задачи и только появление
большого количества новых задач, где
использование рисунка в отрезках
эффективнее старого способа со стрелками,
постепенно убеждает их в необходимости
перейти к новому виду моделирования.
Мы обычно советуем учителям не вводить
новый способ «категорическим требованием».
Пусть ребенок сам постепенно перейдет
на него, а в «переходный период» он может
использовать любой способ моделирования,
лишь бы этот способ помогал ему легко
и правильно решить задачу.
Рассмотрим задачи с различными структурами графических моделей в отрезках.
В ларек привезли 8 ящиков огурцов по 10 кг в каждом. До обеденного перерыва продали 54 кг огурцов. Сколько килограммов огурцов осталось?
Анализ данной задачи удобно проводить, опираясь на графическую модель «в отрезках» в сочетании с элементами краткой записи:
Анализ
рисунка подводит ребенка к плану решения
и записи решения сразу выражением:
10-8-54.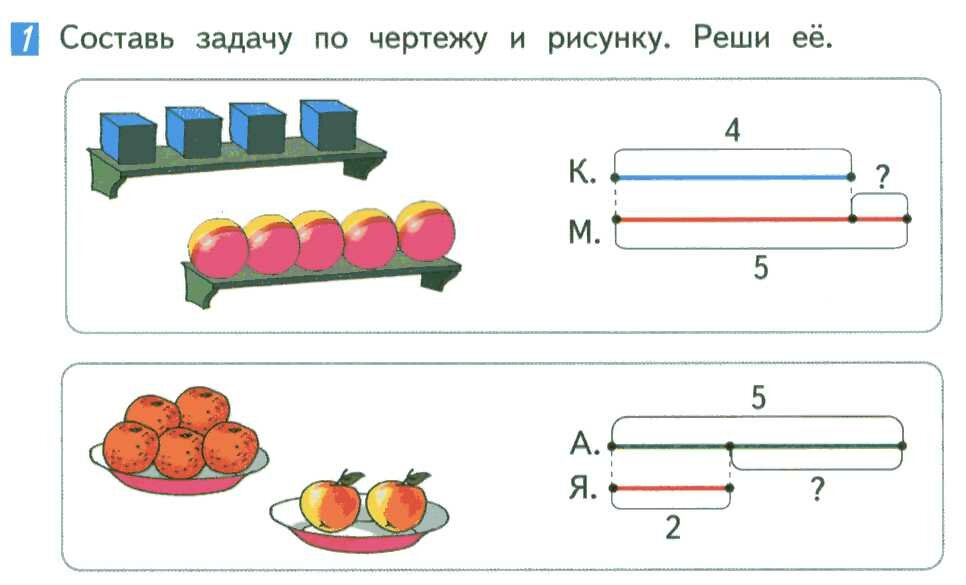
В шкафу стояло 6 глубоких тарелок, мелких в 3 раза больше, чем глубоких, а блюдец в 2 раза меньше, чем мелких тарелок. Сколько блюдец было в шкафу?
Анализируя текст этой задачи, целесообразно сопровождать его построением графической модели в отрезках, используя прием «чтение по частям».
Изобразим количество глубоких тарелок произвольным отрезком и отметим, что он соответствует 6 тарелкам. Так как мелких тарелок в 3 раза больше, отложим ниже отрезок в 3 раза длиннее (3 отрезка такой же длины). Третий отрезок будет обозначать количество блюдец, он вдвое короче второго.
Анализ задачи проводится с опорой на схему: чтобы узнать количество блюдец, надо количество мелких тарелок разделить пополам. Чтобы узнать, сколько было мелких тарелок, надо по 6 взять 3 раза.
Запись решения можно оформить выражением (6 • 3) : 2.
В
один ларек привезли 15 ящиков с фруктами,
в другой — 10 таких ящиков. В первый ларек
привезено фруктов на 60 кг больше, чем
во второй.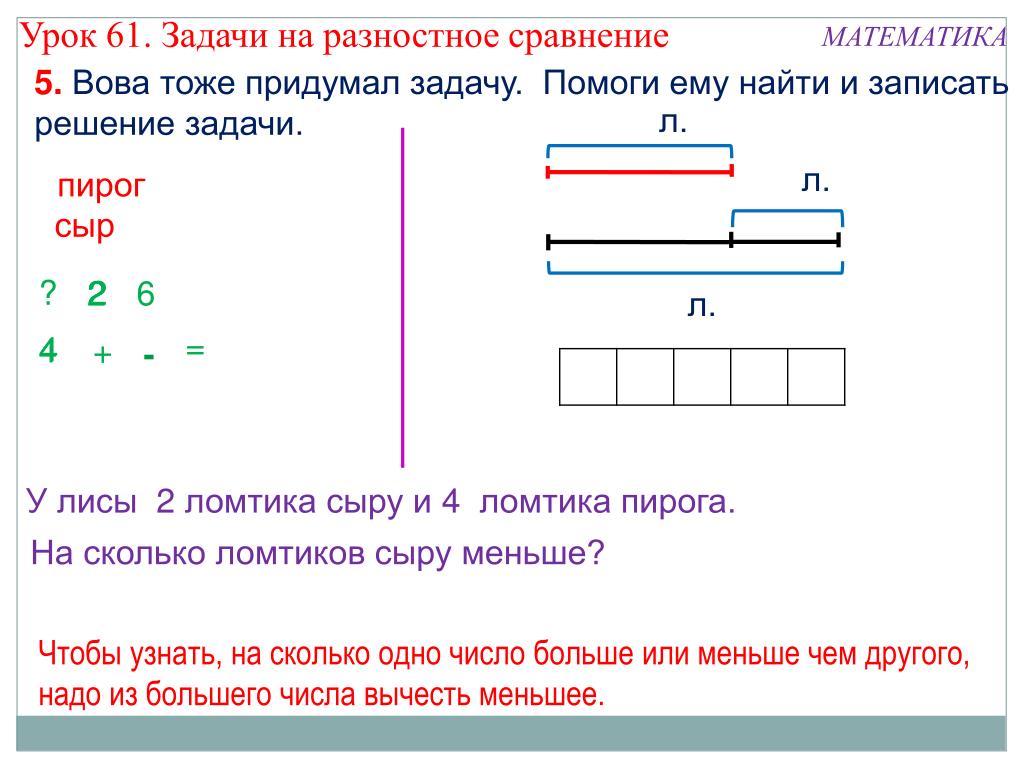
Сколько килограммов фруктов
привезено во второй ларек?
Данная задача содержит три величины, две из которых связаны пропорциональной зависимостью: количество ящиков и общее количество фруктов, третья величина (емкость ящика) является величиной постоянной и играет роль коэффициента пропорциональности. Нагляднее всего такие задачи моделируются на графическом чертеже «в отрезках», хотя в школьной практике для их моделирования чаще используют таблицу. Покажем оба варианта.
Графический вариант:
Визуальный анализ чертежа показывает, что в первом ларьке фруктов больше за счет того, что больше ящиков. Анализ чертежа должен подвести к тому, что на «лишних» 60 кг приходится 5 ящиков. Второй важный момент условия учитель акцентирует с помощью вопроса:
— Что сказано о размерах всех этих ящиков? Какие они все? (Ящики одинаковые.)
— Что можно узнать, если 5 одинаковых ящиков весят 60 кг? (Вес одного ящика,)
После
того, как задача решена, полезно провести
работу над ней, изменяя данные (количество
ящиков, массу избытка), выяснить, что
изменится, если изменить количество
ящиков, но не менять массу избытка
(изменится масса одного ящика) и т.
д.
Дета должны осознать, что, изменяя одну
величину при неизменной постоянной,
нужно обязательно изменить другую
величину (причем точно так же — т. е.
пропорционально).
Данную задачу можно решать и оформив ее условие в таблицу:
Количество ящиков | Масса одного ящика | Масса фруктов |
15 ящ. | ? одинаковая | ? на 60 кг больше |
10 кг | ? | ? |
Таблица
в данном случае является более громоздким
вариантом модели. Планируя использование
таблицы, учитель должен заготовить ее
каркас (рамку) заранее, чтобы не тратить
время на ее вычерчивание на уроке. Удобно
использовать рамку из тонких реек (она
вешается на два гвоздя на доске).
Если
таблица заполнена в процессе анализа
текста на доске, ученикам нет смысла
переносить ее в тетрадь — это занимает
много времени. Таблица удобна при
фронтальном разборе задачи и в том
случае, когда учитель планируй решить
задачу, обратную к данной. Тогда, заменяя
одно из данных вопросом, а Прежний вопрос
— данным, легко построить обратную
задачу той же структуры. Обратная задача
может выглядеть так:
Количество ящиков | Масса одного ящика | Масса фруктов |
? | ? одинаково | ? на 60 кг больше |
10 ящ. | ? | 120 кг |
Графический вариант для обратной задачи выглядит так:
Полезно
обратить внимание учащихся на то, что
если прямую задачу можно было решить
только одним способом, то обратную можно
решить двумя способами.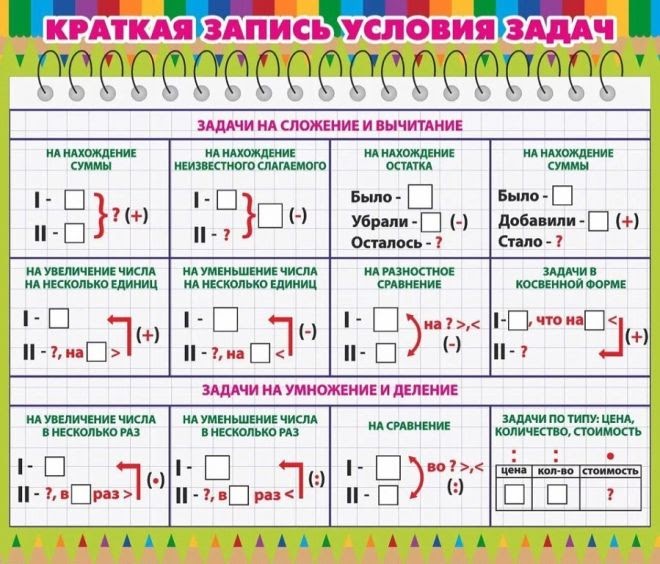
Нагляднее это
видно на графической модели:
I. 1) 120 : 10 – 12 (кг) И. 1) 120 : 10 = 12 (кг)
2) 120 + 60 = 180 (кг) 2) 60 : 12 = 5 (ящ.)
3) 180:,12 = 15 (ящ.) 3) 10 + 5 – 15 (ящ.)
Для формирования умения свободно пользоваться графическим чертежом полезны задания, в которых учащиеся по данной графической модели составляют условие задачи и записывают решение, например:
Составить задачу по чертежу.
При составлении задачи по чертежу нужно подробно провести анализ графической модели, т. е. рассмотреть, как выражены данные, искомое, как показана связь между ними, как понимать каждое условное обозначение.
— О чем будет наша задача? Что изображает верхний отрезок? Известно ли это число?
— Что изображает второй отрезок? Известно ли это число? А что о нем можно сказать по чертежу?
— Что изображает третий отрезок? Что о нем можно сказать по чертежу? Что требуется узнать в задаче? Как это обозначено на чертеже?
При
выполнении подобных заданий ученики
начинают лучше и быстрее разбираться
в математической структуре задачи,
учиться «читать» зависимости, скрытые
в схемах и чертежах.
Из всего многообразия задач, решаемых в 3 и 4 классах, задачи на пропорциональную зависимость между величинами следует выделить в отдельную группу. Пропорциональной зависимостью связаны, как правило, две величины, третья играет роль коэффициента пропорциональности. Наиболее часто используемым способом моделирования для большинства таких задач является таблица, содержащая три столбца (по количеству задействованных величин). Оформление условия и вопроса задачи в таблицу позволяет ученику быстрее сориентироваться как в характере и количестве задействованных в задаче величин, так и в структуре связей между ними.
В одном альбоме 600 марок наклеено на 15 страницах поровну. В другом альбоме наклеено 448 марок и на каждой странице на 8 марок меньше, чем в первом альбоме. Сколько страниц занято марками во втором альбоме?
Анализ текста удобнее отразить в таблице:
Всего марок | Всего страниц | Марок на 1 странице | |
600
шт. | 15 стр. | ? (поровну) | |
448 шт. | ? | ? на 8 шт. меньше | |
Анализ
задачи проводится с опорой на таблицу
(вариант «от данных»). В таблице видно,
что ее первая строка содержит два
известных данных и один вопрос, значит,
начинать решение задачи следует с ответа
на этот вопрос. Затем сравниваются два
данных в третьем столбце по вертикали.
(Можно ли узнать, сколько марок на одной
странице второго альбома, если мы знаем,
сколько их на i странице в первом?) И
затем можно ответить на главный вопрос
задачи. Таблица удобна для работы над
задачей в классе, поэтому многие учителя
предпочитают использовать ее при
проведении фронтальной работы.
Отрицательным моментом этой модели
является то, что это не самостоятельный
прием работы над задачей самого ученика.
Таблицу готовит и руководит ее заполнением
учитель. Дети не чертят таблиц в тетради.
Поэтому этот способ деятельности (эта
модель) многими детьми не присваивается,
т. е. не становится собственным приемом
работы ребенка с задачей.
В противоположность таблице графический рисунок ребенок полностью рисует в тетради сам. Научившись этому на уроках, он и в домашней работе, и на контрольной может использовать этот способ моделирования любой задачи.
С одной грядки собрали 4 мешка картофеля, а с другой б таких же мешков. Масса всего собранного картофеля 480 кг. Найти массу картофеля, собранного с каждой грядки.
В основе данной задачи также лежит понятие прямой пропорциональности, постоянной величиной является масса одного мешка. Это важно подчеркнуть при анализе текста. Моделировать такую задачу можно с помощью чертежа или таблицы. Учителя чаще используют таблицу. Покажем вид рисунка «в отрезках» к этой задаче:
Основная
мысль, которую должны понять дети при
решении этой задачи, заключается в том,
что 480 кг распределяются пропорционально
количеству мешков, которые собраны с
каждой грядки.
Рисунок показывает это
наглядно.
После решения этой задачи полезно составить обратную ей:
На чертеже хорошо видно, почему со второй грядки собрали картофеля на 96 кг больше (так как больше мешков). Значит, разница в 96 кг приходится на 2 мешка, отсюда виден путь решения задачи.
На субботнике 20 школьников убирали классы. Это 1/3 часть тех школьников, которые убирали пришкольный участок. Сколько детей убирали пришкольный участок?
Анализируя данную задачу, лучше начать с ее вопроса:
Отметим, что их количество мы не знаем.
Что известно о школьниках, убиравших классы? (Их было 1/3 от всех и всего 20 человек.)
Разделим отрезок на 3 равные части (приблизительно) и отметим ту часть школьников, которая убирала классы:
— Что
можно сказать о количестве всех школьников
на участке? (Их в 3 раза больше.
)
Обращаем внимание учителя на то, что вопрос детям, почему сделан такой вывод, нецелесообразен — это видно по рисунку.
— Каким действием их можно найти? (Умножением: 20 3 = 60 чел.) Приведенный пример показывает, что достаточно трудные для восприятия многих детей задачи «на нахождение числа по его доле» удобнее всего моделировать рисунком в отрезках, визуально показывающим способ ее решения.
Решение задач на движение в одном направлении с отставанием 4 класс
Тема: Решение задач на движение в одном направлении с отставанием
Цель. Познакомиться с новым видом задач
Задачи: совершенствовать вычислительные навыки и навыки решения задач изученных видов
Отработать правила нахождения скорости сближения, удаления, вдогонку и с отставанием; зависимость между физическими величинами S, t и v (словесные формулировки)
Воспитывать навыки работы в нестандартной ситуации.
Воспитывать уважение к предмету, умение видеть математические задачи в окружающем мире.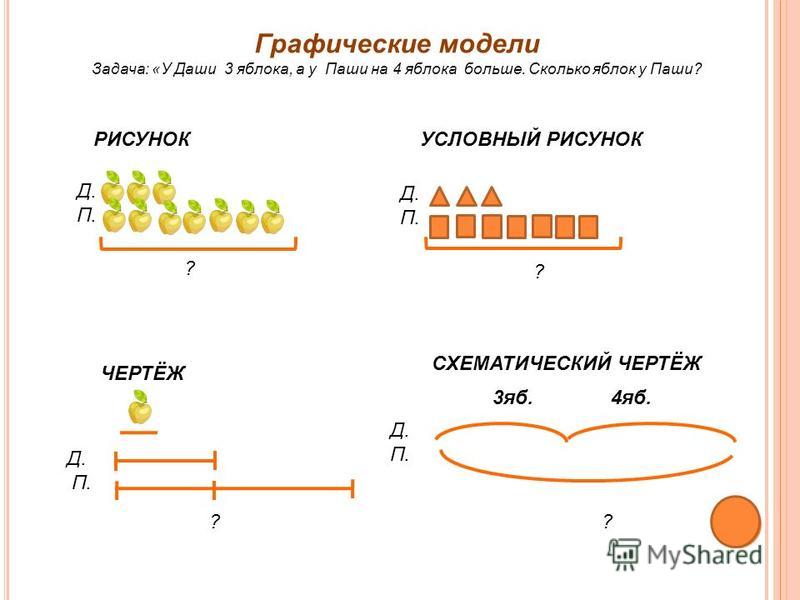
Развивать умение искать различные способы решения задач и выделять рациональные способы решения;
развивать пространственное воображение обучающихся, образное мышление;
совершенствовать графическую культуру.
Оборудование:
1. оформление доски;
2. опорные схемы; формулы.
3. Распечатки тренажёра, теста.
Ход урока.
I) Организация класса
Прозвенел уже звонок!
Время нам начать урок.
Всем известно уж давно
На математике нам нелегко.
Будем учиться ,
Будем трудиться,
Тогда страна сможет
Нами гордиться!
II) Первичная актуализация
1) Подумайте, ребята! – Нужны ли нам умения решать задачи на движение?
– Зачем они нам необходимы? (чтобы не опаздывать на встречи, уметь спланировать время выхода, рассчитать скорость движения, чтобы не было аварий, и т.
д.)
2) Математический диктант
3) – Какие существуют виды задач на движение?
– Движение в противоположном направлении с удалением
– Движение в противоположном направлении навстречу друг другу
– Движение в одном направлении вдогонку
4) – Что общего и в чём различия этих задач?
ОБЩЕЕ : есть объекты движения, есть величины: скорость, время, расстояние
РАЗЛИЧИЯ: направление движения объектов, место отправления значения величин и единицы их измерения.
А вот тема нашего сегодняшнего урока
Решение задач на движение в одном направлении с отставанием
III) Работа по теме урока
Знакомство с новым видом задач
С чего начнём решение задачи?
Составим план решения.
1.
Найдите скорость удаления (V1-V2=Vуд)
2.Найдите расстояние, на которое они удаляются друг от друга за 3 часа
Решение.
1) 90-70=20км/ч- скорость удаления легковой машины от автобуса
2) 20×3=60 км- будет между ними через 3 часа
План:
- вычислите расстояние, которое пройдет за 3 часа легковая машина
- вычислите расстояние, которое пройдет за 3 часа автобус.
- Найдите на сколько больше пройдет машина, чем автобус
- 70 • 3 = 210 км – расстояние проехал автобус
- 210 + 60 = 270 км – проехала легковая машина
- 270 : 3 = 90 км/ч – скорость легковой машины
Второй способ
- 60 : 3 = 20 км/ч – скорость удаления автомобилей
- 70 + 20 = 90 км/ч – скорость движения легковой машины.
найдите скорость удаления 90 – 70 = 20 км/ч
найдите время, через которое автомобили удалятся на 60км
60 : 20 = 3 ч
IV) Первичное закрепление.
Работа с учебником.
1) Приступаем к решению более трудных задач.
Откройте учебник на стр.31. задача № з, рассмотрите схему и составьте задачу по схеме
Определите вид задачи? – Что известно в задаче? – Что надо найти?
Расскажите задачу по схеме.
Попробуйте решить самостоятельно
Прочитайте, каким способом решил задачу
Откройте тетради .
Запишите решение задачи на доску и в тетрадь.
1) 300-200= 100км/ч – скорость удаления
2) 50:100=5 мин
Ответ: расстояние 500м будет между автомобилями через 5 минут
Задача 3(б) самостоятельно
V) Физминутка. (Сидя на стуле)
Любопытная Варвара
смотрит влево, смотрит вправо,
смотрит влево, смотрит вправо.
А потом опять вперёд, тут немножко отдохнёт.
Что там слева, что там справа? Слева, справа, слева, справа.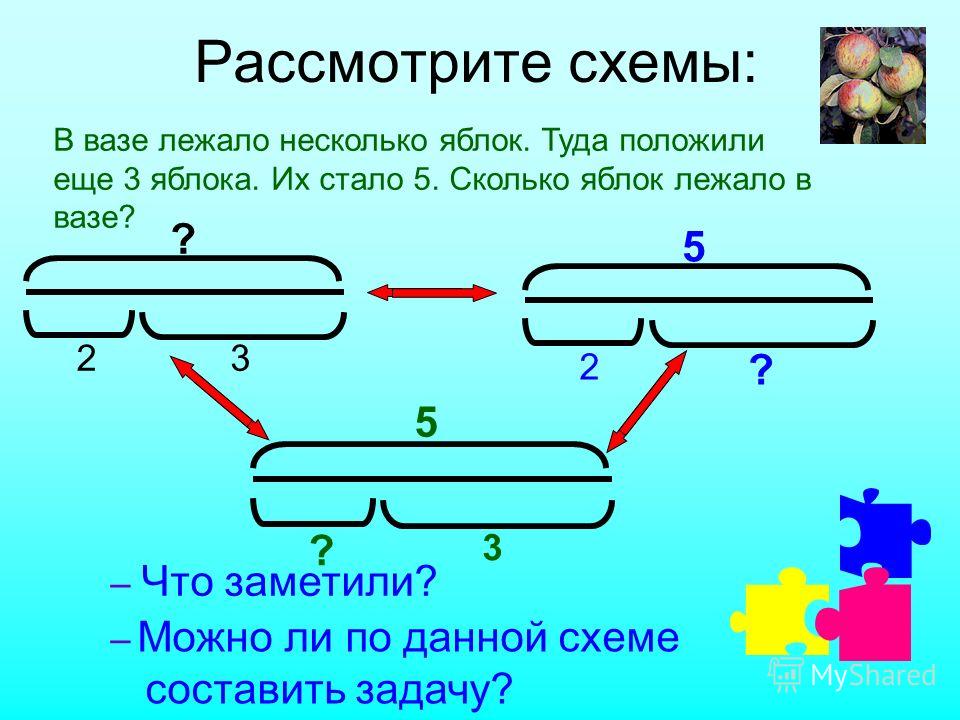
А потом опять вперёд, тут немножко отдохнёт.
Вдруг Варвара смотрит вверх, выше всех, всё дальше вверх.
Возвращается обратно, расслабление приятно.
А теперь посмотрим вниз – мышцы шеи напряглись.
Возвращается обратно, расслабление приятно.
Вверх и вниз, вверх и вниз. Теперь соседу улыбнись.
Мы на пояс руки ставим, локти в стороны расставим.
Повороты начинаем. Правый локоть наблюдаем, теперь левый замечаем.
Правый, левый, правый, левый. Плечики не поднимаем, головою лишь вращаем.
Перед грудью руки сводим, пальцы глазками находим.
Руки плавно поднимаем, глазками их провожаем.
Опускаем, поднимаем, только глазками вращаем, голову не поднимаем.
Воздух плавно выдыхаем.
VI) Систематическое закрепление.
– Можно ли самостоятельно составить задачу на движение? Как?
Что для этого надо сделать?
( выбрать объекты движения, направление движения, место отправления, задать значение измерения величин, определить, что будет искомым)
1) Составление задачи по схеме движения:
– Определите вид задачи? – Что известно в задаче? – Что надо найти?
Из двух городов, расстояние между которыми равно 65 км, выехали одновременно в противоположных направлениях два автомобиля. Один из них шел со скоростью 80 км/ч, а другой – 110 км/ч. На каком расстоянии друг от друга будут автомобили через 3 часа после выезда?
2) Составление плана решения задачи (2 способа рассмотреть)
Записать решение любым способом 80*3=240(км) (80+110)=190 (км/ч)
110*3=330(км) 190*3=570(км)
240+330=570(км) 570+65=635(км)
570+65=635(км)
Ответ.
Через 3 часа расстояние будет 635 км.
VIII) Самостоятельная работа.
Стр.31 № 6
Уравнения
ПРОВЕРКА. Проверьте свою работу самостоятельно.
– Кто не допустил ошибок при решении задачи? МОЛОДЦЫ!
XI) Итог урока:
– Чему мы учились на уроке?
– Что вам понравилось?
Что было трудно?
Домашнее задание:
Составить задачу на движение, выполнить схему и решение.
Просмотр содержимого документа
«Решение задач на движение в одном направлении с отставанием 4 класс »
Тема: Решение задач на движение в одном направлении с отставанием
Цель.
Познакомиться с новым видом задач
Задачи: совершенствовать вычислительные навыки и навыки решения задач изученных видов
Отработать правила нахождения скорости сближения, удаления, вдогонку и с отставанием; зависимость между физическими величинами S, t и v (словесные формулировки)
Воспитывать навыки работы в нестандартной ситуации.
Воспитывать уважение к предмету, умение видеть математические задачи в окружающем мире.
Развивать умение искать различные способы решения задач и выделять рациональные способы решения;
развивать пространственное воображение обучающихся, образное мышление;
совершенствовать графическую культуру.
Оборудование:
1. оформление доски;
2. опорные схемы; формулы.
3. Распечатки тренажёра, теста.
Ход урока.
I) Организация класса
Прозвенел уже звонок!
Время нам начать урок.
Всем известно уж давно
На математике нам нелегко.
Будем учиться ,
Будем трудиться,
Тогда страна сможет
Нами гордиться!
II) Первичная актуализация
1) Подумайте, ребята! – Нужны ли нам умения решать задачи на движение?
– Зачем они нам необходимы? (чтобы не опаздывать на встречи, уметь спланировать время выхода, рассчитать скорость движения, чтобы не было аварий, и т.д.)
2) Математический диктант
3) – Какие существуют виды задач на движение?
Движение в противоположном направлении с удалением
Движение в противоположном направлении навстречу друг другу
Движение в одном направлении вдогонку
4) – Что общего и в чём различия этих задач? ( Слайд № 4)
ОБЩЕЕ : есть объекты движения, есть величины: скорость, время, расстояние
РАЗЛИЧИЯ: направление движения объектов, место отправления значения величин и единицы их измерения.
А вот тема нашего сегодняшнего урока
Решение задач на движение в одном направлении с отставанием
III) Работа по теме урока
Знакомство с новым видом задач
С чего начнём решение задачи?
Составим план решения.
1.Найдите скорость удаления (V1-V2=Vуд)
2.Найдите расстояние, на которое они удаляются друг от друга за 3 часа
Решение.
90-70=20км/ч- скорость удаления легковой машины от автобуса
20×3=60 км- будет между ними через 3 часа
План:
вычислите расстояние, которое пройдет за 3 часа легковая машина
вычислите расстояние, которое пройдет за 3 часа автобус.
Найдите на сколько больше пройдет машина, чем автобус
70 • 3 = 210 км – расстояние проехал автобус
210 + 60 = 270 км – проехала легковая машина
270 : 3 = 90 км/ч – скорость легковой машины
Второй способ
60 : 3 = 20 км/ч – скорость удаления автомобилей
70 + 20 = 90 км/ч – скорость движения легковой машины.
найдите скорость удаления 90 – 70 = 20 км/ч
найдите время, через которое автомобили удалятся на 60км
60 : 20 = 3 ч
IV) Первичное закрепление. Работа с учебником.
1) Приступаем к решению более трудных задач.
Откройте учебник на стр.31. задача № з, рассмотрите схему и составьте задачу по схеме
Определите вид задачи? – Что известно в задаче? – Что надо найти?
Расскажите задачу по схеме.
Попробуйте решить самостоятельно
Прочитайте, каким способом решил задачу
Откройте тетради .
Запишите решение задачи на доску и в тетрадь.
1) 300-200= 100км/ч – скорость удаления
2) 50:100=5 мин
Ответ: расстояние 500м будет между автомобилями через 5 минут
Задача 3(б) самостоятельно
V) Физминутка. (Сидя на стуле)
Любопытная Варвара
смотрит влево, смотрит вправо,
смотрит влево, смотрит вправо.
А потом опять вперёд, тут немножко отдохнёт.
Что там слева, что там справа? Слева, справа, слева, справа.
А потом опять вперёд, тут немножко отдохнёт.
Вдруг Варвара смотрит вверх, выше всех, всё дальше вверх.
Возвращается обратно, расслабление приятно.
А теперь посмотрим вниз – мышцы шеи напряглись.
Возвращается обратно, расслабление приятно.
Вверх и вниз, вверх и вниз. Теперь соседу улыбнись.
Мы на пояс руки ставим, локти в стороны расставим.
Повороты начинаем. Правый локоть наблюдаем, теперь левый замечаем.
Правый, левый, правый, левый. Плечики не поднимаем, головою лишь вращаем.
Перед грудью руки сводим, пальцы глазками находим.
Руки плавно поднимаем, глазками их провожаем.
Опускаем, поднимаем, только глазками вращаем, голову не поднимаем.
Воздух плавно выдыхаем.
VI) Систематическое закрепление.
– Можно ли самостоятельно составить задачу на движение? Как?
Что для этого надо сделать?
( выбрать объекты движения, направление движения, место отправления, задать значение измерения величин, определить, что будет искомым)
1) Составление задачи по схеме движения:
– Определите вид задачи? – Что известно в задаче? – Что надо найти?
Из двух городов, расстояние между которыми равно 65 км, выехали одновременно в противоположных направлениях два автомобиля. Один из них шел со скоростью 80 км/ч, а другой – 110 км/ч. На каком расстоянии друг от друга будут автомобили через 3 часа после выезда?
2) Составление плана решения задачи (2 способа рассмотреть)
Записать решение любым способом 80*3=240(км) (80+110)=190 (км/ч)
110*3=330(км) 190*3=570(км)
240+330=570(км) 570+65=635(км)
570+65=635(км)
Ответ. Через 3 часа расстояние будет 635 км.
VIII) Самостоятельная работа.
Стр.31 № 6
Уравнения
ПРОВЕРКА. Проверьте свою работу самостоятельно.
– Кто не допустил ошибок при решении задачи? МОЛОДЦЫ!
XI) Итог урока:
– Чему мы учились на уроке?
– Что вам понравилось?
Что было трудно?
Домашнее задание:
Составить задачу на движение, выполнить схему и решение.
| ||||||||
Классификация (ИЛС)
Используйте бинарную систему классификации для разделения объектов, затем
обосновать свою схему. Классификация Candy I (NYSED) Разработайте две системы бинарной классификации, используя выборку конфет. Классификация Candy II (NYSED) Разработка бинарная система классификации с использованием конкретных объектов. Классификация Candy III (NYSED) Используйте свойства конфет для построения дерева классификации. * Классификация Горные породы (KDE) Разработка схем классификации на основе наблюдаемые свойства горных пород. Тестирование пищевых продуктов (NYSED) Определить относительное количество масел в пище.
Mystery Card 1 (NYSED) Используйте
электрический тестер, чтобы определить, где электричество течет между
круги на загадочной карте. Mystery Card 2 (NYSED) Используйте электрический тестер, чтобы определить, где электричество течет между круги на загадочной карте. Mystery Card 3 (NYSED) Используйте электрический тестер, чтобы определить, где электричество течет между круги на загадочной карте. Pathfinder (KDE) Идентифицировать полные схемы с досками-головоломками. Контейнеры (TIMSS) Исследование Влияние материалов контейнера на теплопередачу. Сохраняйте спокойствие (CCSSO) Определите какой тип контейнера лучше всего использовать для хранения напитков прохладно в жаркий день. Температурная школа (KDE)
Соотнесите охлаждение и нагревание с окружающей температурой и
среды.
Магнитные испытания (ILS) Наблюдайте и предскажите, какие объекты притянет магнит. Магнитное картирование (CCSSO) Исследуйте, как можно повлиять на компас, поместив его рядом с разными объектами.
Плавающий карандаш (NAEP) Сравните плавучесть карандаша в пресной и соленой воде. вода. Восходящие воды (KDE) Соотнесите вес и водоизмещение различных шаров.
Создание шариков (KDE) Devise
техника, чтобы определить, сколько шариков можно разобрать
заданного объема материала. Измерение: длина, объем, и температура (ILS) Выполнение обычных лабораторных процедур и сообщить о результатах. Измерение: с помощью Баланс (ILS) Выполнение лабораторных процедур и отчет полученные результаты.
Яйца и Ramp (NYSED) Продемонстрировать передачу энергии измеряя расстояния, различные шары перемещают чашку. * Птица Яйца (NS) Определите, какие яйца лучше всего подходят для скалистых утесов. среды. Наклон (RAND) Определить
силы, необходимые для перемещения грузовика по наклонной плоскости с весом
и наклоны как переменные. Таинственные ящики (ILS) Делайте наблюдения и прогнозы относительно неизвестных объектов в закрытых коробках. Наблюдение Объекты (NYSED) Наблюдайте за движением маятника и пружинный маятник, объясняющий сходства и различия между двумя видами движения. Свингеры (KDE) Поэкспериментируйте с маятником, чтобы выяснить, почему он может качаться с разной скоростью в разное время. Swings (CCSSO) Исследование переменных может показаться, что это влияет на движение маятника или «качание».
Цветные точки 1 (NYSED)
обесцвечивание цветных чернил водой. Цветные точки 2 (NYSED) Наблюдать обесцвечивание цветных чернил водой. Цветные точки 3 (NYSED) Наблюдать обесцвечивание цветных чернил водой. Цветной Капли (NYSED) Изучите свойства двух жидкостей и их смесь. Открытие Проблема твердых отходов (LCESC) Изучать и сортировать отходы в мусорном баке, категоризация и составление графиков элементы на графике и предложить решение для уменьшения количество твердых отходов в мусорном ведре.
* Упаковка
Материалы (NYSED) Проверка растворимости различных предметов
используется в упаковке. Пластиковая упаковка (KDE) Сравните качество и цену различных видов пластика кухонная пленка. Лупы (NYSED) Манипуляции с прозрачными и непрозрачными материалами для увеличения строчные буквы. [Верх] | ||||||||
| ||||||||
* Птица
Яйца (NS) Определите, какие яйца лучше всего подходят для скалистых утесов.
Люди, взаимодействующие с окружающей средой (KDE) Изучите характеристики сред и жителей. Беги ради своей жизни (NYSED) Читать рассказ о хищническом происшествии и нарисовать картину получившегося следы животных.
Следуйте по этим следам (NYSED) Напишите рассказ, описывающий события, основанный на изображении животного. треки.
Пульс (TIMSS) Наблюдайте за изменениями
в частоте пульса при воздействии стрессоров.
Животные по частям (TEKS) Находит части тела животных из кусочков пазла, собирает загадку и называет животное. Эй, посмотри на меня! (ТЕКС) Наблюдение за особенностями мучных червей. Идентификация существ (NYSED) Определите трех существ, используя классификационный ключ. Насекомые и пауки (ILS) Сконструируйте насекомое или паука, затем обоснуйте дизайн. Больше закусок из ящерицы (TEKS)
Наблюдение за различными стадиями развития мучных червей
и упорядочивает изображения, чтобы показать жизненный цикл, и рисует
стадии развития мучного червя. Мифические животные (ТЕКС) Создайте воображаемое животное, собрав изображения тела части изображений реальных животных. Исследование дерева (NS) Измерение набор листьев с линейкой и анализировать данные. Чьи части у меня есть? (ТЕКС) Узнает животных на картинке, выбирает и называет тело часть на карточке и сопоставляет часть тела с конкретным животным. [Верх] | ||||||||
| ||||||||
* Классификация
Горные породы (KDE) Разработка схем классификации на основе наблюдаемых
свойства в горных породах. Ты видишь то же, что и я? (ТЕКС)
Осмотрите террариум, чтобы провести мозговой штурм и объяснить роль
камни, почва и вода в террариуме Междисциплинарная задача: погода (MDOE) Эта серия заданий для 3 класса тематически связаны с погодой и требуют навыков в науке, чтении, письмо и словесность. Минералы (CCSSO) Сравнить и определить минералы с помощью скрэтч-теста.
Globe_IT_ES1 (ГЛОБУС) Элементарный (3-4 класс) Исследовательский тест – Времена года – ГЛОБУС Подразделение земных систем. Globe_IT_ES2 (ГЛОБУС) Элементарный
(3-4 класс) Исследовательский тест – Установление связей1
– Подразделение земных систем GLOBE. Globe_IT_ESp (ГЛОБУС) Первичный (Класс К-2) Исследовательский тест – Установление связей1 – Подразделение земных систем ГЛОУБ. Globe_NCTE_ES1 (ГЛОБУС) Элементарный Деятельность NCTE – Денсиометр1 – Подразделение GLOBE EarthSystems. Globe_NCTE_ES2 (ГЛОБУС) Элементарный Деятельность NCTE – Clinometer1 – Подразделение GLOBE EarthSystems. Globe_NCTE_ES3 (ГЛОБУС) Элементарный Деятельность NCTE — Compass1 — подразделение GLOBE EarthSystems. Globe_NCTM_ES1 (ГЛОБУС) Элементарный Деятельность NCTM – Clinometer1 – Подразделение земных систем GLOBE. Globe_NCTM_ES2 (ГЛОБУС) Элементарный
Деятельность NCTM – Clinometer2 – Подразделение земных систем GLOBE. Globe_NCTM_ES3 (ГЛОБУС) Элементарный Деятельность NCTM – Clinometer3 – Подразделение земных систем GLOBE. Протокол Globe_PT_ES1 (GLOBE) Тест – денсиометр – GLOBE Earth Systems Unit. Протокол Globe_PT_ES2 (GLOBE) Испытание – Клинометр – Подразделение земных систем GLOBE. Протокол Globe_PT_ES3 (GLOBE) Тест – Компас – GLOBE Earth Systems Unit. Наблюдение вверх, вверх и в сторону (TEKS) перехода воды из жидкого состояния в газообразное при испарении.
Руководство по ископаемым (CCSSO) Разработать «Руководство по ископаемым
Руководство», которое включает в себя чертежи и письменные описания для
каждое ископаемое.
Globe_NCTE_LC1 (ГЛОБУС) Элементарный Деятельность NCTE — Budding1 — подразделение GLOBE LandCover. Globe_NCTM_LC1 (GLOBE) Элементарный Деятельность NCTM – Бутонизация – Группа GLOBE LandCover. Globe_NCTM_LC2 (GLOBE) Элементарный Деятельность NCTM — Качественная обложка1 — GLOBE LandCover Ед. изм. Globe_NCTM_LC3 (GLOBE) элементарный Деятельность NCTM — качественное покрытие2 — GLOBE LandCover Ед. изм. Globe_NCTM_LC4 (GLOBE) элементарный Деятельность NCTM — Качественная обложка3 — GLOBE LandCover Протокол Globe_PT_LC1 (GLOBE)
Тест – MUC – Устройство GLOBE LandCover. Протокол Globe_PT_LC2 (GLOBE) Тест – Кластер – Устройство GLOBE LandCover. Протокол Globe_PT_LC3 (GLOBE) Тест – Полевое исследование – Устройство GLOBE LandCover. Протокол Globe_PT_LC4 (GLOBE) Тест – Биометрия – GLOBE LandCover Unit. Протокол Globe_PT_LC5 (GLOBE) Тест – Деревья – GLOBE LandCover Unit. Протокол Globe_PT_LC6 (GLOBE) Тест – Биомасса – Устройство GLOBE LandCover. Globe_NCTM_S1 (ГЛОБУС) Элементарный Деятельность NCTM – Температура почвы – GLOBE Soils Unit. Globe_NCTM_S2 (ГЛОБУС) Элементарный
Деятельность NCTM – Влажность почвы – Подразделение почв GLOBE. Протокол Globe_PT_S1 (GLOBE) Тест – Влажность почвы – GLOBE Soils Unit. Протокол Globe_PT_S2 (GLOBE) Тест – Температура почвы – GLOBE Soils Unit. Globe_NCTE_HY1 (ГЛОБУС) Элементарный Деятельность NCTE – pH воды – Гидрологическая группа GLOBE. Globe_NCTE_HY2 (ГЛОБУС) Элементарный Деятельность NCTE — Температура воды — GLOBE Hydrology Ед. изм. Globe_NCTM_HY1 (ГЛОБУС) Элементарный Деятельность NCTM — Температура воды — GLOBE Hydrology Ед. изм. Протокол Globe_PT_HY1 (GLOBE)
Испытание – pH воды – Гидрологическая установка GLOBE. Протокол Globe_PT_HY2 (GLOBE) Тест – Температура воды – Гидрологическая группа GLOBE.
Globe_IT_ATM1 (ГЛОБУС) Элементарный (3-4 класс) Исследовательский тест – Атмосферный блок ГЛОУБ. Globe_IT_ATMp (GLOBE) Первичный (класс К-2) Исследовательский тест – Атмосферный блок ГЛОУБ. Globe_NCTE_ATM1 (ГЛОБУС) Элементарная активность NCTE-Осадки – Атмосфера GLOBE Ед. изм. Globe_NCTE_ATM2 (ГЛОБУС) Элементарная деятельность NCTE – Температура воздуха – Атмосфера GLOBE Ед. изм. Глобус_NCTE_ATM3 (ГЛОБУС)
Элементарная деятельность NCTE — Твердые осадки — GLOBE
Блок атмосферы. Globe_NCTM_ATM1 (ГЛОБУС) Элементарная деятельность NCTM – Осадки – Блок атмосферы GLOBE. Globe_NCTM_ATM2 (ГЛОБУС) Элементарная активность NCTM — температура воздуха — атмосфера GLOBE Ед. изм. Глобус_NCTM_ATM3 (ГЛОБУС) Элементарная деятельность NCTM — Твердые осадки — GLOBE Блок атмосферы. Протокол Globe_PT_ATM1 (GLOBE) Тест – Осадки – Атмосферный модуль GLOBE. Протокол Globe_PT_ATM2 (GLOBE) Тест – Осадки – Атмосферный блок GLOBE. Протокол Globe_PT_ATM3 (GLOBE) Тест – Температура воздуха – Блок атмосферы GLOBE. [Верх] | ||||||||
| ||||||||
* Упаковка
Материалы (NYSED) Проверка растворимости различных предметов
используется в упаковке. Некоторые из его частей (KDE) Изучите два вида обычных машин и узнайте, что их части делают. [Вверх] | ||||||||
| ||||||||
Открытие
Проблема твердых отходов (LCESC) Осмотр и сортировка отходов
предметы в мусорном баке, классификация и составление графиков предметов
на графике и предложить решение по уменьшению количества
твердых отходов в мусорный бак. Еда, которую мы едим (CCSSO) Изучение пищевая пирамида, узнайте о ежедневных потребностях и спланируйте питание на один день. [Вверх] |
среды.
Схемы работы по искусству и дизайну 4 класса
- Дом
- Недавно добавленные
- Схемы работы
- Планы урока
- Планы занятий на семестр
- Первичная домашняя работа и экзамены
- Основные примечания
- Записи о работе
- Свяжитесь с нами
- Уход за собой
- Выберите схемы работы по классам
- Художественные и дизайнерские схемы работы (все классы)
- PP2 Художественные и дизайнерские схемы работы
“>
Схемы работы по искусству и дизайну 1 класс - Схемы работы по искусству и дизайну 2 класса
- Схемы работы по искусству и дизайну 3 класса
- Схемы работы по искусству и дизайну 4 класс
- Схемы работы по искусству и дизайну 5 класс
- Схемы работы по искусству и дизайну 6 класс
- Все схемы работы 4 класса
- Схемы работы по сельскому хозяйству 4 класс
- Схемы работы по искусству и дизайну 4 класс
- Схемы работы CRE 4 класса
- 4 класс Английский Схемы работы
- Немецкие схемы работы 4 класс
- Схемы работы H. R.E. 4 класс
- 4 класс Домашняя наука Схемы работы
- Схемы работы на языке коренных народов 4 класс
- Схемы работы ИРЭ 4 класса
- Схемы работы на языке жестов в Кении для 4 класса
- Схемы работы суахили 4 класс
- Математика 4 класс Схемы работы
- Музыкальные схемы работы 4 класс
- Схемы работы по физическому воспитанию 4 класса
- 4 класс Научно-технические схемы работы
- Схемы работы по обществознанию 4 класс
R.E. 4 классСхемы работ > 4 класс > Искусство и дизайн
10-НЕДЕЛЬНАЯ ВЕРСИЯ: 4 КЛАСС КЛБ ИСКУССТВО И КРАФТ -СХЕМЫ РАБОТ-СРОК 2(1)
Купить сейчас 100,00 крон
Схемы работ > 4 класс > Искусство и дизайн
2021/2022 4 КЛАСС КЛБ VISIONAR ХУДОЖЕСТВЕННО-КРАФТНАЯ ДЕЯТЕЛЬНОСТЬ СХЕМЫ РАБОЧИХ ТЕР.