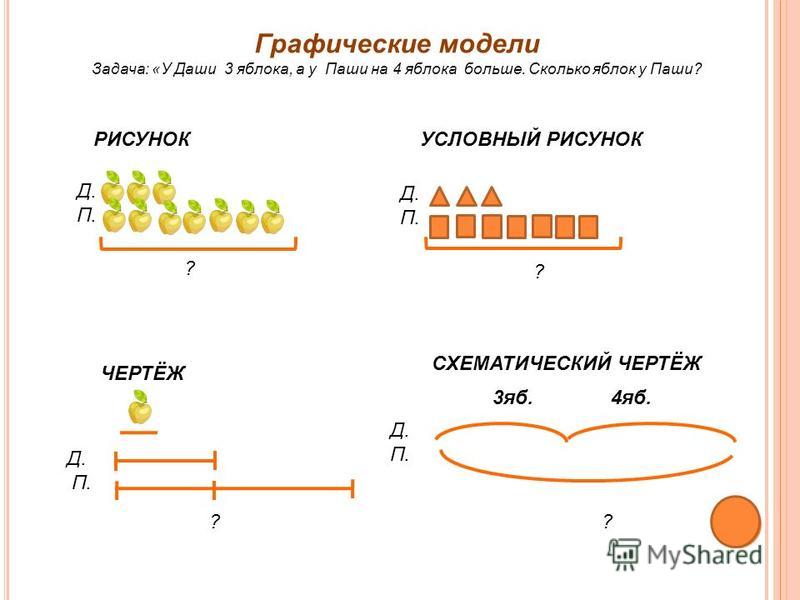
Схематический рисунок к задаче по математике 3 класс: Схематический рисунок к задаче 3 класс по математике

Страница 45 – ГДЗ Математика 3 класс. Моро, Бантова. Учебник часть 1

1. Главная
2. ГДЗ
3. 3 класс
4. Математика
5. Моро, Бантова. Учебник
6. Табличное умножение и деление
7. Страница 45. Часть 1

Вернуться к содержанию учебника

Табличное умножение и деление

Вопрос

1. В городки играли 6 ребят, а в футбол — в 3 раза больше. Сколько всего ребят играло в эти игры?

Сделай схематический чертёж к задаче и реши её.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

2.

На уроке труда мальчик сделал 6 звёздочек, а фонариков в 2 раза меньше. Сколько всего звёздочек и фонариков сделал мальчик?

Сделай к задаче схематический рисунок и реши её.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

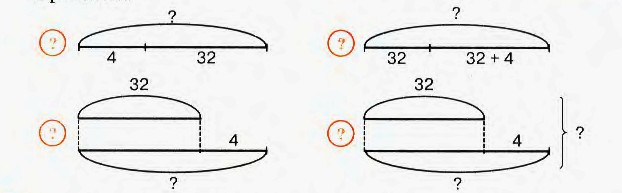
3. Длина первого отрезка 18 см, а длина второго в 3 раза меньше. На сколько сантиметров дли­на второго отрезка меньше длины первого?

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

5.

6 • 9	42 : 6	18 : 2 + 7 • 3	6 • 4	83 – 65
9 • 5	35 : 7	6 • 5 – 24 : 3	4 • 8	17 + 46
6 • 7	48 : 8	21 : 3 – 35 : 5	8 • 5	52 + 39
9 • 3	54 : 6	6 • 7 + 6 • 3	9 • 4	76 – 28

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

6. Используя данные отрезки, начерти 2 прямо­угольника с одинаковым периметром, но с раз­ными длинами сторон.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

Запиши такие 8 чисел, которые делятся на 6 без остатка.

Ответ

Поделись с друзьями в социальных сетях:

Вернуться к содержанию учебника

---

ГДЗ по математике 3 класс учебник Моро, Волкова 1 часть

---

• Тип: ГДЗ, Решебник.
• Автор: Моро М. И., Волкова С. И., Бантова М. А.
• Год: 2020.
• Серия: Школа России (ФГОС).
• Издательство: Просвещение.

❤️️Ответ к странице 45. Математика 3 класс учебник 1 часть. Автор: М.И. Моро.

Решебник – страница 45Готовое домашнее задание

Номер 1.

В городки играли 6 ребят, а в футбол – в 3 раза больше. Сколько всего ребят играло в эти игры?
Сделай схематический чертеж к задаче и реши ее.

Ответ:

1) 6 ∙ 3 = 18 (р.) – играли в футбол.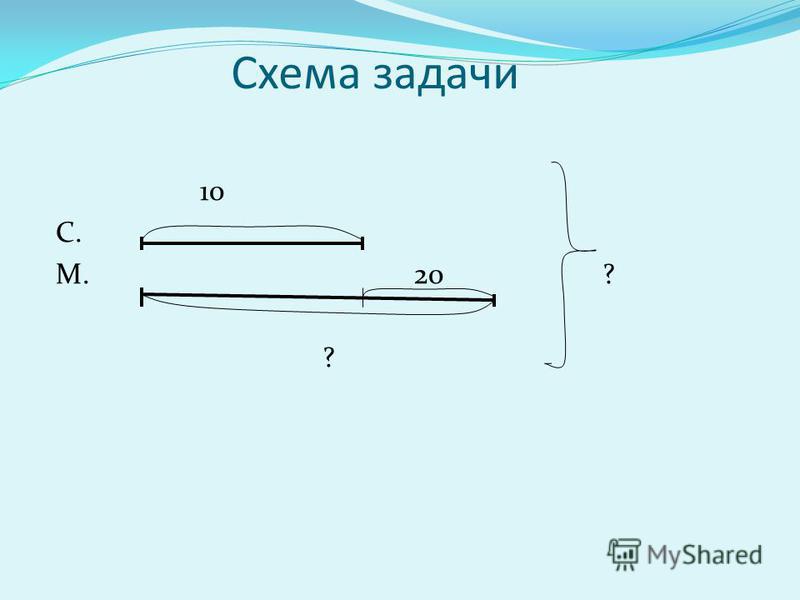 2) 6 + 18 = 24 (р.) Ответ: 24 ребенка играли в игры.

Номер 2.

На уроке труда мальчик сделал 6 звездочек, а фонариков в 2 раза меньше. Сколько всего звездочек и фонариков сделал мальчик?
Сделай к задаче схематический рисунок и реши ее.

Ответ:

1) 6 : 2 = 3 (шт.) – фонарики. 2) 3 + 6 = 9 (шт.) Ответ: 9 фигур сделали мальчики на уроке.

Номер 3.

Длина первого отрезка 18 см, а длина второго в 3 раза меньше. На сколько сантиметров длина второго отрезка меньше длины первого?

Ответ:

1) 18 : 3 = 6 (см) – длина второго отрезка. 2) 18 − 6 = 12 (см) Ответ: длина второго отрезка на 12 см меньше длины первого отрезка.

Номер 4.

Ответ:

Номер 5.

Ответ:

6 ∙ 9 = 54     42 : 6 = 7 9 ∙ 5 = 45     35 : 7 = 5 6 ∙ 7 = 42     48 : 8 = 6 9 ∙ 3 = 27     54 : 6 = 9

6 ∙ 4 = 24     83 − 65 = 18 4 ∙ 8 = 32     17 + 46 = 63 8 ∙ 5 = 40     52 + 39 = 91 9 ∙ 4 = 36     76 − 28 = 48

Номер 6.

Используя данные отрезки, начерти 2 прямоугольника с одинаковым периметром, но с разными длинами сторон.

Ответ:

Р = (3 + 2) ∙ 2 = 5 ∙ 2 = 10 см – 1 прямоугольника. Р = (4 + 1) ∙ 2 = 5 ∙ 2 = 10 см. – 2 прямоугольника.

Задание внизу страницы

Запиши такие 8 чисел, которые делятся на 6 без остатка.

Ответ:

6, 12, 18, 24, 30, 36, 42, 48.

Рейтинг

Выберите другую страницу

1 часть

Учебник Моро	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

2 часть

4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

Помощь учащимся с ограниченными физическими возможностями научиться составлять математические задачи

Добавить в избранное

Джеффри МакКормак и Ян Мэтисон

Два поезда отправляются одновременно из городов, расстояние между которыми составляет 120 километров.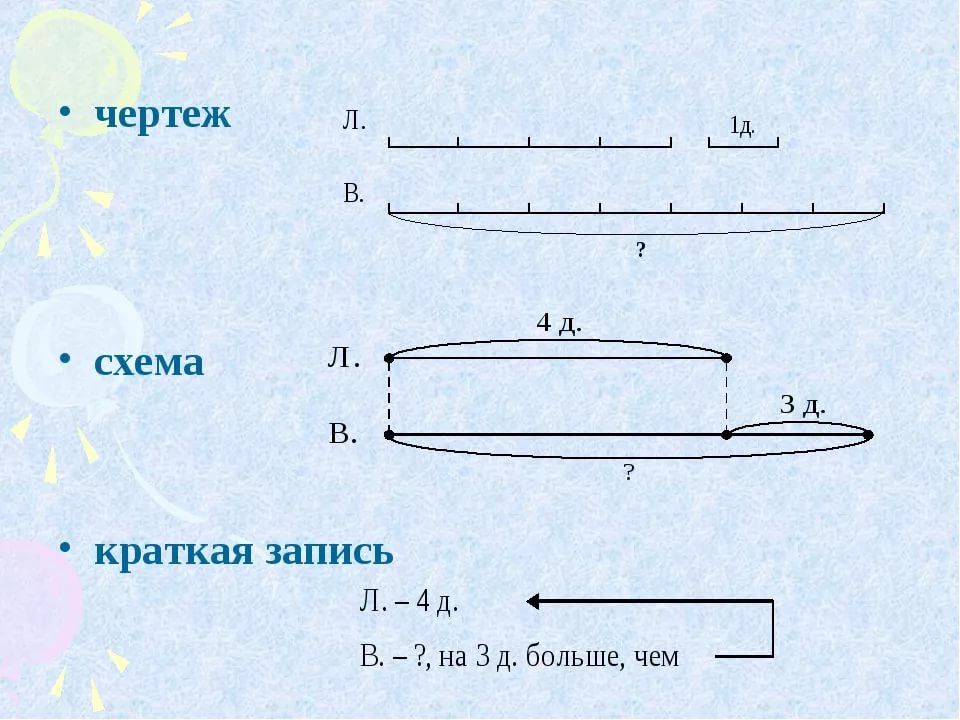 Первый поезд едет со скоростью 40 км/ч, а второй поезд едет со скоростью 60 км/ч. Сколько минут до столкновения?

Если вам приходилось решать задачу со словами, подобную этой, возможно, вы чувствовали некоторую тревогу, пытаясь понять смысл вопроса и выбрать стратегию для его решения. Возможно, вас не удивит, что решение текстовых задач может оказаться сложной задачей для многих учащихся. Для учащихся с ограниченными возможностями обучения (LDs) текстовые задачи могут быть особенно сложными.

Учащиеся с LD чаще, чем обычно развивающиеся учащиеся, испытывают трудности с осмыслением и выбором подходящей стратегии при решении проблем (van Garderen, 2007). Кроме того, учащиеся с LD могут выбирать менее успешные «стратегии решения» (например, метод проб и ошибок), а не стратегии представления (например, построение диаграмм; van Garderen, Scheuermann, & Jackson, 2012). Для всех учащихся одной из наиболее эффективных стратегий решения текстовых задач является разработка диаграмм или, как они известны в литературе, представлений (van Garderen & Montague, 2003).

Щелкните здесь, чтобы получить доступ к статье на веб-сайте LD@school о визуальном представлении.

Часть 1: Чем могут помочь диаграммы

Создание диаграмм для решения математических задач может помочь учащимся во многих отношениях (Stylianou, 2010). В начале процесса диаграммы можно использовать как инструмент для записи информации о проблеме в процессе решения. Когда учащийся начинает концептуализировать проблему, диаграммы могут стать инструментом для изучения альтернативных способов понимания проблемы. Даже когда решение найдено, диаграммы можно использовать для мониторинга и оценки решения.

Несмотря на свою полезность, создание диаграмм может быть сложным процессом, состоящим из многих этапов (van Garderen, Scheuermann, & Poch, 2014). Студенты должны декодировать вербальную информацию и переводить ее в визуальную информацию — процесс, который требует, чтобы учащиеся идентифицировали и синтезировали информацию, прежде чем связать ее с предыдущими знаниями.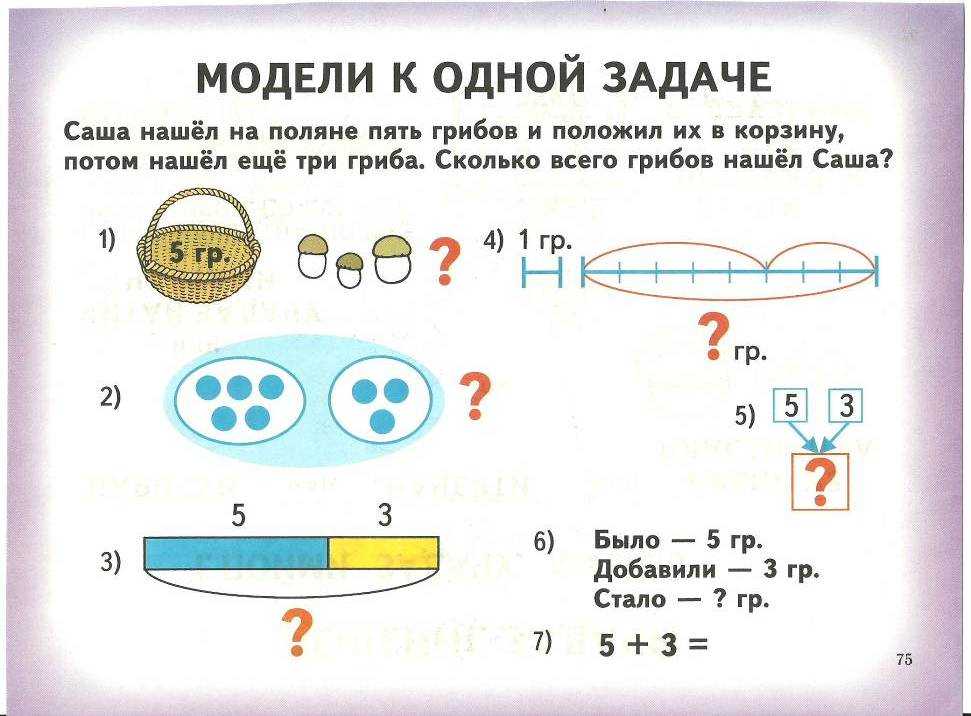 Затем учащиеся должны определить подходящую форму диаграммы в зависимости от типа текстовой задачи. После выбора типа диаграммы, которая будет использоваться, учащиеся должны создать диаграммы, точно соответствующие содержанию словесной задачи. В более сложных текстовых задачах учащимся, возможно, даже придется изменить исходную диаграмму, чтобы включить новую информацию. Этот процесс может быть когнитивно утомительным и, следовательно, дополнительным испытанием для учащихся с LD, которые обладают когнитивным дефицитом (Rosenzweig, Krawec, & Montague, 2011).

Щелкните здесь, чтобы получить доступ к статьям LD@school об оперативной памяти и LD.

Нажмите здесь, чтобы получить доступ к статьям LD@school, посвященным исполнительным функциям и LD.

Умение работать с диаграммами требует навыков в пяти различных направлениях (van Garderen et al., 2014):

1. Концептуальное понимание предполагает понимание того, что такое диаграмма и как ее можно использовать.
2. Процедурная беглость включает в себя создание диаграммы, представляющей проблему.
3. Стратегическая компетентность предполагает использование диаграммы для представления, решения и отслеживания прогресса в решении проблемы.
4. Адаптивное рассуждение включает обоснование того, насколько диаграмма была полезна при решении проблемы.
5. Наконец, продуктивное расположение включает в себя признание ценности диаграмм для решения проблем и уверенность в их использовании, когда это уместно.

Учащиеся с LD и использование диаграмм

Учащиеся с LD используют диаграммы для решения текстовых задач по математике менее эффективно, чем их сверстники (van Garderen et al., 2012). Кроме того, диаграммы, создаваемые учащимися с LD, оказываются более низкого качества, чем у их сверстников, а учащиеся с LD используют диаграммы реже, чем их сверстники (van Garderen & Montague, 2003). К счастью, исследования показали, что, когда их специально обучают создавать и использовать их, учащиеся с LD способны изучать стратегии представления, такие как диаграммы (например, Hutchinson, 19).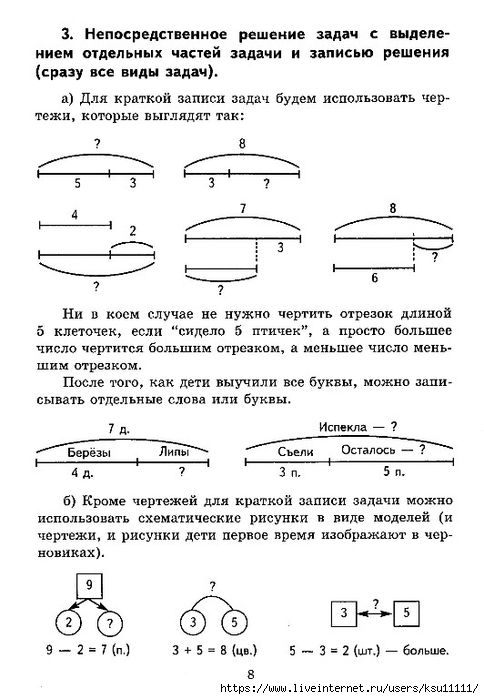 86).

Хотя использование диаграмм является эффективной стратегией решения текстовых задач для учащихся с ограниченными возможностями, реализация этой стратегии сопряжена со своими проблемами. Если у учащихся плохие процедурные и концептуальные знания, им может быть сложнее создавать и использовать значимые диаграммы (van Garderen & Scheuermann, 2015). Кроме того, учащиеся должны использовать исполнительные функции, чтобы сосредоточить внимание и игнорировать посторонние детали при построении схемы (Uesaka & Manalo, 2012). Эти процессы требуют усилий, и, как и в случае со всеми стратегиями, если предполагаемая относительная выгода от диаграмм не стоит затрат, учащиеся будут избегать их использования (Uesaka & Manalo, 2012; van Garderen & Scheuermann, 2015).

Основная проблема для всех учащихся, особенно для тех, у кого LD, заключается в том, что создание эффективных диаграмм затруднено. Прежде чем учащиеся смогут разработать диаграмму, они должны уметь визуализировать проблему — навык, который обычно развивается в возрасте от 8 до 11 лет (van Garderen & Montague, 2003). Даже когда учащиеся могут визуализировать проблему, перевод этой визуализации во внешние образы (например, диаграммы на бумаге) проблематичен. Студенты также могут не записывать информацию эффективно, потому что они сосредотачиваются на посторонних деталях, неправильно обозначают диаграмму или исключают важную информацию. Наиболее проблематично то, что учащиеся могут думать, что диаграммы — это просто визуальное представление проблемы, и не понимать, что диаграммы отображают относительную и количественную информацию о проблеме.

Часть 2: Как научить учащихся использовать диаграммы для решения задач

Согласно van Garderen and Scheuermann (2015), обучение учащихся тому, как использовать диаграммы для решения текстовых задач, состоит из двух отдельных этапов. Прежде чем научиться использовать диаграммы для решения задач, учащиеся должны научиться создавать диаграммы. Учащиеся должны знать, что, как обсуждалось ранее, эффективные диаграммы требуют большего, чем визуальное представление объектов, присутствующих в словесной задаче.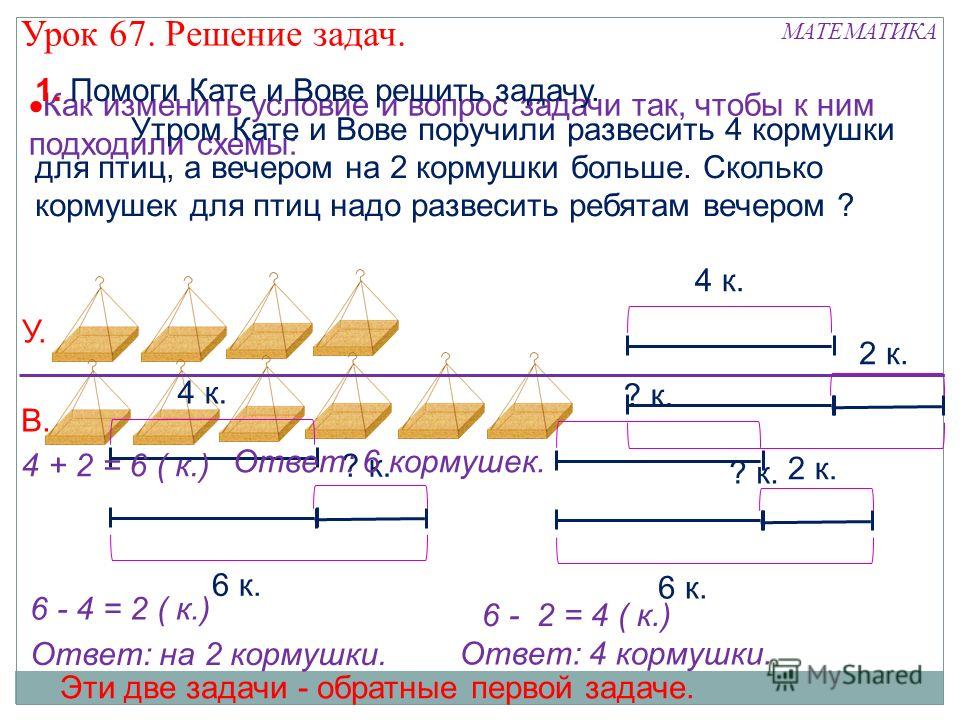 Без прямых инструкций по построению диаграмм учащиеся могут не полностью понять, как можно использовать диаграммы, и эта компетенция известна как метапредставление. Метарепрезентативная компетентность — это способность учащегося применять знания о диаграммах для надлежащего выбора, создания и использования диаграмм для решения математических задач (van Garderen, Scheuermann, & Jackson, 2012).

Чтобы помочь учащимся развить свою метарепрезентативную компетентность, учителя должны научить (а) что такое диаграммы, (б) почему диаграммы используются, (в) когда следует использовать диаграммы, (г) какой тип диаграмм подходит для математической задачи, (e) как создать диаграмму и (f) как использовать диаграмму. Для учащихся важно иметь широкое представление о диаграммах, потому что, хотя некоторые задачи естественным образом поддаются построению диаграмм, не все задачи подходят. Например, учащиеся чаще используют диаграммы при решении текстовых задач, связанных с длиной или расстоянием, чем при решении менее пространственных задач (Uesaka & Manalo, 2012). Прямые инструкции по построению диаграмм важны для учащихся с LD, потому что диаграммы должны быть неотъемлемым компонентом процесса решения проблемы, а не последним шагом (van Garderen, 2007).

Учащиеся должны понять, что диаграммы — это больше, чем просто рисунки. Неэффективные диаграммы, известные в литературе как графических диаграмм , изображают визуальное появление переменных в текстовой задаче (например, рисунок персонажа в текстовой задаче; например, van Garderen & Montague, 2003). Эффективные диаграммы (известные как схематические диаграммы ) выходят за рамки визуализации объектов в задаче; они представляют содержание проблемы и изображают реляционную информацию (ван Гардерен, 2007). Схематические диаграммы чрезвычайно полезны для текстовых задач по математике и могут быть перенесены из разных тем математики, включая геометрию и вероятность, а также из разных классов (Zahner & Corter, 2010).

Как только учащиеся поймут, что диаграммы являются когнитивными инструментами, заменяющими мыслительный процесс и отражающими его, им необходимо научиться использовать их для решения математических задач.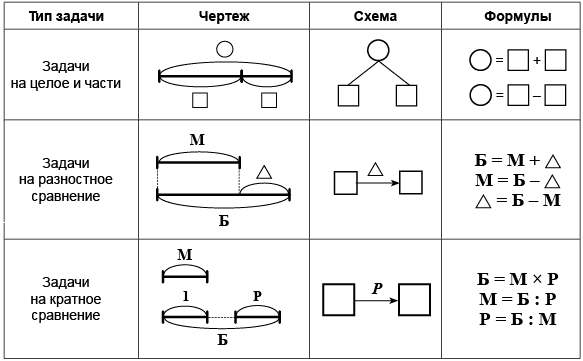 На втором этапе учащиеся должны усвоить, что использование диаграмм требует трехэтапного процесса:

(a) Спросите: сосредоточьтесь на том, что нужно сделать,

(b) Сделайте: действуйте и/или производите и

(c) Проверьте: убедитесь, что диаграмма помогает решить проблему.

Хотя эти шаги кажутся линейными, учащиеся должны знать, что они повторяются (van Garderen & Scheuermann, 2015).

Часть 3: Примеры графических и схематических диаграмм

Следующие задачи из четырех слов включены для иллюстрации различий между графическими и схематическими диаграммами. Диаграммы ниже также демонстрируют, что диаграммы делают больше, чем просто визуализируют проблему; диаграммы являются инструментами для решения проблемы.

Магазин комиксов находится в 4,4 км к западу от дома Веры. Магазин видеоигр находится в 2,8 км к западу от дома Веры. Как далеко магазин комиксов от магазина видеоигр?

Иллюстрированный

Учащиеся с LD могут совершить ошибку, сосредоточив слишком много внимания на деталях рисунков. Этот студент, возможно, потратил слишком много времени на рисование зданий и добавление посторонней информации, такой как компас. Излишнее внимание к деталям могло быть причиной того, что студент неправильно обозначил расстояния.

Схема

Этот ученик использовал схему, которая включает меры длины. Включив реляционную информацию, такую ​​как расстояние на числовой прямой, этот студент смог лучше осмыслить и решить проблему.

Готовя пять рогаликов с пиццей для своих четырех друзей и себя, Лейла случайно сожгла два рогалика с пиццей. Теперь им предстоит разделить оставшуюся пиццу-бублики. Какое наибольшее количество пиццы-рогалика может съесть каждый человек, если у всех их одинаковое количество?

Иллюстрированный

Учащиеся более склонны интуитивно использовать диаграммы для решения определенных типов задач. Например, задачи со словами, связанные с расстоянием (см. предыдущую задачу со словами) и общими целыми (этот вопрос), легче представить, потому что они предполагают конкретные отношения и суммы.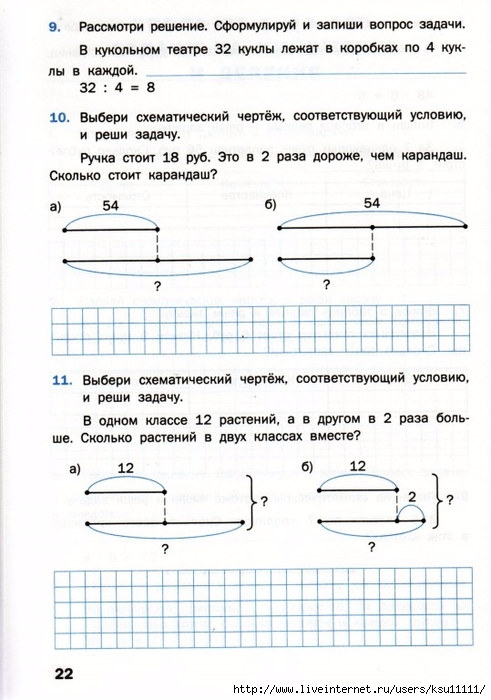 К сожалению, когда учащиеся с LD пытаются изобразить задачу в виде диаграммы, они, как правило, доходят только до рисования объектов задачи. Этот студент знал, что вопрос требует, чтобы он разделил три предмета между пятью людьми, но не знал, как использовать диаграмму, чтобы продвигать свои мысли.

Схема

Даже если учащиеся не в состоянии понять, что три рогалика можно разделить на пятые, они могут представить пятерых друзей, одновременно тянущих один и тот же рогалик. Используя диаграмму, иллюстрирующую, как друзья делят каждый рогалик, учащийся может понять, что при равном распределении каждый друг будет брать по одной пятой от каждого из трех рогаликов, всего три пятых. Также важно отметить, что, не рисуя лица Лейлы и ее друзей, студент смог исключить визуальную информацию, которая не была необходимой для решения задачи. Вместо того, чтобы рисовать лица, ученик использовал цифры (1-5) для обозначения друзей, тем самым упрощая визуализацию.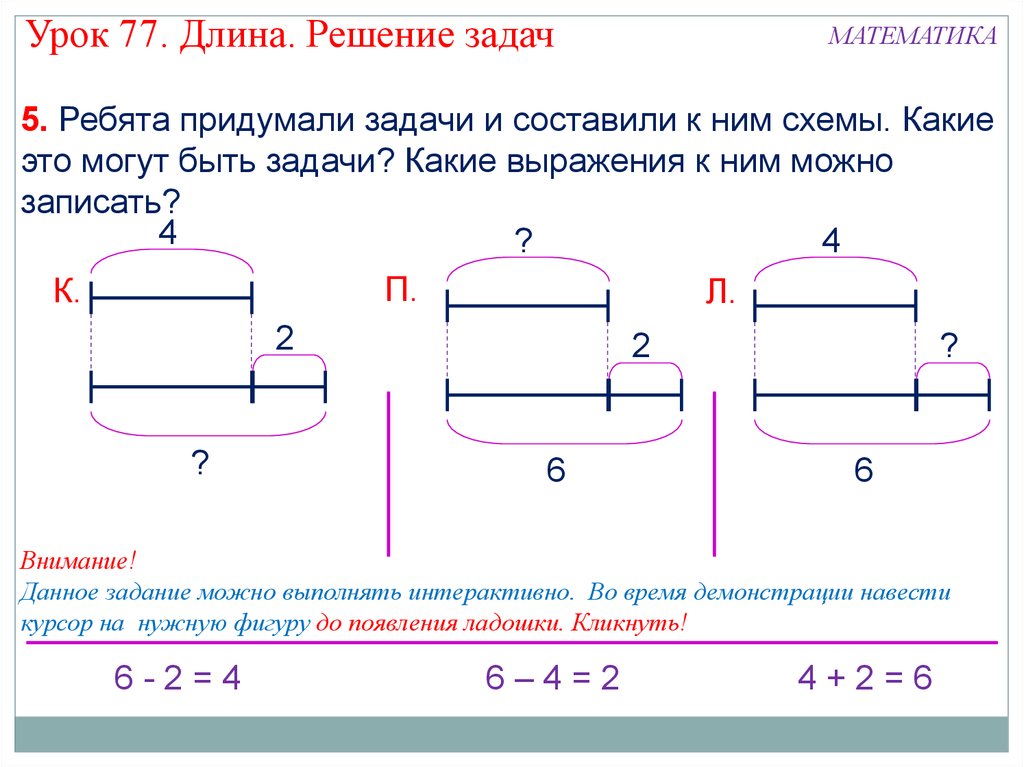

В прошлом месяце в зоомагазине было продано в четыре раза больше котят, чем ящериц. Если бы в прошлом месяце зоомагазин продал еще 18 ящериц, количество проданных котят и ящериц было бы равным. Сколько котят было продано в прошлом месяце?

Иллюстрированный

Составление диаграмм текстовых задач на отношения обычно более сложно для учащихся, чем словесных задач на расстояния. Не всегда может быть ясно, как включать реляционную информацию. Хотя этот студент смог визуализировать, что одна ящерица была продана на каждые четыре проданных котенка, он не смог определить, как эта информация связана с дополнительными 18 ящерицами, которые были бы равны количествам.

Одним из способов представления реляционной информации в виде диаграммы является использование столбцов, как показано здесь. На этом этапе учащийся может не знать количество каждого из столбцов, но использует столбцы для представления неизвестного количества. Ученик может представить себе, что было продано в четыре раза больше котят, чем ящериц, а разница между количествами составляет 18.

Схема

должны представлять шесть домашних животных. Диаграмма, которая теперь завершена, помогла учащемуся визуализировать вопрос, а также предоставила визуальную стратегию для решения вопроса.

Эти визуализации неизвестных величин могут стать первым шагом к пониманию алгебраических формулировок.

Ахмед участвует в 78-километровом триатлоне. Ему нужно проплыть 3 км. Ему нужно проехать на велосипеде в четыре раза больше расстояния, чем нужно пробежать. Какое расстояние он проедет на велосипеде в триатлоне?

Иллюстрированный

Для этой текстовой задачи учащийся нарисовал линию расстояния, потому что понял, что расстояние является релевантной переменной. К счастью, учащийся смог использовать линию для решения первого шага задачи (т. е. найти расстояние, которое не проплыл), но застрял на этом месте.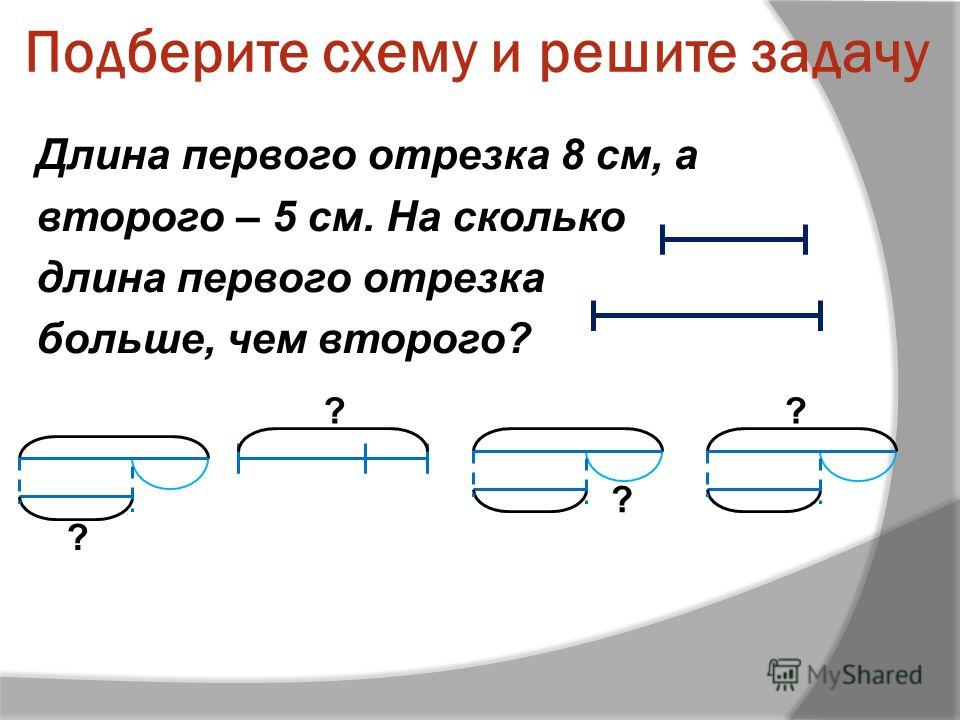 Учащийся не смог использовать диаграмму для решения второго шага задачи (т. е. определить пройденное на велосипеде расстояние).

Схема

В этом примере учащийся использует два типа визуализации для решения задачи. Как и в приведенном выше ответе, этот ученик рисует линию, чтобы показать дистанцию ​​плавания и дистанции без плавания. Для второго шага задачи учащийся создает относительные столбцы (в нижней части диаграммы), чтобы показать, что спортсмен проехал на велосипеде в четыре раза больше, чем пробежал, а общее расстояние составило 75 километров. Опять же, диаграмма не просто визуализирует проблему; диаграмма представляет собой стратегию ее решения.

Диаграммы могут быть ценной стратегией при решении текстовых задач, но, что более важно, диаграммы позволяют учащимся думать и решать задачи по-новому. Учащимся с LD диаграммы могут помочь в организации информации, планировании решения и реализации решения — всех процессах, которые могут показаться им сложными! В качестве стратегии решения проблем использование диаграмм легко адаптируется и является динамичным, и это дает преподавателям прекрасную возможность следить за тем, как учащиеся думают, и при необходимости оказывать поддержку. В то время как обучение студентов эффективному использованию диаграмм займет некоторое время, успехи будут длительными, и стратегия может иметь решающее значение для некоторых студентов.

Ссылки

Hutchinson, NL (1986). Инструкция по представлению и решению алгебраических задач с подростками с ограниченными возможностями обучения (Неопубликованная докторская диссертация). Университет Саймона Фрейзера, Ванкувер, Британская Колумбия.

Розенцвейг, К., Кравец, Дж., и Монтегю, М. (2011). Использование метакогнитивной стратегии учащимися восьмого класса с нарушениями обучаемости и без них во время решения математических задач: анализ мыслей вслух. Журнал неспособности к обучению, 44 , 508-520. doi: 10.1177/0022219410378445

Стилианоу, Д. (2010). Представления учителей о репрезентации математики в средней школе. Журнал образования учителей математики, 13 , 325–434. doi: 10.1007/s10857-0109143-y.

Уэсака Ю. и Манало Э. (2012 г. ). Связанные с заданием факторы, влияющие на спонтанное использование диаграмм в математических задачах. Прикладная когнитивная психология, 26, 251–260. doi: 10.1002/acp.1816

ван Гардерен, Д. (2007). Обучение студентов с LD использовать диаграммы для решения математических текстовых задач. Journal of Learning Disability, 40, 540–553. doi: 10.1177/00222194070400060501

ван Гардерен, Д., и Монтегю, М. (2003). Визуально-пространственное представление, решение математических задач и учащиеся с разными способностями. Исследование и практика проблем с обучаемостью, 18 , 246–254. doi:10.1111/1540-5826.00079

ван Гардерен, Д., и Шойерманн, А. (2015). Диаграммы словесных задач: стратегический подход к обучению. Вмешательство в школу и поликлинику, 50 , 282–290. doi: 10.1177/1053451214560889

ван Гардерен Д., Шойерманн А. и Джексон К. (2012). Изучение того, как учащиеся с разными способностями используют диаграммы для решения математических задач. Ежеквартально по вопросам неспособности к обучению, 36 145–160. doi: 10.1177/0731948712438558

ван Гардерен Д., Шойерманн А. и Поч А. (2014). Ставит перед учащимися проблемы с обучаемостью и показывает им высокий уровень успеваемости при использовании диаграмм в качестве инструмента визуализации для решения математических текстовых задач. ZDM Математическое образование, 46 , 135–149. doi: 10.1007/s11858-013-0519-1

Захнер, Д., и Кортер, Дж. Э. (2010). Процесс решения вероятностных задач: Использование внешних визуальных представлений. Математическое мышление и обучение, 12 , 177–204. doi: 10.1080/10986061003654240

Связанные ресурсы LD@school

Нажмите здесь, чтобы получить доступ к научно обоснованной статье «Визуальное представление в математике».

Нажмите здесь, чтобы получить доступ к видеоролику «Использование совместного опроса учителей для поддержки учащихся с ограниченными возможностями по математике» и прилагаемому Руководству для зрителей.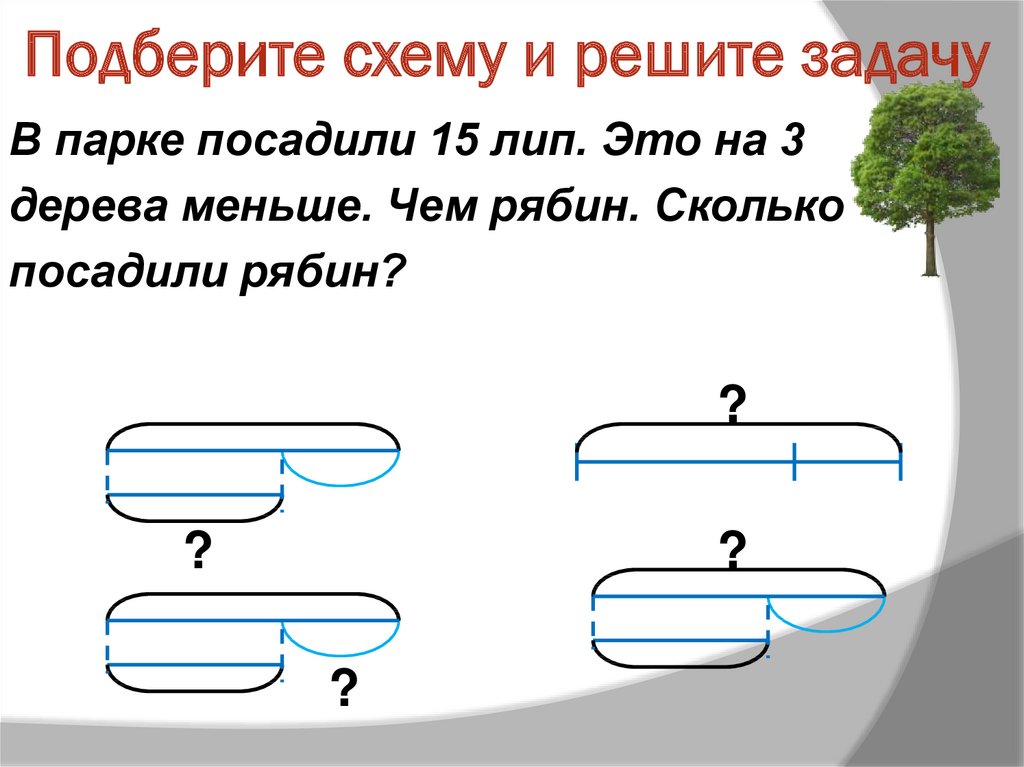

Нажмите здесь, чтобы получить доступ к веб-семинару «Понимание дискалькулии развития: нарушение способности к обучению математике».

Нажмите здесь, чтобы получить доступ к статье, основанной на фактических данных, «Вмешательства, основанные на фактических данных, для учащихся с математическими отклонениями: один размер не подходит всем».

Нажмите здесь, чтобы получить доступ к статье, основанной на фактических данных, «Конкретные – репрезентативные – абстрактные: стратегия обучения математике».

Щелкните здесь, чтобы получить доступ к научно обоснованной статье “Математическая эвристика”.

Нажмите здесь, чтобы получить доступ к статье, основанной на фактических данных, «Четкое обучение: стратегия обучения чтению, письму и математике для учащихся с ограниченными возможностями обучения».

Нажмите здесь, чтобы получить доступ к практической статье «Считаем до 99».

Джеффри — аспирант педагогического факультета Королевского университета, специализирующийся на познании. Он является учителем, сертифицированным Педагогическим колледжем Онтарио, с 9-летним опытом преподавания в начальной школе. Он работал инструктором в Королевском университете, преподавал и создавал онлайн-курсы для преподавателей. В настоящее время он проводит исследования по нескольким темам, включая проблемы с обучаемостью, аутизм, эмоциональное благополучие и развитие молодежи.

 

 

Ян Мэтисон является аспирантом программы докторантуры в области образования в Королевском университете, специализирующейся на обучении и познании. Наряду с преподавательским и исследовательским опытом в Королевском университете, Ян также имеет опыт работы учителем в начальной школе школьного совета округа Лаймстоун.

Рассказывайте и записывайте время с точностью до минуты и измеряйте интервалы времени в минутах. Решите текстовые задачи, включающие сложение и вычитание временных интервалов в минутах, например, представив задачу на диаграмме с числовыми линиями.

Экспорт

Распечатать

Связанные точки доступа

Альтернативная версия этого контрольного показателя для учащихся со значительными когнитивными нарушениями.

Связанные ресурсы

Проверенные ресурсы, которые преподаватели могут использовать для обучения концепциям и навыкам в этом эталонном тесте.

Уроки STEM – Активность по моделированию

Стрижка в спешке:

В это время спешки, чтобы подстричься, ученики суммируют прошедшее время, чтобы найти общее время, проведенное в парикмахерской, и время ухода из салона. Они должны использовать эту информацию, чтобы определить, какой салон лучше всего подходит для новой семьи по соседству. Студенты отправят письмо клиенту, объясняющее их процедуру ранжирования парикмахерских.

Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для того, чтобы выявить мысли учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.

Феи спешат на помощь!:

Во время этого задания учащиеся будут использовать отрывки для чтения и таблицы данных, чтобы разработать стратегию, позволяющую определить, какая конструкция парашюта является наилучшей, чтобы помочь феям решить их проблему.

Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для того, чтобы выявить мысли учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.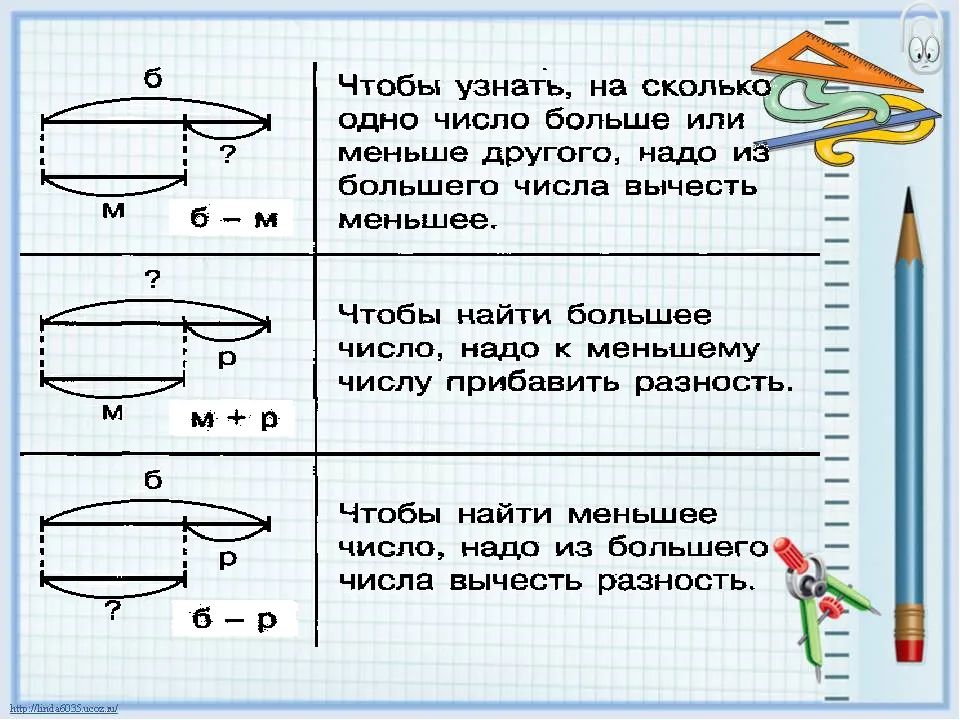

Групповые уроки пения:

Учащиеся третьего класса сами решают, какое учреждение исполнительского искусства им выбрать для групповых уроков пения. Они будут применять навыки умножения, деления и времени для определения времени с точностью до минуты и временных интервалов. Студенты будут совместно работать в группе, чтобы проанализировать эту деятельность по выявлению моделей (MEA) и участвовать в совместном обсуждении, которое включает критическое мышление более высокого уровня. Они напишут аргументированные письма о том, какое учреждение исполнительского искусства является лучшим выбором.

Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для выявления мыслей учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.

Сколько длится ваш урок музыки?:

В этом MEA учащиеся третьего класса должны будут ранжировать пакеты уроков игры на музыкальных инструментах на основе продолжительности, частоты и качества уроков. Часть задания включает в себя определение учащимися прошедшего времени уроков на основе времени их начала и окончания. Им также необходимо будет рассчитать общую недельную стоимость уроков, исходя из количества предлагаемых уроков в неделю.

Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для выявления мыслей учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.

Планирование учебного дня: создание собственного расписания занятий.:

Группа учащихся была выбрана для помощи в составлении расписания занятий на учебный год. Учащиеся должны будут использовать параметры, установленные учителем и директором, а также собственный опыт в отношении того, как им лучше всего учиться, чтобы составить расписание учебного дня, включающее все предметы и работу во время, отведенное на обед и специальные занятия. области. Затем учащиеся должны будут адаптировать созданные ими расписания с учетом дополнительных соображений учителя и директора. Этот MEA потребует, чтобы учащиеся использовали свои математические навыки для измерения временных интервалов и свои навыки ELA, чтобы написать письмо, обосновывающее и объясняющее расписание, которое они создали.

Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для выявления мыслей учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.

Время играть!:

Это MEA 3-го класса, в котором учащимся предлагается определить прошедшее время, чтобы найти идеальный день для другого ученика, чтобы остаться дома и заняться домашними делами.

Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для того, чтобы выявить мысли учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.

Формирующие оценки MFAS

Найдите время:

Учащимся предлагается решить две задачи на вычитание, связанные со временем.

Расчет времени:

Учащиеся определяют время, отображаемое на аналоговых часах, с точностью до минуты.

Затраченное время:

Учащиеся определяют интервалы времени в минутах, зная время начала и время окончания на аналоговых часах.

Сколько сейчас времени?:

Ученикам предлагается решить две задачи на сложение, связанные со временем.

Оригинальные учебники для учащихся по математике – классы K-5

Считать каждую минуту:

В этом интерактивном учебном пособии вы научитесь читать аналоговые и цифровые часы с точностью до минуты.

Ресурсы для учащихся

Проверенные ресурсы, которые учащиеся могут использовать для изучения концепций и навыков в этом эталонном тесте.

Оригинальный учебник для студентов

Считать каждую минуту:

В этом интерактивном учебном пособии вы научитесь читать аналоговые и цифровые часы с точностью до минуты.

Тип: оригинальное учебное пособие для учащихся

Образовательная игра

Прошедшее время:

Этот интерактивный Java-апплет позволяет пользователю попрактиковаться в определении прошедшего времени с помощью аналоговых или цифровых часов. Используя режим «Просмотр», пользователь переводит часы с начального времени на конечное, а апплет вычисляет прошедшее время. Используя режим «Угадай», пользователь должен рассчитать прошедшее время между заданным временем начала и окончания. Три уровня сложности позволяют пользователю практиковаться с шагом в час, пять минут или одну минуту. Дополнительная функция подсчета очков позволяет пользователю отслеживать правильность числа, хотя эта функция не является обязательной.

Тип: Обучающая игра

Образовательное программное обеспечение/инструмент

Электронная лаборатория Интерактивная игра Elapsed Time on a Clock:

Учащиеся могут попрактиковаться в определении прошедшего времени в этой простой в использовании математической онлайн-игре. Он также поставляется с листом для печати для отслеживания прогресса.

Тип: Программное обеспечение/инструмент для обучения

Руководство

Решите задачки на прошедшее время с помощью числовой прямой:

В этом видеоруководстве Академии Хана вы узнаете, как решить задачи на прошедшее время с помощью числовой прямой.