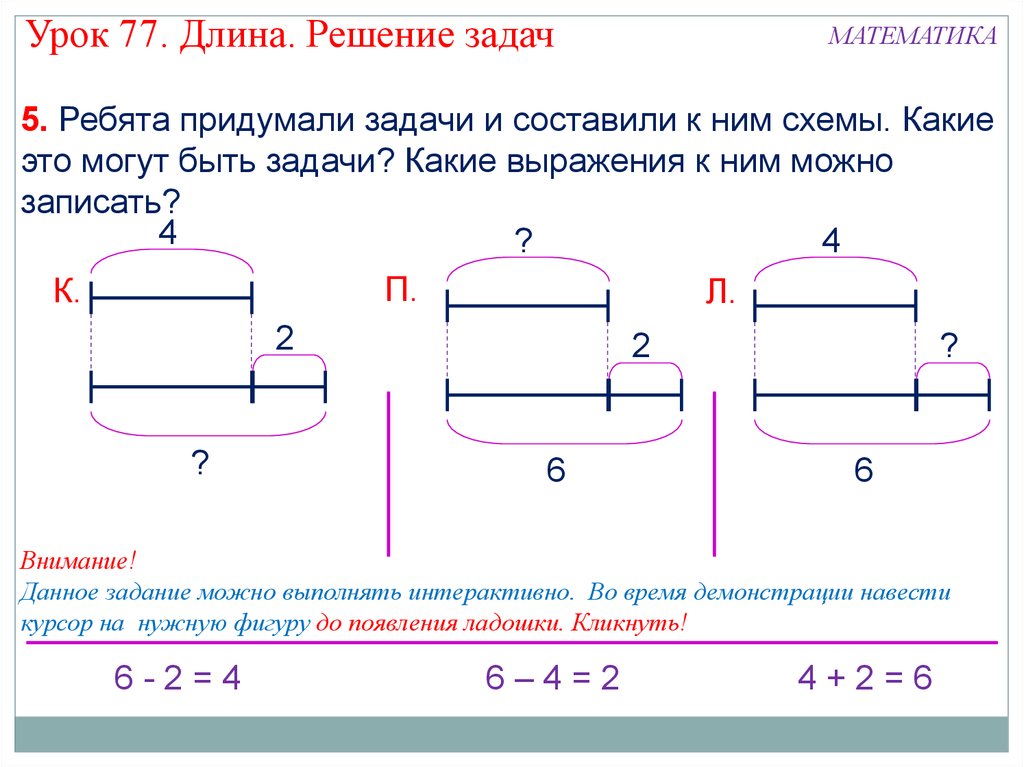
Схема задачи по математике 2 класс: Схемы к задачам по математике 2 класс

ГДЗ по математике 2 класс учебник Моро, Волкова 1 часть

---

• Тип: ГДЗ, Решебник.
• Автор: Моро М. И., Волкова С. И., Бельтюкова Г. В.
• Год: 2020.
• Серия: Школа России (ФГОС).
• Издательство: Просвещение.

Решебник – страница 29Готовое домашнее задание

Номер 1.

В коробке было 10 карандашей. Когда из коробки взяли несколько карандашей, в ней осталось 6 карандашей. Сколько карандашей взяли? Рассмотри краткую запись и схематический чертеж к задаче. Объясни, как составлен этот схематический чертеж. Реши задачу.

Ответ:

10 – 6 = 4 (к.) – взяли. Ответ: 4 карандаша.
Схема составлена так, что нам известно первое слагаемое – 6 (количество оставшихся карандашей в коробке) и 10 (сколько карандашей в коробке было). Найти нужно количество взятых карандашей.

Номер 2.

У Тани несколько значков. Она подарила 2 значка подруге, и у нее осталось 5 значков. Сколько значков было у Тани?
1) Какой схематический чертеж подходит к этой задаче?
2) Составь по другому чертежу задачу, реши ее.

Ответ:

2 + 5 = 7 (зн.) – было у Тани. Ответ: 7 значков.
1) К этой задаче подходит первый схематический чертеж.
2) У Тани было 7 значков. Она подарила 2 значка подруге. Сколько значков осталось у Тани? 7 – 2 = 5 (зн.) – осталось у Тани. Ответ: 5 значков.

Номер 3.

Начерти 2 отрезка: длина первого 6 см, а второго на 20 мм меньше. Чему равна длина второго отрезка в миллиметрах?

Ответ:

6 см = 60 мм 60 – 20 = 40 мм 40 мм – длина 2 отрезка

Номер 4.

Ответ:

18 – 9 + 6 = 15    9 + 5 – 4 = 10 11 – 7 + 8 = 12    13 – 8 + 5 = 10

Номер 5.

Ответ:

9 + 9 – 1 = 17    19 – 9 + 1 = 11    90 + 9 – 1 = 98 8 + 8 – 1 = 15    28 – 8 + 2 = 22    80 + 8 – 1 = 87 7 + 7 – 1 = 13    37 – 7 + 3 = 33    70 + 7 – 1 = 76 6 + 6 − 1 = 11    46 – 6 + 4 = 44    60 + 6 – 1 = 65

Номер 6.

Продолжи запись двузначных чисел.

Ответ:

Задание внизу страницы

Ответ:

40 + 9 + 1 = 50    17 − 7 + 5 = 15

Задание на полях страницы

Цепочка:

Ответ:

15 − 8 = 7 7 + 10 = 17 17 − 9 = 8 8 + 4 = 12 12 − 7 = 5 5 + 6 = 11

Рейтинг

Выберите другую страницу

1 часть

Учебник Моро	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95

2 часть

4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

Страница 41 – ГДЗ Математика 2 класс.

Моро, Бантова. Учебник часть 1

1. Главная
2. ГДЗ
3. 2 класс
4. Математика
5. Моро, Бантова. Учебник
6. Числовые выражения
7. Страница 41. Часть 1

Вернуться к содержанию учебника

Числовые выражения

Вопрос

1.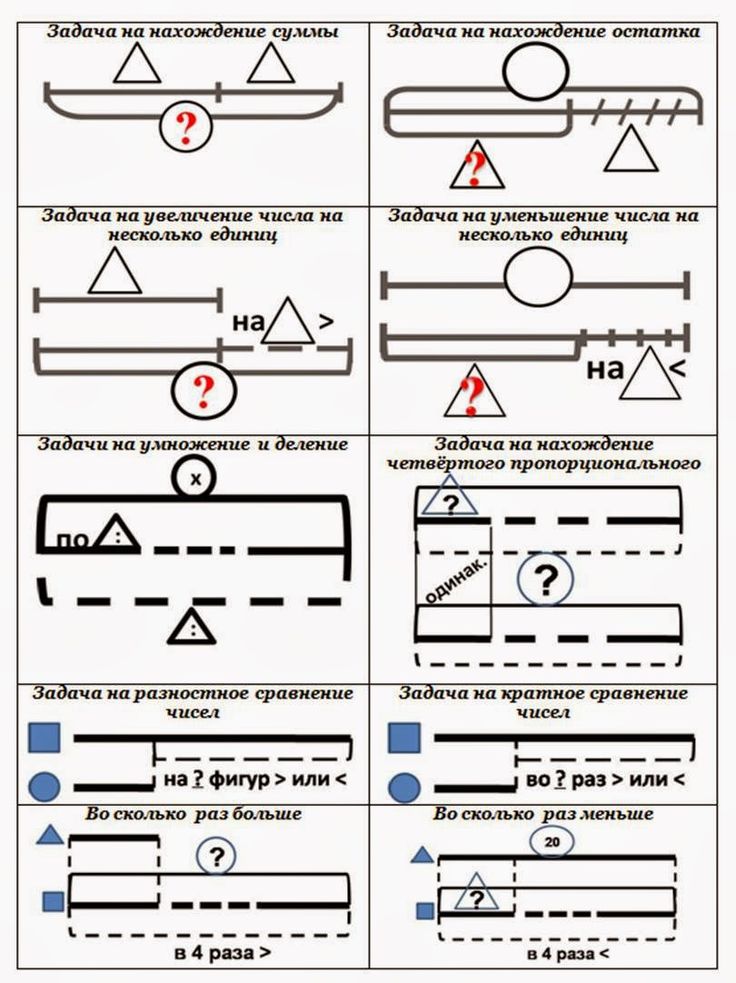 Сравни выражения, поставив знак “больше” (>), “меньше” (<) или “равно” (=).

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

2. В буфете было 12 чашек. Из этих чашек на стол поставили сначала 4 чашки, а потом ещё 3 чашки. Сколько чашек осталось в буфете?
Рассмотри разные способы решения этой задачи и объясни, что узнавали каждым действием.

1) 12 – 4 – 3 = 5 (ч.)        2) 12 – (4 + 3) = 5 (ч.)

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

3. Составь по краткой записи задачу и реши её.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

4.  

13 – 7 + 6	80 + 0 + 3	18 – 9
12 – 6 + 7	70 – 0 + 9	17 – 9
11 – 5 + 8	0 + 90 + 5	17 – 8

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

5. Начерти такие ломаные и найди длину каждой из них в миллиметрах.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

Составь по задаче выражение и реши её.

Утром надоили от коровы 6 л молока, а вечером – на 2 л больше. Сколько литров молока надоили утром и вечером вместе?

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

Ответ

Поделись с друзьями в социальных сетях:

Вернуться к содержанию учебника

---

Чтобы решить описанную ниже проблему, попробуйте использовать ленточную диаграмму.

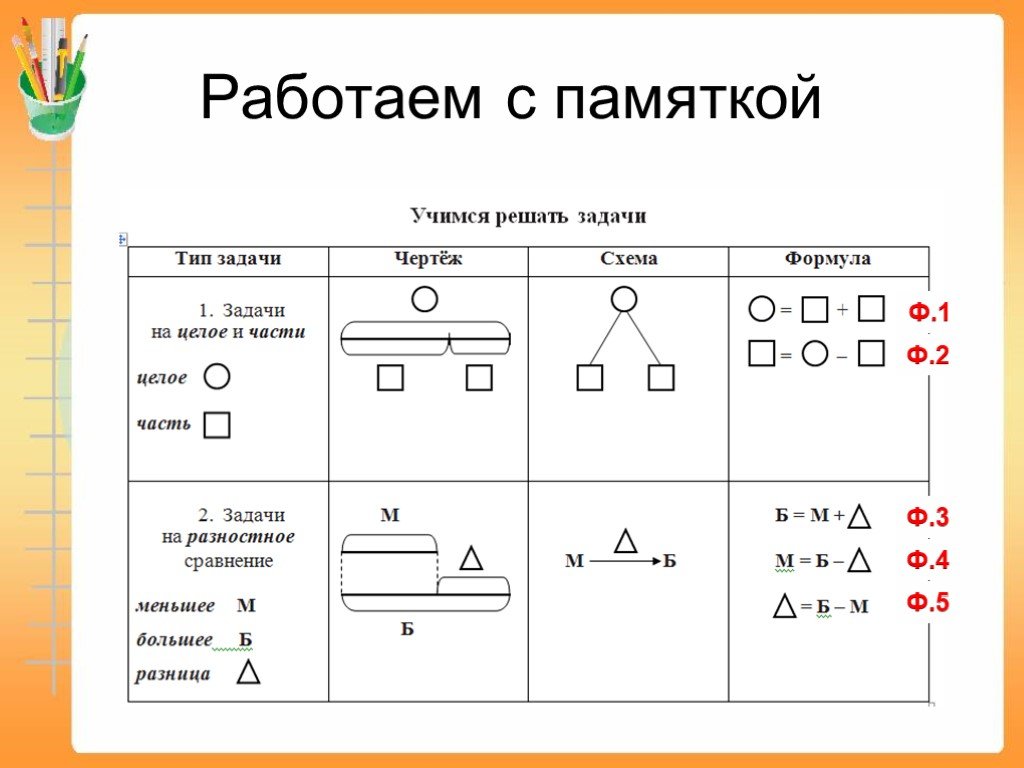Это пример того, как разные подходы к решению математических задач могут упростить решение сложных задач — The 74

Основные новостные агентства уделяют мало времени освещению математики, так что представьте мое удивление — и удовольствие — увидеть, что это одна из самых популярных статей этого лета в The Из всех тем New York Times обратилась к «порядку операций». История завершалась словами: «Давайте уделять больше времени обучению наших студентов более красивым, интересным и вдохновляющим частям математики. Наш чудесный предмет заслуживает лучшего».

Как педагог, который последние 16 лет преподавал математику, я не могу не согласиться. И это заставило меня задуматься: что может быть еще одной общей проблемой, с которой сталкиваются учителя, и почему бы не обсудить ее с читателями?

Итак, приступим.

В моем классе я часто сталкиваюсь с родителями, интересующимися, что им нужно больше изучать концептуальную математику, чем когда они росли, и почему учащимся нужны несколько стратегий для решения задач. Некоторые считают, что достаточно просто выучить стандартный алгоритм решения математической задачи (2+2=4, 6×8=48 и т. д.). Некоторые, кто действительно не любил математику, могли бы даже сказать, что этого более чем достаточно.

Я согласен с тем, что учащиеся должны изучить набор правил или процедур, которым можно следовать при выполнении расчетов. В некоторых случаях это лучший инструмент для работы.

Но в большинстве случаев учащимся нужны варианты — больше инструментов в их наборе инструментов. Могут быть лучшие способы решения проблемы, и, зная несколько стратегий, учащиеся понимают, какую операцию или алгоритм использовать в данной ситуации. Они также получают более глубокое представление о математике и о том, как применять ее в повседневной жизни.

Все еще со мной? Хорошо, рассмотрим следующую задачу.

У Зои было несколько марок. Она отдала 2/5 Лайонелу. 1/3 остатка она использовала для отправки благодарственных писем. У нее осталось 14 марок. Сколько марок у нее было, когда она начинала?

Эту задачу очень сложно решить, если вы знаете только алгебраический подход или стандартный алгоритм. Какие числа стоят в левой части уравнения? Какие идут справа? Каких переменных не хватает? Каков порядок операций?

Но с помощью ленточных диаграмм, математической модели, используемой сегодня, которая помогает учащимся визуализировать числа, пятиклассник может решить задачу менее чем за минуту. Вот как.

В детском саду учащиеся учатся делить числа на единицы, используя концептуальный подход, начиная с конкретных примеров, таких как яблоки, кубики или марки.

В третьем классе изучают понятие дробей, например, две марки из пяти равны 2/5 от общего числа марок.

К пятому классу учащиеся могут использовать этот метод, чтобы легко решить задачу с марками, описанную выше, за четыре шага.

1. Поскольку Зоя отдала две пятых своих марок Лайонелу, мы знаем, что это можно разделить на пять единиц, и что Лайонел получил две из них. Осталось три единицы.

2. Мы знаем, что треть остатка — одна из трех единиц — была использована для отправки благодарственных писем.

3. Мы знаем, что оставшиеся две единицы равны 14 и имеют одинаковый размер. 14 разделить на 2 равно семи маркам в каждой единице.

4. Теперь легко умножить семь марок на пять единиц, чтобы получить ответ: 35 марок.

Да, мы могли бы поставить задачу так:

Но насколько тяжелее запомнить это ученикам? Для взрослых забудьте об этом.

Мы ограничиваем наших учеников, если даем им только один набор инструментов для решения математических задач. В школьных округах по всей стране все чаще используют концептуальные подходы к обучению математике , С каждым днем ​​появляется все больше доказательств того, что учащиеся преуспевают.

Они любят математику. Более того, они и мы говорим о математике. Я называю это победой.

LauraMarie Coleman работает с учителями и обучает их профессиональному развитию для Great Minds . Ранее она была классным руководителем специального образования и инструктором, работающим с учащимися и учителями альтернативного и специального образования в классах K-8 в Бингемтоне, штат Нью-Йорк.

По теме:

Подпишитесь на информационный бюллетень The 74

Получайте подобные истории прямо на свой почтовый ящик. Подпишитесь на рассылку новостей 74

Диаграммы Венна: упражнения | Purplemath

IntroSet Not’nSets Exercises

Purplemath

Текстовые задачи на диаграмме Венна обычно дают вам две или три классификации и кучу чисел. Затем вы должны использовать данную информацию, чтобы заполнить диаграмму и выяснить оставшуюся информацию. Например:

Содержание продолжается ниже

MathHelp.com

В этой вселенной есть две классификации: студенты, изучающие английский язык, и студенты, изучающие химию.

Сначала я нарисую свою вселенную для сорока учеников, с двумя перекрывающимися кругами, помеченными суммой в каждом:

(Ну, ладно, это овалы, но их всегда называют «кругами». )

Пять студентов изучают оба предмета, поэтому я поставлю «5» в перекрытии:

Теперь я учёл пять из 14 студентов, изучающих английский язык, оставив девять студентов, изучающих английский язык, но не изучающих химию, поэтому я поставлю «9».” в части “только английский” круга “английский”:

Я также учёл пятерых из 29 студентов-химиков, оставив 24 студента, изучающих химию, но не английский язык, поэтому я поставлю “24” в ” Только химия» часть кружка «Химия»:

Это говорит мне о том, что в общей сложности 9 + 5 + 24 = 38 студентов изучают либо английский язык, либо химию (или оба). Это дает мне ответ на часть (b) пункта это упражнение. Это также оставляет двух учеников пропавшими без вести, поэтому они должны быть теми, кто не посещает ни один класс, что является ответом на часть (а) этого упражнения. Я поставлю «2» в рамку, но вне двух кружков :

В последней части этого упражнения меня спрашивают о вероятности того, что данный студент изучает химию, но не английский язык. Из сорока студентов 24 изучают химию, но не английский язык, что дает мне вероятность:

24/40 = 0,6 = 60%

1. Два студента не изучают ни один предмет.
2. По крайней мере, в одном из классов учатся 38 учеников.
3. Существует 60% вероятность того, что случайно выбранный ученик в этой группе изучает химию, но не английский язык.

---

• Много лет назад я обнаружил, что мой (ныне покойный) кот любил очаровательных маленьких гекконов, которые жили в кустах и ​​лозах моего двора, когда я жил в Аризоне. Предположим, что за месяц он выложил на мой ковер следующее:

  .
  • шесть серых гекконов,
  • двенадцать гекконов, отбросивших хвосты, чтобы избежать поимки, и
  • пятнадцать гекконов, которых он немного пожевал

  Дополнительно:

  • только один из гекконов был серым, обгрызенным и бесхвостым;
  • двое были серые и бесхвостые, но не прожеванные;
  • двое были серыми и обглоданными, но не бесхвостыми.

  Если в этом месяце на моем ковре осталось 24 геккона, и все гекконы были по крайней мере одним из «серых», «бесхвостых» и «обжеванных», сколько было бесхвостых и обжеванных , а не серый?

Если я буду работать с этим шаг за шагом, используя то, что мне дали, я смогу понять, что мне нужно, чтобы ответить на вопрос. Это проблема, для решения которой требуется некоторое время и несколько шагов.

Мне сказали, что у каждого геккона есть по крайней мере одна из характеристик, поэтому каждый является членом по крайней мере одного из кругов. Это значит, что вне кругов ничего не будет; круги будут объяснять все в этой конкретной вселенной.

Был один геккон, серый, бесхвостый и обглоданный, поэтому я нарисую диаграмму Венна с тремя перекрывающимися кругами и поставлю «1» в центре перекрытия:

Два геккона были серыми и бесхвостый, но не пережеванный, поэтому «2» идет в остальной части совпадения между «серым» и «бесхвостым».

Двое из них были серыми и обжеванными, но не бесхвостыми, поэтому “2” идет в остальной части совпадения между “серым” и “обжеванным”.

Поскольку всего шесть гекконов были серыми, а 2 + 1 + 2 = 5 этих гекконов уже учтены, это говорит мне о том, что остался только один, который был только серым.

Таким образом, мне нужно знать, сколько из них были бесхвостыми и обглоданными, но не серыми, о чем и просит задача. Но, поскольку я не знаю, сколько из них были только пережеванными или только бесхвостыми, я пока не могу вычислить значение ответа для оставшегося участка перекрытия.

Мне нужно работать со значением, которое я еще не знаю, поэтому мне нужна переменная. Я позволю “ x ” обозначать это неизвестное количество бесхвостых, пожеванных гекконов.

Я знаю общее количество пожеванных гекконов (15) и общее количество бесхвостых гекконов (12). После вычитания это дает мне выражения для оставшихся частей диаграммы:

Только разжевываемые на:

15 – 2 – 1 – x = 12 – x

Только хруппомазы:

12 – 2 – 1 – x = 9- x

всего 24 геккона за месяц, поэтому сложение всех участков кругов диаграммы дает мне: (все из «серого» круга) плюс (неизвестное из оставшегося перекрытия) плюс (единственное-пережеванное) плюс ( единственно-бесхвостый), или:

(1 + 2 + 1 + 2) + ( x )

+ (12 − ​​ x ) + (9 − x )

= 27 − x = 24

Решая, я получаю x = 3.