Схема к задаче на умножение: Схемы решения задач на умножение и деление
Этап урока | Деятельность учителя | Деятельность ученика | Примечания |
I.Орг.момент. | Прозвенел звонок и смолк , Начинается урок! Мы за парты тихо сели , И соседа не задели! Ножки на пол мы поставим, Спинки ровно разогнем Локотки на стол поставим Домик к носу поднесём Руку левую на стол Сверху правую кладём! Добрый день , ребята, меня зовут Оксана Сергеевна, сегодня я проведу у вас урок математики. Проверьте , у каждого должен быть на парте учебник, тетрадь, пенал, дневник,смайлик. | ||
II. Устный счет III.Актуализация знаний IV.Изучение нового материала РАЗМИНКА V.Итог урока РЕФЛЕКСИЯ | Сегодня у нас начинается грандиозная стройка. Мы будем строить новый дом «Дом-Знаний». И от того каким он будет зависит только от вас. Каждое выполненное задание на сегодняшнем уроке – это этаж нашего дома. Готовы? Начинаем! . Закладка фундамента. Как быстрее посчитать сумму всех чисел, из которых она состоит? (ищем способ решения данного выражения) 9 * 8 + 6 * 3 + 1 + 8 = 72 + 18 + 9 = 99 1. В одном ряду сидели 23 ученика, в другом – на 5 учеников меньше. Сколько учеников сидело во втором ряду? (18 учеников)
Строительство 1 этажа. Ребята, как вы думаете какая тема сегодняшнего урока?? Какие цели поставим себе на урок?? Открываем тетради, записываем число и классная работа.
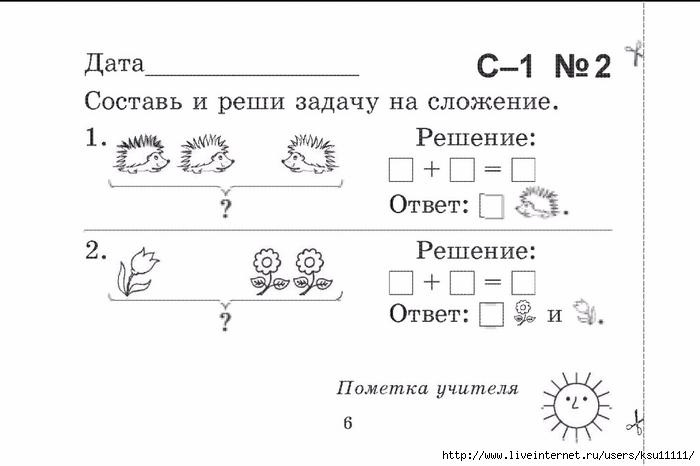
Открываем учебник на стр.109. №1 Решение задач Прочитайте её и обсудите в парах. Обратите внимание у вас есть схема к данной задаче, на нее вы можете опираться при решении задачи. Проверка(фронатально) Записываем решение задачи в тетрадь. 2) Решаем задачу под № 2 С.110 (самостоятельно) Проверка(фронтально) на доске . Итак, строительство идет полным ходом, но нам с вами нужно передохнуть.
VI. Строительство 3 этажа. Составление задач по таблице. По вариантам выполняем 2 ученика работают у доски, остальные в тетрадях
ИЛИ № 8 на стр.111 Глядя на построенный дом, давайте вспомним что мы сегодня делали на уроке? -Что повторили? На партах у каждого лежат смайлики, поднимите тот смайл, который характеризует ваше отношение к сегодняшнему уроку. Вы научились и можете помочь другим. Спасибо за работу! Урок окончен! | даааа Фундамент Ответы детей Ответы детей | На слайде выражения На слайде задачи Наглядности к задаче вывешиваю на доске Фронтальная работа Работа в парах Индивидуальная работа На доске вывешивается задача Вывешиваю таблицу к задаче. Раздаю карточки с заданием «дополни предложения» задание взято из учебника ( с.111 № 10). |
Решаем и пишем правильно — Сайт Беляевой Ирины Анатольевны
Порядок выполнения действий
Leave a comment
1. Найдите значения выражений по двум разным схемам. Почему с одними и теми же числами и действиями получились разные результаты? Потому что отличается порядок выполнения действий: в первом выражения они выполнены слева направо, а во втором справа налево. Вывод: нельзя менять порядок действий 2. Рассмотрим выражение, составленное только с помощью действий сложения и вычитания: 7 – 2 + 3 – 5. С этими действиями знакомятся в школе в 1 классе….
Найдите значения выражений по двум разным схемам. Почему с одними и теми же числами и действиями получились разные результаты? Потому что отличается порядок выполнения действий: в первом выражения они выполнены слева направо, а во втором справа налево. Вывод: нельзя менять порядок действий 2. Рассмотрим выражение, составленное только с помощью действий сложения и вычитания: 7 – 2 + 3 – 5. С этими действиями знакомятся в школе в 1 классе….
Read More >>
Задачи на деление
Какие задачи решают делением? Схемы задач на деление можно получить из схем задач на умножение, ведь деление — это действие, обратное умножению. Из каждой схемы задач на умножение получаются по две схемы задач на деление.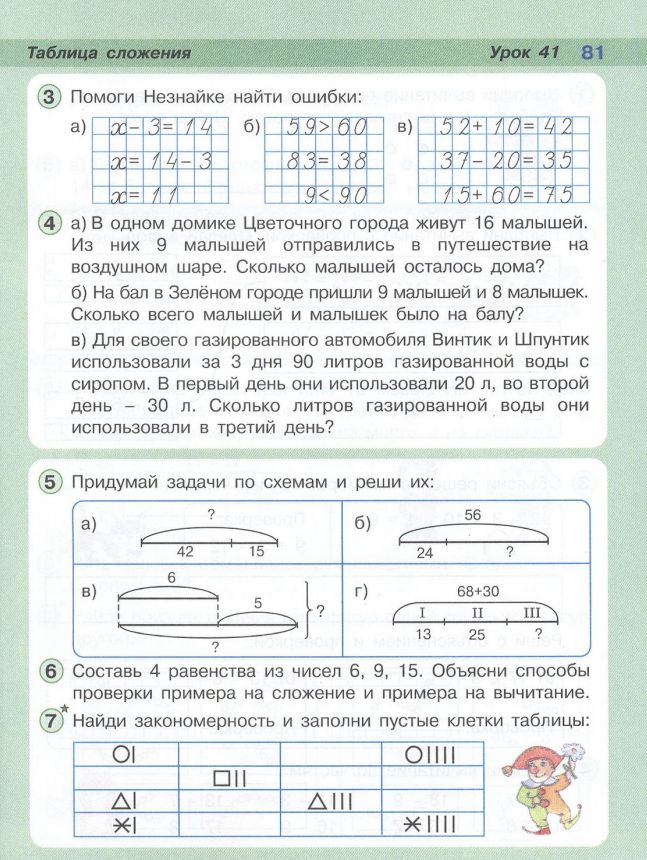 В первой из них даны: произведение с и 1-й множитель а, неизвестен 2-й множитель. Во второй даны: произведение с и 2-й множитель b, неизвестен 1-й множитель. Схема 1 а. Есть сколько-то _ _ _ ,…
В первой из них даны: произведение с и 1-й множитель а, неизвестен 2-й множитель. Во второй даны: произведение с и 2-й множитель b, неизвестен 1-й множитель. Схема 1 а. Есть сколько-то _ _ _ ,…
Read More >>
Задачи на умножение
Leave a comment
Какие задачи решают умножением? Речь пойдет о часто встречающихся схемах задач, где требуется применить умножение. Схема 1.Есть b _ _ _ , в каждом по а … .Сколько … в них всего? Ответ: а ∙ b … . Как получить из этой схемы конкретные задачи? Как обычно: нужно вместо букв а и b ставить какие-нибудь числа, а вместо пропусков — подходящие существительные (для пунктира из точек — одно и то…
Read More >>
Задачи на вычитание
Leave a comment
Какие задачи решают вычитанием? Раз вычитание — это действие, обратное сложению, то можно догадаться, как получить схемы задач на вычитание.
Read More >>
Задачи на сложение
Leave a comment
Простые и составные задачи Простые задачи от составных отличаются не уровнем сложности, а количеством выполняемых арифметических действий. Простая задача подразумевает выполнение только одного действия, а составная – более одного. Поэтому составную задачу можно представить в виде цепочки простых подзадач, позволяющих в конечном итоге ответить на вопрос задачи. И таких цепочек может быть не одна, то есть задача может иметь несколько решений.
Read More >>
Углы
Leave a comment
Уважаемые читатели, пришла пора познакомиться с геометрической фигурой – угол. Посмотрите на аппликацию, из каких фигур составлена ракета? Правильно, из треугольников, четырехугольников и шестиугольников. А какое слово спрятано в названиях этих фигур? Совершенно верно, угол. Так что же это за фигура? Сначала разберемся, что из себя представляет прямая линия. Вообразите себе тонкую нить, натянутую между двумя гвоздиками. А теперь представьте, что эти два гвоздика разлетаются в разные стороны до бесконечности….
Read More >>
Единицы длины
Leave a comment
Когда возникает необходимость изучить какой-либо объект, то наравне с такой характеристикой, как вес, называют и его размеры. Чтобы определить названные параметры, мы сравниваем их с международным эталоном массы (1 кг) и эталоном длины (1 м). Для удобства введены с помощью приставок ещё дольные и кратные единицы измерения, отличающиеся от основной величины в 10, 100, 1000 и т. д. раз. Кратная единица – единица величины, в целое число раз большая основной единицы. Дольная единица – единица…
Чтобы определить названные параметры, мы сравниваем их с международным эталоном массы (1 кг) и эталоном длины (1 м). Для удобства введены с помощью приставок ещё дольные и кратные единицы измерения, отличающиеся от основной величины в 10, 100, 1000 и т. д. раз. Кратная единица – единица величины, в целое число раз большая основной единицы. Дольная единица – единица…
Read More >>
Измерение времени
Leave a comment
В наши дни используют механические и электронные часы. Электронные часы просто показывают количество пройденных часов и минут от начала суток. Сутки начинаются ночью с нуля часов и нуля минут. 12 часов проходит от этого времени до полудня, а потом ещё 12 часов от полудня до полуночи.
Read More >>
Двузначные числа
Leave a comment
Десятки Когда речь идёт о больших числах, то счёт удобно вести десятками или даже сотнями, тысячами и т.д. Если взять один десяток каких-то предметов, то говорят, что взяли десять: 10, если два десятка – двадцать: 20, три десятка – тридцать: 30, четыре десятка – сорок: 40, пять десятков – пятьдесят: 50, шесть десятков – шестьдесят: 60, семь десятков – семьдесят: 70, восемь десятков – восемьдесят: 80, девять десятков – девяносто:…
Read More >>
Перестановка слагаемых
Leave a comment
Мальчик держит несколько флажков. На рисунке мы видим слева от него два синих флажка в правой руке и с другой стороны – один красный флажок в левой руке. Найдём, сколько всего флажков держит мальчик. Для этого к двум синим флажкам прибавим один красный флажок. Получаем три флажка: 2 + 1 = 3. Но вот мальчик поменял флажки местами. Теперь слева от него один красный флажок, а с другой стороны –…
На рисунке мы видим слева от него два синих флажка в правой руке и с другой стороны – один красный флажок в левой руке. Найдём, сколько всего флажков держит мальчик. Для этого к двум синим флажкам прибавим один красный флажок. Получаем три флажка: 2 + 1 = 3. Но вот мальчик поменял флажки местами. Теперь слева от него один красный флажок, а с другой стороны –…
Read More >>
28.3: Использование диаграмм для представления умножения
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 40303
Lesson
Давайте используем диаграммы с площадями для поиска продуктов.
Упражнение \(\PageIndex{1}\): оценка продукта
Для каждого из следующих товаров выберите наилучшую оценку его стоимости. Будьте готовы объяснить свои рассуждения.
Будьте готовы объяснить свои рассуждения.
- \((6.8)\cdot (2.3)\)
- \(1.40\)
- \(14\)
- \(140\)
- \(74\cdot (8.1)\)
- \(5.6\)
- \(56\)
- \(560\)
- \(166\cточка (0,09)\)
- \(1.66\)
- \(16.6\)
- \(166\)
- \((3.4)\cdot (1.9)\)
- \(6,5\)
- \(65\)
- \(650\)
Упражнение \(\PageIndex{2}\): подключение площадных диаграмм к вычислениям с целыми числами
- Вот три способа нахождения площади прямоугольника, который составляет \(24\) единиц на \(13\) единиц.
 Верхний правый прямоугольник, горизонтальная сторона, 4, площадь, 40. Нижний левый прямоугольник, вертикальная сторона, 3, площадь 60. Нижний правый прямоугольник, площадь, 12 .Диаграмма 2, прямоугольник разделен по горизонтали на 2 прямоугольника. Верхний прямоугольник, вертикальная сторона 10, горизонтальная сторона 24, площадь 240. Нижний прямоугольник, вертикальная сторона 3, площадь 72. Диаграмма 3, прямоугольник разделен вертикально на 2 прямоугольника. Левый прямоугольник, вертикальная сторона, 13, горизонтальная сторона, 20, площадь, 260. Правый прямоугольник, горизонтальная сторона, 4, площадь, 52.
Верхний правый прямоугольник, горизонтальная сторона, 4, площадь, 40. Нижний левый прямоугольник, вертикальная сторона, 3, площадь 60. Нижний правый прямоугольник, площадь, 12 .Диаграмма 2, прямоугольник разделен по горизонтали на 2 прямоугольника. Верхний прямоугольник, вертикальная сторона 10, горизонтальная сторона 24, площадь 240. Нижний прямоугольник, вертикальная сторона 3, площадь 72. Диаграмма 3, прямоугольник разделен вертикально на 2 прямоугольника. Левый прямоугольник, вертикальная сторона, 13, горизонтальная сторона, 20, площадь, 260. Правый прямоугольник, горизонтальная сторона, 4, площадь, 52.- Что общего у диаграмм? Чем они похожи?
- Чем они отличаются?
- Если бы вам нужно было найти площадь прямоугольника размером 37 на 19 единиц, какой из трех способов разложения прямоугольника вы бы использовали? Почему?
- Возможно, вы знакомы с различными способами записи вычислений умножения.
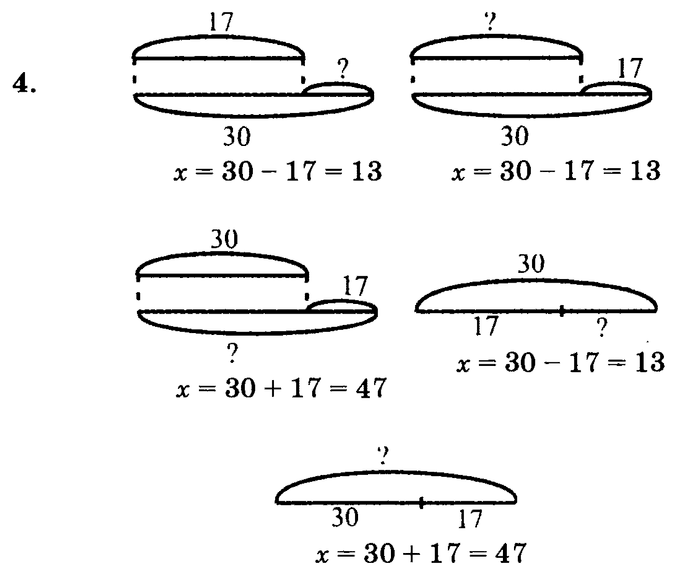 Вот два способа вычислить 24 умножить на 13.
Вот два способа вычислить 24 умножить на 13.
Обсудите с вашим партнером:
- Каким образом в расчете А получается каждый из частичных произведений? Например, откуда взялось число 12?
- Как в расчете B получаются 72 и 240?
- Посмотрите на диаграммы в первом вопросе. Какая диаграмма соответствует расчету А? Какой из них соответствует расчету B?
- Как частичные произведения в расчете A и 72 и 240 в расчете B связаны с числами на диаграммах?
- Используйте два следующих метода, чтобы найти произведение 18 и 14, затем сравните полученные значения.
- Расчет численно.
- Вот прямоугольник размером 18 на 14 единиц. Найдите его площадь в квадратных единицах, разложив его. Покажите свои рассуждения.
- Сравните значения \(18\cdot 14\), полученные двумя способами. Если они не совпадают, проверьте свою работу.
- Используйте апплет, чтобы проверить свои ответы и изучить собственные сценарии. Чтобы настроить значения, переместите точки на концах сегментов.
Упражнение \(\PageIndex{3}\): подключение площадных диаграмм к вычислениям с десятичными дробями
- Диаграммы с областями можно использовать для представления произведений десятичных дробей. Вот диаграмма с площадями, представляющая \((2.4)\cdot (1.3)\).
 Верхний правый прямоугольник, вертикальная сторона, 1, горизонтальная сторона, 0 точек 4. Нижний левый прямоугольник, вертикальная сторона, 0 точек 3, горизонтальная сторона, 2. Нижний правый прямоугольник, вертикальная сторона, 0 баллов 3, горизонтальная сторона, 0 баллов 4.
Верхний правый прямоугольник, вертикальная сторона, 1, горизонтальная сторона, 0 точек 4. Нижний левый прямоугольник, вертикальная сторона, 0 точек 3, горизонтальная сторона, 2. Нижний правый прямоугольник, вертикальная сторона, 0 баллов 3, горизонтальная сторона, 0 баллов 4.- Найдите область, представляющую \((0.4)\cdot (0.3)\)? Обозначьте эту область площадью \(0,12\).
- Пометьте каждый из других регионов соответствующими областями.
- Найдите значение \((2.4)\cdot (1.3)\). Покажите свои рассуждения.
- Вот два способа вычисления \(2,4\) умножить на \(1,3\).
 Первый ряд: 2 балла 4. Второй ряд: знак умножения, 1 балл 3. Горизонтальная черта. Третий ряд: 0 баллов 7 2. Четвертый ряд: плюс 2 балла 4. Горизонтальная линия. Пятый ряд: 3 п. 1 2.
Первый ряд: 2 балла 4. Второй ряд: знак умножения, 1 балл 3. Горизонтальная черта. Третий ряд: 0 баллов 7 2. Четвертый ряд: плюс 2 балла 4. Горизонтальная линия. Пятый ряд: 3 п. 1 2.Проанализируйте расчеты и обсудите с партнером:
- Откуда в расчете А берутся 0,12 и другие частичные произведения? Откуда в расчете Б берутся 0,72 и 2,4? Как рассчитываются другие числа, выделенные синим цветом?
- Почему в каждом расчете числа, выделенные синим цветом, выстроены вертикально именно так, как они есть?
- Найдите произведение \((3.1)\cdot (1.5)\), нарисовав и обозначив площадную диаграмму. Покажите свои рассуждения.
- Покажите, как вычислять \((3.1)\cdot (1.5)\), используя числа без диаграммы. Будьте готовы объяснить свои рассуждения. Если вы застряли, используйте примеры из предыдущего вопроса, чтобы помочь вам.
- Используйте апплет, чтобы проверить свои ответы и изучить собственные сценарии. Чтобы настроить значения, переместите точки на концах сегментов.

Готовы ли вы к большему?
Сколько гектаров принадлежит вашей школе? Сколько это моргенов?
Упражнение \(\PageIndex{4}\): Использование метода частичных произведений
- Пометьте диаграмму с площадями, чтобы представить \((2.5)\cdot (1.2)\) и найти этот продукт.
- Разложите каждое число на его единицы с основанием десять (единицы, десятые и т. д.) и запишите их в полях с каждой стороны прямоугольника.
- Обозначьте области A, B, C и D их площадями. Покажите свои рассуждения.
- Найдите продукт, представленный на диаграмме с областями. Покажите свои рассуждения.
- Вот два способа вычисления \((2.5)\cdot (1.2)\). Каждое число в рамке обозначает площадь одного или нескольких регионов на диаграмме площади.
 Второй ряд: знак умножения, 1 балл 2. Горизонтальная черта. Третий ряд: 0 баллов 1. Четвертый ряд: 0 баллов 4. Пятый ряд: 0 баллов 5. Шестой ряд: плюс 2. Горизонтальная линия. Седьмой ряд: 3 п. 0 0. Расчет Б, 5 ряд. Первый ряд: 2 балла 5. Второй ряд: знак умножения, 1 балл 2. Горизонтальная черта. Третий ряд: 0 баллов 5. Четвертый ряд: плюс 2 балла 5. Горизонтальная линия. Пятый ряд: 3 балла 0 0,
Второй ряд: знак умножения, 1 балл 2. Горизонтальная черта. Третий ряд: 0 баллов 1. Четвертый ряд: 0 баллов 4. Пятый ряд: 0 баллов 5. Шестой ряд: плюс 2. Горизонтальная линия. Седьмой ряд: 3 п. 0 0. Расчет Б, 5 ряд. Первый ряд: 2 балла 5. Второй ряд: знак умножения, 1 балл 2. Горизонтальная черта. Третий ряд: 0 баллов 5. Четвертый ряд: плюс 2 балла 5. Горизонтальная линия. Пятый ряд: 3 балла 0 0,- В полях рядом с каждым номером укажите букву (буквы) соответствующего региона (регионов).
- Какие два числа в расчете B нужно перемножить, чтобы получить 0,5?
Какие числа нужно перемножить, чтобы получить 2,5?
Резюме
Предположим, мы хотим вычислить произведение двух чисел, записанных в десятичной системе счисления. Чтобы объяснить, как это сделать, мы можем использовать то, что мы знаем о десятичных числах и площади прямоугольников.
Вот схема прямоугольника со сторонами 3,4 единицы и 1,2 единицы.
Рисунок \(\PageIndex{9}\)Его площадь в квадратных единицах равна произведению
\((3. 4)\cdot (1.2)\)
4)\cdot (1.2)\)
Чтобы вычислить это произведение и найти площадь прямоугольника, мы можем разложить длину каждой стороны на десятичные единицы, \(3,4=3+0,4\) и \(1,2=1+0,2\), разложив прямоугольник на четыре меньших подпрямоугольника.
Рисунок \(\PageIndex{10}\): диаграмма с областями. Прямоугольник, разделенный на 4 прямоугольника, A, B, C, D. D, вертикальная сторона, 1, горизонтальная сторона, 3. C, вертикальная сторона, 1, горизонтальная сторона, 0 баллов 4. B, вертикальная сторона, 0 баллов 2, горизонтальная сторона, 3. A, вертикальная сторона, 0 баллов 2, горизонтальная сторона, 0 баллов 4.Мы можем переписать произведение и расширить его дважды:
\(\begin{aligned} (3.4)\cdot (1.2)&=(3+0.4)\cdot (1+0.2) \\ &= (3+0.4) )\cdot 1+(3+0.4)\cdot 0.2 \\ &=3\cdot 1+3\cdot (0.2)+(0.4)\cdot 1+(0.4)\cdot (0.2)\end{выровнено}\ )
В последнем выражении каждый из четырех членов называется частичным произведением. Каждое частичное произведение дает площадь подпрямоугольника на диаграмме. Сумма четырех частичных произведений дает площадь всего прямоугольника.
Сумма четырех частичных произведений дает площадь всего прямоугольника.
Вышеприведенные горизонтальные расчеты можно представить как два вертикальных расчета.
Рисунок \(\PageIndex{11}\): Два вертикальных расчета по 3 балла 4 раза по 1 баллу 2. Первый расчет, 7 строк. Первый ряд: 3 балла 4. Второй ряд: знак умножения, 1 балл 2. Горизонтальная черта. Третий ряд: 0 баллов 0 8, А. Четвертый ряд: 0 баллов 6, Б. Пятый ряд: 0 баллов 4, С. Шестой ряд: плюс 3, Г. Горизонтальная линия. Седьмой ряд: 4 п. 0 8. Второй расчет, 5 рядов. Первый ряд: 3 балла 4. Второй ряд: знак умножения, 1 балл 2. Горизонтальная черта. Третий ряд: 0 п. 6 8, А плюс Б. Четвертый ряд: плюс 3 п. 4, С плюс Г. Горизонтальная линия. Пятый ряд: 4 балла 0 8.Расчет слева является примером метода частичных произведений. Он показывает значения каждого частичного произведения и букву соответствующего подпрямоугольника. Каждое частичное произведение дает площадь:
- A равно 0,2 единицы на 0,4 единицы, поэтому его площадь равна 0,08 квадратной единицы.

- B имеет размер 3 на 0,2 единицы, поэтому его площадь равна 0,6 кв.
- C имеет размер 0,4 на 1 единицу, поэтому его площадь равна 0,4 квадратной единицы.
- D составляет 3 единицы на 1 единицу, поэтому его площадь равна 3 квадратным единицам.
- Сумма частичных произведений равна \(0,08+0,6+0,4+3\), поэтому площадь прямоугольника равна 4,08 квадратных единиц.
Расчет справа показывает стоимость двух продуктов. Каждое значение дает общую площадь двух подпрямоугольников:
- Объединенные области A и B имеют площадь 0,68 квадратных единиц; 0,68 — это значение \((3+0,4)\cdot 0,2\).
- Объединенные области C и D имеют площадь 3,4 квадратных единиц; 3,4 — это значение \((3+0,4)\cdot 1\).
- Сумма значений двух произведений равна \(0,68+3,4\), поэтому площадь прямоугольника равна 4,08 квадратных единиц.
Практика
Упражнение \(\PageIndex{5}\)
Вот прямоугольник, разделенный на четыре меньших прямоугольника.
Для каждого выражения выберите вложенный прямоугольник, площадь которого в квадратных единицах соответствует выражению.
- \(3\cточка (0,6)\)
- \((0.4)\cdot 2\)
- \((0.4)\cdot (0.6)\)
- \(3\cточка 2\)
Упражнение \(\PageIndex{6}\)
Вот диаграмма с площадями, представляющая \((3.1)\cdot (1.4)\).
Рисунок \(\PageIndex{13}\)- Найдите площади подпрямоугольников A и B.
- Какова площадь прямоугольника 3,1 на 1,4?
Упражнение \(\PageIndex{7}\)
Нарисуйте площадную диаграмму, чтобы найти \((0,36)\cdot (0,53)\). Пометьте и организуйте свою работу, чтобы за ней могли следить другие.
Упражнение \(\PageIndex{8}\)
Найдите все продукты. Покажите свои рассуждения.
- \((2.5)\cdot (1.4)\)
- \((0,64)\cdot (0,81)\)
Упражнение \(\PageIndex{9}\)
Завершите расчеты, чтобы каждый из них показал правильную сумму.
(Из модуля 5.2. 2)
Упражнение \(\PageIndex{10}\)
Диего купил 12 мини-маффинов за 4,20 доллара.
- При таком раскладе, сколько Диего заплатил бы за 4 мини-булочки?
- Сколько мини-маффинов мог купить Диего на 3 доллара? Объясните или покажите свои рассуждения. Если вы застряли, рассмотрите возможность использования таблицы.
| количество мини-маффинов | цена в долларах |
|---|---|
| \(12\) | \(4. 20\) 20\) |
(Из модуля 2.4.2)
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Теги

Ленточные диаграммы: визуализация математики — руководство для умного обучения
Что такое ленточные диаграммы в математике?
Ленточная диаграмма, иногда называемая линейчатой моделью, моделью длины или полосой дробей, представляет собой вид визуальной модели, используемой при обучении математике для демонстрации числовых отношений и облегчения решения учащимися различных чисел и задач.
Ленточная диаграмма представляет собой прямоугольную полосу или прямоугольник, который можно разделить по-разному для представления известных и неизвестных величин.
Общая идея заключается в том, что с помощью рисунка или изображения учащиеся могут лучше визуализировать проблему, а затем решить, какую операцию им следует использовать для получения ответа.
Как они используются на уроках математики?
Ленточные диаграммы на самом деле являются довольно гибкими визуальными инструментами, которые можно использовать при изучении различных тем и при решении различных типов текстовых задач.
Как правило, ленточные диаграммы используются в качестве инструмента, помогающего учащимся визуализировать задачи и операции, которые их просят выполнять (сложение, вычитание, умножение и деление), что может быть особенно полезно при решении текстовых задач.
Главный принцип заключается в том, что, рисуя модель, учащиеся учатся выбирать различные переменные, данные в словесной задаче, то, что им нужно найти, а затем могут выяснить, какие операции и методы им нужно использовать для решения задачи. обсуждаемый.
Различные стратегии построения ленточных диаграмм
В целом, родители и учителя могут использовать ленточные диаграммы для решения различных математических задач по-разному.
Часть-Часть Целое/Равные части целогоВообще говоря, первая ленточная диаграмма, которую изучают большинство учащихся, представляет собой модель часть-часть-целое.
В сущности, сверху помещается большой прямоугольник, представляющий целую сумму.
Под ним находится прямоугольник того же размера, разделенный на две или более частей, представляющих различные части, которые могут составить целое.
В зависимости от задачи они могут быть разного размера (представлять два разных числа — например, при сложении или вычитании) или одинаковыми по размеру.
Стержень можно даже разбить на несколько отдельных частей, как это происходит при умножении и делении.
Студенты получают некоторую информацию, но быстро понимают, что они найдут и заполнят недостающие части.
Сравнительная ленточная диаграммаСравнительная ленточная диаграмма, как следует из названия, представляет собой интуитивно понятный и наглядный способ решения проблем, когда есть разница в количествах и когда есть известный/неизвестный компонент.
Они могут быть идеальными, например, при решении задач, которые задают учащимся такие вещи, как:
- Насколько больше
- Насколько больше
- На сколько меньше
- Больше
- Меньше
- И так далее
Подобно моделям «Часть-Часть-Целое», сравнительные полосовые диаграммы имеют две полосы, расположенные одна над другой, чтобы учащиеся могли сразу понять разницу в длине между ними, а в скобках указаны соответствующие числа и итоги.
Идея заключается в том, что именно эти наглядные столбцы могут стать легкой отправной точкой для понимания различий в суммах.
Более того, однако, мы обнаружили, что они могут сделать понимание и разбор задач на сравнение слов немного проще для учащихся, особенно с учетом большого разнообразия словарного запаса и терминов, которые могут использоваться в этих задачах (выше, чем, шире, больше, чем , столько же, сколько меньше, меньше, больше, дороже и т. д.).
Использование ленточных диаграмм для решения более сложных задач
Одно из распространенных заблуждений состоит в том, что ленточные диаграммы используются только для основных операций, таких как сложение, вычитание, умножение и деление.
Реальность такова, что они довольно гибкие и могут быть использованы в более сложной математике и для более сложных и сложных текстовых задач, которые часто бросают учеников.
Например, ленточные диаграммы можно использовать для иллюстрации и решения задач соотношения, как показано ниже.
Как эффективно настроить ленточную диаграмму
Важно помнить, что ленточные диаграммы — это инструмент, и хороший родитель, обучающийся на дому, не может быть слишком жестким, когда дело доходит до его точного использования и применения.
Само собой разумеется, что при решении любых задач необходимо помнить об уникальной личности, понимании, способностях и навыках учащегося.
Тем не менее, есть несколько шагов, которые будут выполняться в большинстве программ при обучении учащихся использованию ленточных диаграмм. Обычно это:
- Внимательно и до конца прочитайте вопрос.
- Выделите или обведите любую важную информацию, содержащуюся в вопросе, уделяя особое внимание цифрам и важным словам или фразам (больше, вместе, столько).
- Найти переменные «кто» и «что» – в частности:
- Кто проблема о/ о чем проблема о
- Что отсутствует
03
- Перечитывая ключевую фразу вопроса (и обращая особое внимание на отдельные фразы – сколько, сколько всего, кто/что больше, на сколько и т.
 д. ), решите, какую операцию необходимо использовать решить проблему.
д. ), решите, какую операцию необходимо использовать решить проблему. - Нарисуйте и подпишите столбцы, используя собранную информацию
- Просмотрите задачу, чтобы убедиться, что столбцы имеют смысл с учетом представленной информации
- Завершите расчет, используя операцию, чтобы получить ответ
Почему в некоторых учебных программах используются ленточные диаграммы
Системный подход к решению сложных текстовых задач
Младшие школьники часто испытывают затруднения при решении текстовых задач по разным причинам.
Во-первых, текстовые задачи (в отличие от вычислительных упражнений) включают в себя гораздо больше, чем математику.
Вместо простой математической задачи учащиеся внезапно сталкиваются с абзацем слов и чисел.
В этом нагромождении слов они должны отследить много разной информации, выяснить, что важно, определить, в чем на самом деле состоит вопрос (поскольку он обычно замаскирован специальной математической лексикой) и, наконец, они должны выяснить что делать.
Ленточные диаграммы могут помочь учащимся, предоставив им готовый и систематический метод решения этих задач.
Чтобы построить ленточную диаграмму, учащиеся должны разобрать важную информацию, собрав информацию о:
- В чем проблема
- Какая информация мне предоставлена
- Какая информация отсутствует
Как учащиеся получают больше практики в построении ленточных диаграмм, они могут стать более искусными в выделении ключевой информации, игнорировании ненужной информации и определении ключевых математических терминов в качестве подсказок к тому, о чем предполагается операция.
Кроме того, по мере того, как они получают больше опыта в рисовании этих диаграмм, они могут лучше организовывать и представлять эту информацию осмысленным и организованным образом, что полезно для учащихся, которым трудно показать свою работу или сообщить свои мысли лаконично или математически.
Визуальный подход, помогающий младшим учащимся с абстрактными понятиями
Еще одна проблема со словами заключается в том, что они часто заставляют учащихся рассуждать или думать над задачами абстрактно.
Как правило, в возрасте до 12 лет учащиеся гораздо лучше видят мир в конкретных терминах, чем понимают абстракции.
Конечно, они мыслят логически и по большей части могут понимать символы, но лучше всего они понимают вещи, наблюдая их напрямую.
Словесная задачка с участием двух поездов, мчащихся по пути между двумя городами, или разница в возрасте между несколькими детьми, или разные размеры разных предметов, или разные цены — все это может быть очень трудным для детей, чтобы понять.
Обучение построению ленточной диаграммы может помочь младшим учащимся, позволяя им видеть и работать с визуальным (и конкретным) представлением информации вопроса, а не просто полагаться на письменное слово.
Более мягкое введение в алгебраическое мышление
Тем не менее, важно отметить, что, несмотря на то, что ленточные диаграммы наглядны, они все же остаются в некоторой степени символическими и стандартизированными, в определенной степени абстрагированными от различных тем и персонажей, которые появляются в текстовой задаче.
В конце концов, учащиеся работают с прямоугольниками, и их не просят буквально рисовать каждую задачу.
В результате они по-прежнему могут действовать, чтобы помочь детям привыкнуть к алгебраическому мышлению, то есть к способности представлять, обобщать или рассуждать через проблему, используя абстрактные математические символы и отношения.
Имеются убедительные доказательства их полезности.
Поскольку многие педагоги (и родители) решают текстовые задачи несколько иначе, чем привыкли многие педагоги (и родители), некоторые задаются вопросом, оказывает ли использование ленточных диаграмм при решении математических задач какое-либо реальное влияние на успех.
В последние годы проводились исследования по оценке того, насколько хорошо ленточные диаграммы могут помочь учащимся понять и решить математические операции и текстовые задачи.
Выводы из них были весьма положительными. Исследования показали, например, что использование ленточных диаграмм в качестве инструмента может помочь учащимся начальной школы правильно отвечать на текстовые задачи, и есть некоторые свидетельства того, что это может быть эффективным инструментом для исправления ошибок.
Плюсы и минусы использования ленточных диаграмм в обучении на дому
Важно помнить, что ленточные диаграммы — это лишь один из многих инструментов, которые родители и ученики могут использовать для решения текстовых задач.
Также важно отметить, что ленточные диаграммы как инструмент могут иметь свои плюсы и минусы, и их использование в обучении не всегда подходит каждому учащемуся.
Преимущества ленточных диаграмм
Простота обучения как для родителей, так и для учащихсяНаучиться использовать ленточные диаграммы и вплетать их в подход к решению задач на самом деле не так уж сложно, если вы освоите их.
По большому счету, ленточные диаграммы — это просто особый способ набросать ключевые детали вопроса несколькими различными способами, и они могут быть довольно интуитивно понятными как для родителей, так и для учащихся, чтобы учиться и использовать.
Простое для понимания визуальное представление информации о задачах со словами Как упоминалось ранее, создание ленточной диаграммы дает учащимся графическое представление, которое они могут использовать, чтобы лучше понять, что их просят сделать.
Ученикам может быть намного легче увидеть разницу в размерах между двумя или более квадратами, чем с параграфом, включающим поезда, самолеты, одежду, шоколад, людей, рост, размеры и многое другое.
Поощряет учащихся разбивать на части и систематически анализировать текстовые задачиЧтобы правильно построить ленточную диаграмму, учащиеся должны научиться читать предложение, определять ключевые элементы, определять, чего не хватает, и понимать некоторые важные ключевые фразы.
В результате, работа с ленточными диаграммами может помочь учащимся научиться решать текстовые задачи (и излагать их результаты) более организованно и логично.
Легко интегрируется с манипулятивными и практическими учебными объектамиЛенточные диаграммы довольно легко и естественно подходят для практических подходов к обучению математике.
Полоски можно сконструировать из кубиков, монет, палочек или чего-либо еще, что может превратить обучение в мультисенсорную деятельность, которая больше подходит тактильным учащимся.
Недостатки
Не каждому учащемуся нужно использовать ленточные диаграммы (или они хотят этого)Несмотря на то, что ленточные диаграммы являются полезным инструментом, они не являются инструментом, который нужен или который предпочитает использовать каждый учащийся.
Некоторые учащиеся очень легко «решают» текстовые задачи, будучи в состоянии почти интуитивно выбирать ключевую информацию и без проблем обдумывать и представлять их с помощью уравнений и символов.
Другие учащиеся более процедурны по своей природе и не очень заботятся об использовании наглядных материалов и других моделей. Такие учащиеся могут предпочесть более простой, основанный на числах подход к решению текстовых задач (т. е. запоминание ряда шагов, которым нужно следовать), или могут просто хорошо реагировать на дополнительную практику и упражнения.
В любом случае такие учащиеся могут быть разочарованы принуждением к использованию ленточных диаграмм.
Более одаренные студенты-математики могут даже считать этот процесс излишним и обременительным для себя.
Это может замедлить процесс решения задач.Ленточные диаграммы включают идентификацию и сбор информации из словесной задачи, ее организацию и построение модели, которая имеет какой-то смысл с точки зрения масштаба.
Следовательно, настройка ленточных диаграмм и работа с ними может занять некоторое время, особенно когда учащиеся еще не освоились с процессом, что, в свою очередь, может увеличить продолжительность урока математики или практического занятия.
Не применимо ко всем задачам со словами по математике
Хотя они, как правило, хорошо работают для большинства задач со словами, связанных с операциями и даже алгеброй, создание ленточных диаграмм не всегда имеет смысл (и даже не работает) со всеми типами математических задач.
Статистика и геометрия, например, могут иметь интересные и сложные текстовые задачи, связанные с ними, но не обязательно поддаются использованию в качестве объектов ленточных диаграмм и требуют собственных моделей и алгоритмов для подражания.
В каких учебных программах используются ленточные диаграммы и другие более простые математические инструменты?
Ленточные диаграммы, в частности, наиболее заметно (хотя и не исключительно) характерны для программ, основанных на сингапурском подходе к математике, и эти программы, как правило, довольно хорошо помогают родителям и учащимся в пошаговом использовании. -шаговый способ.
Сингапурский подход к математике (названный так, поскольку он изначально был разработан в качестве основной учебной программы по математике для учащихся начальной школы в Сингапуре) — это концептуальный математический метод, направленный на обучение учащихся почему отстает от математики и почему она работает именно так, а также критически мыслить и решать математические задачи, не слишком полагаясь на запоминание и тренировку.
При этом, а также путем обучения для достижения мастерства, эти программы, как правило, дают учащимся более глубокое понимание числовых отношений, хорошую беглость математики и навыки решения задач по сравнению с более традиционными программами.
Сингапурский метод или подход очень сильно верит в то, что они называют стадиями конкретного-графического-абстрактного обучения, т. е. плавно переводя учащегося с конкретной стадии понимания через стадию визуального моделирования и, наконец, к точке, где учащийся чувствует себя комфортно используя абстрактные символы и уравнения.
Наряду с числовыми связями, ленточные диаграммы (которые в этих программах чаще называются столбчатыми моделями), как правило, удобно вписываются в визуальную/графическую стадию обучения.
Если этот тип математической программы вас интересует или у вас есть ученик, которому, по вашему мнению, было бы полезно подходить к математическим задачам более наглядно, например, с помощью ленточных диаграмм, то мы настоятельно рекомендуем следующие программы.
Singapore Math
Один из самых известных и широко используемых примеров сингапурского подхода в сообществе домашнего обучения. Singapore Math предлагает тщательную и строгую учебную программу по математике для учащихся K-8, в которой особое внимание уделяется практическому обучению и визуальному представлению математики. проблемы.
проблемы.
Предлагая несколько различных изданий (Основная математика и Измерения), визуально насыщенные книги Singapore Math поощряют более глубокий и критический подход к математике, который на протяжении многих лет воспитывал очень сильных и способных студентов-математиков
Прочтите наш подробный обзор Singapore Math
Прочитайте наш подробный обзор их последней учебной программы Primary Mathematics 2022 Edition
Math in Focus
Выпущенный в 2009 году, подготовленный Маршаллом Кавендишем и опубликованный Houghton Mifflin Harcourt, Math in Focus также основан на сингапурском подходе. , преподает математику аналогичным образом, а также предлагает строгую и тщательную учебную программу по математике.
Сингапур Math и Math in Focus похожи, и разница в основном заключается в том, что Math in Focus разработана как традиционная школьная книга, затрагивает немного больше содержания и, как правило, имеет немного больше встроенной дифференциации.

 Как называются компоненты действия деления?
Как называются компоненты действия деления? 
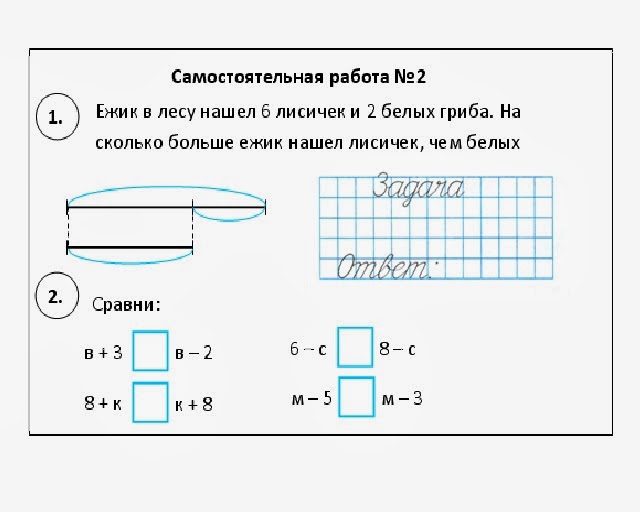
 , и количество апельсинов 4 штуки)
, и количество апельсинов 4 штуки) 
