Сериация для дошкольников в картинках: Книга: “Что такое сериация? Развивающая тетрадь для детей дошкольного и младшего школьного возраста” – Савенков, Савенкова. Купить книгу, читать рецензии | ISBN 5931340882
1 c53vq 1 презентация, доклад
Коррекционная работа по формированию логических операций.
Формирование сериации.
Формирование логических операций.
Интеллектуальные операции — это система умственных действий, включающих целый ряд разнообразных логических актов: анализа, синтеза, сравнения, обобщения, классификации, умозаключения и т. д.
С целью формирования понятия сохранения детям предлагаются следующие упражнения.
Раскладывание шашек разного цвета.
I вариант. Раскладывание 7 голубых и 7 красных шашек в два ряда в определенном пространственном соответствии. Задается вопрос: «У меня столько же голубых шашек, сколько и красных? То же количество?»
II вариант. Раскладывание 7 голубых и 7 красных шашек следующим образом: в первом ряду голубые шашки сдвинуты и занимают небольшое пространство; втором ряду красные шашки раздвинуты и занимают большее пространство.
III вариант. Красные шашки раздвинуты, голубые сдвинуты. Упражнение проводится аналогичным образом.
IV вариант. 7 зеленых и 9 желтых квадратов раскладываются в два ряда так, чтобы оба ряда занимали одинаковое пространство. Задается вопрос: «Одинаковое ли количество квадратов в обоих рядах?»
2. Упражнения на провоцирующее соответствие.
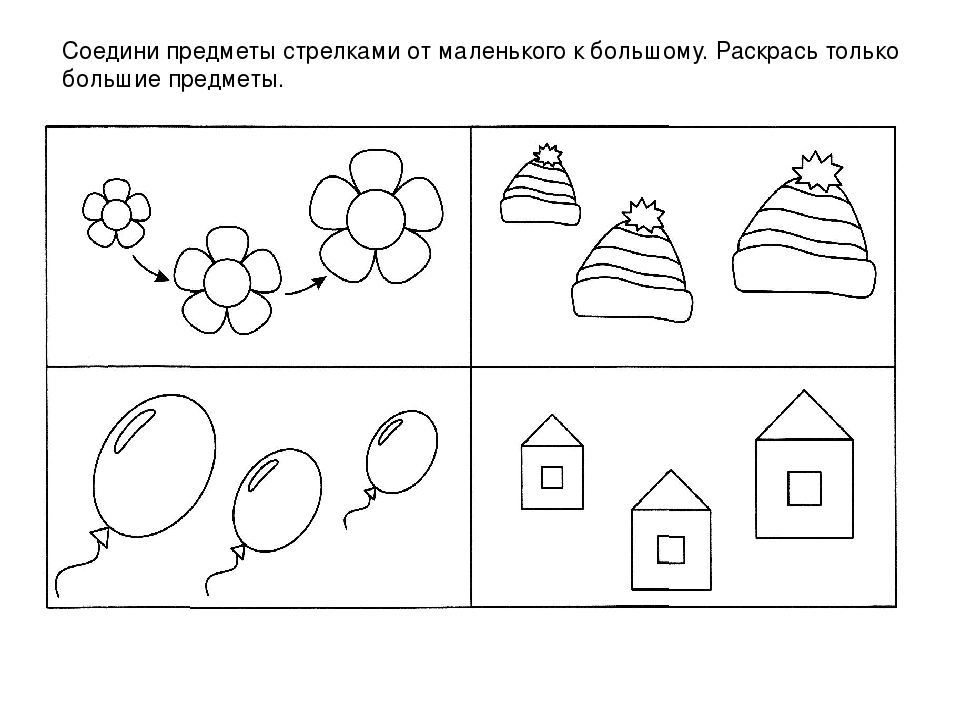
I вариант. Ребенку даются две картинки, изображающие лестницы: одна лестница большая, вторая — маленькая. На каждой из них стоит человечек на седьмой ступеньке. Педагог задает вопрос: «Скажи, какой человечек прошел больше ступенек?» Часто дети показывают человечка на большой лестнице.
II вариант. Ребенку предъявляются две картинки с изображением тарелок. На первой картинке 12 маленьких тарелок, расположенных на небольшом пространстве; на второй картинке — 12 больших тарелок такой же формы, но расположенных на более широком пространстве. Задаются те же вопросы, что и в первом варианте. Аналогичные упражнения проводятся с использованием других предметов (с бусами, карандашами и т.д.).
Сериация – это:
Способность составления серий из предметов по выделенному свойству.
Операция распределения объектов классификации в упорядоченные ряды
Этапы формирования сериации у детей с дискалькулией:
I этап – уточнение глобальной операции без регулярной последовательности действий;
II этап – интуитивная сериация с нащупыванием конструкций, с трудностями включения новых элементов в конструируемую серию;
III этап – определенная сериация с систематической координацией отношений предметов или действий.
На втором этапе используются следующие упражнения:
Первая серия упражнений — ранжирование предметов, геометрических фигур по величине, длине, насыщенности цвета и другим признакам.
1. Ранжирование 5 полосок, длина каждой из которых увеличивается на 1 см по отношению к предыдущей. Дается инструкция: «Разложи полоски в таком порядке — от самой маленькой к самой большой». Затем предлагаются 10 полосок и изменяется инструкция: «Разложи полоски от самой большой до самой маленькой». В дальнейшем задание усложняется через уменьшение разницы в размере полосок до 0,5 см.
2. Распределение квадратов по величине
3. Раскладывание кругов по величине
Раскладывание кругов по величине
4. Сравнение скорости транспортных средств.
5. Сериация сюжетных картинок, данных в беспорядке
Вторая серия упражнений — проводятся в речевой форме с одновременным закреплением сравнительной лексики.
1. Этот вид упражнений проводится на материале первой серии. Различие заключается в том, что ребенок, сравнивая предметы, оформляет результаты сравнения в речевой форме, в вербальном плане. В результате тренировки ученики должны овладеть следующими прилагательными: маленький—большой, маленький—средний— большой, самый маленький—самый большой, огромный и т.д.
2. Детям предлагается рисунок, изображающий детей разного роста, стоящих в очереди Задаются вопросы: «Скажи, кто самый низкий?», «Кто самый высокий?», «Как ты скажешь о девочке с собакой?», «Какой этот мальчик по отношению к мальчику с мячом?» и т. д. На заключительном этапе выполнения задания дается инструкция: «Покажи детей по очереди, начиная с самого высокого и кончая самым низким». Позже дается задание показать детей в последовательности, начиная с самого низкого.
д. На заключительном этапе выполнения задания дается инструкция: «Покажи детей по очереди, начиная с самого высокого и кончая самым низким». Позже дается задание показать детей в последовательности, начиная с самого низкого.
Третья серия упражнений — проводятся на числовом материале (закрепление порядкового значения числа).
1. Раскрасить числа разным цветом: 2 и 4 — синим, 1 и 5 — красным, 3 — желтым.
2. Определить, кто какой по счету в очереди.
Детям предлагается рисунок, изображающий детей разного роста, стоящих в очереди. Педагог задает следующие вопросы: «Сколько детей в очереди за мороженым? Кто четвертый в очереди? Какая по счету девочка с собакой? Кто стоит после третьего в очереди? Кто стоит перед пятым в очереди?» И т. д.
3. Определить, на какой жердочке птица.
Детям предъявляется картинка с изображением забора и птицы, а также фишка с изображением птицы. Педагог задает следующие вопросы: «На какой жердочке сидит птица? Сколько жердочек должна перепрыгнуть птица, чтобы сесть на пятую жердочку? Покажи 6 первых жердочек. Покажи 3 последние жердочки. Сколько жердочек надо перепрыгнуть птице, чтобы оказаться на последней?»
Определить, на какой жердочке птица.
Детям предъявляется картинка с изображением забора и птицы, а также фишка с изображением птицы. Педагог задает следующие вопросы: «На какой жердочке сидит птица? Сколько жердочек должна перепрыгнуть птица, чтобы сесть на пятую жердочку? Покажи 6 первых жердочек. Покажи 3 последние жердочки. Сколько жердочек надо перепрыгнуть птице, чтобы оказаться на последней?»
4. Нахождение чисел, разбросанных на листе, в порядке их увеличения.
5. Определение места чисел в ряду.
Предлагаются задания типа: считай от 13 до 27 и обратно; считай от 22 до 29 и обратно; назови соседей числа 7, 20, 32 …, назови число на 1 больше 6, 27, 33, 47 …
6. Письменные упражнения:
— дополнение числовых рядов, например: 8, 7, , 4; 22, 23, , 26; 65, 64, 61;
— з аполнение решеток с последовательностью чисел.
Развитие зрительного восприятия составлением сериации как важнейшей составляющей сенсорного воспитания детей с нарушениями зрения старшего дошкольного возраста
Цель: научить детей составлять сериационные
ряды по сенсорным эталонам, познакомить с
основными принципами сериации и чередования.
- Что такое “сериация”?
- Сериация – это одна из важнейших мыслительных операций.
Суть ее составляет установление последовательных взаимосвязей, упорядочивание различий.
Простейший пример сериации – сбор ребенком обычной пирамидки.
Сериация является фундаментом понимания и правильного обращения с различными шкалами, инструментами измерения, а также лежит в основе представлений о порядковых числительных, об арифметических и геометрических прогрессиях.
Сериация способствует развитию:
- зрительного восприятия,
- зрительного внимания,
- мышления (в большей степени таких операций, как анализ, сравнение, классификация),
- зрительно-двигательной координации (“глаз – рука”),
- ориентировки в микропространстве,
- мелкой моторики
Проблемы, с которыми сталкиваются дети с нарушениями зрения при составлении сериации:
- несформированность представлений о сенсорных эталонах или их фрагментарность,
- трудности в анализе образца и в сравнении сенсорных эталонов,
- ошибки в узнавании близких между собой сенсорных эталонов,
- неумение выстроить элементы сериации по предложенному педагогом пространственному расположению,
- действия простыми способами составления
сериации: пробы и ошибки, перебор вариантов.

Основной принцип при обучении составлению сериации – это принцип от простого к сложному:
- от основного признака – цвета (в онтогенезе ребенка он появляется как первый эталон) к форме и величине.
- от основного цвета к оттенкам, от простых форм и величин к сложным.
- от малого количества элементов (2, 3) к большему количеству.
- от чередования по одному признаку к чередованию по нескольким признакам.
- от пошагового показа, к зрительному образцу и к действию по словесной инструкции.
- от использования зрительных ориентиров, обозначающих пространственное положение элементов в ряду, и без них.
- от использования линии , обозначающей ряд и без нее.
- от размещения элементов по горизонтальной
линии к раскладыванию по вертикали, по диагонали,
по волнистой линии, по кругу и пр.

Основные способы действия при раскладывнии сериации:
- Действия силой
- Перебор вариантов
- Пробы и ошибки
- Практическое примеривание (наложение, приложение)
- Зрительное соотнесение
Действия силой и перебор вариантов являются примитивными способами действия, которые свойственны детям раннего возраста и для детей с нарушением интеллекта.
Практическое примеривание и зрительное соотнесение являются самыми совершенными способами действия.
Одной из разновидностей сериации является чередование.
Чередование – это повторение элементов ряда по какому-либо признаку.
Например, составление ряда чередования по оттенкам основного цвета.
В старшем дошкольном возрасте рекомендуется
работа с оттенками оранжевого, фиолетового,
голубого цветов, при этом важно закреплять и
другие оттенки основных цветов, с которыми дети
знакомились в младшем возрасте.
При составлении ряда по оттенкам важно подобрать фон так, чтобы элементы не сливались с ним и не искажался сам оттенок элемента.
Составление ряда по оттенкам цветов.
Перед ребенком можно поставить 2 задачи по развитию цветовосприятия:
- выделение оттенка из группы красно-оранжево-коричнево-фиолетовых,
- выделение оттенка из “своей” группы основного цвета, например, выделение бордового из группы малиновых и красных оттенков.
А также закрепить представления о четырехугольниках: квадрате, прямоугольнике, трапеции.
Составление ряда по чередованию объемных форм.
В старшем дошкольном возрасте необходимо
закреплять представления о таких объемных
формах, как шар, куб, цилиндр, конус, располагая их
в сериационных рядах, а также комбинируя их в
различных пространственных модальностях. Тем
самым, мы закрепляем и пространственные
представления.
Составление ряда по величине, закрепление представлений о длине, при различном расположении элементов в микропространстве (горизонтально, вертикально).
Составление ряда по таким понятиям величины, как высота и толщина.
Составление ряда по чередованию элементов по такому признаку, как направление.
При составлении ряда по чередованию можно предложить усложнение – составление по двум признакам, например, цвет и направление элементов.
При этом выбор цвета элемента может осуществляться из тех цветов, которые не присутствуют в образце. Тем самым, закрепляется не только ориентировка в пространстве и пространственная терминология, но и цветовосприятие.
При составлении рядов по чередованию сенсорные признаки элементов можно комбинировать: форма и величина, форма и направление элементов, форма и количество.
Рекомендуется предлагать детям задания на
активизацию мыслительной деятельности:
“Правильно ли я составила ряд?”, “Найди
ошибку”.
Составление ряда по трем сенсорным признакам: например, форма, оттенок, направление.
Ребенку старшего дошкольного возраста можно предложить составить ряд из близких оттенков и фигур, например, из четырехугольников (квадрат и ромб, квадрат и трапеция), закрепляя представления о них.
Сформированные сенсорные представления и умение составлять сериацию дают возможность детям отразить свой накопленный сенсорный опыт в продуктивной деятельности.
Например, при составлении узоров на предметах одежды способом штампования. В процессе работы дети выбирают желаемую форму и цвет из множества предложенных штампиков и палитр, а затем составляют ряды по чередованию элементов по сенсорным эталонам, украшая предметы одежды.
Развитие логического мышления детей старшего дошкольного возраста средствами занимательной математики
1. Развитие логического мышления детей старшего дошкольного возраста средствами занимательной математики
РАЗВИТИЕ ЛОГИЧЕСКОГОМЫШЛЕНИЯ ДЕТЕЙ
СТАРШЕГО ДОШКОЛЬНОГО
ВОЗРАСТА СРЕДСТВАМИ
ЗАНИМАТЕЛЬНОЙ
МАТЕМАТИКИ
Февраль 2014
2.
 Актуальность темыАКТУАЛЬНОСТЬ ТЕМЫ
Актуальность темыАКТУАЛЬНОСТЬ ТЕМЫДетский сад – первая и очень ответственная ступень
общей системы образования.
Цель: вырастить детей людьми, умеющими думать,
хорошо ориентироваться во всем, что их окружает, правильно
оценивать различные ситуации, с которыми они сталкиваются
в жизни, принимать самостоятельные решения.
От ребенка, пришедшего в первый класс, сразу же
требуется достаточно высокий уровень развития логического
мышления, необходимый для успешного усвоения программы.
Овладев логическими операциями, ребенок станет более
внимательным, научиться мыслить ясно и четко, сумеет в
нужный момент сконцентрироваться на сути проблемы,
убедить других в своей правоте.
3. Роль логического мышления
РОЛЬ ЛОГИЧЕСКОГО МЫШЛЕНИЯСпособность логически мыслить позволяет:
– понимать происходящее вокруг,
– вскрывать существенные стороны, связи в предметах и явлениях
окружающей действительности,
– делать умозаключения, решать различные задачи, проверять эти
решения,
– доказывать, опровергать словом.

Логическое мышление — это умение оперировать абстрактными
понятиями, это мышление путем рассуждений и опровержений.
Старший дошкольный возраст является сензитивным для развития
логического мышления.
Условия развития мышления ребенка – предметная деятельность и
общение, целенаправленные воздействия взрослого. Формировать и
развивать логическое мышления можно с детьми любого уровня развития и
любого возраста
4. Занимательный математический материал
ЗАНИМАТЕЛЬНЫЙ МАТЕМАТИЧЕСКИЙМАТЕРИАЛ
Сущность занимательности новизна, необычность, неожиданность.
Занимательный математический
материал:
активизирует умственную
деятельность,
заинтересовывает математическим
материалом,
увлекает и развлекает детей,
развивает ум,
расширяет, углубляет
математические представления,
закрепляет полученные знания и
умения.
5. Цель и задачи
ЦЕЛЬ И ЗАДАЧИЦель – развитие логического мышления детей.
Задачи:
1.
 Формирование логических приемов умственных действий у
Формирование логических приемов умственных действий удошкольников:
анализа, синтеза, сравнения, классификации,
обобщения.
2. Развитие у детей:
речи (умения рассуждать, доказывать),
произвольности внимания,
познавательных интересов,
творческого воображения.
3. Воспитание:
коммуникативных навыков,
стремления к преодолению трудностей,
уверенности в себе.
желание вовремя прийти на помощь сверстникам.
6. Логические приемы умственных действий – сериация
ЛОГИЧЕСКИЕ ПРИЕМЫ УМСТВЕННЫХДЕЙСТВИЙ – СЕРИАЦИЯ
Сериация — построение упорядоченных возрастающих или
убывающих рядов.
7. Логические приемы умственных действий – анализ и синтез
ЛОГИЧЕСКИЕ ПРИЕМЫ УМСТВЕННЫХДЕЙСТВИЙ – АНАЛИЗ И СИНТЕЗ
Анализ
—
это
мысленное
расчленение чего-либо на части или
мысленное выделение отдельных
свойств предмета.
Синтез
—
соединение
различных элементов в единое
целое, а также мысленное сочетание
отдельных их свойств
Являясь противоположными по своей
сути, анализ и синтез фактически
тесно связаны между собой.
 Они
Ониучаствуют
в
каждом
сложном
мыслительном процессе.
8. Логические приемы умственных действий – анализ и синтез
ЛОГИЧЕСКИЕ ПРИЕМЫ УМСТВЕННЫХДЕЙСТВИЙ – АНАЛИЗ И СИНТЕЗ
Традиционной формой на развитие визуального
анализа являются задания на выбор «лишней»
фигуры (предмета).
Одна фигура отличается от всех других. Какая? Чем
она отличается?
А в этих фигурках найдите лишнюю,
отличающуюся от всех других. Почему она
лишняя?
9. Логические приемы умственных действий – анализ и синтез
ЛОГИЧЕСКИЕ ПРИЕМЫ УМСТВЕННЫХДЕЙСТВИЙ – АНАЛИЗ И СИНТЕЗ
Способность к синтезу формируется у ребенка раньше, чем
способность к анализу.
Если ребенок знает, как это было собрано (сложено,
сконструировано), ему легче анализировать и выделять
составные части.
Для конструирования
используются
различные мозаики,
конструкторы,
кубики, разрезные
картинки,
подходящие по
возрасту.
10.
 Логические приемы умственных действий – анализ и синтезЛОГИЧЕСКИЕ ПРИЕМЫ УМСТВЕННЫХ
Логические приемы умственных действий – анализ и синтезЛОГИЧЕСКИЕ ПРИЕМЫ УМСТВЕННЫХДЕЙСТВИЙ – АНАЛИЗ И СИНТЕЗ
Формирование аналитико-синтетического процесса
через использование игр геометрического конструктора
«Танграм»
«Монгольская
игра»
«Колумбово яйцо»
«Пифагор»
«Волшебный круг»
11. Логические приемы умственных действий – анализ и синтез
ЛОГИЧЕСКИЕ ПРИЕМЫ УМСТВЕННЫХДЕЙСТВИЙ – АНАЛИЗ И СИНТЕЗ
Фигуры, составленные из
плоскостных
геометрических
конструкторов
12. Логические приемы умственных действий – анализ и синтез
ЛОГИЧЕСКИЕ ПРИЕМЫ УМСТВЕННЫХДЕЙСТВИЙ – АНАЛИЗ И СИНТЕЗ
1 задание – найти только те геометрические фигуры, которые
понадобятся для составления зайчика, собачки.
2 задание – найти
предмет, который
составлен из фигур в
рамочке.
(божья коровка)
13. Логические приемы умственных действий – анализ и синтез
ЛОГИЧЕСКИЕ ПРИЕМЫ УМСТВЕННЫХДЕЙСТВИЙ – АНАЛИЗ И СИНТЕЗ
Задание –
сосчитать
геометрические
фигуры в
нарисованных
картинках.
14. Логические приемы умственных действий – сравнение
ЛОГИЧЕСКИЕ ПРИЕМЫ УМСТВЕННЫХДЕЙСТВИЙ – СРАВНЕНИЕ
Сравнение — логический прием умственных действий, требующий
выявления сходства и различия между признаками объекта (предмета,
явления, группы предметов).
15. Логические приемы умственных действий – сравнение
ЛОГИЧЕСКИЕ ПРИЕМЫ УМСТВЕННЫХДЕЙСТВИЙ – СРАВНЕНИЕ
Упражнения на сравнение
Найди двух одинаковых
котят
Найди Буратино, который
отличается от других
16. Задания на развитие зрительного и пространственного восприятия
ЗАДАНИЯ НА РАЗВИТИЕ ЗРИТЕЛЬНОГОИ ПРОСТРАНСТВЕННОГО ВОСПРИЯТИЯ
Задания на поиск геометрических фигур.
Нужно найти круги, овалы и квадраты на картинке слева,
ромбы и круги на картинке справа.
17. Логические приемы умственных действий – классификация
ЛОГИЧЕСКИЕ ПРИЕМЫ УМСТВЕННЫХДЕЙСТВИЙ – КЛАССИФИКАЦИЯ
Классификация — разделение множества на группы по какому-либо признаку,
который называют «основанием классификации».

Классификацию с детьми дошкольного
возраста можно проводить:
• по общему названию;
• по размеру;
• по цвету;
• по форме;
• по другим признакам
не математического характера:
что можно есть и что нельзя;
кто летает, кто бегает, кто
плавает;
кто живет в доме и кто в лесу;
18. Логические приемы умственных действий – классификация
ЛОГИЧЕСКИЕ ПРИЕМЫ УМСТВЕННЫХДЕЙСТВИЙ – КЛАССИФИКАЦИЯ
Классификацию по
признакам
нематематического
характера хорошо
закреплять через
дидактические игры
по типу «Лото».
19. Логические приемы умственных действий – классификация
ЛОГИЧЕСКИЕ ПРИЕМЫ УМСТВЕННЫХДЕЙСТВИЙ – КЛАССИФИКАЦИЯ
Задания на
подбор
смысловой пары
Задания из серии
«Выбери подходящую
картинку» достаточно
сложные.
Здесь проверяется
умение рассуждать,
делать умозаключения.
20. Логические приемы умственных действий – обобщение
ЛОГИЧЕСКИЕ ПРИЕМЫ УМСТВЕННЫХДЕЙСТВИЙ – ОБОБЩЕНИЕ
Обобщение — это оформление в словесной форме результатов
процесса сравнения.

Обобщение формируется в дошкольном возрасте как выделение
и фиксация общего признака двух и более объектов.
21. Логические задачи на нахождение пропущенной фигуры.
ЛОГИЧЕСКИЕ ЗАДАЧИ НАНАХОЖДЕНИЕ ПРОПУЩЕННОЙ
ФИГУРЫ.
Задание:
выявить закономерность
в расположении фигур и
нарисовать фигуру в
пропущенной клетке.
22. Логические задачи на поиск недостающих в ряду фигур.
ЛОГИЧЕСКИЕ ЗАДАЧИ НА ПОИСКНЕДОСТАЮЩИХ В РЯДУ ФИГУР.
1 признак
2 признака
Четыре признака:
форма туловища,
головы,
количество усов,
направление хвоста.
23. Загадки и задачи — шутки математического содержания
ЗАГАДКИ И ЗАДАЧИ — ШУТКИМАТЕМАТИЧЕСКОГО СОДЕРЖАНИЯ
Загадки:
Два конца, два кольца, а посредине гвоздик.
(ножницы)
– Четыре братца под одной крышей живут. (стол)
– Нас семь братьев, летами все равные. А именем
разные. Отгадай, кто мы? (дни недели)
– Кто в году четыре раза переодевается? (земля)
–
Задачи-шутки:
Ты да я, да мы с тобой.
 Сколько нас всего? (Двое)
Сколько нас всего? (Двое)– На столе лежат в ряд 3 палочки. Как сделать
среднюю крайней, не трогая ее? (Переложить
крайнюю.)
– Тройка лошадей пробежала 5 км. По сколько
километров пробежала каждая лошадь? (По 5
км)
–
24. Развивающая среда
РАЗВИВАЮЩАЯ СРЕДАПалочки Кюизенера позволяют моделировать числа, свойства,
отношения, зависимости между ними с помощью цвета и длины.
Первый
этап
25. Развивающая среда
РАЗВИВАЮЩАЯ СРЕДАПалочки Кюизенера –
второй этап.
С помощью палочек Кюизенера
можно решать логические задачи.
26. Развивающие блоки Дьенеша
РАЗВИВАЮЩИЕ БЛОКИ ДЬЕНЕШАБлоки Дьенеша – универсальная развивающая игра, которая позволяет
Познакомить с формой, цветом, размером, толщиной объектов.
Развивать пространственные представления.
Развивать логическое мышление, представление о множестве, операции над
множествами (сравнение, разбиение, классификация, абстрагирование,
кодирование и декодирование информации).

Усвоить элементарные навыки алгоритмической культуры мышления.
Развивать умения выявлять свойства в объектах, называть их, обобщать
объекты по их свойствам, объяснять сходства и различия объектов,
обосновывать свои рассуждения.
Воспитывать самостоятельность, инициативу, настойчивость в достижении
цели.
Развивать творческие способности, воображение, фантазию, способности к
моделированию и конструированию.
Успешно овладеть основами математики и информатики.
ВЫВОД
Развитие логических приемов мышления
должно строится в соответствии с
общедидактическими принципами:
–
–
–
–
–
–
–
сознательности;
активности;
последовательности;
посильности и доступности;
прочности;
наглядности;
«опережающих знаний».
Использование игрового занимательного
математического материала ведет к более
интенсивному развитию компонентов
логического мышления.
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 64 из 64 Виды детской деятельности: игровая, коммуникативная, познавательно-исследовательская, конструктивная. Цели: закрепить умения и навыки детей в создании конструкции; учить выполнять сериацию по величине; развивать внимание, восприятие; воспитывать интерес к конструктивной и игровой коллективной деятельности. Целевые ориентиры дошкольного образования : с интересом рассматривает картинки, сооружает элементарные постройки по образцу, проявляет желание строить большой домик коллективно, отвечает на вопросы при обсуждении построек; принимает участие в сериации предметов по величине. Материалы и оборудование: легкие модули; картинки с изображением разных домов, силуэты деревьев разной величины на подставках; фланелеграф, 3 картинки: маленькое деревце, побольше, большое. Содержание организованной деятельности детей Организационный момент. Воспитатель предлагает детям отправиться на дачу на автобусе. Дети садятся в «автобус» (поставленные попарно стулья), а воспитатель берет в руки игрушечный руль и «везет» детей на дачу. Основная часть. Рассматривание картинок. Воспитатель. Вот мы и приехали на дачу, выходите. (Дети встают со стульев.) На нашей даче, к сожалению, нет дома. Как же мы его построим? (Предложения детей.) У меня есть картинки с изображением разных домов. Посмотрим и сделаем так же. Дети вместе с воспитателем рассматривают разные дома на картинках и отмечают их величину, наличие стен, окон, крыши, входа. Конструирование. Воспитатель предлагает детям построить стены дома из больших мягких модулей, а крышу сделать из плотной материи. Дети под руководством воспитателя строят стены так, чтобы в них оставались не закрытые модулями пространства: окна и дверь. Затем воспитатель кладет сверху стен материю – «крышу». Когда дом будет готов, воспитатель предлагает детям зайти в него по очереди и проверить, крепким ли он получился. Сериация по величине. Воспитатель. Дом на нашей даче есть, а деревьев нет. Давайте их посадим. Но прежде чем посадить, мы должны знать, как они растут. (Выставляет на фланелеграфе изображения трех деревьев: маленького, побольше и самого большого.) Сначала деревце совсем маленькое, потом подрастает, становится больше и вырастает большим, сильным деревом. Запомнили, как растет дерево? (Ответы детей.) Теперь вы попробуйте поставить картинки так же, как я. Воспитатель убирает с фланелеграфа картинки и предлагает желающим детям выставить их на фланелеграфе в правильном порядке. Рефлекия. Воспитатель раздает детям силуэты деревьев на подставках, которые они ставят возле построенного домика.
Литература 1. Аверина, И. Е. Физкультурные минутки в детском саду : практическое пособие / И. 2. Бейлипа, А. Почти забытое наследие немецкого народа // Дошкольное воспитание. – 1990. – № 9. – С. 103–106. 3. Гербова, В. В. Занятия по развитию речи в первой младшей группе детского сада : пособие для воспитателя детского сада / В. В. Гербова, А. И. Максаков. – М. : Просвещение, 1986. 4. Гербова, В. В. Занятия по развитию речи в первой младшей группе детского сада / В. В. Гербова, А. И. Максаков. – М. : Просвещение, 1979. 5. Елисеева, Л. Н. Хрестоматия для маленьких / Л. Н. Елисеева. – М. : Просвещение, 1982. 6. Казакова, Т. Г. Развивайте у дошкольников творчество : конспекты занятий рисованием, лепкой, аппликацией / Т. Г. Казакова. – М. : Просвещение, 1985. 7. Макшанцева, Е. Д. Детские забавы : кн. для воспитателя и муз. руководителя детского сада / Е. Д. Макшанцева. – М. : Просвещение, 1991. – 64 с. 8. От рождения до школы. Примерная общеобразовательная программа дошкольного образования / под ред. 9. Программа воспитания и обучения в детском саду / под ред. М. А. Васильевой, В. В. Гербовой, Т. С. Комаровой. – М. : Мозаика-Синтез, 2009. 10. Сакулина, Н. П. Сенсорное воспитание в детском саду / Н. П. Сакулина, Н. Н. Подьяков, Т. С. Комарова, Л. Е. Журова, Г. А. Туманова, Е. И. Корзакова, В. Н. Аванесова. – М. : Просвещение, 1970. – 214 с. 11. Сенсомоторное развитие детей раннего возраста : программа, конспекты занятий / авт.-сост. Т. П. Высокова. – Волгоград : Учитель, 2010. 12. Сутеев, В. Кто сказал «мяу»? / В. Сутеев. – М. : АСТ : Астрель, 2006. 13. Эмоциональное развитие детей : занятия в первой младшей группе, дидактические игры, работа с семьей / авт.-сост. О. А. Айрих. – Волгоград : Учитель, 2008. Интернет-источники: 14. www.it-n.ru/cjmmunities.aspx? 15. http://www.lowe-tech.com/portfolio/paperplanes.asp 16. 17. www.mdk-arbat.ru/bookcard_aii4.aspx?… 18. festival.1september.ru/subjecta/16/?n=25 19. http://vospitatel.com.ua
⇐ Предыдущая55565758596061626364 Читайте также: Техника нижней прямой подачи мяча Комплекс физических упражнений для развития мышц плечевого пояса Стандарт Порядок надевания противочумного костюма Общеразвивающие упражнения без предметов |
|
Последнее изменение этой страницы: 2019-08-19; просмотров: 130; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
1
Первый слайд презентации: Развитие логического мышления детей дошкольного возраста
Март 2021г
Изображение слайда
2
Слайд 2: Актуальность темы
Детский сад – первая и очень ответственная ступень общей системы образования.
Цель: вырастить детей людьми, умеющими думать, хорошо ориентироваться во всем, что их окружает, правильно оценивать различные ситуации, с которыми они сталкиваются в жизни, принимать самостоятельные решения. Актуальность темы
Актуальность темы
Изображение слайда
3
Слайд 3: Роль логического мышления
Способность логически мыслить позволяет: понимать происходящее вокруг, вскрывать существенные стороны, связи в предметах и явлениях окружающей действительности, делать умозаключения, решать различные задачи, проверять эти решения, доказывать, опровергать словом. Логическое мышление — это умение оперировать абстрактными понятиями, это мышление путем рассуждений и опровержений. Условия развития мышления ребенка – предметная деятельность и общение. Роль логического мышления
Изображение слайда
4
Слайд 4: Цель и задачи
Цель – развитие логического мышления детей.
Задачи:
1. Формирование логических приемов умственных действий у дошкольников:
анализа, синтеза, сравнения, классификации, обобщения.
2. Развитие у детей:
речи (умения рассуждать, доказывать),
произвольности внимания,
познавательных интересов,
творческого воображения.
3. Воспитание:
коммуникативных навыков,
стремления к преодолению трудностей,
уверенности в себе.
желание вовремя прийти на помощь сверстникам.
Цель и задачи
Формирование логических приемов умственных действий у дошкольников:
анализа, синтеза, сравнения, классификации, обобщения.
2. Развитие у детей:
речи (умения рассуждать, доказывать),
произвольности внимания,
познавательных интересов,
творческого воображения.
3. Воспитание:
коммуникативных навыков,
стремления к преодолению трудностей,
уверенности в себе.
желание вовремя прийти на помощь сверстникам.
Цель и задачи
Изображение слайда
5
Слайд 5: Занимательный математический материал
Сущность занимательности – новизна, необычность, неожиданность. Занимательный математический материал: активизирует умственную деятельность, заинтересовывает математическим материалом, увлекает и развлекает детей, развивает ум, расширяет, углубляет математические представления, закрепляет полученные знания и умения.
Изображение слайда
6
Слайд 6: Логические приемы умственных действий – сериация
Сериация — построение упорядоченных возрастающих или убывающих рядов. Логические приемы умственных действий – сериация
Логические приемы умственных действий – сериация
Изображение слайда
7
Слайд 7: Логические приемы умственных действий – анализ и синтез
Анализ — это мысленное расчленение чего-либо на части или мысленное выделение отдельных свойств предмета. Синтез — соединение различных элементов в единое целое, а также мысленное сочетание отдельных их свойств Являясь противоположными по своей сути, анализ и синтез фактически тесно связаны между собой. Они участвуют в каждом сложном мыслительном процессе.
Изображение слайда
8
Слайд 8: Логические приемы умственных действий – анализ и синтез
Традиционной формой на развитие визуального анализа являются задания на выбор «лишней» фигуры (предмета). Одна фигура отличается от всех других. Какая? Чем она отличается?
Логические приемы умственных действий – анализ и синтез
А в этих фигурках найдите лишнюю, отличающуюся от всех других. Почему она лишняя?
Одна фигура отличается от всех других. Какая? Чем она отличается?
Логические приемы умственных действий – анализ и синтез
А в этих фигурках найдите лишнюю, отличающуюся от всех других. Почему она лишняя?
Изображение слайда
9
Слайд 9: Логические приемы умственных действий – анализ и синтез
Способность к синтезу формируется у ребенка раньше, чем способность к анализу. Если ребенок знает, как это было собрано (сложено, сконструировано), ему легче анализировать и выделять составные части. Логические приемы умственных действий – анализ и синтез Для конструирования используются различные мозаики, конструкторы, кубики, разрезные картинки, подходящие по возрасту.
Изображение слайда
10
Слайд 10: Логические приемы умственных действий – анализ и синтез
Формирование аналитико-синтетического процесса через использование игр геометрического конструктора Логические приемы умственных действий – анализ и синтез «Танграм» «Монгольская игра» «Пифагор» «Колумбово яйцо» «Волшебный круг»
Изображение слайда
11
Слайд 11: Логические приемы умственных действий – анализ и синтез
Фигуры, составленные из плоскостных геометрических конструкторов
Изображение слайда
12
Слайд 12: Логические приемы умственных действий – анализ и синтез
1 задание – найти только те геометрические фигуры, которые понадобятся для составления зайчика, собачки. 2 задание – найти предмет, который составлен из фигур в рамочке.
(божья коровка)
2 задание – найти предмет, который составлен из фигур в рамочке.
(божья коровка)
Изображение слайда
13
Слайд 13: Логические приемы умственных действий – анализ и синтез
Задание – сосчитать геометрические фигуры в нарисованных картинках.
Изображение слайда
14
Слайд 14: Логические приемы умственных действий – сравнение
Сравнение — логический прием умственных действий, требующий выявления сходства и различия между признаками объекта (предмета, явления, группы предметов). Логические приемы умственных действий – сравнение
Изображение слайда
15
Слайд 15: Логические приемы умственных действий – сравнение
Найди двух одинаковых котят Найди Буратино, который отличается от других Упражнения на сравнение
Изображение слайда
16
Слайд 16: Задания на развитие зрительного и пространственного восприятия
Задания на поиск геометрических фигур. Задания на развитие зрительного и пространственного восприятия
Нужно найти круги, овалы и квадраты на картинке слева,
ромбы и круги на картинке справа.
Задания на развитие зрительного и пространственного восприятия
Нужно найти круги, овалы и квадраты на картинке слева,
ромбы и круги на картинке справа.
Изображение слайда
17
Слайд 17: Логические приемы умственных действий – классификация
Классификация — разделение множества на группы по какому-либо признаку, который называют «основанием классификации». Логические приемы умственных действий – классификация Классификацию с детьми дошкольного возраста можно проводить: по общему названию; по размеру; по цвету; по форме; по другим признакам не математического характера: что можно есть и что нельзя; кто летает, кто бегает, кто плавает; кто живет в доме и кто в лесу;
Изображение слайда
18
Слайд 18: Логические приемы умственных действий – классификация
Классификацию по признакам нематематического характера хорошо закреплять через дидактические игры
по типу «Лото».
Изображение слайда
19
Слайд 19: Логические приемы умственных действий – классификация
Задания на подбор смысловой пары Задания из серии «Выбери подходящую картинку» достаточно сложные. Здесь проверяется умение рассуждать, делать умозаключения.
Изображение слайда
20
Слайд 20: Логические приемы умственных действий – обобщение
Обобщение — это оформление в словесной форме результатов процесса сравнения. Обобщение формируется в дошкольном возрасте как выделение и фиксация общего признака двух и более объектов. Логические приемы умственных действий – обобщение
Изображение слайда
21
Слайд 21: Логические задачи на нахождение пропущенной фигуры
Задание:
выявить закономерность в расположении фигур и
нарисовать фигуру в
пропущенной клетке.
Изображение слайда
22
Слайд 22: Логические задачи на поиск недостающих в ряду фигур
1 признак 2 признака Четыре признака: форма туловища, головы, количество усов, направление хвоста.
Изображение слайда
23
Слайд 23: Загадки и задачи — шутки математического содержания
Загадки:
Два конца, два кольца, а посредине гвоздик. (ножницы)
Четыре братца под одной крышей живут. (стол)
Нас семь братьев, летами все равные. А именем разные. Отгадай, кто мы? (дни недели)
Кто в году четыре раза переодевается? (земля)
Задачи-шутки:
Ты да я, да мы с тобой. Сколько нас всего? (Двое)
На столе лежат в ряд 3 палочки. Как сделать среднюю крайней, не трогая ее? (Переложить крайнюю. )
Тройка лошадей пробежала 5 км. По сколько километров пробежала каждая лошадь? (По 5 км)
Загадки и задачи — шутки математического содержания
)
Тройка лошадей пробежала 5 км. По сколько километров пробежала каждая лошадь? (По 5 км)
Загадки и задачи — шутки математического содержания
Изображение слайда
24
Слайд 24: Развивающая среда
настольно-печатные игры: Развивающая среда Игра «Заплатки»
Изображение слайда
25
Слайд 25: Развивающая среда
Игры на объемное моделирование: Развивающая среда
Изображение слайда
26
Слайд 26: Развивающая среда
Игра «Стройка»
Игра «Грузовички»
Выбрать карточку-задание.
Так сложить детали-формочки в кузов грузовика, чтобы все детали поместились в кузове машины, не выступая за его края.
Изображение слайда
27
Слайд 27: Развивающая среда
Палочки Кюизенера позволяют моделировать числа, свойства, отношения, зависимости между ними с помощью цвета и длины. Развивающая среда Первый этап
Изображение слайда
28
Слайд 28: Развивающая среда
Палочки Кюизенера – второй этап. Развивающая среда С помощью палочек Кюизенера можно решать логические задачи.
Изображение слайда
29
Слайд 29: Развивающие игры Воскобовича
«Цветной квадрат» Воскобовича Развивающие игры Воскобовича
Изображение слайда
30
Слайд 30: Развивающие игры Воскобовича
«Прозрачный квадрат» Развивающие игры Воскобовича 1 + 2 = 3
Изображение слайда
31
Слайд 31: Развивающие игры Воскобовича
« Чудо КРЕСТИКИ» Развивающие игры Воскобовича
Изображение слайда
32
Последний слайд презентации: Развитие логического мышления детей дошкольного возраста: Вывод
-Развитие логических приемов мышления должно строится в соответствии с общедидактическими принципами. -Использование игрового занимательного математического материала ведет к более интенсивному развитию компонентов логического мышления.
Вывод
-Использование игрового занимательного математического материала ведет к более интенсивному развитию компонентов логического мышления.
Вывод
Изображение слайда
14 серий практических занятий для дошкольников
- Поделиться
- Электронная почта
Что такое упорядоченность и упорядоченность в развитии ребенка и как научить дошкольников упорядочению размеров предметов?
Эти серии упражнений для дошкольников просты и практичны. Они подходят для обучения детей дома или в школе.
Что такое серийность в раннем детстве?
Серия одна из умственных способностей детей приобретают в раннем детстве. Он развивается вместе с другими когнитивными способностями, такими как сопоставление, сортировка и изучение причинно-следственных связей.
Серийность — это форма упорядочивания — или упорядочивания вещей — в соответствии с градуированным порядком , чаще ссылающимся на упорядочивание с точки зрения размера .
В отличие от временного порядка (последовательности), который упорядочивает вещи в том порядке, в котором они происходят во времени , серия заказывает их в соответствии с градациями по размеру.
Также можно провести повествование в соответствии с:
- Color (например, от самых легких до самых темных синих)
- Вкус (сладкий до кислый)
- Звук (мягкий до громкого)
-
- . коснитесь (от самого гладкого до самого грубого).
Эти действия по заказу в основном отвечают на вопрос « Что дальше? ”
В своей работе по развитию детей Пиаже дал термин серия. [источник]
Примеры серий
Некоторые примеры серий, которые вы встретите в повседневной жизни:
- Мерные стаканчики, которые помещаются друг в друга
- Вложенные стаканчики или кубики, с которыми дети могут играть
- Дети, стоящие в линия по высоте порядок
- Цветовая палитра в малярном цехе с градациями оттенков цвета
Что такое серийная деятельность?
Упорядочивание, или упорядочивание, включает в себя задание от детей расположить определенные предметы в порядке в соответствии с критериями, такими как от самого длинного к самому короткому, от самого толстого к самому тонкому, от меньшего к самому большому и т. д.
д.
Эти действия могут принимать форму:
- Бетон Занятия (раскладывание палочек от самой длинной к самой короткой)
- Рисунок Занятия (расположите изображения яблок в порядке от меньшего к большему)
- Аннотация (пронумеруйте элементы на листе от самого длинного до самого короткого или расположите эти числа в порядке от большего к меньшему).
Как вы обучаете последовательностям?
На дошкольном уровне детей следует обучать этому понятию в основном посредством практических занятий с физическими объектами .
Рабочий лист не имеет смысла для ребенка, которому нужно время, чтобы усвоить понятие. Начните с игры и упорядочивания предметов, затем переходите к изображениям предметов. Рабочие листы могут быть введены позже.
Также не обязательно превращать каждую возможность обучения в «урок». Например, просто добавляя мерные чашки и ложки во время игры с водой, дети будут изучать концепцию серий во время игры, именно так усваивается большинство понятий.
Не забывайте учить детей новому словарному запасу, озвучивая то, что они делают во время игры. Используйте такие слова, как:
- Самый высокий
- Самый короткий
- Самый длинный
- Самый тонкий
- Самый толстый
- Самый большой
- наименьший
- LOUST
- Самый мягкий
- Самые грубые
- Световые
- Darkest
, чтобы облегчить мероприятия для младших детей:
- . спрашивать детей «что будет дальше» или «что будет сначала» (раньше других)
Чтобы усложнить задание:
- Предложите больше товаров для заказа
- Предложите все предметы, перемешанные вместе, и попросите ребенка разложить их по порядку
- Составьте последовательность и оставьте несколько ячеек случайным образом, чтобы ребенок мог заполнить их
простые действия, чтобы научить детей концепции упорядочения и упорядочения.
 Замените различные предметы, где это необходимо.
Замените различные предметы, где это необходимо.1. Палочки и соломинки
Соберите палочки снаружи и расположите их от самой короткой к самой высокой или наоборот.
Можно использовать соломинки и нарезать их на разную длину.
2. Фрукты и овощи
Предложите несколько фруктов или овощей одного типа и расположите их в порядке от наименьшего к наибольшему. Используйте один и тот же фрукт, чтобы дети могли сравнивать «яблоки с яблоками», так сказать, вместо того, чтобы путаться из-за разной формы разных фруктов.
3. Наведение порядка
Научите детей аккуратно упаковывать вещи по порядку. Например:
- На летней кухне развесьте кулинарные ложки от самой маленькой до самой большой
- Повесьте одежду по длине в шкаф или на вешалку, когда играете в переодевания
- Упакуйте блоки на полку, начиная с самого большого слева и самого маленького справа
4. Орехи и Болты
Предлагаются гайки и болты всех размеров, которые необходимо расположить по порядку.
Это упражнение также можно использовать для обучения переписке один на один, если вы попросите детей навинтить гайку нужного размера на нужный болт.
5. Вложенные чашки
Поиграйте с вложенными друг в друга чашками и позвольте детям расположить их, складывая их различными способами:
- друг на друга от большего к меньшему, образуя башню
- вложенные друг в друга
- линия по порядку
6. Рисование
Предложите только один цвет краски разных оттенков и позвольте детям поэкспериментировать с оттенками на бумаге.
7. Текстурная игра
В непрозрачный пакет поместите внутрь наждачную бумагу с разной степенью шероховатости и попросите детей вытащить сначала самую гладкую, затем следующую и так далее.
8. Все в очередь
Поставьте членов семьи или детей в ряд в ряд, от самого маленького до самого высокого.
Затем переставьте всех от самых высоких до самых маленьких.
9. Деревянные куклы
Играйте с маленькими деревянными куклами, которые складываются друг в друга. Вы также можете найти деревянные гнездовые яйца.
10. Встряхните и послушайте
Используя несколько одинаковых контейнеров (банки или бутылки), поместите в каждый разное количество бобов, чечевицы или риса. Встряхните каждую бутылку, послушайте звук и закажите их в зависимости от того, сколько бобов, по их мнению, находится в каждом контейнере (от меньшего к большему).
11. Листья
Соберите листья в саду и разложите их по порядку. Старайтесь собирать одинаковые листочки.
12. Контейнерная сортировка
Подготовьте пластиковые бутылки всех размеров и рассортируйте их по высоте.
13. Блоки с основанием 10
Играйте с маленькими кубиками с основанием 10 (количество которых кратно единице). Сложите их рядом друг с другом небольшими стопками, чтобы сравнить их высоту.
Они усовершенствуют свое представление о числах, когда узнают, что 3 — это 3 единицы, 2 — это 2 единицы и т. д.
д.
14. Мерные ложки
Играйте с мерными ложками и мерными чашками во время игры с песком. Сделайте пироги из грязи с помощью мерных чашек и сравните размеры.
Источник:
Хендрик, Х . 1990. Полное обучение: развивающая программа для детей младшего возраста. Третье издание. Издательство Macmillan Publishing Company: Нью-Йорк.
Получите БЕСПЛАТНЫЙ доступ к печатным головоломкам, историям, наборам заданий и многому другому!
Присоединяйтесь к Empowered Parents +, и вы получите загружаемый набор из печатных головоломок, игр и рассказов , а также набор «Обучение через игру» , который включает целый год занятий для детей от 3 до 6 лет.
Бесплатный доступ навсегда.
Регистрация бесплатной учетной записи Grow выполняется быстро и легко и позволит вам добавлять статьи в закладки для последующего чтения на этом веб-сайте, а также на многих веб-сайтах по всему миру, использующих Grow .
- Поделиться
- Электронная почта
ECRP Vol. 4 № 1. Учимся направлять математическое понимание детей дошкольного возраста: профессиональный рост учителя
Исследование и практика раннего детства находится в процессе перехода к программе специального образования для детей младшего возраста в Университете Лойолы в Чикаго после 17 лет работы в Университете Иллинойса в Урбана-Шампейн. Мы в восторге от возможности «передать эстафету» нашим коллегам из раннего детства Лойолы.
Mirar esta página en español
Домашний журнал СодержаниеВыпуска
Том 4 Номер 1
© Автор(ы) 2002
Обучение направить математическое понимание детей дошкольного возраста: Профессиональный рост учителя
Анна
Кирова
Университет Альберты
Амбика
Бхаргава
Оклендский университет
Национальный
Совет учителей математики подчеркивает, что дети младшего возраста
нуждаются в игровых возможностях для развития и углубления своих концептуальных
понимание математики. С точки зрения социал-конструктивизма,
обучение с большей вероятностью произойдет, если взрослые или более компетентные сверстники
опосредовать образовательный опыт детей. Подчеркивая как развитие
и учебные перспективы, эта статья посвящена роли
учителя в организации обучения детей дошкольного возраста математике
пока они играют с повседневными материалами. Профессиональный рост в
три области были определены как критические в обучении учителей
направлять обучение детей младшего возраста математических понятий. Первый
это способность распознавать продемонстрированное детьми понимание
математических понятий, во-вторых, способность использовать математические
язык, чтобы направлять их переход от поведенческих к репрезентативным
понимание математических понятий, а в-третьих, способность
систематически оценивать понимание детьми математических
концепции.
С точки зрения социал-конструктивизма,
обучение с большей вероятностью произойдет, если взрослые или более компетентные сверстники
опосредовать образовательный опыт детей. Подчеркивая как развитие
и учебные перспективы, эта статья посвящена роли
учителя в организации обучения детей дошкольного возраста математике
пока они играют с повседневными материалами. Профессиональный рост в
три области были определены как критические в обучении учителей
направлять обучение детей младшего возраста математических понятий. Первый
это способность распознавать продемонстрированное детьми понимание
математических понятий, во-вторых, способность использовать математические
язык, чтобы направлять их переход от поведенческих к репрезентативным
понимание математических понятий, а в-третьих, способность
систематически оценивать понимание детьми математических
концепции. Контрольные списки, отслеживающие развитие трех основных
математические понятия – однозначное соответствие, классификация,
и сериализацияпредлагаются в качестве инструментов для мониторинга учителями.
обучение детей дошкольного возраста математическим понятиям и плану
соответствующий опыт обучения в детских зонах проксимального
разработка. Создание среды с математическими возможностями
и опосредование детского опыта в этой среде установить
основа для построения, модификации и интеграции математических
понятия у детей раннего возраста.
Контрольные списки, отслеживающие развитие трех основных
математические понятия – однозначное соответствие, классификация,
и сериализацияпредлагаются в качестве инструментов для мониторинга учителями.
обучение детей дошкольного возраста математическим понятиям и плану
соответствующий опыт обучения в детских зонах проксимального
разработка. Создание среды с математическими возможностями
и опосредование детского опыта в этой среде установить
основа для построения, модификации и интеграции математических
понятия у детей раннего возраста.
Лаура только что дочитала рассказ “Златовласка и три медведя” в свой дошкольный класс. Она объявляет, что пришло время для свободная игра. Четырехлетняя Рэйчел некоторое время осматривает комнату. и идет к драматическому центру игры/уборки.
Сегодня этот центр оснащен куклами, другими мягкими игрушками, чашками, тарелками, пластиковая посуда, пластиковые продукты питания, стол, стулья и некоторые нарядная одежда. Рэйчел берет рубашку большого размера и скользит ее ноги в «туфлях мумии». Затем она выводит три чучела мишек разных размеров из коллекции и мест их вокруг стола. Когда она рассаживает медведей на три стула, она бормочет себе под нос: «Ты Папа Медведь» (выбирая самый большой медведь), «ты медведь-мумия» (выбирая медвежонок среднего размера), «а ты Медвежонок» (выбирая самый маленький медведь). Затем Рэйчел подходит к полке и достает одну тарелку и ставит ее перед Папой Медведем; она возвращается к полка, чтобы взять вторую тарелку и поставить ее перед Мамой-Медведицей; а также затем она совершает последний поход, чтобы поставить тарелку перед Медвежонок.
Далее Рэйчел подходит к полке и берет коллекцию. ложек разных размеров. Теперь к ней присоединился 5-летний Тиффани, которая говорит ей, что самому большому медведю нужен самый большой ложка, средний медвежонок – средняя ложка, а медвежонок – самый маленький ложка. «Помните, как сказку о медведях мисс Лора читала нам». Рэйчел смотрит на Тиффани, потом на ложки, потом беспорядочно кладет ложку перед каждым медведем. Тиффани немедленно вступает во владение и переставляет ложки в соответствии с размером медведей. Рэйчел наблюдает несколько секунд, а затем уходит.
Несмотря на то, что
эпизод, подобный этому, не был бы чем-то необычным во многих дошкольных учреждениях.
классах, это оказало особенно сильное влияние на то, как Лора понимала
математические знания своих учеников. Как новый член местного
глава Национального совета учителей математики (NCTM),
Лаура особенно заинтересовалась развитием математических
понятия у ее учеников. Она поняла, что самое замечательное
рост математических знаний происходит между дошкольным
и 2 класса и что это было особенно важно на этом
этап, чтобы сосредоточиться на руководстве развитием детей основных
математические понятия. Тем не менее, отсутствие согласованной учебной программы по математике
для дошкольного учреждения Лауре было трудно решить, какие понятия
были наиболее подходящими для ее детей дошкольного возраста. Как и многие
других учителей, Лаура изо всех сил пыталась понять развитие
математических знаний своих учеников и связать это с ее учебным
решения (Franke & Kazemi, 2001). Она написала в своем дневнике:
Она поняла, что самое замечательное
рост математических знаний происходит между дошкольным
и 2 класса и что это было особенно важно на этом
этап, чтобы сосредоточиться на руководстве развитием детей основных
математические понятия. Тем не менее, отсутствие согласованной учебной программы по математике
для дошкольного учреждения Лауре было трудно решить, какие понятия
были наиболее подходящими для ее детей дошкольного возраста. Как и многие
других учителей, Лаура изо всех сил пыталась понять развитие
математических знаний своих учеников и связать это с ее учебным
решения (Franke & Kazemi, 2001). Она написала в своем дневнике:
Обучение математика всегда была за пределами моей «зоны комфорта». Много коммерческие и созданные учителями математические игры, в том числе наборы животных, фрукты, транспортные средства, формы; настольная счетная игра; классификация досок игры; и различные блесны и большие игральные кости, полезны для усиления взаимно-однозначное соответствие, классификация и сериация.
Однако, при случайном и изолированном использовании эти игры могут не помочь дети полностью усваивают математические концепции, на которых они построены. У меня есть выйти за рамки предоставления некоторой формы математического обучения; я действительно необходимо иметь хорошо продуманную программу по математике. я пытался математические занятия, которые, как я надеялся, будут способствовать обучению. я нарисовал с детьми на большом коврике. Я заставил их каждого снять обувь и решить по цвету, где он должен быть размещен. Это была деятельность мне казалось, что это будет весело и практично, но дети были беспокойны и скучали. Я излагаю небольшие манипуляции с подобными атрибуты и пусть дети исследуют и сортируют в мисках. я поощрял им принести коллекции листьев для научного стола и обсудили цвет и форма.
Хотя дети изучали материалы, Передо мной стояла задача найти способ оценить, какими были дети. учиться и как развивать свои знания.
Как видно из этого
запись в журнале, Лаура почувствовала потребность в прочной концептуальной основе
которые учитывали бы особенности развития
детей дошкольного возраста и будет указывать на среду, которая будет
воспитывать у детей природные математические способности. Такая структура
может помочь Лауре решить, какие математические концепции подходят
для ее учеников и порядок, в котором они должны преподаваться. Лаура
поняла, что эти решения должны быть основаны на ее знаниях
развития математических понятий и на соответствующем
оценка математических знаний детей. Она также поняла
что дошкольные программы должны расширять и углублять концептуальные
знания, которые у маленьких детей уже сформированы к 3 годам
возраста (Пейн, 1990). Новые стандарты NCTM (2000 г.) подчеркивают
что все дети дошкольного возраста нуждаются в возможности исследовать свои
мир и опыт математики через игру. Зная, однако,
оставил у Лоры больше вопросов, чем ответов. Она написала в своем журнале:
Новые стандарты NCTM (2000 г.) подчеркивают
что все дети дошкольного возраста нуждаются в возможности исследовать свои
мир и опыт математики через игру. Зная, однако,
оставил у Лоры больше вопросов, чем ответов. Она написала в своем журнале:
Как использую ли я игры и игровые материалы для улучшения обучения детей? основных математических понятий? Как фасилитатор обучения, как может Я вовлекаю детей в деятельность, которая позволит им дальше конструировать математические понятия? Какой порядок в какие математические понятия развиваются? Какие основные математические понятия? умения и навыки, которые необходимо развивать дошкольникам, чтобы построить прочную основу для их дальнейшего успеха в математике в школе? Как мне убедиться, что я предоставляю возможности для каждого ребенка, как человек, чтобы учиться на его или ее собственном темпе? Что за постоянная оценка будет наиболее полезна при планировании развития подходящий курс по математике? Как я могу еще больше расширить детскую математические знания и навыки, улучшая свою собственную практику и развивая мои познания в преподавании математики?
Наблюдение Лауры эпизода пьесы, в котором участвовали Рэйчел и Тиффани, помогли ей сосредоточить свою работу на следующих конкретных вопросах:
- Какие математические концепции, которые Рэйчел и Тиффани демонстрировали во время игры?
- Как я могу направить их учиться так, чтобы их понимание этих понятий прогрессировало на более высокий уровень?
- Другие дети в моем классе на том же этапе, что и Рэйчел в отношении некоторых эти понятия?
С этими вопросами
в уме Лаура начала свой магистерский проект. Потому что у нас было исследование
интерес к раннему изучению математических понятий, мы стали
надзиратели. В то время наши собственные исследования находились на стадии
разработка ряда удобных для учителей инструментов оценки, которые
облегчить планирование учебного плана в предметной области математики.
Этот проект дал Лоре захватывающую возможность углубить ее
понимание того, как маленькие дети изучают математику. Для нас,
Проект Лауры был как возможность реализовать и задокументировать
использование этих средств в дошкольном классе и получить ее
отзывы об их уместности и полезности для текущей
оценка развития у детей младшего возраста основных математических понятий.
Как руководители Лауры, мы смогли задокументировать посредством наблюдений
и анализ ее дневниковых записей, как она думает о молодых
развитие у детей математических понятий и то, как
ее понимание необходимости согласования учебного плана, обучения,
и оценка выросла.
Потому что у нас было исследование
интерес к раннему изучению математических понятий, мы стали
надзиратели. В то время наши собственные исследования находились на стадии
разработка ряда удобных для учителей инструментов оценки, которые
облегчить планирование учебного плана в предметной области математики.
Этот проект дал Лоре захватывающую возможность углубить ее
понимание того, как маленькие дети изучают математику. Для нас,
Проект Лауры был как возможность реализовать и задокументировать
использование этих средств в дошкольном классе и получить ее
отзывы об их уместности и полезности для текущей
оценка развития у детей младшего возраста основных математических понятий.
Как руководители Лауры, мы смогли задокументировать посредством наблюдений
и анализ ее дневниковых записей, как она думает о молодых
развитие у детей математических понятий и то, как
ее понимание необходимости согласования учебного плана, обучения,
и оценка выросла. В этой статье мы остановимся на основных
области роста в профессиональном развитии Лауры, которые мы считаем
может быть полезным для роста других учителей дошкольного образования.
В этой статье мы остановимся на основных
области роста в профессиональном развитии Лауры, которые мы считаем
может быть полезным для роста других учителей дошкольного образования.
Первый и самый важный
этапом профессионального роста Лауры стала ее повышенная способность
выявить продемонстрированное детьми понимание математических понятий.
Ее наблюдение за реконструкцией истории Рэйчел и Тиффани.
из «Златовласки и трех медведей» привлек внимание Лауры.
к «впечатляющим неформальным математическим силам» (Баруди,
2000, с. 61), которые маленькие дети приносят в класс. Она видела
что в этом эпизоде Рэйчел продемонстрировала свои поведенческие знания,
то есть знание того, как вводить в действие процедуры и роли и реализовывать
несколько математических концепций (Katz & Chard, 2000). Например,
выбирая только медведей из большей коллекции кукол и плюша
игрушки продемонстрировали свое поведенческое знание математической концепции
классификации. Предоставление тарелки для каждого медведя и медведя для
каждый стул демонстрировал свое знание индивидуальной переписки;
упорядочивание медведей по размеру от самого большого к самому маленькому показало ее поведение.
знание серийности. Тиффани также продемонстрировала свое поведение.
знание двойной последовательности путем перестановки ложек в соответствии
с размером медведей после того, как Рэйчел случайно расставила ложки.
Однако более важно то, что Тиффани продемонстрировала свою способность вербализовать
что нужно было сделать, чтобы каждый медведь получил соответствующий
размер ложки. Повышенное внимание Лауры к математическому контексту
взаимодействия между двумя детьми помогло ей распознать
различных стадиях, которых они достигли в своем развитии.
знание серийности. Она также узнала, что маленькие дети
выражать свои математические знания в различных контекстах, которые
не обязательно связаны с «математической деятельностью».
Предоставление тарелки для каждого медведя и медведя для
каждый стул демонстрировал свое знание индивидуальной переписки;
упорядочивание медведей по размеру от самого большого к самому маленькому показало ее поведение.
знание серийности. Тиффани также продемонстрировала свое поведение.
знание двойной последовательности путем перестановки ложек в соответствии
с размером медведей после того, как Рэйчел случайно расставила ложки.
Однако более важно то, что Тиффани продемонстрировала свою способность вербализовать
что нужно было сделать, чтобы каждый медведь получил соответствующий
размер ложки. Повышенное внимание Лауры к математическому контексту
взаимодействия между двумя детьми помогло ей распознать
различных стадиях, которых они достигли в своем развитии.
знание серийности. Она также узнала, что маленькие дети
выражать свои математические знания в различных контекстах, которые
не обязательно связаны с «математической деятельностью». Как
В результате она могла планировать индивидуально подходящий учебный опыт
для них, а также совместный опыт, где они могли бы учиться
друг друга. Она также могла бы поощрять неформальное математическое обучение.
путем создания математической среды и вовлечения детей в математические
разговоры, когда они взаимодействуют с окружающей средой.
Как
В результате она могла планировать индивидуально подходящий учебный опыт
для них, а также совместный опыт, где они могли бы учиться
друг друга. Она также могла бы поощрять неформальное математическое обучение.
путем создания математической среды и вовлечения детей в математические
разговоры, когда они взаимодействуют с окружающей средой.
Следующий этап Лауры профессиональный рост ознаменовался изменением ее понимания роли учителя в обучении детей дошкольного возраста математике концепции. Традиционно акцент в дошкольных учреждениях делается на на том, как усваиваются понятия, а не на том, чему следует учить. Каган (цит. по Jacobson, 1998, стр. 12) указал: «Мы подходил к [раннему образованию] больше с точки зрения развития а не с точки зрения учебного плана. Нам нужно и то, и другое».
Конструктивистская парадигма, основанная на теории Пиаже о познании
развитие уже давно обеспечило теоретическую основу для образовательного
практика, в которой дети усваивали понятия посредством активного участия
с окружающей средой и построили свои собственные знания по мере того, как они
исследовали их окрестности. Применение этой теории к математике
привело к использованию манипулятивных материалов, позволяющих маленьким детям
считать, участвовать в активном обучении и развивать понятия (Каплан,
Ямамото и Гинзберг, 19 лет89). Было замечено, что учитель взял
роль предоставления различных материалов и организации среды
который богат материалами и выбором. Однако в исправленном варианте
принципов соответствующей развитию практики (Бредекамп
& Copple, 1997), Национальная ассоциация образования
лидеров детей младшего возраста (NAEYC) признали, что акцент
на предоставление разнообразия выбора в классе и избегание
обучение детей определенным навыкам было неверно истолковано. Как
В результате в дошкольных учреждениях манипулятивные материалы, как правило,
используется несистематически, что допускает двойную рандомизацию:
один, связанный с появлением манипулятивного материала как такового
а другой определяется различиями в готовности детей
зарегистрировать их (Feuerstein & Feuerstein, 1991).
Применение этой теории к математике
привело к использованию манипулятивных материалов, позволяющих маленьким детям
считать, участвовать в активном обучении и развивать понятия (Каплан,
Ямамото и Гинзберг, 19 лет89). Было замечено, что учитель взял
роль предоставления различных материалов и организации среды
который богат материалами и выбором. Однако в исправленном варианте
принципов соответствующей развитию практики (Бредекамп
& Copple, 1997), Национальная ассоциация образования
лидеров детей младшего возраста (NAEYC) признали, что акцент
на предоставление разнообразия выбора в классе и избегание
обучение детей определенным навыкам было неверно истолковано. Как
В результате в дошкольных учреждениях манипулятивные материалы, как правило,
используется несистематически, что допускает двойную рандомизацию:
один, связанный с появлением манипулятивного материала как такового
а другой определяется различиями в готовности детей
зарегистрировать их (Feuerstein & Feuerstein, 1991). Эта рандомизация
могли помешать реальному концептуальному обучению на какое-то время.
количество детей, которые в противном случае могли бы быть включены в запланированные
деятельность для обучения. Хотя качественное обучение в дошкольном
лет часто носит неформальный характер, эта неформальность не предполагает незапланированного
или бессистемная программа. Изучение математики в дошкольных учреждениях должно
побуждать к размышлению, включать возможности для активного обучения,
и должен быть богат математическим языком. Совсем недавно,
Стандарты NCTM (2000 г.) обращались к проблеме математического содержания,
математический процесс, и важность введения маленьких детей
к языку и правилам математики.
Эта рандомизация
могли помешать реальному концептуальному обучению на какое-то время.
количество детей, которые в противном случае могли бы быть включены в запланированные
деятельность для обучения. Хотя качественное обучение в дошкольном
лет часто носит неформальный характер, эта неформальность не предполагает незапланированного
или бессистемная программа. Изучение математики в дошкольных учреждениях должно
побуждать к размышлению, включать возможности для активного обучения,
и должен быть богат математическим языком. Совсем недавно,
Стандарты NCTM (2000 г.) обращались к проблеме математического содержания,
математический процесс, и важность введения маленьких детей
к языку и правилам математики.
Таким образом роль учителя в активном обучении была замечена больше
в последнее время как решающий. Учитель – это фасилитатор, который создает
среда обучения, которая расширяет математические возможности (NCTM,
1991). Теоретической основой, которая повлияла на это изменение, была концепция Выготского.
(1978, 1986) социально-конструктивистская теория когнитивного развития.
Согласно этой теории, обучение с большей вероятностью произойдет, если взрослые или пожилые
дети опосредуют учебный опыт маленьких детей (Баруди,
2000). Выготский верил в континуум обучения, характеризующийся
дистанция между способностью ребенка самостоятельно решить задачу
и его или ее способность решать проблемы с “максимальной помощью”
под руководством взрослых или более опытных сверстников. Он назвал эту область
где происходит реальное обучение, «зона ближайшего развития».
(ЗПД). Роль учителя, таким образом, состоит в том, чтобы обеспечить «эшафот».
Учитель – это фасилитатор, который создает
среда обучения, которая расширяет математические возможности (NCTM,
1991). Теоретической основой, которая повлияла на это изменение, была концепция Выготского.
(1978, 1986) социально-конструктивистская теория когнитивного развития.
Согласно этой теории, обучение с большей вероятностью произойдет, если взрослые или пожилые
дети опосредуют учебный опыт маленьких детей (Баруди,
2000). Выготский верил в континуум обучения, характеризующийся
дистанция между способностью ребенка самостоятельно решить задачу
и его или ее способность решать проблемы с “максимальной помощью”
под руководством взрослых или более опытных сверстников. Он назвал эту область
где происходит реальное обучение, «зона ближайшего развития».
(ЗПД). Роль учителя, таким образом, состоит в том, чтобы обеспечить «эшафот». помощи» (Berk & Winsler, 19 лет).95), что влечет за собой постоянное
модификация заданий для обеспечения соответствующего уровня
вызов, который позволяет ребенку учиться. Взрослые меняются
качество поддержки в течение учебного занятия, корректировка
помощь в соответствии с уровнем успеваемости ребенка (Berk & Winsler,
1995). Дети учатся через осмысленное, естественное, активное обучение
опыт. Взрослый должен опираться на эти знания и
детей на более высокий уровень понимания.
помощи» (Berk & Winsler, 19 лет).95), что влечет за собой постоянное
модификация заданий для обеспечения соответствующего уровня
вызов, который позволяет ребенку учиться. Взрослые меняются
качество поддержки в течение учебного занятия, корректировка
помощь в соответствии с уровнем успеваемости ребенка (Berk & Winsler,
1995). Дети учатся через осмысленное, естественное, активное обучение
опыт. Взрослый должен опираться на эти знания и
детей на более высокий уровень понимания.
Приняв взгляд Выготского на обучение, Лаура начала
понимать, что она должна решить, какие дальнейшие возможности — не только
материалы, но, что более важно, взаимодействие — ей нужно было обеспечить
для Рэйчел, Тиффани и остальных детей в ее классе.
Только тогда она могла развить и расширить свое понимание математики. осмысленно. Она написала в своем дневнике:
осмысленно. Она написала в своем дневнике:
я нужно сделать физическую среду в моем классе более математической богатый. Мебель детского размера и легко адаптируется для размещения совместная работа. Есть достаточное и удобное пространство на пол с частичным ковровым покрытием для исследования, строительства и работы бетонные материалы. Математические материалы и манипуляторы хранятся в прозрачных корзинах на открытых полках с картинками и в удобном досягаемость детей. Теперь я намерен увеличить количество детей. математическое понимание, помогая им построить знание взаимно однозначного соответствия, классификации и упорядочения.
Для направления детских
изучение концепций, продемонстрированных во время эпизода свободной игры,
Лаура начала понимать необходимость участия в различных ситуациях. которые создают общий язык, связанный с математикой (Franke & Kazemi, 2001). Например, мы смогли наблюдать за ее ежедневными обсуждениями
с детьми, которые включали сравнение противоположностей при выборе
время. Дети и воспитатель обсудили, какие кубики
больше или меньше, какие блоки лучше помещаются в полки: маленькие,
средние, или большие. Они также сделали ежедневной привычкой обсуждать порядок:
кто был первым в очереди, кто был вторым в очереди,
кто был последним в очереди или камбузом, закусщиком.
которые создают общий язык, связанный с математикой (Franke & Kazemi, 2001). Например, мы смогли наблюдать за ее ежедневными обсуждениями
с детьми, которые включали сравнение противоположностей при выборе
время. Дети и воспитатель обсудили, какие кубики
больше или меньше, какие блоки лучше помещаются в полки: маленькие,
средние, или большие. Они также сделали ежедневной привычкой обсуждать порядок:
кто был первым в очереди, кто был вторым в очереди,
кто был последним в очереди или камбузом, закусщиком.
Язык позволяет получать новую информацию, а также
присвоение сложных идей и процессов (Бодрова и Леонг,
1996). Открытые вопросы могут стимулировать расширенное мышление. “Какая
еще?» и «Интересно, что будет, если» можно будет нарисовать
внимание детей к новым способам мышления и взаимодействия. Камии
(1982) объясняет, что важно позволять детям, которые строят
свои математические знания, чтобы сделать это без поддержки учителя
«правильность» или исправление «неправильности» ответа ребенка. Несогласие со сверстниками может помочь ребенку
пересмотреть правильность своего мышления. Социальные взаимодействия
посредством групповых игр являются отличным источником создания новых
математические идеи и могут привести детей к установлению новых связей
и расширить свои рассуждения. Это взаимодействие помогает им стать
более независимым и менее зависимым от учителя как единственного источника
ответов.
Несогласие со сверстниками может помочь ребенку
пересмотреть правильность своего мышления. Социальные взаимодействия
посредством групповых игр являются отличным источником создания новых
математические идеи и могут привести детей к установлению новых связей
и расширить свои рассуждения. Это взаимодействие помогает им стать
более независимым и менее зависимым от учителя как единственного источника
ответов.
Если учебные ситуации были организованы и основаны на развитии
последовательность математических понятий, то учебный план будет отражать
нынешняя стадия понимания детей и обеспечит
возможности для дальнейшего развития в темпе каждого ребенка. В соответствии
Кацу и Чарду (2000), понимая, «как развивается знание,
что они [дети] могут понять, и как они понимают свои
опыт по мере развития является еще одной основой для учебной программы
планирования» (стр.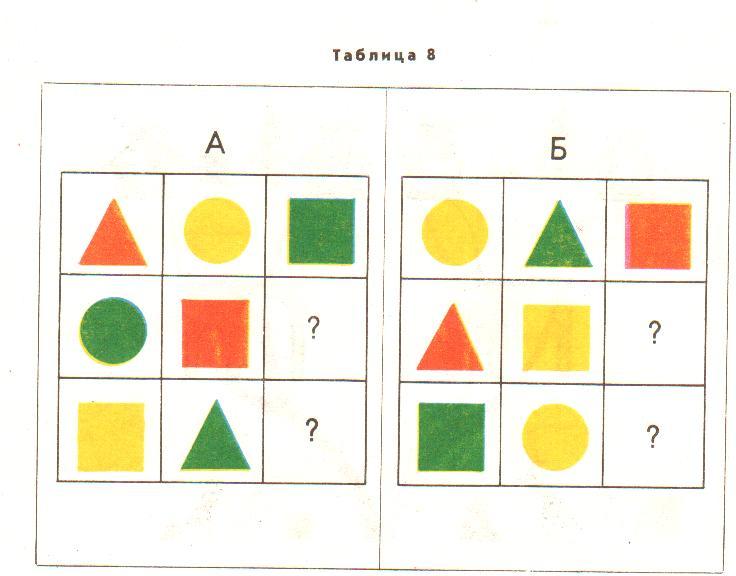 26). Таким образом, взять и Рейчел, и Тиффани из
от поведенческого к репрезентативному знанию (т. е. ментальному или символическому
представления понятий, абстрагированные от прямых и/или косвенных
опыта), Лоре нужно было тщательно спланировать не только физические
расположение ее класса, но, что наиболее важно, ее взаимодействие с
их, чтобы помочь их продвижению по этапам представления
математических понятий.
26). Таким образом, взять и Рейчел, и Тиффани из
от поведенческого к репрезентативному знанию (т. е. ментальному или символическому
представления понятий, абстрагированные от прямых и/или косвенных
опыта), Лоре нужно было тщательно спланировать не только физические
расположение ее класса, но, что наиболее важно, ее взаимодействие с
их, чтобы помочь их продвижению по этапам представления
математических понятий.
Как и большинство педагогов,
Лаура искала способы улучшить согласованность учебной программы,
инструктаж и оценка. Работая над своим магистерским проектом,
она начала думать на более высоком уровне о связи между
учебная программа и оценка. Она поняла, что если цель оценки
заключалась в том, чтобы позволить учителям принимать соответствующие решения для улучшения
понимание учащимися и усвоение математических понятий, а затем
ее собственное глубокое знание этих ключевых понятий, фактов, принципов,
и процессы были необходимы для планирования соответствующей учебной программы
и опыт работы в классе. Таким образом, чтобы иметь возможность направлять обучение детей
математических понятий, она должна была быть основательно
последовательность развития понятий, которые дети усваивают. Только
тогда она могла бы оценить текущий уровень детского понимания
математических понятий и планировать опыт в своей зоне ближайшего
разработка.
Таким образом, чтобы иметь возможность направлять обучение детей
математических понятий, она должна была быть основательно
последовательность развития понятий, которые дети усваивают. Только
тогда она могла бы оценить текущий уровень детского понимания
математических понятий и планировать опыт в своей зоне ближайшего
разработка.
Лаура, однако, поняла, что одних теоретических знаний недостаточно.
для эффективного обучения; ей потребуются соответствующие инструменты для оценки
такое обучение. Оценка и документирование детской работы может
помочь ей спланировать с учетом развития и, что более важно, индивидуально
соответствующий опыт, который будет способствовать обучению детей.
Среди специалистов по раннему развитию общепринято, что наблюдение
является наиболее подходящим методом оценки детей дошкольного возраста и
эта игра предлагает идеальный контекст для наблюдения за детьми и определения
их знание и понимание (Гарви, 1990; Хоус, 1992).
В следующих разделах описано, как Лаура использовала теоретические знания о последовательности развития математических понятий, которые продемонстрировали Рэйчел и Тиффани в игровом эпизоде, чтобы оценить и направлять все учащиеся в изучении этих концепций. Эти понятия являются (1) соответствием и взаимно-однозначным соответствием, (2) множествами и классификацией, и (3) порядок и серия. Детское развитие этих понятий проходит несколько стадий. Мы собрали эти этапы в контрольный список, и Лаура использовала этот контрольный список в своей работе.
Концепция №1: Сопоставление и однозначное соответствие
Как обсуждалось выше,
Размещение Рэйчел по одной тарелке для каждого медведя продемонстрировало ее понимание.
понятия соответствия и однозначного соответствия. Как правило,
дети в возрасте от 2 до 4 лет развивают это понимание
через отношения «более-менее-одинаково» (Кисть,
1972 год; Гельман и Галлистел, 19 лет78). Совпадение является обязательным условием
для консервации; это одно из первых математических понятий
развивать и формирует основу для развития логических
мышление. Индивидуальная переписка является фундаментальным компонентом
понятия числа. Это понимание того, что одна группа
имеет то же количество вещей, что и другой. Предварительно к подсчету
и основой для понимания эквивалентности и концепции
сохранение числа (Чарльсворт и Линд, 1999; Монтегю-Смит,
1997). Как только дети поймут основную переписку один на один,
они могут применить эту концепцию к деятельности более высокого уровня, которая включает в себя
эквивалентность и идея «более или менее» (см. Приложение
Я).
Совпадение является обязательным условием
для консервации; это одно из первых математических понятий
развивать и формирует основу для развития логических
мышление. Индивидуальная переписка является фундаментальным компонентом
понятия числа. Это понимание того, что одна группа
имеет то же количество вещей, что и другой. Предварительно к подсчету
и основой для понимания эквивалентности и концепции
сохранение числа (Чарльсворт и Линд, 1999; Монтегю-Смит,
1997). Как только дети поймут основную переписку один на один,
они могут применить эту концепцию к деятельности более высокого уровня, которая включает в себя
эквивалентность и идея «более или менее» (см. Приложение
Я).
Используя контрольный список, Лаура смогла определить стадию болезни Рэйчел.
понимание концепции взаимной корреспонденции как
при «сопоставлении четных наборов элементов, которые связаны или идут вместе
но не похожи. ” Чтобы поддержать и направить обучение Рэйчел
на следующий уровень той же концепции Лаура предоставила возможности
чтобы она соответствовала нечетным наборам из пяти или более предметов. Она использовала каждый
возможность присоединиться к Рэйчел в игровой зоне по уборке. С использованием
бытовые предметы (как в четном, так и в нечетном количестве), с которыми Рэйчел
был знаком, как чашки и блюдца, ложки и вилки, лопаты и
ведра или наборы пластиковых животных, Лаура смогла идентифицировать
способность сопоставлять одинаковые или не похожие предметы. Когда у Рэйчел
использование этих материалов не указывало на четкую закономерность, спросила Лора.
конкретные вопросы. Например, Лаура принесла несколько пластиковых животных.
добавить к мишкам и использовать небольшие контейнеры. Как раз вовремя
Во время игры она попросила Рэйчел найти по одному животному для каждого контейнера.
” Чтобы поддержать и направить обучение Рэйчел
на следующий уровень той же концепции Лаура предоставила возможности
чтобы она соответствовала нечетным наборам из пяти или более предметов. Она использовала каждый
возможность присоединиться к Рэйчел в игровой зоне по уборке. С использованием
бытовые предметы (как в четном, так и в нечетном количестве), с которыми Рэйчел
был знаком, как чашки и блюдца, ложки и вилки, лопаты и
ведра или наборы пластиковых животных, Лаура смогла идентифицировать
способность сопоставлять одинаковые или не похожие предметы. Когда у Рэйчел
использование этих материалов не указывало на четкую закономерность, спросила Лора.
конкретные вопросы. Например, Лаура принесла несколько пластиковых животных.
добавить к мишкам и использовать небольшие контейнеры. Как раз вовремя
Во время игры она попросила Рэйчел найти по одному животному для каждого контейнера. После неоднократных взаимодействий такого рода Лаура наблюдала за Рэйчел.
играя у водного стола, кладя по одной лягушке на каждый пластиковый лист
в воде. Лора также заметила, что за столом с закусками Рэйчел осторожно
поставил чашку рядом с бумажной салфеткой для каждого ребенка.
После неоднократных взаимодействий такого рода Лаура наблюдала за Рэйчел.
играя у водного стола, кладя по одной лягушке на каждый пластиковый лист
в воде. Лора также заметила, что за столом с закусками Рэйчел осторожно
поставил чашку рядом с бумажной салфеткой для каждого ребенка.
Чтобы перевести Рэйчел от поведенческих к репрезентативным знаниям, Лаура
был осторожен в использовании формулировок, связанных с концепцией сопоставления и
переписка один на один. Богатое социальное взаимодействие с учителями
и более компетентные сверстники могут способствовать расширению возможностей детей
для обучения и превращения поведенческих знаний в репрезентативные
знания. Способность детей использовать такие слова, как недостаточно и
слишком многие продемонстрировали бы высочайший уровень своего понимания
соответствие и взаимное соответствие.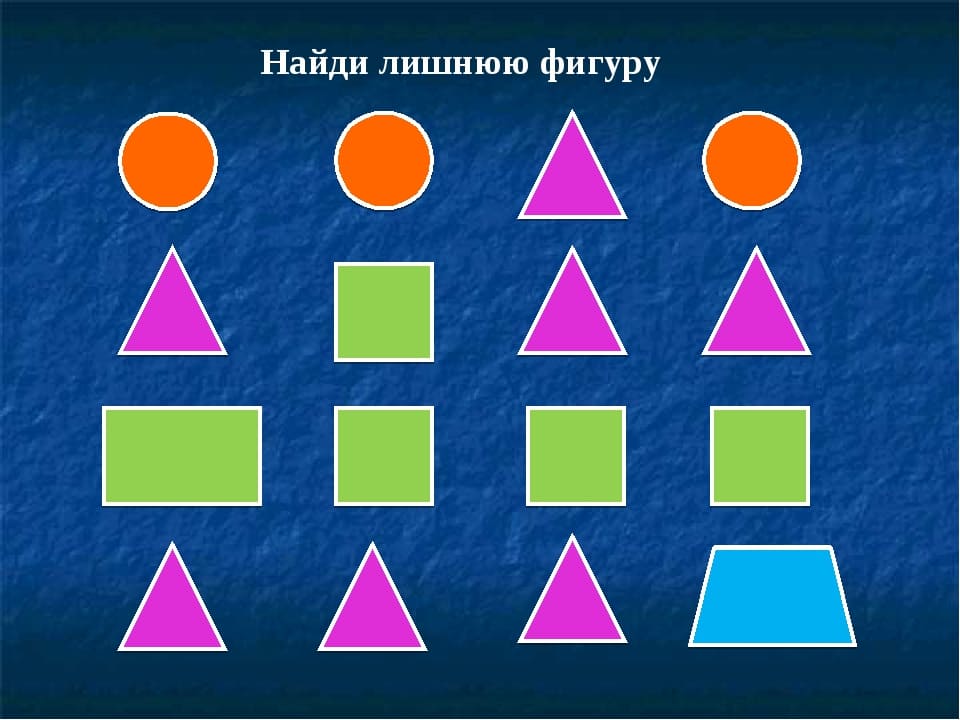 Использование детской литературы.
также способствовал развитию языка, связанного с математикой
концепции.
Использование детской литературы.
также способствовал развитию языка, связанного с математикой
концепции.
Поскольку взаимно однозначное соответствие означает, что одна группа имеет одинаковые
помимо прочего, целью Лауры было помочь не только Рэйчел
но все дети в ее классе, чтобы увидеть отношения в
любой набор материалов. В результате Лаура преобразовала время уборки
к важному «математическому времени», введя сопоставление
игра. Она попросила детей поместить один предмет в контейнер.
или на полке. Выполняя это задание, они должны были сопоставить объект
к объекту, объект к изображению и изображение к изображению (см. Приложение
Я). Она также представила различные коммерческие игры и игры, созданные учителями.
соответствующие виды деятельности, доступные детям в выбранное время. занятия, проводимые учителем, включали в себя корзины с небольшими предметами, разделенные
подносы, щипцы (по желанию, в зависимости от индивидуальных особенностей ребенка)
двигательные навыки), а также кубики от одного до трех или от одного до шести. Эти
деятельность ввела понятие сопоставления: один предмет входит в
одна секция лотка. Одно из занятий, которое дети Лауры
очень понравилось брать шарики из корзины совком для дыни
и положить по одному шарику в каждое отделение лотка для кубиков льда.
Лаура написала в своем дневнике: «Это занятие настолько популярно, что
Я должен внести имена в лист ожидания для тех детей, которые хотят
играть в мраморную игру снова и снова».
занятия, проводимые учителем, включали в себя корзины с небольшими предметами, разделенные
подносы, щипцы (по желанию, в зависимости от индивидуальных особенностей ребенка)
двигательные навыки), а также кубики от одного до трех или от одного до шести. Эти
деятельность ввела понятие сопоставления: один предмет входит в
одна секция лотка. Одно из занятий, которое дети Лауры
очень понравилось брать шарики из корзины совком для дыни
и положить по одному шарику в каждое отделение лотка для кубиков льда.
Лаура написала в своем дневнике: «Это занятие настолько популярно, что
Я должен внести имена в лист ожидания для тех детей, которые хотят
играть в мраморную игру снова и снова».
По мере того, как дети становились более опытными в переписке один на один
навыки, Лаура представила игры с сеткой и коротким путем. Сетчатые игры
карты типа бинго (без букв и цифр), используемые в комбинации
с игральными костями или спиннерами и счетчиками (Moomaw & Hieronymus, 1995).
Teddy Bear Bingo и Candy Land Bingo являются примерами коммерческих
сеточные игры. Эти игры позволили Лоре наблюдать за разными уровнями.
на котором находились дети по уровню развития
соответствия и однозначного соответствия. Для некоторых детей, считая
точки на костях были вызовом; они либо дважды учитываются
или пропущенные пункты. Рэйчел, например, посчитала шесть за «один».
два три; один два три.” Для других счет не представляет
проблема. Они даже могли использовать математический язык, чтобы не
только объяснить, что они делали, но и предсказать, что они
необходимо для победы в игре.
Сетчатые игры
карты типа бинго (без букв и цифр), используемые в комбинации
с игральными костями или спиннерами и счетчиками (Moomaw & Hieronymus, 1995).
Teddy Bear Bingo и Candy Land Bingo являются примерами коммерческих
сеточные игры. Эти игры позволили Лоре наблюдать за разными уровнями.
на котором находились дети по уровню развития
соответствия и однозначного соответствия. Для некоторых детей, считая
точки на костях были вызовом; они либо дважды учитываются
или пропущенные пункты. Рэйчел, например, посчитала шесть за «один».
два три; один два три.” Для других счет не представляет
проблема. Они даже могли использовать математический язык, чтобы не
только объяснить, что они делали, но и предсказать, что они
необходимо для победы в игре. Меган сказала: «У меня шесть, теперь я только
осталось еще три”, и Тиффани сказала: “Один и два
три, теперь мне нужно еще четыре.” Увидев Тиффани, Лора
спросил ее, не хочет ли она сыграть в сетку с Рэйчел. Тиффани,
который получил огромное удовольствие от игры и искал все доступные
возможности играть в нее, с готовностью согласился. Во время взаимодействия
между двумя детьми, Тиффани сказала Рэйчел: “Это
не то, как вы считаете это! Смотреть. Вы идете вот так (показывая на каждую
карандашом и произнести раз, два, три, четыре, пять)». После нескольких повторений Рэйчел смогла самостоятельно сосчитать,
шесть.
Меган сказала: «У меня шесть, теперь я только
осталось еще три”, и Тиффани сказала: “Один и два
три, теперь мне нужно еще четыре.” Увидев Тиффани, Лора
спросил ее, не хочет ли она сыграть в сетку с Рэйчел. Тиффани,
который получил огромное удовольствие от игры и искал все доступные
возможности играть в нее, с готовностью согласился. Во время взаимодействия
между двумя детьми, Тиффани сказала Рэйчел: “Это
не то, как вы считаете это! Смотреть. Вы идете вот так (показывая на каждую
карандашом и произнести раз, два, три, четыре, пять)». После нескольких повторений Рэйчел смогла самостоятельно сосчитать,
шесть.
В играх с дорожками дети бросают кубик или кости, чтобы продвинуть ходок на
путь отчетливо разделенных пространств. Мумо и Иеронимус (1995)
утверждают, что «путевые игры включают в себя стратегии мышления
нужен для игры в сетку на более сложном уровне и разместить дополнительные
акцент на социальном взаимодействии с учителями и сверстниками» (с. 117). Первая игра с коротким путем покрыла путь фишками бинго.
чтобы помочь белке найти орехи. Кости от одного до шести были
используется (рис. 1). Все дети смогли понять
концепция игры с коротким путем со стартом и финишем.
117). Первая игра с коротким путем покрыла путь фишками бинго.
чтобы помочь белке найти орехи. Кости от одного до шести были
используется (рис. 1). Все дети смогли понять
концепция игры с коротким путем со стартом и финишем.
Рисунок 1. Математическая таблица настроена для короткого игра дорожка белка.
Следующее задание на коротком пути было более сложным. Игра со змеей использовалась
кубики unifix в качестве счетчиков и использовали счетчик от одного до шести.
игра в змейку была более сложной для детей, которые еще не освоили
возможность сопоставлять неравные наборы из пяти и более предметов. Рэйчел,
например, с трудом сопоставлял куб unifix с соответствующим
площадь. Квадраты следовали форме «s», а форма
смутил ее. Она пропускала квадраты и сбивалась со счета, когда складывала
кубики. Она не смогла закончить игру. Тиффани, наоборот,
уже был в состоянии предсказать: «У меня трое, а теперь я просто
нужен еще один!” Она также считала квадраты, чтобы увидеть, сколько она
ушла до того, как она закончила. Она играла в игру несколько раз
с большим энтузиазмом. Зная, что Тиффани удалось помочь
Рэйчел научилась считать очки на костях до шести, Лора один раз
снова попросите ее поиграть с Рэйчел. На этот раз Тиффани использовала другой
стратегия, чтобы показать Рэйчел, что ей нужно делать. Она сказала: «Рэйчел,
вы просто кладете палец на следующий квадрат, а затем перемещаете куб». Хотя Рэйчел быстро научилась следовать по изогнутому пути,
номера на спиннере оставались проблемой. Тиффани решила, что
она должна была бы сказать ей, сколько квадратов ей нужно, чтобы переместить ее
куб. Рэйчел была счастлива, что Тиффани помогла ей.
Она не смогла закончить игру. Тиффани, наоборот,
уже был в состоянии предсказать: «У меня трое, а теперь я просто
нужен еще один!” Она также считала квадраты, чтобы увидеть, сколько она
ушла до того, как она закончила. Она играла в игру несколько раз
с большим энтузиазмом. Зная, что Тиффани удалось помочь
Рэйчел научилась считать очки на костях до шести, Лора один раз
снова попросите ее поиграть с Рэйчел. На этот раз Тиффани использовала другой
стратегия, чтобы показать Рэйчел, что ей нужно делать. Она сказала: «Рэйчел,
вы просто кладете палец на следующий квадрат, а затем перемещаете куб». Хотя Рэйчел быстро научилась следовать по изогнутому пути,
номера на спиннере оставались проблемой. Тиффани решила, что
она должна была бы сказать ей, сколько квадратов ей нужно, чтобы переместить ее
куб. Рэйчел была счастлива, что Тиффани помогла ей.
Концепция № 2: Ранняя классификация: создание наборов
В своей реконструкции истории о Златовласке Рэйчел продемонстрировала ее понимание классификации, когда она увидела тождество медведей независимо от их размера. Согласно Sugarman (1983), «классификация существует, когда два или более дискретных события рассматриваться как эквивалентные» (стр. 4). Эта классификация приводит к признание того, что одна группа объектов является частью большей группы. Однако некоторые люди могут относиться к некоторым объектам или группам объектов эквивалентны по разным причинам.
Используя контрольный список, Лаура определила, что у Рэйчел были поведенческие расстройства.
знание классификации по ассоциации и что она продемонстрировала
некоторые знания о включении классов. Таким образом, чтобы направлять обучение Рэйчел
этой концепции Лоре нужно было вовлечь Рэйчел в деятельность, которая
поможет ей понять концепцию класса: включение. Перекус
время предоставило такую возможность. При приготовлении фруктового салата
Лаура спросила Рэйчел: «У нас есть яблоки и бананы в этом фрукте.
салат; Можем ли мы добавить какие-либо другие фрукты?» Также предусмотрено время для уборки.
Лора с возможностью попросить Рэйчел поместить всех животных в
одна коробка. Несколько дней спустя дети делали вид, что продолжают
пикник, и Лора услышала, как Рэйчел сказала детям: «Мы
нужно положить всю еду в корзину для пикника».
другие дети положили еду в корзину, Рэйчел взяла разные
игрушек и положил их в другую коробку, чтобы взять с собой на пикник. В течение
“пикник”, Лора “случайно” положила
мяч в корзине для пикника, и она получила выговор от Рэйчел, которая
сказал: «Это не входит в корзину для пикника».
Перекус
время предоставило такую возможность. При приготовлении фруктового салата
Лаура спросила Рэйчел: «У нас есть яблоки и бананы в этом фрукте.
салат; Можем ли мы добавить какие-либо другие фрукты?» Также предусмотрено время для уборки.
Лора с возможностью попросить Рэйчел поместить всех животных в
одна коробка. Несколько дней спустя дети делали вид, что продолжают
пикник, и Лора услышала, как Рэйчел сказала детям: «Мы
нужно положить всю еду в корзину для пикника».
другие дети положили еду в корзину, Рэйчел взяла разные
игрушек и положил их в другую коробку, чтобы взять с собой на пикник. В течение
“пикник”, Лора “случайно” положила
мяч в корзине для пикника, и она получила выговор от Рэйчел, которая
сказал: «Это не входит в корзину для пикника».
Лора поняла, что на каждом из уровней развития
концепции, было важно, чтобы она поговорила с Рэйчел и спросила ее
чтобы описать, а затем объяснить, что она сделала. Выготский считал
что дети становятся способными думать во время разговора (Bodrova & Leong, 1996). Когда ребенок продемонстрировал понимание поведения
концепции и описала то, что она или он представляли, Лаура
убедиться, что она поговорила с ребенком, чтобы определить, что она
также в состоянии объяснить свои действия. Это обсуждение обеспечило
ребенок действительно понял концепцию и не просто повторял
слова без реального понимания. Использование языка в общих
деятельность позволяет ребенку конструировать смысл, а также демонстрировать
более высокий уровень понимания концепции.
Выготский считал
что дети становятся способными думать во время разговора (Bodrova & Leong, 1996). Когда ребенок продемонстрировал понимание поведения
концепции и описала то, что она или он представляли, Лаура
убедиться, что она поговорила с ребенком, чтобы определить, что она
также в состоянии объяснить свои действия. Это обсуждение обеспечило
ребенок действительно понял концепцию и не просто повторял
слова без реального понимания. Использование языка в общих
деятельность позволяет ребенку конструировать смысл, а также демонстрировать
более высокий уровень понимания концепции.
Большинство очень маленьких детей способны классифицировать предметы. Однако,
маленькие дети не обязательно знают названия цветов, форм,
материалы и пр. Это отсутствие словарного запаса может быть ошибкой
из-за отсутствия знаний или умения классифицировать по одному признаку. Так
учитель должен попросить маленьких детей классифицировать, не используя конкретный
цвета или формы, а используя общие вопросы, такие как «Может ли
вы найдете что-то того же цвета (или формы, или размера, или материала,
д.), как этот?» К тому времени, когда дети демонстрируют, что они
могут классифицировать по двум и более признакам, они уже приобрели
словарный запас для описания конкретных характеристик объекта.
Поэтому учителю уместно спросить детей: «Могут ли
найдешь что-нибудь красное и длинное?»
Так
учитель должен попросить маленьких детей классифицировать, не используя конкретный
цвета или формы, а используя общие вопросы, такие как «Может ли
вы найдете что-то того же цвета (или формы, или размера, или материала,
д.), как этот?» К тому времени, когда дети демонстрируют, что они
могут классифицировать по двум и более признакам, они уже приобрели
словарный запас для описания конкретных характеристик объекта.
Поэтому учителю уместно спросить детей: «Могут ли
найдешь что-нибудь красное и длинное?»
Чтобы помочь Рэйчел развить способность классифицировать по функциям или ассоциациям,
во время уборки Лаура спросила ее: «Можете ли вы положить вещи
что вы рисуете вместе в этой коробке, пожалуйста?» или «Можно
вы найдете в игровом центре все, чем пользуется врач, и положите
их в одном месте, пожалуйста?” Во время драматической игры Лаура спросила
детям собрать все необходимое для открытия продуктового
магазин, чтобы Златовласка могла купить больше продуктов, чтобы сделать кашу
для медведей. Хотя это не характерно для детей дошкольного возраста.
иметь четкое представление о включении и исключении классов,
при задании конкретных вопросов некоторые могут продемонстрировать частичное понимание
концепции. Они особенно склонны понимать, когда
включение в класс связано с личным опытом, таким как посещение
кабинет врача, поход в продуктовый магазин или работа в саду с
родитель (см. Приложение II).
Хотя это не характерно для детей дошкольного возраста.
иметь четкое представление о включении и исключении классов,
при задании конкретных вопросов некоторые могут продемонстрировать частичное понимание
концепции. Они особенно склонны понимать, когда
включение в класс связано с личным опытом, таким как посещение
кабинет врача, поход в продуктовый магазин или работа в саду с
родитель (см. Приложение II).
Графики — это более сложный способ классификации. Простой групповой бар графики подходят для развития детей дошкольного возраста и позволяют дети работают вместе и учатся друг у друга. Гистограммы которые отчетливо отображают информацию, дают детям возможность попрактиковаться в создание и сравнение наборов:
Хороший график возникает из естественного желания детей делиться информацией со своими сверстниками, количественно оценить результаты и сравнить результаты.
Графики могут быть особенно мотивирующими для когнитивно развитых детей так как они провоцируют высокий уровень мышления. (Мумо и Иеронимус, 1995, с. 170)
С приближением Хэллоуина, Лора привлекла детей к построению графиков на основе предсказаний. Она представил тыквы с графиком под названием «Как растут тыквы?» (Фигура 2). Тыквы, выращиваемые различными способами, иллюстрируют выбор: на тыквенном дереве, на тыквенном кусте, на лиане или под землей. Имена детей были на картонных прямоугольниках и были доступны чтобы они выбрали. Лаура позвала детей по отдельности и снова представил каждый вариант и попросил их назвать свое имя по тому, как, по их мнению, растут тыквы.
Это занятие еще раз показало, что маленькие дети думают по-другому
или не имеют знаний, предполагаемых взрослыми..jpg) Большинство
дети правильно выбрали, что тыквы росли на лианах. Сид, однако
заявил: «Тыквы растут под землей, как картофель». Джейми
тоже выбрала подполье, но не смогла объяснить свой выбор. На вопрос,
она сказала: «Потому что они [тыквы] делают». После детей
и учитель закончил обсуждение, Лаура показала классу
несколько фотографий тыквенной грядки и тыкв на лозе. Она спросила
если бы кто-нибудь мог видеть, как растут тыквы. Все дети
согласился, что тыквы действительно растут на виноградных лозах.
Большинство
дети правильно выбрали, что тыквы росли на лианах. Сид, однако
заявил: «Тыквы растут под землей, как картофель». Джейми
тоже выбрала подполье, но не смогла объяснить свой выбор. На вопрос,
она сказала: «Потому что они [тыквы] делают». После детей
и учитель закончил обсуждение, Лаура показала классу
несколько фотографий тыквенной грядки и тыкв на лозе. Она спросила
если бы кто-нибудь мог видеть, как растут тыквы. Все дети
согласился, что тыквы действительно растут на виноградных лозах.
Рисунок 2. Графический дисплей «Как работают тыквы Расти?»
Концепция №3: Порядок и серийность
В описанном выше игровом эпизоде Рэйчел также продемонстрировала свою
поведенческое понимание серий путем систематического размещения
медведей от большего к меньшему. Заказ – это более высокий уровень
сравнивать (видеть различия) и включает в себя сравнение более чем
два объекта или более двух наборов. Заказ или серия включает в себя
размещение более двух объектов или наборов с более чем двумя элементами
в последовательность. Упорядочивание также включает в себя размещение объектов в определенной последовательности.
от первого до последнего, и это является необходимым условием для создания паттернов. Заказ
лежит в основе нашей системы счисления (например, 2 больше 1,
3 больше 2 и т. д.).
Заказ или серия включает в себя
размещение более двух объектов или наборов с более чем двумя элементами
в последовательность. Упорядочивание также включает в себя размещение объектов в определенной последовательности.
от первого до последнего, и это является необходимым условием для создания паттернов. Заказ
лежит в основе нашей системы счисления (например, 2 больше 1,
3 больше 2 и т. д.).
Лора увидела из контрольного списка, что следующий этап развития
последовательность этого понятия – двойная серия. Во время игрового эпизода
Рэйчел не понимала этой концепции, как она продемонстрировала, когда
она расставила ложки хаотично, а не по размеру
медведи. На самом деле, когда старший ребенок, Тиффани, напомнил ей, что
самому большому медведю нужна была самая большая ложка, Рэйчел проигнорировала ее, и
когда Тиффани продолжила, Рэйчел ушла.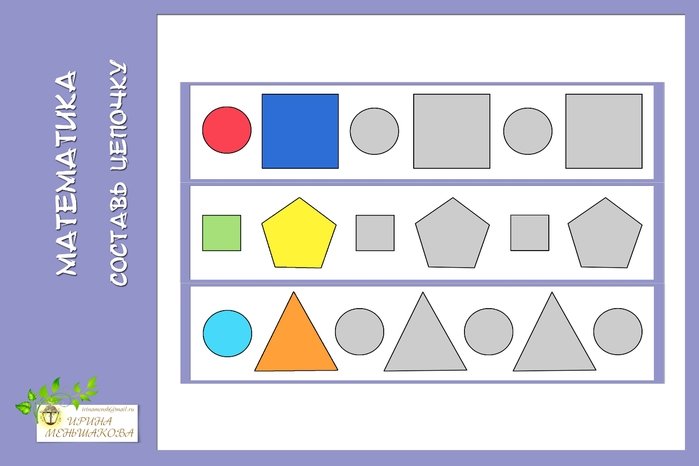 Такие истории, как «Златовласка.
и три медведя» часто используются для иллюстрации
концепция двойной серии. Тем не менее, поскольку Рэйчел не уловила
концепции с первого чтения Лора решила предоставить чашки и
ложки, животные и миски разных размеров, которые можно было использовать для
двойная серия. Позже в учебном году Лора заметила Рэйчел.
объясняя концепцию двойной серии Эмили в том же
способ, которым Тиффани попыталась объяснить концепцию Рэйчел.
Лора услышала, как Эмили наконец воскликнула: «Я поняла — большая миска
идет с большой собакой!” Компетентные сверстники могут моделировать концепции
и направлять обучение менее компетентного ребенка во время совместных занятий.
Совместная деятельность заставляет участников уточнять и уточнять
свое мышление (Бодрова и Леонг, 1996).
Такие истории, как «Златовласка.
и три медведя» часто используются для иллюстрации
концепция двойной серии. Тем не менее, поскольку Рэйчел не уловила
концепции с первого чтения Лора решила предоставить чашки и
ложки, животные и миски разных размеров, которые можно было использовать для
двойная серия. Позже в учебном году Лора заметила Рэйчел.
объясняя концепцию двойной серии Эмили в том же
способ, которым Тиффани попыталась объяснить концепцию Рэйчел.
Лора услышала, как Эмили наконец воскликнула: «Я поняла — большая миска
идет с большой собакой!” Компетентные сверстники могут моделировать концепции
и направлять обучение менее компетентного ребенка во время совместных занятий.
Совместная деятельность заставляет участников уточнять и уточнять
свое мышление (Бодрова и Леонг, 1996).
Лора также вовлекла всех детей в процесс обучения, который
может помочь им получить как поведенческие, так и репрезентативные знания
понятия порядка и серийности. Среди них были вопросы к детям
выстраиваться по высоте перед выходом на игру, ставя персонажей
в своих картинах в соответствии с их размером, выстраивая в ряд звуки от
от самого громкого к самому тихому, и окрашивание объектов в соответствии с их оттенком
от самого светлого к самому темному или наоборот. Последовательность событий во время
экскурсия была еще одним опытом обучения, который Лора предоставила
ее учеников, что было связано с пониманием сериализации. Кроме того,
Лора добросовестно использовала математический язык, когда
дети играли с кубиками, матрешками и т.д. Немного
конкретные вопросы, которые она задавала, были: «Можете ли вы найти блок, который
меньше этого?” или “Можете ли вы найти что-то, что
больше, чем эта чашка?» Играя с игрушечными машинками,
она попросила ребенка расставить машинки по порядку от самой большой к самой маленькой
или от меньшего к большему. Лаура также принесла в класс свою
собственная коллекция из 17 сосновых шишек гигантских шишек секвойи из
Калифорнии до очень крошечных сосновых шишек из саженцев вечнозеленых деревьев.
Дети были рады узнать, где она собирала их и
как разные виды сосен имеют сосновые шишки разного размера.
Им нравилось расставлять их по порядку от самого маленького до самого большого.
наоборот. Хотя большинство детей использовали метод проб и ошибок, чтобы поставить
их по порядку, почти все они смогли пронумеровать по крайней мере
9конусов от большего к меньшему. Один ребенок даже смог
упорядочить все 17 из них. Серийность в обратном порядке была более сложной
и нуждался в большом количестве словесных подсказок со стороны учителя.
включение словаря, такого как первый, второй, третий и т.
Лаура также принесла в класс свою
собственная коллекция из 17 сосновых шишек гигантских шишек секвойи из
Калифорнии до очень крошечных сосновых шишек из саженцев вечнозеленых деревьев.
Дети были рады узнать, где она собирала их и
как разные виды сосен имеют сосновые шишки разного размера.
Им нравилось расставлять их по порядку от самого маленького до самого большого.
наоборот. Хотя большинство детей использовали метод проб и ошибок, чтобы поставить
их по порядку, почти все они смогли пронумеровать по крайней мере
9конусов от большего к меньшему. Один ребенок даже смог
упорядочить все 17 из них. Серийность в обратном порядке была более сложной
и нуждался в большом количестве словесных подсказок со стороны учителя.
включение словаря, такого как первый, второй, третий и т. д.
помогли детям развить репрезентативное знание серийности
(см. Приложение III).
д.
помогли детям развить репрезентативное знание серийности
(см. Приложение III).
Когда учителя постоянно
контролировать и оценивать понимание детей, они могут опираться на
знания детей в контекстах, значимых для
дети. Контрольные списки служили средством для картирования детских
понимание некоторых математических понятий в дошкольном возрасте Лауры
школьный класс. Лаура использовала эти контрольные списки не для оценки или определения
мастерство, а для сбора информации, которая может быть использована для учебной программы
разработка. Она использовала эти контрольные списки, чтобы определить конкретные
этапы развития понятий у каждого ребенка, а затем
спланировать соответствующие материалы и учебный опыт для поддержки
обучение детей в зоне ближайшего развития этого
концепция. Лаура осторожно отметила, что помимо демонстрации
поведенческое понимание дети также были в состоянии описать
и объяснить свои действия. Объяснение детьми своих действий.
помогли Лауре определить, что существует истинное понимание
понятие и что они не были просто повторением слов без реального
понимание. Текущая оценка позволила ей контролировать отдельные
прогресса детей и, таким образом, сосредоточиться на обучении детей
этих понятий. Контрольные списки помогли Лауре принять решение о
обеспечение развивающих занятий детей
она работала с. Она написала в своем дневнике:
Лаура осторожно отметила, что помимо демонстрации
поведенческое понимание дети также были в состоянии описать
и объяснить свои действия. Объяснение детьми своих действий.
помогли Лауре определить, что существует истинное понимание
понятие и что они не были просто повторением слов без реального
понимание. Текущая оценка позволила ей контролировать отдельные
прогресса детей и, таким образом, сосредоточиться на обучении детей
этих понятий. Контрольные списки помогли Лауре принять решение о
обеспечение развивающих занятий детей
она работала с. Она написала в своем дневнике:
контрольный список помог мне организовать мои уроки в логическом порядке от от простого к более сложному. Я научился быть внимательным наблюдателем и слушать детей не только за математическим столом, но и во время свободный выбор и игровое время.
Я смог приспособиться к детскому индивидуальному потребности в различных предматематических занятиях. Я согласовал учебную программу и оценка, чтобы дать мне более четкое представление об этапах развития математических понятий соответствия и однозначного соответствия, классификация и сериация.
Систематический, но гибкий
использование контрольных списков в любом дошкольном классе может облегчить учителям
принятие решения о том, как организовать класс, какие вопросы
спросить, и какие ресурсы предоставить для развития каждого
ребенок (Хелм, Бенеке и Штайнхаймер, 1997). Как Лаура, другие
учителя могут использовать эти контрольные списки, наблюдая за небольшими группами
дети, работающие вместе, или отдельные дети, участвующие в
деятельность. Контрольные списки также можно использовать для индивидуальных интервью. оценивать детей, которые не проявляют понимания во время работы
самостоятельно или в группах. Кроме того, контрольные списки могут быть использованы
для оценки успеваемости, чтобы определить, как дети выполняют
конкретные задачи, воспроизводящие реальный жизненный опыт (Биллман и Шерман, 19 лет).96).
оценивать детей, которые не проявляют понимания во время работы
самостоятельно или в группах. Кроме того, контрольные списки могут быть использованы
для оценки успеваемости, чтобы определить, как дети выполняют
конкретные задачи, воспроизводящие реальный жизненный опыт (Биллман и Шерман, 19 лет).96).
Учителя могут использовать контрольные списки так часто, как считают необходимым
составить схему развития детей и понимания понятий. К
определить уровень понимания на начало года,
контрольный список можно использовать в первые несколько недель программы.
Было бы полезно провести эту оценку для всех детей.
во время произвольной деятельности. Тогда роль учителя могла
предоставлять разнообразные материалы, которые позволяют детям
демонстрировать спонтанно и естественно свои поведенческие знания
математических понятий.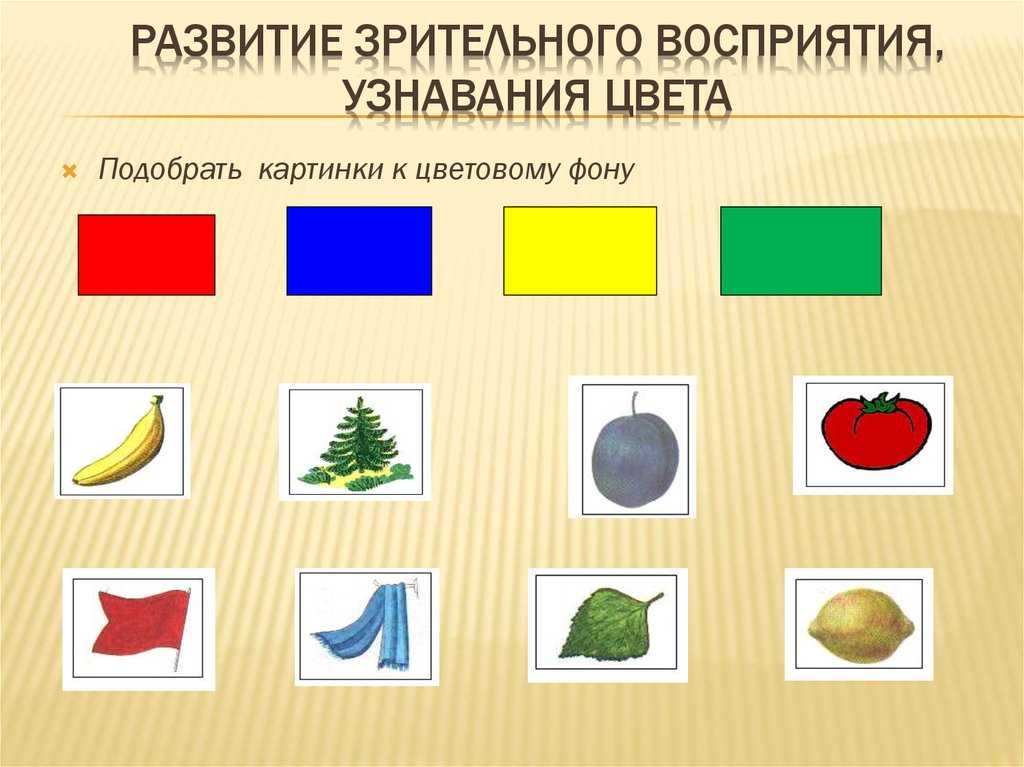 Затем эта исходная информация может быть
используется при принятии решения о том, какой опыт может быть полезен для отдельных
детей и для небольших групп детей, которые нуждаются в подобном опыте.
Предоставив детям возможность продемонстрировать свои
поведенческие знания через активное участие в материалах,
воспитателям необходимо общение с детьми. Когда учителя используют
языком математики в таких взаимодействиях детям помогают
перейти от одного уровня поведенческих знаний к другому,
или от поведенческого к репрезентативному пониманию концепции.
Лора заметила, что дети в целом стали более осведомлены о
математика привела к гораздо большему количеству спонтанного использования математических навыков в классе.
Она записала в своем журнале:
Затем эта исходная информация может быть
используется при принятии решения о том, какой опыт может быть полезен для отдельных
детей и для небольших групп детей, которые нуждаются в подобном опыте.
Предоставив детям возможность продемонстрировать свои
поведенческие знания через активное участие в материалах,
воспитателям необходимо общение с детьми. Когда учителя используют
языком математики в таких взаимодействиях детям помогают
перейти от одного уровня поведенческих знаний к другому,
или от поведенческого к репрезентативному пониманию концепции.
Лора заметила, что дети в целом стали более осведомлены о
математика привела к гораздо большему количеству спонтанного использования математических навыков в классе.
Она записала в своем журнале:
Пластик животных классифицировали и ранжировали.
Использованы цветные блоки. создавать сложные геометрические узоры. Строительные блоки были используется все более сложным образом. Здание из блоков на начало учебного года было одноуровневым и линейным. По мере того, как проект продвигался и дети становились более опытными, здание из блоков стало многоуровневым и более абстрактным. числа календаря пересчитывались много раз в течение дня с более способным дети помогают своим менее способным друзьям определить имена числовые символы. Этот рост математических знаний привел в какие-то детские дома. Несколько родителей сказали мне, что их дети стали очень интересоваться математикой вне школы. Мать Меган, например, сказала мне, что она копирует «все»: семейная обувь, банки в шкафу, хлопья, конфеты и даже игрушки ее младшего брата.
Периодические и систематические
использование чек-листов необходимо для мониторинга развития
понятий у каждого ребенка. Датировка наблюдений при использовании
контрольные списки обеспечивают запись роста и развития каждого ребенка
и помогает выявить детей с аналогичным уровнем понимания
в любой момент времени. Этот процесс информирует учителя о решениях
о необходимости направлять процесс обучения для каждого ребенка. “Качественный
оценки информируют учебные решения и позволяют учителям
контролировать прогресс отдельных детей, уделяя особое внимание тому, как дети
думают о математике» (NTCM, 2000, стр. 6). Когда учителя
знать, какие математические понятия они хотят, чтобы дети понимали
и этапы, через которые они развиваются, они могут планировать осмысленные
опыт обучения и оценивать успехи детей (Richardson
и Салкельд, 19 лет95). Когда учителя планируют развитие детей,
они также должны учитывать интересы детей и
этапы развития. Очень важно дать детям время для
свободная игра, которая позволяет им исследовать математические понятия. Пока
дети вовлечены в деятельность, учитель может наблюдать и
затем стать активными в управлении их обучением. Это взаимодействие будет
помочь детям перейти от поведенческих к репрезентативным
понимание математических понятий. Таким образом, гибкий, но систематический
использование приведенных здесь контрольных списков может помочь учителям дошкольных учреждений
развитие математических знаний детей. Они также предоставляют
средство для учителей, чтобы систематически исследовать свою собственную практику
и принимать обоснованные решения о встречах с отдельными детьми.
потребности в математическом обучении. Следующая запись в журнале явно
передает собственное чувство Лауры профессионального роста:
Когда учителя планируют развитие детей,
они также должны учитывать интересы детей и
этапы развития. Очень важно дать детям время для
свободная игра, которая позволяет им исследовать математические понятия. Пока
дети вовлечены в деятельность, учитель может наблюдать и
затем стать активными в управлении их обучением. Это взаимодействие будет
помочь детям перейти от поведенческих к репрезентативным
понимание математических понятий. Таким образом, гибкий, но систематический
использование приведенных здесь контрольных списков может помочь учителям дошкольных учреждений
развитие математических знаний детей. Они также предоставляют
средство для учителей, чтобы систематически исследовать свою собственную практику
и принимать обоснованные решения о встречах с отдельными детьми.
потребности в математическом обучении. Следующая запись в журнале явно
передает собственное чувство Лауры профессионального роста:
Во время В этом проекте я развил навыки исследователя.
я систематически изучил свою собственную практику и внес много коррективов, чтобы приспособить мои вновь обретенные математические способности. Я научился планировать уроки и выполнение математических заданий, соответствующих уровню развития для детей. По мере того, как я становился более осведомленным и приобретал некоторые уверенности, я начал развивать свой профессиональный голос. Большинство дети, их родители и администрация моей школы очень восторженно воспринял весь проект. Дети волнение по поводу математики было непрерывным.
Все цитаты из журнала учителя включены с ее разрешения.
Баруди, Артур Дж. (2000). Действительно ли обучение математике для детей от трех до пяти лет смысл? Дети младшего возраста, 55 (4), 61–67.
Берк, Лаура Э.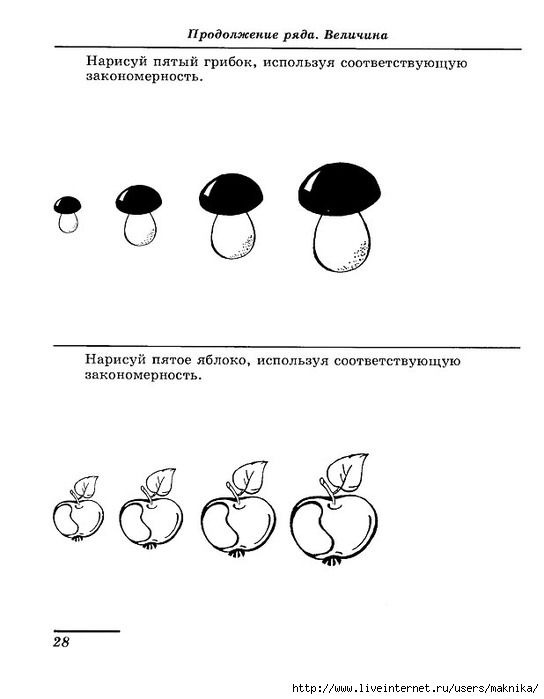 и Уинслер, Адам. (1995). Подмости детские
обучения: Выготский и дошкольное образование. Вашингтон,
округ Колумбия: Национальная ассоциация образования детей младшего возраста. ЭД
384 443.
и Уинслер, Адам. (1995). Подмости детские
обучения: Выготский и дошкольное образование. Вашингтон,
округ Колумбия: Национальная ассоциация образования детей младшего возраста. ЭД
384 443.
Биллман, Джин и Шерман, Дженис А. (1996). Наблюдение и участие в установках раннего детства. Нидхэм-Хайтс, Массачусетс: Эллин и Бэкон.
Бодрова, Елена, и Леонг, Дебора Дж. (1996). Инструменты разум: Выготский подход к дошкольному образованию. Колумбус, Огайо: Меррилл. ЭД 455 014.
Бредекамп, Сью, и Коппл, Кэрол (ред.). (1997). Развитие соответствующая практика в программах для детей младшего возраста (Rev. ed.). Вашингтон, округ Колумбия: Национальная ассоциация образования молодежи. Дети. ЭД 403 023.
Браш, Лорелей Р. (1972). Детская концепция сложения и
вычитание: отношение формальных и неформальных понятий. Неопубликовано
докторская диссертация, Корнельский университет.
(1972). Детская концепция сложения и
вычитание: отношение формальных и неформальных понятий. Неопубликовано
докторская диссертация, Корнельский университет.
Чарльзворт, Розалинда и Линд, Карен К. (1999). Математика и наука для детей младшего возраста (3-е изд.). Вашингтон, округ Колумбия: Делмар.
Фейерштейн, Реувен и Фейерштейн, С. (1991). Опосредованное обучение опыт: Теоретический обзор. В Reuven Feuerstein, Pnina S. Кляйн и Авраам Дж. Танненбаум (ред.), Опосредованное обучение опыт (MLE): теоретические, психологические и учебные последствия (стр. 3-51). Лондон: Фройнд.
Франке, Меган Лоеф и Каземи, Элхам. (2001). Учимся учить математика: Сосредоточьтесь на студенческом мышлении. Теория на практике, 40 (2), 102-109. ЭДж 627 349.
Гарви, Кэтрин. (1990). Играть. Кембридж, Массачусетс: Гарвардский университет
Нажимать.
(1990). Играть. Кембридж, Массачусетс: Гарвардский университет
Нажимать.
Gelman, Rochel, & Gallistel, CR (1978). Понимание ребенка числа. Кембридж, Массачусетс: Издательство Гарвардского университета.
Хелм, Джуди Харрис; Бенеке, Салли; и Штайнхаймер, Кэти. (1997). Документирование обучения детей. Детское образование, 73 (4), 200-205. ЭДж 544 885.
Хоус, Кэролли. (1992). Совместное строительство притворства. Олбани: Государственный университет Нью-Йорка Press. ЭД 385 337.
Джейкобсон, Линда. (1998). Специалисты продвигают математику, естественные науки для дошкольников. Education Week [онлайн], 16 (26). Доступно: http://www.edweek.com/ew/ewstory.cfm?slug=26early.h27&keywords=experts%20promote.
Камии, Констанс. (1982). Номер в дошкольном и детском саду:
Образовательные последствия теории Пиаже. Вашингтон, округ Колумбия:
Национальная ассоциация образования детей младшего возраста. ЭД
220 208.
(1982). Номер в дошкольном и детском саду:
Образовательные последствия теории Пиаже. Вашингтон, округ Колумбия:
Национальная ассоциация образования детей младшего возраста. ЭД
220 208.
Каплан, Рошель Г.; Ямамото, Такаши; и Гинзбург, Герберт П. (1989). Обучение математическим понятиям. В Лорен Б. Резник и Леопольд Э. Клопфер (редакторы), К учебной программе по мышлению: Текущие когнитивные исследования (стр. 59-82). Александрия, Вирджиния: Ассоциация для надзора и разработки учебных программ. ЭД 328 871.
Кац, Лилиан Г. и Чард, Сильвия К. (2000). Привлечение детей умы: проектный подход (2-е изд.). Стэмфорд, Коннектикут: Ablex. ЭД 456 892.
Монтегю-Смит, Энн. (1997). Математика в детском саду. Лондон, Англия: Издательство Дэвида Фултона.
Мумо, Салли и Иеронимус, Бренда. (1995). Больше, чем счет. Цельные математические занятия для дошкольников и детского сада. Сент-Пол, Миннесота: Redleaf Press. ЭД 386 296.
Национальный совет учителей математики. (1991). Профессиональный стандарты преподавания математики. Рестон, Вирджиния: Автор. ЭД 344 779.
Национальный совет учителей математики. (2000). Профессиональный стандарты преподавания математики. Рестон, Вирджиния: Автор.
Пейн, Джозеф Н. (1990). Математика для самых маленьких. Рестон, Вирджиния: Национальный совет учителей математики. ЭД 326 393.
Ричардсон, Кэти, и Салкельд, Лесли. (1995). Преобразование математики
учебный план. В Сью Бредекамп и Терезе Роузгрант (ред.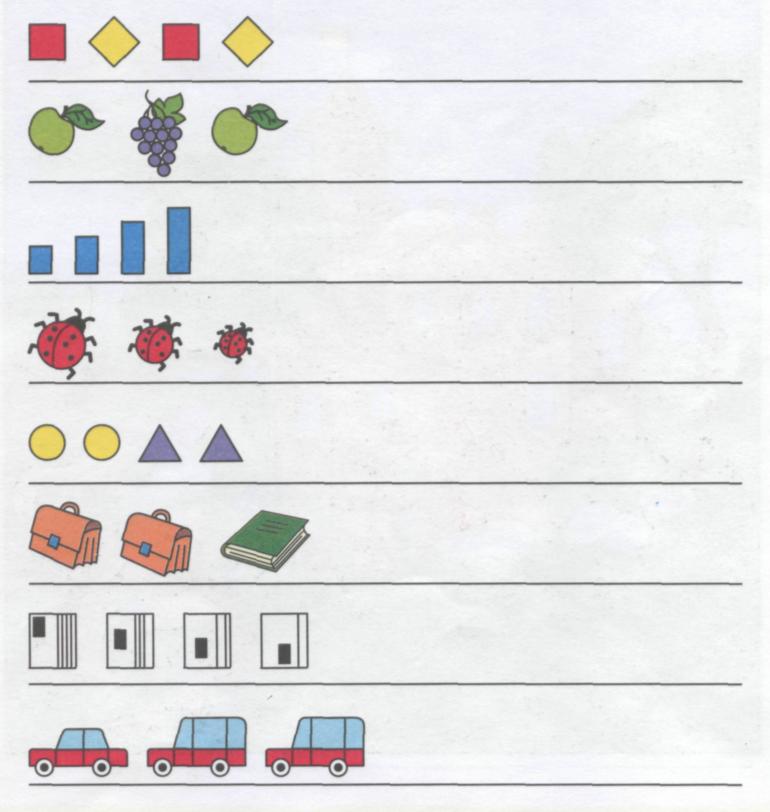 ), Reaching
потенциалы: Преобразование учебной программы и оценки для детей младшего возраста (Том 2, стр. 23-42). Вашингтон, округ Колумбия: Национальная ассоциация
Воспитание детей младшего возраста. ЭД
391 598.
), Reaching
потенциалы: Преобразование учебной программы и оценки для детей младшего возраста (Том 2, стр. 23-42). Вашингтон, округ Колумбия: Национальная ассоциация
Воспитание детей младшего возраста. ЭД
391 598.
Шугарман, Сьюзен. (1983). Детская ранняя мысль: Развитие в классификации. Кембридж, Англия: Кембриджский университет Нажимать.
Выготский, Л. С. (1978). Разум в обществе: Развитие высшего психологические процессы (Майкл Коул, Вера Джон-Штайнер, Сильвия Скрибнер и Эллен Соуберман, ред. и пер.). Кембридж, Массачусетс: Издательство Гарвардского университета.
Выготский, Л. С. (1986). Мысль и язык (Алексей Козулин, пер.). Кембридж, Массачусетс: MIT Press.
Контрольный список для дошкольных предматематических понятий
Сопоставление и взаимное соответствие
| Имя ребенка _ __________________ | |||
| Концепции/этапы разработки | сент.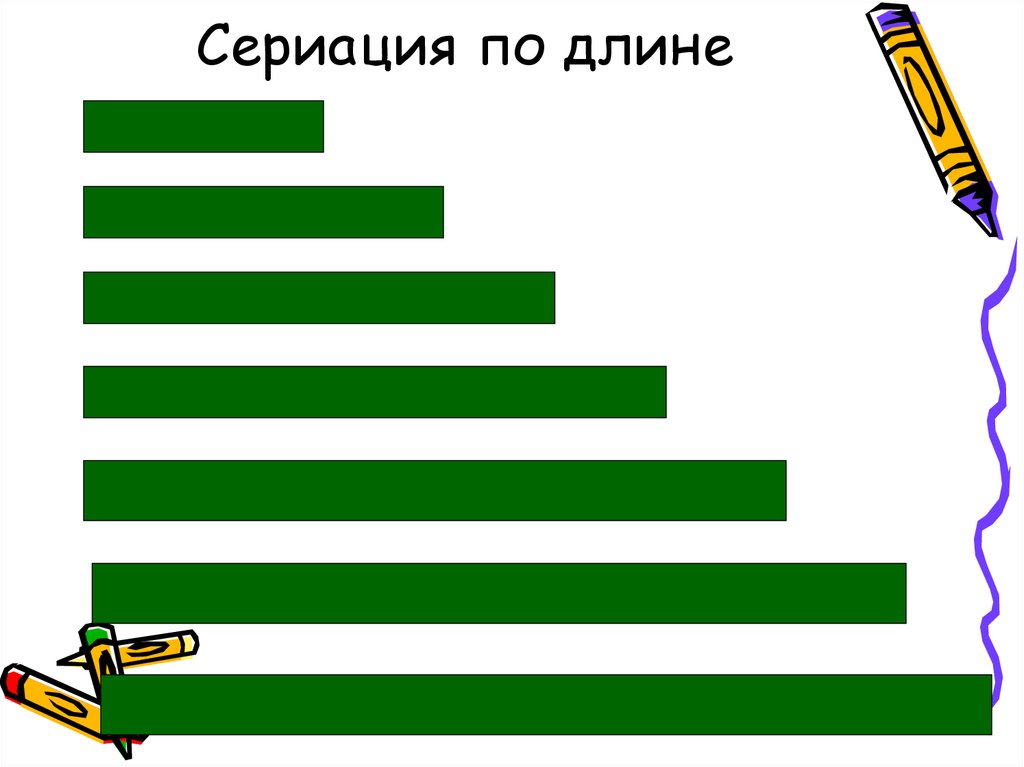 -окт. -окт. | дек.-янв. | апрель-май |
|---|---|---|---|
Сопоставление непохожих родственных предметов | |||
| 1. Соответствует различным, но не похожим друг на друга предметам | |||
| 2. Подходит для четных наборов, состоящих из 5 или менее предметов | |||
| 3. Подходит для неравномерных наборов из 5 или более предметов | |||
| 4. Использует соответствующую лексику при сопоставлении наборов (например, слишком много, недостаточно) | |||
Соответствие аналогичным товарам | |||
5. Подходит для 2 одинаковых предметов Подходит для 2 одинаковых предметов | |||
| 6. Сочетается даже с наборами из 5 или менее предметов | |||
| 7. Подходит для неравномерных комплектов5 или более предметов | |||
| 8. Использует соответствующую лексику при сопоставлении одинаковых наборов (например, слишком много, недостаточно) | |||
| КЛЮЧ К КОНТРОЛЬНЫМ СПИСКАМ | |
|---|---|
| Демонстрирует поведенческие знания концепции | |
| Демонстрирует поведенческие и репрезентативные знания концепта | |
| 0 | Демонстрирует частичное поведенческое знание концепции |
| 00 | Демонстрирует частичное репрезентативное знание концепции |
| Х | Делает не демонстрировать какое-либо знание концепции |
Контрольный список для дошкольных предматематических понятий
Наборы классификации
| Имя ребенка ___________________ | |||
| Концепции/этапы разработки | сент. -окт. -окт. | дек.-янв. | апрель-май |
|---|---|---|---|
| 1. Умеет группировать одинаковые предметы | |||
| 2. Сортирует объекты по 1 признаку — цвету, форме, размеру, материалу, рисунку, текстуре | |||
| 3. Классифицирует по 2 атрибутам | |||
| 4. Классифицирует по 3 атрибутам | |||
| 5. Описывает, что было сделано при классификации по 1, 2 или 3 признакам | |||
6.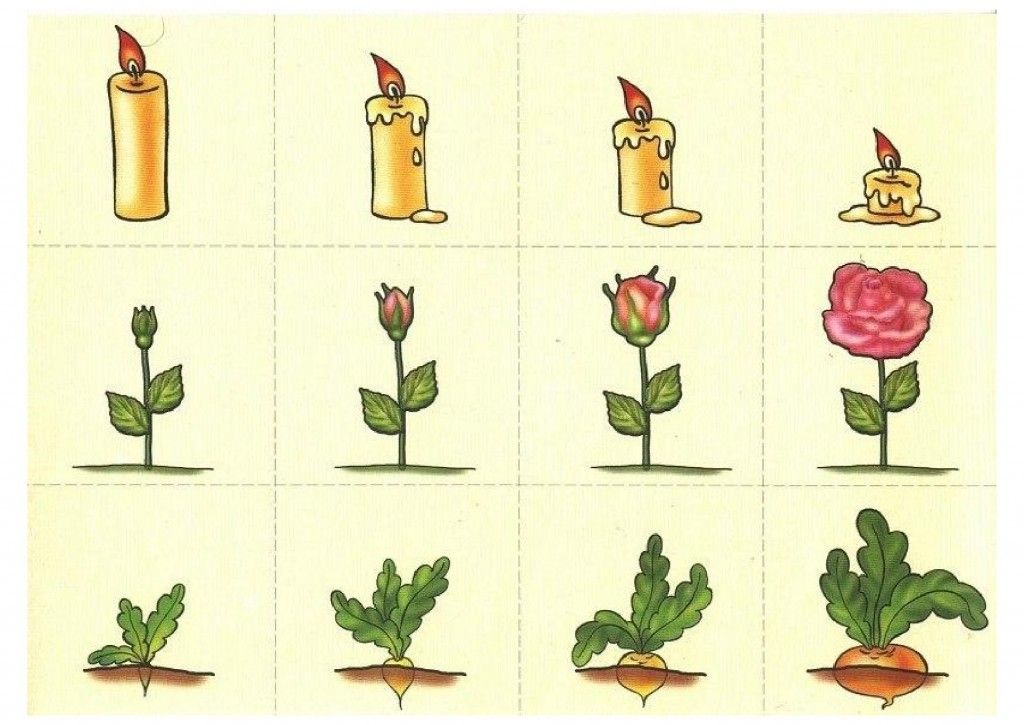 Объясняет, что было сделано при классификации по 1, 2 или 3 признакам Объясняет, что было сделано при классификации по 1, 2 или 3 признакам | |||
| 7. Классификация по функциям | |||
| 8. Описывает и/или объясняет, что было сделано | |||
| 9. Классифицируется по ассоциации | |||
| 10. Описывает и/или объясняет, что было сделано | |||
| 11. Понимает исключение класса | |||
12. Понимает включение классов Понимает включение классов | |||
| 13. Описывает и/или объясняет, что было сделано | |||
| 14. Классификация по номеру | |||
| КЛЮЧ К КОНТРОЛЬНЫМ СПИСКАМ | |
|---|---|
| Демонстрирует поведенческие знания концепции | |
| Демонстрирует поведенческие и репрезентативные знания концепта | |
| 0 | Демонстрирует частичное поведенческое знание концепции |
| 00 | Демонстрирует частичное репрезентативное знание концепции |
| Х | Делает не демонстрировать какое-либо знание концепции |
Контрольный список для дошкольных предматематических понятий
Порядок и серия
| Имя ребенка ___________________ | |||
| Концепции/этапы разработки | сент. -окт. -окт. | дек.-янв. | апрель-май |
|---|---|---|---|
| 1. Сравнение противоположностей (например, длинное/короткое, большое/маленькое и т. д.) | |||
| 2. Заказывает 3 предмета в случайном порядке | |||
| 3. Заказывает 3 предмета методом проб и ошибок | |||
| 4. Систематически заказывает 3 предмета | |||
| 5. Серии в обратном порядке | |||
6.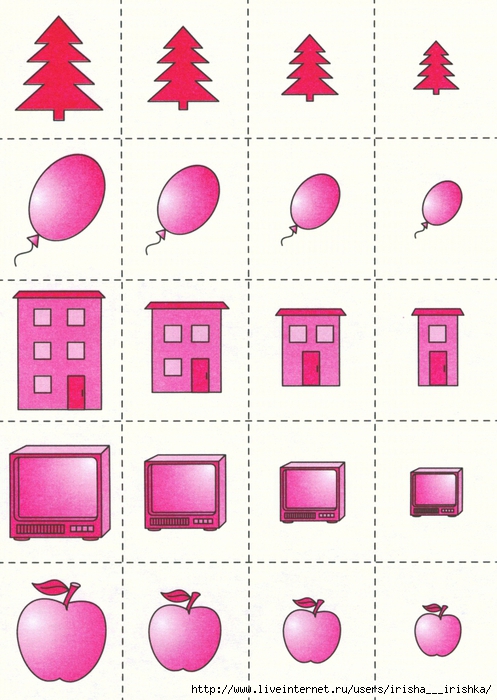 Выполняет двойную серию Выполняет двойную серию | |||
| 7. Описывает, что было сделано | |||
| 8. Объясняет, что было сделано | |||
| КЛЮЧ К КОНТРОЛЬНЫМ СПИСКАМ | |
|---|---|
| Демонстрирует поведенческие знания концепции | |
| Демонстрирует поведенческие и репрезентативные знания концепта | |
| 0 | Демонстрирует частичное поведенческое знание концепции |
| 00 | Демонстрирует частичное репрезентативное знание концепта |
| Х | Делает не демонстрировать какое-либо знание концепции |
Анна Кирова
является доцентом кафедры начального образования
в Университете Альберты, Эдмонтон, Альберта, Канада. Ее исследования
интересы находятся в областях профессионального развития учителей через
вовлечение в рефлексивную практику, раннее изучение математики
концепции, использование детьми младшего возраста компьютерных технологий в гендерных
свободная от предубеждений среда в классе, а также культурно и лингвистически
разнообразный детский опыт одиночества и изоляции в школе.
Ее исследования
интересы находятся в областях профессионального развития учителей через
вовлечение в рефлексивную практику, раннее изучение математики
концепции, использование детьми младшего возраста компьютерных технологий в гендерных
свободная от предубеждений среда в классе, а также культурно и лингвистически
разнообразный детский опыт одиночества и изоляции в школе.
Анна
Кирова
Доцент
Департамент начального образования
Педагогический факультет
Университет Альберты
Эдмонтон, AB T6G 2G5
Канада
Телефон: 780-492-4273, доб. 263
Факс: 780-492-7622
Электронная почта: [email protected]
Амбика Бхаргава — доцент кафедры
Развитие и детские исследования в Оклендском университете, Рочестер,
Мичиган. Ее исследовательские интересы сосредоточены на роли взрослого
в создании условий, способствующих обучению. В частности, три
ответвления этого потока касаются разработки математических
концепции у детей дошкольного возраста, использование компьютера маленькими детьми,
и создание в классе среды, свободной от гендерных предубеждений.
Ее исследовательские интересы сосредоточены на роли взрослого
в создании условий, способствующих обучению. В частности, три
ответвления этого потока касаются разработки математических
концепции у детей дошкольного возраста, использование компьютера маленькими детьми,
и создание в классе среды, свободной от гендерных предубеждений.
Амбика
Бхаргава
Доцент
Департамент человеческого развития и детских исследований
Школа образования и социальных служб
Оклендский университет
Рочестер, Мичиган 48309
Электронная почта: [email protected]
Я лучший: задание по измерению
Необходимые материалы Каждой группе потребуются четыре обычных предмета домашнего обихода, каждый из которых является самым большим по определенному признаку. (Примеры показаны, но вы можете выбрать другие объекты.):
(Примеры показаны, но вы можете выбрать другие объекты.):
● один объект самый высокий (пустая бутылка из-под воды с крышкой)
● один объект самый широкий (форма для пирога из фольги)
● один объект имеет наибольшую вместимость (контейнер для хранения продуктов)
● один объект самый тяжелый (пакет со льдом)
Кроме того, дайте каждой группе емкость с водой или песком (желательно на подносе, чтобы не было беспорядка), а также мерный стакан или другое приспособление для черпания.
Упражнение
Это задание было вдохновлено работой в классе, описанной в программе Early Math Collaborative’s Большие идеи ранней математики (2014) . В книге описывается, как дети сравнивают предметы на песочном столике по-разному, основываясь на разных признаках.
Попросите участников работать в группах по четыре человека (или как можно ближе к этому числу). Дайте каждой группе набор из четырех предметов, как описано выше. Выбирайте объекты, которые являются «лучшими» только с точки зрения одного атрибута или измерения. Например, выбирая объект как самый высокий, убедитесь, что он не имеет наибольшей ширины, вместимости или веса.
Выбирайте объекты, которые являются «лучшими» только с точки зрения одного атрибута или измерения. Например, выбирая объект как самый высокий, убедитесь, что он не имеет наибольшей ширины, вместимости или веса.
Объясните, что маленькие дети часто добродушно соревнуются в повседневной жизни. Например, один ребенок может сказать, что его башня самая большая из всех, а другой может сказать, что его рюкзак тяжелее, чем у другого ребенка. Эти виды сравнений можно использовать, чтобы помочь детям развить представление об измерении и выучить язык для сравнения объектов. Таким образом, эта деятельность включает в себя несколько видов сравнений, которые могут быть сделаны детьми.
Разрешить участникам брать в руки и рассматривать каждый из четырех объектов. Затем назначьте объект каждому участнику. Объясните, что каждый участник будет утверждать, что «мой объект является величайшим», а затем должен обосновать, почему его объект является величайшим, основываясь на одном из его атрибутов. Объясните, что участники могут выстраивать объекты в ряд, обращаться с ними или использовать имеющийся песок или воду, чтобы наполнить их, чтобы помочь им разработать и изложить свои кейсы.
Объясните, что участники могут выстраивать объекты в ряд, обращаться с ними или использовать имеющийся песок или воду, чтобы наполнить их, чтобы помочь им разработать и изложить свои кейсы.
После того, как у участников будет время придумать обоснование, пусть каждый участник представит свои объекты другим в своей небольшой группе и кратко скажет, почему их объект является самым большим. Например, вот некоторые, но не все аргументы, которые могли привести участники.
После того, как участники изложат свои доводы, предложите им обсудить другие свойства объектов. Например, участник со сковородкой из фольги может сказать: «У моей сковороды не самая большая вместимость, но я думаю, что она вторая по вместимости». Другие учащиеся могут использовать песок или воду, чтобы изменить свойство своих объектов. Например, участник может сказать: «Бутылка с водой самая высокая, но если я наполню ее песком, думаю, она будет и самой тяжелой». Предложите участникам обсудить в своих малых группах различные способы измерения, манипулирования и сравнения объектов.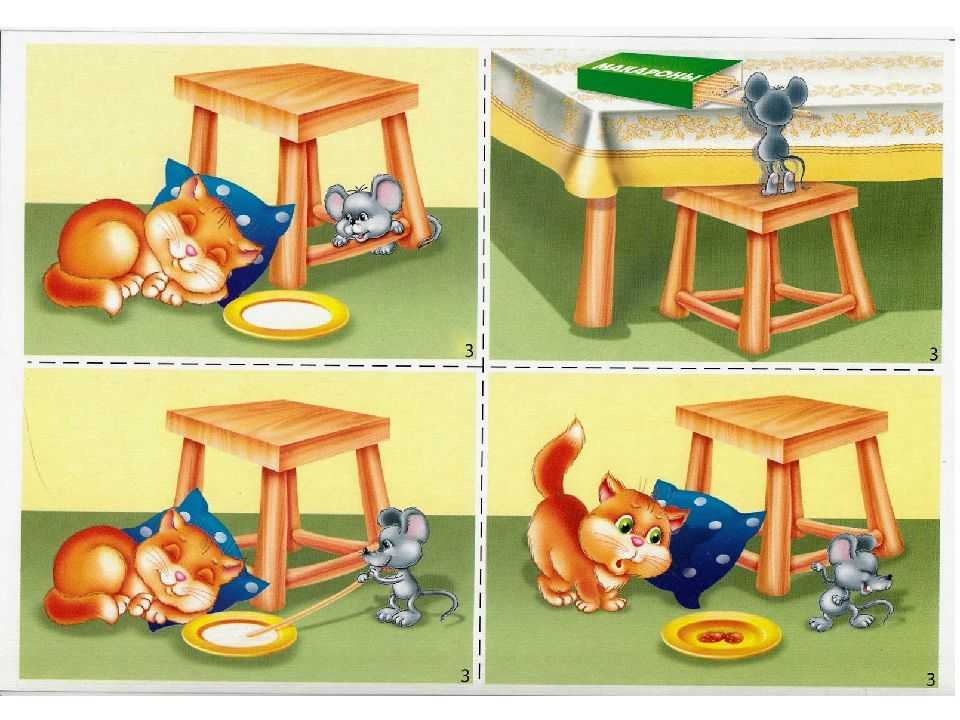
Обсуждение/обсуждение
Соберитесь всей группой, чтобы обсудить, что участники узнали из этого занятия. Ниже приведены некоторые возможные вопросы для обсуждения, которые можно использовать для обсуждения после выполнения задания:
- Что вы думаете об этом задании? Как вы думаете, почему я представил его вам?
- Вас что-то удивило? (Некоторые участники могут сказать, что они не думали о том, чтобы маленькие дети думали о емкости или весе, а не только о длине, когда обучали измерениям.)
- Было ли легче сделать ящик для одних предметов, чем для других? (Например, более высокий объект заметно выше других, но в него нужно было бы насыпать песок или жидкость, чтобы доказать, что контейнер для хранения продуктов имеет наибольшую вместимость.)
- Как вы думаете, можно ли использовать подобное упражнение в дошкольном возрасте?
- На какие качества вы ожидаете, что маленький ребенок будет уделять больше всего внимания? (Участники могут указать, что многих детей больше всего интересует рост, потому что это очень важная характеристика самих детей.
 )
) - Думаете, маленьким детям было бы трудно понять, что один объект может быть и самым большим, и самым маленьким? (Например, бутылка с водой имеет наибольшую высоту, но также и наименьшую ширину среди всех объектов. Форма для пирога имеет наибольшую ширину, но наименьшую высоту.)
- Может ли существовать объект, который мог бы быть величайшим в одном из двух способов в зависимости от того, как вы его сориентируете? (Другими словами, что-то высокое, если его держать в вертикальном положении, и широкое, если его положить горизонтально?) Как, по-вашему, справится с этим маленький ребенок?
- Можете ли вы придумать другие способы изменить эту задачу? (Например, не могли бы вы предоставить объект, который является «величайшим» одновременно более чем в одном отношении, например, самым высоким и самым тяжелым?)
Попросите участников вернуться к упражнению после сеанса, отражая свой опыт в письменной форме. Используйте их ответы, чтобы сформировать свое собственное учение.
Дополнение
Вы можете расширить это задание, показав, как можно использовать книжку с картинками для развития у детей понимания измерений (раздаточный материал доступен здесь)
Ссылки
Сотрудничество по ранней математике в Эриксоновском институте (2014 г.). Большие идеи ранней математики: что должны знать учителя маленьких детей (Первое изд.). Бостон: Пирсон.
Сарама, Дж., и Клементс, Д.Х. (2009). Исследования в области математического образования в раннем детстве: траектории обучения маленьких детей. Нью-Йорк: Рутледж.
Добро пожаловать. | Департамент образования
В вашем поиске использовано слишком много выражений И/ИЛИ. В этот поиск были включены только первые 7 терминов. К сожалению, страница, которую вы ищете, больше не существует, была перемещена или в настоящее время недоступна. Мы выполнили поиск по ключевым словам на основе страницы, которую вы пытаетесь открыть. Соответствующие параметры поиска были предоставлены ниже.
Соответствующие параметры поиска были предоставлены ниже.
Введите ключевые слова
О поискеИстория штата Мэн и онлайн-ресурсы
Мэн История и Интернет Ресурсы … Использование наборов первичных источников (совместно представлено Мэн DOE , Мэн Историческое общество, Мэн Государственный архив, … Мэн Государственные служащие Talking Civics & Gov ‘t с сенатором Ангусом Кингом Говоря гражданское право и …
Государственные чиновники, обществоведение и гражданский дискурс
… Государственные чиновники Talking Civics & Gov ‘t с сенатором Ангусом Кингом Говоря о гражданских правах и… сенатор Сьюзен Коллинз Говоря гражданское право и Gov ‘t с Rep.
 Jared Golden
Talking Civics & Gov ‘t with Rep. … NewsHour)
Презентация PBS NewsHour
Mid- Технический центр штата Мэн / Веб-страница Дэйва Бордмана …
Jared Golden
Talking Civics & Gov ‘t with Rep. … NewsHour)
Презентация PBS NewsHour
Mid- Технический центр штата Мэн / Веб-страница Дэйва Бордмана …Гражданско-активные студенты и студенческий голос
… Эллен Дэниелс – Коалиция гражданской миссии Иллинойса Презентация Папка ресурсов … Час новостей) Новости PBSЧас Презентация Mid- Технический центр штата Мэн / Веб-страница Дэйва Бордмана … с государственными служащими Мэн Talking Civics & Gov ‘t с сенатором Ангусом Кингом Говоря гражданское право и …
Ежемесячные информационные бюллетени ESEA 2021
… для 22 ФГ была автоматизирована и будет производиться Департаментом образования штата Мэн с использованием сертификата NEO … Джессике Карон, Title IA, по адресу Jessica.
 s.caron@ мэн . правительство .
Раздел V 23 ФГ. Право на участие
23 ФГ… информацию можно найти на https://www. мэн . gov / doe /learning/esea/contact . Также ваш отзыв …
s.caron@ мэн . правительство .
Раздел V 23 ФГ. Право на участие
23 ФГ… информацию можно найти на https://www. мэн . gov / doe /learning/esea/contact . Также ваш отзыв …Учитель на пенсии
Учитель Пенсионер … перечисление взносов работодателя См. Мэн Штат Пенсионное Системное законодательство: Заголовок 5 – … – https://www. мэн . gov / doe / сайты / maine . правительство . doe / файлы / встроенные – файлы /FY20_RFL_prelimED279_Presented27Feb2019. pdf …
Ежемесячный информационный бюллетень ESEA
… Часы работы во вторник, 24 августа Свяжитесь с Cheryl.
 Lang @ maine . gov или вашему региональному координатору программы для получения ссылки. … здесь: https://www. мэн . gov / doe / сайты / maine . правительство . doe / файлы / встроенные – файлы /Grants4ME%20Access%20v4. pdf .
Для …
Lang @ maine . gov или вашему региональному координатору программы для получения ссылки. … здесь: https://www. мэн . gov / doe / сайты / maine . правительство . doe / файлы / встроенные – файлы /Grants4ME%20Access%20v4. pdf .
Для …Летняя программа общественного питания (SFSP)
… для всех детей в возрасте 18 лет и младше на утвержденных объектах SFSP в районах со значительной концентрацией малообеспеченных … Программа общественного питания Онлайн-обучение Как пройти Мэн Курс Bright Track Код доступа к обучению: maine111 … другие округа считаются сельскими https://www.fns.usda. gov /sfsp/rural-designations-summer-food-service-program …
Ежемесячный информационный бюллетень ESEA
… 9 ноября, 9:00 Свяжитесь с Cheryl.
 Lang @ maine . gov или у вашего регионального координатора программы для ссылки.) … здесь: https://www. мэн . гов / лань / сайты / мейн . правительство . doe / файлы / встроенные – файлы /Grants4ME%20Access%20v4. pdf .
Для …
Lang @ maine . gov или у вашего регионального координатора программы для ссылки.) … здесь: https://www. мэн . гов / лань / сайты / мейн . правительство . doe / файлы / встроенные – файлы /Grants4ME%20Access%20v4. pdf .
Для …Ежемесячный информационный бюллетень ESEA
… (Свяжитесь с вашим региональным координатором программы или Cheryl.Lang@ maine . gov для ссылки.) Общие и специальные обновления… здесь: https://www. мэн . правительство / лань / сайты / мейн . правительство . doe / файлы / встроенные – файлы /Grants4ME%20Access%20v4.
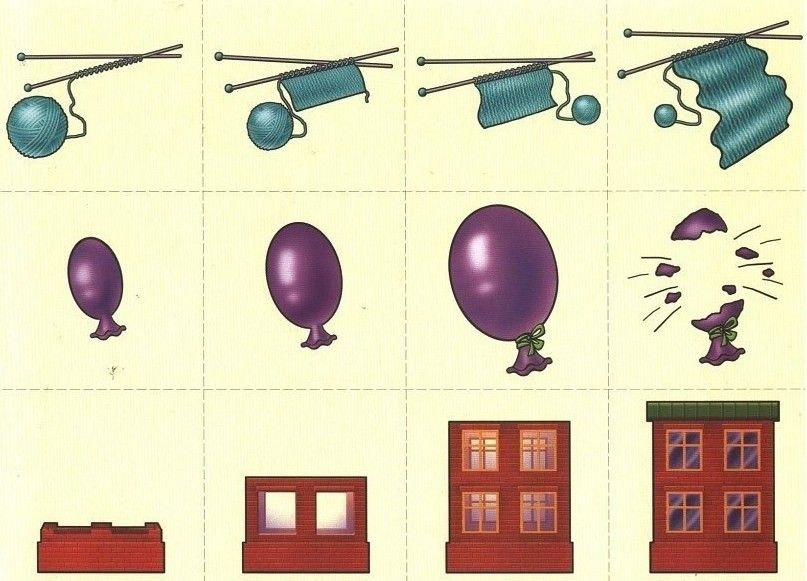 pdf .
Для …
pdf .
Для …Годовая финансовая отчетность на конец года
… Требования Загрузите следующие файлов в NEO Financial до 30 августа. Фактические … материалы в статусе «перенесено» считаются полученными до Мэн Министерство энергетики США .
Сохранение, классификация и серия — Моник М. Чураешкенази, доктор философии, психолог.
Теория когнитивного развития Пиаже представляет собой теоретическую основу, созданную в 1930-х годах швейцарским психологом Жаном Пиаже. Основанная на естественном развитии человеческого интеллекта, теория Пиаже фокусируется на конкретных действиях людей и на том, как они взаимодействуют в своей внутренней и внешней среде (Нанс, 2017). Парадигма также сравнивает умы детей и взрослых, потому что социальное и когнитивное развитие понимаются в разных аспектах, поскольку оно связано со стадиями когнитивного развития. Социальный работник Анджела Освальт утверждает, что «младенцы и маленькие дети понимают мир совсем иначе, чем взрослые, и, играя и исследуя, их разум учится мыслить таким образом, который лучше соответствует реальности» (без даты, пункт 1). Кроме того, теория Пиаже основана на четырех стадиях развития: сенсомоторной, предоперационной, конкретно-операционной и формально-операциональной (McLeod, 2015). И такие этапы основаны на развитии детских мыслей и идей через умственную прогрессию. Тема этой недели будет посвящена этапу конкретной операции, который концентрируется на основных понятиях, связанных с когнитивным развитием.
Социальный работник Анджела Освальт утверждает, что «младенцы и маленькие дети понимают мир совсем иначе, чем взрослые, и, играя и исследуя, их разум учится мыслить таким образом, который лучше соответствует реальности» (без даты, пункт 1). Кроме того, теория Пиаже основана на четырех стадиях развития: сенсомоторной, предоперационной, конкретно-операционной и формально-операциональной (McLeod, 2015). И такие этапы основаны на развитии детских мыслей и идей через умственную прогрессию. Тема этой недели будет посвящена этапу конкретной операции, который концентрируется на основных понятиях, связанных с когнитивным развитием.
Конкретно-операциональная стадия
Конкретно-оперативная стадия является третьей фазой теории Пиаже и представляет собой значительный переходный процесс прогрессии интеллектуального развития ребенка, поскольку на ней начинается «логическое или операциональное мышление» (McLeod, 2015). Другими словами, дети начали решать проблемы и находить решения без использования физических объектов или других вещей, помогающих их мыслительному процессу, и полагаться на рациональное мышление при принятии решений. На этом этапе дети довольно молоды (от семи до 11 лет), поэтому крайне важно наблюдать за прогрессом во внутренней и внешней среде. По словам Сола Маклеода (2010), на этапе конкретной операции дети взрослеют, формируют мнение, понимают методологии разумного мышления и сохраняют.
На этом этапе дети довольно молоды (от семи до 11 лет), поэтому крайне важно наблюдать за прогрессом во внутренней и внешней среде. По словам Сола Маклеода (2010), на этапе конкретной операции дети взрослеют, формируют мнение, понимают методологии разумного мышления и сохраняют.
Три фазы
Конкретно-операционная фаза фокусируется на трех элементах: сохранении, классификации и упорядочении. Сохранение — это концепция того, что вещи остаются неизменными, даже если другие элементы изменяются, что основано на рациональном мышлении. Согласно теории Пиаже, консервация или логическое мышление должны проявляться на этапе конкретной операции, а возраст созревания приходится на возраст от семи до одиннадцати лет (McLeod, 2010). Примером понимания сохранения может быть способность ребенка идентифицировать два одинаковых объекта как одинаковые, независимо от порядка, размещения или местоположения. Я посмотрел два видео двух детей, которых тестировали на стадии консервации. Мальчику было приблизительно четыре года, а девочке около восьми или девяти лет. Оба они были испытаны на равном количестве жидкости в стакане (одинакового размера и формы). Оба согласились, что стакана с голубым веществом было равное количество в обоих стаканах. Когда инструкторы налили один из стаканов жидкости в более высокие стаканы, было два разных ответа. Мальчик сказал инструктору, что в более высоком стакане было больше жидкости. Он верил в это, потому что стакан был больше (то есть выше), поэтому количество жидкости увеличилось. Девушка заявила, что количество жидкости осталось прежним, потому что не имело значения, в какой предмет наливали жидкость, так как изначально было установлено, что оба стакана содержат одинаковое количество. Этот пример показывает восприятие двух детей разного возраста и то, как они понимают сохранение. Важно, когда дети старше, чтобы понять эту концепцию, потому что это больше, чем просто логические рассуждения; вместо этого он также основан на опыте обучения и образовании, таких как математика и естественные науки (т.
Мальчику было приблизительно четыре года, а девочке около восьми или девяти лет. Оба они были испытаны на равном количестве жидкости в стакане (одинакового размера и формы). Оба согласились, что стакана с голубым веществом было равное количество в обоих стаканах. Когда инструкторы налили один из стаканов жидкости в более высокие стаканы, было два разных ответа. Мальчик сказал инструктору, что в более высоком стакане было больше жидкости. Он верил в это, потому что стакан был больше (то есть выше), поэтому количество жидкости увеличилось. Девушка заявила, что количество жидкости осталось прежним, потому что не имело значения, в какой предмет наливали жидкость, так как изначально было установлено, что оба стакана содержат одинаковое количество. Этот пример показывает восприятие двух детей разного возраста и то, как они понимают сохранение. Важно, когда дети старше, чтобы понять эту концепцию, потому что это больше, чем просто логические рассуждения; вместо этого он также основан на опыте обучения и образовании, таких как математика и естественные науки (т. е. числа, длина, жидкость, масса, площадь, вес и объем) (Эпштейн, 2014).
е. числа, длина, жидкость, масса, площадь, вес и объем) (Эпштейн, 2014).
Классификация — это просто группировка свойств по отношению к другим типам. Это важная концепция для понимания детьми, особенно для решения проблем. Примером классификации может служить способность ребенка группировать определенные объекты по цвету, форме, размеру, количеству и/или сходству. Очень важно, чтобы дети понимали классификацию, потому что это концепция знания того, что отличается, а что одинаково. Авторы Джеппсон и Майерс-Уоллс заявляют, что дети изначально классифицируют объекты по тому, что они видят, слышат и чувствуют, и требуется время, чтобы понять другие элементы помимо этого (nd, para. 2.). По мере развития познавательных способностей детей они узнают, как некоторые объекты связаны друг с другом, а также назначение каждого из них. Наконец, есть сортировка, которая позволяет группировать объекты по высоте, весу и/или важности. Примером упражнения на упорядочение может быть следующее: дети упорядочивают предметы от низких к высоким, от тонких к большим, от маленьких к большим или по важности и т. д. Поскольку сериация имеет дело с размером, весом или величиной, это очень важная концепция, которую дети должны освоить в школе, особенно в математике и естественных науках.
д. Поскольку сериация имеет дело с размером, весом или величиной, это очень важная концепция, которую дети должны освоить в школе, особенно в математике и естественных науках.
Заключение
Теория Пиаже включает три важные фазы, которые указывают на стадию конкретной операции в когнитивном развитии. Сохранение, классификация и сериация являются важными этапами, отвечающими за когнитивное развитие ребенка. Основываясь на логическом мышлении, различении и организации, три фразы считаются зрелыми элементами, которые дети должны понимать в возрасте от семи до одиннадцати лет и которые отвечают за расширение их умственных способностей. Важно, чтобы каждому этапу обучали детей, чтобы они могли понять окружающий мир. Внутренняя и внешняя среда имеет решающее значение для когнитивного развития детей, и, если ее не преподавать, она может ухудшить их интеллектуальную способность рационализировать, понимать и принимать решения.
Ссылки
Эпштейн, В. (2014). Задачи консервации. Чему Пиаже научил меня о детях. Воспитание детей и Наставничество. Получено с https://www.kars4kids.org/blog/conservation-tasks-what-piaget-taught-me-about-children/ (по состоянию на 1 марта 2018 г.).
(2014). Задачи консервации. Чему Пиаже научил меня о детях. Воспитание детей и Наставничество. Получено с https://www.kars4kids.org/blog/conservation-tasks-what-piaget-taught-me-about-children/ (по состоянию на 1 марта 2018 г.).
Джеппсон, Дж. и Майерс-Уоллс, доктор философии, CFLE, Дж. А. (без даты). Понимание одинакового и разного (классификация). Университет Пердью. Получено с https://www.extension.purdue.edu/providerparent/Child%20Growth-Development/UnderstandingSameDiff.htm (по состоянию на 1 марта 2018 г.).
Маклеод, С. (2015). Жан Пиаже. Просто психология. Получено с https://www.simplypsychology.org/piaget.html (по состоянию на 1 марта 2018 г.).
Маклеод, С. (2010). Бетонно-эксплуатационная стадия. Получено с https://www.simplypsychology.org/concrete-operational.html (по состоянию на 1 марта 2018 г.).
Нэнси, С. (2017). Психология сохранения и ее связь с другими областями науки. Психология сохранения. Получено с http://conservationpsychology.org/science/relationship-with-sciences (по состоянию на 1 марта 2018 г.).
Получено с http://conservationpsychology.org/science/relationship-with-sciences (по состоянию на 1 марта 2018 г.).
Освальт, А. (без даты). Развитие ребенка и подростка: обзор Жан Пиаже и развитие ребенка. Галф Бенд Центр. Получено с https://www.gulfbend.org/poc/view_doc.php?type=doc&id=7929&cn=28 (по состоянию на 1 марта 2018 г.).
20 бесплатных печатных карточек с последовательностями для дошкольников
Печатные формы
Этот пост может содержать партнерские ссылки.
Начните создавать прочную основу для математики и чтения, познакомив своих дошкольников с последовательностями. Эти бесплатных печатных карточек секвенирования помогут вам начать работу.
Мне понравилось делиться заданиями по секвенированию для дошкольников.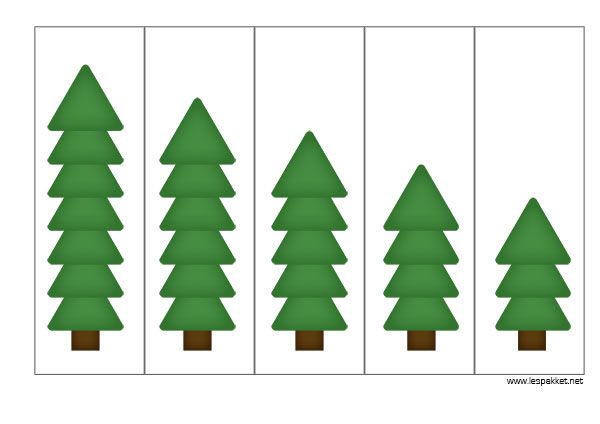 Они так важны для того, чтобы помочь малышам научиться наводить порядок в окружающем их мире.
Они так важны для того, чтобы помочь малышам научиться наводить порядок в окружающем их мире.
Секвенирование также является строительным блоком для раннего развития навыков математики и грамотности. Эти карточки с последовательностями — отличный способ дать дошкольникам возможность попрактиковаться в последовательностях действий, с которыми они уже знакомы.
Карточки последовательностей
Дети начнут понимать порядок, в котором происходят события, когда вы представите эти бесплатных распечатываемых карточек последовательностей для детей . Homeschool Preschool
Вашим маленьким любителям спорта понравится этот бесплатный набор на тему мини-бейсбола . В нем вы найдете карточки с вырезками и страницу для записей, чтобы дети могли записывать последовательность. 3 динозавра
Этот набор из бесплатных рабочих листов охватывает 15 тем, включая личную гигиену и сезонные мероприятия. Totschooling
Totschooling
Ваши дети могут не только упорядочить эти карточки жизненного цикла лягушек , но и распечатать несколько копий, чтобы превратить их в увлекательную игру на запоминание. Дождливый день, мама
Ничто так не говорит о лете, как смор! Вашим детям понравится эта корона-секвенатор s’mores . Затем обязательно ознакомьтесь с ее реквизитом для ролевых игр. Они такие милые! Books and Giggles
Этот мини-набор на тему Рождества Христова идеально подходит для праздников. Дети могут раскладывать карточки по порядку, отмечать порядок на карточках с клипсами, а затем записывать последовательность на странице для письма. 3 динозавра
Детям понравится заказывать события в этом наборе Весенних карточек для печати . Это отличный способ познакомить дошкольников с секвенированием! Homeschool Preschool
Если вы изучаете растения и/или семена в дошкольном учреждении, обязательно загрузите эти карточек секвенирования растений . Они станут отличным дополнением к вашей научной деятельности. File Folder Fun
Они станут отличным дополнением к вашей научной деятельности. File Folder Fun
Дети могут изучить порядок вещей с помощью этих трехэтапных головоломок . Каждая головоломка включает в себя действия, с которыми ваши дошкольники столкнутся в своей повседневной жизни. Домашнее дошкольное учреждение
Дети могут попрактиковаться в счете до десяти, раскладывая эти карточек с изображением уточек в ряд в порядке от 1 до 10. Домашнее обучение My Kinetic Kids
Мне нравится этот набор из карты последовательности снеговика используют слова сначала, затем, затем и последний в дополнение к использованию порядковых номеров. 3 динозавра
Не пропустите эти карточек весенней последовательности , которые включают в себя головоломки, коврик для последовательности и страницу повествования для карточек последовательности из 3 шагов. Homeschool Preschool
Если вы ищете забавную игру для своих детей, чтобы поиграть в это Рождество, попробуйте эти веселые карточки-последовательности рождественских историй . Хитрый класс
Хитрый класс
Этот набор карточек для определения последовательности жизненного цикла содержит карточки для кур, собак, змей, рыб, лягушек и некоторых насекомых. Pinay Homeschooler
Эти карточки-последовательности гусениц помогут дошкольникам научиться распознавать закономерности и понимать, как события происходят в определенном порядке. Лягушки и феи
Осень – идеальное время года, чтобы попрактиковаться в последовательности приготовления яблочного пирога . 3 Динозавры
Головоломки с пропуском счета помогают детям практиковать порядок чисел. Эти головоломки помогут детям попрактиковаться в счете до 1, 2, 5 и 10. Life Over C’s
Эта последовательность действий «Как одеваться зимой» для дошкольников — отличное наглядное пособие, помогающее малышам практиковать самостоятельность. одеваться этой зимой. Homeschool Preschool
Создание шаблонов — это еще один способ попрактиковаться в построении последовательности, поскольку дети пытаются определить, что будет дальше, на основе предоставленного шаблона. это Набор карточек с узорами из палочек от эскимо содержит 12 карточек, с которыми дети могут практиковаться. Пластилин для Платона
это Набор карточек с узорами из палочек от эскимо содержит 12 карточек, с которыми дети могут практиковаться. Пластилин для Платона
Вот еще один забавный набор полосок с узорами для детей. Эти полоски с изображением медвежонка предназначены для использования с радужными жетонами медведя. Вы можете взять несколько радужных медведей из своего набора , если у вас их нет под рукой. Измеренная мама
Этой зимой дошкольники могут практиковаться в составлении последовательности с помощью этого набора из карточек с последовательностями «как слепить снеговика» . Они идеально подходят для ваших зимних уроков. Домашнее обучение Дошкольное учреждение
Учебные материалы
Головоломки-последовательности — отличный способ развивать навыки решения проблем! В этих головоломках дети упорядочивают размер, числа, от семени до цветка, приготовления яблочного пирога и многого другого.
Этот набор из 26 четырехшаговых карточек идеально подходит для самых маленьких. И они пронумерованы сзади, чтобы их можно было проверить самостоятельно.
Карточки последовательности изображений поможет вам начать строить прочную основу для логического мышления ваших дошкольников. Какие из них вы попробуете в первую очередь?
Больше развлечений для дошкольников
5,9 К акции
- Поделиться82
Почтовые теги: #Упражнения по секвенированию#Карточки для секвенирования#Обучение секвенированию
Похожие сообщения
Печатные формы
Летние рабочие листы для дошкольников
Этот пост может содержать партнерские ссылки. Преподаете ли вы этим летом или просто ищете что-нибудь интересное, эти летние рабочие листы для дошкольников — то, что вам нужно! Эти рабочие листы включают игры, наборы заданий и образовательные страницы с забавными летними темами, которые обязательно понравятся вашим дошкольникам! Не пропустите эти летние мероприятия для дошкольников ! Они идут…
Читать дальше Дошкольные летние рабочие листыПродолжить
Печатные формы
Autumn I Spy Preschool Game
Этот пост может содержать партнерские ссылки. Не упустите шанс загрузить и распечатать набор игр для дошкольников «Осень, я шпионю»! Он идеально подходит для счета и визуальной дискриминации для детей. Игры «Я шпион» для детей — отличный, неброский способ укрепить счет, зрительное различение и мелкую моторику. Играете ли вы в игру устно или…
Не упустите шанс загрузить и распечатать набор игр для дошкольников «Осень, я шпионю»! Он идеально подходит для счета и визуальной дискриминации для детей. Игры «Я шпион» для детей — отличный, неброский способ укрепить счет, зрительное различение и мелкую моторику. Играете ли вы в игру устно или…
Подробнее Autumn I Spy Preschool GameПродолжить
Печатные формы
Рабочие листы по отслеживанию алфавита
Этот пост может содержать партнерские ссылки. Рабочие листы для отслеживания алфавита — отличный инструмент, который нужно иметь под рукой для практики письма. Этот 27-страничный пакет готов к печати! Эти бесплатные печатные рабочие листы с алфавитом идеально подходят для практики чистописания. Они содержат как прописные, так и строчные буквы, чтобы помочь вам научиться распознавать буквы…
Читать далее Рабочие листы по отслеживанию алфавитаПродолжить
Печатные формы
Transportation ABC Letter Practice
Этот пост может содержать партнерские ссылки. Детям дошкольного и детсадовского возраста понравятся эти страницы для практики букв ABC на транспорте! Увеличьте масштаб и загрузите свою копию сегодня! Добавьте эти рабочие листы к своим транспортным мероприятиям для дошкольников. Дети будут работать над распознаванием букв и практикой письма, укрепляя при этом мелкую моторику рук. Отслеживание этих букв…
Детям дошкольного и детсадовского возраста понравятся эти страницы для практики букв ABC на транспорте! Увеличьте масштаб и загрузите свою копию сегодня! Добавьте эти рабочие листы к своим транспортным мероприятиям для дошкольников. Дети будут работать над распознаванием букв и практикой письма, укрепляя при этом мелкую моторику рук. Отслеживание этих букв…
Читать дальше Практика письма в транспортной азбукеПродолжить
Печатные формы
Детские стишки для дошкольников
Этот пост может содержать партнерские ссылки. Эти дошкольные детские стишки очень интересны для малышей. Практикуйте раннюю грамотность и математические навыки с вашими любимыми стишками Mother Goose! Страницы с заданиями в этих детских стишках идеально подходят для детей в возрасте от 3 до 5 лет! Вы можете использовать их для обучения потешкам, началу звуков, счету и т. д.
Подробнее Дошкольные детские стишкиПродолжить
Печатные формы
Letter to Santa Template Printables
Этот пост может содержать партнерские ссылки.

 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
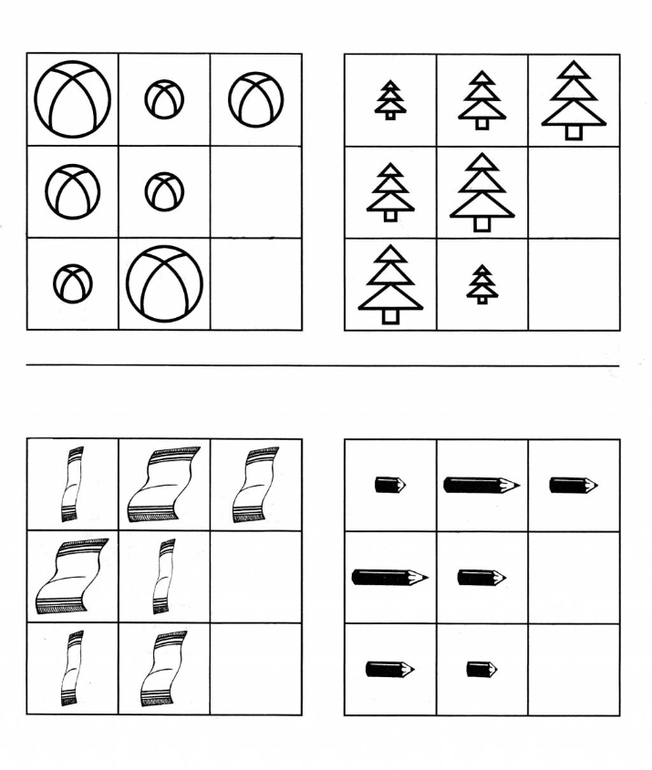
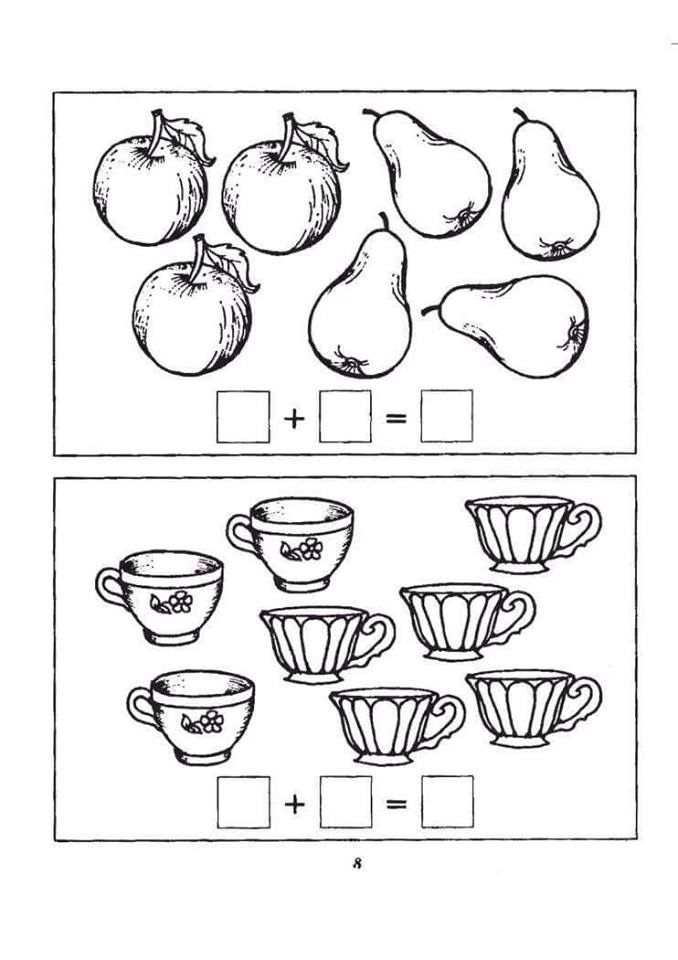
 Е. Аверина. – М. : Айрис-Пресс, 2009.
Е. Аверина. – М. : Айрис-Пресс, 2009. Н. Е. Вераксы, Т. С. Комаровой, М. А. Васильевой. – М. : Мозаика-Синтез, 2014.
Н. Е. Вераксы, Т. С. Комаровой, М. А. Васильевой. – М. : Мозаика-Синтез, 2014. doshvozrast.ru/ozdorov/fizkultura10.htm
doshvozrast.ru/ozdorov/fizkultura10.htm su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь – 161.97.168.212 (0.007 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь – 161.97.168.212 (0.007 с.)