Счеты абак как пользоваться: Счёт на абаке и ментальная арифметика: janemouse — LiveJournal

секреты ментальной арифметики для первоклассников

Содержание статьи

• Что это такое?
• Преимущества использования
• Как работать?
• Как складывать и вычитать?
• Умножение и деление
• Правила

Среди необычных дидактических пособий для детей свое место занимают счеты абакус, которые помогут улучшить математические навыки и весело и с пользой провести время. Предлагаем познакомиться с тем, что они собой представляют и как ими пользоваться.

Что это такое?

Сами счеты, которые положены в основу методики, появились более 2,5 тысячелетий назад. Также можно встретить названия «абак» или «соробан». Эти счеты исполняли в древнейших государствах функции современных калькуляторов и помогали отсчитывать десятки. Впоследствии они стали использоваться в ментальной арифметике.

Внешний их вид довольно прост: абак представляет собой рамку прямоугольной формы, которая разделена перекладинами с нанизанными на них косточками. Вверху, над разделительной полосой, расположена всего одна линия, каждый элемент которой означает пять. Снизу находятся ряды с четырьмя косточками, обозначающими единицу.

Линии косточек означают поочередно единицы (первая правая), десятки (вторая правая), сотни, тысячи. Если первая правая косточка поднята, то на счетах выложена цифра 1 или наименьшее десятичное значение (если расчеты ведутся, например, в миллиардах). Распределение чисел таково:

• нижние косточки – это 1,2,3 и 4, соответственно, если подняты 2 из них, то счеты показывают число два;
• если верхняя косточка поднята, число меньше, чем 5; если опущена на разделительную линию – больше;
• верхняя опущена, три нижние подняты – это число 8.

Аналогичным образом можно выложить любое число.

Преимущества использования

Работа со счетами не только помогает развивать мелкую моторику дошкольника, но и тренирует сразу оба полушария его головного мозга, позволяет наладить взаимосвязи между ними. Кроме того, можно выделить несколько достоинств методики:

1. Интерес. Малышам нравится перебирать косточки, при правильном подходе родителей из абакуса можно сделать тренажер, занятия на котором будут искренне нравиться ребенку.
2. Использование счетов позволяет избежать заучивания и стимулирует образное мышление.
3. При регулярных тренировках со временем удастся перевести ребенка от работы с реальным абакусом к воображаемой.
4. Дети учатся находить нестандартные варианты решения проблемы.
5. Постепенно обретают уверенность в себе, становятся более самостоятельными.
6. Очень хорошо развивается мышление.

Вот почему счеты считаются мощнейшим пособием в ментальной арифметике, то есть обучении быстрому счету.

Как работать?

Познакомимся с инструкцией по использованию абакуса в домашней работе со старшими дошкольниками и первоклассниками. В целом японские счеты могут заинтересовать детей от 5–6 до 10–11 лет. Они помогают научить совершать в уме различные арифметические действия: сложение, вычитание и даже умножение.

Как же пользоваться таким пособием?

1. Положить счеты на поверхность стола, добившись того, чтобы никакие посторонние предметы не мешали нормальному движению косточек.
2. Поставить их «на ноль» — ни один из шариков не должен касаться разделительной полосы.

Далее на конкретном примере рассмотрим суть работы. Допустим, нам необходимо сложить 1 и 2. Для этого при помощи большого пальца перемещаем к разделительной полосе сначала одну косточку. Потом – две. Считаем результат – 3.

Но как быть, если надо сложить, например, 5 и 3. Цифр гораздо больше, чем косточек. Действовать следует так: косточка, расположенная над разделительной полосой – это 5. Поэтому ее следует опустить. А три косточки из нижнего ряда, наоборот, поднять. Получится 8.

На счетах можно отложить и трехзначные числа. Например, 175 будет выглядеть так:

1. На первой линии опускается верхняя (пятерка).
2. На второй – опускается верхняя (5) и поднимаются две нижние (2).
3. На третьей – поднимается одна нижняя (1).

Сначала может показаться, что все слишком сложно и научиться будет нереально не только дошкольнику, но и взрослому. Но на практике зачастую бывает достаточно показать ребенку пару примеров, он довольно быстро разберется и начнет считать.

Как складывать и вычитать?

После того как малыш научился выкладывать числа, можно приступать к обучению простейшим арифметическим действиям.

Сначала рассмотрим сложение, к примеру, 36+23:

1. Устанавливается первое число, 36.
2. Далее его следует разделить на простые цифры – 3 и 6.
3. После этого на соответствующих линейках провести сложение единиц с единицами, десятков и десятками. Получается: 3+2 (десятки) и 6+3 (единиц).
4. Кости на линейках перемещаются соответствующим образом.

Если бы косточек получилось больше 9, нужно было прибавить единицу на соседней линейке.

Вычитание проводится по такой же системе, начиная с меньшего порядка. В случае, если из меньшего числа вычитается большее, происходит следующее: их переставляют, а на соседней линейке убирают косточку.

Такая система счета кажется сложной только при описании, на деле же стоит попробовать – и ребенку непременно понравится.

Умножение и деление

Они также не вызовут особых затруднений у тех, кто знает таблицу умножения (от 1 до 10). Рассмотрим пример. Надо умножить 13х3. Сначала пример делится на два действия:

10 х 3 = 30

3 х 3 = 9.

На счетах сначала набирается 30, потом добавляется еще 3. И становится понятно, что ответ на пример – 39.

Деление полностью аналогично, однако результаты не складываются, а вычитаются.

Правила

Специалисты по ментальной арифметике разработали ряд правил, которых следует придерживаться при занятиях с абакусом.

1. Ставить пальцы необходимо определенным образом. Работают только большой и указательный, остальные сжаты в кулак. Большим поднимаются косточки по одной, указательным – опускаются. Оба движутся по направлению слева направо.
2. «Набор» чисел ведется одной рукой. Вторая придерживает счеты таким образом, чтобы не закрывать обзор.
3. Верхнюю косточку поднимает и опускает исключительно указательный палец.

Занятия проводятся дважды в неделю, действовать следует по принципу «от простого к сложному», не допуская переутомления ребенка.

Интересно, что при желании счеты можно изготовить своими руками, работа не отнимет много сил и времени.

Таков абакус, научиться считать на котором могут как дети, так и взрослые. Самое главнее правило успеха – регулярные занятия.

Как считать на древних приспособлениях для счета

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Борисов А.Е. 1

---

1МБОУ “СОШ № 40 им. Героя Советского Союза В.А. Скугаря”

Пинчук Н.Н. 1

---

1ГБОУ ДО РК “ДДЮТ”

Автор работы награжден дипломом победителя III степени

Диплом школьникаСвидетельство руководителя

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Введение

Человечество научилось пользоваться простейшими счётными приспособлениями тысячи лет назад. Наиболее востребованной оказалась необходимость определять количество предметов, используемых в меновой торговле. Одним из самых простых решений было использование весового эквивалента меняемого предмета. Для этих целей использовались простейшие балансирные весы.

С потребностью более сложного счета были изобретены счетные доски, применявшиеся для арифметических вычислений приблизительно с V века до н. э. в Древней Греции, Древнем Риме, Древнем Китае и в других странах.

Общие принципы счетных досок — разделение линиями на полосы, счёт осуществлялся с помощью размещённых на полосах камней или других подобных предметов. Камешек для греческой счетной доски (абак) назывался псифос; от этого слова было произведено название для счёта — псифофория, «раскладывание камешков». У римлян камешек называли калькулюс, а счет на абаке получил название калькуляция. И сейчас подсчет расходов называют калькуляцией, а человека, выполняющего этот подсчет – калькулятором, также называется современный электронный прибор для счета. Среди применяющихся в современности вариантов абака — русские счёты и японский соробан.

Древние приспособления для счета заинтересовали меня при изучении темы «История развития вычислительной техники». Как древние приспособления для счета способствовали развитию вычислительной техники?

Актуальностьмоей работы состоит в том, что в наше время сложных информационных технологий важно понимать, что стояло у истоков зарождения вычислительной техники, как потребность в счете и обработке сложных вычислений способствовала развитию вычислительной техники и привела к появлению сложных современных вычислительных систем.

Выдвигаемая гипотеза:

Древние приспособления для счета позволяли выполнять сложные вычисления.

Цель:изучить способы счета на древних приспособлениях посредством проведения эксперимента.

Задачи:

изучить теоретический материал;

изучить способы математических действий на приспособлениях;

изготовить соробан;

провести эксперимент по выполнению вычислений на приспособлениях для счета;

зафиксировать результаты вычисления при помощи фотографий;

сделать выводы по полученным результатам.

В ходе проведения работы мною был изучен теоретический материал из источников, указанных в списке. Прочитана книга Гутер Р.С., От абака до компьютера. М.: Знание. -1981 г.-180 с., которая вызвала интерес к более углубленному изучению древних приспособлений для счета, практическому их использованию. Вместе с папой изготовлен соробан. Из других источников литературы, таких как Берназани Д. Соробан/Абакус: Справочное пособие 2013 г.-150 с. и Депман И.Я. История арифметики: Пособие для учителей, Издание второе, исправленное, М.: Просвещение, 1965 г.- 416 с.

Изучены способы счета на соробане и русских счетах. Произведен анализ и сделаны выводы по проделанной работе. Для представления защиты работы публике сделана презентация в Power Point.

Описание древних приспособлений счета

Абак

Предшественником абака была пыльная доска или доска, которая покрывалась песком. Путем разделения пыльного полотна на ряды острой палочкой, представлялись различные значения чисел.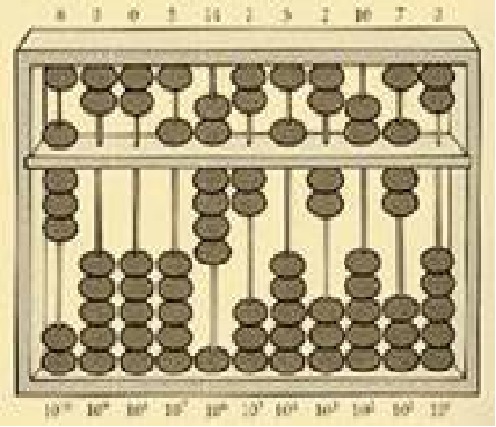 Это достигалось с использованием различных знаков, которые рисовались вдоль линий. Позднее, в Древнем Риме использовали доски, сделанные из камня, бронзы, слоновой кости. На сделанных углублениях считали камешками, косточками.

В неаполитанском музее древностей хранится римский абак, представляющий собой доску с прорезанными полосками, вдоль которых передвигались камешки. На доске располагалось восемь длинных полосок и восемь коротких, расположенных над длинными. Над каждой длинной полоской имеется обозначение, описывающее назначение полоски (слева на право):

– означает, что полоска используется для отложения разряда миллионов;

– для отложения разряда сотен тысяч;

– разряда десятков тысяч;

– разряда тысяч;

– разряда сотен;

– разряда десяток;

– разряда единиц.

– означает, что эта полоска используется для отложения унций.

На семи левых длинных полосках располагали четыре камешка, каждый из которых приравнивался к единице соответствующего разряда числа. На семи левых коротких полосках располагали по одному камешку, обозначавшего пять единиц разряда. Восьмая длинная полоса (служившая для отсчета унций) содержала пять камешков, каждый из которых обозначал единицу разряда унции. Восьмая короткая содержала один камешек, обозначающий шесть единиц. На доске справа имелись две короткие полоски с одним камешком означавшие: – пол унции; – четверть унции. Одна длинная полоска с двумя камешками означала: – шестая часть унции.

Чаще всего абаком пользовались для денежных расчетов налогов и торговли.

Счет на абаке сменил более древний счет на пальцах.

Соробан

Соробан – это японские счёты, которые появились в Японии в XVI веке. Соробан является потомком абака.

Соробан состоит из нечётного количества вертикально расположенных спиц. Каждая спица представляет собой цифру. Обычно их 13, но встречаются соробаны и с 21, 23, 27 или даже с 31 спицей. Бо́льшее количество спиц позволяет набирать большие числа, или представлять сразу несколько чисел на одном соробане.

На каждой спице нанизано по 5 костяшек, причём верхняя костяшка на каждой спице отделена от нижних перегородкой.

Четыре нижние костяшки называются «земными», и каждая представляет собой единицу.

Верхняя костяшка называется «небесной» и считается за пять «земных».

В начальных классах японских школ, до сих пор обучают детей счету на соробане.

Русские счеты

Появились в России на рубеже XV — XVI веков и активно применялись в торговле вплоть до последнего десятилетия XX века. В русских счётах, используется десятичная система счисления и возможность оперировать четвертями, десятыми и сотыми дробными долями. С момента своего возникновения счёты практически не изменились.

С появлением дешёвых электронных калькуляторов счёты практически полностью вышли из употребления. Ещё раньше, в начале 1980-х годов, обучение пользованию счётами было исключено в СССР из школьной программы.

На Русских счетах одиннадцать полос спиц с костями.

Дробная часть начинается со спицы с 4-мя костями. И от нее вниз располагается еще три спицы для дробной части.

Вверх от дробной части идут спицы по 10 костей, начиная с разряда единиц до миллиона.

Способы вычислений на древних приспособлениях для счета

Способ и метод счета на абаке

В исходном положении в «обнуленном» устройстве все камни выровнены по нижнему краю, а верхний ряд по верхнему краю.

В первую полоску ставили столько камешков, сколько в числе единиц, во вторую полоску – сколько в нем десятков, в третью – сколько сотен, и так далее. В верхнем разделе каждый камешек равен 5 в первой полоске, 50 во второй и так далее. Три правые полоски предназначались для счета дробями.

Вычисления производились слева на право.

Сравнивая древний абак и русские счеты, можно заметить, что процесс вычислений совершался пятеричной системой счета, выкладывание камешек происходило снизу в верх, а в русских счетах процесс вычислений совершался десятеричной системой счета и передвижение косточек происходило справа налево.

Способ и метод счета на соробане

Счеты представляют собой рамку, разделенную перекладиной. В верхней части расположена одна линия косточек. Каждая косточка в ней означает «пять». Внизу расположены ряды косточек, в каждом из которых по 4 косточки. Каждая из них обозначает «один». Для удобства вычисления начинают с самого среднего ряда.

Для обнуления соробана счеты слегка ударяют о стол. После этого двумя пальцами отодвигают верхние бусинки от перегородки.На соробане работают всегда сверху вниз большим и указательным пальцами обеих рук.

Набор числа на соробане. Сложение

Сначала нужно отложить первое слагаемое в центре. Ряд за рядом формируя общее число, поразрядно. Все действия на соробане осуществляют слева направо. Сначала откладывается старший разряд и так до младшего, по порядку. Затем также слева направо поразрядно необходимо произвести прибавление следующего числа. Если разряд переполняется косточками, нужно добавить одну бусинку к старшему разряду (слева).

Например, 254+333=587:

1)Откладываем 254

2)Прибавляем 333

3)Получаем 587

Вычитание

Вычитание происходит по той же системе, что и сложение. Разница в том, что при

недостаче бусинок их берут у старшего разряда.

333-254=79

Откладываем 333, затем вычитаем из него 254

Получаем 79

Способ и метод счета на русских счетах

В исходном положении в «обнуленных» счетах все костяшки выровнены по правому краю (как показано на рисунке). Каждый ряд костяшек представляет собой разряд числа, единицы находятся над четырьмя костяшками. Выше единиц – десятки, сотни и т.д., ниже – четверти, десятые и сотые. С таким раскладом удобно считать деньги, где в ходу есть копейки. Черным цветом выделены центральные костяшки (для удобства).

м

Набор числа:

Если мы хотим установить какое-нибудь число на счетах (для совершения с ним в дальнейшем арифметических действий), то необходимо просто передвинуть нужные костяшки налево. Например, для набора числа «3 251,5» передвигаем 2 четвертака (или 5 десятых), 1 единицу, 5 десяток, 2 сотни и 3 тысячи.

Сложение

Чтобы сложить на счетах два числа, нужно просто набрать костяшками одно число, а затем перенести налево каждый разряд второго числа, начиная с нижних рядов. Если вдруг выясняется, что костяшек в каком-то ряду не хватает, то в этом ряду нужно оставить столько костяшек, сколько не хватает, а на уровне выше перекинуть влево еще 1 костяшку. Чтобы лучше разобраться, как правильно складывать числа на счетах, посмотрим пример ниже (987 + 134 = 1 121):

Вычитание

Вычитание на счетах производится точно таким же образом как сложение, сверху вниз. Если костяшек в ряду не хватает, в этом ряду нужно оставить (10-x) костяшек, где x-число не хвативших костяшек, а в ряду выше нужно убрать одну костяшку (сдвинуть ее вправо). Ниже пример (121 – 98 = 23):

Умножение

Для того, чтобы умножить число на 2 или на 3, нужно просто сложить данное число с собой два раза или три раза соответственно. Умножение на 4 производится как умножение на 2 с последующим умножением на 2 полученного результата. Умножение на 5, это деление на 2 , а потом умножение на 10. В этом случае, после деления на 2 переносятся разряды (костяшки) на уровень выше. Умножение на большие числа осуществляется при помощи комбинации описанных методов.

Умножение на счетах является не самым быстрым и простым.

Деление

Деление на русских счетах является достаточно сложной процедурой. Если пример удобный, допустим, необходимо разделить 280 на 2, тогда действительно, нужно просто из каждого ряда отодвинуть направо половину костяшек и тогда получится 140. Но иные примеры в большинстве своем требуют сложных алгоритмов.

Эксперимент с древними приспособлениями счета

Задача:

Расстояние от Москвы до Екатеринбурга по железной дороге 1667км., от Екатеринбурга до Новосибирска 1524 км. и от Москвы до Иркутска 5042 км. Чему равно расстояние от Новосибирска до Иркутска по железной дороге?

3.1 Решение задачи по математике при помощи соробана

Сначала сложим расстояние от Москвы до Екатеринбурга и от Екатеринбурга до Новосибирска:

1667+1524=3191 (км.)

Получаем 3191

Затем из расстояния от Москвы до Иркутска вычтем полученную сумму

5042-3191=1851 (км.)

Получаем ответ 1851 (км.)

Ответ: расстояние от Новосибирска до Иркутска по железной дороге равно 1851 (км).

3.2. Решение задачи по математике при помощи русских счет

Так же для начала сложим расстояние от Москвы до Екатеринбурга и от Екатеринбурга до Новосибирска:

1667+1524=3191(км.)

Получаем 3191 (км.)

Из расстояния от Москвы до Иркутска вычтем полученную сумму

5042-3191=1851(км.)

Ответ: расстояние от Новосибирска до Иркутска по железной дороге равно 1851(км.).

Вывод

Благодаря исследованию, я узнал о различных видах древних приспособлений счета. Изучив методы и способы счета могу сделать вывод, что разные приспособления счета имели различные свойства, так, например, абак позволял вычислять способом сложения, вычитания, умножения и деления, а так же позволял выполнять действия с дробями. Но абак имел свои недостатки: невозможность сохранить результат, из него мог выпасть камешек, в результате весь расчет сбивался.

На протяжении нескольких столетий соробан активно применяется для обучения детей в странах Азии. В Европе и Америке заинтересовались соробаном в XXI веке. А в нашей стране первые школы обучения ментальной арифметике появились в 2013 году. Современные японцы считают, что и сегодня обучение счету с использованием соробана имеет ряд преимуществ по сравнению с традиционным подсчетом на бумаге. Этот метод тренирует мозг, увеличивая количество нейронных связей, и способствует развитию интеллекта и творческих способностей. Хорошо заменяет калькулятор при выполнении домашнего задания по математике начальной школы. Позволяет совершать такие математические действия как сложение, вычитание, умножение и деление.

Недостаток соробана заключается, что невозможно сохранить результат вычислений.

Вычисления на русских счетах, позволяет так же выполнять многие математические действия: сложение, вычитание, умножение, деление, и выполнять действия с дробями, которые будут изучаться мною в дальнейшем.

Недостатки использования русских счет заключаются в том, что нельзя сохранить результат, большие по размеру.

Гипотеза мною доказана на примерах: сложные математические вычисления можно выполнять на древних приспособлениях для счета. Возможно сложение, вычитание больших чисел до миллиарда и более. Конкретно на моем соробане до миллиона.

Таким образом, я считаю, что древние приспособления для счета, а именно, русские счеты и соробан являются достойными предшественниками современной вычислительной техники.

Список использованных источников и литературы

Апокин И. А., Майстров Л.Е. История вычислительной техники. М.: Наука, 1990г.- 400 с.

2. Берназани Д. Соробан/Абакус: Справочное пособие ,2013 г.-150 с.

3. Гутер Р.С., От абака до компьютера. М.: Знание. -1981 г.-180 с.

4. Депман И.Я. История арифметики: Пособие для учителей,

Издание второе, исправленное, М.: Просвещение, 1965 г.- 416 с.

Интернет ресурсы:

https://ru.wikipedia.org/wiki

http://all-ht.ru/inf/history/p_0_4.html

Просмотров работы: 1318

Абакус – как научиться считать, способы обучения и правила применения

Абак (с греческого языка переводится как «таблица») — древние счеты, которые продолжают пользоваться большой популярностью среди детей и взрослых. Такой спрос обусловлен тем, что существует множество разнообразных методик, как считать на абакусе. Ознакомление с ними поможет быстро и легко обучить учеников, развив в них необходимые для школьной программы математические навыки.

Содержание

• История и общие понятия
  • Виды абакуса
  • Устройство и основные элементы
  • Правильное распределение бусин
• Инструкция по применению
  • Положение пальцев и простые примеры
  • Сложение/вычитание и умножение/деление

История и общие понятия

Возможно, в это трудно поверить, но, несмотря на научно-технический прогресс, счеты абакус не считаются пережитком прошлого, активно используются по сей день в некоторых странах. К примеру, китайские и японские торговцы, применяющие механическое средство калькуляции для работы с большими числами, не являются редкостью, хотя эти страны не только не отстают, но и, напротив, лидируют в развитии, демонстрируя настоящее экономическое и техническое чудо.

Виды абакуса

Трудно найти более оптимальный инструмент для усвоения навыков ментальной арифметики, чем обычные счеты. Между тем подобные навыки помогают научиться быстро считать без использования таких популярных в последнее время вспомогательных средств, как электронный калькулятор, эксплуатация которого только ухудшает математические способности.

Неудивительно, что в древности люди считали гораздо лучше, чем их потомки, пусть даже и весьма примитивными способами. Так, долгое время в ход шли пальцы рук и ног, пока, наконец-то, не была придумана новая счетная система, дошедшая до настоящего времени, пусть и в усовершенствованном виде. Речь шла о прототипе абакуса, с помощью которого люди получили возможность выполнять более сложные вычисления.

Всего же сегодня выделяют три счетные системы, каждая из которых имеет свои особенности. В этот перечень входят:

• Суан Пэн (Suan-Pan). Китайский аналог абака, который также представлен в виде деревянной прямоугольной рамки с поперечными прутьями для косточек. Примечательно, что вплоть до 1850 года это древнее счетное средство имело по 2 шара в верхнем ряду и 5 в нижнем (2/5), но после обозначенной даты привычная схема была изменена, в результате чего на соответствующих палубах осталось по 1 и 5 (1/5) косточек.
• Соробан. Так называли счеты в Японии, фактически этот прототип и стал примером для современного приспособления, получив схематическое расположение бусин 1/4. Во всем остальном техника этой разновидности абакуса мало чем отличается от китайской, предполагая применение похожих счетных методик. Что касается отличий, то они также имеются. И стоит отметить, что именно этот вариант сегодня используется активнее всего, причем не только в Японии, но и во многих других странах, включая постсоветское пространство.
• Русские счеты. Эта модель была изобретена в Царской России в XVII столетии, имеет широкое практическое применение и по сей день. Отличительная характеристика российского аналога абакуса заключается в том, что он получил по 10 шаров на каждой планке. Они уложены по схеме 4/2/4, кроме двух рядов с 4 бусинами.

Трудно переоценить роль абакуса в ментальной арифметике, поэтому неудивительно, что человечество неоднократно пробовало изменить счеты, пытаясь изобрести еще более удобное схематическое расположение костей и их количество на каждой палубе. Например, в 1958 году известный китайский ученый Ли Кай Чен разработал одноименную модификацию, представляющую собой своеобразный гибрид соробана и абакуса.

Устройство и основные элементы

Современные счеты, которые применяются на уроках ментальной математики, называются не только абакусом, но и абаком, а также линейкой. Все они в основном являются преемниками старого доброго японского соробана, практически не отличаясь друг от друга. Так, в классическом виде устройство состоит из следующих элементов:

• Жесткая деревянная или пластиковая рамка прямоугольной формы, размер которой может варьироваться от самого миниатюрного до внушительного, предназначаясь для коллективного обучения и счета.
• Поперечные спицы из дерева или металла, число которых может варьироваться как в большую, так и в меньшую сторону.
• Бусины (они же косточки, шары или шармы). Обычно применяется по пять таких шаров на каждой спице.
• Вертикальная планка, предназначенная для разделения костей на две части. В современных абакусах верхний (небесный) ряд включает в себя по одной такой бусине, которой присваивается значение 5, тогда как нижний (земной) содержит по четыре единицы, но с минимальным значением — 1.

Распределяются эти шарики и спицы в особом порядке, начиная свой отсчет с верхнего ряда справа налево. Увеличение чисел происходит в каждом последующем ряду посредством умножения на 10.

Правильное распределение бусин

Так как начальное значение у верхнего и нижнего ряда разные, то и их изменение в бо́льшую сторону будет происходить по индивидуальным схемам. Таблица числовых эквивалентов для каждой спицы выглядит следующим образом:

	Небесные бусины	Земные бусины
Первый ряд	5	1
Второй	50	10
Третий	500	100
Четвертый	5000	1000
Пятый	50 000	10 000
Шестой	500 000	100 000
Седьмой	5 000 000	1 000 000
Восьмой	50 000 000	10 000 000

Еще проще ориентироваться по схематической картинке или названиям рядов, которые можно присваивать самостоятельно, облегчая тем самым процесс изучения особенностей счетного механизма. В качестве примера можно привести следующие условные обозначения рядов:

• 1-й ряд — единицы со значением 0,001;
• 2-й — десятки с 0,01;
• 3-й — сотни с 0,1;
• 4-й — тысячи с 1;
• 5-й — десятки тысяч с 10;
• 6-й — сотни тысяч со 100;
• 7-й — миллионы с 1000;
• 8-й — десятки миллионов с 10 000.

Чтобы понять, как правильно считать на абакусе, необходимо научиться распределять числа на нем. Базовый принцип распределения осуществляется исходя из следующих основных законов механического счета на абаке:

• На первой спице с верхней единичной бусиной принимается наименьшее значение (десятичное, если счет ведется на десятки). Если же необходимо решить пример с миллиардными значениями цифр, то первому шарику присваивается соответствующее значение, тогда как для вычисления десятичных дробей принято считать в тысячных. Все последующие в рамке спицы учитываются вместе с десятикратным умножением.
• На каждой спице находится по пять костяшек, верхняя из которых имеет значение 5. Ее опущенное положение указывает на то, что используемое в вычислении число больше пяти и, наоборот, поднятое свидетельствует о том, что оно не доходит до этого значения.
• Единичные костяшки, расположенные под разделительной планкой, считаются полностью, если имеют поднятое положение.
• В случае когда верхняя бусина находится в опущенном положении, а нижние в поднятом, к пяти необходимо добавить столько единиц, сколько насчитывается в земном ряду. Если же последние находятся в опущенном положении, то к вычислению принимается одна только верхняя бусина, которая имеет значение 5.

Поначалу освоение этой лесенки может показаться очень сложной задачей, но буквально через несколько минут интенсивной тренировки даже первоклассник покажет быстрый правильный набор и распределение, после чего можно приступать и к устному счету.

Инструкция по применению

Сегодня вовсе не обязательно посещать специальную школу для изучения устного счета на абакусе. Вместо этого можно попробовать онлайн-тренажеры с разными уровнями, предназначенные не только для начинающих, но и для продвинутых счетоводов.

Положение пальцев и простые примеры

Вне зависимости от степени сложности выбранного задания, определяющее значение будет иметь положение пальцев, для чего была разработана специальная техника, облегчающая счет. Так, в случае применения японского абакуса необходимо задействовать только два пальца: указательный и большой. Согласно старинным схемам, большой палец предназначается для того, чтобы править костяшками из нижней палубы, тогда как указательный годится для всех бусин без исключения.

Кроме того, важную роль в этом вопросе играет и характер выполняемой счетной операции, ведь если, к примеру, речь идет о вычитании шариков земного ряда, то лучше всего делать его с помощью указательного пальца при прибавлении большим. В то же время для управления костяшками из небесной планки специалисты советуют ограничиваться одним только указательным пальцем, невзирая на то, что нужно сделать — прибавить или отнять.

Разобравшись с положением пальцев и кистей в целом, можно приступать к вычислению, начиная с установки счетов на горизонтальную поверхность и перевода всех их бусин в нулевое положение. Далее можно привести несколько элементарных примеров, как считать на абакусе, выполнив сложение следующих чисел:

«1+3». Чтобы сложить эти простейшие числа, необходимо перевести одну костяшку из земного ряда в сторону разделительной планки, а потом добавить к ней еще три бусинки, получив значение «4».

Выполнение вычисления до пяти предполагает перенесение одной бусины в сторону разделительной планки с одновременным перемещением всех остальных костяшек в нижнее положение.

Для получения числа «7» следует добавить еще две костяшки к разделительной планке, получив один небесный шарик, соответствующий пяти, и два земных, равных двум (5+2=7).

Для выполнения более сложных вычислений рекомендуется придерживаться того же алгоритма действий. В качестве наглядного примера можно привести число 372, для набора которого следует выставить в первом ряду две земные бусины, соответствующие единицам, во втором одну небесную и две земные (5+2=7), а в третьем три из земного, что равно трем сотням.

Сложение/вычитание и умножение/деление

Набив руку в наборе однозначных и многозначных чисел и научившись прибавлять и отнимать самые простые из них, можно смело переходить на следующий, более сложный уровень. И прежде всего речь идет о сложении и вычитании двухзначных чисел. К примеру, посчитать, сколько будет 27+43, на абакусе можно будет следующим образом:

Прежде всего на счетах набираются оба числа с обязательным разложением их на простые составляющие (7 и 3 к единицам, 2 и 4 к десяткам).

После этого выполняется простейшее попарное сложение цифр — 2+4 и 7+3.

Из-за того что при сложении единиц получается 10, необходимо привести все костяшки в этом ряду в нулевое положение, добавив единицу к ряду десяток, получив в итоге 30.

Так как добавляются не только единицы, но и десятки, то к полученным 30 необходимо прибавить еще 4, в результате чего должно остаться 7 десятков, разложенных на одну небесную пятерку и 2 земные единички из ряда десятых.

Вычитание выполняется на основе аналогичного алгоритма, но только в обратную сторону, предполагающую отнимание десятых и добавление единиц, если таковые будут образовываться в остатке. Что касается умножения, то с ним также не должно возникнуть никаких трудностей, нужно только освоить таблицу умножения от 0 до 10.

Само решение выполняется в два этапа, которые предполагают разложение каждого числа на десятки и единицы с последующим их перемножением. Если же для расчета используются трехзначные и более сложные числа, следует придерживаться одного простого правила, согласно которому сначала перемножаются десятки, потом единицы с десятками и наоборот, а после сами единицы. Проще говоря, счет ведется от большего к меньшему с последовательным их набором на абакусе. По аналогии выполняется и деление, главное, не сбиться и соблюдать очередность выполняемых операций.

Предыдущая

МатематикаУмножение и деление – примеры решения задач по математике для 3 класса

Следующая

МатематикаСвойства сложения – основные законы, формулы и правила

Как использовать счеты AL с ЛЮБОЙ учебной программой — с видео

Используете ли вы Saxon или Singapore, Math Mammoth или Math U See, счеты AL могут помочь вашим детям лучше понять сложение и вычитание и помочь им развить более глубокое чувство числа. (Если вы не читали мой предыдущий пост о том, почему я так люблю AL Abacus, вы можете сначала щелкнуть туда, чтобы получить представление о том, что делают счеты, прежде чем погрузиться в этот пост.)

Я начал писать длинный, сложный пост о том, как преподавать на счетах в вашей домашней школе, когда я понял, что на самом деле хочу просто сесть с вами и показать вам. Итак, я сделал четыре коротких видеоролика , которые демонстрируют, как использовать AL Abacus для обучения:

• начальное добавление
• арифметика в уме с двузначными числами
• как складывать трехзначные числа с перегруппировкой
• как вычитать трехзначные числа с перегруппировкой

Я также описал пять шагов к использованию счетов AL с любым уроком сложения или вычитания, а также как перевести вашего ребенка от использования счетов к решению задач на бумаге или в уме. В конце концов, цель использования счетов состоит в том, чтобы понимать математику так хорошо, чтобы вы не нужны счеты. Этот пост покажет вам, как!

Преимущество счетов в том, что вы действительно можете использовать их в любой учебной программе по математике, чтобы помочь вашему ребенку закрепить основы понимания чисел, сложения и вычитания. Для каждого из приведенных ниже видеороликов я взял задачу из другой учебной программы (в данном случае — Singapore Primary Mathematics 2A) и «перевел» ее на счеты.

Видео: Как научить простому сложению на счетах AL Abacus

Во многих учебных программах простое сложение представлено в виде кучи неорганизованных объектов для счета. Использование счетов помогает вашему ребенку видеть числа как группы, а не просто объекты, которые нужно считать по одному.

 

Видео: Как обучать математике в уме на AL Abacus

Счеты отлично подходят для обучения детей тому, как использовать свое понимание разрядности для решения задач по математике в уме.

Видео: Как обучать многозначному сложению на AL Abacus

Счеты облегчают перегруппировку и обмен при обучении многозначному сложению или вычитанию.

Видео: Как научить многозначному вычитанию на AL Abacus

Теперь, когда у вас есть общее представление о том, как преподавать с помощью счетов, вот пять шагов, которые помогут вам использовать счеты AL с вашей учебной программой .

1. Решите, какую сторону счетов использовать.

Счеты имеют две стороны. Используйте пустую сторону (с кружком AL в правом верхнем углу) для вычислений в уме до 100. Используйте сторону с пометкой 1000, 100, 10, 1, если вы работаете с большими числами или если вы выполняете какую-либо перегруппировку или торгуете. (как при двузначном вертикальном сложении или вычитании).

Используйте эту сторону для счета в уме до 100.

2. Познакомьте ребенка со счетами.

Прежде чем приступить к новой концепции, дайте ребенку немного времени, чтобы понять, как работают счеты. Введите несколько цифр на счетах, и пусть ваш ребенок скажет, какую цифру показывают бусины. Затем назовите ребенку число и попросите его ввести правильное количество бусин. (См. мой предыдущий пост, где показаны изображения чисел, введенных на счетах.) Например, если вы хотите научить своего ребенка складывать многозначные числа, попросите его ввести трех- и четырехзначные числа на маркированной стороне. счеты.

3. Переведите понятие, которое вы преподаете, на счеты.

Здесь пригодится учебник для учащихся или руководство для учителя. Взгляните на картинки, которые они используют для иллюстрации концепции, и переведите их на счеты, как я сделал в видеороликах выше. Делайте это медленно, проработайте несколько примеров и убедитесь, что каждый шаг имеет смысл для вашего ребенка. Задавайте много вопросов, чтобы проверить понимание, особенно когда речь идет о перегруппировке и торговле.

4. Позвольте вашему ребенку использовать счеты, когда он начнет использовать новую концепцию для решения задач.

Держите счеты под рукой и дайте ребенку использовать их при выполнении первых нескольких заданий с новой концепцией. Это поможет укрепить его понимание и действительно закрепит новую концепцию.

5. Поощряйте ребенка переходить к решению математических задач без счетов.

На этой неделе подруга пошутила, рассказывая об успеваемости дочери по математике: «Счеты помогают ей понять, что она делает. Но я не хочу, чтобы ей приходилось носить такую ​​в сумочке, когда она станет взрослой, чтобы внести сдачу!» Она абсолютно права! Цель использования счетов (или любых других манипулятивных средств) состоит в том, чтобы в конце концов в них больше не было необходимости. Манипуляторы — это инструмент , помогающий детям понять, что они делают, чтобы они могли перейти к решению проблем на бумаге или в уме.

Чтобы счеты не стали костылем, постепенно уменьшайте использование счетов ребенком по мере освоения новой концепции. Например, вот как вы можете отучить своего ребенка от счетов при изучении многозначного сложения:

• Сначала используйте счеты для решения каждой задачи, аккуратно меняя бусины, чтобы перегруппировать их.
• После того, как ваш ребенок полностью поймет концепцию перегруппировки, предложите ему ввести только первое сложение на счетах, а затем  представьте, что добавляет бусины для второго сложения. Например, если ваш ребенок складывает 265 + 379, он может ввести 265 на проводах, но только визуализировать , передвигая бусины вверх для 379.
• Как только она сможет надежно решать задачи таким образом, уберите счеты. Вытаскивайте его только в том случае, если ваш ребенок запутался или застрял, но в остальных случаях поощряйте его решать задачи на бумаге.

Купите собственные счеты AL здесь, чтобы начать пожинать плоды для своих детей.

(Ссылки выше могут быть партнерскими ссылками. Когда вы покупаете товар по партнерской ссылке, вы помогаете поддерживать этот сайт без каких-либо дополнительных затрат для вас. Спасибо!)

Happy Math!

 

 

Как вы используете счеты?

ИСКУССТВО ЯЗЫКА — Литература

Задумывались ли вы когда-нибудь.

..

• Как пользоваться счетами?
• Когда были изобретены счеты?
• Кто-нибудь еще пользуется счетами?

Теги:

Просмотреть все теги

• abaci,
• абакаст,
• счеты,
• счеты,
• добавить,
• Африка,
• алгебра,
• Азия,
• бамбук,
• бусина,
• расчет,
Калькулятор
• ,
• исчисление,
• китайский,
• компьютер,
конфигурация
• ,
• счет,
устройство
• ,
• разделить,
• Геометрия,
• Греческий,
• изобретений,
• Математика,
• математик,
• математика,
• умножить,
• номер,
• персидский,
• позиция,
• Роман,
• вычесть,
• шумерский,
система
• ,
• технология,
• тригонометрия,
• Абаци,
• Абацист,
• Счеты,
• Счеты,
• Добавить,
• Африка,
• Алгебра,
• Азия,
• Бамбук,
• Бусина,
• Расчет,
• Калькулятор,
• Исчисление,
• китайский,
• Компьютер,
• Конфигурация,
• Подсчет,
• Устройство,
• Разделить,
• Геометрия,
• Греческий,
• Изобретения,
• Математика,
• Математик,
• Математика,
• Умножить,
• Номер,
• персидский,
• Должность,
• Роман,
• Вычесть,
• шумерский,
Система
• ,
• Технология,
• Тригонометрия

Сегодняшнее чудо дня было вдохновлено миссис Меган из Вудбери, штат Миннесота. Миссис Меган Уондерс , « Как вы используете счеты? «Спасибо, что ДУМАЕТЕ вместе с нами, миссис Меган!

Какой твой любимый предмет в школе? Не говорите обед или перерыв! Это всеобщие любимцы! Что касается популярных предметов, то некоторые ученики предпочитают английский язык. Другим учащимся могут нравиться естественные науки или история. Дети, умеющие считать, могут найти математику своим любимым уроком дня.

Чем старше вы становитесь, тем сложнее становятся ваши уроки математики. Вы когда-нибудь изучали алгебру? Как насчет геометрии или тригонометрии? Если да, то вы знаете, что быстро выходите за пределы работы, которую вы можете делать в своей голове. Для более продвинутых предметов необходим калькулятор.

Еще до изобретения калькуляторов и компьютеров люди работали с системами счисления. А как же самые ранние люди на Земле? У них не было языка, не говоря уже о системах счисления для базовой математики. Так как же они следили за вещами?

Первые люди, вероятно, обращались к природным объектам, чтобы вести счет. Камни и палки можно было легко использовать для подсчета и отслеживания объектов. Однако когда началась торговля, торговцам понадобился способ производить базовые расчеты и считать большие числа.

Первые счетные устройства, вероятно, были сделаны из канавок, вырезанных в песке или дереве, по которым можно было перемещать мелкие предметы, такие как бусы и галька. Со временем эти устройства были заменены каркасом из бамбука или дерева. Они содержат стержни, веревки или проволоки, по которым бобы или бусины могут свободно скользить.

Это раннее устройство было известно как счеты или счетная рамка. Если у вас есть несколько счетов, их называют счетами или счетами. Человек, использующий счеты, известен как абакист.

Счеты использовались веками. На самом деле, они до сих пор часто используются купцами и торговцами. Никто точно не знает, когда впервые были изобретены счеты. Однако историки знают, что версии абаков появлялись в разных культурах на протяжении всей истории.

Например, шумерские счеты могли быть первыми. Он был изобретен еще в 2700 году до н. э. Со временем версии счетов использовались древними персами, греками, римлянами и китайцами.

Вы когда-нибудь пользовались счетами? Если да, то вы знаете, что бусины можно перемещать, чтобы отслеживать подсчитанные объекты. Более сложные абаки могут даже помочь вам складывать, вычитать, умножать и делить!

Common Core, Научные стандарты следующего поколения и Национальный совет по социальным исследованиям.»> Стандарты: CCRA.L.3, CCRA.L.6, CCRA.R.1, CCRA.R.2, CCRA.R.4, CCRA.R.10, CCRA.SL.1, CCRA.W.4

Интересно, что дальше?

Завтрашнее чудо дня черно-синее и читается повсюду!

Попробуйте

Мы говорили вам, что вы можете рассчитывать на сегодняшнее Чудо Дня для получения удовольствия от обучения! Продолжайте веселиться, проверив следующие занятия с другом или членом семьи:

• У вас есть счеты дома, чтобы попрактиковаться? Если нет, не волнуйтесь! Вы можете попрактиковаться в счете на японских или китайских счетах, подключившись к Интернету и отправившись попробовать эти виртуальные счеты! Поделитесь ссылкой с друзьями и объясните им, что вы узнали об абаках!
• Чувствуете себя лукавым? Знаете ли вы, что можете сделать свои собственные счеты? Это так! Вам просто нужно несколько принадлежностей и помощь взрослого друга или члена семьи. Будь креативным! Не стесняйтесь использовать интересные бусины, чтобы ваши самодельные счеты отражали вашу индивидуальность.
• Мы далеко ушли от счетов. Сегодня в нашем распоряжении есть множество инструментов, которые помогают нам считать и вычислять математические задачи, с которыми мы сталкиваемся ежедневно. С помощью взрослого друга или члена семьи оцените все способы счета и счета дома и в школе. У вас дома есть таймер? Как насчет карманного калькулятора? У вас есть компьютер или смартфон в школе? Какие еще у вас есть инструменты и устройства, которые могут помочь вам считать или решать математические задачи? Составьте список всех инструментов или устройств, о которых вы только можете подумать.

Wonder Sources

• https://www.ee.ryerson.ca/~elf/abacus/history.html (по состоянию на 25 февраля 2021 г.)
• https://history-computer.com/abacus-complete -history-of-the-abacus/ (по состоянию на 25 февраля 2021 г.)
• https://kb.osu.edu/bitstream/handle/1811/78206/OJSM_65_Spring2012_58. pdf (по состоянию на 25 февраля 2021 г.)

Ты понял?

Проверьте свои знания

Wonder Words

• рамка
• стержни
• бусины
• алгебра
• калькулятор
• канавки
• версии
• культур
• историков

Примите участие в конкурсе Wonder Word Challenge

Оцените это чудо

Поделись этим чудом

×

ПОЛУЧАЙТЕ СВОЕ ЧУДО ЕЖЕДНЕВНО

Подпишитесь на Wonderopolis и получайте Wonder of the Day® по электронной почте или SMS

Присоединяйтесь к Buzz

Не пропустите наши специальные предложения, подарки и рекламные акции. Узнай первым!

Поделись со всем миром

Расскажите всем о Вандополисе и его чудесах.

Поделиться Wonderopolis

Wonderopolis Widget

Хотите делиться информацией о Wonderopolis® каждый день? Хотите добавить немного чуда на свой сайт? Помогите распространить чудо семейного обучения вместе.

Добавить виджет

Ты понял!

Продолжить

Не совсем!

Попробуйте еще раз

Как пользоваться счетами

 

Из учебных советов, вторник

 

Алекс: Всем привет! И добро пожаловать в очередной выпуск «Советов для учителей» во вторник, у нас очень  специальный выпуск для вас сегодня с единственным и неповторимым Марком Эштоном, генеральным директором Фонда помощи слепым детям, как дела, Марк?

Марк: У меня сегодня все отлично, Алекс, спасибо, что пригласил меня.

Алекс: Абсолютно, большое спасибо за то, что вы были, не могли бы вы немного рассказать людям дома о том, как вы связались с FBC?

Марк: Ну, почти 27 лет назад у меня родился сын Макс, и когда ему поставили диагноз болезни Лебера, и мы… Фонд помощи слепым детям появился на нашем пороге на следующий день, чтобы начать раннее вмешательство, и, в конце концов, он ходил здесь в дошкольное учреждение, ходил в государственную школу, а теперь работает на сенатора США. Итак, это был отличный путь, и именно так я стал членом совета директоров, а затем, в конце концов, генеральным директором.

Алекс: Что ж, нам повезло, и мы гордимся тем, что вы командуете нашим кораблем.

Марк: [кивает и улыбается] Спасибо, спасибо.

Алекс: Абсолютно, так что несколько недель назад мы провели, э-э, во вторник «Советы преподавателям» с Линн Гриллет об абаке, а затем Марк обратился ко мне и сказал, что за все эти годы его так и не научили пользоваться счетами. счеты.

Марк: [кивает в знак согласия]

Алекс: Вот я и подумал, что это прекрасная возможность дать небольшой урок для домашних. У тебя есть счеты? [достает счеты]

Марк: [держит счеты] У меня есть счеты.

Алекс: Хорошо, мы собираемся сделать это зеркально, так что это будет немного сложно, но я чувствую себя хорошо.

Марк: [легко посмеивается]

Алекс: Итак, да, найдите минутку, чтобы нормально посмотреть на свои счеты.

Марк: Хорошо. [Марк держит счеты лицом к себе]

Алекс: [Алекс держит счеты лицом к себе] У нас есть – он весь в бисере, это первое, что бросается в глаза; эти бусины представляют собой различные разряды чисел. Итак, на правом краю наших счетов находится колонка единиц. Если вы должны были поднять одну бусину, вы установили номер один [передвигает бусину вверх по счету и продолжает делать это для бусинок 2-4]. Затем мы можем продолжить через два, три, четыре, но теперь у нас все кончились бусины. Итак, что мы делаем, так это сдвигаем их обратно вниз [сдвигаем все бусины обратно вниз] , а затем спуститесь вниз по бусинкам нашей пятерки. [опускает пятую бусину вниз]

Марк: [следует за счетами] Итак, верно?

Алекс: Базовый – Итак, да [в ответ Марку] Это стоит пять, и это стоит пять от того разряда, в котором вы находитесь, так что вот пять, вот пятьдесят, пятьсот, пять тысяч, все путь до пяти триллионов. [проводит пальцем по «пяти» бусинам]  Так что вы можете сделать что-то

Марк: [удивленно кивает головой] О!

Алекс: Итак, вы можете сделать серьезных математических расчетов на счетах — вплоть до столбца триллионов, но я не думаю, что мы доберемся до этого сегодня, Марк, так что не волнуйтесь.

Марк: [легко смеется] Спасибо, спасибо, маленькие шажки.

Алекс: По сути, чтобы установить число, все зависит от того, касается ли оно этой полосы посередине, то есть для числа восемь. Посмотрим, смогу ли я сделать это в обратном порядке. [хрюкает и пытается отобразить число 8 через счеты лицом к аудитории] О, хорошо, у меня есть моя пятерка и три единицы.

Марк: [Попытки продолжить] 

Алекс: Итак, вы установили номер —

Марк: Хорошо, спасибо.

Алекс: 35 – поехали! Итак, вот проверка вашего понимания, Марк, без каких-либо объяснений столбца десятков вы можете установить число 64?

Марк: [Шепотом ведет себя через него] 

Алекс: Красиво! 64, вот и все!

Марк: Верно?

Алекс: Да, именно так! Итак, у вас есть…

Марк: Ничего себе, хорошо.

Алекс: 50, 10, это 60. Так что это очень логичный, понятный инструмент, особенно для тех, кто уже имеет представление о числах; но счеты — прекрасное средство для обучения первоначальным способностям к числам учеников с нарушениями зрения, потому что все они полностью тактильны. О, одна из моих любимых частей в этом, похоже, у тебя уже есть довольно четкие счеты, даже если ты встряхнешь их, чтобы четки двигались.

Марк: [Встряхивает счеты] Нет, это совершенно новое, я только что забрал из нашей библиотеки.

Алекс: [смеется] О, хорошо, прямо из AIRT.

Марк: Ага! [кивает головой и смеется]

Алекс: Это хорошо, счеты Криса Крамера, так что да, они остаются покрытыми пластинами, они не двигаются, пока вы намеренно не задействуете их.

Марк: Да-

Алекс: Хорошо!

Марк: Сзади войлок сзади, да.

Алекс: Давайте попробуем сделать какое-нибудь простое сложение, начнем с три плюс семь. Теперь, Марк, можем ли мы сделать это в любом порядке?

Марк: Не знаю, учитель!

Алекс: Семь плюс три — это то же самое, что три плюс семь?

Марк: Да.

Алекс: Да, потому что сложение коммутативно, так с какого числа ты хочешь начать — с трех или с семи?

Марк: О, так что я могу начать с пяти, семи…

Алекс: Семь, хорошо, и мы собираемся использовать то, что называется Метод подсчета, , так что многие люди делают ошибку на этом этапе.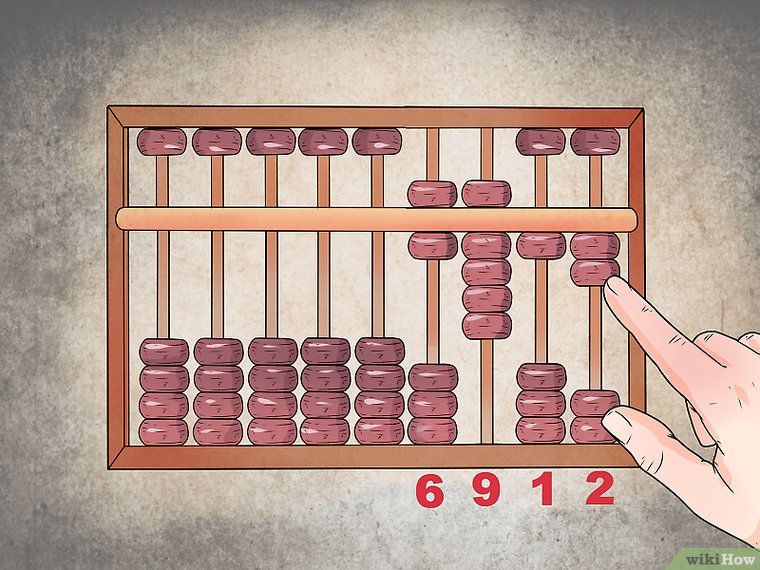 Поэтому вместо следующей скорости, которую они поднимали вверх, они говорили восемь, но тогда вы не знаете, сколько еще цифр, поэтому первая цифра, которую вы поднимаете, будет означать единицу.

Марк: [Следует за Алексом] Один.

Алекс: А потом два.

Марк: Два.

Алекс: Но вот и все, у нас закончились бусинки, а нам еще осталось одну. Мы очищаем всю колонку единиц, скользим вниз на десятую бусину — или скользим вверх на десятую, простите, и говорим «три».

Марк: Три.

Алекс: Ты пропустил одну бусину.

Марк: О. [закрепляет бусину]

Алекс: Ну вот, это один из самых важных шагов, когда вы учите ученика пользоваться счетами. Как использовать этот синтез над баром, мне нравится считать это…

Марк: Извините, это только на пять, а не на десять?

Алекс: Что ты имеешь в виду?

Марк: Хорошо, я просто пытаюсь понять это. Итак, это число прямо сейчас означает одиннадцать. Нет, это значит десять.

Алекс: Всего десять,

Марк: Да.

Алекс: Было бы одиннадцать. [отображает на счетах число одиннадцать]

Марк: О, спасибо. Хорошо. [кивает головой в понимании] 

Алекс: Хорошо, это имеет смысл?

Марк: Так и есть.

Алекс: Ладно, пойдем в другую сторону, сделаем вычитание. Сделаем шестнадцать минус восемь.

Марк: [Вычитает шестнадцать минус восемь на счетах] Десять?

Алекс: Ну вот, красиво, да. Красиво и чисто, да. Итак, теперь мы собираемся начать обратный отсчет, начиная с одного, какой первый шаг, по вашему мнению, мы должны сделать?

Марк: Один.

Алекс: Один — отлично.

Марк: шестнадцать минус сколько? Мне жаль.

Алекс: Восемь.

Марк: Хорошо, один. Я заберу пять?

Алекс: Ты понял.

Марк: Пять.

Алекс: Итак, тебе нужно сделать еще кое-что. [указывает на счеты] Поднимите свои бусинки — все.

Марк: Все, почему все?

Алекс: Хорошо, значит, мы только что достигли — функционально — числа пятнадцать.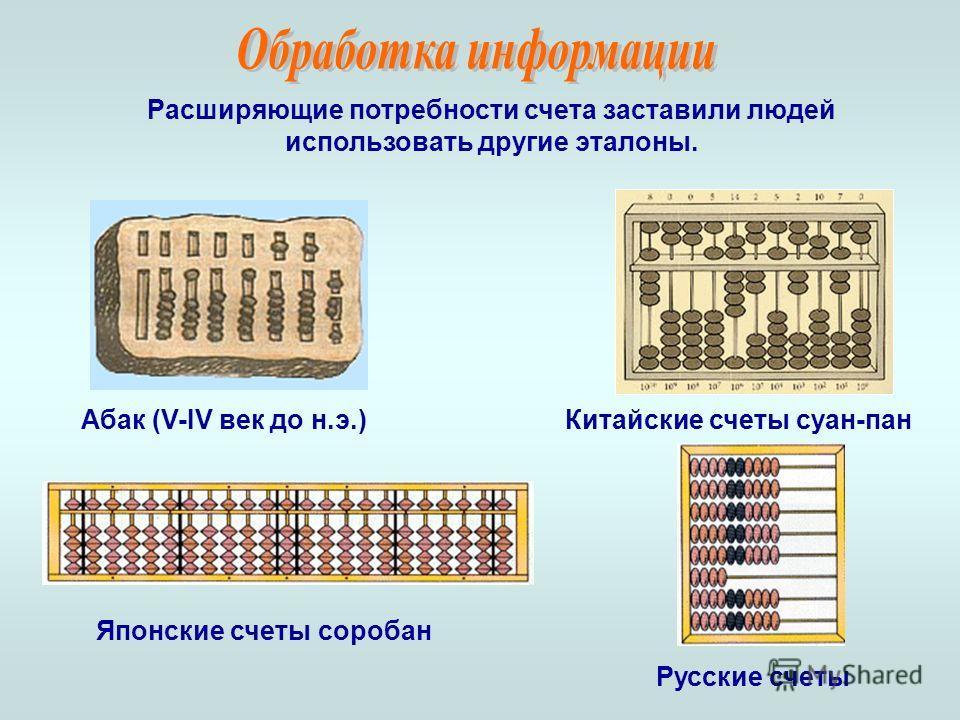 Мы забрали одного из шестнадцати. Когда вы считаете в обратном порядке, вы не идете от десяти до конца или от пятнадцати до десяти, вы идете от пятнадцати до четырнадцати.

Марк: Ооо, ладно, по одной бусине за раз. Хорошо.

Алекс: Итак, два. Три, четыре, пять, шесть — у всех кончились бусы. Так что подумайте об этом со своим чувством числа, мы на десяти, нам нужно идти к девяти.

Марк: [Говорит сам с собой]

Алекс: Ну вот! Красиво, вот так.

Марк: Вау, шрифт Брайля было намного легче выучить.

Алекс: О, я не мог не согласиться с вами по этому поводу. Марк [смеется] Хорошо…

Марк: У меня была возможность, Алекс, когда Макс был ребенком, выучить шрифт Брайля вместе с ним, а Макс просто этого не сделал. Не принеси домой счеты. Он просто оставил его в школе, так что у меня никогда не было этого опыта, но я получил опыт изучения шрифта Брайля, как и он, и, гм, очевидно, я выучил его с помощью зрения, но, гм, это совершенно новый мир. Спасибо.

Алекс: Абсолютно! Итак, мы на пяти, нам осталось передвинуть еще три числа.

Марк: Подожди, мы еще не добрались?

Алекс: Похоже на правильный ответ шестнадцать минус восемь?

Марк: Уже восемь, верно, Боже мой. Итак, мы должны пройти пять, шесть, семь, восемь.

Алекс: Что, D=мы напортачили? О, кажется, я отвлекся на счет. Ладно, мы отвлеклись на середину, и это…

Марк: Прости…

Алекс: [Заикаясь] Делать это перед зеркалом оказалось намного сложнее, чем я думал. Хорошо, теперь у меня есть шестнадцать. Я убираю один, два, три, четыре, пять, шесть, семь, восемь.

Марк: Хорошо.

Алекс: Мой ответ, конечно, восемь.

Марк: Вау. Пять плюс три, то есть восемь.

Алекс: Ммм, и, в конце концов, это становится очень моторным процессом. Это не так, это не так — вы не просто думаете о математике, вы думаете о шагах. Хорошо, последнее испытание на счетах для вас сегодня, Марк. Вы можете отложить его, я отложу свой, потому что мы собираемся решить эту задачу полностью тактильно. Итак, мы собираемся установить непрерывный зрительный контакт во время следующей задачи. Хорошо, ты хочешь сделать сложение или вычитание?

Марк: Дополнение для меня, если не возражаете

Алекс: Конечно, абсолютно. Давайте сделаем двузначное число двузначным; давайте сделаем тридцать шесть плюс четырнадцать.

Марк: Хорошо [смеется]  Хорошо, тридцать шесть, так что я только что поставил тридцать шесть плюс четырнадцать, так что мне нужно идти, э-э, раз, два, три, четыре. [смотрит на счеты]  Я жульничал, я смотрел вниз! Тридцать шесть плюс четырнадцать, э-э, я пытаюсь сделать это цифрами здесь…. [бормочет]

Алекс: Не смотри вниз! Это обман, давайте посмотрим, что у вас есть!

[Алекс и Марк держат счеты]

Марк: Нет? (Счета — разные значения)

Алекс: Мы получили тридцать шесть плюс четырнадцать, тридцать шесть плюс четыре — сорок, плюс десять — пятьдесят. Итак, я…

Марк: [Марк понимает свою ошибку и исправляет ее] Ты прав! О чувак.

Алекс: Итак, я задал вам очень сложный вопрос, я дал вам две части синтеза, которые вы должны были сделать, вы должны были пересечь свою черту девяток в десятую позицию, и вы должны были преобразовать гм, сорок в пятьдесят. Так что я сделал довольно сложной задачей.

Марк: Я просто хочу извиниться перед всеми вашими зрителями, я плохо учусь, и я надеюсь, что они вынесли из этого что-то, кроме того факта, что я не умею считать, или, э, что Я не очень хорошо учусь, но я надеюсь, что сегодня они чему-то научились.

Алекс: Абсолютно, надеюсь, мы показали всем, что счеты — даже несмотря на то, что у вас были некоторые проблемы с последней задачей — это относительно быстрое для понимания устройство, которое имеет большую практическую, очень математическую ценность.

Марк: Что ж, Алекс, это было… это было здорово, и это доказывает, что такие инструменты важны, и это важно для наших студентов по всей стране, и я рад, что вы в состоянии показать мне немного родителей.