Рукописные цифры: Распознавание цифр, написанных от руки, с помощью Machine Learning — NTA на vc.ru
Распознавание цифр, написанных от руки, с помощью Machine Learning — NTA на vc.ru
Каждый день люди сталкиваются с огромным количеством данных, но, несмотря на переход к электронному документообороту, встречаются документы, которые отсканированы человеком и содержат рукописный текст, в том числе цифры, даты, подписи и пр.
1144 просмотров
Распознавание рукописного текста – это огромная проблема, так как существует всего 10 цифр, а почерк человека может сильно варьироваться. И порой с задачей распознания рукописного текста не справляется даже сам человек, что уж говорить о почерке врача 😊
Классификация рукописного текста или цифр очень важна на практике, это поможет сократить время на разбор огромного количества данных.
В этой статье я хочу рассмотреть распознавание рукописных цифр от 0 до 9, с использованием известного набора данных digits библиотеки Scikit-learn, применяя классификатор логистической регрессии.
Кратко о наборе данных digits
Область данных digits содержит некоторое множество наборов данных, которые могут быть полезны для тестирования задач анализа данных и прогнозирования результатов.
Для того чтобы работать с распознаванием рукописного текста, вам понадобятся следующие библиотеки: matplotlib, sklearn, scipy.
На примере встроенного набора данных библиотеки sklearn — digits рассмотрим выполнение распознавания цифр. Для этого импортируем его, чтобы начать использовать.
import sklearn.datasets dd = datasets.load_digits() print(dd.DESCR)
Область данных digits представляет собой словарь, в котором содержатся данные, целевые объекты, изображения, а также названия объектов и описание набора данных с названиями целевых объектов и пр.
Я ориентируюсь на наборе данных и целевой функции, извлечем два списка в две разные переменные.
m_d=dd[‘data’] tt=dd[‘target’] print(len(m_d)) import matplotlib.pyplot as pltt %matplotlib inline def show_cifr(index): pltt.imshow(dd.images[index],cmap=pltt.cm.gray_r, interpolation=’nearest’) pltt.title(‘Цифра: ‘ + str(dd.target[index])) pltt.show() show_cifr(8)
Давайте рассмотрим 3 модели: классификатор опорных векторов, классификатор деревьев решений и классификатор случайного леса, для того чтобы понять, как работает каждая из моделей на одном наборе данных.
Классификатор опорных векторов
Задача этого алгоритма заключается в том, чтобы найти гиперплоскость в n-мерном пространстве, где n – это число признаков, чтобы проклассифицировать все точки данных.
from sklearn import svm svm = svm.SVC(gamma = 0.001, C=100.) svc.fit(m_d[:1790], tt[:1790]) pr = svc.predict(m_d[1791:]) pr, tt[1791:]
На выходе мы получили 100% совпадение, где 1791 значение используется для обучения, а 6 входных данных используются для тестирования.
Классификатор деревьев решений
В классификаторе дерева решений применяется простая идея решения задачи классифкации. Задается ряд тщательно продуманных вопросов об атрибутах тестовой записи. Каждый раз, когда будет задан вопрос – на выходе получаем ответ до тех пор, пока не будет сделан вывод о классовой метке записи.
from sklearn.tree import DecisionTreeClassifier
dt = DecisionTreeClassifier(criterion = ‘gini’)
dt.fit(m_d[:1550] , tt[:1550])
pr2 = dt.predict(m_d[1551:]
import sklearn.
metrics.accuracy_score
import sklearn.metrics.confusion_matrix
confusion_matrix(tt[1551:], pr2)
accuracy_score(tt[1551:], pr2)
Как можно видеть, классификатор дерева решений плохо работает с данными. Вы можете попробовать повысить точность путем настройки гиперпараметров DTC.
Классификатор случайного леса
Случайный лес – является контролируемым алгоритмом обучения. Его используют как для классификации, так и для регрессии.
При случайном лесе можно создать деревья решений на случайно выбранных выборках набора данных и получают прогноз каждого дерева и впоследствии выбирают лучшее решение с помощью голосования.
import sklearn.ensemble.RandomForestClassifier rc = RandomForestClassifier(n_estimators = 150) rc.fit(m_d[:1400], tt[:1400]) pr3 = rc.predict(m_d[1401:]) accurace_store(tt[1401:], pr3)
Таким образом, мы можем увидеть, что случайный лес отлично работает на меньшем количестве данных в сравнении с деревом решений. Оценка точности составляет 92%.
Согласно гипотезе, при настройке гиперпараметра с помощью различных моделей можно достичь более 96% точности распознавания рукописного набора данных. Но прежде необходимо убедиться, что тестовые данные будут хорошими, иначе модель может быть перегружена.
Удачи в кодировании! 😊
Поиск
- 1-10 – 126669 pезультаты
- следующая
Cобственный текст
Pазмер очень маленькиймаленькийсреднийбольшойочень большой
Bосстановить
Pезультаты
102030
Сортировать по
idимярейтингзагрузкинисходящий порядоквосходящий порядок
Категория
ЛюбаяГотическиеДругиеКельтскиеПрописныеСовременныеСредневековыеИллюзорныеC завитушкамиДекоративныеДругиеЗападныеИскаженныеКиношныеКомиксныеКонтурныеМилитариМультфильмыПревосходныеРазъеденныеРетроСовременныеСтарой школыТехноТрёхмерныеУстрашающиеФутуриЦифровыеИностранныеАрабскиеБенгальскиеБирмаВьетнамскиеГреческиеГрузинскиеДругиеИзраильскиеКириллическиеКитайскиеКорейскиеЛаосскиеЛатинскиеМексиканскиеМонгольскиеРусскиеСиллабическиеТаитянскиеТибетскиеЦ.
-ЕвропейскиеЭфиопскиеЮникодЯпонскиеОсновныеБез засечекДругиеРавноширинныеС засечкамиПраздничныеДень ВалентинаПасхаРождествоХеллоуинРастровыеПиксельныеРукописныеГраффитиКаллиграфияКистьРукописныеТрешевыеШкольныеСимвольныеАзиатскиеВ стиле БрайляВ стиле ужасовДругиеЖивотныеИгровыеИнопланетныеИскусствоМилитариМультфильмыПищевыеПриродныеРуническиеСимволическиеСпортивныеСтаринныеФантастическиеЧеловеческиеШтрих-кодЭзотерические
Tаблица символов ЛюбаяЕвропейские алфавитыЛатинскийБазовая латиницаЛатиница-1 дополнительнаяРасширенная латиница-AРасширенная латиница-BРасширенная латиница-ЦРасширенная латиница-ДДополнительное расширение латиницыДекоративные варианты буквМалые варианты символовСимволы полной и половинной шириныКириллицаКириллицаДополнение к кириллицеРасширенная Кириллица-AРасширенная Кириллица-БГреческое письмоГреческое письмоРасширение греческого письмаАрмянское письмоКоптское письмоГрузинское письмоГрузинское письмоГрузинское дополнениеАфриканские рукописные шрифтыЭфиопское письмоЭфиопское письмоЭфиопское расширенное письмоЭфиопское дополнениeДругие африканские рукописные шрифтыН’КООсмания (Осман Юсуф Кенадида)Древнеливийское письмоВаиCредне-восточные рукописные шрифтыАрабское письмоАрабское письмоАрабское дополнениeАрабское декоративное письмо-ААрабское декоративное письмоИвритСирийское письмоТаана (мальдивское письмо)Aмериканские рукописные шрифтыУнифицированное слоговое письмо канадских коренных жителейПисьмо чероки (чироки)Дезерет (мормонское письмо)Филиппинские рукописные шрифтыБухид, мангиан (Филиппины)Письмо хануну (разновидность деванагари) (Филиппины)Тагальская письменностьТагбануа (Филиппины)Индийские рукописные шрифтыБенгальское, ассамское письмоДеванагари (индийское слоговое письмо)Гуджаратское письмоГурмукхи (синдхское, пенджабское письмо)Каннада (каннада)ЛепхаЛимбуМалайское письмоОл ЧикиПисьмо ория (одри, уткали) (Индия)СаураштраСингальское письмоСилоти НагриТамильское письмоПисьмо телугуЮго-восточные азиатскиеБалийскийБугийскийЦхамКайаКхмерское письмоКхмерские символыЛаосское письмоБирманское письмоНовый Тайский ЛeРеджангскаяСуданскийТайский ЛеТайское (сиамское) письмоВосточно-азиатские рукописные шрифтыИдиографы ханДальневосточные унифицированные иероглифыДальневосточные унифицированные иероглифы, расширение-АДальневосточные унифицированные иероглифы pасширениe-БИдеографы, совместимые с дальневосточными языкамиИдеографы, совместимые с дальневосточными языками – ДополнениеКамбунPадикалы и ударенияДополнительные ключи к иероглифамКандзи (ключи к иероглифам)ККЯ-штрихиОписания идеограммКитайский алфавитКитайское слоговое письмоРасширение к бопомофо (Китай)Японский алфавитХирагана (японское письмо)Катакана (японское письмо)Катакана, фонетическое расширениеКорейский алфавитКорейское слоговое письмоХангул джамо (корейские буквы)Корейское совместимое письмоСлоговое письмо ицзу (и)Слоговое письмо ицзу (и)Корни письма ицзу (и)Центрально-азиатские рукописные шрифтыКхароштхиMонгольское письмоПагспаТибетское письмоДругие рукописные шрифтыФонетический алфавит Шовиан (Бернард Шоу)Cтаринные рукописные шрифтыДревнегреческийСтароитальянские числаДревнегреческая музыкальная нотацияКлинописьКлинописьКлинообразные цифры и знаки препинанияУгаритская клинописьЛинейный bЛинейная слоговая азбука БЛинейные идеограммы БДругие старинные рукописные шрифтыЭгейские числаДревние символыКарийскoе письмоСчетные палочкиКиприотская слоговая азбукаГлаголическое письмоГотическое письмоЛицианЛидийское письмоОгамическое письмо (древнеирландское)Староитальянскoе письмоФестский дискФиникийское письмоРуническое письмоПунктуацияЗнаки пунктуацииЗнаки пунктуацииДополнительнaя пунктуацияИдеографические символы и знаки препинанияИдеографические символы и знаки препинанияДекоративные дальневосточные формыВертикальные формыЗакрытые и квадратныеБуквы и цифры в кружочкахДальневосточные буквы и месяцы в кружочкахДальневосточные совместимые символыДиакритические знакиДиакритические знакиОбъединённые диакритические знаки для символовОбъединённые диакритические знаки – дополнениeДиакритические знаки половинной шириныФонетические символыФонетические знакиФонетические расширенияФонетические расширения – дополнениeКатакана, фонетическое расширениесимволы для тоновСимволы изменения пробелаMатематические символыЧисла и цифрыЧисловые формыВерхние и нижние индексыБуквоподобные символыБуквоподобные символыМатематические буквенно-цифровые символыCтрелки и операторыСтрелкиДополнительные стрелки-АДополнительные стрелки-БМатематические операторыМатематические операторыДополнительные математические операторыРазличные математические символы-АРазличные математические символы-БГеометрические символыГеометрические фигурыЧасти рамок (бывшая псевдографика)Заполняющие знакиTехнические символыЗначки управляющих кодовРазличные технические знакиЗначки оптического распознавания символовCимволыРазличные символыШрифт БрайляСимволы графической разметки текстаРазличные символыРазличные символы и стрелкиТай Ксуан ДжингСимволы гексограмм И-Цзина (Китай)Mузыкальные нотыДревнегреческая музыкальная нотацияВизантийские музыкальные символыМузыкальные символыДенежные символыИгровые символыМаджонг плиткиДомино плиткиЛичное пользованиеСпециальные символыМеткиСелекторы варианта начертаниРазличные дополнительные модификаторы
Oсобенные глифы ЛюбыеУдарения (частичные)Ударения (полные)ЕвроCмайликиСимволы игральных картMузыка
Tип шрифта ЛюбойTrueTypeOpenTypePostScript Type 1
Лицензия ЛюбаяGNU/GPLБесплатнаяДля личного пользованияБесплатная с возможностью пожертвованияУсловно бесплатнаяДемоНеизвестная
Поддерживаемая платформа Юникод Macintosh Microsoft
Cтиль шрифта ЛюбойHегативPегулярныйЖирныйЗачеркнутыйКосойКурсивныйОбьведенныйПодчеркнутый
Насыщенность шрифта ЛюбаяУльтра-светлыйЭкстра-светлыйСветлыйПолу-светлыйСредний (нормалный)Полу-жирныйЖирныйЭкстра-жирныйУльтра-жирный
Ширина шрифта ЛюбаяУльтра-сжатыйЭкстра-сжатыйСжатыйСредне-сжатыйСредний (нормальный)Полу-розширенныйРозширенныйЭкстра-розширенныйУльтра-розширенный
Классификация шрифта ЛюбойНе квалифицированныйЗасечки в старом стилеТрадиционные засечкиСовременные засечкиПолужирные засечкиБрусковые засечкиЗарезервированныйСвободные засечкиБез засечекОрнаментальныеРукописныеСимвольные
- Ударения (частичные)
- Ударения (полные)
- Евро
Sacramento-Regular.
ttf
Загрузить @font-face
- Ударения (частичные)
Intro Inline.otf
Загрузить @font-face
- Евро
OneDirection.ttf
Загрузить @font-face
- Ударения (частичные)
- Ударения (полные)
- Евро
Parisienne-Regular.ttf
Загрузить @font-face
- Ударения (частичные)
- Ударения (полные)
- Евро
OpenSans-Bold.ttf
Загрузить @font-face
- Ударения (частичные)
- Ударения (полные)
- Евро
OpenSans-Light.ttf
Загрузить @font-face
- Ударения (частичные)
- Ударения (полные)
- Евро
OpenSans-Regular.ttf
Загрузить @font-face
The Avengers.otf
Загрузить @font-face
- Евро
LONDO___.
TTF
Загрузить @font-face
- Cмайлики
- Символы игральных карт
1 Minecraft-Regular.otf
Загрузить @font-face
- 1-10 – 126669 pезультаты
- следующая
MNIST, Янн ЛеКун, Коринна Кортес и Крис Берджес База данных
MNIST рукописных цифр, Янн ЛеКун, Коринна Кортес и Крис Берджес
Это хорошая база данных для людей, которые хотят попробовать методы обучения и методы распознавания образов на реальных данных с минимальными затратами усилия по предварительной обработке и форматированию.
На сайте доступны четыре файла:
train-images-idx3-ubyte.gz:
изображения обучающей выборки (9912422 байта)
train-labels-idx1-ubyte.gz:
Метки обучающего набора (28881 байт)
t10k-images-idx3-ubyte.gz:
изображения тестового набора (1648877 байт)
t10k-labels-idx1-ubyte.gz:
метки набора тестов (4542 байта)
обратите внимание, что ваш браузер может распаковать эти файлы, не сообщая вам .
Если загруженные вами файлы имеют больший размер, чем указано выше, они были
несжатый вашим браузером. Просто переименуйте их, чтобы удалить расширение .gz.
Некоторые люди спрашивали меня: «Мое приложение не может открыть ваши файлы изображений».
Эти файлы не имеют стандартного формата изображений. Вы должны написать
ваша собственная (очень простая) программа для их чтения.
Формат файла описан
внизу этой страницы.
Исходные черно-белые (двухуровневые) изображения из NIST были нормализованы по размеру. чтобы поместиться в поле размером 20×20 пикселей с сохранением соотношения сторон. Результирующий изображения содержат уровни серого из-за используемой техники сглаживания по алгоритму нормализации. изображения были центрированы в изображении 28×28 путем вычисления центра масс пикселей и перевода изображения чтобы расположить эту точку в центре поля 28×28.
При использовании некоторых методов классификации (в частности, методов на основе шаблонов, таких как SVM и K-ближайшие соседи), частота ошибок улучшается, когда цифры центрируются ограничивающей рамкой, а не центром масс. если ты делать такого рода предварительную обработку, вы должны сообщить об этом в своем публикации.
База данных MNIST была создана на основе специальной базы данных NIST 3 и
Специальная база данных 1, содержащая бинарные изображения рукописных цифр. НИСТ
изначально обозначал SD-3 в качестве своего тренировочного набора, а SD-1 – в качестве тестового.
установлен. Однако SD-3 намного чище и легче распознается, чем SD-1.
причину этого можно найти в том, что СД-3 собирали среди
Сотрудники бюро переписи населения, а СД-1 — среди старшеклассников.
Чтобы сделать разумные выводы из обучающих экспериментов, необходимо, чтобы
результат не зависит от выбора обучающей выборки и теста среди
полный комплект образцов. Поэтому необходимо было создать новую базу данных.
путем смешивания наборов данных NIST.
Учебный набор MNIST состоит из 30 000 паттернов из SD-3 и 30 000 шаблонов от SD-1. Наш тестовый набор состоял из 5000 паттернов. из SD-3 и 5000 шаблонов из SD-1. Тренировочный набор из 60 000 шаблонов содержит примеры примерно 250 писателей. Мы убедились, что наборы авторов обучающего набора и тестового набора не пересекались.
SD-1 содержит 58 527 цифровых изображений, написанных 500 разными авторами.
В отличие от SD-3, где блоки данных от каждого записывающего устройства появлялись в
последовательности, данные в SD-1 зашифрованы.
Идентификационные данные писателя для SD-1
доступны, и мы использовали эту информацию, чтобы расшифровать писателей. Мы тогда
разделить SD-1 на две части: персонажи, написанные первыми 250 писателями, вошли в
наш новый тренировочный набор. Остальные 250 писателей были включены в наш тест.
установлен. Таким образом, у нас было два набора почти по 30 000 примеров в каждом. Новый тренинг
набор был дополнен достаточным количеством примеров из SD-3, начиная с шаблона #
0, чтобы составить полный набор из 60 000 тренировочных шаблонов. Точно так же новый тест
набор был дополнен образцами SD-3, начиная с шаблона № 35 000, чтобы сделать
полный набор из 60 000 тестовых шаблонов. Только часть из 10 000 тестовых изображений
(5000 из SD-1 и 5000 из SD-3) доступны на этом сайте. Полный
Доступен обучающий набор из 60 000 образцов.
Многие методы были протестированы с этим обучающим набором и тестовым набором. Здесь
несколько примеров. Подробности о методах приведены в следующем
бумага. В некоторых из этих экспериментов использовалась версия базы данных, в которой
входные изображения, где устранены перекосы (путем вычисления главной оси формы
которая находится ближе всего к вертикали, и сдвигая линии так, чтобы она
вертикально).
В некоторых других экспериментах обучающая выборка была дополнена
искусственно искаженные версии исходных обучающих выборок. Искажения
представляют собой случайные комбинации сдвигов, масштабирования, перекоса и сжатия.
| КЛАССИФИКАТОР | ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА | ЧАСТОТА ОШИБОК ТЕСТА (%) | Справочник |
| Линейные классификаторы | |||
| линейный классификатор (1-слойный NN) | нет | 12,0 | ЛеКун и др. 1998 |
| линейный классификатор (1-слойный NN) | устранение перекоса | 8,4 | ЛеКун и др. 1998 |
| попарно-линейный классификатор | устранение перекоса | 7,6 | ЛеКун и др. 1998 |
| K-ближайшие соседи | |||
| K-ближайшие соседи, Евклидово (L2) | нет | 5,0 | ЛеКун и др. 1998 |
| K ближайших соседей, Евклидова (L2) | нет | 3,09 | Кеннет Уайлдер, У. Чикаго |
| K-ближайшие соседи, L3 | нет | 2,83 | Кеннет Уайлдер, У. Чикаго |
| K-ближайшие соседи, Евклидово (L2) | устранение перекоса | 2,4 | ЛеКун и др. 1998 |
| K ближайших соседей, Евклидова (L2) | устранение перекосов, удаление шума, размытие | 1,80 | Кеннет Уайлдер, У. Чикаго |
| K-ближайшие соседи, L3 | устранение перекосов, удаление шума, размытие | 1,73 | Кеннет Уайлдер, У. Чикаго |
| K-ближайшие соседи, L3 | выравнивание, удаление шума, размытие, сдвиг на 1 пиксель | 1,33 | Кеннет Уайлдер, У. Чикаго |
| K-ближайшие соседи, L3 | выравнивание, удаление шума, размытие, сдвиг на 2 пикселя | 1,22 | Kenneth Wilder, U. Chicago |
| K-NN с нелинейной деформацией (IDM) | смещаемые кромки | 0,54 | Кейзерс и др. IEEE PAMI 2007 |
| K-NN с нелинейной деформацией (P2DHMDM) | смещаемые кромки | 0,52 | Кейзерс и др. IEEE PAMI 2007 |
| K-NN, касательное расстояние | субдискретизация до 16×16 пикселей | 1,1 | ЛеКун и др. 1998 |
| K-NN, сопоставление контекста формы | извлечение признаков контекста формы | 0,63 | Белонги и др. IEEE PAMI 2002 |
| Усиленные культи | |||
| Усиленные культи | нет | 7,7 | Kegl et al., ICML 2009 |
| изделия из усиленных культей (3 термина) | нет | 1,26 | Kegl et al. , ICML 2009 |
| усиленные деревья (17 листьев) | нет | 1,53 | Кегл и др., ICML 2009 |
| пни на чертах Хаара | Характеристики Хаара | 1,02 | Kegl et al., ICML 2009 |
| продукт пней на Haar f. | Характеристики Хаара | 0,87 | Kegl et al., ICML 2009 |
| Нелинейные классификаторы | |||
| 40 PCA + квадратичный классификатор | нет | 3,3 | ЛеКун и др. 1998 |
| 1000 РБФ + линейный классификатор | нет | 3,6 | ЛеКун и др. 1998 |
| SVM | |||
| SVM, ядро Гаусса | нет | 1,4 | |
| SVM степени 4 полинома | устранение перекоса | 1,1 | ЛеКун и др. 1998 |
| Сокращенный полином SVM степени 5 | устранение перекоса | 1,0 | ЛеКун и др. 1998 |
| Виртуальный SVM deg-9 poly [искажения] | нет | 0,8 | ЛеКун и др. 1998 |
| Виртуальный SVM, deg-9 poly, 1 пиксель с дрожанием | нет | 0,68 | DeCoste and Scholkopf, MLJ 2002 |
| Virtual SVM, deg-9 poly, 1 пиксель с дрожанием | устранение перекоса | 0,68 | DeCoste and Scholkopf, MLJ 2002 |
| Virtual SVM, deg-9 poly, 2-пиксельное дрожание | устранение перекоса | 0,56 | DeCoste and Scholkopf, MLJ 2002 |
| Нейронные сети | |||
| 2-слойная нейронная сеть, 300 скрытых единиц, среднеквадратическая ошибка | нет | 4,7 | ЛеКун и др. 1998 |
| 2-х слойный NN, 300 HU, MSE, [искажения] | нет | 3,6 | ЛеКун и др. 1998 |
| 2-слойный NN, 300 HU | устранение перекоса | 1,6 | ЛеКун и др. 1998 |
| 2-слойный NN, 1000 скрытых блоков | нет | 4,5 | ЛеКун и др. 1998 |
| 2-х слойный NN, 1000 HU, [перекосы] | нет | 3,8 | ЛеКун и др. 1998 |
| 3-слойный NN, 300+100 скрытых блоков | нет | 3,05 | ЛеКун и др. 1998 |
| 3-х слойный NN, 300+100 HU [перекосы] | нет | 2,5 | ЛеКун и др. 1998 |
| 3-слойный NN, 500+150 скрытых блоков | нет | 2,95 | ЛеКун и др. 1998 |
| 3-х слойный NN, 500+150 HU [перекосы] | нет | 2,45 | ЛеКун и др. 1998 |
| 3-слойный NN, 500+300 HU, softmax, кросс-энтропия, уменьшение веса | нет | 1,53 | Хинтон, неопубликовано, 2005 г. |
| 2-слойный NN, 800 HU, кросс-энтропийные потери | нет | 1,6 | Simard et al., ICDAR 2003 |
| 2-слойная нейронная сеть, 800 HU, кросс-энтропия [аффинные искажения] | нет | 1,1 | Simard et al., ICDAR 2003 |
| 2-слойный NN, 800 HU, MSE [упругие искажения] | нет | 0,9 | Simard et al., ICDAR 2003 |
| 2-слойный NN, 800 HU, кросс-энтропия [упругие искажения] | нет | 0,7 | Simard et al., ICDAR 2003 |
| NN, 784-500-500-2000-30 + ближайший сосед, RBM + обучение NCA [без искажений] | нет | 1,0 | Салахутдинов и Хинтон, AI-Stats 2007 |
| 6-слойный NN 784-2500-2000-1500-1000-500-10 (на GPU) [упругие искажения] | нет | 0,35 | Чиресан и др. Нейронные вычисления 10, 2010 г. и arXiv 1003.0358, 2010 г. |
| комитет 25 НН 784-800-10 [упругие перекосы] | нормализация ширины, наклон | 0,39 | Мейер и др. ICDAR 2011 |
| глубокая выпуклая сетка, предварительная тренировка без опор [без искажений] | нет | 0,83 | Денг и др. Интерреч 2010 |
| Сверточные сети | |||
| Сверточная сеть Ленет-1 | субдискретизация до 16×16 пикселей | 1,7 | ЛеКун и др. 1998 |
| Сверточная сеть Ленет-4 | нет | 1,1 | ЛеКун и др. 1998 |
| Сверточная сеть ЛеНэт-4 с К-НН вместо последнего слоя | нет | 1,1 | ЛеКун и др. 1998 |
| Сверточная сеть LeNet-4 с локальным обучением вместо последнего слоя | нет | 1,1 | ЛеКун и др. 1998 |
| Сверточная сеть ЛеНэт-5, [без искажений] | нет | 0,95 | ЛеКун и др. 1998 |
| Сверточная сеть ЛеНэт-5, [огромные искажения] | нет | 0,85 | ЛеКун и др. 1998 |
| Сверточная сеть ЛеНэт-5, [искажения] | нет | 0,8 | ЛеКун и др. 1998 |
| Сверточная сеть Boosted LeNet-4, [искажения] | нет | 0,7 | ЛеКун и др. 1998 |
| Извлекатель обучаемых признаков + SVM [без искажений] | нет | 0,83 | Лауэр и др., Распознавание образов 40-6, 2007 г. |
| Извлекатель обучаемых признаков + SVM [упругие искажения] | нет | 0,56 | Лауэр и др., Распознавание образов 40-6, 2007 г. |
| Извлекатель обучаемых признаков + SVM [аффинные искажения] | нет | 0,54 | Лауэр и др. , Распознавание образов 40-6, 2007 |
| неконтролируемые разреженные признаки + SVM, [без искажений] | нет | 0,59 | Labusch et al., IEEE TNN 2008 |
| Сверточная сеть, кросс-энтропия [аффинные искажения] | нет | 0,6 | Simard et al., ICDAR 2003 |
| Сверточная сеть, кросс-энтропия [упругие искажения] | нет | 0,4 | Simard et al., ICDAR 2003 |
| большой конв. нетто, случайные черты [без искажений] | нет | 0,89 | Ranzato et al., CVPR 2007 |
| крупный конв. сеть, функции unsup [без искажений] | нет | 0,62 | Ranzato et al., CVPR 2007 |
| крупный конв. нетто, unsup pretraining [без искажений] | нет | 0,60 | Ranzato et al. , NIPS 2006 |
| крупные конв. сетка, предварительная тренировка unsup [упругие искажения] | нет | 0,39 | Ranzato et al., NIPS 2006 |
| крупные конв. нетто, unsup pretraining [без искажений] | нет | 0,53 | Jarrett et al., ICCV 2009 |
| большая/глубокая конв. сетка, 1-20-40-60-80-100-120-120-10 [упругие перекосы] | нет | 0,35 | Чиресан и др. IJCAI 2011 |
| комитет из 7 съездов сетка, 1-20-П-40-П-150-10 [упругие перекосы] | нормализация ширины | 0,27 +-0,02 | Чиресан и др. ICDAR 2011 |
| комитет из 35 конв. сетка, 1-20-П-40-П-150-10 [упругие перекосы] | нормализация ширины | 0,23 | Чиресан и др. CVPR 2012 |
Ссылки
- [LeCun et al.
, 1998a] - Y. LeCun, L. Bottou, Ю. Бенжио и П. Хаффнер. «Градиентное обучение применяется для распознавания документов». Протоколы IEEE , 86(11):2278-2324, ноябрь 1998 г. [онлайн-версия]
, 1998a]ФОРМАТЫ ФАЙЛОВ ДЛЯ БАЗЫ ДАННЫХ MNIST
Данные хранятся в очень простом формате файла, предназначенном для хранения векторов. и многомерные матрицы. Общая информация об этом формате приведена на конец этой страницы, но вам не нужно читать это, чтобы использовать файлы данных.Все целые числа в файлах сначала сохраняются в старших разрядах (старший разряд) формат, используемый большинством процессоров сторонних производителей. Пользователи процессоров Intel и другие машины с низким порядком байтов должны переворачивать байты заголовка.
Есть 4 файла:
train-images-idx3-ubyte: изображения обучающего набора
train-labels-idx1-ubyte: метки обучающего набора
t10k-images-idx3-ubyte: тестовый набор изображений
t10k-labels-idx1-ubyte: ярлыки тестового набора
Обучающий набор содержит 60 000 примеров, а тестовый набор — 10 000 примеров.
Первые 5000 примеров тестового набора взяты из исходного Учебный набор NIST. Последние 5000 взяты из оригинального теста NIST. установлен. Первые 5000 чище и проще, чем последние 5000.
ФАЙЛ ОБУЧАЮЩЕГО НАБОРА (train-labels-idx1-ubyte):
[смещение] [тип] [значение] [описание]0000 32-битное целое число 0x00000801(2049) магическое число (сначала MSB)
0004 32-битное целое число 60000 Количество предметов
0008 байт без знака ?? этикетка
0009 байт без знака ?? этикетка
……..
xxxx байт без знака ?? этикетка
Значения меток от 0 до 9.
ФАЙЛ ИЗОБРАЖЕНИЯ ТРЕНИРОВОЧНОГО КОМПЛЕКТА (train-images-idx3-ubyte):
[смещение] [тип] [значение] [описание]0000 32-битное целое число 0x00000803(2051) магическое число
0004 32-битное целое число 60000 количество изображений
0008 32-битное целое число 28 количество рядов
0012 32-битное целое число 28 Число столбцов
0016 байт без знака ?? пиксель
0017 байт без знака ?? пиксель
.
……. xxxx байт без знака ?? пиксель
пикселей организованы построчно. Значения пикселей от 0 до 255. 0 означает фон (белый), 255 означает передний план (черный).
ФАЙЛ ЭТИКЕТКИ НАБОРА ТЕСТОВ (t10k-labels-idx1-ubyte):
[смещение] [тип] [значение] [описание]0000 32-битное целое число 0x00000801(2049) магическое число (сначала MSB)
0004 32-битное целое число 10000 Количество предметов
0008 байт без знака ?? этикетка
0009 байт без знака ?? этикетка
……..
xxxx байт без знака ?? этикетка
Значения меток от 0 до 9.
ФАЙЛ ИЗОБРАЖЕНИЯ НАБОРА ТЕСТОВ (t10k-images-idx3-ubyte):
[смещение] [тип] [значение] [описание]0000 32-битное целое число 0x00000803(2051) магическое число
0004 32-битное целое число 10000 количество изображений
0008 32-битное целое число 28 количество рядов
0012 32-битное целое число 28 Число столбцов
0016 байт без знака ?? пиксель
0017 байт без знака ?? пиксель
.
……. xxxx байт без знака ?? пиксель
пикселей организованы построчно. Значения пикселей от 0 до 255. 0 означает фон
(белый), 255 означает передний план (черный).
ФОРМАТ ФАЙЛА IDX
формат файла IDX — это простой формат для векторов и многомерных изображений. матрицы различных числовых типов.Основной формат
магическое число
размер в измерении 0
Размер
в размерности 1
Размер
в размере 2
…..
размер в размере N
данные
Магическое число представляет собой целое число (сначала старший бит). Первые 2 байта всегда 0.
Третий байт кодирует тип данных:
0x08: беззнаковый байт
0x09: байт со знаком
0x0B: короткий (2 байта)
0x0C: целое (4 байта)
0x0D: число с плавающей запятой (4 байта)
0x0E: двойной (8 байт)
4-й байт кодирует количество измерений вектора/матрицы: 1 для векторов, 2 для матриц….
Размеры в каждом измерении представляют собой 4-байтовые целые числа (сначала старший бит, старший разряд,
как и в большинстве процессоров не Intel).
Данные хранятся как в массиве C, т.е. индекс в последнем измерении
меняется быстрее всего.
Удачного взлома.
Цифровые изображения в наборе MNIST были первоначально выбраны и экспериментировали Крис Берджес и Коринна Кортес, используя нормализация ограничивающей рамки и центрирование. Версия Яна Лекуна, которая на этой странице используется центрирование по центру масс внутри окно большего размера.
Ян ЛеКун, профессор
Институт математических наук Куранта
Нью-Йоркский университет
Коринна Кортес, научный сотрудник
Google Labs, New York
corinna at google dot com
Часть 5. Обучение сети чтению рукописных цифр | by Tobias Hill
В этой заключительной статье мы увидим, на что способна эта реализация нейронной сети. Мы бросим на него один из самых распространенных наборов данных (MNIST) и посмотрим, сможем ли мы обучить нейронную сеть распознавать рукописные цифры.
Это пятая и последняя часть из серии статей:
- Часть 1: Основание.
- Часть 2. Градиентный спуск и обратное распространение.
- Часть 3. Реализация на Java.
- Часть 4: Лучше, быстрее, сильнее.
- Часть 5. Обучение сети чтению рукописных цифр.
- Extra 1: Как я увеличил точность на 1% за счет увеличения данных.
- Экстра 2: Детская площадка MNIST.
База данных MNIST содержит рукописные цифры и имеет обучающий набор из 60 000 образцов и тестовый набор из 10 000 образцов. Цифры располагаются по центру изображения фиксированного размера 28×28 пикселей.
Этот набор данных очень удобен для всех, кто просто хочет изучить свою реализацию машинного обучения. Требует минимальных усилий по предварительной обработке и форматированию.
Весь код этого маленького эксперимента доступен здесь. Этот проект, конечно же, также зависит от реализации нейронной сети.
Чтение наборов данных в Java очень просто.
Формат данных описан на страницах MNIST.
Каждая цифра в классе DigitData. Этот класс, конечно, содержит данные (т. е. ввод) и метку (т. е. ожидание). Я также добавил небольшую хитрость для улучшения toString() класса DigitData:
Вызов toString() на самом деле дает вывод данных в кодировке ascii:
Это удобно при проверке того, какие цифры сеть путает с другими цифрами. Мы вернемся к этому в конце этой статьи.
Граничные слои задаются нашими данными:
- Входной слой принимает каждый пиксель изображения в качестве входных данных и должен иметь размер 28 x 28 = 784.
- Выходной слой представляет собой классификацию. Цифра от 0 до 9, т.е. размер 10.
Скрытые слои требуют дальнейшего изучения и тестирования. Я попробовал несколько разных макетов сети и понял, что получить хорошую точность с чудовищной сетью не так уж и сложно. Как следствие, я решил снизить количество скрытых нейронов, просто чтобы посмотреть, смогу ли я получить приличные результаты.
Я полагаю, что установка с ограничениями могла бы научить больше тому, как получить дополнительный процент точности. Я решил установить максимальное количество скрытых нейронов на 50 и начал исследовать, чего я могу достичь.
Сначала у меня был неплохой результат с воронкообразной структурой только с двумя скрытыми слоями, и я продолжал исследовать это. Например, первый с 36, а второй с 14 нейронами.
784 входных ⇒ 36 скрытых ⇒ 14 скрытых ⇒ 10 выходных нейронов
После некоторых проб и ошибок я решил использовать две функции активации, которые не были представлены в предыдущих статьях этой серии. Leaky ReLU и Softmax .
Leaky ReLU — это вариант ReLU. Единственное отличие состоит в том, что он не полностью плоский для отрицательных входов. Вместо этого он имеет небольшой положительный градиент.
Первоначально они были разработаны для решения проблемы, связанной с тем, что часть ReLU с нулевым градиентом может отключать нейроны.
Также см. этот вопрос на Quora, чтобы узнать, когда и почему вы можете захотеть протестировать Leaky ReLU вместо ReLU.
Softmax — это функция активации, которую вы обычно используете в выходном слое при классификации. Хорошая вещь с softmax заключается в том, что она дает вам категориальное распределение вероятностей — Он покажет вам вероятность для каждого класса в выходном слое. Итак, предположим, что мы отправили цифровые данные, представляющие цифру 7, через сеть, она может вывести что-то вроде:
Как вы можете видеть, вероятность наибольшая для цифры 7. Также обратите внимание, что сумма вероятностей равна 1.
Softmax также может конечно, использовать с порогом, так что, если ни один из классов не получит вероятность выше этого порога, мы можем сказать, что сеть ничего не распознала во входных данных.
Плохая сторона Softmax заключается в том, что она не так проста, как другие функции активации. Это становится немного уродливее как в прямом, так и в обратном проходе.
Это фактически сломало мою абстракцию активации, где я до появления softmax мог определить активацию только как саму функцию для прямого прохода, fn(), и производный шаг этой функции для обратного распространения, dFn().
Причина, по которой Softmax сделала это, заключается в том, что ее dFn() ( ∂ o/∂i ) может использовать последний фактор из цепного правила, ∂ C/∂o , , чтобы сделать расчеты более понятными/упрощенными. Следовательно, абстракцию активации пришлось расширить, чтобы иметь дело с вычислением произведения ∂C/∂i .
Во всех других функциях активации это просто умножение:
Но в softmax это выглядит так (см. функцию dCdI() ниже):
Подробнее о Softmax в целом читайте здесь и о том, как рассчитывается производная от Softmax здесь .
Обычно моя установка:
Итак, приступим к обучению!
Цикл обучения прост.
- Я перемешиваю обучающие данные перед каждой эпохой ( Эпоха — это то, что мы называем полным циклом обучения всех доступных обучающих данных , в нашем случае 60 000 цифр) и передаю их через сеть с установленным флагом обучения true .
- После каждой 5-й эпохи я также запускаю тестовые данные через сеть и регистрирую результаты, но не обучаю сеть при этом.
Код выглядит следующим образом:
И прогон всего набора данных выполняется партиями и параллельно (как уже было показано в прошлой статье):
Единственная недостающая часть цикла выше — это знать, когда остановиться …
Как упоминалось ранее (при введении регуляризации L2), мы действительно хотим избежать переобучения сети. Когда это происходит, точность обучающих данных может повышаться, а точность тестовых данных начинает снижаться. Мы отслеживаем это с помощью StopEvaluator. Этот служебный класс сохраняет скользящее среднее частоты ошибок тестовых данных, чтобы определить, когда она окончательно начала снижаться. В нем также хранится информация о том, как выглядела сеть при лучшем тестовом прогоне (попытка найти пик этого тестового прогона).
Код выглядит следующим образом:
При схеме сети, показанной выше (50 скрытых нейронов, Нестеров и L2 настроены так же, как указано выше), я постоянно обучаю сеть до частоты ошибок около 2,5% .
В рекордном прогоне частота ошибок составляла всего 2,24%, но я не думаю, что это имеет значение, если только большинство моих прогонов не будут примерно такими же. Причина в том, что перенастройка гиперпараметров взад и вперед, попытка побить рекорд на тестовых данных (хотя это и весело) также может означать, что мы переоснащаем к тестовым данным . Другими словами: я, возможно, нашел удачное сочетание параметров, которое работает очень хорошо, но все же не так хорошо на невидимых данных.
Итак, давайте взглянем на несколько цифр, которые сеть обычно путает:
Это всего лишь несколько примеров. Также доступны несколько других бордюров. Вполне логично, что сети довольно трудно классифицировать их, и причина связана с тем, что мы обсуждали в заключительном разделе первой части этой серии: некоторые из этих точек в пространстве 784D просто слишком далеко от своих. группа цифр и, возможно, ближе к какой-либо другой группе точек/цифр. Или на естественном языке: они больше похожи на какую-то другую цифру, чем на ту, которую они должны представлять.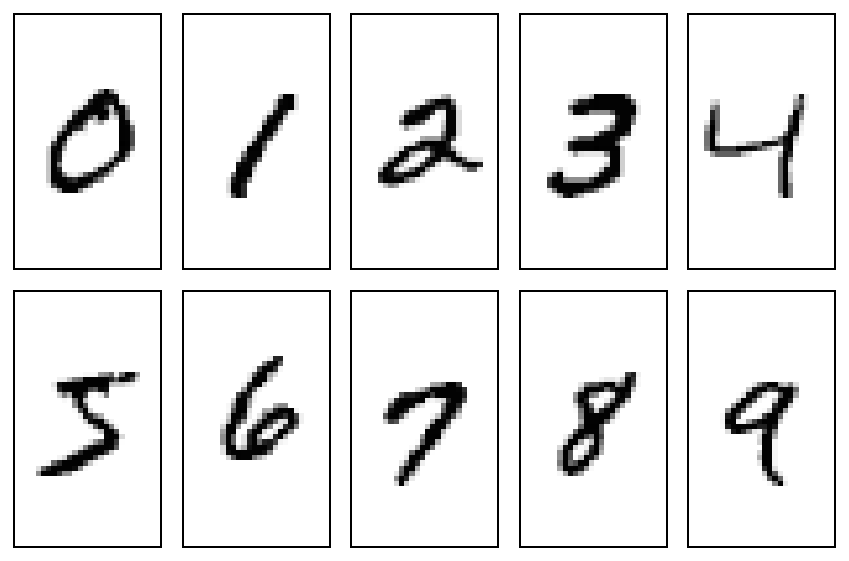
Это не значит, что мы не заботимся об этих тяжелых случаях. Наоборот. Мир — поистине неоднозначное место, и машинное обучение должно уметь справляться с двусмысленностью и нюансами. Вы знаете, чтобы быть менее похожим на машину («Утвердительно») и более человечным («Нет проблем»). Но я думаю, что это указывает на то, что решение не всегда находится в имеющихся данных. Довольно часто контекст дает подсказки, необходимые человеку для правильной классификации (или понимания) чего-либо… например, плохо написанной цифры. Но это другая большая и увлекательная тема, выходящая за рамки данного введения.
Это была пятая и последняя часть этой серии. Я многому научился, когда писал это, и я надеюсь, что вы узнали что-то, читая это.
Отзывы приветствуются!
Это ресурсы, которые я считаю лучше, чем большинство других. Пожалуйста, погрузитесь, если вы хотите немного глубже понять:
- 3 Blue 1 Browns фантастические видео о нейронных сетях (4 эпизода)
- блестящий учебник Майкла Нильсенса (несколько глав)
- Стэнфордский курс CS231n.
