Решить задачу 2 класс: Логические задачи для 2 класса с ответами по математике, задания для детей 8-9 лет – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Быстро решаем задачи по математике. 2 класс (Елена Нефёдова, Ольга Узорова)

164 ₽

119 ₽

+ до 24 баллов

Бонусная программа

Итоговая сумма бонусов может отличаться от указанной, если к заказу будут применены скидки.

Купить

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

Осталось мало

В наличии в 190 магазинах. Смотреть на карте

Пособие “Учимся решать задачи по математике. 2 класс” разработано известными педагогами-практиками О. В. Узоровой и Е. А. Нефёдовой, авторами более 500 учебных пособий для начальной школы. Занимаясь по этой книге, ребёнок научится решать простые и составные задачи всех типов, делать по ним краткие записи, выполнять чертежи и рисовать схемы, правильно оформлять решение. .Для начального образования. .

Описание

Характеристики

АСТ

На товар пока нет отзывов

Поделитесь своим мнением раньше всех

Как получить бонусы за отзыв о товаре

Сделайте заказ в интернет-магазине

Напишите развёрнутый отзыв от 300 символов только на то, что вы купили

Дождитесь, пока отзыв опубликуют.

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Книга «Быстро решаем задачи по математике. 2 класс» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене. Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом другом регионе России, вы можете оформить заказ на книгу Елена Нефёдова, Ольга Узорова «Быстро решаем задачи по математике. 2 класс» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.

Решение задач. Закрепление 2 класс

Решение задач. Закрепление

2 класс

ГОУ ЛНР « Артемовская средняя

школа № 8»

Классный руководитель:

Елена Анатольевна Чевокина

2 класс

30 марта Классная работа

Минутка каллиграфии

Разминка для ума Вставь нужные числа НАПРИМЕР:

Тема урока : Решение задач. Закрепление

Цель: закрепить умение решать задачи на нахождение неизвестного третьего слагаемого; навыки устного счета; развивать

логическое мышление и внимание

Работаем по учебнику

с. 77. Упр.10

(задание

на полях учебника)

Задача 3 с.77

— Прочитай задачу. Найди главные слова для краткой записи. (Заготовила, выпито, осталось)

— Как ты понимаешь первое предложение в задаче: «Семья заготовила 10 двухлитровых банок яблочного сока»? (В одну банку входит 2 л , и таких банок всего было 10)

— Запиши в тетради условие задачи кратко.

Заготовили — ?, 10 б. по 2 л

Выпили — ?

Осталось — 2 л

— Можем ли мы сразу ответить на вопрос задачи? ( Да или нет. )

— Почему не можем? (Неизвестно, сколько всего литров сока заготовили)

— Каким действием это можно узнать? (Умножением)

— Делай запись в тетради: Решение:

— Выполни умножение и поясни, что узнали:

1)2·10 = 20 (л)

заготовили;

— Что узнаем вторым действием? (Сколько литров сока выпили)

2)20 – 2 = 18 (л)

Ответ: 18 литров сока выпито за зиму.

Задача 4 с.77

5 кг

4кг

13 кг

13 – 5=

Найди, запиши несколько

правильных способов решения.

5 + 4=

13 – 4 – 5=

13 – (5 + 4)=

Решай задачу, работай самостоятельно по своему составленному плану

План

1. Подумать и понять смысл задачи

2. Заполнить схему

3. Записать решения разными способами

4. Записать ответ

5. Найти способ проверки решения задачи

6. Самопроверка

У тебя получилось! Ты молодец!

Работай самостоятельно по учебнику

Упр. 1 (с. 77) Устное выполнение

Упр. 2 (с. 77) Ученики решают задание с комментарием вслух, с подробным объяснением действий

Хочешь отдохнуть? Давай повеселимся, как мартышки!

Физкультминутка

Мы веселые мартышки,

Мы играем громко слишком.

Все ногами топаем,

Все руками хлопаем,

Надуваем щечки.

Скачем на носочках.

Дружно прыгнем к потолку,

Пальчик поднесем к носку.

И друг другу даже

Язычки покажем.

Шире рот откроем,

Гримасы все состроим.

Как скажу я слово «три»,

Все с гримасами замри.

Раз, два, три!

Я знаю. У тебя всё получится! Продолжение работы по учебнику Упр. 5 (с. 77) — Прочитай задание. — Какими действиями можно записать решение? (Сложением, умножением.) — А какой способ рациональнее? Почему решение способом умножения удобнее? — Выполни задание письменно. Решение запиши умножением. Набери одинаковыми монетами:

15 руб ; 8 руб ; 10 руб Упр. 7 (с. 77) Самостоятельное выполнение Упр. 8 (с. 77) Самостоятельное выполнение Дополнительно выполни на уроке: Задание под чертой. «Проверь себя» (с. 77) Самостоятельное выполнение

Давай отдохнем! Разгадай РЕБУС

Разгадка РЕБУСА:

Миш -ка / РУКА

№ 1 2 3 4

ура

БУКВА №: 2, 1, 4

ОТВЕТ:

Мишура

Как ты усвоил(а) урок? Твой ответ:

Подведение итогов урока:

Оцени сам(а) свою работу на уроке от 1 до 5 баллов.

Ответь на вопросы:

— Чем мы занимались на уроке?

— Тебе понравился урок?

— Что тебе было интересно?

— Все тебе было понятно на сегодняшнем уроке?

— Где можно применить полученные знания?

Домашнее задание:

1. Учебник. Упр. 9 (с. 77).

2. Тетрадь с печатной основой: с. 78. Упр.1,2

3. Выполни домашнее задание.

Ты умница!

СПАСИБО ЗА ВНИМАНИЕ!

УРОК ОКОНЧЕН!

словесных задач: пропорции

Горячая математика

А соотношение это сравнение двух чисел. Можно написать через двоеточие ( 1 : 5 ) , или используя слово “к” ( 1 к 5 ) , или как дробь: 1 5

Пример 1:

Во дворе есть пруд 12 солнечная рыба и 30 светящиеся радуги.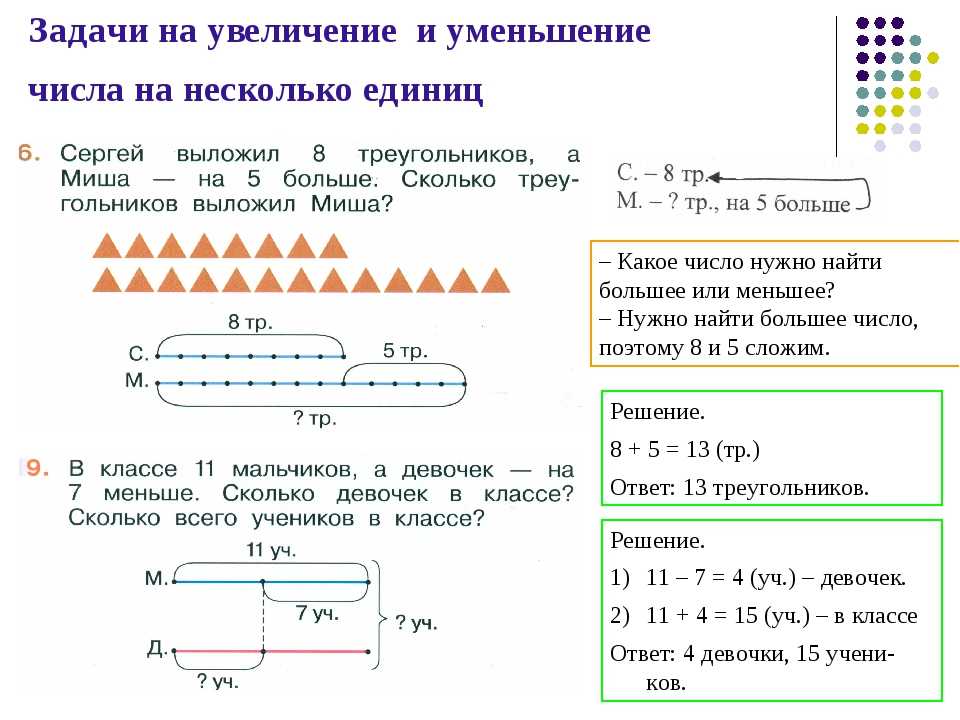

Напишите соотношение солнечников и радужных светил в простейшая форма .

Запишите соотношение в виде дроби.

12 30

Сейчас уменьшить дробь .

2 5

Таким образом, соотношение солнечная рыба для радужных светил является 2 : 5 .

(Обратите внимание, что отношение светит радуга солнечной рыбе это взаимный : 5 2 или 5 : 2 .)

Внимательно прочитайте текстовые задачи, чтобы проверить, соответствует ли соотношение, о котором вас спрашивают,

часть общего или отношение одной части к другой части .

Пример 2:

В классе г-жи Экпебе есть 32 студенты, из них 20 девочки. Напишите соотношение девочек и мальчиков.

Осторожный! Не пиши 20 32 … это доля общий количество учащихся, которые являются девушками. Нам нужно соотношение девочек и мальчиков.

Вычесть 20 от 32 найти количество мальчиков в классе.

32 − 20 “=” 12

Есть 12 мальчики в классе. Итак, соотношение девочек и мальчиков равно 20 : 12 .

Вы можете уменьшить это отношение так же, как вы уменьшаете дробь. Оба числа имеют общий факт 4 , поэтому разделите оба на 4 .

В простейшем виде это соотношение равно 5 : 3 .

Некоторые задачи на соотношение слов требуют решения пропорции.

Пример 3:

В рецепте указано масло и сахар в соотношении 2 : 3 . Если вы используете 6 чашек масла, сколько чашек сахара вы должны использовать?

Соотношение 2 : 3 означает, что для каждого 2 чашки сливочного масла, вы должны использовать 3 чашки сахара.

Здесь вы используете 6 чашки сливочного масла или 3 раз столько.

Итак, вам нужно умножить количество сахара на 3 .

3 × 3 “=” 9

Итак, вам нужно использовать 9 чашки сахара.

Вы можете думать об этом с точки зрения эквивалентных дробей:

2 3 “=” 6 9

Словесные задачи – Полный курс алгебры

Навыки
в н
A L G E B R A

Содержание | Дом

Примеры

Проблемы

ЗАДАЧИ СЛОВА требуют практики перевода словесного языка на алгебраический язык. См. Урок 1, Задача 8. Тем не менее, текстовые задачи делятся на разные типы. Ниже приведены некоторые примеры.

Пример 1. x ± b = c . Все проблемы, подобные следующей, в конечном итоге приводят к уравнению в такой простой форме.

Джейн потратила 42 доллара на обувь. Это было на 14 долларов меньше, чем в два раза больше, чем она потратила на блузку. Сколько стоила блузка?

Раствор. У каждой задачи со словами есть неизвестный номер. В этой задаче это цена блузки. Всегда позволяйте x представлять неизвестное число. То есть пусть x ответьте на вопрос.

Пусть х , то сколько она потратила на блузку. В задаче указано, что “Это”, то есть 42 доллара США, было на 14 долларов США меньше, чем удвоенное x .

Вот уравнение:

2 x − 14	=	42.

2 x	=	42 + 14 (Урок 9)

	=	56.

x	=	56 2

	=	28.

Блузка стоит 28 долларов.

Пример 2. В классе b мальчиков. Это в три с лишним раза больше, чем у девочек. Сколько девочек в классе?

Решение. Опять же, пусть x представляет собой неизвестное число, которое вас просят найти: Пусть x будет количеством девочек.

(Хотя b неизвестно — это идея определенного числа — это не то, что вас просят найти.)

Задача утверждает, что “Это” — b — в три раза больше, чем в четыре раза x :

	4 х + 3	=	б .
	Следовательно,
	4 х	=	б − 3

x		=	б − 3 4	.

Решение здесь не числовое, потому что оно будет зависеть от значения b . Это тип «буквального» уравнения, который очень распространен в алгебре.

Пример 3. Целое равно сумме частей.

Сумма двух чисел равна 84, и одно из них на 12 больше другого. Какие два числа?

Решение. В этой задаче нас просят найти два числа. Поэтому пусть х будет одним из них.

Пусть x будет первым числом.

Тогда другое число будет еще 12, x + 12.

В задаче указано, что их сумма равна 84:

= 84

Линия размером x + 12 является группирующим символом, называемым vinculum . Это избавляет нас от написания скобок.

У нас есть:

2 x	=	84 − 12

	=	72.

х	=	72 2

	=	36.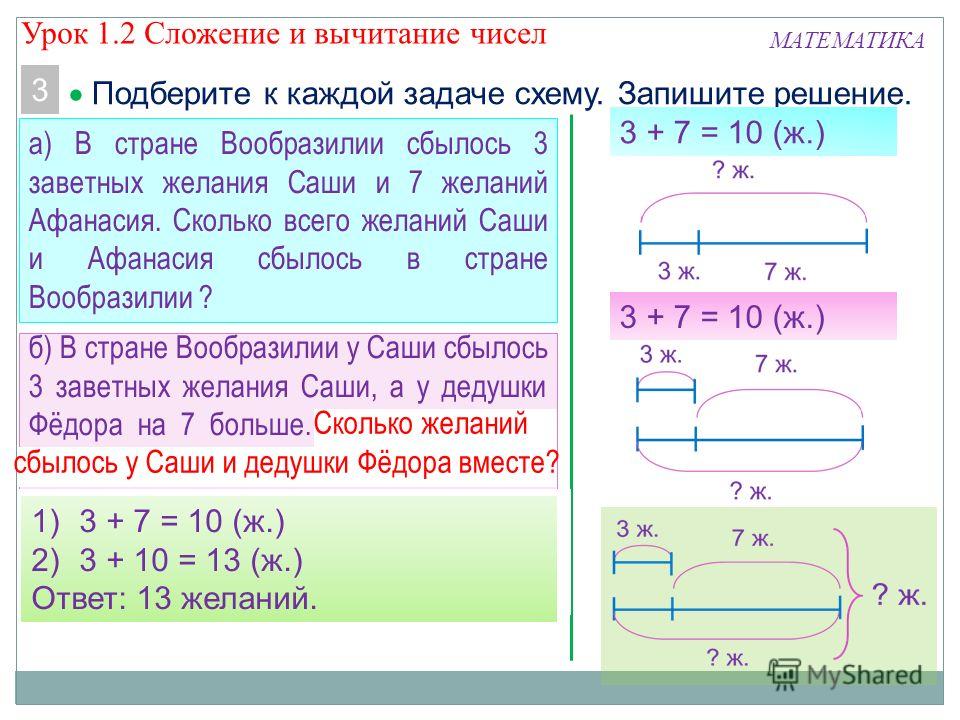

Это первый номер. Поэтому другой номер

х + 12 = 36 + 12 = 48.

Сумма 36 + 48 равна 84.

Пример 4. Сумма двух последовательных чисел равна 37. Что это такое?

Раствор . Два последовательных числа подобны 8 и 9 или 51 и 52.

Пусть x будет первым числом. Тогда число после него будет x + 1.

В задаче указано, что их сумма равна 37:

= 37

2 x	=	37 − 1

	=	36.

x	=	36 2

	=	18.

Два числа 18 и 19.

Пример 5. Одно число на 10 больше другого.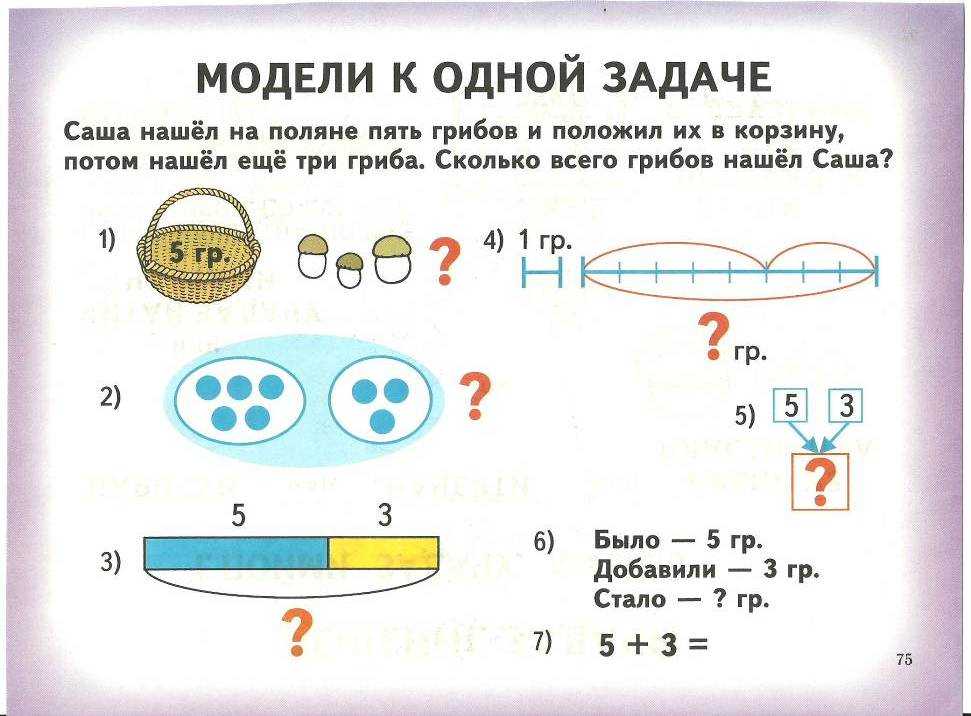 Сумма удвоенного меньшего плюс трехкратного большего равна 55. Какие это два числа?

Решение. Пусть x будет меньшим числом.

Тогда большее число будет на 10 больше: x + 10.

Проблема гласит:

2 х + 3( х + 10)	=	55.
Это означает
2 x + 3 x + 30	=	55. Урок 14.

5 x	=	55 – 30 = 25.

x	=	5.

Это меньшее число. Большее число на 10 больше: 15.

Пример 6. Разделите 80 долларов между тремя людьми так, чтобы у второго было в два раза больше, чем у первого, а у третьего было на 5 долларов меньше, чем у второго.

Раствор .

Пусть x будет тем, сколько получит первый человек.

Тогда второй получает в два раза больше, 2 x .

А третий получает на 5 долларов меньше, 2 x − 5.

Их сумма $80:

5 х	=	80 + 5

x	=	85 5

	=	17.

Столько получает первый человек. Поэтому второй получает

2 x	=	34.

И третий получает
2 x − 5	=	29.

Сумма 17, 34 и 29 на самом деле равна 80.

Пример 7. Нечетные числа. Сумма двух последовательных нечетных чисел равна 52. Какие два нечетных числа?

Раствор . Во-первых, четное число кратно 2: 2, 4, 6, 8 и т. д. В алгебре принято представлять четное число как 2 n , где под вызовом переменной n подразумевается, что n будет принимать целочисленные значения: n = 0, 1, 2, 3, 4 и так далее.

Нечетное число на 1 больше (или на 1 меньше), чем четное число. Итак, мы представляем нечетное число как 2 n + 1.

Пусть 2 n + 1 будет первым нечетным числом. Тогда в следующем будет еще 2 — это будет 2 n + 3. Задача утверждает, что их сумма равна 52:

2 n + 1 + 2 n + 3

52.

Теперь мы решим это уравнение для n , а затем заменим решение на 2 n + 1, чтобы найти первое нечетное число. У нас есть:

4 п + 4	=	52

4 нет	=	48

нет	=	12.

Следовательно, первое нечетное число равно 2 · 12 + 1 = 25. Следующее число равно 27. Их сумма равна 52.

Проблемы

Задача 1. У Джули есть 50 долларов, что на восемь долларов больше, чем у Джона. Сколько у Джона? (Сравните пример 1.)

Во-первых, что вы позволите представлять x ?

Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите “Обновить” (“Reload”).
Сначала решай задачу сам!

Неизвестное число — сколько у Джона.

Что такое уравнение?

2 х + 8 = 50.

Вот решение:

х = 21

долларов США

Задача 2. Карлотта потратила на рынке 35 долларов. Это на семь долларов меньше, чем в три раза больше, чем она потратила в книжном магазине; сколько она там потратила?

Вот уравнение.

3 х – 7 = 35

Вот решение:

х = 14

долларов США

Задача 3. Есть b черных шариков. Это в четыре раза больше, чем количество красных шариков. Сколько красных шариков? (Сравните пример 2.)

Вот уравнение.

2 х + 4 = б

Вот решение:

х =

б − 4
2

Задача 4. Джанет потратила 100 долларов на книги. Это было на тысяч долларов меньше, чем в пять раз больше, чем она потратила на обед. Сколько она потратила на обед?

Вот уравнение.

5 х – к = 100

Вот решение:

х =

100 + к
5

Задача 5. Целое равно сумме частей.

Сумма двух чисел равна 99, и одно из них на 17 больше другого. Какие два числа? (Сравните пример 3.)

Вот уравнение.

Вот решение:

x	=	41

x + 17	=	58

Задача 6. Класс из 50 учеников делится на две группы; в одной группе на восемь меньше, чем в другой; сколько в каждой группе?

Вот уравнение.

Вот решение:

x	=	29

x − 8	=	21

Задача 7. Сумма двух чисел равна 72, и одно из них в пять раз больше другого; какие два числа?

Вот уравнение.

х + 5 х = 72.

Вот решение:

х = 12, 5 х = 60,

Задача 8. Сумма трех последовательных чисел равна 87; кто они такие? (Сравните пример 4.)

Вот уравнение.

Вот решение:

28, 29, 30.

Задача 9. Группа из 266 человек состоит из мужчин, женщин и детей. Мужчин в четыре раза больше, чем детей, и вдвое больше, чем женщин. Сколько каждого из них?

(Чему можно приравнять x — количеству мужчин, женщин или детей?)

Пусть х	=	Количество детей. Тогда

4 x	=	Количество мужчин. И

2 x	=	Количество женщин.

Вот уравнение:

х + 4 х + 2 х = 266

Вот решение:

х = 38, 4 х = 152, 2 х = 76,

Задача 10. Разделите 79 долларов между тремя людьми так, чтобы у второго было в три раза больше, чем у первого, а у третьего было на два доллара больше, чем у второго. (Сравните пример 6.)

Вот уравнение.

Вот решение:

11 долларов США, 33 долларов США, 35 долларов США.

Задача 11. Разделите 15,20 доллара между тремя людьми так, чтобы у второго было на один доллар больше, чем у первого, а у третьего было на 2,70 доллара больше, чем у второго.

Вот уравнение.

Вот решение:

3,50 доллара США, 4,50 доллара США, 7,20 доллара США.

Задача 12. Два последовательных нечетных числа таковы, что первое, умноженное на три, больше второго в 5 раз. Что это за два нечетных числа?

(см. пример 7, где мы представляем нечетное число как 2 n + 1.)

Раствор . Пусть первое нечетное число будет 2 n + 1.

Тогда следующий будет 2 n + 3 — потому что будет еще 2.

Задача утверждает, т. е. уравнение:

	3(2 n + 1)	=	2(2 н + 3) + 5.
Это означает:
	6 п + 3	=	4 п + 6 + 5.
	2 нет	=	8.
	п	=	4.

Следовательно, первое нечетное число равно 2 · 4 + 1 = 9.

Быстро решаем задачи по математике. 2 класс (Елена Нефёдова, Ольга Узорова)

Как получить бонусы за отзыв о товаре

Решение задач. Закрепление 2 класс

словесных задач: пропорции

Словесные задачи – Полный курс алгебры

Добавить комментарий Отменить ответ