Решение задачи по математике 3 класс школа россии: ГДЗ Решебник Математика 3 класс Учебник Школа России «Просвещение» Моро, Бантова, Бельтюкова.

ГДЗ по математике 3 класс учебник Моро, Волкова 1 часть

---

• Тип: ГДЗ, Решебник.
• Автор: Моро М. И., Волкова С. И., Бантова М. А.
• Год: 2020.
• Серия: Школа России (ФГОС).
• Издательство: Просвещение.

❤️️Ответ к странице 29. Математика 3 класс учебник 1 часть. Автор: М.И. Моро.

Решебник – страница 29Готовое домашнее задание

Номер 1.

Ответ:

Номер 2.

Ответ:

9 ∙ 2 = 18     7 ∙ 3 = 21 18 : 9 = 2     21 : 7 = 3 18 : 2 = 9     21 : 3 = 7
24 : 3 = 8     12 : 2 = 6 3 ∙ 8 = 24     12 : 6 = 2 24 : 8 = 3      6 ∙ 2 = 12

Номер 3.

Ответ:

8 см 3 мм > 38 мм    35 см < 3 дм 6 см 83 мм > 38 мм          35 см < 36 см
56 мм = 5 см 6 мм    67 дм > 6 м 5 дм 56 мм = 56 мм          67 дм > 65 дм

Номер 4.

Каждое четное число от 12 до 18 увеличь на 50, а каждое нечетное уменьши на 9.

Ответ:

12, 13, 14, 15, 16, 17, 18.
12 + 50 = 62 13 − 9 = 4 14 + 50 = 64 15 − 9 = 6 16 + 50 = 66 17 − 9 = 8 18 + 50 = 68

Номер 5.

Реши задачи.
1) Масса подушки 2 кг. Узнай массу 6 таких подушек.
2) Ведро вмещает 10 л воды. Из бочки взяли 30 л воды. Сколько ведер воды взяли из этой бочки?
Проверь решение: составь и реши задачу, обратную данной.

Ответ:

Задача 1:

2 ∙ 6 = 12 (кг) Ответ: 12 кг масса 6 подушек.
Задача 2:

30 : 10 = 3 (в.) Ответ: из бочки взяли 3 ведра воды.
Обратная задача: Ведро вмещает 10 л. воды. Из бочки взяли 3 ведра воды. Сколько литров воды взяли из бочки?

10 ∙ 3 = 30 (л) Ответ: 30 литров воды взяли из бочки.

Номер 6.

Для школьной столовой привезли сухие фрукты: яблок 30 кг, а груш на 6 кг меньше. Объясни, что узнаешь, выполнив вычисления: 30 − 6   &nbsp30 + (30 − 6)

Ответ:

30 − 6 – сколько кг груш привезли в столовую. 30 + (30 − 6) – сколько кг сухих фруктов привезли в столовую.

Номер 7.

В саду собрали 26 корзин слив, груш на 6 корзин больше, чем слив, а яблок на 5 корзин больше, чем груш. Сколько корзин яблок собрали в саду?

Ответ:

1) 26 + 6 = 32 (к.) – груш собрали. 2) 32 + 5 = 37 (к.) Ответ: 37 корзин яблок собрали.

Номер 8.

Проверь, магические ли это квадраты.

Ответ:

Да, магические.
В 1-ом и по горизонтали, и по вертикали сумма чисел равна – 30. Во 2-ом сумма чисел равна – 75.

Рейтинг

Выберите другую страницу

1 часть

Учебник Моро	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

2 часть

4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

Ваше сообщение отправлено!

+

«Решение задач на увеличение числа в несколько единиц»

МКОУ СОШ №4 г. Хасавюрт

Открытый урок по математике.

3 класс. УМК «Школа России»

Тема: «Решение задач на увеличение числа в несколько единиц»

Провела: учительница начальных классов

Хасаева З.М.

28.11.2014

Цели:

• Отрабатывать умение решать задачи на увеличение числа в несколько единиц и на увеличение числа на несколько единиц;

• Закрепить знание таблицы умножения и деления, порядок выполнения действий;

• Совершенствовать вычислительные навыки, развивать познавательные способности, внимание;

• Развивать логическое мышление, умение размышлять.

Оборудование: карточки с заданиями, проектор, презентация.

Ход урока:

1. Организационный момент.

В наше время, чтобы строить

И машиной управлять,

Помни, друг, что надо прочно

Математику познать.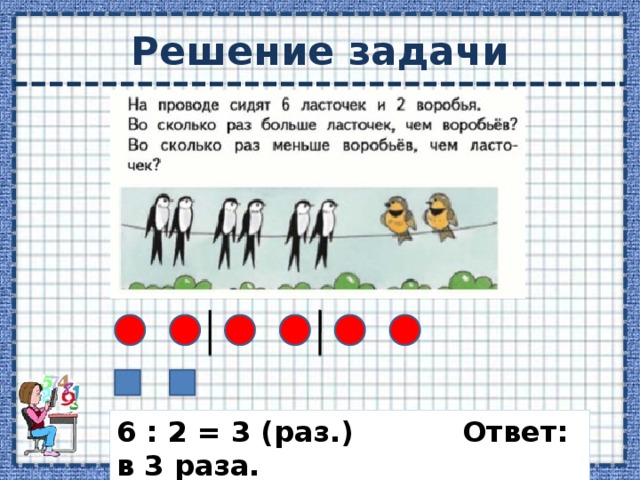

1. Сообщение темы и целей урока.

– Ребята, сегодня на уроке мы с вами повторим таблицу умножения, порядок выполнения действий, порешаем задачи на увеличение числа в несколько раз. (Слайд 1)

– Сейчас мы с вами будем строить дом. И каждый из вас будет принимать активное участие в его строительстве. Вот такой дом должен получиться у нас. (Слайд 2) Перед тем, как начать стройку, нам нужно выбрать очень красивое место. Что это будет за место вы узнаете, решив задачу.

III. Устный счет.

– Помни о том, что без устного счёта не сдвинется с места любая работа.

• Уменьшите 13 на 5;

• Найдите сумму чисел 6 и 6;

• Найдите разность чисел 70 и 60;

• Увеличьте 8 в 3 раза;

• Уменьшите 15 в 5 раз;

• Найдите произведение чисел 19 и 7;

• Найдите частное чисел 40 и 8.

Задача на смекалку:

В двух залах 50 стульев. Когда из одного зала вынесли 10 стульев, то в залах стульев осталось поровну. Сколько стульев было в каждом зале? (Слайд 3)

Теперь нам нужно заложить фундамент.

Ребята, посмотрите на ряд чисел. (Слайд4)

4 5 7 8 9 1 3 2

(Дети втечение 6-10 секунд смотрят на них. Затем цифры закрываются и задаются вопросы.)

• Какие цифры вы запомнили?

• Назови соседей числа 5? 3?

• Сколько всего цифр было на слайде?

• Какие две первых цифры?

• Какие три последних?

– Хорошо, ребята! Мы с вами заложили фундамент дома. (Слайд 5)

– Какую форму он имеет? (Форму прямоугольника)

– Что такое прямоугольник? (Четырёхугольник, у которого все углы прямые, а противоположные стороны равны)

– Давайте найдем периметр прямоугольника со сторонами 5 см и 6 см. Что такое периметр? (Сумма длин всех сторон многоугольника)

IV. Работа по теме урока:

–Запишите в тетрадях число, классная работа.

– Дальше, ребята нам нужно возвести стены дома. А для этого необходимо произвести расчеты, выполним примеры на порядок действий.

(Детям раздаются карточки)

– Самостоятельно решаете, а затем проверим. (Слайд 6, 7, 8, 9)

– Нужно сделать крышу дома с трубой. (Слайд 9) Откройте учебник на с. 28 задача № 3.

– О ком говорится в задаче? (О спортсменах)

– Что мы знаем о них? (Мальчиков – 6к. по 4 человека, Девочек – 5 к. по 3 человека)

– Что нужно найти? (Сколько человек принимало участие в соревнованиях?)

Поиск решения от главного вопроса.

1. 6х4=24 (ч.) – мальчиков.

2. 5х3=15 (ч.) – девочек.

3. 24+15=39 (ч.)

Ответ: 39 человек принимало участие в соревнованиях.

(Один ученик работает у доски, остальные в тетрадях). Проверка.

V. Физминутка.

Утром бабочка проснулась,

Потянулась, улыбнулась:

Раз – росой она умылась,

Два – изящно покружилась,

Три – нагнулась и присела,

На четыре – улетела.

VI. Закрепление.

– Ребята, какой же дом без окон и дверей?

– На доске записаны примеры, необходимо вставить пропущенный множитель.

5*…=35 …*6=36

7*…=42 5*…=45

…*8=40 …*3=21

…*2=18 8*…=56

…*7=27 …*2=12

10*…=90 10*…=80

– Молодцы! Посмотрите, мы с вами достигли своей цели: построили великолепный дом. (Слайд 9) Наш дом так понравился Маше, что она решила в нём жить!

V. Итог урока. Выставление оценок.

– Ребята, понравился вам сегодня урок?

-Что повторили и закрепили?

– Спасибо за урок.

Местный округ Запад / Когнитивное обучение (CGI)

•  

   

  Математика для детей младшего возраста	Математика для детей: когнитивно-ориентированное обучение	Расширение детской математики: дроби и десятичные дроби	Математическое мышление: интеграция арифметики и алгебры
  Математические обмены: руководство молодыми математиками на собраниях малых групп	Осмысление: преподавание и изучение математики с пониманием	Стать учителем математики, которого вы хотели бы иметь	Преобразование задач с выбором номера K-3
  Хоровой счет и сборники счета	Упражнения на распознавание чисел 3–5 классы	Преднамеренный разговор	Делаем разговоры о цифрах

  
  

   

   

   

   

  НОВЫЕ ТОВАРЫ:

   

  • Elementary: Математический проект UCLA MATH AT HOME (счет коллекций, игра в карты дома, что вы замечаете? Интересно?)

   

  •      Раннее детство (EEC-K): https://sites. google.com/view/cgieec-k/home  

     

  • Линда Леви Публикация в блоге:Занимаемся математикой с ребенком, помогая решать задачи; Предложения для родителей и учителей

   

  Исследование компьютерной графики, отвечающее критериям центра обмена информацией (папка на Google Диске)

    

  Таблица 1: Ресурсы CGI PD

  Когнитивное руководство (CGI) PD	РЕСУРС (Нажмите на ссылку для доступа к ресурсу)
  ВИДЕО СЕРИИ PD LAUSD CGI LEADERSHIP	Видео о лидерстве
  ИНТЕРВЬЮ С УЧИТЕЛЯМИ LAUSD И ВИДЕО КЛАССА	Интервью с учителями и видео
  ДЕТСКАЯ МАТЕМАТИКА: CGI 2 ND EDITION BOOK STUDY (LD WEST 2018)	Учебные материалы
  Совместные исследовательские структуры для поддержки внедрения CGI на школьных объектах (для преподавателей математики/руководителей математики)	Структуры цикла совместного запроса, поддерживающие реализацию CGI

  Таблица 2: Ссылки и ресурсы для поддержки внедрения компьютерной графики в классе

  ТЕМА CGI	РЕСУРС
  Долгосрочное планирование CGI	Шаблоны планирования блока CGI
  Разминка CGI или упражнения на определение числа и рассуждение	Банки задач и разработка задач Планирование Обучение Оценка Глядя на студенческие работы Инструменты наблюдения для постоянного улучшения	Какой из них не принадлежит Ресурсы для учителей   Ресурсы для обучения хоровому счету   Number Talk/Number Talk Images Учебные ресурсы   Способы составления числа Учебные материалы   Верно Неверно Числовые предложения Папка драйвера Google   Ресурсы для обучения числовым строкам
  Решение проблем	Типы проблем	Типы проблем для операций
  	Банк задач и разработка задач Планирование с задачами	Задачи по типу задачи CGI Сложение и вычитание   Умножение и деление   Дроби: задачи на равные доли и множественные группы Десятичные задачи   Наборы задач на мультипликативную концепцию (НОВОЕ ЗАДАНИЕ 2–5 классы) Промежуточный класс (2-5) Подсказки в журнале по математике (НОВЫЙ ПУНКТ) Многоэтапные насыщенные задачи из проекта по элементарной математике Наборы словесных задач CGI по уровням обучения (Центр обучения учителей математики CGI)
  	Траектории/структуры решения проблем	Траектории решения задач с целыми числами (синтезировано из книги Children’s Mathematics: CGI)    Структуры равного совместного использования и групповой стратегии (обновленные версии расширенной детской математики: схемы дробей и десятичных знаков)
  	Шаблоны планирования для решения проблем CGI Постановка и распаковка проблем Выявление мышления/конференций учащихся Привлечение учащихся к идеям друг друга с помощью стратегии Share	Руководство по планированию и обучению CGI для решения проблем Шаблон планирования для постановки и раскрытия проблем  Шаблоны планирования для стратегического обмена Numberless Word Problems Сообщение в блоге и ресурсы Адаптация уроков из учебников к потребностям учащихся (НОВЫЙ ЭЛЕМЕНТ)
  	*Оценка   * Любая задача любого дня может быть использована в качестве формирующего оценивания для выявления и использования доказательств мышления учащихся	Из проекта по элементарной математике K-1 Оценочные материалы интервью по развитию Материалы для начальной оценки по десятичному разряду (от позднего первого до начала второго класса) Материалы для оценки по десятичной системе счисления (2-й и третий класс) Оценка мультипликативного мышления (для каждого класса с 3 по 5) Диагностические оценки CGI K-5 Прослушивание обзора детского мышления Ресурсы для оценки диагностики CGI на осень и весну Неформальные оценки понимания математики CGI (от CGI Math TLC) НОВЫЙ ПУНКТ CGI Числовая оценка стратегии фактов Оценка и сбор данных
  	Глядя на студенческие работы	Сортировка рабочих инструментов учащихся Траектории стратегий задач CGI (фреймворки) Инструменты и протоколы анализа работы учащихся Инструменты и формы для математических конференций
  Подсчет коллекций	Задачи и разработка задач Планирование Обучение Оценка	Подсчет ресурсов коллекций
  Игры	Карточные игры дома (математический проект Калифорнийского университета в Лос-Анджелесе: математика дома)
  Приступая к настройке среды обучения математике CGI и наборов математических инструментов CGI	Ресурсы для начала работы Развитие математического мышления школьников и академические беседы Сообщение в блоге НОВЫЙ ПУНКТ Математические инструменты CGI
  Дополнительные ресурсы	CGI ДОСТОЙНЫЕ ЗАДАЧИ ПО РЕШЕНИЮ ПРОБЛЕМ ВЕБ-САЙТЫ: НОВЫЕ ДОБАВЛЕННЫЕ: МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ С КУЛЬТУРНЫМ И ОБЩЕСТВЕННЫМ КОНТЕКСТАМИ (ЗАДАНИЯ ДЛЯ 3-5 КЛАССОВ): https://bit. ly/MathModelingContextsTasksGr3-5  Иллюстративная математика (проблемные задачи K-5):  https://www.illustrativemathematics.org/content-standards  NC Department of Public Instruction Elementary Math K-2 (достойные CGI-задачи): Home NC Department of Public Instruction Elementary Math 3-5 (CGI Worthy CGI CGI Worthy CGI Task-Based Tasks): Home НОВОЕ ДОБАВЛЕНО: МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ С ТРЕМЯ ЗАДАЧАМИ ОТ ГРЭМА ФЛЕТЧЕРА И ДРУГИХ: https://gfletchy.com/3-act-lessons/   ДРУГИЕ ВЕБ-САЙТЫ CGI Математический проект UCLA Center X: Раннее детство (EEC-K): https://centerx.gseis.ucla.edu/math-project/early-childhood/ Начальный уровень: https://centerx.gseis.ucla.edu/math-project/elementary/     DREME (Развитие и исследования в области раннего математического образования): https://dreme. stanford.edu/    Центр обучения учителей математики CGI: https://www.cgimath-tlc.org/   Проект по элементарной математике: Project Services   Обучение — это решение проблем:       https://www.teachingisproblemsolving.org/ Преобразование задания с помощью выбора чисел и контекстов, связанных с жизнью и опытом ваших детей      http://bit.ly/TransformingTaskwNumberChoice   Шаблоны форм задачи решения проблем CGI   СТАТЬИ, СВЯЗАННЫЕ С CGI, для профессиональных обучающих сообществ (PLC): Статьи лидеров математики по вопросам преподавания стандартных алгоритмов Статьи по стандартным алгоритмам обучения Базовый фон для учителей CGI  CGI и статьи по теме  ОБЫЧНЫЕ ВЕБ-САЙТЫ ПО ЧИСЛУ И ОБОСНОВАНИЮ Числовые строки: сообщество разработчиков числовых строк: https://numberstrings. com/   Какой из них не принадлежит: http://wodb.ca/   Изображения для разговора по номерам: http://ntimages.weebly.com/   Визуальные шаблоны: https://buildingmathematicians.wordpress.com/visual-patterns/   Berkeley Everett Math Visuals: https://mathvisuals.wordpress.com/ и 5 недель упражнений на распознавание чисел   Центр обучения математике: Домашняя математика (какой из них не принадлежит, сколько?, сегодняшнее число, такое же другое) : https://mathathome.mathlearningcenter.org/search   Сплат! для учителей начальных классов НОВЫЙ ПУНКТ: Стив Уайборни Сайт: https://stevewyborney.com/2018/09/splat-for-google-slides-40-уроки/ Организованные ресурсы Splat, куратор Джейми Гарнер: https://docs.google.com/document/d/1q_8j1rILDWxBeRrpef95D9fbj2h_np1-sGsHKI-PQLU/mobilebasic   Хоровой счет: творческий математический планировщик хорового счета и инструмент хорового счета (для доступа необходимо создать учетную запись. Когда вы увидите описание инструмента, нажмите НАЧАТЬ ХОРОВОЙ СЧЕТ, чтобы использовать инструмент)  Teacher Education by Design (TEDD.org): Математическая разминка CGI (Умственная математика (Разговоры о числах), Числовые строки, Верно-ложные предложения, Быстрые изображения, Хоровой счет, Коллекция счетов): TEDD.org: Элементарная математика

   

   

   

•  

  Компьютерная графика дома

  • Математический проект Калифорнийского университета в Лос-Анджелесе МАТЕМАТИКА ДОМА (Считаем коллекции, Играем в карты дома, Что вы замечаете? Интересно?)

   

  • Линда Леви Публикация в блоге: Занятия с ребенком по математике — содействие решению задач; Предложения для родителей и учителей

   

   

   

  Начало работы с компьютерной графикой для учащихся, не имевших опыта решения задач с использованием собственных стратегий Сообщение в блоге ( НОВЫЙ ПУНКТ)

• ПРЕДСТОЯЩИЕ ТРЕНИНГИ CGI

  Комментарии (-1)

Что можно и чего нельзя делать при обучении решению задач по математике

Вы здесь: Главная → Статьи → Решение проблем

Многие студенты-математики в США боятся, если не в ужасе, математических задач. В целом они считаются трудными.

С чего бы это? Это совершенно не имеет смысла. Я не могу себе представить, чтобы дети не любили словесные задачи только потому, что им нужно найти ответ на что-то (задачу), или потому, что задача объяснена словами. Например, даже большинство из нас, взрослых, очарованы головоломками.

Кроме того, эта боязнь текстовых задач точно не может появиться в 1-м классе. Сюжетные задачи в первом классе очень простые, например: «На озере пять уток, а на берегу три. Сколько всего уток?» Часто в учебнике по математике даже есть картинка. Я не могу представить, чтобы дети чувствовали, что это трудно.

Я чувствую, что вызывает для этой трудности во много раз:

1. Преобладают одношаговые словесные задачи в конце уроков отработки конкретной операции в младших классах. Это побуждает детей просто находить числа и использовать изучаемую операцию линейным образом, как если бы все задачи со словами решались с помощью «рецепта».
2. Во многих школьных учебниках недостаточно ХОРОШИХ словесных задач . Обычно они включают в себя множество одношаговых задач, а затем несколько отдельных уроков по решению проблем, которые обычно подчеркивают конкретную стратегию решения проблем (так что у вас снова есть «правило», которое решает проблемы на этом уроке).
3. Учителя боятся текстовых задач, поэтому пропускают их.

Рассмотрим 1 и 2 подробнее.

1. Одношаговые словесные задачи преобладают в конце уроков, отрабатывающих определенную операцию

Вы часто видите это в начальных классах. Дети упражняются, возможно, в многозначном умножении, возможно, в вычитании с использованием заимствований, возможно, в делении десятичных дробей. После задач на вычисления идут задачи со словами, которых, как ни странно, 9.0720 решается с помощью точной операции, только что отработанной !

Это выходит за рамки уроков по четырем операциям. Разве вы не замечали: если урок посвящен теме X, то и задачи в словесной форме также относятся к теме X!

Когда дети снова и снова подвергаются таким урокам, они понимают, что даже не читать задачу слишком внимательно, это менее сложно для их умственного развития. Зачем беспокоиться? Просто возьмите два числа и разделите (или умножьте, или сложите, или вычтите) их, и все.

Этому, конечно же, способствует и тот факт, что словесные задачи в конце таких уроков, как правило, содержат только два числа . Так что, даже если вы не поняли СЛОВО в задаче, вы могли бы это сделать! Просто попробуйте: следующая выдуманная задача на ФИНСКОМ языке… и, допустим, она найдена в длинном уроке деления. Теперь я предполагаю, что вы НЕ знаете финского языка, но можете ли вы его решить?

Kaupan hyllyillä on 873 lakanaa, 9:ää эри вария. Joka väriä on саман верран. Kuinka monta lakanaa on kussakin värissä?

Наведите указатель мыши на пустое пространство внизу, чтобы увидеть перевод (выделите его).

В магазине 873 листа 9 разных цветов. Для каждого цвета одинаковое количество листов. Сколько листов каждого цвета?

Использование множества подобных задач вскоре приводит к проблеме: дети «узнают» (разумно) это негласное правило:

“Задачи со словами в учебниках по математике решаются с помощью некоторой процедуры или правила, которые вы найдете в начале этого конкретного урока . ”

Как избежать этой ужасной ситуации? Перепутайте словесные задачи так, чтобы не все они решались только что изученной операцией. Другая идея состоит в том, чтобы дать учащимся набор коротких текстовых задач для анализа, чтобы вместо того, чтобы искать ответы, они определяли, какие операции необходимы для получения ответа.

2. Во многих школьных учебниках недостаточно задач на ХОРОШЕЕ слово.

Под хорошими задачами я подразумеваю многоступенчатые задачи, которые повышают сложность по классам и способствуют развитию логического мышления детей.

Одношаговые задачи хороши для 1-го и 2-го классов, а тут и там смешиваются с другими. Но детям нужно начинать решать многоэтапные задачи как можно раньше, в том числе в 1-м и 2-м классах.

Посмотрите на этот пример задачи из русского учебника для четвертого класса:

Древний художник нарисовал на стенах пещеры сцены охоты, в том числе 43 фигурки животных и людей. Фигурок животных было на 17 больше, чем людей. Как сколько фигур людей нарисовал художник?

Похожая задача есть в сингапурском учебнике для 5 класса:

Раджу и Сэми поделили между собой 410 долларов. Раджу получил на 100 долларов больше, чем Сэми. Сколько денег получил Сэми?

Ничего особенного. Вы можете решить их, например, вычитая из общей суммы разницу в 17 или 100 долларов, а затем разделив оставшуюся сумму поровну:

410 долларов – 100 долларов = 310 долларов, а затем разделите 310 долларов поровну между Раджу и Сэми, что даст каждому по 155 долларов. Дайте Раджу 100 долларов. Итак, у Сэми было 155 долларов, а у Раджу — 255 долларов.

Что касается фигур, 43 − 17 = 26, а затем разделите это поровну: 13 и 13. Итак, 13 фигурок людей и 30 фигурок животных.

НО в США такого рода задачи обычно вводятся в Алгебра 1 – девятый класс , И они решаются только с использованием алгебраических средств.

Вот еще один пример, от которого я, помню, был ошеломлен, найденный в современном учебнике по алгебре США:

Найдите два последовательных числа, произведение которых равно 42.

Третьеклассники должны знать умножение достаточно хорошо, чтобы быстро найти, что 6 и 7 подходят к задаче! Зачем использовать «обратную лопату» (алгебру) для задачи, которую можно решить с помощью «маленькой лопаты» (простое умножение)!

Я знаю, что некоторые будут спорить и говорить: «Его цель — научиться составлять уравнение». Но для этой цели я бы использовал большее число, а не 42. Разве такие простые задачи в учебниках по алгебре не побуждают студентов забывать здравый смысл и простую арифметику?

Другой пример, задача 3 класса из России:

Мальчик и девочка собрали 24 ореха. Мальчик собрал в два раза больше орехов как девушка. Сколько собрал каждый?

Можно нарисовать мальчика и девочку, нарисуйте два кармана для мальчика и один для девочки. Это визуальное представление легко решает проблему .

Вот пример задачи по русскому языку для 6-8 классов:

Древняя проблема. Летящий гусь встретил в воздухе стаю гусей и сказал: “Здравствуйте, сто гусей!” Вожак стада ответил ему: «Есть нас не сотня. Если бы нас было столько, сколько есть, и еще столько же, и половина еще много и на четверть больше и ты, гусь, тоже летал с нами, то там нас было бы сто». Сколько гусей было в стае?

(Лично я бы составил уравнение для этого, но это можно сделать и без алгебры.)

Пожалуйста, ознакомьтесь с этими ресурсами для задач с хорошими словами.

Цель текстовых задач

Одной из целей текстовых задач является подготовка детей к реальной жизни . Это относится, например, к проблемам с покупками.

Другая, очень важная цель сюжетных задач состоит в том, чтобы просто развивать у детей логическое и абстрактное мышление и умственную дисциплину . Примечание: одношаговые словесные задачи точно не помогут!

Третий; некоторые учителя используют довольно сложные сценарии или модели из реальной жизни, чтобы мотивировать учащихся . Я видел это, например, в программе алгебры.

Проблема в том, что такие задачи требуют много времени и руководства со стороны учителя. Единственный верный способ развить хорошие навыки решения проблем – это… РЕШИТЬ МНОГО ХОРОШИХ ПРОБЛЕМ . Они не обязательно должны быть реальными или включать неудобные числа (например, в реальной жизни). Реалистичные, сложные задачи могут быть хороши для «приправы», но не для «основного блюда». «Фантастические» (нереальные) проблемы — это нормально.

План решения проблем

В большинстве учебников по математике представлен какой-либо план решения задач, смоделированный по образцу описания процесса решения задач Джорджа Полиа из его книги How to Solve It . Эти шаги для решения проблемы:

1. Разобраться в проблеме.
2. Разработайте план.
3. Выполнить план.
4. Оглянитесь назад.

Эти шаги соответствуют здравому смыслу и носят общий характер.

ОДНАКО мне не нравится представлять этот план ученикам. Я думаю, что мы могли бы и должны выделить первый и последний шаги, но я также чувствую, что часто мы не можем «втиснуть» решение проблемы в два простых шага: разработку плана и его выполнение.

В сложных задачах фактическое решение проблемы становится процессом , посредством которого решатель мысленно «проверит» прогресс и исправляет себя, если прогресса нет. Вы можете пойти по одному маршруту, заметить, что это не сработает, вернуться немного назад и выбрать другой маршрут.

Другими словами, разработка планов и их выполнение могут происходить несколько одновременно, и решатель перемещается между ними туда и обратно.

Шаги, описанные выше, хороши, если учащиеся понимают, что эти шаги не всегда просты или прямолинейны и не всегда следуют последовательно. Вы можете составить план, начать его выполнять и вдруг что-то заметите и поймете, что даже не поняли проблему правильно!

Рассмотрим идею мастер/ученик . Пусть ваши ученики будут учениками, которые наблюдают за тем, что вы, учитель, делаете, решая задачи перед классом. Выберите проблему, решения которой вы не знаете заранее. Вы можете сначала попробовать неправильный подход, но это нормально. Объясни свои мысли. Это покажет учащимся настоящий пример решения реальных проблем!

См., например, мой мыслительный процесс решения проблем здесь: Доказательство — это процесс: доказательство свойства логарифмов.

Как насчет стратегий решения проблем?

Стратегии решения проблем, которые мы часто встречаем в школьных учебниках, — это нарисовать картинку, найти закономерность, решить более простую задачу, работать в обратном порядке или разыграть проблему. Опять же, они часто берутся из книги Polya How to Solve It . Он тратит много страниц, объясняя и приводя примеры различных эвристик решения проблем или общих стратегий.

Эти стратегии или эвристики, конечно, очень полезны. Однако мне не нравятся уроки по решению проблем, которые можно найти в школьных учебниках и которые концентрируются на одной стратегии за раз. Видите ли, на таком уроке у вас есть задачи, которые решаются с помощью заданной стратегии, так что это еще больше подчеркивает мысль о том, что решение текстовых задач всегда следует какому-то заранее установленному рецепту.

Лучшим подходом было бы решать хорошие сложные задачи еженедельно или раз в две недели. Варьируйте проблемы и способы их решения. Естественно используйте различные стратегии решения проблем в примерах решений, которые вы предоставляете, но не ограничивайте мышление учащихся, называя урок какой-то конкретной стратегией.

Так что нам делать?

Обучение решению задач, вероятно, не так сложно, как может показаться. Первым шагом будет, конечно, то, что вы, учитель, не должны бояться проблем. Прочтите книгу Поля.

Затем найдите несколько хороших задач для решения (см. ресурсы ниже) и предложите учащимся решать задачи в рамках своего обычного обучения математике. Обсудите решения. Объясните им различные стратегии в контексте решения проблем. Не заблуждайтесь, думая, что текстовые задачи из учебника достаточно хороши, потому что это может быть не так.

Иногда самостоятельно моделируйте процесс решения проблем, как описано выше.

Все отлично сойдется. Как я уже сказал, главное, что помогает учащимся стать экспертами в решении задач, — это много практики в решении задач!

---

И, наконец, шутка Линн Нордстром:

Заблуждение студента при решении задач

Правило 1: По возможности избегайте чтения задачи. Чтение задачи только отнимает время и вызывает путаницу.

Правило 2: Извлеките числа из задачи в том порядке, в котором они появляться. Следите за числами, написанными словами.

Правило 3: Если правило 2 дает три или более чисел, лучшая ставка добавление их вместе.

Правило 4: Если есть только 2 числа, которые примерно равны одинакового размера, то вычитание должно дать наилучшие результаты.

Правило 5: Если есть только два числа и одно намного меньше чем другой, затем разделите, если он идет поровну — иначе умножить.

Правило 6: Если проблема требует формулы, выберите формула, в которой достаточно букв, чтобы использовать все числа дано в задаче.

Правило 7: Если кажется, что правила 1-6 не работают, сделайте последнее отчаянная попытка. Возьмем набор чисел, найденный правило 2 и выполнить около двух страниц случайных операций используя эти числа. Вы должны обвести около пяти или шесть ответов на каждой странице на случай, если один из них оказывается ответ. Вы можете получить частичное похвала за старание.

Я надеюсь, что ваши ученики не подходят к вышеприведенной шутке.

Источники и дополнительные ресурсы

Проблемы со словом в России и Америке — статья Андрея Тоома. Это расширенная версия выступления на собрании Шведского математического общества в июне 2005 года.

Любимые пазлы
Коллекция любимых математических головоломок для детей, собранная на моем конкурсе головоломок. Большинству из них требуются только четыре основные операции, поэтому они хорошо подходят для детей младшего школьного возраста и старше.

Список веб-сайтов, посвященных текстовым задачам и решению задач
Используйте эти сайты, чтобы найти хорошие словесные задачи для решения. Большинство бесплатно!

Как решить: новый аспект математического метода Джорджа Полиа.
Классическая и превосходная книга по решению проблем. Идеи Полии лежат в основе большинства «планов» и стратегий решения проблем, представленных сегодня в учебниках по математике. Как это решить популяризировал эвристику, искусство и науку открытий и изобретений.