Решение задач во 2 классе по математике: Задачи по математике для 2 класса, 3500 занимательных заданий с ответами и решением
Урок математики во 2-м классе по теме “Решение задач”
Дидактическая цель урока: cоздать условия для закрепления знаний и умений.
Тип урока: урок комплексного применения знаний и умений.
Задачи урока.
- Развивающие: развивать операции мышления: анализ, синтез, сравнение, классификацию; моделирующую деятельность; пространственное мышление.
- Образовательные: продолжить формирование умения читать задачу; соотносить её текст с готовым решением, сравнивать тексты, моделировать текст задачи с помощью отрезков, находить различные способы решения задач, совершенствовать вычислительные умения. Для расширения знаний по математике использовать межпредметные связи с литературным чтением и окружающим миром.
- Воспитательные: побуждать интерес к
познанию окружающего мира, воспитывать гуманное
отношение ко всему, что нас окружает.

Методы обучения: сочетание репродуктивного и проблемно – поискового методов.
Формы познавательной деятельности учащихся: индивидуальная, групповая, фронтальная.
Средства обучения:
- учебник математики 2 класс. Истомина Н. Б.
- демонстрационный материал: книга А. Экзюпери «Маленький принц», звёзды, схемы задач, магнитофон.
- раздаточный материал: карточки с заданиями, дифференцированные по уровням сложности.
ХОД УРОКА
I. Организационный момент
Если хочешь строить мост,
Управлять машиной в поле
.Наблюдать движенье звёзд,
Иль вести ракету ввысь–
Хорошо работай в школе,
Добросовестно учись!
Организация класса, проверка готовности к
уроку, задание положительной мотивации.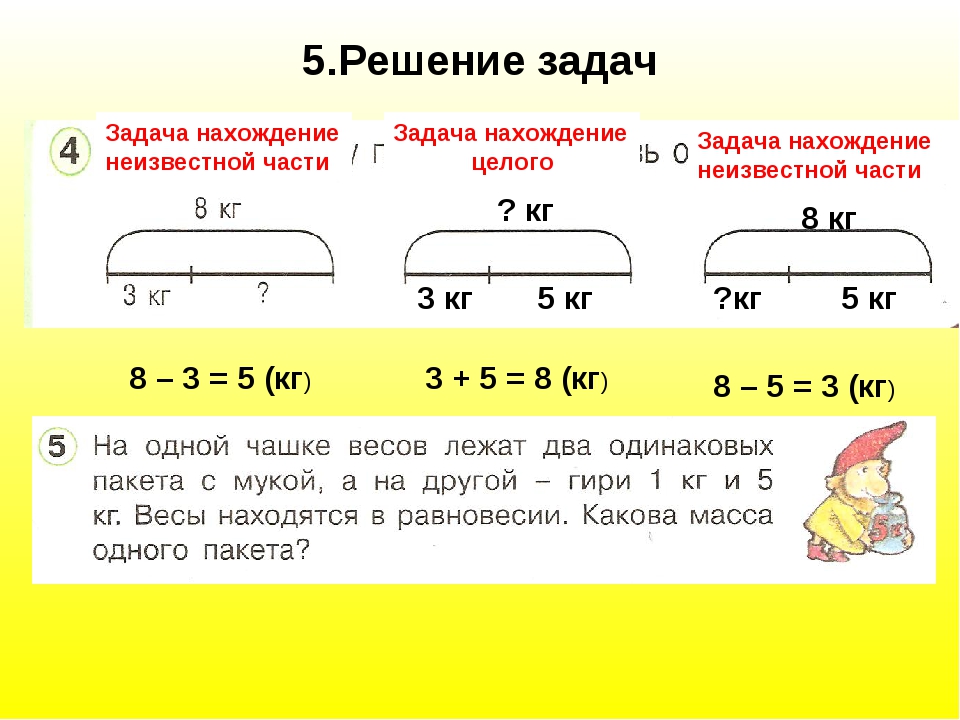
II. Сообщение темы и цели урока
– Каждый урок – открытие. Сегодня на уроке новой темы у нас не будет, но я надеюсь, что открытие сделает для себя каждый. Наш урок необычный, сегодня вы будете учёными. Учёные делают открытия. Они постоянно решают сложные задачи. Чтобы решать задачи верно, нужно считать без ошибок. Вот и мы на уроке будем решать задачи и производить вычисления. В какой области будут наши исследования, вы узнаете выполнив устный счёт.
III. Устный счёт
– Как и учёные, работать будем творческими группами. Несколько ребят получат индивидуальные задания.
1. Индивидуальная работа на карточках
1) Реши головоломку:
– сумма на каждой линии должна равняться 10;
– можно использовать только числа 1, 2, 3, 4, 5:
– каждое число можно использовать только
один раз.
2) Сколько созвездий на небе?
2. Фронтальная работа.
Математический диктант
Фронтальная работа.
Математический диктант
– Ответы записывайте на полосках бумаги в строку
1. Насколько 8 больше 3?
2. Первое слагаемое 40, второе 10. Найдите сумму.
3. Уменьшаемое 38, вычитаемое 2. Найдите разность.
4. Увеличьте 8 на 5.
5. Уменьшите 18 на 9.
6. Какое число надо прибавить к 20, чтобы получить
60?
8. Найдите сумму чисел 40 и 20.
9. Найдите разность чисел 60 и 1.
Проверим что получилось. (Ответы с буквами.)
– Расположите в порядке убывания и расшифруйте
слово. Мы узнаем первое слово имени уже знакомого
вам литературного героя. Кто сразу не догадался,
назовёт имя героя, посмотрев на книгу.
Маленький принц подскажет вам, в какой области
будут наши исследования. «Звёзды принадлежат
всем людям. Но каждый смотрит на них по-своему. Страннику звёзды укажут путь. Для других они –
всего лишь крошечные огоньки на небе. Для
третьих, учёных, звёзды – это задачки, которые
надо решить».
Страннику звёзды укажут путь. Для других они –
всего лишь крошечные огоньки на небе. Для
третьих, учёных, звёзды – это задачки, которые
надо решить».
– Как вы думаете, о чём будут задачи, которые мы
будем решать?
Проверка индивидуальных заданий с выносом на доску.
3. Межпредметные связи с окружающим миром.
– Как в головоломке расположены звёзды?
– Как называется группа звёзд?
– Что можно сказать об этих звёздах?
– Сколько созвездий на небе?
IV. Работа по теме
1. Анализ текстов задач с недостающими данными, с противоречивым условием и вопросом.
Самостоятельная работа. Прочитайте тексты. Если текст является задачей – ставьте рядом знак «+», если нет – знак «–» .
- На ночном небе появилась туча и закрыла 30 звёзд. Сколько звёзд видно на небе?
- В созвездии Большая Медведица 21 звезда.
 Из
них 7 звёзд образуют ковш.
Из
них 7 звёзд образуют ковш. - В созвездии Жирафа 9 звёзд, в созвездии Лебедя – 7. Насколько больше звёзд в созвездии Жирафа, чем в созвездии Льва?
- В созвездии Рака 15 звёзд. Среди них есть красные, жёлтые и белые звёзды. Белых звёзд – 5, жёлтых – 3. Сколько красных звёзд?
– Текст, который является задачей, решим в тетради.
2. Решение задач
– Составим схему.
Решение:
- 5 + 3 = 8 (зв.) – белых и жёлтых.
- 15 – 8 = 7 (зв.) – красных.
Ответ: красных звёзд 7.
– Есть другие способы решения задачи? Проговорить устно.
3. Постановка вопросов по данному условию
– Какие ещё вопросы можно поставить к этой
задаче?
– На сколько белых звёзд больше, чем жёлтых?
– Сколько белых и жёлтых звёзд?
– Выберите схемы, соответствующую поставленным
вопросам.
4. Самостоятельная работа
Решение задач по вариантам:
Физминутка
Упражнение для релаксации «Сотвори в себе Солнце»
В природе есть Солнце. Оно светит и греет.
Давайте сотворим Солнце в себе. Сядьте поудобнее,
расслабьтесь, закройте глаза, руки на колени
ладонями вверх, представляйте всё, о чём я
буду говорить.
Представьте в своём сердце маленькую звёздочку.
Мысленно направляйте к ней лучик, который несёт
любовь. Мы чувствуем, что звёздочка увеличилась.
Направляем лучик, который несёт мир, добро.
Звёздочка растёт. Здоровье, радость, нежность.
Звёздочка растёт, становится большой и тёплой
как Солнце. Ей тесно у вас. Руки в стороны. Она
несёт тепло и добро всем-всем-всем.
V. Работа по учебнику
Самостоятельная работа по вариантам:
Учебник математики № 165 (2, 4 ст. )
)
1 в – 2 ст 2 в – 4 ст
69 –
6
83 – 3
38 –
3
54 – 40
26 –
2
96
– 60
57 –
5
42 – 20
78 –
7
85
– 50
29 –
2
94
– 40
– Продолжите столбики по этому же правилу. Взаимопроверка.
IV. Геометрический материал
– Последнее наше открытие. В учебнике
«Наглядная геометрия» № 6. Представьте , что в
созвездии четыре звезды. Как их можно соединить?
Как назвать? На кого или на что будут похожи
эти созвездия? Соедините звёздочки так, чтобы
получились разные ломаные линии, состоящие из
трёх звеньев. Дайте названия созвездиям.
Рассмотрите все варианты.
Как их можно соединить?
Как назвать? На кого или на что будут похожи
эти созвездия? Соедините звёздочки так, чтобы
получились разные ломаные линии, состоящие из
трёх звеньев. Дайте названия созвездиям.
Рассмотрите все варианты.
VII. Итог урока
– Над чем мы работали на уроке?
– Что запомнилось, понравилось?
– Какой литературный герой помог провести урок?
– Подводя итоги урока, вспомним одно хорошее
правило, которое всегда выполнял Маленький
принц: «Я держусь правила. По утрам, как только
приведёшь себя в порядок, наведи порядок на своей
планете, да постарайся на совесть».
– Как вы оцениваете нашу сегодняшнюю работу?
VIII. Рефлексия
– Минутку подумайте и оцените результат своей работы. Выберите из трёх сигнальных карточек, ту, которая подходит вам.
– красную – если вы уверены, что хорошо работали на уроке и всё поняли;
– зелёную – если вы считаете, что в материале разобрались, но есть некоторая неуверенность;
– жёлтую – если считаете, что в новой теме разобрались ещё недостаточно.
IX. Домашнее задание
Составьте и решите задачу о любом созвездии.
Приложение
9 | 6 | 48 | ||||||
8 | 4 | 38 | 5 | |||||
3 | 56 | 0 | 54 | Виталик во время каникул прочитал 12 книг, а его младшая сестра Маша 4 книги. Во сколько раз меньше книг прочитала Маша? | 2 группа | 3 группа | 4 группа | |
– 14 – 7 | – 14 – 7 | – 14 – 7 | – 14 – 7 | |||||
мальчики девочки во меньше | мальчики девочки во меньше | мальчики девочки на больше | мальчики девочки на меньше | |||||
2 | 1 | 14 | ||||||
7 | 3 | 4 | 10 | |||||
9 | 6 | 5 | 11 | |||||
Презентация ” Решение задач. Путешествие в космос” 2 класс
библиотека
материалов
Содержание слайдов
Номер слайда 1
Номер слайда 2
Номер слайда 3
Учитель начальных классов Хромова Светлана Николаевна Урок математики во 2 классе по УМК «Перспектива»
Номер слайда 4
В 1960 году Юрий Гагарин начал готовиться к полету в космос. Работал упорно, с полной отдачей сил.
Работал упорно, с полной отдачей сил.
Номер слайда 5
. Чтоб сегодня наш урок, Всем пошёл ребятам впрок, Постарайтесь всё понять, Слушать, думать и вникать!
Номер слайда 6
БОРТОВОЙ ЖУРНАЛ Маршрутный лист 12 22 32 ……
Номер слайда 7
12 апреля 1961 года на старте прозвучало его знаменитое «Поехали»!
Номер слайда 8
КЛЮЧЕВОЕ СЛОВО УРОКА 29 – 19 = 4 + 3х6 = (80-70)+6= 26 + 14 = 40 – 35 = 90 : 10 =
Номер слайда 9
КЛЮЧЕВОЕ СЛОВО УРОКА 40-а 22-ч 16-а 10-д 9-а 5-з
Номер слайда 10
КЛЮЧЕВОЕ СЛОВО УРОКА ЗАДАЧА
Номер слайда 11
Номер слайда 12
Номер слайда 13
КЛАСТЕР ЗАДАЧА условие вопрос решение ответ
Номер слайда 14
СТАРТОВАЯ ПОДГОТОВКА
Номер слайда 15
СТАРТОВАЯ ПОДГОТОВКА
Номер слайда 16
СТАРТОВАЯ ПОДГОТОВКА
Номер слайда 17
И так! Внимание ! Взлёт! Наша ракета помчалась вперёд! Прощально мигнут и растают вдали Огни золотые любимой Земли!
Номер слайда 18
Номер слайда 19
Номер слайда 20
Номер слайда 21
. М.кратер- 15 ч. Б.кратер-? ч. на 65 > } ?Ч..
М.кратер- 15 ч. Б.кратер-? ч. на 65 > } ?Ч..
Номер слайда 22
ГАЛАКТИКА ЗАДАЧ Станция «Сочиняй-ка» Маленький кратер возьмёт в себя 15 человек. А большой кратер на 65 человек больше. Сколько человек возьмут в себя оба кратера?
Номер слайда 23
ГАЛАКТИКА ЗАДАЧ Станция «Сочиняй-ка» 15+65=80(ч. )-возьмёт большой кратер. 2) 15+80=95(ч.) Ответ: 95 человек возьмут оба кратера.
)-возьмёт большой кратер. 2) 15+80=95(ч.) Ответ: 95 человек возьмут оба кратера.
Номер слайда 24
ГАЛАКТИКА ЗАДАЧ Станция «Отдыхай-ка»
Номер слайда 25
ГАЛАКТИКА ЗАДАЧ Станция «Отдыхай-ка»
Номер слайда 26
К космическому полёту долго и упорно готовились 12 космонавтов. Они работали над собой, не покладая сил. Наконец, настал торжественный день отбора самых достойных космонавтов. Когда все построились, то выбрали самых сильных, ловких и умелых. А на Земле осталось 7 космонавтов. Сколько космонавтов были удостоены чести полететь в космос ?
Они работали над собой, не покладая сил. Наконец, настал торжественный день отбора самых достойных космонавтов. Когда все построились, то выбрали самых сильных, ловких и умелых. А на Земле осталось 7 космонавтов. Сколько космонавтов были удостоены чести полететь в космос ?
Номер слайда 27
К полёту готовились 12 космонавтов. Когда несколько космонавтов полетели , то на Земле осталось 7 . Сколько полетело в космос ?
Номер слайда 28
1) Осталось – 7 косм. Полетело – ? косм. 2) 12 косм.
3) ? косм. 7 ? 12
Полетело – ? косм. 2) 12 косм.
3) ? косм. 7 ? 12
Номер слайда 29
Решение: 12 –7= 5(косм.) Ответ: 5 космонавтов полетело в космос.
Номер слайда 30
Космонавт взял в космос 18 тюбиков картофельного пюре и 12 тюбиков мясного пюре. Съел он 20 тюбиков с космической пищей. Сколько тюбиков осталось?
Номер слайда 31
1) 18 – 12 + 20 = 2) 20 – ( 18 – 12) = 3) 18 + 12 – 20 =
Номер слайда 32
18 + 12 – 20 = 20 (тюб. ) Ответ: 20 тюбиков осталось
) Ответ: 20 тюбиков осталось
Номер слайда 33
1) У Димы 27 марок на тему «Космос», а у Серёжи 10. Сколько марок у Димы? 2) Собаки Белка и Стрелка пробыли в космосе одни сутки. А собаки Ветерок и Уголёк 23 дня. Кто был в космосе больше и на сколько?
Номер слайда 34
108 минут длился первый полет в космос Космический корабль « ВОСТОК»
Номер слайда 35
1 вариант: стр. 62 №3,6 2 вариант :стр.64 №3,4
62 №3,6 2 вариант :стр.64 №3,4
Номер слайда 36
РЕФЛЕКСИЯ Из полета возвратились Мы на землю приземлились. Как слетал ты? Расскажи! И звезду всем покажи!
Номер слайда 37
РЕФЛЕКСИЯ справился, всё решил сам решал с помощью было трудно
Номер слайда 38
РЕФЛЕКСИЯ справился, всё решил сам решал с помощью было трудно
Номер слайда 39
МОЛОДЦЫ!
Тест: Тест по математике “Решение задач”
Тест по математике “Решение задач”
Тест составлен для контроля и отработки умения решать текстовые задачи. Тест состоит из 18 вопросов. Выполняя тестовые задания, ученик должен выбрать один верный ответ из предложенных.
Тест состоит из 18 вопросов. Выполняя тестовые задания, ученик должен выбрать один верный ответ из предложенных.
Математика 2 класс | Автор: Исаева Анжелика Владимировна | ID: 801 | Дата: 2.1.2014
“;} else {document.getElementById(“torf1″).innerHTML=””;}; if (answ.charAt(1)==”1″) {document.getElementById(“torf2″).innerHTML=””;} else {document.getElementById(“torf2″).innerHTML=””;}; if (answ.charAt(2)==”1″) {document.getElementById(“torf3″).innerHTML=””;} else {document.getElementById(“torf3″).innerHTML=””;}; if (answ.charAt(3)==”1″) {document.getElementById(“torf4″).innerHTML=””;} else {document.getElementById(“torf4″).innerHTML=””;}; if (answ.charAt(4)==”1″) {document.getElementById(“torf5″).innerHTML=””;} else {document.getElementById(“torf5″).innerHTML=””;}; if (answ.charAt(5)==”1″) {document.getElementById(“torf6”). innerHTML=””;} else {document.getElementById(“torf6″).innerHTML=””;};
if (answ.charAt(6)==”1″) {document.getElementById(“torf7″).innerHTML=””;} else {document.getElementById(“torf7″).innerHTML=””;};
if (answ.charAt(7)==”1″) {document.getElementById(“torf8″).innerHTML=””;} else {document.getElementById(“torf8″).innerHTML=””;};
if (answ.charAt(8)==”1″) {document.getElementById(“torf9″).innerHTML=””;} else {document.getElementById(“torf9″).innerHTML=””;};
if (answ.charAt(9)==”1″) {document.getElementById(“torf10″).innerHTML=””;} else {document.getElementById(“torf10″).innerHTML=””;};
if (answ.charAt(10)==”1″) {document.getElementById(“torf11″).innerHTML=””;} else {document.getElementById(“torf11″).innerHTML=””;};
if (answ.charAt(11)==”1″) {document.getElementById(“torf12″).innerHTML=””;} else {document.getElementById(“torf12″).innerHTML=””;};
if (answ.charAt(12)==”1″) {document.getElementById(“torf13″).innerHTML=””;} else {document.getElementById(“torf13″).innerHTML=””;};
if (answ.charAt(13)==”1″) {document.
innerHTML=””;} else {document.getElementById(“torf6″).innerHTML=””;};
if (answ.charAt(6)==”1″) {document.getElementById(“torf7″).innerHTML=””;} else {document.getElementById(“torf7″).innerHTML=””;};
if (answ.charAt(7)==”1″) {document.getElementById(“torf8″).innerHTML=””;} else {document.getElementById(“torf8″).innerHTML=””;};
if (answ.charAt(8)==”1″) {document.getElementById(“torf9″).innerHTML=””;} else {document.getElementById(“torf9″).innerHTML=””;};
if (answ.charAt(9)==”1″) {document.getElementById(“torf10″).innerHTML=””;} else {document.getElementById(“torf10″).innerHTML=””;};
if (answ.charAt(10)==”1″) {document.getElementById(“torf11″).innerHTML=””;} else {document.getElementById(“torf11″).innerHTML=””;};
if (answ.charAt(11)==”1″) {document.getElementById(“torf12″).innerHTML=””;} else {document.getElementById(“torf12″).innerHTML=””;};
if (answ.charAt(12)==”1″) {document.getElementById(“torf13″).innerHTML=””;} else {document.getElementById(“torf13″).innerHTML=””;};
if (answ.charAt(13)==”1″) {document. getElementById(“torf14″).innerHTML=””;} else {document.getElementById(“torf14″).innerHTML=””;};
if (answ.charAt(14)==”1″) {document.getElementById(“torf15″).innerHTML=””;} else {document.getElementById(“torf15″).innerHTML=””;};
if (answ.charAt(15)==”1″) {document.getElementById(“torf16″).innerHTML=””;} else {document.getElementById(“torf16″).innerHTML=””;};
if (answ.charAt(16)==”1″) {document.getElementById(“torf17″).innerHTML=””;} else {document.getElementById(“torf17″).innerHTML=””;};
if (answ.charAt(17)==”1″) {document.getElementById(“torf18″).innerHTML=””;} else {document.getElementById(“torf18″).innerHTML=””;};
}
}
getElementById(“torf14″).innerHTML=””;} else {document.getElementById(“torf14″).innerHTML=””;};
if (answ.charAt(14)==”1″) {document.getElementById(“torf15″).innerHTML=””;} else {document.getElementById(“torf15″).innerHTML=””;};
if (answ.charAt(15)==”1″) {document.getElementById(“torf16″).innerHTML=””;} else {document.getElementById(“torf16″).innerHTML=””;};
if (answ.charAt(16)==”1″) {document.getElementById(“torf17″).innerHTML=””;} else {document.getElementById(“torf17″).innerHTML=””;};
if (answ.charAt(17)==”1″) {document.getElementById(“torf18″).innerHTML=””;} else {document.getElementById(“torf18″).innerHTML=””;};
}
}
Получение сертификата
о прохождении теста
Презентация “Решение задач.
 Закрепление” 2 класс
Закрепление” 2 класс
«Решение задач» Закрепление. 2 класс
Тема урока: «Решение задач» Закрепление.
Цель урока:
совершенствовать вычислительные навыки и умение решать задачи;
решение уравнений, работа с величинами;
Пробуждать интерес к предмету через игру.
Логическая разминка
- Из леса нужно привезти 9 брёвен. На машину можно
Положить не больше 4 брёвен. Сколько раз придётся
съездить в лес, чтобы привезти все брёвна?
- Как сделать, чтобы у прямоугольного стола стало
5 углов ?
- Если курица стоит на одной ноге, она весит 1 кг. Сколько
она будет весить, когда встанет на две ноги?
Задача от Мурки
Корова Мурка в день съедает 15 кг сена, а телёнок Гаврюша – на 10 кг сена меньше. Сколько всего сена в день съедают корова и телёнок?
Сколько всего сена в день съедают корова и телёнок?
Проверка
Корова – 15 кг
Телёнок – ? на 10 кг меньше
- 15 – 10 = 5(кг) – съедает телёнок.
- 15 + 5 = 20(кг)
Ответ: 20 кг сена в день съедают корова и телёнок.
?
Задание от галчонка
Галчонок Хватайка прыгал по дорожке: сначала 3 шага вперёд, затем 4 шага вправо, потом 5 шагов назад.
5 см
3 см
4 см
3 + 4 + 5 = 12 (см)
Восстановите
– 1 =
39 + 1=
+ 5 =
– 4 =
Решите цепочку.
-3
+40
+8
-30
-8
-20
23
2
10
52
60
32
20
9 дм 1 м 99 см 9 дм 1 ч 10 мин 53 – 20 – 3 = 30 97 – 50 – 7 35 “Сравни
91 см 9 дм
1 м 99 см
9 дм
1 ч 10 мин
53 – 20 – 3 = 30
97 – 50 – 7 35
Самостоятельная работа
2 вариант
1 вариант
80 – 6
40 + 56
54 + 6
75 – 30
1. 70 + 20
70 + 20
1.50 + 20
47+ 50
47 + 30
60 – 42
60 – 48
35 + 4
25 + 4
70 – 7
30 + 65
44 + 6
85 – 30
2. 88 – 7 * 98 – 7
64 – 20 * 30 + 24
2. 79 – 6 * 97 – 7
54 – 20 * 20 + 24
Оцените себя
4
3
2
1
Урок математики 2 класс. учебных задач и выбирать способы действия;
Конспект урока по математике.
Конспект урока по математике. Учитель: Виссарионова И.Е. Класс: 2 «А» Дата: 24.12.2018 г Предмет: математика УМК «Школа России» Тема: «Что узнали. Чему научились.» Раздел: «Устные вычисления» Урок 54 Тип:
Чему научились.» Раздел: «Устные вычисления» Урок 54 Тип:
Технологическая карта урока математики.
Технологическая карта урока математики. Предмет УМК Время проведения урока Класс ФИО учителя Тема урока Тип урока Цель урока Задачи урока Методы обучения Педагогические технологии Формы организации работы
ПодробнееВершинина Анна Владимировна
МБОУ «СОШ 76» Урок математики ( 27) Сложение и вычитание в пределах 100. Образовательная программа: Материально-техническое обеспечение: Тип урока: Цель: Задачи: Формируемые УУД: Вершинина Анна Владимировна
ПодробнееТехнологическая карта урока
Технологическая карта урока Учитель: Класс Предмет: Авторы учебника: Тарасова Екатерина Антоновна 1Г Математика В. Н. Рудницкая, Т.В.Юдачёва (Начальная школа XXI века) Тема урока. Прибавление числа 5. Тип
Н. Рудницкая, Т.В.Юдачёва (Начальная школа XXI века) Тема урока. Прибавление числа 5. Тип
2 класс. Личностные результаты
2 класс Личностные результаты У учащегося будут сформированы: понимание того, что одна и та же математическая модель отражает одни и те же отношения между различными объектами; элементарные умения в проведении
ПодробнееМетапредметные результаты
1. ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ Личностные результаты У учащегося будут сформированы: -понимание того, что одна и та же математическая модель отражает одни и те же отношения между различными объектами; -элементарные
ПодробнееДата: Класс: 1-А
Дата: 26.02.2014 Класс: 1-А Тема. Упражнения на усвоение названий компонентов при сложении и вычитании. Сравнение выражений и чисел. Подготовительные упражнения к решению задач в два действия. Измерение
Подготовительные упражнения к решению задач в два действия. Измерение
КОНСПЕКТ УРОКА МАТЕМАТИКИ
КОНСПЕКТ УРОКА МАТЕМАТИКИ Учитель: Вихрова Оксана Николаевна Класс: 4. Дата проведения: 13.10.15 г. Тема: Доли. Получение и образование долей. Тип урока: Открытие нового знания. Цели урока: Предметные:
ПодробнееТехнологическая карта урока 50
Урок математики в 1 Д классе по теме “Решаем задачи” (УМК “Начальная школа XXI век”) Учитель: Нигматуллина Татьяна Семеновна, МБОУ “СШ 21”, г. Нижневартовск. Технологическая карта урока 50 Тип урока Тема
Подробнее3 класс (1-4). Программа Истоминой Н.Б.
3 класс (1-4). Программа Истоминой Н.Б. Тема: «ПЯТИЧНАЧНЫЕ И ШЕСТИЗНАЧНЫЕ ЧИСЛА». ( Первый урок.) Цель урока: ввести понятие «пятизначные» числа, научить читать и записывать такие числа. Задачи: ОБРАЗОВАТЕЛЬНЫЕ:
Задачи: ОБРАЗОВАТЕЛЬНЫЕ:
Технологическая карта урока
Технологическая карта урока Общая часть Предмет Математика Класс, ФИО 1дополнительный класс Тема урока Тип урока Цель Планируемые образовательные результаты ПИСЬМЕННОЕ СЛОЖЕНИЕ ДВУЗНАЧНЫХ ЧИСЕЛ С ПЕРЕХОДОМ
ПодробнееУрок математики в 1Б классе по программе «Школа России» по теме: «Задачи в два действия». Первый урок в теме, когда дети переходят от решения задач-цепочек к решению задач в два действия. Цели деятельности
ПодробнееТехнологическая карта урока математики
Технологическая карта урока математики Тема урока: Задачи с величинами цена, количество, стоимость. Тип урока: открытие нового знания (в технологии деятельностного метода) Класс: 2 класс Учитель: Волошина
ПодробнееУрок математики во 2 классе
Урок математики во 2 классе Автор: Матвеева С. А., учитель начальных классов Тема: Приемы вычислений для случаев вида 36-2, 36-20 Цели урока: 1. Познакомить детей с приемами устных вычислений вида 36-2,
А., учитель начальных классов Тема: Приемы вычислений для случаев вида 36-2, 36-20 Цели урока: 1. Познакомить детей с приемами устных вычислений вида 36-2,
Планируемые результаты
Личностные Планируемые результаты У обучающегося будут сформированы: начальные (элементарные) представления о самостоятельности и личной ответственности в процессе обучения математике; начальные представления
Подробнее«Числовые и буквенные выражения».
Муниципальное казѐнное общеобразовательное учреждение «Дуровская средняя общеобразовательная школа» Сафоновского района Смоленской области «Числовые и буквенные выражения». Учитель математики I категории
ПодробнееКонспект урока во 2 классе
Конспект урока во 2 классе Тема: Вычитание двузначных чисел с переходом через разряд Цель: Знакомство с приемами вычитания двузначного числа из двузначного с переходом через разряд Задачи: – познакомить
ПодробнееРабочая программа по математике 2 класс
МБОУ «Кипринская основная общеобразовательная школа» Рабочая программа по математике 2 класс Составитель: учитель нач. классов Пыстогова В. В. 2018 2019 учебный год 1 Пояснительная записка Рабочая программа
классов Пыстогова В. В. 2018 2019 учебный год 1 Пояснительная записка Рабочая программа
Технологическая карта урока математики.
Технологическая карта урока математики. Андреева Надежда Николаевна Тема урока «Умножение десятичных дробей на натуральное число» (5 класс) Цели (задачи) урока образовательные: Формировать умения выполнять
ПодробнееТехнологическая карта урока
Технологическая карта урока ФИО учителя: Сидорова Сусанна Петровна Класс: 1 класс УМК: «Школа России» Предмет: математика Тема: Перестановка слагаемых Тип урока: урок «открытия» нового знания Цель: вывести
ПодробнееПояснительная записка
Пояснительная записка Рабочая программа по предмету «Математика» для 2 класса разработана на основе требований к результатам освоения основной образовательной программы начального общего образования Лангепасского
ПодробнееКонспект урока математики
Конспект урока математики Класс: 1а ГБОУ СОШ 185 с углублённым изучением английского языка Учитель: Федотова Н. Н. Тема урока: «Задачи в два действия» Цель урока: познакомить с составными задачами, состоящими
Н. Тема урока: «Задачи в два действия» Цель урока: познакомить с составными задачами, состоящими
1. ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ
1. ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ Личностные результаты У учащегося будут сформированы: -понимание того, что одна и та же математическая модель отражает одни и те же отношения между различными объектами; -элементарные
Подробнее«Прямая. Луч. Отрезок.»
«Прямая. Луч. Отрезок.» Урок математики во 2-м классе ХОД УРОКА Деятельность учителя Организационный момент Устный счет. 1)Найди закономерность и вставь пропущенные числа. Кто быстрее назовет весь ряд?
ПодробнееТехнологическая карта
1. Ф.И.О. учителя: Шевякова Тамара Анатольевна 2. Урок математики в 3 классе ФГОС 3. Тема: Знакомство с понятием «Дробное число» 4. Место и роль урока в изучаемой теме: урок освоения новых знаний Цель
Место и роль урока в изучаемой теме: урок освоения новых знаний Цель
Кромского района Орловской области
Муниципальное бюджетное общеобразовательное учреждение Кромского района Орловской области «Черкасская средняя общеобразовательная школа» Конспект урока математики по теме: «Порядок выполнения действий.
ПодробнееПояснительная записка
Пояснительная записка Рабочая программа по математике для 2 класса составлена с учётом: – Федерального государственного образовательного стандарта начального общего образования второго поколения, утверждённого
Подробнее6 урок из 7 части речи
Технологическая карта урока Предмет: русский язык класс: 3 Учитель: Корякова Анастасия Александровна Тема урока Место урока по теме (в разделе/главе) Разбор глагола как 6 урок из 7 части речи Тип урока
ПодробнееТехнологическая карта урока
Технологическая карта урока Приложение 2. Тема: Конкретный смысл действия умножения. Тип урока: урок первичного предъявления знаний Цель: создать условия для организации совместной деятельности учащихся
Тема: Конкретный смысл действия умножения. Тип урока: урок первичного предъявления знаний Цель: создать условия для организации совместной деятельности учащихся
Урок математики в 1 классе
Учитель: Бажутова С.Г. Тема: Единица длины сантиметр. Урок математики в 1 классе Цель урока: формирование представлений о единице длины (сантиметре) как единой принятой мерке, путем сравнения различных
ПодробнееУрок математики в 4Г классе
Тема: «Записываем числовые последовательности». Урок математики в 4Г классе Цели урока: формирование умения записывать числовые последовательности, вычисляя несколько первых членов данной последовательности;
ПодробнееРешение задач онлайн
Решение Ваших математических задач в онлайн режиме. Бесплатная версия программы предоставляет Вам только ответы. Если вы хотите увидеть полное
решение, Вы должны зарегистрироваться для бесплатной полной пробной версии.
Если вы хотите увидеть полное
решение, Вы должны зарегистрироваться для бесплатной полной пробной версии.
Другие программы
Основы математики
Онлайн программа решения математических задач предлагает Вам решение в режиме онлайн задач с дробями, корнями, метрическими преобразованиями.
Вы можете найти площадь и объем прямоугольника, окружности, треугольника, трапеции, куба, цилиндра, конуса, пирамиды, шара.
Вы можете упростить, найти значение, объединять и умножать выражения.
Онлайн программа решения задач курса предварительной алгебры (геометрии)
Вы можете решать все задачи с основного раздела математики а также координатных задач, простых уравнений, неравенств, упрощать выражения.
Вы можете подсчитывать выражения, объединить выражения и умножать / делить выражения.
Онлайн программа решения задач по алгебре
Мы рекомендуем Вам зарегистрироваться для этой онлайн программы.Решите Ваши задачи (уравнения, неравенства, радикалы, построение графиков, решение полиномов) в онлайн режиме.

Если Ваша домашняя работа включает в себя математические уравнения, неравенства, функции, многочлены, матрицы, значит регистрация для тестовой версии – это правильный выбор.
Онлайн программа решения задач по тригонометрии
Находит значения всех типов выражений (синус, косинус, тангенс, котангенс, секанс, косеканс), уравнений, неравенств.
Строит графики тригонометрических функций.
Тригонометрия прямоугольного треугольника.
Онлайн программа решения задач курса предварительной алгебры
Включает в себя все вышеперечисленное функции плюс нахождение пределов (LIM), сумм, матриц.
Онлайн программа решения задач курса высшей математики
Решение задач c определенными, неопределенными интегралами.
Онлайн программа решения статистических задач
Решайте задач с нахождением вероятности, комбинаторные задачи.
Статистические задачи – найти среднее (арифметическое, геометрическое, квадратическое) значение, распределение, нормальное распределение, т-распределение.
Онлайн программа успешно проводит тестирование статистических гипотез
Урок второго класса Счет до решения задач
Чтобы начать урок, я снова ввожу пустую числовую строку. Я даю каждому студенту пустую числовую строку на полосе предложений. Прошу сделать отметку прямо у левого края. Затем я приказываю им положить 2 пальца и сделать еще одну отметку. Я прошу их повторять это до тех пор, пока числовая строка у них не будет отмечена четными пробелами.
Затем я прошу их поставить цветную фишку на отметку у левого края. Я говорю им, чтобы они представили, что это число 18.Я прошу их использовать числовую линию, чтобы сосчитать 10 и найти на 10 больше 18. Мы проверяем наши ответы. Теперь прошу переместить фишку на отметку в правом конце строки. Я прошу их представить, что это число равно 25. Я прошу их сосчитать 10 и найти 10 меньше 25.
Я повторяю это еще с несколькими числами. Я хочу усилить концепцию «десять больше, десять меньше» как способ понять сложение и вычитание десятков.
Затем я разбиваю класс на 3 группы в зависимости от их понимания числовой линии из неформальных оценок предыдущего урока.
Группе, которая может использовать числовую прямую для решения задач, выдается контрольный документ с текстовыми задачами, требующими сложения двухзначных чисел. Их просят работать вместе с партнерами или в одиночку, чтобы решать проблемы, используя свою числовую линию, если это необходимо для поддержки их мышления.
Группа, которая имеет некоторое представление о числовой строке, но испытывает трудности с пустой строкой, будет работать с родителем, чтобы найти число в строке, а затем добавить к нему второе число. Здесь цель состоит в том, чтобы учащиеся поняли, что им не всегда нужно начинать с левой отметки.Им нужно подумать о том, какое число они добавляют, то есть далеко ли оно от числа, с которого они начинают, или очень близко. Если он далеко, они должны считать по 2 или 10. Группа вместе примет некоторые решения об отправных точках, а затем решит проблемы.
Группа, которая все еще не понимает, как работает числовая линия (они всегда хотят начинать с 1, даже если они ищут число 89), будет работать со мной, чтобы найти одно число относительно другого, считая единицы или Комбинации 2 и установка фишек на два числа.Если учащиеся овладеют этим навыком, мы попробуем начать с однозначного числа и добавить второе однозначное число.
Математика / Решение задач в общем ядре
ОбзорИспользование моделей – важный шаг, помогающий учащимся перейти от конкретной манипулятивной работы с текстовыми задачами к абстрактному этапу создания уравнения для решения контекстных задач. Научившись использовать простые модели для представления ключевых математических соотношений в словесной задаче, учащиеся могут легче разбираться в словесных задачах, распознавать как числовые отношения в данной задаче, так и связи между типами задач, и успешно решать задачи с уверенностью их решения разумны.
Важность Почему моделирование текстовых задач важно?
У студентов часто возникают проблемы со словами. Многие студенты просто ищут какие-то числа и что-то с ними делают, надеясь, что они решат проблему.
Учащиеся должны выработать привычку сначала разбираться в проблеме. Диаграмма или модель часто фокусируются на понимании проблемы, а не просто на получении ответа. Затем модель можно использовать для создания продуманного уравнения.Модель и уравнение можно использовать в качестве проверки рассуждений после того, как учащийся получит решение.
Решение проблем не заканчивается на ответе. Процесс должен продолжаться после «получения ответа» на рассуждение о том, имеет ли ответ смысл.
Что такое моделирование текстовых задач?
Модели на любом уровне могут варьироваться от простых до сложных, от реалистичных до представительных. Молодые студенты часто решают начальные словесные задачи, разыгрывая их и моделируя их с реальными объектами проблемной ситуации, например.грамм. плюшевых мишек или игрушечных машинок. Со временем они расширяются до использования репрезентативных рисунков, сначала рисуя рисунки, которые реалистично изображают элементы проблемы, а затем переходят к многоцелевым представлениям, таким как круги или счетные метки. После множества конкретных опытов с реальными задачами со словами, включающими соединение и разделение или умножение и разделение объектов, учителя могут переводить учащихся на рисунки с перевернутой буквой V и гистограммы, которые являются многоцелевыми графическими организаторами, привязанными к определенным типам задач со словами.
Моделирование базовых числовых отношенийПростые диаграммы, иногда известные как числовые связи, треугольники фактов, ситуационные диаграммы или графические изображения, все чаще появляются в учебных материалах. Но способности учащихся решать проблемы и относительное мышление выиграют, если будут более рутинно использовать эти диаграммы и модели.
Маленькие дети могут начать видеть числовые отношения, существующие в семье фактов, благодаря использованию модели, из которой они выводят уравнения.Связь чисел и перевернутая буква V – это одна простая модель, которая помогает учащимся увидеть отношения сложения / вычитания в семействе фактов и может использоваться с задачами со словами, требующими простого соединения и разделения. Связь чисел, а затем модель перевернутой буквы V могут быть адаптированы для семейств фактов умножения и деления. Кроме того, учащиеся могут подумать о взаимосвязях между числами в перевернутой букве V в формальных терминах, , сложение, и , сумма , или, проще, , часть, и , всего , как показано на схемах ниже.
Конкретный пример для данной суммы 10 будет следующим, в зависимости от того, какой элемент проблемы неизвестен.
6 + 4 =? 6+? = 10? + 4 = 1
4 + 6 =? 10-6 =? 10 – 4 =?
Несмотря на то, что они часто используются с семействами фактов и изучением основных фактов, диаграммы с числовыми связями и перевернутые буквы V также могут хорошо работать при решении текстовых задач.Студентам необходимо подумать о том, что они знают и чего не знают в словесной задаче – известны ли обе части или только одна из них? Правильно разместив известные величины на перевернутой V-диаграмме, учащиеся с большей вероятностью определят полезное уравнение для решения проблемы и увидят результат как разумный для ситуации. Например, рассмотрим следующую задачу:
У Закари было 10 вагонов. Захари подарил своему брату 3 вагона. Сколько вагонов сейчас у Закари?
Студенты должны определить, со сколькими суммами Захари начал (всего или целиком ), и сколько он отдал ( часть от общего числа ).Итак, им нужно узнать, сколько осталось (другая часть из общего числа ). Следующая перевернутая V-диаграмма представляет отношения между номерами этой проблемы:
3 +? = 10 или 10 – 3 =?, Значит, у Закари осталось 7 вагонов.
По мере того, как учащиеся переходят к умножению и делению, модель перевернутой буквы V все еще может использоваться либо в режиме повторного сложения, либо в режиме умножения. Ситуации разделения не требуют новой модели; деление рассматривается как обратное умножению или ситуация, когда один из факторов неизвестен.
Опять же, перевернутая V-диаграмма может быть полезна при решении задач умножения и деления слов. Например, рассмотрим следующую задачу:
Фонг посадил 18 растений томатов в 3 ряда. Если в каждом ряду было одинаковое количество растений, сколько растений было в каждом ряду?
Студенты могут видеть, что они знают продукт и количество строк. Число В строке неизвестно. Любая из приведенных ниже диаграмм может помочь решить эту проблему, убедив учащихся, что шесть раз подряд – разумный ответ.
Хотя перевернутая V-диаграмма может быть расширена до многозначных чисел, она обычно используется с проблемами, связанными с базовыми семействами фактов. Расширение использования модельной диаграммы с перевернутой буквой V должно усилить взаимосвязь между числами в семействе фактов, что сделает его полезным и быстрым визуальным средством для решения простых задач со словами с дополнительным преимуществом использования и увеличения удержания основных фактов.
Модели и типы задач для вычисленийПо мере того, как дети переходят к работе с многозначными числами, учителя могут переводить учащихся на чертежи ленточных диаграмм / гистограмм, быстрые наброски, которые помогают учащимся увидеть взаимосвязь между важными числами в словесной задаче и определить, что известно и неизвестно в ситуации.
Знакомя учащихся с грифельными моделями, учитель получает важные наглядные пособия, помогающие учащимся думать о математических отношениях между числами в заданной задаче со словом.
С ленточной диаграммой / гистограммой отношения между числами во всех этих типах задач становятся более прозрачными и помогают студентам перебросить мышление от работы с манипуляторами и рисования картинок к символической стадии написания уравнения для ситуации. При рутинном использовании диаграмм и хорошо организованных обсуждениях учителями ученик начнет понимать части словесной задачи и то, как эти части соотносятся друг с другом.
Проблемы частично-частично-целиком. Задачи Part-Part-Whole полезны с задачами со словами, которые относятся к совокупности вещей, например коллекции. Обычно это более статичные ситуации, включающие два или более подмножества целого набора. Рассмотрим проблему,
Коул имеет 11 красных блоков и 16 синих блоков. Сколько всего блоков у Коула?
Учащиеся могут построить простой прямоугольник из двух частей, чтобы обозначить два известных набора блоков (части / дополнения).Неважно, чтобы части прямоугольника были точно пропорциональны числам в задаче, но некоторое внимание к их относительному размеру может помочь в решении проблемы. Неизвестным в этой задаче является то, сколько их всего (всего / всего / суммы), что обозначено скобкой (или перевернутой буквой V) над полосой, обозначающей общее количество двух наборов блоков. Первая барная модель ниже отражает информацию в задаче о блоках Коула.
11 + 16 =? Итак, у Коула всего 27 блоков.
Аналогичная модель будет работать для проблемы, когда известна вся сумма, но одна из частей (недостающее слагаемое) неизвестна. Например:
У Коула было 238 блоков. 100 из них были желтыми. Если все блоки Коула синие или желтые, сколько их было синими?
Следующая модель стержня может быть полезна в решении этой проблемы.
100 +? = 238 или 238 – 100 =? Итак, у Коула 138 синих блоков.
Ответ должен быть немного больше 100, потому что 100 + 100 равно 200, но здесь всего 238, поэтому синих блоков должно быть немного больше 100.
Столбиковую модель «часть-часть-целая» можно легко расширить до больших чисел и других числовых типов, таких как дроби и десятичные дроби. Рассмотрим задачу:
Летисия прочитала 7 ½ книг для читателей. Всего она хочет прочитать 12 книг. Сколько еще книг ей нужно прочитать?
Первая диаграмма ниже отражает эту проблему. Любая проблема со словом, которую можно рассматривать как части и целое, реагирует на диаграммы моделирования стержней. Если у задачи есть несколько слагаемых, учащиеся просто рисуют на полосе достаточно частей, чтобы отразить количество слагаемых или частей, и указывают, является ли одна из частей или целое / сумма неизвестными, как показано на втором рисунке ниже.
12 – 7 ½ =? или 7 ½ +? = 12, поэтому Летиции нужно прочитать еще 4 ½ книги.
Задачи соединения (сложения) и разделения (вычитания).
Студенты, которые не могут решить, нужно ли им прибавлять или вычитать, а затем умножать или делить, находят организационный потенциал гистограммы невероятно полезным.
У Марии было 20 долларов. Она получила еще 11 долларов за присмотр за детьми. Сколько у нее сейчас денег? Рассмотрим эту задачу объединения:
Студенты могут определить, что начальная сумма в 20 долларов является одной из частей, 11 долларов – другой частью (добавочная сумма), а неизвестным является сумма / вся сумма или сколько денег она есть сейчас.Первая диаграмма ниже помогает представить эту проблему.
Рассмотрим соответствующую ситуацию с вычитанием:
У Марии был 31 доллар. Часть денег она потратила на новый компакт-диск. У Марии осталось 16 долларов.
Вторая диаграмма выше представляет эту ситуацию. Студенты могут использовать модель, чтобы помочь им определить, что общая сумма сейчас составляет 31 доллар, одна из частей (вычитающее изменение) неизвестна, поэтому другая часть – это те 16 долларов, которые у нее остались.
Проблемы сравнения. Проблемы со сравнением обычно считались трудными для детей. Частично это может быть связано с акцентом на вычитание, который используется в задачах со словами, которые включают ситуации «убрать», а не нахождение «разницы» между двумя числами. Интересно, что исследования в странах, которые часто используют гистограммы, показали, что учащиеся не находят задачи сравнения намного более сложными, чем задачи «часть-часть-целое» (Yeap, 2010, стр. 88-89).
Модель с двумя стержнями может помочь сделать задачи сравнения менее загадочными.В основном, задачи сравнения включают две величины (либо одна величина больше другой, либо они равны) и разницу между величинами. Можно нарисовать две полосы, по одной для каждой величины, причем разница будет представлена пунктирной областью, добавленной к меньшему количеству. Например, учитывая задачу:
Тамека участвовал в 26 окружных ярмарках. Ее друг Джексон проехал 19 поездок. На сколько аттракционов ездил Тамека больше, чем Джексон?
Учащиеся могут создать диаграмму столбцов сравнения, показанную ниже, где большее количество, 26, является более длинным столбцом.Пунктирная часть показывает разницу между количеством поездок Джексона и Тамеки, или насколько больше у Тамека, чем у Джексона, или на сколько дополнительных поездок Джексон должен был бы проехать, чтобы иметь такое же количество поездок, как и Тамека.
26-19 =? или 19+? = 26; разница в 7, так что Тамека проехал еще 7 аттракционов.
Задачи сравнения выражают несколько различных формулировок отношений. Если Тамека проехал на 7 аттракционов больше, чем Джексон, то Джексон проехал на 7 аттракционов меньше, чем Тамека.Варианты схемы модели с двойной полосой могут сделать для учащихся более наглядными отношения, сформулированные по-разному. Студентам часто бывает полезно осознать, что в какой-то момент обе величины имеют одинаковое количество, как показано на модели ниже пунктирной линией, проведенной от конца прямоугольника, представляющего меньшее количество. Но у одной из величин больше, на что указывает область справа от пунктирной линии на более длинной полосе. Разницу между количествами можно определить путем вычитания 19 из 26 или сложения от 19 до 26 и получения 7, что означает, что 26 на 7 больше, чем 19, или 19 означает, что на 7 меньше 26.
Задачи со словами сравнения особенно проблематичны для изучающих английский язык, поскольку вопрос можно задать несколькими способами. Изменение полос сравнения может сделать вопросы более прозрачными. Вот несколько вариантов ответов на вопросы о двух количествах поездок, на которых ездили Тамека и Джексон:
- На сколько аттракционов проехал Тамека больше, чем Джексон?
- На сколько поездок Джексон совершил меньше поездок, чем Тамека?
- Сколько еще поездок пришлось бы проехать Джексону, чтобы проехать столько же поездок, что и Тамека?
- На сколько меньше поездок пришлось бы проехать Тамеке, чтобы проехать столько же поездок, что и Джексон?
Сравнения также могут быть мультипликативными.Рассмотрим проблему:
В коллекции Хуана 36 компакт-дисков. Это в 3 раза больше дисков, чем у его брата Маркоса. Сколько компакт-дисков у Маркоса?
В этой ситуации ученики должны построить модель стержня, показанную ниже слева, из 3 частей. Студенты могут разделить 36 на 3 равные группы, чтобы показать количество, которое нужно взять 3 раза, чтобы создать в 3 раза больше компакт-дисков для Хуана.
36 ¸ 3 =? или 3 раза? = 36 12 + 12 + 12 =? (или 3 x 12 =?)
, так что у Маркоса 12 компакт-дисков.Итак, у Хуана 36 компакт-дисков.
Аналогичная модель может использоваться, если большее количество неизвестно, но меньшее количество и мультипликативное отношение известны. Если проблема была:
У Хуана есть компакт-диски. У него в 3 раза больше компакт-дисков, чем у Маркоса, у которого 12 компакт-дисков. Сколько компакт-дисков у Хуана?
Как видно на диаграмме вверху справа, студенты могут положить 12 в коробку, чтобы показать количество компакт-дисков, которые есть у Маркоса; затем продублируйте это 3 раза, чтобы увидеть, что у Хуана в 3 раза больше компакт-дисков.Тогда общее количество, которое есть у Хуана, будет суммой этих трех частей.
Задачи умножения и деления. Та же модель, что и для мультипликативных сравнений, также будет работать для основных задач умножения слов, начиная с однозначных множителей. Рассмотрим проблему:
У Аланы было 6 пакетов жевательной резинки. В каждой упаковке 12 штук жевательной резинки. Сколько всего жевательных резинок у Аланы?
В следующей линейчатой модели для визуализации проблемы используется повторное сложение умножения.
12 + 12 + 12 + 12 + 12 + 12 = 72 (или 6 x 12 = 72)
, так что у Аланы 72 кусочка жевательной резинки.
По мере того, как учащиеся переходят к многозначным множителям, они могут использовать модель с многоточием, чтобы упростить гистограмму. Например:
Сэм пробегает 32 км в день в течение апреля, чтобы подготовиться к гонке. Если Сэм бегает каждый день месяца, сколько всего километров он пробежал в апреле?
30 x 32 км = 30 x 30 км + 30 x 2 км = 960 км
Сэм пробежал 960 км за 30 дней апреля.
Поскольку деление – это обратное умножение, в задачах деления слов будет использоваться модель мультипликативного столбца, в которой произведение (делимое) известно, но один из факторов (делитель или частное) неизвестен.
Задачи, связанные со ставками, дробями, процентами и несколькими шагами. По мере того, как учащиеся переходят в старшие классы, они могут применять новые концепции и многоступенчатые задачи со словами к чертежам моделей стержней. Скемп (1993) определил, что реляционное мышление имеет решающее значение для развития математики.Учащийся должен уметь расширять свое мышление на основе моделей, которые они использовали ранее, связывая и адаптируя свои знания к новым ситуациям.
Рассмотрим задачу о скорости и расстоянии:
Фонг проехала 261 милю, чтобы увидеться с бабушкой. В среднем она разгонялась до 58 миль в час. Сколько времени ей понадобилось, чтобы добраться до дома бабушки?
Следующая модель строится на основе модели «часть-часть-целое» с использованием формата повторяющегося сложения для умножения и деления. Предполагается, что учащиеся имеют опыт использования модели для задач деления, частные которых являются не просто целыми числами.По мере того, как они наращивают (или делят) 261 милю, они рассчитывают, что пять 58-х будут соответствовать 5 часам путешествия, а оставшиеся 29 миль будут представлены половинным квадратом, поэтому решение состоит в том, что Фонг займет 5½ часов. времени в пути, чтобы добраться до дома бабушки.
Даже более сложную проблему скорости можно решить с помощью комбинации подобных моделей. Рассмотрим эту задачу:
Сью и ее подруга Энн вместе отправились в путешествие. Сью проехала первые 2/5 поездки, а Энн проехала 210 миль за последние 3/5 поездки.Средняя скорость Сью составляла 60 миль в час, а Энн – 70 миль в час. Как долго у них была поездка?
Есть несколько способов, которыми учащиеся могут комбинировать или изменять базовую модель стержня. Одно из решений может заключаться в следующем, где первое неизвестное – сколько миль проехала Сью. Полоса, разделенная на пятые части, показывает, как рассчитать километры, которые проехала Сью. Поскольку мы знаем, что 210 миль, которые проехала Энн, составляют 3/5 всего пути, каждая из ящиков Анны, каждая из которых представляет 1/5 пути, составляет 70 миль. Таким образом, Сью проехала две части по 70 миль, или 140 миль, что составляет 2/5 от общей поездки.
Теперь диаграмму необходимо расширить, чтобы показать, как рассчитать количество часов. Участок 210 миль Анны, разделенный на ее скорость 70 миль в час, займет 3 часа, как указано в следующем расширении диаграммы. Расстояние Сью в 140 миль теперь необходимо разделить на сегменты со скоростью 60 миль в час, чтобы определить время ее вождения, равное 2 1/3 часа. Таким образом, общая поездка в 350 миль займет 5 1/3 часа времени вождения, учитывая две нормы вождения.
Рассмотрим более простую многоступенчатую задачу:
Роберто купил 5 спортивных напитков по 1 доллару.25 каждый. Роберто дал кассиру 20 долларов. Сколько сдачи он получил обратно?
Опять же, у учащихся могут быть вариации, когда они начинают расширять использование диаграмм в многоэтапных или более сложных задачах. Некоторые ученики могут использовать сразу две диаграммы, как показано ниже слева. Другие могут указывать вычисления на одной диаграмме, как показано на диаграмме справа.
Имея рутинный опыт моделирования стержней, учащиеся могут расширить использование моделей для решения задач, связанных с отношениями, которые могут быть выражены с помощью переменных.Рассмотрим эту простую задачу, которую можно представить алгебраически:
Каллан и Авриель собрали в общей сложности 190 ошибок для научного проекта. Каллан собрал на 10 ошибок больше, чем Авриель. Сколько жуков собрал Каллан?
Пусть n равно количеству ошибок, собранных Авриель, а n + 10 равно количеству ошибок, собранных Калланом. Студенты могут создать следующую модель:
Поскольку n + n = 180 (или 2 n = 180), n = 90.Таким образом, Каллан собрал 90 + 10 или 100 ошибок, а Авриэль собрала 90 ошибок, всего 190 ошибок, собранных вместе.
При использовании модельного метода учащиеся должны переводить информацию и отношения в словах в визуальные представления, которые являются моделями. Они также должны манипулировать и преобразовывать визуальные представления, чтобы генерировать информацию, полезную при решении заданных проблем.
Понимание структуры словесной задачи включает в себя знание того, как связана математическая информация в данной текстовой задаче и как выделить компоненты, необходимые для решения проблемы.Чертежи ленточной диаграммы / гистограммы могут помочь учащимся лучше определять переменные, участвующие в проблеме, а также отношения между ними. Эта способность сосредотачиваться на отношениях между числами в данной задаче и распознавать математическую структуру как особый тип проблемы является частью реляционного мышления – критически важным навыком для успеха в алгебре. Использование перевернутой буквы V и гистограммы в предалгебраическую работу в классах K-7 может сделать учащихся более подготовленными к формальному изучению алгебры.
Это отличный сайт для практики решения проблем – моделирования задач с помощью ленточной диаграммы / гистограммы.
Стратегии решения проблем Word для учащихся K – 4 классов [Бесплатные шаблоны]
Стратегии решения математических задач должны начинаться еще в детском саду или первый класс! Поскольку в последние годы чтению научной литературы уделяется больше внимания, мы можем рассматривать текстовые задачи как часть жанра научной литературы. Загрузки для сегодняшнего сообщения включают несколько шаблонов или графических органайзеров, которые помогут студентам найти связь между задачами со словами и уравнениями, которые представляют эти проблемы.
Как учитель математики, я много раз слышал, что «мы все учителя чтения», и этот пост покажет, как связаны эти две области, как математика, так и чтение, поскольку ученики создают представления, которые помогают им перейти от слов к уравнениям и наоборот. Кроме того, возьмите мои загружаемые шаблоны для нескольких представлений ниже! Используя эти шаблоны для разработки уроков, вы можете соответствовать многим Стандартам математической практики, которые лежат в основе стратегий решения математических словесных задач.
- SMP 1: разбираться в проблемах и настойчиво их решать
- SMP 2: Размышляйте абстрактно и количественно
- SMP 4: Модель с математикой
- SMP 7: Найдите и используйте структуру
Манипулятивное и визуальное представление математических словесных задач тесно связаны. Эти представления представляют собой стратегии решения математических задач, которые могут использовать учащиеся. Я надеюсь, что вы терпите меня, когда я расскажу немного об истории того, что я узнал об обучении студентов с помощью манипуляций и репрезентаций.В 1960-х Джером Брунер ввел термины активный, иконический и символический, чтобы описать, как ученики продвигаются от использования манипуляторов к созданию рисунков, основанных на манипуляциях, к использованию только чисел и символов. Сегодня мы можем назвать эти шаги конкретными, репрезентативными (полубетонными) и абстрактными. Сингапурская математика использует термины конкретный, графический и абстрактный. Все эти три набора терминов относятся к одной и той же основной стратегии мастерского использования манипуляторов для демонстрации математической идеи, затем ученики излагают эту идею с помощью бумаги и карандаша (повторно представляют ее) и, наконец, используют для обозначения только числа и символы. представляют это.
Я бы посоветовал студентам сначала поработать с такими манипуляторами, как счетчики плюшевых мишек, маленькие кубики или даже бобы. Они помогают показать взаимосвязь между ситуациями, о которых учащиеся читают в словесной задаче. Лучше всего, чтобы они использовали шаблон для представления своей идеи, используя десятикратную рамку, числовую связь, массив или модель области и ленточную диаграмму (полубетонные, графические или пиктограммы). Наконец, они поймут значение уравнения (абстрактное или символическое представление), когда они его напишут.
Если вы ищете стратегии решения задач по математике в детском саду до 4-го класса, вы найдете нижеприведенные загружаемые шаблоны очень полезными. Используя шаблоны, вы можете дать учащимся стратегии для чтения текстовых задач и создания представлений для их решения или даже дать им представление и попросить их создавать текстовые задачи. Используйте эти загружаемые шаблоны, чтобы дать учащимся стратегии решения математических задач, включающие сложение, вычитание, умножение и деление. Распечатайте их и используйте сегодня в своем классе!
Детский сад и 1 класс – добавление
Ожидается, что в младших классах учащиеся только прибавят.Типичная проблема со словами может быть такой: «У Криса три апельсина и два яблока. Сколько фруктов у Криса вместе? » Студенты могут смоделировать задачу, используя кубики разного цвета. В загружаемом шаблоне есть место для вопроса, после чего учащиеся могут нарисовать рисунок на основе своих манипуляций. Ключевые полуабстрактные представления для этих студентов – десять рамок и числовые связи. В частности, с числовыми связями учащиеся должны думать о частях и итогах. Наконец, студенты пишут дополнительное предложение.
Для добавления доступны два шаблона. В первом есть один десятифрейм, предназначенный для детского сада, где ученики добавляют только в пределах десяти. Во втором есть две десятичные рамки, ориентированные на первый класс, где ученики складывают в пределах двадцати. Студентов продвинутого уровня можно подтолкнуть к представлению своих дополнительных предложений с помощью числовой линии, но это не входит в эту загрузку.
1 и 2 классы – сложение и вычитание
По мере того, как учащиеся переходят в 1-й и 2-й классы, они узнают о взаимосвязи между сложением и вычитанием.Концептуально это отличается от ранней работы с простым добавлением. Стратегии решения проблем со сложением слов с двумя слагаемыми могут быть шаблонными. Два числа в словарной задаче необходимо сложить, но когда учащиеся сталкиваются с текстовыми задачами с отсутствующей частью, у них должны быть стратегии и представления, чтобы думать о частях и целых.
В шаблоне для сложения и вычитания вы найдете числовые связи и ленточную диаграмму. Каждый шаблон имеет рамку с двумя числовыми связями, одна с удаленной «целиком», а другая – с одной из «частей».Студенты должны прочитать задачу и решить, является ли проблема типом отсутствующей части или отсутствующей целой. Здесь нам нужно связать чтение с математикой. Точно так же учащиеся должны заполнить ленточную диаграмму, используя идеи части и целого, но на этот раз используя знак «?» или буква как переменная, обозначающая неизвестное.
Наконец, учащиеся должны написать хотя бы одно предложение сложения или вычитания, чтобы представить проблему с помощью знака «?» или переменная для неизвестного. Затем они могут написать числовое предложение, показывающее «решение», вместо вопросительного знака или переменной.Студентов продвинутого уровня можно подтолкнуть к представлению числовых предложений с помощью числовой линии, но это не входит в эту загрузку.
Классы 3 и 4 – умножение и деление
Опираясь на работу во втором классе, учащиеся 3 и 4 классов должны применять стратегии решения словесных задач, включающие умножение и деление. Эти задачи требуют другого представления, чем стратегии математических задач со словами, включающие сложение и вычитание.
Загружаемый шаблон для классов 3 и 4 включает место для модели массива, модели области и ленточной диаграммы. Для ясности: учащиеся могут представлять задачи умножения и деления слов, используя любое из этих трех представлений:
Вы можете видеть, что эта серия абстрактных представлений умножения и деления переходит от более конкретных (полуабстрактных) версий, где вы можете считать точки или квадраты, к более абстрактным версиям, где студенты переходят от счета к поиску решений.Это также помогает учащимся на начальном этапе использовать переменные для представления неизвестных, поскольку они могут маркировать отсутствующие части модели области или массива буквой.
В последнем поле загружаемого шаблона студентам предлагается написать уравнение, используя переменную или вопросительный знак для неизвестного, а затем «решить» его. Под решением я подразумеваю не использование алгебраических шагов (т. Е. Деление обеих сторон на три), а вместо этого просто написать «x = 7» в случае примера, приведенного непосредственно выше.Учащиеся могли использовать любую форму рассуждений, в том числе вернуться к использованию физических счетчиков и разделить их на равные группы.
Как стандарты математической практики связаны с использованием шаблоновЯ хочу поделиться некоторыми мыслями о том, как эти загружаемые шаблоны можно использовать для разработки стратегий учащихся по решению математических словесных задач и использования Стандартов математической практики (SMP).
SMP 1: разбираться в проблемах и настойчиво их решать.
Когда студентов просят составить схему, они должны четко понимать, что такое части и целое. Предоставление им представлений, таких как числовые связи, модели площадей и массивов или ленточные диаграммы, помогает им понять проблемы и взаимосвязи элементов, которые они обнаруживают при чтении слова «проблема».
SMP 2: Размышляйте абстрактно и количественно.
Когда учащиеся создают представление, такое как в Загрузке 4 (3 прямоугольника «x» равны 21), это абстрактное представление.Он ничего не говорит о том, в чем проблема. Когда ученики читают задачу о количестве (три игрушки общей стоимостью 21 доллар) и составляют ленточную диаграмму, они переходят от количеств к абстракциям. Другой способ использования этих шаблонов – заполнить ленточную диаграмму (или модель массива или области) и попросить учащихся заполнить остальные поля. Другими словами, ученики будут создавать свои собственные задачи с текстом из ленточной диаграммы. Они начинают с абстрактного представления и приходят к количественной идее (это может быть 21 яблоко и три человека или 21 шоколад и три коробки и т. Д.).
SMP 4: Модель с математикой.
Такие модели, такие как модели с областями и ленточные диаграммы, если они будут введены на раннем этапе, помогут учащимся, когда они используют модели с областями в старших классах для моделирования более сложных задач.
SMP 7: Ищите и используйте структуру.
Чтение задач со словами, а затем создание представлений с использованием шаблонов поможет студентам найти ключевые слова и их отношение к структуре частей и целых, строк и столбцов, факторов, итогов и делителей.Просмотр общих базовых структур с использованием числовых связей, десяти рамок, моделей площадей и массивов, а также ленточных диаграмм помогает укрепить общие базовые структуры, которые появляются в различных текстовых задачах.
РезюмеЗагрузите и используйте мои бесплатные шаблоны, чтобы помочь студентам установить связь между задачами со словами и уравнениями, которые представляют эти проблемы. Когда вы это сделаете, вы будете вовлекать учащихся в использование изложенных выше Стандартов математической практики, давая им возможность представить себе словесные проблемы в своей голове и создать представления, показывающие взаимосвязь задействованных количеств.
Задачи по математике для 2-го класса – миссис Лутц и мисс Уилл
2 класс
GO Math
2016-2017
Цели и цели обучения
Глава 1: Числовые концепции
000 3 · Классифицируйте числа до 20 как четные или нечетные.
· Напишите уравнения с равными слагаемыми для представления четных чисел.
· Используйте разряд для описания значений цифр в двузначных числах.
· Напишите 2-значные числа в развернутой форме.
· Записывайте двузначные числа в форме слова, развернутой и стандартной форме.
· Применяйте концепции разряда, чтобы найти эквивалентные представления чисел.
· Решайте проблемы, находя различные комбинации десятков и единиц для представления 2-значных чисел, используя стратегию «найти образец».
· Расширить последовательности подсчета в пределах 100 на 1, 5 и 10
· Расширить последовательности подсчета в пределах 1000 на 1, 5, 10 и 100 секунд.
Глава 2: Числа до 1000
· Записывайте трехзначные числа в развернутой и стандартной форме.
· Применяйте концепции разряда, чтобы найти эквивалентные представления чисел.
· Определите на 10 больше, на 10 меньше, на 100 больше или на 100 меньше, чем любое заданное число
· Расширьте числовые шаблоны, считая на 10 или 100.
· Решайте проблемы, связанные со сравнением чисел, используя стратегию «создать модель».
· Сравните 3-значные числа, используя символы <, = и>.
Глава 3: Основные факты и взаимосвязи
· Используйте двойные факты как стратегию для нахождения сумм для почти двойных фактов.
· Вспомните суммы основных фактов, используя свойства и стратегии.
· Вызов сумм для сложения фактов, используя стратегию «сделать десять».
· Найдите суммы трех слагаемых, применяя коммутативные и ассоциативные свойства сложения.
· Используйте обратную зависимость сложения и вычитания, чтобы вспомнить основные факты.
· Вспомните различия основных фактов, используя умственные стратегии.
· Найдите различия на числовой прямой, чтобы разработать мысленную стратегию разложения для упрощения фактов.
· Используйте линейчатые модели для представления различных ситуаций сложения и вычитания.
· Решайте проблемы с участием равных групп, используя стратегию «разыграй все».
· Напишите уравнения, используя повторное сложение, чтобы найти общее количество объектов в массивах.
Глава 4: 2-значное дополнение
· Найдите сумму, разделив однозначное сложение, чтобы двузначное сложение стало кратным 10.
· Используйте компенсацию для развития гибкое мышление для сложения 2-х цифр.
· Применяйте концепцию разряда при использовании стратегии разделения для двухзначного сложения.
· Модель 2-значного сложения с перегруппировкой.
· Нарисуйте быстрые картинки и запишите сложение двух цифр, используя стандартный алгоритм.
· Запишите сложение двух цифр, используя стандартный алгоритм.
· Практикуйте сложение двух цифр с перегруппировкой и без нее.
· Перепишите задачи горизонтального сложения по вертикали в стандартном формате алгоритма.
· Решайте задачи, связанные со сложением двух цифр, используя стратегию «нарисовать диаграмму».
· Представляйте ситуации сложения числовыми предложениями, используя символ для неизвестного числа.
· Найдите суммы трех двузначных чисел.
· Найдите суммы четырех двузначных чисел.
Глава 5: Вычитание двух цифр
· Разделите однозначное вычитание на части, чтобы вычесть его из двузначного числа.
· Разделите 2-значное вычитаемое, чтобы вычесть его из 2-значного числа.
· Модель вычитания двух цифр с перегруппировкой.
· Нарисуйте быстрые картинки и запишите двузначное вычитание с помощью стандартного алгоритма.
· Запишите двузначное вычитание, используя стандартный алгоритм.
· Практикуйте вычитание двух цифр с перегруппировкой и без нее.
· Перепишите задачи горизонтального вычитания по вертикали в формате стандартного алгоритма.
· Используйте сложение, чтобы найти различия.
· Решайте задачи вычитанием двух цифр, используя стратегию «нарисовать диаграмму».
· Представляйте ситуации вычитания числовыми предложениями, используя символ неизвестного числа.
· Анализируйте текстовые задачи, чтобы определить, какие операции использовать для решения многоступенчатых задач.
Глава 6: Сложение и вычитание 3-х цифр
- Нарисуйте быстрые картинки для представления 3-значного сложения.
- Примените концепцию разряда при использовании стратегии разделения для 3-значного сложения.
- Запишите сложение трех цифр по стандартному алгоритму с возможностью перегруппировки единиц.
- Запишите сложение трех цифр, используя стандартный алгоритм с возможной перегруппировкой десятков.
- Запишите сложение трех цифр по стандартному алгоритму с возможной перегруппировкой единиц и десятков.
- Решайте задачи, связанные с вычитанием трех цифр, используя стратегию «создать модель».
- Запишите сложение трех цифр с использованием стандартного алгоритма с возможной перегруппировкой сотен.
- Запишите 3-значное сложение с использованием стандартного алгоритма с возможной перегруппировкой сотен и десятков.
- Запись вычитания с использованием стандартного алгоритма, когда в уменьшаемом значении есть нули.
Глава 7: Деньги и время
- Найдите общую стоимость коллекций десятицентовиков, никелей и пенсов.
- Отсортируйте монеты в коллекции по стоимости, а затем найдите общую стоимость.
- Представьте денежные суммы меньше доллара с использованием двух различных комбинаций монет.
- Покажите один доллар разными способами.
- Найдите и запишите общую ценность денег для сумм, превышающих доллар.
- Решайте словесные задачи, связанные с деньгами, используя стратегию «разыграй это».
- Сообщите и запишите время с точностью до часа и получаса.
- Сообщите и запишите время с точностью до 5 минут.
- Укажите и запишите время, используя A.M. и П.
Глава 8: Длина в обычных единицах
- Используйте конкретные модели для измерения длины объектов в дюймах.
- Сделайте дюймовую линейку и используйте ее для измерения длины предметов.
- Оцените длину предметов, мысленно разделив их на дюймы.
- Измерьте длину объектов с точностью до дюйма с помощью дюймовой линейки.
- Решайте задачи сложения и вычитания, связанные с длинами объектов, используя стратегию «нарисовать диаграмму».
- Измерьте длину объектов в дюймах и футах, чтобы изучить обратную зависимость между размером и количеством единиц.
- Оцените длину предметов в футах.
- Выберите подходящие инструменты для измерения различной длины.
- Измерьте длину объектов и используйте линейный график для отображения данных измерений.
Глава 9: Длина в метрических единицах
- Используйте конкретную модель для измерения длины объектов в сантиметрах.
- Оцените длину объектов в сантиметрах, сравнив их с известной длиной.
- Измерьте длину предметов с точностью до сантиметра с помощью сантиметровой линейки.
- Измерьте длину объектов в сантиметрах и метрах, чтобы изучить обратную зависимость между размером и количеством единиц.
- Оцените длину объектов в метрах.
- Измерьте, а затем найдите разницу в длине двух объектов.
Глава 10: Данные
· Соберите данные в опросе и запишите эти данные в итоговую таблицу.
· Интерпретируйте данные в графических изображениях и используйте эту информацию для решения проблем.
· Создавайте графические изображения для представления данных.
· Интерпретируйте данные в виде гистограмм и используйте эту информацию для решения проблем.
· Создавайте гистограммы для представления данных.
· Решайте проблемы, связанные с данными, используя стратегию построения графика.
Глава 11: Понятия геометрии и дроби
· Определите трехмерные формы.
· Определите трехмерные формы по количеству граней, ребер и вершин.
· Создавайте трехмерные формы, используя кубы и другие объекты.
· Назовите 3-4-5-6-сторонние формы в соответствии с количеством сторон и вершин,
· Определите углы в двухмерных формах.
· Сортировка двухмерных фигур по их атрибутам.
· Разделите прямоугольники на квадраты одинакового размера и найдите общее количество этих квадратов.
· Определите и назовите равные части кругов и прямоугольников половинками, третями или четвертями.
· Формы разделов для отображения половин, третей или четвертей.
· Определите и опишите одну равную часть как половину трети или четверть целого.
· Решайте задачи, связанные с разделением целых на равные доли, используя стратегию «нарисовать диаграмму».
Как научить загадывать слова
Эта запись в блоге посвящена обучению учащихся 1-го и 2-го классов различным стратегиям решения словесных задач. Начиная с 1-го класса, учащиеся начнут решать задачи со словами в следующих областях математики Common Core: Операции и алгебраическое мышление, Число и операции по основанию 10, Геометрия и Измерение и данные.Ко второму классу учащиеся расширяют свои предыдущие знания и применяют еще больше стратегий решения словесных задач в этих областях. Важно научить студентов различным стратегиям, чтобы они могли найти наиболее подходящие для их стиля обучения.
Различные типы проблем со словами
В математике используется много разных типов задач со словами. Студенты должны хорошо разбираться в различных стилях текстовых задач. Кроме того, очень важно, чтобы они знали, какие стратегии задачи со словами подходят для каждого стиля задачи.Сегодня мы обсудим стратегии объединения, разделения, части-части-целого, отсутствующей части, сравнения и многоэтапных задач со словами.
Проблемы с соединением слов. Эти проблемы включают 3 числа, начальную сумму, сумму сдачи и итоговую сумму. Студенты складывают и сводят суммы.
Задачи с разделением слов. Эти задачи похожи на задачи с объединением, но просят учащихся разделить или вычесть суммы.
Задачи со словом «часть-часть-целое» – В словесных задачах «часть-часть-целое» используются только 2 числа, которые образуют единое целое.
Задачи с отсутствующими частями – в задачах этого типа учащиеся решают, чтобы найти недостающую часть в задаче «часть-часть-целое».
Проблемы со словами сравнения. Задачи сравнения связаны с поиском разницы между двумя значениями. Они склонны использовать такие слова, как «больше» и «меньше».
Многоступенчатые задачи со словами. Этот стиль задачи включает более одной операции. Учащиеся могут использовать комбинацию сложения и вычитания в многоступенчатых словесных задачах 1-го и 2-го класса.Начиная с 3-го класса, ученики также будут использовать умножение и деление.
Создание мнемонического устройства
При обучении студентов стратегиям решения словесных задач было бы неплохо начать с диаграммы привязки мнемонических приемов, такой как эта. Эта таблица BURST послужит очень важным наглядным пособием в вашем классе. Это поможет вашим ученикам запомнить важные детали и шаги в решении словесных задач. Это также поможет им исключить информацию в слове «проблема», которая не нужна для ее решения.
Стратегия BURST означает:
- B ox важные числа и математическая информация
- U укажите вопрос или формулировку действия
- R задайте вопрос
- S как ваша работа
- T укажите свой ответ и опишите свою рассуждения
Начать моделирование
Моделирование того, как использовать стратегию BURST проблем со словами с различными стилями проблем со словами, имеет важное значение.Этот пошаговый процесс поможет вашим ученикам критически осмыслить проблемы, используя эту стратегию. Моделирование во время группового обучения и небольших групп поможет вам обслужить всех ваших учеников на их уровне. Задавая управляемые вопросы, учащиеся узнают, как выделять важную информацию, вопрос и находить ответ. Ключевым моментом является моделирование того, как использовать стратегию проблемы со словами BURST с каждым стилем задачи со словами.
Предлагайте различные способы решения проблемы
Несмотря на то, что существует множество стратегий решения словесных задач, важно помочь учащимся найти стратегию или стратегии, которые лучше всего подходят для их стиля обучения.Некоторым ученикам будет полезно нарисовать картинку, в то время как другие предпочитают использовать уравнения. Кинестетические ученики могут решить, используя манипуляторы, чтобы разыграть проблему. Ключевым моментом является предоставление учащимся возможности использовать наиболее подходящую для них стратегию.
Когда включать проблемы со словами
Во время урока по математике учителя должны задавать текстовые задачи ближе к концу урока. Это гарантирует, что стандарт и навыки будут изучены в первую очередь в явной форме. Студентам нужно время, чтобы попрактиковаться в этом навыке, прежде чем применять его к более сложным задачам со словами.Как учитель, руководствуйтесь здравым смыслом, чтобы определить, готовы ли ваши ученики к задачам со словами. Некоторые ученики могут быть готовы раньше других, и именно здесь время в малых группах полезно. Это дает возможность повторного обучения, дополнительной практики и обогащения.
Нужно научить решать проблемы со словом виртуально?
Если вам нужен эффективный и увлекательный способ для ваших учеников отработать словесные задачи в цифровом формате, особенно во время дистанционного обучения, эти ресурсы по математическим задачам со словами для вас! Их можно заполнить через Google Slides и поделиться через Google Classroom.
Нужно нарисовать Часть A, чтобы показать свою работу и решить вашу проблему?
- Щелкните стрелку раскрывающегося списка рядом с «инструментом линии» в Google Slides. Прокрутите вниз и выберите инструмент для рисования каракулей.
- Учащиеся также могут решать свои математические задачи со словами в Google Draw, а затем загружать их в Google Classroom или вставлять этот рисунок в Часть A своей задачи Google Slides.
- Другой вариант: студенты могут решить задачу на бумаге или с помощью манипуляторов, а затем сфотографировать свою работу и вставить ее в свой слайд.
Ресурсы, помогающие разобраться в задачах со словами
Эти комплекты ресурсов по проблемам слов для 1-го и 2-го класса доступны как в бумажной, так и в цифровой версиях. Они поставляются в комплекте с плакатами и закладками по стратегии BURST для словесных задач, ключами ответов, рубриками и разнообразными задачами с короткими ответами.
У меня также есть блок 2-го класса, в котором есть готовые уроки и групповые задания по математике. Вышеупомянутые продукты являются дополнительными задачами по устранению проблем со словом для применения всех стандартов Common Core.Приведенный ниже блок – это блок о том, КАК учить словесные задачи. Он соответствует одному определенному математическому стандарту.
Щелкайте кнопками нужной ссылки.
Большое спасибо за чтение! Я надеюсь, что у вас появятся новые идеи по обучению задачам со словами и как включить их в свои уроки математики.
Ищете другие статьи в математическом блоге, чтобы почитать?
Поддержка семей Bridges Grade 2
Следующий набор игр и занятий поможет вашему ребенку практиковать некоторые из этих навыков дома.
Дополнение
Math Lines В этой игре соревнуйтесь в парных числах, которые в сумме дают целевую сумму. Перед тем, как ваш ребенок начнет играть, просмотрите пары чисел, которые в сумме дают целевую сумму. Вы можете даже посмотреть на разные способы составить число, используя игровые фишки, шарики или монетки.
Сложение с манипуляторами Игроки видят и слышат проблему сложения. Они могут перетащить шарики на рабочую поверхность, чтобы помочь им разобраться в проблеме. Игра включает пять уровней сложения, начиная с простых задач с 1 цифрой.Для повышения уровня игроки должны набрать не менее 70%. Аудио-направления.
Вычитание
Вычитание всплывающих шариков Просмотрите задачу вычитания и лопните воздушные шары, чтобы найти решение. Доступны три уровня сложности, а также аудио направления.
Очистить сложение Создайте числовые предложения, которые в сумме дают целевые числа. Зарабатывайте звезды для дополнительных очков и очистите поле до истечения таймера.
Деньги
Коробка для монет Узнайте, как считать, собирать, обменивать и менять монеты.Плитки с монетами помогают вам подсчитывать, когда вы узнаете ценность каждой монеты.
Научитесь считать деньги Игроки считают деньги, складывая монеты и купюры в ящик. По мере того, как учащиеся осваивают уровни, игра становится все сложнее. Уровень 1, считайте до 99 центов. Уровень 2, сосчитайте до 10 долларов. Уровень 3, сосчитайте до 100 долларов. Также выберите уровень новичка (используя любую комбинацию монет) или уровень эксперта (используя наименьшее количество купюр и монет).
Геометрия
Концентрация Щелкните режим фигур, чтобы играть в игру, в которой каждой форме соответствует ее имя.
Geoboard App С помощью этой виртуальной географической доски ученики натягивают ленты вокруг колышков, чтобы делать открытия о формах. Доступны версии для iPad и онлайн.
Дроби
Другие игры
По ссылкам ниже приведены некоторые из лучших игр для учащихся начальной математики, в которые можно играть дома. Просмотрите сайты, чтобы найти другие занятия для вашего ребенка.
ABCya! Математические игры на этом сайте, смоделированные на основе уроков начальной школы, были одобрены учителями или созданы ими.
Cyberchase На популярном шоу PBS есть сайт с примерно 50 играми и мероприятиями, а также видеороликами, посвященными математическим понятиям.
Johnnie’s Math Page Используйте этот онлайн-индекс, чтобы найти в Интернете сотни интерактивных математических игр, упорядоченных по концепциям.
Национальная библиотека виртуальных манипуляторов Этот сайт Университета штата Юта, организованный по классам и математической концепции, содержит широкий выбор виртуальных манипуляторов.
Mathwire.com | Решение проблем: Gr. К-2
Главная | Список от А до Я | Стандарты | ТемыРесурсы по решению проблем: K-2
Решение проблем: классы К-2
Эти задачи предназначены для учащихся классов K-2:
- Пазлы на сотнях квадратов: Ученики школы Порт-Монмут-Роуд в Кинсбурге, штат Нью-Джерси, используют шаблоны для сборки сотен головоломок.& nbsp Учителя создают головоломки, которые различаются как по количеству, так и по размеру частей, чтобы дифференцировать это задание и наилучшим образом удовлетворить разнообразные потребности учащихся в классе.
- Задачи о животных просят учащихся решать задачи о домашних и животных.
- Проблемы с едой: учащиеся решают задачи, связанные с едой, рисуя, чтобы выяснить, сколько всего было съедено печенья, пиццы, кексов.
- Задачи «Зимние забавы» используют снеговиков, чтобы вовлекать детский сад в решение задач.
- Наибольшая сумма предлагает учащимся расположить заданные цифры, чтобы получить наибольшую сумму.
- Наименьшая сумма предлагает учащимся расположить заданные цифры, чтобы получить наименьшую сумму.
- Наибольшая разность предлагает учащимся расположить указанные цифры так, чтобы получить наибольшую разницу.
- Наименьшая разница предлагает учащимся расположить указанные цифры так, чтобы получить наименьшую разницу.
- Bean Bags оценивает понимание учащимися значения разряда с помощью длинных чисел и кубов с основанием десять.
- Digit Game – 1 предлагает ученикам составить как можно большее число, используя три цифры, которые вытащил каждый игрок. & nbsp Учащиеся должны определить победителя игры и объяснить, как они решили, кто победил.
- Digit Game – 2 похожа на Digit Game -2 и может использоваться для дополнительной практики.
- Ice Cream Treat касается комбинаций монет и внесения сдачи.
- Пицца Лакомство касается комбинаций монет и внесения сдачи.
- Quilt Square Challenge : Первоклассники школы Флинн в Перте, Амбой, штат Нью-Джерси, использовали блоки для квилтинга и коврики для квилтинга, чтобы воссоздать образцы блоков лоскутного одеяла 4×4 и 9×9. & nbsp См. «Вызов Quilt Square Challenge» на веб-странице Quilts, чтобы получить дополнительную информацию об этом упражнении и загрузить блоки и маты для учащихся.
- Образцы фигур: образцы фигур, которые заставляют учащихся рисовать то, что будет дальше. & nbsp Учителя должны попросить учащихся объяснить, откуда они знают, что будет дальше, чтобы у учащихся развивалась способность объяснять свое мышление.
- Class Gardens измеряет понимание учащимися территории и периметра.
- Модели роста рыб: Первоклассники школы Флинн в Перт-Амбой, штат Нью-Джерси, искали закономерности в росте рыбы из книги Мэрилин Бернс по алгебраическому мышлению. & nbsp Учащиеся использовали блоки шаблонов для создания рыбок каждого возраста, систематизировали данные в виде Т-диаграммы, а затем предсказали, какие рыбы постарше захотят, на основе найденных ими шаблонов.
- Bay Street требует от учащихся проанализировать структуру номеров домов на Bay Street.Учащиеся записывают узор, который они видят, и используют этот числовой узор, чтобы вписать отсутствующие номера домов.
- King Street требует от учащихся проанализировать структуру номеров домов на King Street. Учащиеся записывают узор, который они видят, и используют этот числовой узор, чтобы вписать отсутствующие номера домов.
- Задачи с узорами: визуальные узоры, требующие от учащихся рисовать то, что будет дальше. & nbsp Учителя должны попросить учащихся объяснить, откуда они знают, что будет дальше, чтобы у учащихся развивалась способность объяснять свое мышление.
- Образцы фигур: образцы фигур, которые заставляют учащихся рисовать то, что будет дальше. & nbsp Учителя должны попросить учащихся объяснить, откуда они знают, что будет дальше, чтобы у учащихся развивалась способность объяснять свое мышление.
- Winter Patterns для изучения выкройки используются снеговики, санки и рукавицы.
- Счет за минуту: Первоклассники в школе Флинн в Перт-Амбой, штат Нью-Джерси, использовали стикеры, чтобы построить линейный график того, насколько высоко они могут считать за минуту.Затем учащиеся проанализировали данные, чтобы решить, насколько высоко может рассчитывать большинство первоклассников.
- Дни рождения требует, чтобы учащиеся интерпретировали данные в виде гистограммы.
- Fair Game оценивает понимание учащимися вероятности в играх со спиннером.
- Четно-нечетная игра требует, чтобы учащиеся интерпретировали данные в таблице подсчетов.
- «Любимые домашние животные» требует, чтобы учащиеся проанализировали информацию в таблице подсчета любимых домашних животных.
- Любимое мороженое требует от учащихся проанализировать информацию в таблице подсчетов о шоколаде и ванильном мороженом.
- Pet Survey требует, чтобы учащиеся использовали данные в таблице частот, чтобы построить гистограмму и ответить на вопросы о ней.
- Сбор данных орла и решки требует от учащихся решить, является ли игра с подбрасыванием двух монет справедливой или нет, если один игрок выигрывает, если совпадают монеты (обе орла или оба решки), а другой игрок выигрывает, если монеты не совпадают (одна решка и одна решка).
- Конусы мороженого: Учителя первого класса в школе Флинн в Перте, Амбой, штат Нью-Джерси, попросили учеников выяснить, сколько различных 3-мерных рожков мороженого они могли бы приготовить, используя шоколадное, ванильное и клубничное мороженое.Пары учащихся использовали вырезы из конусов и совков, чтобы собрать их, а затем записали различные комбинации.
- Светофоры требуют от учащихся использовать метод упорядоченного подсчета, чтобы определить, сколько разных светофоров можно сделать с помощью комбинации красных, зеленых и желтых блоков. & nbsp Учащиеся могут использовать соединяющие кубы, чтобы моделировать светофоры и записывать комбинации, раскрашивая лист соответствующим образом.
Авторские права © 2006-2010 – Терри Кавас – Все права защищены.
.


 Ч. 2. . – М.: «Вентана-Граф», 2011г.
Ч. 2. . – М.: «Вентана-Граф», 2011г. Чистописание.
Чистописание. Чем похожи?
Чем похожи? Отпускаем Колобка в путь. Он встречает зайца. Поможем ему уйти от зайца. Сейчас работаем в группах по составлению задач по схеме.
Отпускаем Колобка в путь. Он встречает зайца. Поможем ему уйти от зайца. Сейчас работаем в группах по составлению задач по схеме. А остальные группы предполагают вопрос и доказывают почему.
А остальные группы предполагают вопрос и доказывают почему. Работаете в парах
Работаете в парах 6
6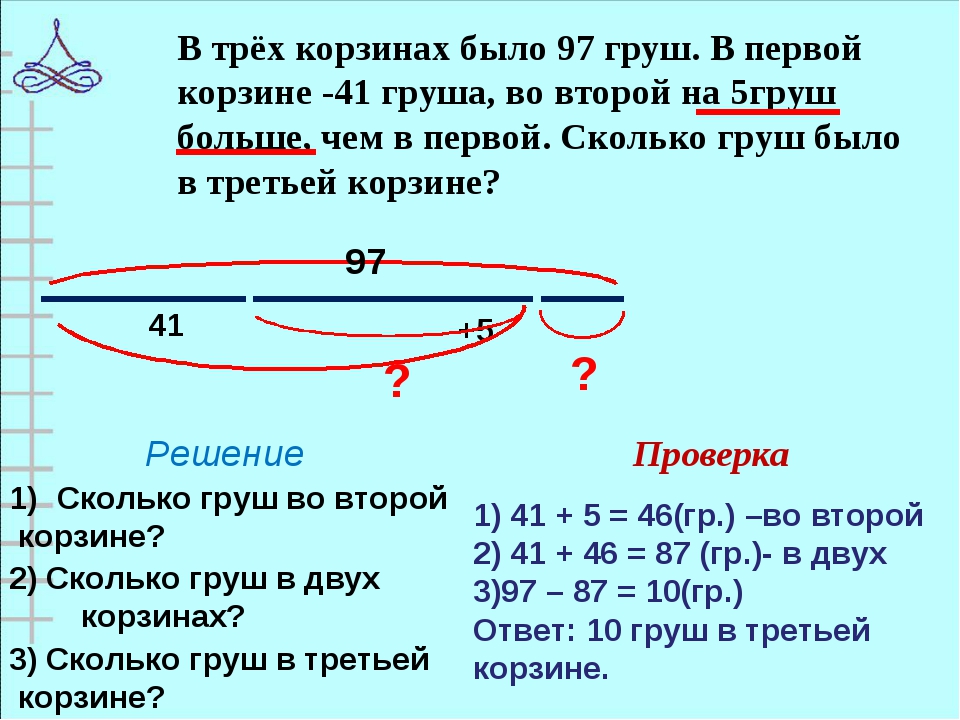 Литература
Литература