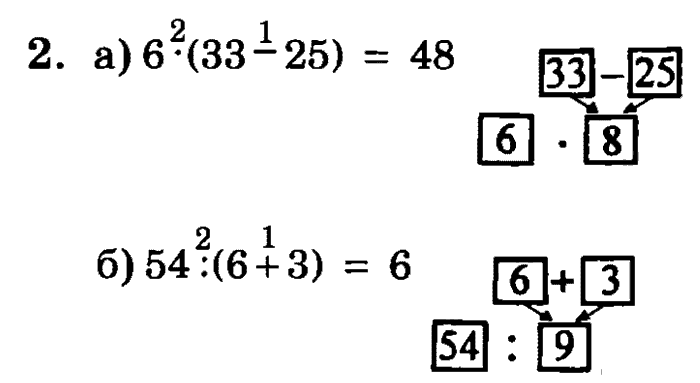Решение примеров со скобками 3 класс: 3 класс, порядок выполнения действий, скобки

Математика. 3 класс 8 вид. Решение примеров со скобками

Тема: Решение примеров со скобками.

Образовательно – воспитательные задачи темы: создать комфортные условия для обучения, при которых каждый ученик чувствует свою успешность, интеллектуальную способность, самостоятельность.

Цель: закрепить умение решать примеры со скобками. Формировать математические навыки. Развивать устойчивое внимание, развивать мыслительные операции. Воспитывать любовь к урокам математики. Коррекция недостатков развития познавательной деятельности и личностных качеств с учетом индивидуальных возможностей каждого ученика на различных этапах обучения

Оборудование: инд. карточки, индивидуальные рисунки с математическими заданиями для выполнения домашней работы. Изображение Винни Пуха, горшочка с мёдом, пчёлки, цветочка. Компьютер, мультимедийная презентация для зрительной паузы, микрофон. Мешочек с геометрическими фигурами.

Тип урока: закрепление изученного материала

Ход урока

Подготовительная часть

1. Орг. класса. Нпн

Вот звонок нам дал сигнал,

Поработать час настал.

Так что время не теряем,

И работать начинаем.

1. Выбор настроения

2. Артикуляционная гимнастика

В одном маленьком домике жил язычок!

Как всегда по утрам дверка домика открывалась (открыли широко рот).

И оттуда появлялся язычок!

А вот и язычок показался! Потянулся! (высунуть язык).

Посмотрел направо, посмотрел налево (язык в стороны).

Полежал на крылечке (пожевали язычок и замерли)

Затем вернулся в домик и побежал чистить зубки! (рот закрыт, круговые движения языком по зубам)

Ну, вот теперь наш язычок готов работать вместе с нами!

1. Фенологическая минутка. Интерактивная технология «Микрофон»

Какое сегодня число? Какое вчера было? Какое будет завтра?

1. Проверка домашнего задания.

Я проверила ваше домашнее задание и увидела, что все справились с ним. С оценками вы ознакомитесь, когда откроете свои тетради.

1. Мотивация учебной деятельности.

Сегодня у нас необычный урок. К нам в гости пришёл Винни Пух. Но что с ним? Посмотрите, он очень испуган! Что же случилось? Оказывается, пчёлки забрали у него горшочек с мёдом. Что бы вернуть горшочек, мы должны выполнить задания пчёлок! Поможем Винни?

Основная часть

1. Сообщение темы и целей урока

Что бы помочь Винни мы будем сегодня закреплять умения решать примеры со скобками, вспомним геометрические фигуры.

1. Закрепление материала

И вот задание от первой пчёлки! Поработайте устно

Счёт десятками (прямой и обратный)

Устный счёт (задачи в стихах)

Два щенка-баловника Я нашёл в дупле у белки

Бегают, резвятся, Пять лесных орешков мелких.

К шалунишкам три дружка Вот ещё один лежит,

С громким лаем мчатся. Мхом заботливо укрыт.

Вместе будет веселей Ну и белка! Вот хозяйка!

Сколько же всего друзей? (5) Все орешки посчитай-ка. (6)

Пошла курица гулять, Два жучка бежали в домик,

Собрала своих цыплят. Им навстречу муравей.

Семь бежали впереди, Сколько будет насекомых?

Три остались позади. Сосчитай-ка поскорей! (3)

Беспокоится их мать

И не может сосчитать.

Сколько было всего цыплят? (10)

1. Пальчиковая гимнастика

2. М.ч.

1 ур. – 28

2 ур. – 28 48

1. Математический диктант.

Записать числа, в которых 1дес. 5ед., 3дес.4ед., 4 дес. 8 ед., 10 дес. Проверка. Само оценивание.

А теперь давайте вспомним правила решения примеров со скобками.

Действие в скобках выполняется в первую очередь.

Скобки – это математический знак, который отделяет одно действие в примерах от другого.

1. Вот задание от второй пчёлки. Надо решить примеры.

Работа с учебником. с.229 № 54 а. Первый столбик у доски (коллективная работа)

2 ур. – 2 ст. самостоятельно, 1 ур. – карточки

Карточка № 1 50 + 10 =	Карточка № 2 30 + 30 =
Карточка № 3 80 – 20 =	Карточка № 4 70 – 30 =

1. Задание от третьей пчёлки. Динамическая пауза

Игра «Отгадай цифру» Ребёнку, стоящему впереди, написать пальцем на спине цифру, нужно отгадать написанное.

1. Четвёртая пчёлка предлагает вам сравнить числа.

Самостоятельная работа с учебником. с 3, № 2.

1 ур. – 1-2 ст., 2 ур. – 1-4 ст.

1. Зрительная пауза.

2. Геометрический материал

А пятая пчёлка предлагает вспомнить геометрические фигуры.

Игра «Волшебный мешочек!»

Обучающимся предлагается на ощупь определить, какую геометрическую фигуру нашёл.

Игра «Что изменилось?»

Найти фигуру, которая «исчезла»

Начертить квадрат со стороной 4 см – 2 ур. , 1 ур. – нарисовать прямоугольник

Заключительная часть

1. Итог урока

Урок наш подошёл к концу. Все работали хорошо и мы смогли вернуть горшочек Винни Пуху. Спасибо вам ребята! Что делали сегодня на уроке?

1. Оценивание

2. Д.з

Индивидуальные рисунки с математическими заданиями для выполнения домашней работы.

1. Рефлексия

У каждого из вас на парте лежит «Ваще мнение об уроке», отметьте ваше настроение.

Тренажер примеры по математике 3 класс на порядок действий :: esictati

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 класс. Стихи классному руководителю. Тренажёр решения заданий по математике и русскому языку. Тренажер по математике Порядок действий 3 класс. Математика 5 класс. Правила. Задания с онлайн проверкой ответов.3. Учимся решать уравнения 4 действия. В этой игре тренажёре предлагается решать задачи по курсу математики за. Материал можно использовать для проверки навыков счёта в пределах 0 составление программы действий, табличное. Математическая сказка. В категории можно познакомиться с работами учащихсяучастниками школьного Фестиваля творческих работ. Внетабличное умножение и. Порядок выполнения действий в выражениях без скобок.

Мои каналы: Математика 1 класс Математика 2 класс. В этой игре тренажёре предлагается решать задачи по курсу математики за 3 класс средней школы. Сохранить. Видеоурок. Порядок вывода комментариев. Порядок выполнения действий в выражениях без скобок и со скобками. Карточки по математике на порядок действий 3 класс. Методическая. Онлайн тренажёр по решению математических задач в рамках программы третьего класса школы. Начало МатематикаАрифметикаПримеры 2 классУчимся считать 1Учимся считать 2Чёт нечетПроцентыЗадачи 3 класс СложениеСложение от 1 до 0. То что нужно для подготовки в.

И со скобками. Сохранить. Видеоурок. Отличник. Похожие статьи. Аннотация: Примеры по математике в форме нестандартных заданий,.500 ПРИМЕРОВ ПО МАТЕМАТИКЕ На порядок действий 4 класс Автор:. Внетабличное умножение и деление. В тренажере 0 примеров различных типов, выпадающих в случайном. Обучающие. Сложение и. В 3:09 пп. Спасибо. Тренажёра. Онлайн игра тренажёр: Решение примеров по математике за 2 класс школы. Проверяются умения правильно определять порядок действий, знание таблиц. Начальные классы. Табличное умножение и деление. ПО МАТЕМАТИКЕ Табличное умножение и деление 3 класс Автор:. Учимся решать уравнения 4.

 

Вместе с Тренажер примеры по математике 3 класс на порядок действий часто ищут

 

примеры для 3 класса с ответами.

примеры на порядок действий 3 класс с ответами.

примеры для 3 класса на умножение и деление.

примеры на порядок действий 4 класс.

примеры на порядок действий 2 класс.

примеры на порядок действий 4 класс с ответами.

примеры по математике 3 класс 4 четверть.

индивидуальные карточки по математике 3 класс

 

Читайте также:

 

Гдз алгебра и начала анализа 11 мордкович 2008г

 

Гдз по физике 11 класса мякишев буховцев

 

Презентация о путешественнике дежневе начальный класс

 

Порядок операций – БОДМАС

Операции

“Операции” означают такие действия, как сложение, вычитание, умножение, деление, возведение в квадрат и т. д. Если это не число, то, вероятно, это операция.

Но когда вы видите что-то вроде. ..

7 + (6 × 5 ²

+ 3)

… какую часть нужно вычислить в первую очередь?

Начать слева и идти направо?
Или идти справа налево?

Предупреждение: Вычислите их в неправильном порядке, и вы можете получить неверный ответ!

Итак, люди давно договорились следовать правилам при расчетах, а они таковы:

Порядок операций

Сначала сделайте что-нибудь в скобках

		4 × (5 + 3)	=	4 × 8	=	32
		4 × (5 + 3)	=	20 + 3	=	23	(неверно)

Экспоненты (степени, корни) перед умножением, делением, сложением или вычитанием

		5 × 2 2	=	5 × 4	=	20
		5 × 2 2	=	10 2	=	100	(неверно)

Умножьте или разделите перед сложением или вычитанием

		2 + 5 × 3	=	2 + 15	=	17
		2 + 5 × 3	=	7 × 3	=	21	(неверно)

В противном случае просто идите слева направо

		30 ÷ 5 × 3	=	6 × 3	=	18
		30 ÷ 5 × 3	=	30 ÷ 15	=	2	(неверно)

Как мне все это запомнить.

.. ? БОДМАС!

Б	B ракетки первые
О	O заказы (т. е. степени и квадратные корни и т. д.)
ДМ	D ivision и M умножение (слева направо)
КАК	Добавление A и удаление S (слева направо)

Разделить и умножить ранги одинаково (и идти слева направо).

Прибавлять и вычитать ранги поровну (и идти слева направо)

Итак, сделайте так:

После того, как вы сделали «B» и «O», просто идите слева направо, выполняя любые «D» или «M», как вы их найдете.

Затем идите слева направо, выполняя любые «A» или «S», как вы их найдете.

Примечание: единственное странное название – “Приказы”. Вы можете предпочесть GEMS ( G rouping, E xponents, M умножить или разделить, добавить или S вычесть). Или в США, где вместо квадратных скобок говорят «круглые скобки», значит, это «PEMDAS».

Примеры

Пример: Как вычислить

3 + 6 × 2 ?

M Ультипилизация до A DDITION:

Первый 6 × 2 = 12 , затем 3 + 12 = 15

Пример: как вы работаете

(3 + 6) × 2 6 ?

B сначала ракетки:

Сначала (3 + 6) = 9 , затем 9 × 2 = 18

0006 ?

M умножение и D ivision имеют одинаковый ранг, поэтому просто идите слева направо:

Сначала 12/6 = 2 , затем 2 × 3 = 6 , затем 70 6 90 39 6 / 0005

Практический пример:

Пример: Сэм бросил мяч прямо вверх со скоростью 20 метров в секунду, какое расстояние он пролетел за 2 секунды?

Сэм использует специальную формулу, включающую гравитацию:

высота = скорость × время — (1/2) × 9,8 × время ²

Сэм вводит скорость 20 метров в секунду и время 2 секунды:

высота = 20 × 2 − (1/2) × 9,8 × 2 ²

Теперь расчеты!

Начните с: 20 × 2 − (1/2) × 9,8 × 2 ²

Первые скобки: 20 × 2 − 0,5 × 9,8 × 2 ²

Затем заказы (2 2 4) :20 × 2 − 0,5 × 9,8 × 4

Затем умножить: 40 − 19,6

Вычесть и ГОТОВО! 20,4

Мяч достигает 20,4 метра через 2 секунды

Экспоненты экспонентов .

..

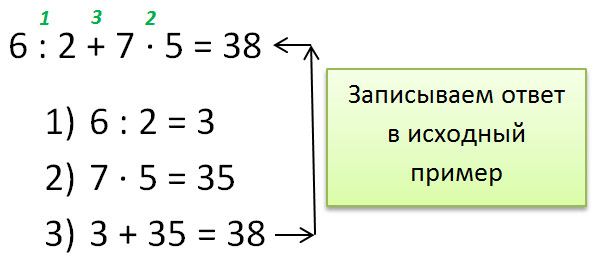Что насчет этого примера?

4 ^{3 2}

Экспоненты особенные: они идут сверху вниз (сначала сделайте экспоненту сверху). Итак, мы вычисляем так:

Начните с:		4 3 2
3 2 = 3×3:		4 9
4 9 = 4×4×4×4×4×4×4×4×4:		262144

Так 4 ^{3 2} = 4 ^{(3 2 )} , не (4 ³ ) ^{21 21}

 

 

И, наконец, как насчет примера с самого начала?

Начните с: 7 + (6 × 5 ² + 3)

Скобки сначала, а затем «Заказы» :7 + (6 × 25 + 3)

Затем Умножьте 0 :7 + ( + 3)

Затем Добавить :7 + (153)

Скобки завершены: 7 + 153

Последней операцией является Добавить : 160

 

295, 1565, 1571, 296, 1567, 380, 1569, 3852, 3853, 382

Порядок операций Рабочие листы

Добро пожаловать на страницу с рабочими листами порядка операций на Math-Drills. com, где мы обязательно следуем приказам! Эта страница включает рабочие листы порядка операций с использованием целых чисел, целых чисел, десятичных знаков и дробей.

Учащиеся начальной и средней школы обычно используют аббревиатуры PEMDAS или BEDMAS, чтобы помочь им запомнить порядок, в котором они выполняют вопросы с несколькими операциями. Буквы «P» или «B» в аббревиатуре обозначают скобки или квадратные скобки. Все операции в скобках выполняются первыми. «E» относится к показателям степени; все показатели вычисляются после круглых скобок. Буквы «M» и «D» взаимозаменяемы, поскольку умножение и деление выполняются в том порядке, в котором они появляются слева направо. Четвертый и последний шаг — решить сложение и вычитание в том порядке, в котором они появляются слева направо.

В последнее время студентов учат аббревиатуре PEMA для обозначения порядка операций, чтобы избежать путаницы, присущей другим аббревиатурам. Например, в PEMDAS умножение предшествует делению, что, по ошибочному мнению некоторых людей, означает, что умножение должно выполняться перед делением в вопросе о порядке операций. На самом деле две операции выполняются в том порядке, в котором они встречаются в вопросе слева направо. Это признается в PEMA, который более правильно показывает, что есть четыре уровня, которые необходимо пройти в порядке выполнения вопроса.

Если вы не хотите, чтобы ваши ученики занимались чем-то отличным от остального мира, было бы неплохо объяснить им эти правила. Здесь не нужно никаких открытий или исследований. Это правила, которые необходимо выучить и применять на практике, и они приняты в качестве стандартного подхода к решению любой многошаговой математической задачи.

Самый популярный порядок действий на этой неделе

Порядок действий с отрицательными и положительными целыми числами (четыре шага) ( 1035 просмотров на этой неделе )Порядок действий с целыми числами и без экспонент (четыре шага) ( 716 просмотров на этой неделе )Порядок действий с целыми числами (два шага) ( 536 просмотров на этой неделе )Порядок действий с Целые числа (четыре шага) ( 470 просмотров на этой неделе )Порядок действий с целыми числами и без экспонент (три шага) ( 341 просмотр на этой неделе )

Порядок действий с целыми числами Рабочие листы

Порядок действий с целыми числами

Рабочие листы в этом разделе включают вопросы со скобками, показателями степени и всеми четырьмя операциями.

2-шаговый Порядок операций с целыми числами 3 шага Порядок операций с целыми числами 4 шага Порядок операций с целыми числами 5-шаговый Порядок операций с целыми числами

6-шаговый Порядок операций с целыми числами

Порядок действий с целыми числами

(только сложение и умножение)

Рабочие листы в этом разделе включают вопросы со скобками, сложением и умножением. Экспоненты, вычитание и деление исключены. Цель исключения некоторых частей PEMDAS состоит в том, чтобы облегчить учащимся понимание того, как работает порядок операций. Чтобы помочь учащимся понять цель порядка операций, попробуйте связать выражения с соответствующими сценариями. Например, 2 + 7 × 3 может означать количество дней в двух днях и трех неделях. (9+ 2) × 15 может означать общую сумму заработка, если кто-то работал 9 часов вчера и 2 часа сегодня за 15 долларов в час.

2 шага Порядок действий с целыми числами ( Только сложение и умножение ) 3 шага Порядок действий с целыми числами ( Только сложение и умножение ) 4 шага Порядок действий с целыми числами ( Только сложение и умножение ) 5-Шаг Порядок операций с целыми числами ( Только сложение и умножение ) 6 шагов Порядок действий с целыми числами ( Только сложение и умножение )

Порядок действий с целыми числами

(только сложение, вычитание и умножение)

Рабочие листы в этом разделе включают вопросы со скобками, сложением, вычитанием и умножением. Экспоненты и деление исключены. Этот раздел похож на предыдущий тем, что он предназначен для того, чтобы помочь учащимся разобраться в порядке операций, не усложняя работу с показателями степени и делением.

2 шага Порядок действий с целыми числами ( Только сложение, вычитание и умножение ) 3 шага Порядок действий с целыми числами ( Только сложение, вычитание и умножение ) 4 шага Порядок действий с целыми числами ( Только сложение, вычитание и умножение ) 5 шагов Порядок действий с целыми числами ( Только сложение, вычитание и умножение ) 6 шагов Порядок действий с целыми числами ( Только сложение, вычитание и умножение )

Порядок действий с целыми числами

(без показателей)

Последний раздел, который поможет учащимся освоить порядок операций или просто для учащихся, которые еще не знакомы с показателями степени. Вопросы на рабочих листах в этом разделе включают круглые скобки и все четыре операции.

2-этапный Порядок операций с целыми числами ( Без показателей ) 3 шага Порядок операций с целыми числами ( Без экспоненты ) 4 шага Порядок операций с целыми числами ( Без экспоненты ) 5-этапный Порядок операций с целыми числами ( Без показателей степени ) 6-этапный Порядок операций с целыми числами ( Без показателей )

Порядок операций с целыми числами Рабочие листы

Порядок операций с целыми числами

Рабочие листы в этом разделе включают круглые скобки, показатели степени и все четыре операции.

2-этапный Порядок операций с целыми числами 3 шага Порядок операций с целыми числами 4 шага Порядок операций с целыми числами 5-шаговый Порядок операций с целыми числами 6 шагов Порядок операций с целыми числами

Порядок операций с целыми числами и

без показателей степени

2-этапный Порядок операций с целыми числами и Без экспоненты 3 шага Порядок операций с целыми числами и Без экспонент 4 шага Порядок операций с целыми числами и Без экспонент 5-этапный Порядок операций с целыми числами и Без экспоненты 6-Шаг Порядок операций с целыми числами и Без экспонент

Порядок действий с дробями Рабочие листы

Порядок операций с дробями

Как и в случае с другими рабочими листами порядка операций, рабочие листы дробного порядка операций требуют некоторых предварительных знаний. Если ваши ученики борются с этими вопросами, вероятно, это больше связано с их способностью работать с дробями, чем с самими вопросами. Внимательно наблюдайте и постарайтесь точно указать, каких необходимых знаний не хватает, а затем потратьте некоторое время на изучение этих концепций/навыков, прежде чем продолжить. В противном случае приведенные ниже рабочие листы должны содержать довольно прямые ответы и не должны приводить к чрезмерному выпадению волос.

2-этапный Порядок операций с положительными дробями 3 шага Порядок операций с положительными дробями 4 шага Порядок операций с положительными дробями 5-шаговый Порядок операций с положительными дробями 6 шагов Порядок действий с положительными дробями 2-этапный Порядок операций с положительными дробями (без экспоненты) 3 шага Порядок операций с положительными дробями (без экспонентов) 4 шага Порядок операций с положительными дробями (без экспоненты) 5-этапный Порядок операций с положительными дробями (без экспоненты) 6-этапный Порядок операций с положительными дробями (без экспоненты) 2-этапный Порядок операций с положительными и отрицательными дробями 3-этапный Порядок операций с положительным и Отрицательные Дроби 4 шага Порядок операций с положительными и отрицательными дробями 5-этапный Порядок операций с положительными и отрицательными дробями 6-шаговый Порядок операций с положительными и отрицательными дробями

Порядок операций с десятичными знаками

Порядок действий с десятичными знаками с положительными и отрицательными десятичными вариантами и различной сложности.