Ребусы с цифрой 2: Nothing found for Rebusy-s-chislami-i-ciframi%23kak-ih-reshat – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Учимся разгадывать ребусы

Тема внеклассного занятия: Учимся разгадывать ребусы.

Цель: Познакомить учащихся с правилами расшифровки ребусов, научить их решать ребусы.

Задачи:

знакомство учащихся с историей возникновения ребусов;
знакомство детей со способами зашифровки слов;
развитие внимания, воображения и логического мышления учащихся;
воспитание терпения и настойчивости в достижении цели.

Оборудование: компьютер, карточки с ребусами, толковый словарь

Ход занятия:

Организационный момент

– Здравствуйте, ребята! Мы продолжаем наше путешествие по стране Математика. Сегодня вы познакомитесь с еще одним городом в этой удивительной стране – городом Ребусы.

Основная часть занятия.

– Ребята, а что такое ребусы?

– Ребус – это шифровка, носящая развлекательный характер (посмотрим по словарю). В ребусах текс зашифровывается с помощью рисунков, предметов, цифр, букв и т.д. Ребусы появились очень давно, в эпоху возрождения письменности (рисунчатое письмо). В 15 – 16 веках ребусы становятся модным увлечением у народа и при королевских дворах во Франции, Германии, Англии, Италии, а с 1845г и в России. Само название произошло от старинного латинского выражения, которое в переводе на русский язык означает: «Не словами, а при помощи букв».

Это наскальная надпись из Северной Америки. Она повествует о том, как вождь по имени Майенгук отправился в путь на 5 каноэ. Путешествие длилось 3 дня (3 солнца под изогнутым небосводом). Орел – символ храбрости. Другие животные – это изображения добрых духов хранителей.

Составление ребусов – это умственный труд. Иногда для этого требуется много времени. Но какое удовольствие получаешь, когда ребус разгадан. Знание правил составления и расшифровки ребусов позволяет разгадать любой ребус.

Что надо знать, чтобы расшифровать ребус?

Если в ребусе между двумя картинками стоит знак «+», то нужно сложить названия рисунков. Например: слово «семья» можно изобразить, написав цифру 7 и букву Я, и поставить между ними знак «+».

Если рисунок перевернут «вверх тормашками», название его следует читать наоборот. Например: вместо слова «нос» получается слово «сон»
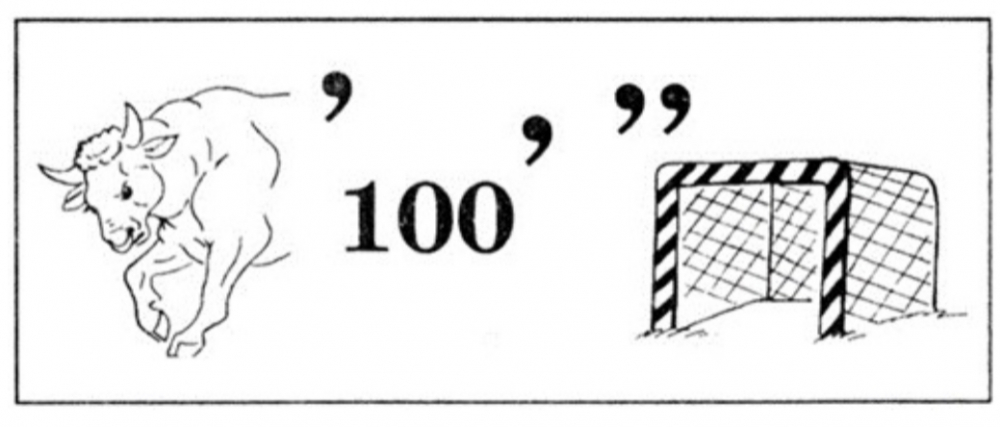
Когда перед рисунком стоит запятая, от названия предмета следует отбросить первую букву. Например: из слова «муха» получается слово «уха».

Запятая после рисунка указывает на то, что в названии предмета следует отбросить последнюю букву. Например: из слова «стол» получается слово «сто».

Две запятые перед или после картинки означают, что надо отбросить от названия две буквы. Однако надо помнить, что обилие запятых перегружает рисунок и делает ребус неоригинальным.

(восемь)

Существуют ребусы, в которых используются только буквы. Здесь нужно использовать различные предлоги. Например: если внутри буквы «о» изобразить цифру 7, то получится слово «восемь».

С (наст) Слово «наст» можно получить, нарисовав букву «т» поверх «с».

Л Слово «подвал» можно изобразить, нарисовав под цифрой 2 букву «л».

Если в ребусах встречаются зачеркнутые над рисунками (около рисунка) буквы, надо выбросить указанные буквы из названия предмета. Например: изобразив зачеркнутую букву «к» около рисунка крота, получим слово «рот»

Знак равенства между буквами над каким-либо рисунком предполагает замену одной на другую. Иногда делают по-другому: зачеркивают букву, которую надо заменить, а рядом ставят ту букву, на которую надо поменять. Например: Если над изображением лука стоит «у = а», следует читать «лак»

У=А

Цифры над рисунком указывают, что следует изменить порядок букв в слове. Например: если над изображением куста поставить цифры 3,4,2,1, получится слово «стук»

3, 4, 2, 1

– Вот такие правила помогают нам разгадывать ребусы.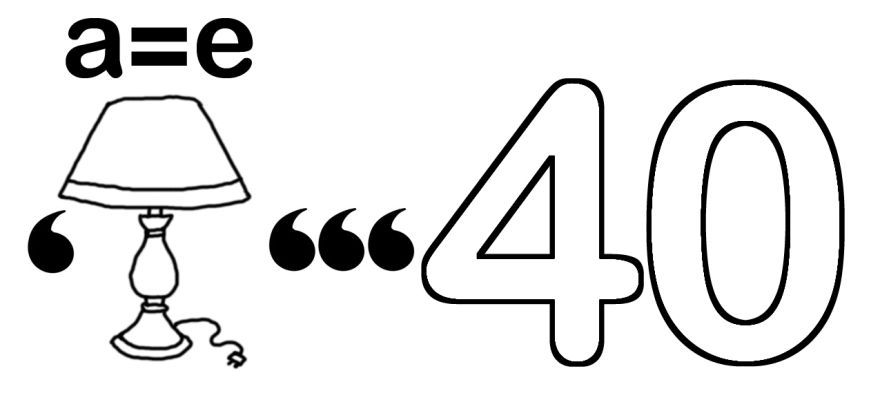 Но не думайте, что этот процесс такой легкий. Встречаются «хитрые» ребусы, над разгадкой которых приходится немало потрудиться.

Выполнение тренировочных упражнений.

– А сейчас мы будем разгадывать различные ребусы. Не забывайте про правила – помощники, с которыми вы познакомились, (ребусы нарисованы на карточках и прикреплены на доску) (см. приложение к уроку).

Ученики расшифровывают слово, а один из них объясняет, как он это сделал.

Самостоятельная работа учащихся.

– Молодцы, ребята! Понравилось вам разгадывать ребусы? А теперь давайте сделаем так: вы сами превратитесь в шифровальщиков. Помните о правилах «шифровки» и не забывайте самого главного: рисунки в ребусах должны быть ясными и точными.

– А теперь будем разгадывать ваши ребусы.

Итог занятия.

– Что такое ребус?

– Назовите правила зашифровки или расшифровки слов?

Рефлексия.

– У вас на партах лежат кружки, нарисуйте на них….., а вот что? Вы узнаете, расшифровав ребус:

НАСТРОЕНИЕ

Приложение к занятию

Внеклассное занятие для 1-4 классов ” Учимся разгадывать кроссворды”.

Тема внеклассного занятия: Учимся разгадывать ребусы.

Цель: Познакомить учащихся с правилами расшифровки ребусов, научить их решать ребусы.

Задачи:

знакомство учащихся с историей возникновения ребусов;
знакомство детей со способами зашифровки слов;
развитие внимания, воображения и логического мышления учащихся;
воспитание терпения и настойчивости в достижении цели.

Возраст детей: 9 – 10 лет.

Оборудование: компьютер, карточки с ребусами, толковый словарь

Ход занятия:

Оргмомент.

Когда вы слушаете, вы забываете,
Когда вы видите, вы понимаете,
Когда вы действуете, вы научаетесь.

Основная часть занятия.

– Ребята, а что такое ребусы?

Что надо знать, чтобы расшифровать ребус?

Если в ребусе между двумя картинками стоит знак «+», то нужно сложить названия рисунков. Например: слово «семья» можно изобразить, написав цифру 7 и букву Я, и поставить между ними знак «+».

Если рисунок перевернут «вверх тормашками», название его следует читать наоборот. Например: вместо слова «нос» получается слово «сон»
Когда перед рисунком стоит запятая, от названия предмета следует отбросить первую букву. Например: из слова «муха» получается слово «уха».

(восемь)

С (наст) Слово «наст» можно получить, нарисовав букву «т» поверх «с».

Л Слово «подвал» можно изобразить, нарисовав под цифрой 2 букву «л».

Если в ребусах встречаются зачеркнутые над рисунками (около рисунка) буквы, надо выбросить указанные буквы из названия предмета. Например: изобразив зачеркнутую букву «к» около рисунка крота, получим слово «рот»

Знак равенства между буквами над каким-либо рисунком предполагает замену одной на другую. Иногда делают по-другому: зачеркивают букву, которую надо заменить, а рядом ставят ту букву, на которую надо поменять. Например: Если над изображением лука стоит «у = а», следует читать «лак»

У=А

Цифры над рисунком указывают, что следует изменить порядок букв в слове. Например: если над изображением куста поставить цифры 3,4,2,1, получится слово «стук»

3, 4, 2, 1

Выполнение тренировочных упражнений.

Ученики расшифровывают слово, а один из них объясняет, как он это сделал.

Самостоятельная работа учащихся.

– А теперь будем разгадывать ваши ребусы.

Итог занятия.

– Что такое ребус?

– Назовите правила зашифровки или расшифровки слов?

Рефлексия.

– У вас на партах лежат кружки, нарисуйте на них….., а вот что? Вы узнаете, расшифровав ребус:

НАСТРОЕНИЕ

Приложение к занятию

математическая головоломка · Caffeinspiration

8 мая 2022 г. · 2751 слов · 13 минут чтения

На днях я видел математическую головоломку в Hacker News. Он читается следующим образом:

Два числа выбраны случайным образом, оба являются положительными целыми числами, меньшими 100. Сэнди сообщается сумма чисел, а Питеру – произведение чисел.
Затем между Сэнди и Питером происходит этот диалог:
Питер: Я не знаю цифр.
Сэнди: Я не знаю цифр.
Питер: Я не знаю цифр.
Сэнди: Я не знаю цифр.
Питер: Я не знаю цифр.
Сэнди: Я не знаю цифр.
Питер: Я не знаю цифр.
Сэнди: Я не знаю цифр.
Питер: Я не знаю цифр.
Сэнди: Я не знаю цифр.
Питер: Я не знаю цифр.
Сэнди: Я не знаю цифр.
Питер: Я не знаю цифр.
Сэнди: Я не знаю цифр.
Питер: Я знаю числа.
Какие числа?

На первый взгляд это выглядит непроницаемым, но я бы посоветовал вам подумать над этим, если хотите. Я подробно расскажу, как это работает и как это решить (с помощью компьютера).

Ниже спойлеры, будьте осторожны

Опять же, на первый взгляд, эта информация не выглядит полезной, но фокус в том, что каждый раз, когда они говорят, что не знают ответа, другая сторона может сузить варианты ответа. какие могут быть числа. Если вы сделаете это достаточное количество раз, останется только одна пара чисел, после чего Питер узнает ответ.

Мне было полезно подумать об этом с разных точек зрения. Во-первых, предположим, что у нас есть список всех пар чисел — мы можем думать о них как о наших кандидатах. Для упрощения предположим, что порядок не имеет значения (

(1, 2) совпадает с (2, 1) ), и мы просто отслеживаем один из дубликатов.

кандидаты: [
  (1, 1),
  (1, 2),
  (1, 3),
  (1, 4),
  ...
  (99, 99)
]

Давайте также представим большое представление всех возможных суммирует и произведения и пары чисел, которые составляют эти суммы и произведения. Допустим, это карты, где ключи — это суммы/произведения, а значения — списки пар, составляющих эти суммы/произведения. Кроме того, предположим, что и Сэнди, и Питер полностью знакомы с этими картами.

суммы: {
  2: [(1, 1)], # Единственная пара, которая в сумме дает 2, это (1, 1)
  3: [(1, 2)],
  4: [(1, 3), (2, 2)], # Для 4 у нас есть две пары: (1, 3) и (2, 2)
  5: [(1, 4), (2, 3)],
  6: [(1, 5), (2, 4), (3, 3)],
  # И так далее.  
  ...
  198: [(99, 99)]
}
продукты: {
  1: [(1, 1)], # Единственная пара, которая при умножении дает 1, это (1, 1)
  2: [(1, 2)],
  3: [(1, 3)],
  4: [(1, 4), (2, 2)], # Для 4 у нас есть две пары: (1, 4) и (2, 2)
  # И так далее.
  ...
  9801: [(99, 99)]
}

Хитрость заключается в тех записях, которые состоят только из одной пары.

Давайте сначала посмотрим на Питера. Питер знает произведение двух чисел. Питер может найти этот продукт на карте продуктов – если есть только одна пара, которая составляет этот продукт, то эти должно быть числом ! Когда Питер говорит нам, что не знает чисел, это означает, что товар не должен быть товаром, имеющим только одну пару . Это означает, что каждый раз, когда Питер не знает, мы можем удалить каждую пару, которая является единственной парой для продукта, и эти пары можно удалить из списка потенциальных кандидатов.

Давайте посмотрим на приведенные выше списки и первое требование Питера. В начале у нас есть полный список пар-кандидатов, полная карта из сумм и полная карта из товаров карта. Поскольку Петр знает произведение, когда он говорит «я не знаю чисел», это означает, что он просмотрел возможные пары, из которых состояло это произведение, и нашел несколько потенциальных пар — иначе он бы сразу знал числа. Это означает, что мы можем дисквалифицировать продукты, состоящие из одной пары. 1 как произведение, например, получается только путем умножения пары (1, 1) . Поскольку мы знаем, что Петр не сразу знает это как решение, значит, это не может быть (1, 1) .

Точно так же, если бы произведение было

9801 , Питер сразу бы понял, что пара равна (99, 99) . Поскольку он пока не может сказать наверняка, значит, числа не должны быть (99, 99) .

Теперь мы можем удалить всех кандидатов, которые были единственными факторами, из которых состоял продукт. Для первого раунда это, в частности, 1 , умноженное на каждое простое число, и каждое простое число, умноженное на другое простое число, в результате чего получается число больше 100. Важно отметить, что мы также можем удалить их и их произведения/суммы из продукты карта и суммы карта.

# После отбраковки кандидатов из первого тура
кандидаты: [
  (̶1̶,̶ ̶1̶)̶,̶
  (̶1̶,̶ ̶2̶)̶,̶
  (̶1̶,̶ ̶3̶)̶̶,̶
  (1, 4),
  ...
  (̶9̶9̶,̶ ̶9̶9̶)̶
 ]
суммы: {
  2̶:̶ ̶[̶(̶1̶,̶ ̶1̶)̶]̶,
  3̶:̶ ̶[̶(̶1̶,̶ ̶2̶)̶]̶,
  4: [(̶1̶,̶ ̶3̶)̶, (2, 2)],
  5: [(1, 4), (2, 3)],
  6: [(̶1̶,̶ ̶5̶)̶, (2, 4), (3, 3)],
  # И так далее.
  ...
  198: [(99, 99)]
}
продукты: {
  1̶:̶ ̶[̶(̶1̶,̶ ̶1̶)̶]̶,̶
  2̶:̶ ̶[̶(̶1̶,̶ ̶2̶)̶]̶,̶
  3̶:̶ ̶[̶(̶1̶,̶ ̶3̶)̶]̶,̶
  4: [(1, 4), (2, 2)],
  # И так далее.
  ...
  9̶8̶0̶1̶:̶ ̶[̶(̶9̶9̶,̶ ̶9̶9̶)̶]̶
}
# Примечание: в приведенном выше коде используется зачеркнутый код - если это выглядит смешно на вашем экране, приносим свои извинения!
# В этом случае отбраковка остается за читателем.

Вот в чем хитрость. Поскольку пространство возможных кандидатов было уменьшено, это означает, что возможные кандидаты, составляющие каждую сумму и произведение, также были сокращены. Давайте посмотрим на обновленные кандидата , суммы и продукта , заполнив еще несколько ранее пропущенных значений:

кандидаты: [
  (1, 4),
  (1, 6),
  (1, 8),
  ...
  (88, 90)
]
суммы: {
  4: [(2, 2)],
  5: [(1, 4), (2, 3)],
  6: [(2, 4), (3, 3)],
  # И так далее.
  ...
  178: [(88, 90)],
  179: [(80, 99)]
}
продукты: {
  4: [(1, 4), (2, 2)], # Для 4 у нас есть две пары: (1, 4) и (2, 2)
  # И так далее.
  ...
  7920: [(88, 90), (80, 99)]
}

Теперь очередь Сэнди сказать, что она не знает цифр. Поскольку Сэнди знает сумму , опять же это должно означать, что сумма не может быть любой суммой только с одной парой в качестве опции в суммирует , поэтому мы можем снова отбросить эти пары. В обновленной структуре суммирует мы видим, что 4 теперь состоит только из одной пары кандидатов, (2, 2) . Если бы сумма равнялась 4, Сэнди сразу бы знала, какая это пара, но раз она этого не знает, значит, пара не может быть (2, 2) , и мы можем удалить ее из кандидатов.

Каждый раунд мы дисквалифицируем потенциальных кандидатов. Потому что мы также можем удалить их из сумм и продуктов в качестве потенциальных вариантов, это означает, что каждый главный герой каждый раз работает над новой коллекцией, предоставляя немного больше информации каждый раз, когда они говорят, что не знают номер.

Этот шаблон будет продолжаться, каждый раз удаляя определенное количество параметров. В какой-то момент Питер наконец говорит, что знает числа — наконец, остался только один продукт с одной потенциальной парой, и это ответ. Важно, чтобы он сводился к одному продукту, иначе было бы несколько ответов! Вот почему в этой версии Питер утверждает, что знает ответ после 14 раундов, потому что он ограничивает ответ одной парой (хотя есть и другие варианты — см. далее).

Это было бы немного сложно сделать вручную, но, к счастью, компьютер сделает это за нас.

N = 100
# Вспомогательные функции для регенерации структур данных сумм/произведений каждый раунд. 
# Не оптимально, но это для развлечения.
def generate_sums (кандидатные_пары):
    суммы = {}
    для пары кортежей в парах кандидатов:
        (i, j) = tuple_pair
        сумма = я + j
        если сумма не в суммах:
            суммы[сумма] = [кортеж_пара]
        еще:
            суммы[сумма].append(tuple_pair)
    суммы возврата
def generate_products (кандидатные_пары):
    продукты = {}
    для пары кортежей в парах кандидатов:
        (i, j) = tuple_pair
        продукт = я * j
        если продукт не в продуктах:
            продукты [продукт] = [tuple_pair]
        еще:
            продукты[продукт].append(tuple_pair)
    возврат продуктов
защита find_pairs():
    # Сначала сгенерируйте все возможные пары от (1, 1) до (N-1, N-1).
    кандидат_пары = установить ()
    для i в диапазоне (1, N):
        для j в диапазоне (i, N):
            кандидат_пары.добавить((я, к))
    # Переключайтесь между сообщениями Питера или Сэнди каждый раунд (произведение или сумма)
    do_not_know_product = Истина
    раунд = 1
    пока верно:
        суммы = генерировать_суммы (кандидатные_пары)
        продукты = generate_products (кандидатные_пары)
        # Во-первых, проверьте, не остался ли один товар с одной парой.
  если раунд == 15:
            для продукта в продуктах:
                если len(products[product]) == 1:
                    print('Питер: я знаю числа')
                    печать (продукты [продукт] [0])
                    возвращаться
        если делать_не_знать_продукт:
            print('Питер: я не знаю цифр')
            # Просмотр продуктов. Для любого продукта, который имеет только одну пару,
            # мы можем удалить их из числа кандидатов на следующий тур.
            для продукта в продуктах:
                если len(products[product]) == 1:
                    tuple_pair = продукты[продукт][0]
                    # Удалить из кандидатов.
                    кандидат_пары.удалить(кортеж_пара)
            do_not_know_product = Ложь
        еще:
            print('Сэнди: я не знаю цифр')
            # Пройтись по суммам. Для любого продукта, который имеет только одну пару,
            # мы можем удалить их из числа кандидатов на следующий тур.
            на сумму в суммах:
                если len(суммы[сумма]) == 1:
                    tuple_pair = суммы[сумма][0]
                    # Удалить из кандидатов.  
                    кандидат_пары.удалить(кортеж_пара)
            do_not_know_product = Истина
        раунд += 1
если __name__ == '__main__':
    найти_пары()

Выполнение, которое приводит к следующему, как и головоломка, но теперь включает ответ:

Питер: я не знаю цифр
Сэнди: я не знаю цифр
Питер: я не знаю цифр
Сэнди: я не знаю цифр
Питер: я не знаю цифр
Сэнди: я не знаю цифр
Питер: я не знаю цифр
Сэнди: я не знаю цифр
Питер: я не знаю цифр
Сэнди: я не знаю цифр
Питер: я не знаю цифр
Сэнди: я не знаю цифр
Питер: я не знаю цифр
Сэнди: я не знаю цифр
Питер: я знаю числа
(77, 84)

Вот пара! 77 и 84.

Интересно, что в рамках отладки этого решения я обнаружил, что могут быть разные ответы при разном количестве раундов. Пока есть один продукт, состоящий из одной пары, это может быть ответом. Мы можем обновить функцию find_pairs , чтобы проверять потенциальные решения на различных длинах раундов (и останавливаться, прежде чем мы дойдем до бесконечности):

защита find_pairs():
    # Сначала сгенерируйте все возможные пары от (1, 1) до (N-1, N-1). 
    кандидат_пары = установить ()
    для i в диапазоне (1, N):
        для j в диапазоне (i, N):
            кандидат_пары.добавить((я, к))
    # Переключайтесь между сообщениями Питера или Сэнди каждый раунд (произведение или сумма)
    do_not_know_product = Истина
    раунд = 1
    пока верно:
        суммы = генерировать_суммы (кандидатные_пары)
        продукты = generate_products (кандидатные_пары)
        name = 'Питер:' if do_not_know_product else 'Сэнди:'
        потенциал_финал = Нет
        # Во-первых, проверьте, не остался ли один товар с одной парой.
        если делать_не_знать_продукт:
            count_unique_product_pairs = 0
            для продукта в продуктах:
                если len(products[product]) == 1:
                    count_unique_product_pairs += 1
                    потенциал_финал = продукты[продукт][0]
            если count_unique_product_pairs == 1:
                print(name, 'Я мог бы узнать цифры после',
                      раунд, 'раунды:', потенциал_финал)
        еще:
            count_unique_sum_pairs = 0
            на сумму в суммах:
                если len(суммы[сумма]) == 1:
                    count_unique_sum_pairs += 1
                    потенциал_финал = суммы[сумма][0]
            если count_unique_sum_pairs == 1:
                print(name, 'Я мог бы узнать цифры после',
                      раунд, 'раунды:', потенциал_финал)
        num_candidates_before_cull = длина (кандидатные_пары)
        если делать_не_знать_продукт:
            # Просмотр продуктов.  Для любого продукта, который имеет только одну пару,
            # мы можем удалить их из числа кандидатов на следующий тур.
            для продукта в продуктах:
                если len(products[product]) == 1:
                    tuple_pair = продукты[продукт][0]
                    # Удалить из кандидатов.
                    кандидат_пары.удалить(кортеж_пара)
            do_not_know_product = Ложь
        еще:
            # Пройтись по суммам. Для любого продукта, который имеет только одну пару,
            # мы можем удалить их из числа кандидатов на следующий тур.
            на сумму в суммах:
                если len(суммы[сумма]) == 1:
                    tuple_pair = суммы[сумма][0]
                    # Удалить из кандидатов.
                    кандидат_пары.удалить(кортеж_пара)
            do_not_know_product = Истина
        раунд += 1
        # Если мы не удалили ни одной пары, возможно, мы попали в бесконечный цикл и хотим
        # остановиться.
        если len(candidate_pairs) == num_candidates_before_cull:
            возвращаться

Используя эту версию, мы теперь получаем следующее:

Сэнди: Я мог узнать числа после 6 раундов: (72, 99)
Питер: Я мог узнать числа после 7 раундов: (81, 88)
Сэнди: Я мог узнать числа после 8 раундов: (70, 99)
Питер: Я мог узнать числа после 9 раундов: (77, 90)
Сэнди: Я мог узнать числа после 10 раундов: (72, 95)
Питер: Я мог узнать цифры после 11 раундов: (76, 90)
Сэнди: Я мог узнать цифры после 12 раундов: (70, 96)
Питер: Я мог узнать цифры после 13 раундов: (80, 84)
Сэнди: Я мог узнать числа после 14 раундов: (66, 98)
Питер: Я мог узнать числа после 15 раундов: (77, 84)

Это означает, что головоломка может состоять из нескольких различных комбинаций раундов, и либо Сэнди, либо Питер говорят, что знают ответ! По моему мнению, показ 15 «я не знаю» делает головоломку еще более запутанной, что добавляет головоломки.

Сколько раундов идет? Здесь мы видим, что он может прогрессировать до тех пор, пока не останется отбракованных кандидатов — для N = 100 мы проходим 15 раундов, прежде чем остановимся. Как это выглядит для другого значения N? Мы можем легко исследовать это, и я думаю, что здесь есть забавный вопрос: каково наименьшее значение N, на которое есть ответ?

Для самого низкого уровня мы можем просто сделать следующее, добавив n в качестве аргумента:

определение найти_пары (n):
    # Сначала сгенерируйте все возможные пары от (1, 1) до (N-1, N-1).
    кандидат_пары = установить ()
    для i в диапазоне (1, n):
        для j в диапазоне (i, n):
            кандидат_пары.добавить((я, к))
    # ... все остальное то же самое
если __name__ == '__main__':
    для i в диапазоне (100):
        печать('N =', я)
        найти_пары (я)
        Распечатать('*****')

 Н = 0
*****
Н = 1
*****
Н = 2
Питер: Я мог знать числа после 1 раунда: (1, 1)
*****
Н = 3
*****
Н = 4
*****
Н = 5
*****
Н = 6
*****
Н = 7
*****
Н = 8
*****
Н = 9*****
Н = 10
Питер: Я мог знать числа после 3 раундов: (1, 4)
Сэнди: Я мог узнать числа после 4 раундов: (2, 3)
Питер: Я мог знать числа после 5 раундов: (1, 6)
Сэнди: Я мог узнать числа после 6 раундов: (3, 4)
Питер: Я мог знать числа после 7 раундов: (2, 6)
Сэнди: Я мог узнать числа после 8 раундов: (4, 4)
Питер: Я мог узнать числа после 9 раундов: (2, 8)
*****
. .. гораздо больше

Похоже, что самый низкий номер N = 2 , что не очень весело, потому что единственная пара (1, 1) . Не очень интересная загадка! Следующий – N = 10 для значений 1-9, что можно сделать за 3-9 ходов. Это довольно интересно, так как мы могли бы сформулировать загадку по-другому, хотя большое количество чисел и раундов делает ее еще более запутанной.

Я думаю, что еще одна интересная вещь заключается в том, что для некоторых значений N нет решения! Давайте посмотрим на N = 4 , где числа 1-3. Эти таблицы довольно легко написать от руки:

кандидаты: [
  (1, 1),
  (1, 2),
  (1, 3),
  (2, 2),
  (2, 3),
  (3, 3)
]
суммы: {
  2: [(1, 1)],
  3: [(1, 2)],
  4: [(2, 2), (1, 3)],
  5: [(2, 3)],
  6: [(3, 3)]
}
продукты: {
  1: [(1, 1)],
  2: [(1, 2)],
  3: [(1, 3)],
  4: [(2, 2)],
  6: [(2, 3)],
  9: [(3, 3)]
}

Хорошо, если мы удалим все продукты, состоящие из одной пары, у нас не останется ни одной пары, что логично. Поскольку не все значения N приводят к решению, это также означает, что пытаться рассуждать о проблеме при низких значениях N очень сложно, поскольку на самом деле это не приводит к решению!

В общем, забавная головоломка. Вот несколько закрывающих дополнительных вопросов для вас:

Какая разница, кто говорит первым: Питер или Сэнди?
Что произошло бы, если бы у нас был третий человек, который знал бы абсолютное значение чисел, вычитаемых друг из друга? Имеет ли значение порядок трех?
Что, если этот третий человек знал вычитаемые числа, где порядок чисел имел значение?

Головоломки с разрядностью (для двузначных чисел)

Эти самокорректирующиеся математические головоломки — забавный способ попрактиковаться в разрядности (и они также представляют собой хорошую альтернативу рабочим листам)

Не секрет, что я большой поклонник математических головоломок.

Это увлекательный и практический способ попрактиковаться и повторить математические темы.

Отличные новости? Большинству детей они, кажется, действительно нравятся.

Этот пост посвящен головоломкам с разрядностью. Эти распечатанные пазлы предназначены для двузначных чисел и станут отличным занятием для любого ребенка, которому нужно работать с десятками и единицами.

Подобные головоломки отлично подходят для отдыха от рабочих листов или рабочих тетрадей — никаких карандашей, никакого письма, только много-много математических задач.

Готовы заглянуть? Читай дальше!

Расскажите мне об этих головоломках с разрядными значениями

Этот математический ресурс состоит из 20 отдельных прямоугольных головоломок с разрядными значениями .

Каждая отдельная головоломка разделена на четыре части следующим образом:

Каждая из четырех частей головоломки показывает одно и то же двузначное число , представленное по-разному :

в виде числа (54)
в расширенной форме (50 + 4)
в виде десятичных блоков (показаны как 5 стержней по десять и 4 единицы)
в словесной форме («5 десятков и 4 единицы»)

В набор входят 20 различных чисел в виде головоломок. Это: 23, 14, 86, 54, 49, 61, 32, 46, 29, 51, 93, 72, 11, 37, 68, 35, 77, 81, 59 и 91.

Связано: 5 причин почему головоломки с числами ОТЛИЧНЫ для маленьких детей

Подготовка

Сначала распечатайте 20 головоломок. Я бы порекомендовал распечатать на картоне и/или заламинировать. Одна головоломка печатается на одном листе бумаги/карточки формата Letter.

Все пазлы написаны черными чернилами для удобства печати.

Выполните . Убедитесь, что все головоломки напечатаны на бумаге или карточке одного цвета. В противном случае вы вполне можете обнаружить, что ваш ребенок или ученики сопоставляют кусочки головоломки в соответствии с их цветом и полностью игнорируют математику!

После печати вырежьте каждую головоломку, а затем разрежьте каждую на четыре части по волнистым линиям.

Как мне использовать эти головоломки с разрядностью?

Сначала решите, сколько головоломок вы хотите использовать. Хотя головоломок в этом ресурсе 20, я бы рекомендовал начинать не более чем с десяти. Вы всегда можете использовать остальные десять в следующий раз.

Затем смешайте все кусочки головоломки.

Задача состоит в том, чтобы снова собрать прямоугольные пазлы.

В каждой головоломке четыре разные части должны представлять одно и то же число.

Связанный: Что такое расширенная форма в математике?

Вы говорите, что эти головоломки самовосстанавливающиеся ? Что это вообще значит?!

Это означает, что линии разреза (линии, которые делят каждую прямоугольную головоломку на четыре части) уникальны.

Четыре части головоломки соберутся вместе, только если математика верна.

Почему это важно?

Ну, это дает вашему ребенку мгновенную обратную связь о том, правильно ли он сопоставил части или нет, и, следовательно, правильно ли он понимает математику.

Такая мгновенная обратная связь и означает, что ребенок с большей вероятностью сможет решать головоломки самостоятельно, без значительного вмешательства взрослых.

Учимся разгадывать ребусы

Внеклассное занятие для 1-4 классов ” Учимся разгадывать кроссворды”.

математическая головоломка · Caffeinspiration

8 мая 2022 г. · 2751 слов · 13 минут чтения

Головоломки с разрядностью (для двузначных чисел)

Добавить комментарий Отменить ответ