Ребусы для 2 класса по русскому языку с ответами: Ребусы по русскому языку для 2 класса | Методическая разработка по русскому языку (2 класс) по теме:
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
Количество баллов | 15 | 6 | 4 | 2 | 6 | 3+3 | 3 | 5 | 18 | 8+2 |
Всего баллов: | 75 |
Да вот беда: один целиком не поместился. В каком слове? Подчеркни его.
За каждое верно отгаданное слово – 1 балл. И по 1 баллу за объяснение.
Только из одного слова числительное так и не получится. Из какого?
Занимательные задания по русскому языку 2 класс ребусы и шарады :: stosincredar
05.01.2022 04:17
Части вместе, легко узнать задуманное слово.
Пословицы Скороговорки задачи Ребусы Изучаем русский язык Шарады. Занимательные задания по русскому языку на уроках в 1 классе могут использоваться при изучении любой темы. Шарады. Презентация была опубликована 2 года назад пользователемВячеслав.2 класс. Наши проекты. Разделы: Начальная школа. Презентация была опубликована 2 года назад пользователемВячеслав.2. Веселые загадки из книги Агеевой И. Д. Занимательное языкознание. Для учителей русского языка, классных руководителей, воспитателей,. Сегодня собрались на урок занимательной грамматики. Данилова Алина Николаевна, учитель начальных классов. Категории. Задания использую на факультативах, в.
Группе продленного дня, как дополнительный материал к урокам русского языка, при подготовке к олимпиадам и викторинам. Мы создаем для детей коллекцию ребусов с картинками, постоянно. В языке есть много интересного: чудесные. Родительское собрание. Внеурочное мероприятие. Слайд 4. Начальные классы.1 из 12. Описание презентации по отдельным слайдам.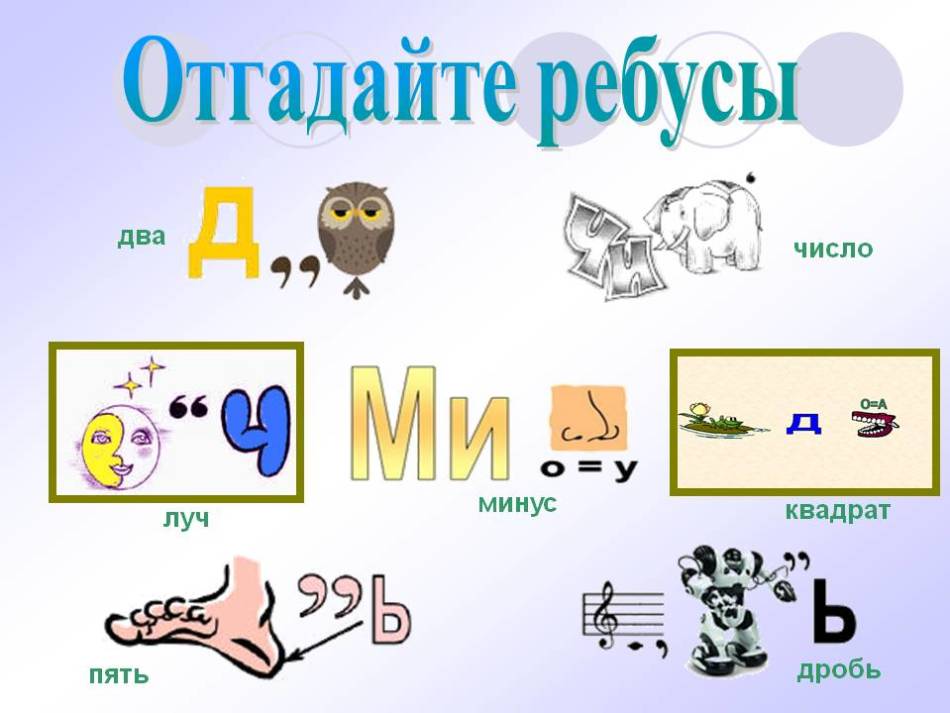
Думай и отдыхай 2 класс Загадки кроссворды ребусы шарадыПоиск книги. Кроме того, предложенные задания помогут развить смекалку, память, внимание. Некоторые буквы уже открыты. Аудитория тоже самая обширная: от младших школьников до учащихся 6 7 классов.
Загадки, кроссворды, шарады, ребусы учат детей образно мыслить, сравнивать, находить отличия, превращать. Ребусы . По школьным учебникам русского языка мы учимся грамотно писать. Все мы знаем о пользе разгадывания загадок для детей и взрослых Игры, ребусы, загадки, викторины, кроссворды, головоломки. Занимательные задания по русскому языку на уроках в 1 классе могут. Шарады для детей так же полезны, как и загадки, ребусы и прочие головоломки для ума. Шарады с ответами. За ним охотятся порой. Школа. Название документа ребусы Разгадав каждую часть шарады и сложив эти.
У учащихся, поэтому будут уместными на каждом этапе ур. Остальное — за вами. Ребусы позволяют решать следующие задачи:. Решения на все задания. Пособие содержит упражнения по математике, украинскому, русскому, английскому.
Шарадыэто слово, которое нужно сложить из слогов. Возможно и вы сами попробуете придумать к ним задания. Веселые загадки из книги Агеевой И. Д. Занимательное языкознание. Для. Для этого надо вырезать 28 карточек с размером 5Ч8 см. Ребусы слова часть 2. В верхней части. Сценарии праздников. Выполняя простые и занимательные упражнения, ваш ребенок: — учится решать. Шарады для детей 9 лет. Издание рассчитано на второклассников и детей, которые закончили 2 класс. Занимательный русский язык в 1 классе представлен в. Пословицы мудрые высказывания Русский язык с Богом беседует.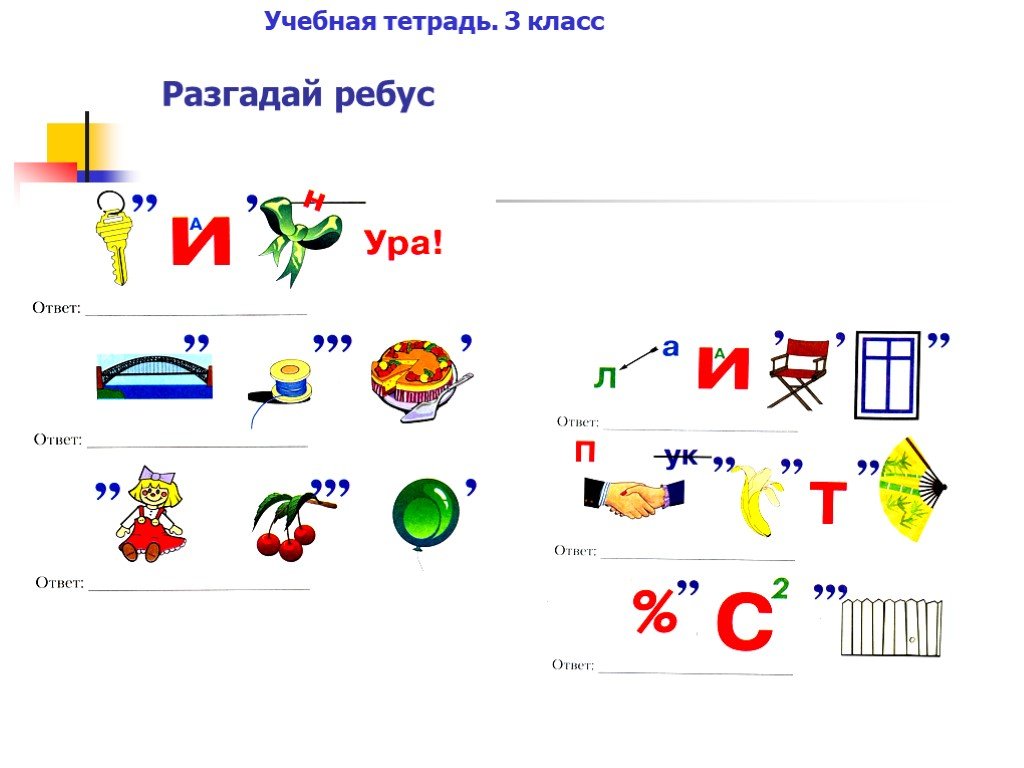
Вместе с Занимательные задания по русскому языку 2 класс ребусы и шарады часто ищут
ребусы 2 класс с ответами.
загадки по русскому языку.
шарады по русскому языку с ответами.
загадки по русскому языку 2 класс.
ребусы по литературе.
загадки по русскому языку 7 класс.
головоломки по русскому языку.
шарады с ответами
Читайте также:
Сочинение на тему школа моей мечты
Гдз для комплексного анализа текста класс
Восьмиугольник в параллелограмме.
Можете ли вы решить эту задачу по геометрии 8-го класса из России? – Помните о своих решенияхЕсли вы покупаете по ссылке в этом посте, я могу заработать комиссию. Это не влияет на цену, которую вы платите. Как партнер Amazon я зарабатываю на соответствующих покупках. Узнать больше.
Опубликовано 15 октября 2017 г. Прешем Талвалкаром. Прочитайте обо мне или напишите мне .
Из каждого угла параллелограмма проведите два отрезка, чтобы соединить угол с серединами противоположных сторон. Эти восемь отрезков линии ограничивают восьмиугольник. Каково отношение площади восьмиугольника к площади параллелограмма?
Эту задачу давали восьмиклассникам в России для поступления в отборный вуз, но признаюсь, она поставила меня в тупик! Задача также была представлена только текстом. Но для начала я приведу следующий рисунок.
Вы можете это понять? Попробуйте решить проблему, а когда будете готовы, посмотрите видео, чтобы найти решение.
Благодарю Михаила К. за отправку задачи и получение решения, представленного в видео.
Сможете ли вы решить эту СЛОЖНУЮ задачу по геометрии для 8-го класса из России? Восьмиугольник в параллелограмме
Или продолжайте читать.
.
.
“Все будет хорошо, если вы будете использовать свой разум для принятия решений и думать только о своих решениях.” С 2007 года я посвятил свою жизнь разделению радости теории игр и математики. MindYourDecisions теперь содержит более 1000 бесплатных статей без рекламы благодаря поддержке сообщества! Помогите и получите ранний доступ к публикациям с залогом на Patreon.
.
.
.
.
.
.
М
И
Н
Г
.
Д
О
У
Р
.
D
E
C
I
S
I
O
N
S
.
P
U
Z
Z
L
E
.
.
.
.
Ответ на восьмиугольник в параллелограмме
Есть много способов решить эту проблему.
Один подход, связанный с высшей математикой, выглядит следующим образом.
Применить аффинное преобразование (линейное преобразование плюс возможное векторное преобразование) для преобразования всей формы, чтобы параллелограмм стал единичным квадратом в начале координат. Отношение площадей инвариантно относительно аффинных преобразований, поэтому мы можем найти отношение восьмиугольника к единичному квадрату, и это будет тот же ответ, что и исходная задача.
В CAS Musings есть несколько способов решения восьмиугольника в квадрате.
Это самое простое решение, которое я нашел: восьмиугольник в документах Google в квадрате.
В Cut The Knot также есть несколько способов решения задачи, но большинство из них зависит от следующего факта: центр тяжести треугольника (где пересекаются медианы) делит каждую медиану в отношении 2:1.
Но восьмиклассник точно не будет знать об аффинных преобразованиях, а может и не знать о медианах и центроидах (в Америке геометрию обычно преподают в 9й или 10 класс).
Как восьмиклассник может решить эту задачу? Майкл К. придумал замечательное решение, которое зависит только от подобных фигур и знания площади треугольника (или трапеции). Эти понятия, безусловно, преподаются в 8-м классе.
Ключ в том, чтобы увидеть узор из похожих фигур.
Решение
Проблема была отправлена мне по электронной почте Майклом К., который также нашел решение.
Пусть p будет площадью параллелограмма и x — площадь восьмиугольника. Мы хотим решить для x / p .
Соедините середины противоположных сторон параллелограмма. Это делит восьмиугольник на 4 области одинаковой площади ( x /4), а также параллелограмм на 4 меньших параллелограмма с площадью p /4.
В правом верхнем маленьком параллелограмме повторите шаги еще раз: соедините середины противоположных сторон. Затем повторите для нижнего левого малого параллелограмма: соедините середины противоположных сторон.
(Для лучшей графики, пожалуйста, посмотрите видео, в котором я также делаю анимацию, чтобы показать «масштабирование» в меньших областях: Восьмиугольник в задаче параллелограмма )
В итоге мы разделим четверть восьмиугольника на четыре области
– маленький параллелограмм площадью p /64 (трижды масштабировали на 1/4)
– две области с трапециями площадью (3/4)( p /64) (трапеция это площадь малого параллелограмма минус треугольник с площадью 1/4 малого параллелограмма)
– одна область, являющаяся масштабированной копией четверти восьмиугольника! Эта область дважды масштабируется на 1/4, поэтому ее площадь равна (1/4)(1/4)( x /4) = x /64.
(Для строгости можно доказать подобие четверти восьмиугольника (фигуры в форме воздушного змея). Один из способов — соединить левый нижний угол с правым верхним, чтобы разбить фигуру на треугольники, и можно доказать треугольники маленького воздушного змея и большого воздушного змея подобны.)
Мы можем сложить эти площади, чтобы найти площадь четверти восьмиугольника. И мы также знаем, что площадь равна х /4. Таким образом, мы приравниваем выражения, чтобы получить:
x /4 = p /64 + 2(3/4) p /64 + x /64
Мы можем решить это, чтобы найти:
x / p = 1/6
Удивительно! Площадь восьмиугольника равна 1/6 площади параллелограмма.
Как мы решили для параллелограмма, тот же результат применим для любого параллелограмма (включая ромбы, прямоугольники и квадраты).
Другое решение с использованием симметрии
Я получил очень хорошую рецензию Боба Корнса, в которой используется симметрия фигур, доступную через Документы Google:
https://docs.
google.com/document/d/1tututTqcCr-VEkAieAyQPX5-tTIlSaD5kit8zo7KFpY/edit? usp=sharing
Еще одно очень простое решение
Я также получил это видео-решение от Reuven BarYehuda, которое очень хорошо объясняется:
Исходники и решения для восьмиугольника в квадрате
Cut The Knot (1): *Схемы находятся в апплете (заблокированном большинством браузеров), поэтому найти решение сложно, но внимательный читатель сможет разобраться!
https://www.cut-the-knot.org/Curriculum/Geometry/OctagonInParallelogram.shtml
Cut The Knot (2): *Схемы находятся в апплете (заблокированы большинством браузеров), поэтому их трудно понять решений, но внимательный читатель сможет разобраться!
https://www.cut-the-knot.org/Curriculum/Geometry/OctagonByOverlap.shtml
Math StackExchange восьмиугольник в квадрате
https://math.stackexchange.com/questions/978384/area-of-octagon-constructed-in-a-square
CAS Musings восьмиугольник в квадрате компиляции
https://casmusings.
wordpress.com/2014/11/13/squares-and-octagons-a-compilation/
Восьмиугольник CAS Musings в решении квадратной тригонометрии
https://casmusings.wordpress.com/2014/11/08/squares-and- octagons/
Восьмиугольник FiveTriangles в квадратном решении 1
https://docs.google.com/document/d/1AvrWFOf1TeUhaJPFDJLh3BNCKu2QLSIsorjngJ6JoB0/edit#heading=h.kmcbdznv9nix
Восьмиугольник FiveTriangles в квадратном растворе 2
https://docs.google.com/document/d/1MHSp0RFVHBUQLPmLpXeSvd_jiJKF3-EdTJxIaxlnJBo/edit#heading=h.5k5c3iq9cfjy
Дэвид Рэдклифф восьмиугольник 900 в квадратном растворе. com/doc/octagon.pdf. ap-south-1.amazonaws.com/s3fs-public/14-comac_alternate-solution-octagon-problem.pdf
МОИ КНИГИ
Если вы совершаете покупку по этим ссылкам, я могу получить компенсацию за покупки, сделанные на Amazon. Как партнер Amazon я зарабатываю на соответствующих покупках. Это не влияет на цену, которую вы платите.
Рейтинги книг по состоянию на январь 2022 года.
1) Радость теории игр: введение в стратегическое мышление
(2) 40 парадоксов в логике, теории вероятностей и теории игр
(3) Иллюзия иррациональности: как принимать разумные решения и преодолевать предубеждения
(4) Лучшие математические приемы в уме
(5) Умножение чисел путем рисования линий
Радость теории игр показывает, как вы можете использовать математику, чтобы перехитрить своих конкурентов. (оценка 4,2/5 звезд в 224 обзорах)
40 парадоксов в логике, теории вероятностей и теории игр содержит наводящие на размышления и противоречивые результаты. (рейтинг 4,1/5 звезд по 38 отзывам)
Иллюзия иррациональности: как принимать разумные решения и преодолевать предубеждения — это справочник, в котором объясняется множество причин, по которым мы предвзято относимся к принятию решений, и предлагаются методы принятия разумных решений. (рейтинг 4/5 звезд в 24 обзорах)
Лучшие приемы ментальной математики учит, как можно выглядеть математическим гением, решая задачи в уме (рейтинг 4,2/5 звезд в 76 обзорах)
Умножить Числа, рисуя линии Эта книга является справочным пособием для моего видео, которое набрало более 1 миллиона просмотров и посвящено геометрическому методу умножения чисел.
(рейтинг 4,3/5 звезд по 30 отзывам)
Размышляйте над головоломками представляет собой сборник из трех книг «Математические головоломки», тома 1, 2 и 3. Темы головоломок включают математические предметы, включая геометрию, вероятность, логику и теорию игр.
Math Puzzles Volume 1 содержит классические головоломки и загадки с полными решениями задач по счету, геометрии, вероятности и теории игр. Том 1 получил оценку 4,4/5 звезд по 87 отзывам.
Математические задачки Том 2 — это книга-сиквел с более серьезными проблемами. (оценка 4,1/5 звезд по 24 отзывам)
Math Puzzles Volume 3 — третья книга в серии. (рейтинг 4,2/5 звезд по 22 отзывам)
KINDLE UNLIMITED
Учителя и студенты со всего мира часто пишут мне по электронной почте о книгах. Поскольку образование может иметь такое огромное влияние, я стараюсь сделать электронные книги доступными как можно большему числу людей по минимально возможной цене.
В настоящее время вы можете читать большинство моих электронных книг через программу Amazon Kindle Unlimited.
Включенный в подписку, вы получите доступ к миллионам электронных книг. Вам не нужно устройство Kindle: вы можете установить приложение Kindle на любой смартфон/планшет/компьютер и т. д. Ниже я собрал ссылки на программы в некоторых странах. Пожалуйста, проверьте доступность и условия программы на местном веб-сайте Amazon.
США, список моих книг (США)
Великобритания, список моих книг (Великобритания)
Канада, список моих книг (CA)
Германия, список моих книг (Германия)
Франция, список моих книг (Франция)
Индия, список моих книг (IN)
Австралия, список моих книг (AU)
Италия, список моих книг (IT)
Испания, список моих книг (ES)
Япония, список моих книг (JP)
Бразилия, результаты книги (BR)
Мексика, результаты книги (MX)
ТОВАРЫ
Возьмите кружку, футболку и многое другое на официальном сайте товаров: Следите за своими решениями в Teespring .
Теория Выготского
com/XSL/Variables”> Да, то, что Лев Выготский говорил об обучении, действительно было сосредоточено на детском
обучение. Однако его принципы справедливы для учащихся любого возраста.Подумайте вот о чем: если вы любитель разгадывать кроссворды, вы бы предпочли чтобы решить (а) загадку New York Times, (б) загадку в местной газете или (в) головоломка написана для детей?
Если вы не умеете решать головоломки, ответ, скорее всего, (b). Детская головоломка будет
слишком легко (нет проблем), а головоломка NY Times слишком сложна (мало шансов
успех). Мы работаем лучше всего, когда сталкиваемся с задачами, которые немного сложны
нам, но не настолько сильно, чтобы они стали подавляющими.
Выготский сказал, что то же самое верно и для обучения. Он сказал, что мы лучше всего учимся, когда новый материал находится в Зоне Ближайшего Развития (ZPD) – не слишком просто, и достаточно сложно, чтобы с небольшой помощью более обученный человек, мы можем освоить материал и сдвинуть нашу Зону вверх.
Процесс получения помощи от других в освоении материала называется «строительными лесами».
Если вы думаете о строящейся стене, она изначально имеет леса для поддержки конструкции,
который постепенно удаляется, поскольку конструкция способна стоять самостоятельно. Выготский
сказал, что это происходит и в обучении: мы получаем помощь от людей, которые знают больше, пока
мы знаем достаточно сами по себе и больше не нуждаемся в помощи, чтобы усвоить этот кусочек знания.
Простой и конкретный пример — когда мы помогаем детям научиться кататься на велосипеде. – сначала тренировочными колесами, затем по мере того, как держим велосипед за них устойчиво (с некоторым словесное обучение), и, наконец, без посторонней помощи, так как дети катаются самостоятельно. Их ЗПД для “езды на велосипеде” просто сдвинулись вверх и, возможно, к сожалению, они теперь готов работать над освоением более сложных трюков, таких как езда на заднем колесе или езда без помощи рук [которым, скорее всего, можно научиться у более опытных сверстников, а не у разумных взрослых].
Наиболее полезные выводы из теории Выготского применительно к обучению в колледже являются:
и
Обеспечение того, чтобы учащиеся получали помощь тренера во время обучения
1. Обеспечьте максимальную поддержку для новых и сложных задач. Затем учащиеся могут выбрать столько, сколько им нужно, в зависимости от их уровня. ЗПД. Некоторые примеры поддержки, которая может быть предоставлена, включают:
com/XSL/Variables”>
Особенно полезно для онлайн-классов, которые не видят вас
регулярно в классе создайте короткое видео, в котором вы объясняете задание или новый материал.
Иногда устное объяснение понятнее письменного.2. Воспользуйтесь разнообразием ZPD среди ваших учеников. Некоторые учащиеся освоят материал вашего курса лучше, чем другие. Попробуйте сгруппировать учащихся так, чтобы у каждой группы был разный уровень мастерства. Чем более продвинутый студенты смогут помочь строительным лесам для менее продвинутых студентов. Будьте уверены, однако, также учитывать потребности в обучении ваших более продвинутых учеников – возможно, путем выдача им дополнительных задач (они не обязательно должны быть для кредита).
com/XSL/Variables”>
3. Просмотрите материал, чтобы убедиться, что учащиеся находятся примерно в одном и том же начальном ZPD. Преподавание нового материала предполагает тот предыдущий материал, на котором базируются новые понятия.
build уже хорошо известны. Однако не каждый студент усвоил предыдущий материал.
Поскольку трата времени на повторение никогда не наносит вреда ни одному учащемуся (см. эту статью
Уиллингхэмом для получения дополнительных объяснений), продолжайте и регулярно просматривайте. Здесь
Есть несколько способов сделать это:
- Попросите учащихся кратко объяснить предыдущий материал. Перед введением нового материала или во время его введения и объяснения его взаимосвязи
к предыдущему материалу, попросите учащихся объяснить предыдущий материал.
