Раскраска состав числа 3: ИЗУЧАЕМ СОСТАВ ЧИСЛА – РАСПЕЧАТАЙ и ИГРАЙ :: Игры, в которые играют дети и Я
ИЗУЧАЕМ СОСТАВ ЧИСЛА – РАСПЕЧАТАЙ и ИГРАЙ :: Игры, в которые играют дети и Я
Здравствуйте-здравствуйте!
Сегодня покажу новые математические раскраски на изучение состава числа и поделюсь парой страничек, может, и вам пригодится.
Еще покажу несколько фото-моментов с урока – это для тех, кому интересно заглянуть ко мне на урок.
В начале занятия стараюсь делать массажную разминку для пальчиков. Одна из моих любимых разминок – с карандашами. В проекте ИГРАнаУРА – 2 будет игровой месяц с массажными играми, постараюсь к тому времени зафотографировать карандашную разминку. А пока, для интересующихся, могу предложить подборку упражнений с карандашами в в моей группе Вконтакте ЛАДОШКИ_NL, там я собираю интересные и полезные идеи для занятий по развитию мелкой моторики.Доминошки!
У меня много разных заданий с домино, но начали с простого – “переводили” точки в числа. Посчитай сколько точек – запиши число. Еще отрабатывали порядок действий – поработал с доминошкой – переверни, чтобы не сбиться.

Я обязательно уделяю время организационным вопросам: заостряю внимание детей на то как, где, зачем и почему именно так лучше делать.
Каждый получает свой набор доминошек, а значит надеяться не на кого – нужно включать голову и выполнять задания самостоятельно.
А это наши папочки для листочков с заданиями.
А это задание “найди и раскрась” на внимание. После того как дети познакомились с таким видом заданий – можно давать их уже и для самостоятельной работы.
Вот, например, после или перед занятием я проверяю домашние задания, а чтобы дети были при деле – даю им такие раскраски.
Дети: а что же здесь получится?
Я: это вы мне расскажете, если правильно выполните задание))
У некоторых ребят уже появилась даже своя методика раскрашивания!
Молодцы! Мыслят!
Ну и СОСТАВ ЧИСЛА.
За два занятия выяснила, что состав числа дети не знают((( примеры решают со скрипом… для некоторых даже 1+1 – “надо подумать”.
Состав числа это важно!
Сейчас меня закидают тапками методисты))) но общепринятые “домики” меня не устраивают – не работают они… дети не запоминают, что из чего состоит…
Только частые повторения могут дать результат, но просто зубрить – не наш метод)))
Так родились раскраски на изучение-закрепление состава числа.
Начали с саааамого простого.
Как я работаю с таким заданием:
Рассматриваем задание. Выбираем цвет. Договариваемся, что будем решать примеры так: шагаем по строчкам, пример за примером – “читаем” пример, решаем, смотрим в таблицу с ответами, каким цветом нужно раскрашивать клеточку с получившимся результатом, и только потом раскрашиваем.
Две строки проговариваем и решаем вместе, а дальше уже каждый работает самостоятельно.
Если всё решили правильно, то получится узнаваемая картинка.
Ребёнок: ай… я ошибся… ааа что теперь делать. ..
..
Я: не расстраиваться, мы же с вами учимся! Хорошо, что ты увидел ошибку. Почему ошибка закралась в твой листочек?
Ребенок: я торопился…
Сделал вывод сам – в следующий раз вероятнее всего вспомнит свой опыт и, прежде чем раскрасить, проверит.
Я стараюсь подталкивать детей искать причины их ошибок.Моё пособие
СОСТАВ ЧИСЛА: от 1 ДО 10
Статья авторская
и предназначена только для частного ознакомления.
Копирование и публикация в других источниках
без моего письменного согласия
ЗАПРЕЩЕНЫ.
Автор: Наталья Чистоклетова
Новости моего блога можно получать на вашу любимую почту,
а подписаться можно
ИГРАЙТЕ С РАДОСТЬЮ
НАТАЛЬЯ ЧИСТОКЛЕТОВА
ЧИСЛОВЫЕ ПИРАМИДЫ: СОСТАВ ЧИСЛА В ПРЕДЕЛАХ 10
Здравствуйте-здравствуйте!
Дорогие мои читательницы, поздравляю вас с чудесным весенним праздником – 8 Марта!
Чтобы там не говорили, а хорошо, что этот праздник есть, правда ведь? ))))
Я желаю вам солнечного настроения и побольше улыбающихся людей вокруг!
Ну а у меня вот уже 8 месяцев праздник каждый день с #мой_сын_Сема ))) поэтому я с удовольствием работаю ночью даже 8 Марта )))
Спешу показать вам еще одно пособие, чтобы тот, кто очень захочет, смог приобрести его с праздничной скидкой.
Покажу пособие “ЧИСЛОВЫЕ ПИРАМИДЫ: СОСТАВ ЧИСЛА В ПРЕДЕЛАХ 10″, но я не только его покажу, а и подарю 10 страниц для скачивания – пусть это будет маленький восьмомартовский подарок от меня.
Все мои пособия в первую очередь я делаю для своих занятий. Я по ним реально работаю. Как я с ними работаю – это отдельная история, но скажу, что я делаю всегда гораздо больше, чем мне надо на момент создания, чтобы был выбор в будущем. Это не хомячество – это экономия времени ПОТОМ.
Каждый год у меня новые группы и каждый год я адаптирую свою программу под конкретную группу, поэтому в моих пособиях часто задания представлены несколькими уровнями. Пришли слабенькие – им задание попроще, пришли сильные – им потруднее. Это я к чему? Если вы приобретаете у меня пособия – оценивайте возможности и уровень подготовки ваших детей, давайте им задания по силам.
Ну и о пособии)))
Числовые пирамиды, которые я покажу ниже – задания на изучение-закрепление состава числа в пределах 10. Также эти задания развивают умение логически мыслить и делать выбор.
От этих пирамид в восторге я и, самое главное, мои ребята их восприняли на ура.
Для начала я покажу, что собой представляют числовые пирамиды – смотрите картинки ниже. Первая картинка (левая) – это варианты заданий, вторая (правая) – варианты решения, обратите внимание, что некоторые пирамидки могут быть решены по-другому, всё зависит от выбора.
Опытным путем я пришла к тому, что эти пирамидки должны быть на отдельных карточках – одна числовая пирамида – это одна карточка! Когда ребенок видит целую страницу заданий, он впадает в уныние))) “огооо сколько…”, а когда он видит маленькую карточку, то таких мыслей не возникает – для него мало, значит просто… А вот сколько он сможет решить таких карточек за один присест, он даже и не догадывается! Решаются пирамидки легко, конечно, при условии, что вы отобрали для знакомства сначала простые пирамидки и уделили время для объяснения и совместного решения! Важно не только ЧТО вы даёте детям, а и то, КАК вы это подаёте.
Мои карточки я заламинировала, дороговато на первый взгляд получается, но карточки ведь многоразовые – сделал один раз и пользуйся до бесконечности)))
Чем еще мне нравятся ламинированные карточки? Ошибся – стёр!
Эти карточки я использую для самостоятельной работы. Работаем 5-10 минут.
Беру на урок 50 карточек, каждый берет столько, сколько хочет! Решает – берет еще и так до тех пор, пока группа не решит все 50 карточек.
Т.е. один может решить 10 карточек, другой 3 – каждый работает в своем темпе.
Никто не ждёт, что будет на доске или у соседа подсказка – ведь у каждого своя уникальная карточка! Сидят пыхтят – только посматривают, кто сколько решил, стараются догнать и перегнать – “а ты сколько решил?”
Работа кипит! Что остаётся мне? Я проверяю карточки по первому “я решил!”, если вижу ошибку – возвращаю карточку, ребенок ищет ошибку, переделывает. Что скажу – я с трудом за ними успеваю))) так, что хоть работа и самостоятельная, я тоже с ними работаю)))
А это на фото ниже ученица, которая вдохновила меня на создание пособия “ПИШИ ЦИФРЫ ПРАВИЛЬНО!” ))) Она получает домой дополнительные задания с роботами, а остальные завистливо на неё смотрят и выпрашивают у меня дополнительные задания и себе.
 Получила “заказ” от детей “еще роботов!”))))
Получила “заказ” от детей “еще роботов!”))))Вот так мы щелкаем простые числовые пирамиды)) Ведь есть пирамиды сложнее! Моим ученикам с ними еще предстоит познакомиться, а вам я их покажу)))
Ниже 10 страниц с числовыми пирамидами на состав числа 1, 2, 3, 4, 5, 6, 7, 8, 9,10. На каждое число одна страница. На одной странице 9 пирамидок. Итого вы получаете в подарок 90 числовых пирамидок!
Обратите внимание: есть пирамидки простые – в них много данных, и есть сложные пирамидки, в них заложены разные варианты решений, т.е. одну и ту же пирамидку можно решить разными способами.
В полной версии пособия 130 страниц!
130 х 9= 1170 разных пирамидок!
Не следует давать детям СРАЗУ все пирамидки)))
Например, учим состав числа 5 – отобрали простые пирамидки на состав числа 5, закрепляем состав числа 5 – добавили сложные пирамидки на состав числа 5.
Работаем поэтапно, идём от простого к сложному!
Ребенок освоил состав чисел 1, 2, 3, 4 – смешали карточки сначала простые, потом добавили сложные.
Таким образом этим пособием можно пользоваться целый год!
На какой возраст эти задания?
Младшим школьникам – эти задания в самый раз будут!
Я даю эти задания своим шестилеткам, моим пятилеткам пока, например, будет сложно.
Стоит ли раньше шести лет давать эти пирамидки?
В группе я бы не советовала, а в индивидуальной работе, можно попробовать.
Можно ли купить эту тысячу пирамидок?
Если вы скачали и апробировали подарочный вариант числовых пирамидок (см 10 страниц для скачивания выше), поделитесь вашими впечатлениями.
Еще раз с ПРАЗДНИИИИКОМ!!!!!!!
Статья авторская
и предназначена только для частного ознакомления.
Копирование и публикация в других источниках
без моего письменного согласия
ЗАПРЕЩЕНЫ.
Автор: Наталья Чистоклетова
Новости моего блога
можно получать на вашу любимую почту,
ИГРАЙТЕ С РАДОСТЬЮ
НАТАЛЬЯ ЧИСТОКЛЕТОВА
Сложение с переходом через десяток. Малыш и Карлсон на крыше | Сложение с переходом через десяток. Утёнок-футболист |
Выражения в несколько действий. (Два варианта) Динозаврик | Нахождение неизвестного слагаемого. (Два варианта) Домик Кроша |
Нахождение неизвестного уменьшаемого, вычитаемого. (Два варианта) Пин | Выражения в два действия. Сложение и вычитание с переходом через десяток. (Два варианта) Мальвина |
Выражения в два действия. Сложение и вычитание без перехода через 10. (Два варианта) Домик | Нахождение неизвестного слагаемого. (Два варианта) Единорог |
| Состав числа 11, 12. Домик | Состав числа 11, 12, 13. Медведь с удочкой |
Состав числа 11, 12, 13, 14.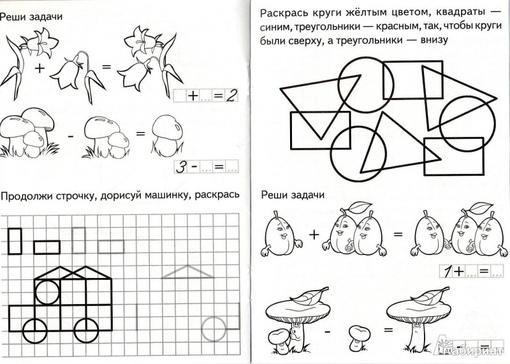 Мамонтенок Мамонтенок | Состав числа 11, 12, 13, 14, 15. Сова |
| Состав числа 11, 12, 13, 14, 15, 16. Мышь | Состав числа 11, 12, 13, 14, 15, 16, 17. Серфинг |
Состав чисел в пределах 20. (Два варианта) Дом – Мойдодыр | Состав чисел второго десятка. (Два варианта) Мандала слоники |
Числа четные и нечетные. Нахождение неизвестного вычитаемого. (Два варианта) Месяц | Состав чисел в пределах 20. (Два варианта) Мышка на скейте |
Числа четные и нечетные. Нахождение неизвестного уменьшаемого. (Два варианта) Ёжик и гриб | Состав числа 11, 12, 13, 14, 15. Поросенок на воздушном шаре |
Выражения в 2-4 действия. Сложение и вычитание в пределах 20. Кот и мышонок Кот и мышонок | Выражения в 2-3 действия. Сложение и вычитание в пределах 20. Карлсон |
| Вычитание единицы в пределах 20. Поросенок Фунтик | Прибавление единицы в пределах 20. Космонавт |
| Прибавление единицы в пределах 20. Гном | Прибавление и вычитание единицы в пределах 20. Баба Яга |
Карточки для проверки знаний по теме ” Числа от 1 до 10. Состав чисел.”
Выберите документ из архива для просмотра:
Выбранный для просмотра документ +1 -1.pptx
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:Увеличь на 1 Уменьши на 1 Увеличь на 1 Уменьши на 1 Увеличь на 1 Уменьши на 1 Увеличь на 1 Уменьши на 1
Выбранный для просмотра документ +2 -2. pptx
pptx
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:4 + 2 = 4 – 2 = 1 + 2 = 7 – 2 = 6 + 2 = 9 – 2 = 3 + 2 = 10 –2 = 5 + 2 = 5 – 2 = 7 + 2 = 8 – 2 = 6 + 2 = 6 – 2 = 2 + 2 = 3 – 2 = 4 + 2 = 4 – 2 = 1 + 2 = 7 – 2 = 6 + 2 = 9 – 2 = 3 + 2 = 10 –2 = 5 + 2 = 5 – 2 = 7 + 2 = 8 – 2 = 6 + 2 = 6 – 2 = 2 + 2 = 3 – 2 = 4 + 2 = 4 – 2 = 1 + 2 = 7 – 2 = 6 + 2 = 9 – 2 = 3 + 2 = 10 –2 = 5 + 2 = 5 – 2 = 7 + 2 = 8 – 2 = 6 + 2 = 6 – 2 = 2 + 2 = 3 – 2 = 4 + 2 = 4 – 2 = 1 + 2 = 7 – 2 = 6 + 2 = 9 – 2 = 3 + 2 = 10 –2 = 5 + 2 = 5 – 2 = 7 + 2 = 8 – 2 = 6 + 2 = 6 – 2 = 2 + 2 = 3 – 2 =
Выбранный для просмотра документ Проверка знаний +3, – 3. pptx
pptx
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:4 + 3 = 1 + 3 = … – 3 = 6 8 – 3 = 10 – 3 = … + 3 = 8 2 + 3 = 3 + 3 = … – 3 = 4 9 – 3 = 4 – 3 = … + 3 = 9 7 + 3 = 6 + 3 = … – 3 = 3 6 – 3 = 7 – 3 = … + 3 = 7 5 + 3 = 5 – 3 = … – 3 = 7 9 – 3 = 4 – 3 = … + 3 = 9 7 + 3 = 6 + 3 = … – 3 = 3 6 – 3 = 7 – 3 = … + 3 = 7 5 + 3 = 5 – 3 = … – 3 = 7 4 + 3 = 1 + 3 = … – 3 = 6 8 – 3 = 10 – 3 = … + 3 = 8 2 + 3 = 3 + 3 = … – 3 = 4 4 + 3 = 1 + 3 = … – 3 = 6 8 – 3 = 10 – 3 = … + 3 = 8 2 + 3 = 3 + 3 = … – 3 = 4 9 – 3 = 4 – 3 = … + 3 = 9 7 + 3 = 6 + 3 = … – 3 = 3 6 – 3 = 7 – 3 = … + 3 = 7 5 + 3 = 5 – 3 = … – 3 = 7 9 – 3 = 4 – 3 = … + 3 = 9 7 + 3 = 6 + 3 = … – 3 = 3 6 – 3 = 7 – 3 = … + 3 = 7 5 + 3 = 5 – 3 = … – 3 = 7 4 + 3 = 1 + 3 = … – 3 = 6 8 – 3 = 10 – 3 = … + 3 = 8 2 + 3 = 3 + 3 = … – 3 = 4
Выбранный для просмотра документ Проверка знаний 0т 6 до 10 – копия.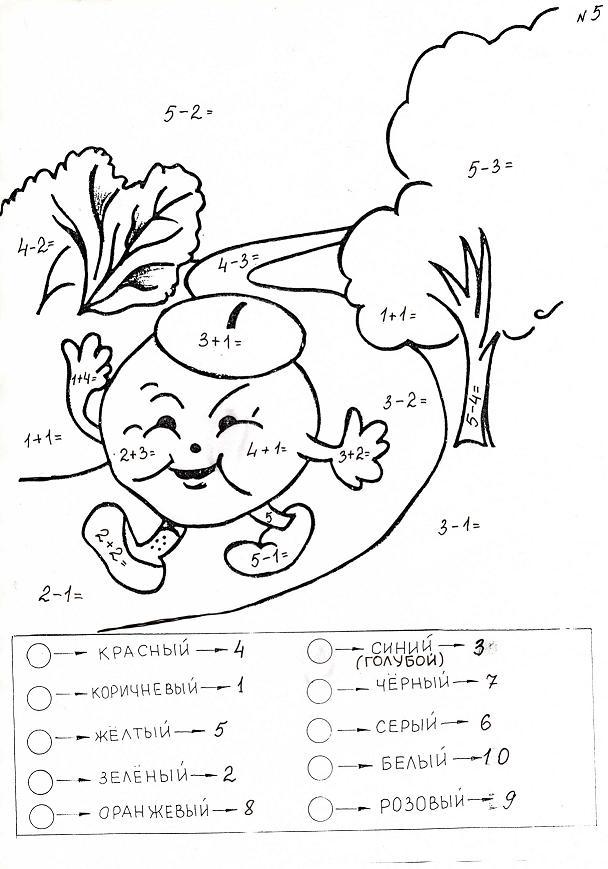 pptx
pptx
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:Выбранный для просмотра документ Проверка знаний 0т 6 до 10.pptx
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:7 – 3 = 8 – 5 = 10 – 2 = 3 + 6 = 7 + 3 = 5 + 4 = 6 – 4 = 9 – 5 = 7 – 2 = 5 + 2 = 6 + 4 = 4 + 4 = 8 – 6 = 10 – 3 = 9 – 2 = 9 – 3= 8 – 3 = 10 – 4 = 5 + 2 = 6 + 4 = 4 + 4 = 8 – 6 = 10 – 3 = 9 – 2 = 9 – 3= 8 – 3 = 10 – 4 = 7 – 3 = 8 – 5 = 10 – 2 = 3 + 6 = 7 + 3 = 5 + 4 = 6 – 4 = 9 – 5 = 7 – 2 = 7 – 3 = 8 – 5 = 10 – 2 = 3 + 6 = 7 + 3 = 5 + 4 = 6 – 4 = 9 – 5 = 7 – 2 = 5 + 2 = 6 + 4 = 4 + 4 = 8 – 6 = 10 – 3 = 9 – 2 = 9 – 3= 8 – 3 = 10 – 4 = 5 + 2 = 6 + 4 = 4 + 4 = 8 – 6 = 10 – 3 = 9 – 2 = 9 – 3= 8 – 3 = 10 – 4 = 7 – 3 = 8 – 5 = 10 – 2 = 3 + 6 = 7 + 3 = 5 + 4 = 6 – 4 = 9 – 5 = 7 – 2 =
Выбранный для просмотра документ Проверка знаний 10 2. pptx
pptx
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:8 – 3 = 6 + 4 = 5 + 5 = 5 + 4 = 10 – 3 = 9 – 7 = 9 – 3 = 8 – 4 = 7 + 3 = 8 – 6 = 8 + 2 = 3 + 5 = 2 + 7 = 8 – 7 = 6 + 3 = 8 – 3 = 6 + 4 = 5 + 5 = 5 + 4 = 10 – 3 = 9 – 7 = 8 – 6 = 8 + 2 = 3 + 5 = 2 + 7 = 8 – 7 = 6 + 3 = 9 – 3 = 8 – 4 = 7 + 3 = 8 – 3 = 6 + 4 = 5 + 5 = 5 + 4 = 10 – 3 = 9 – 7 = 9 – 3 = 8 – 4 = 7 + 3 = 8 – 6 = 8 + 2 = 3 + 5 = 2 + 7 = 8 – 7 = 6 + 3 = 8 – 3 = 6 + 4 = 5 + 5 = 5 + 4 = 10 – 3 = 9 – 7 = 8 – 6 = 8 + 2 = 3 + 5 = 2 + 7 = 8 – 7 = 6 + 3 = 9 – 3 = 8 – 4 = 7 + 3 =
Выбранный для просмотра документ Проверка знаний 10. pptx
pptx
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:8 – 3 = 6 + 4 = 5 + 5 = 5 + 4 = 10 – 3 = 9 – 7 = 9 – 3 = 8 – 4 = 7 + 3 = 8 – 6 = 8 + 2 = 3 + 5 = 2 + 7 = 8 – 7 = 6 + 3 = 8 – 3 = 6 + 4 = 5 + 5 = 5 + 4 = 10 – 3 = 9 – 7 = 8 – 6 = 8 + 2 = 3 + 5 = 2 + 7 = 8 – 7 = 6 + 3 = 9 – 3 = 8 – 4 = 7 + 3 = 8 – 3 = 6 + 4 = 5 + 5 = 5 + 4 = 10 – 3 = 9 – 7 = 9 – 3 = 8 – 4 = 7 + 3 = 8 – 6 = 8 + 2 = 3 + 5 = 2 + 7 = 8 – 7 = 6 + 3 = 8 – 3 = 6 + 4 = 5 + 5 = 5 + 4 = 10 – 3 = 9 – 7 = 8 – 6 = 8 + 2 = 3 + 5 = 2 + 7 = 8 – 7 = 6 + 3 = 9 – 3 = 8 – 4 = 7 + 3 =
Выбранный для просмотра документ Проверка знаний 2 3.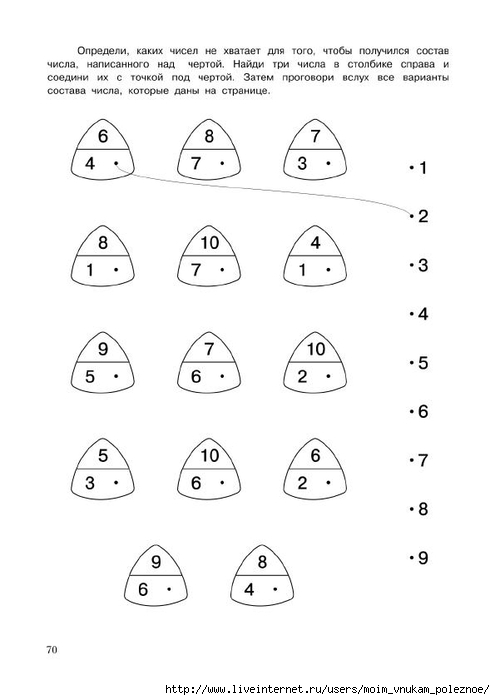 pptx
pptx
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:Беридзе Кристина
Выбранный для просмотра документ Проверка знаний 4 5 – копия 2.pptx
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:Выбранный для просмотра документ Проверка знаний 4 5 – копия 3. pptx
pptx
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:Выбранный для просмотра документ Проверка знаний 4 5 – копия.pptx
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:Выбранный для просмотра документ Проверка знаний 4 5.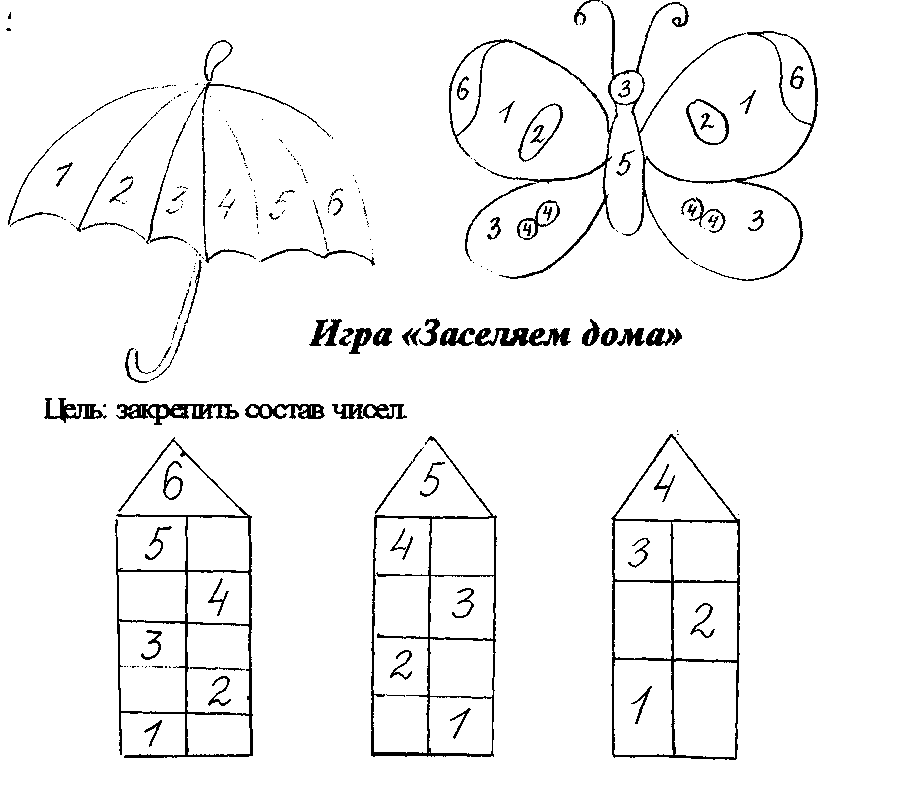 pptx
pptx
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:Выбранный для просмотра документ Проверка знаний 6.pptx
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:Выбранный для просмотра документ Проверка знаний 7.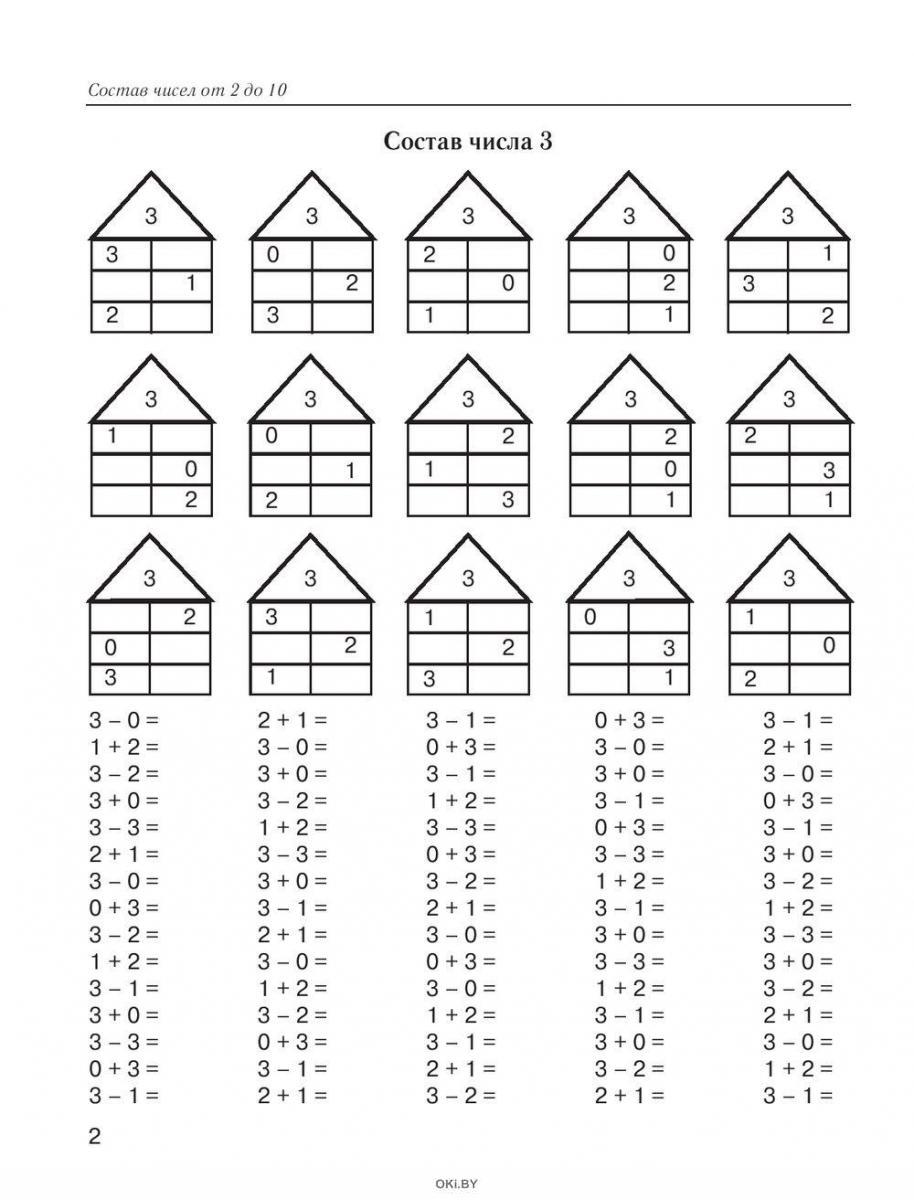 pptx
pptx
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:Выбранный для просмотра документ Проверка знаний 8.pptx
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:Выбранный для просмотра документ Проверка знаний 3 4.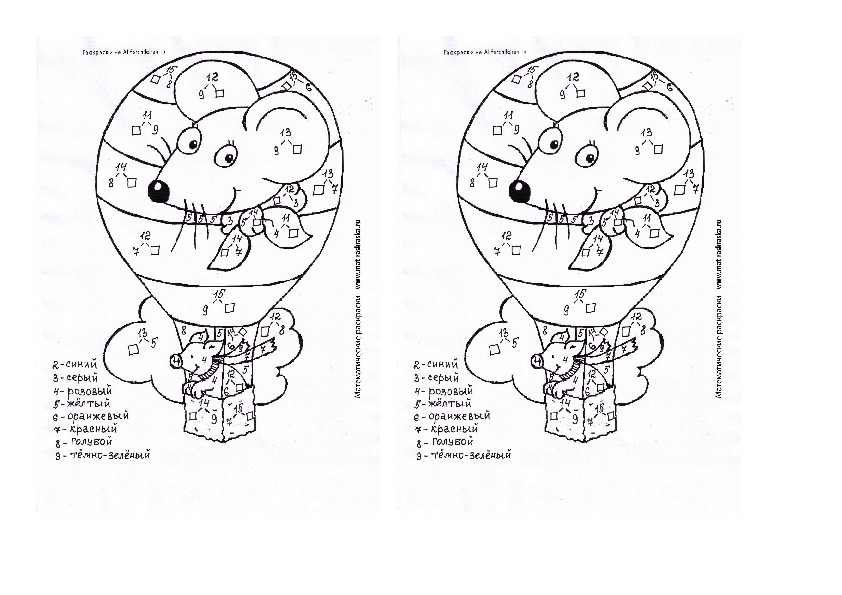 pptx
pptx
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:Выбранный для просмотра документ Проверка знаний 6 – 8 неравенства.pptx
Состав числа 3. Цифра 3.
Конспект урока «Математические представления» в 3 классе
для обучающегося надомного обучения с умеренной умственной отсталостью
«Состав числа 3. Цифра 3»
Цель урока: Расширить знания ребенка о числах и цифрах.
Задачи урока:
Образовательные:
Познакомить обучающегося с образованием числа 3 (путем присчитывания одной единицы к предшествующему числу) и названием числа 3;
Познакомить обучающегося с графическим изображением цифры 3.
Коррекционно-развивающие:
Коррекция логического мышления посредством решения упражнений и заданий.
Развивать мыслительные операции, формировать умение делать выводы о проделанной работе путем решения проблемной ситуации.
Воспитательные:
Воспитывать положительную мотивацию к учению, любознательность.
Воспитывать трудолюбие и самостоятельность.
Оборудование: учебные принадлежности; счетные палочки; образец правильного написания цифры 3; набор предметных картинок с изображением клоунов (веселый, грустный, удивленный), с изображением цветов (красный, желтый, зеленый, синий), с изображением предметов от 1 до 3; с изображением предметов «Один-много»; пазлы «Большой-маленький»; ноутбук с видео-фрагментом для музыкальной зарядки; колпак и нос Клоуна.
План урока:
Организационный момент, введение в игровую ситуацию
Актуализация знаний, повторение пройденного, устный счет до 2.

Проблемная ситуация
Постановка темы и целей урока
«Открытие» нового знания.
Музыкальная физкультминутка.
Знакомство с письмом цифры 3. Работа в тетради.
Включение нового знания в систему знаний.
Задание на дом.
Подведение итогов урока.
Рефлексия
Ход урока:
Организационный момент, введение в игровую ситуацию
Учитель: Здравствуй Рузиль! Сегодня на наш урок пришли гости. Давай поздороваемся с ними и начнем наш урок.
Скажи, пожалуйста, какое у тебя настроение? (радостное)
Выбери смайлик. Ты нам рад? (да)
Давай начнем урок с нашей любимой пальчиковой гимнастики.
Пальчиковая игра «Котики».
Раз, два, три, четыре! Хлопаем в ладошки.
Жили котики в квартире. Хлопаем сначала кулаками,
потом в ладошки (повторяем 2 раза)
Первый котик был большой, Показываем большой палец и показывая
«Во!» поднимаем руку вверх
Любопытным был второй, Показываем указательный палец
и помощью него делаем полукруг и ставим на глаз, показывая любопытство
Третий – танцевать умел, Машем тремя пальцами, как бы танцуя
А четвертый – песни пел, Сгибаем и разгибаем четвертый палец
Ну а пятый, хоть и мал,
Сказки деткам сочинял. Хлопаем в ладошки.
Дружно жили котики, Гладим сначала свои ладошки
Мягкие животики. а потом животики.
Актуализация знаний, повторение пройденного, устный счет до 2.
Учитель: Рузиль, давай покажем гостям, чему мы с тобой научились.
Игра «Большой – маленький»
Учитель: Рузиль посмотри на эти рисунки, выбери одинаковые предметы и скажи какой из них большой, а какой маленький.
Ребенку предлагается собрать пазл, выделяя словами «Большой – маленький».
Игра «Цвета»
Учитель: Молодец, Рузиль! А теперь скажи лимон какого цвета? (Желтый)
А божья коровка? (красный). А кубик? (синий). А лягушка? (зеленый)
Давай эти животных и предметов посадим в вагоны поезда соответствующего цвета.
Игра «Один – много»
Учитель: Молодец, Рузиль! А теперь посмотри на рисунки и скажи, где много, а где один? Собери в левую сторону количество предметов из одного, а в другую сторону количество предметов, где много.
Устный счет до 2-х
Учитель: Молодец, Рузиль! А теперь посмотри на следующие рисунки и скажи с какими числами мы знакомы? (показываю число 1 и 2)
Учитель: Какое число больше? (число 2)
Проблемная ситуация
Учитель: К нам сегодня в гости придут клоуны. Ты знаешь кто такой клоун?
Ты знаешь кто такой клоун?
Ученик: Да
Учитель: Клоун – это артист, который выступает в цирке. Ты бывал в цирке?
Ученик: Нет
Учитель: Давай встретимся и познакомимся с клоуном.
Сначала пришел удивленный клоун. Сколько клоунов пришло? (один). Выбери 1 звездочку и поставь внизу клоуна. А теперь выбери число «Единицу» и поставь на клоуна. Молодец!
Учитель: Давай, как этот клоун, сделаем удивленное лицо.
Ребенок высоко поднимает брови, широко открывает глаза и рот.
Учитель: Пришел еще один клоун. Какое настроение у этого клоуна? (радостное). Сделай радостное лицо.
Ребенок улыбается.
Учитель: Сколько клоунов пришло? (1). Поставь внизу клоуна еще одну звездочку, а на клоуна «Единицу».
Сколько стало клоунов? Давай, посчитаем. (два). Выбери число «Два» и поставь между клоунами.
Клоунам надо одеться для выступления. Сколько колпачков они привезли с собой? Давай посчитаем (два)
Хватит ли каждому клоуну по колпачку? (да)
Почему ты думаешь, что хватит? (Потому что, клоунов два и колпачков тоже два. Два и два – поровну)
Но клоуны не умеют считать и волнуются, достанется ли каждому колпачок. Что нужно сделать, чтобы они увидели, что колпачков столько же, сколько их? (Надеть колпачки)
Ребенок надевает колпачки на голову клоунов.
Постановка темы и целей урока
Раздается стук в дверь. Пришел опоздавший клоун. У него грустное лицо.
Учитель: Кто это? (клоун). Какое у него лицо? (грустное).
Сделай грустное лицо.
Ребенок опускает вниз уголки губ, немного прикрывает глаза.
Учитель: Как ты думаешь, почему грустит клоун? (Потому что, он опоздал)
Хорошо ли опаздывать? (Нет)
Сколько клоунов еще пришло? (один). Поставь внизу клоуна еще звездочку, а на клоуна «Единицу».
А сколько было, пока не пришел этот клоун? (два).
Сколько теперь стало клоунов? (три)
Учитель: Молодец! Три! Сегодня мы с тобой познакомимся с цифрой 3, узнаем из каких чисел она образуется, научимся соотносить число 3 с количеством предметов и научимся писать её в тетради.
(показываю картинку с числом «3»)
«Открытие» нового знания.
Учитель: Рузиль, если мы не знаем, какое число следует за числом, мы спрашиваем у взрослого. Давай я тебе еще раз покажу, как надо считать до 3-х.
Учитель дотрагивается рукой до каждого клоуна и говорит «Один», «Два», «Три». Затем обводит пальцем все перечисленные предметы и говорит «Всего три предмета». Ребенок повторяет за учителем.
Учитель: При счете за числом 2 идет число 3.
Как получилось 3 клоуна? (Было два, пришел один)
Чего теперь больше? Клоунов или колпачков? (Клоунов больше, колпачков меньше)
Как сделать так, чтобы клоунов и колпачков было поровну? (Дать еще один колпачок)
На последнего клоуна ребенок надевает колпачок.
Учитель: Поровну ли теперь клоунов и колпачков? (да)
Сколько колпачков? (три)
Сколько клоунов? (три)
Три и три – поровну.
Музыкальная физкультминутка.
Учитель: Давай мы тоже с тобой переоденемся в клоунов и немножко потанцуем.
На ребенка надевается нос и колпачок клоуна и под музыкальное сопровождение мультфильма «Малышарики» – «Умные песенки. Разминка» ребенок танцует, повторяя движения за учителем.
Работа в тетради. Знакомство с письмом цифры 3.
Учитель предлагает обучающемуся работу в рабочей тетради «Математика для малышей», часть 2. (стр. 6).
Объясняет и показывает алгоритм написания цифры 3.
1) Знакомство с цифрой 3.
Учитель: Число три обозначается математическим знаком – цифрой три. Посмотри, как выглядит цифра 3.
Это – месяц дугой, ниже месяц другой.
А теперь – посмотри: получилась цифра …
Число три записывают знаком – цифра 3.
Учитель: А сейчас мы будем писать цифру 3. При письме мы ручку держим правильно и сидим прямо!
2) Письмо цифры 3. Работа в тетради .
Работа в тетради .
Учитель: Посмотри, как правильно надо писать цифру 3.
Обведи цифру на карточке (образец написания) пальцем, ручкой.
Напиши ручкой цифру 3 в воздухе.
Работа в рабочей тетради.
Учитель: Возьми простой карандаш и подчеркни самую красивую цифру.
Включение нового знания в систему знаний.
Продолжение работы в рабочей тетради «Математика для малышей», часть 2. (стр. 6, 7).
Игра «Домик для чисел» (состав числа 3)
Учитель: Поиграем в игру «Домик». Нужно расселить числа в домик под номером 3.
Задание на дом.
В классных тетрадях написать цифру 3, 0, Ɛ3.
Раскрасить цифру 3.
Подведение итогов урока.
Учитель: С каким числом мы сегодня познакомились? (3)
Из каких чисел состоит число три? (2 и 1)
Рефлексия
Учитель: Тебе понравился урок? (да)
Теперь оцени свою работу на сегодняшнем уроке и покажи того клоуна, который передает твоё настроение.
Учитель: Спасибо за работу, урок окончен!
Для дополнительной работы:
Раскраски Цифры, счет. Раскраски с цифрами и примерами.
Русские народные аудиосказки
- Волшебные (62)
- Про животных (42)
- Бытовые (27)
- Русские народные аудиосказки (все) (131)
Русские аудиосказки
- Бианки В.
 В. (31)
В. (31) - Козлов С.Г. (29)
- Абрамцева Н.К. (27)
- Сутеев В.Г. (23)
- Прокофьева С.Л. (22)
- Пляцковский М.С. (20)
- Усачёв А.А. (20)
- Бажов П.П. (17)
- Мамин-Сибиряк Д.Н. (14)
- Толстой А.Н. (13)
- Заходер Б.В. (12)
- Михалков С.В. (12)
- Салтыков-Щедрин М.Е. (12)
- Остер Г.Б. (12)
- Успенский Э.Н. (10)
- Иванов А.А. (9)
- Пушкин А.С. (8)
- Цыферов Г. (7)
- Онисимова О. (7)
- Берестов В.Д. (6)
- Одоевский В.Ф. (6)
- Пермяк Е.А. (4)
- Крюкова Т.Ш. (3)
- Огурцова Л.В. (3)
- Катаев В.П. (2)
- Телешов Н.Д. (2)
- Маркин Г. (1)
- Епифановы А. и А. (1)
- Волков А. (0)
- Русские аудиосказки (все) (333)
Зарубежные аудиосказки
- Ганс Христ. Андерсен (54)
- Братья Гримм (50)
- Дональд Биссет (25)
- Харрис Д.Ч. (24)
- Родари Дж. (12)
- Киплинг Р.
 (11)
(11) - Хогарт Энн (11)
- Астрид Линдгрен (11)
- Шарль Перро (11)
- Уайльд О. (6)
- Стюарт П. (4)
- Вильгельм Гауф (4)
- Поттер Б. (1)
- Топелиус С. (1)
- Зарубежные аудиосказки (все) (225)
Сборник аудиосказок
- Сказки Диснея (47)
- Сказки-мультфильмы (40)
- Классические шедевры (9)
- Любимые сказки (6)
- Сборник аудиосказок (все) (102)
Аудиосказки народов мира
- Британские аудио-и (44)
- Белорусские аудио-и (32)
- Восточные аудио-и (31)
- Латышские аудио-и (22)
- Украинские аудио-и (19)
- Скандинавские аудио-и (17)
- Арабские аудио-и (3)
- Аудиосказки народов мира (все) (168)
3-раскраска NP Complete – GeeksforGeeks
Предварительное условие: NP-полнота, раскраска графика
Задача K-раскраски графа : Задача K-раскраски для неориентированных графов – это присвоение цветов узлам графа таким образом, чтобы никакие две соседние вершины не имели одинаковый цвет, а использовалось не более цветов. для завершения раскраски графика.
для завершения раскраски графика.
Постановка задачи : Для графа G (V, E) и целого числа K = 3 задача состоит в том, чтобы определить, можно ли раскрасить граф, используя не более 3 цветов, чтобы не было двух соседних вершин. имеют одинаковый цвет.
Explanation :
Экземпляр проблемы – это вход, указанный для проблемы. Примером задачи 3-раскраски является неориентированный граф G (V, E) , и задача состоит в том, чтобы проверить, есть ли возможное назначение цветов для каждой из вершин V , используя только 3 разных цвета. с каждым соседом по-разному. Поскольку проблема NP-Complete – это проблема, которая присутствует как в NP , так и в NP-hard , доказательство утверждения, что проблема является NP-полной, состоит из двух частей:
- Сама проблема в NP класса .
- Все другие задачи в классе NP могут быть сведены к этому за полиномиальное время (B полиномиально сводится к C, обозначается как B ≤ P C )
Если выполняется только 2-е условие , проблема называется NP-Hard .
Но невозможно свести каждую проблему NP к другой проблеме NP, чтобы постоянно демонстрировать ее NP-полноту. Следовательно, чтобы показать, что проблема является NP-Complete, тогда доказательство того, что проблема находится в NP , и любая NP-Complete задача сводится к i.е., если B является NP-полным и B≤P C , то для C в NP, то C является NP-полным. Таким образом, можно сделать вывод, что задача о K-раскраске графа является NP-полной, используя следующие два утверждения:
Проблема с 3-мя раскрасками находится в NP:
Если какая-либо проблема находится в NP, то, учитывая сертификат, который является решением проблемы и экземпляром проблемы (График G (V, E) и назначение цветов {c 1 , c 2 , c 3 } , где каждой вершине назначается цвет из этих трех цветов {c 1 , c 2 , c 3 } ), то можно проверить (проверить, правильно ли данное решение), что сертификат выдан за полиномиальное время. Это можно сделать следующим образом:
Это можно сделать следующим образом:
Для каждого ребра {u, v} в графе G убедитесь, что цвет c (u)! = C (v)
Следовательно, назначение может быть проверено на правильность за полиномиальное время графа относительно его ребер O (V + E).
Задача 3-раскраски NP-Hard:
Чтобы доказать, что задача 3-раскраски является NP-Hard, выполните редукцию от известной NP-Hard задачи к этой задаче. Выполните редукцию, из которой задача 3-SAT может быть сведена к задаче 3-раскраски.Предположим, что задача 3-SAT имеет формулу 3-SAT из m предложений по n переменным, обозначенным как x 1 , x 2 ,…, x n . Затем график можно построить по формуле следующим образом:
- Для каждой переменной x i Построить вершину v i На графике и вершину v i ’ , обозначая отрицание переменной x i .

- Для каждого предложения c в m добавьте 5 вершин, соответствующих значениям c1, c1,…, c5.
- Три вершины разных цветов добавляются дополнительно для обозначения значений True, False и Base (T, F, B) соответственно.
- К этим трем дополнительным вершинам T, F, B добавляются ребра для образования треугольника.
- Кромки добавляются между вершинами v i и v i ’ и основанием (B), чтобы образовать треугольник.
Следующие ограничения верны для графика G:
- Для каждой из пар вершин v i и v i ’ , либо одной из них присваивается значение ИСТИНА, а другой – ЛОЖЬ.
- Для каждого предложения c в предложениях m по крайней мере один из литералов должен содержать значение ИСТИНА, чтобы значение было истинным.
Таким образом, для каждого пункта c = (u V v V w) в формуле можно построить небольшой граф OR-гаджета с помощью входных узлов u, v, w, и подключить выходной узел гаджета как к False, так и Базовые специальные узлы.
Рассмотрим формулу f = (u ’V v V w’) И (u V v V w ’)
Теперь сокращение может быть доказано двумя следующими утверждениями:
Предположим, что формула 3-SAT имеет удовлетворительное назначение, тогда в каждом предложении должен быть хотя бы один из литералов x i истина, следовательно, соответствующий v i может быть назначен ИСТИННОМУ цвету, а v i ‘ – ЛОЖНО.Теперь, расширяя это, для каждого предложения соответствующий граф OR-гаджета может быть трехцветным. Следовательно, граф может быть трехцветным.
Будем считать, что граф G 3-раскрашиваем, поэтому, если вершине vi присваивается истинный цвет, соответственно переменная x i присваивается true. Это сформирует задание юридической истины. Кроме того, для любого пункта C j = (x V y V z) не может быть, чтобы все три литерала x, y, z были ложными. -, Fe4 [Fe (CN) 6] 3, Nh5NO3, so42-, ch4cooh, cuso4 * 5h3o).
-, Fe4 [Fe (CN) 6] 3, Nh5NO3, so42-, ch4cooh, cuso4 * 5h3o).
Степень окисления атома – это заряд этого атома после ионного приближения его гетероядерных связей. Степень окисления является синонимом степени окисления. Определить степень окисления по структуре Льюиса (рис. 1a) даже проще, чем по молекулярной формуле (рис. 1b). Степень окисления каждого атома может быть рассчитана путем вычитания суммы неподеленных пар и электронов, которые он получает от связей, из числа валентных электронов.Связи между атомами одного элемента (гомоядерные связи) всегда делятся поровну.
Рис. 1. Различные способы отображения степеней окисления этанола и уксусной кислоты. R – это сокращение для любой группы, в которой атом углерода присоединен к остальной части молекулы связью C-C. Обратите внимание, что замена группы CH 3 на R не изменяет степень окисления центрального атома. → Скачать изображение высокого качества При работе с органическими соединениями и формулами с несколькими атомами одного и того же элемента легче работать с молекулярными формулами и средними степенями окисления (рис. 1d).Органические соединения можно записать таким образом, что все, что не меняется до первой связи C-C, заменяется сокращением R (рис. 1c). В отличие от радикалов в органических молекулах, R не может быть водородом. Поскольку электроны между двумя атомами углерода распределены равномерно, группа R не изменяет степень окисления атома углерода, к которому она присоединена. Вы можете найти примеры использования на странице Разделите окислительно-восстановительную реакцию на две полураакции.
1d).Органические соединения можно записать таким образом, что все, что не меняется до первой связи C-C, заменяется сокращением R (рис. 1c). В отличие от радикалов в органических молекулах, R не может быть водородом. Поскольку электроны между двумя атомами углерода распределены равномерно, группа R не изменяет степень окисления атома углерода, к которому она присоединена. Вы можете найти примеры использования на странице Разделите окислительно-восстановительную реакцию на две полураакции.
Правила присвоения степеней окисления
- Степень окисления свободного элемента всегда равна 0.
- Степень окисления одноатомного иона равна заряду иона.
- Фтору в соединениях всегда присваивается степень окисления -1.
- Щелочные металлы (группа I) всегда имеют степень окисления +1.
- Щелочноземельным металлам (группа II) всегда присваивается степень окисления +2.
- Кислород почти всегда имеет степень окисления -2, за исключением пероксидов (H 2 O 2 ), где она равна -1, и соединений с фтором (OF 2 ), где она равна +2.

- Водород имеет степень окисления +1 в сочетании с неметаллами, но имеет степень окисления -1 в сочетании с металлами.
- Алгебраическая сумма степеней окисления элементов в соединении равна нулю.
- Алгебраическая сумма степеней окисления иона равна заряду иона.
Определение степени окисления для органических соединений
- Степень окисления любого химически связанного углерода может быть определена путем добавления -1 для каждого дополнительного электроположительного атома (H, Na, Ca, B) и +1 для каждого еще электроотрицательного атома (O, Cl, N, P) и 0 для каждого атома углерода, непосредственно связанного с представляющим интерес углеродом.Например:
Состав
Этот тип словообразования, в котором новые слова образуются путем объединения двух или более основ, является одним из трех наиболее продуктивных типов современного английского языка, два других – это преобразование и аффиксация . Составные слова, хотя их количество определенно меньше, чем производных или корневых слов, все же представляют собой одну из наиболее типичных и специфических черт структуры английского слова.
1.1. Группы и подгруппы соединений.
Есть как минимум три аспекта композиции, которые представляют особый интерес.
Первый – структурный аспект. Составы неоднородны по структуре. Традиционно выделяют три типа: нейтральный, морфологический и синтаксический.
В нейтральных компаундах процесс компаундирования осуществляется без каких-либо связывающих элементов, путем простого сопоставления двух стеблей, как в черный дрозд, витрина, спальня, высокий потолок (), и т. Д.Есть три подтипа нейтральных соединений в зависимости от структуры составляющих стеблей.
Приведенные выше примеры представляют подтип, который можно описать как простые нейтральные соединения: они состоят из простых основ без аффиксов.
Соединения, которые имеют аффиксы в своей структуре, называются производными или производными соединениями. Например. голубоглазый, златовласый, леди-убийца (), кинозритель (), меломан (), первокурсник (,), поздно пришедший (), новичок (), рано встающий (), злодей (). Продуктивность этого типа подтверждается значительным количеством сравнительно недавних формирований, таких как подросток, няня, двухэтажный (корабль или автобус с двумя палубами). На этом шаблоне придумано множество несуразных слов, что еще раз доказывает его высокую продуктивность, например (гусиный мясник (история убийства).
Третий подтип нейтральных соединений называется сокращенными соединениями. Эти слова имеют в своей структуре укороченную (сокращенную) основу: TV-set, V-day (День Победы), G-man (правительственный агент ФБР), футболка, и т. Д.
Морфологические соединения немногочисленны. Этот тип непродуктивный. Он представлен словами, в которых две составные основы объединены соединяющей гласной или согласной, например Англосакс, ручная работа (), ремесло (), представитель (), государственный деятель ().
В синтаксических составах мы находим особенность специфически английской структуры слов. Эти слова образуются из отрезков речи, сохраняя в своей структуре многочисленные следы синтагматических отношений, характерных для речи: артикли, предлоги, наречия, как в существительных lily-of-the-valley (), Мастер на все руки. (), бездельник (,), свекровь (). Синтаксические отношения и грамматические модели, существующие в современном английском языке, можно четко проследить в структурах таких составных существительных, как know-all (), know-nothing (e), go-between (), whodunit (). Последнее слово (означающее «детектив»), очевидно, произошло от грамматического варианта группы слов , кто (сделал) это.
В этой группе соединений мы находим большое количество неологизмов, и детальных единиц является одним из них.
Структура большинства словосочетаний прозрачна и ясно выдает происхождение этих слов от словосочетаний.
1.2. Семантический аспект составных слов.
Другой предмет интереса – семантический аспект составных слов, то есть вопрос соотношения отдельных значений составных частей и действительного значения составного слова. Можно ли рассматривать значение составного слова как сумму составляющих его значений?
Чтобы попытаться ответить на этот вопрос, давайте рассмотрим следующие группы примеров.
(1) Аудитория, спальня, столовая, спальный вагон, читальный зал, танцевальный зал.
Эта группа, кажется, представляет собой соединения, значения которых действительно можно описать как сумму составляющих их значений. Тем не менее, в последних четырех словах мы можем отчетливо заметить небольшое изменение значения. Первый компонент в этих словах, если рассматривать его как свободную форму, обозначает действие или состояние чего-либо или того, что охарактеризовано этим словом. Тем не менее, спальный вагон – это не машина, которая спит (ср. спящий ребенок ), и танцевальный зал не танцует на самом деле (ср. танцующих пар ).
Сдвиг смысла становится более заметным во второй группе примеров.
(2) Доска, черный дрозд, футбол, болтун (), леди-убийца, бездельник ().
В этом соединении один из компонентов (или оба) изменили свое значение: доска – это не доска и не обязательно черная, футбол – не мяч, а игра, болтун – не ящик, а человек, и женщина-убийца. никого не убивает, а просто мужчина, очаровывающий женщин.Во всех этих соединениях значение всего слова не может быть определено как сумма составляющих его значений.
Тем не менее, несмотря на некоторую корректировку семантической структуры слова, значения составляющих составных частей этой второй группы все еще прозрачны: сквозь них можно увидеть значение всего комплекса. По крайней мере, ясно, что blackbird – это какая-то птица и что никчемный не является комплиментом.
(3) В третьей группе соединений процесс определения значения
целиком из тех составных частей невозможно. Ключ к значению, кажется, был утерян: божья коровка () не птица, а насекомое, талбой не мальчик, а предмет мебели.
Соединения, значения которых не соответствуют отдельным значениям их составных частей (2-я и 3-я группа), называются идиоматическими соединениями, в отличие от первой группы, известной как неидиоматических соединений.
Предлагаемое подразделение на три группы основано на степени семантического единства составных частей, третья группа представляет собой крайний случай сплоченности, когда составляющие значения смешиваются, чтобы произвести совершенно новое значение.
Композиция – не такой гибкий способ создания новых слов, как преобразование, но достаточно гибкий, как убедительно показывают примеры nonce-слов. Среди словосочетаний встречается множество выразительных и красочных слов.Они также сравнительно лаконичны, вбирают в одно слово идею, которая в противном случае потребовала бы целой фразы (ср. В отеле было полно выходных и В отеле было полно людей, проводящих там выходные ).
И лаконичность, и выразительность составных слов хорошо проиллюстрированы английскими сложными прилагательными, обозначающими цвета (ср. белоснежный как белый как снег ).
:
4.Сочинение. Виды композиции. Критерии соединений.
В виде Английские словосочетания состоят из свободных форм, трудно подобрать отличить их от фраз. Комбинированный верх собака ‘a человек, занимающий главное место », например, хотя формально разбита, не более и не менее поддается семантическому анализу, чем комбинация аутсайдеров ‘a человек, который пережил худшую встречу », и все же мы считаем первый (верх собака) как фраза и второй (аутсайдер) как слово.Насколько это оправдано? На самом деле проблема даже в более сложный, чем предполагает этот изолированный пример. Разделение соединения из фраз, а также из производных – непростая задача, и ученые не пришли к единому мнению по вопросу о соответствующих критериях. В Ниже приводится краткий обзор различных решений и различных комбинации критериев, которые были предложены.
В проблема естественно сводится к проблеме определения слова границы на языке. Уместно процитировать Э.Нида кто пишет, что «критерии определения словосочетаний в язык бывает трех типов: (1) фонологический, (2) морфологический, (3) синтаксический. Как правило, одного типа критериев недостаточно для установление слова-единицы. Скорее комбинация двух или трех типы имеет важное значение “. Э. Нида не упоминает графический критерий твердости или написание через дефис. Эта недооценка письменного языка кажется быть ошибкой. Для современного литературного языка письменный форма так же важна, как и устная.Если мы примем определение написанное слово как часть текста с пустого на пустой, должны принять графический критерий как логическое следствие. Это может Однако можно утверждать, что в английском правописании нет последовательности в этом отношении. С разными словарями и разными авторами а иногда даже у одного и того же автора написание меняется, так что одно и то же подразделение может существовать в твердом написании: директор, громкоговоритель, с дефис: директор, громкоговоритель и с перерывом между компонентами: голова господин, громко оратор.Сравнить также: авиакомпания, воздуховод, воздуховод, спичечный коробок, спичечный коробок, спичечный коробок, разрушение, расставаться. Более того, соединения, которые кажутся построенными по одному образцу и имеют аналогичные семантические отношения между составляющими могут быть записаны иначе: учебник, разговорник и справочник книга. Еще если принять во внимание сравнительную частоту твердых или написание рассматриваемых комбинаций через дефис, критерий довольно надежный. Эти три типа написания не обязательно должны указывать разные степени смыслового слияния.Иногда расстановка переносов может служить эстетические цели, помогающие избежать слов, которые будут выглядеть слишком длинными, или в целях удобства, чтобы сделать синтаксические компоненты более понятными для глаз: миролюбивый нации, старомодные идеи.
Слово-композиция является продуктивным типом словообразования, в котором новые слова производятся путем объединения двух и более стеблей. Например: кемпинг, синяя птица, побелка, свекровь, комбинезон.
Типы состава:
——- Нейтральный
——- Морфологический
——- Синтаксический
Нейтральный соединения – два стебли соединяются без каких-либо соединительных элементов: чучело, золотая рыбка, плакса (плакса).
Подтипы нейтральных соединений:
– простой нейтральные соединения – состоят из простых стеблей без аффиксов: подсолнечник, спальня, blackbird
– производственный, или производные соединения – имеют в своей структуре аффиксы: длинноногие, широкий кругозор
– контрактный соединения – имеют в своем составе укороченную ножку (усеченный корень): H-bag (сумочка), телевизор (телевизор), A-bomb (атомная бомба), День Победы (День Победы).
Морфологический соединения – компоненты соединены связывающим элементом («o», «i», «s»): видеофон, микрочип; трагикомический, кустарный; мастер.
Синтаксис соединения образуются целыми фрагментами речи: военный корабль), Незабудка, свекровь.
типов соединений в соответствии с их значением
—- Неидиоматические – соединения, значения которых можно описать как сумму значения их составляющих: класс, спальня, родина, вечернее платье.
—- Идиоматический – значение соединений нельзя описать как простую сумму его составные части: доска, футбол, убийца женщин; божья коровка (тумбочка), синий чулок.
Основы композиции: структура ценностей | Мадди Цвета
– Автор: Дан дос Сантос
Создавая свои композиции, я склонен мыслить триатическими аранжировками переднего, среднего и заднего плана. Чтобы усилить взаимосвязь между каждой из этих различных глубин, я пытаюсь ограничить каждую область общим диапазоном значений; в пользу черного, белого или серого.
Например, вы можете позволить фону использовать преимущественно белые тона, средний план – преимущественно серые, а передний план – преимущественно черные тона.Или вы можете отменить это.
Конечно, подойдет любая комбинация из этих трех значений, и существует партий комбинаций.
Ограничивая свои ценности в каждой из этих областей, вы визуально усиливаете ощущение глубины своего изображения, тем самым делая силуэты очень легко читаемыми… и это важно! Разборчивость важна для хорошей картинки. Мутные ценностные структуры мешают зрителю различать формы, особенно в мелком масштабе. Вот почему вы увидите технику, которая так часто используется в карточном искусстве.Когда ваше произведение искусства будет воспроизведено на высоте всего несколько дюймов, высококонтрастные композиции работают особенно хорошо.
Подобные схемы триптических ценностей легко увидеть в работах старых мастеров, особенно в гравюрах Гюстава Доре. Вот три примера Dore, каждый из которых демонстрирует различное расположение черного, белого и серого, чтобы подчеркнуть разницу между передним, средним и фоном.
| ФОН: БЕЛЫЙ СРЕДНИЙ ФОН: СЕРЫЙ ФОН: БЕЛЫЙ |
| ФОН: СЕРЫЙ СРЕДНИЙ ФОН: ЧЕРНЫЙ ФОН: БЕЛЫЙ |
| ФОН: ЧЕРНЫЙ СРЕДНИЙ ФОН: БЕЛЫЙ ФОН: СЕРЫЙ |
Говард Пайл, Эндрю Лумис и многие другие иллюстраторы реализовали аналогичный метод, но вместо этого использовали 4 значения: белый, почти белый, черный и почти черный.

