Простые уравнения 4 класс примеры: Карточки. Сложные уравнения 4 класс | Тренажёр по математике (4 класс) на тему: – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Карточки для отработки навыков решать уравнения. 3 – 4 класс. | Тренажёр по математике (3, 4 класс) на тему:

Опубликовано 23.03.2018 – 12:46 – Дашиева Ирина Долгорсуруновна

Индивидуальные карточки для отработки навыка решать простые и составные уравнения.

Скачать:

Предварительный просмотр:

Ф. И. ___________________

Реши уравнения:

Ф. И. ___________________

Реши уравнения:

Ф. И. ___________________

Реши уравнения:

х : 8 = 3648

х=

х : 8 = 3648

х=

х : 8 = 3648

х=

832 ∙ х = 3328

х=

832 ∙ х = 3328

х=

832 ∙ х = 3328

х=

х ∙ 605 = 6050

х=

х ∙ 605 = 6050

х=

х ∙ 605 = 6050

х=

Х : 75 = 7350

х=

Х : 75 = 7350

х=

Х : 75 = 7350

х=

6786 : х = 87

х=

6786 : х = 87

х=

6786 : х = 87

х=

564 ∙ х = 9588

х=

564 ∙ х = 9588

х=

564 ∙ х = 9588

х=

5951 : х = 541

х=

5951 : х = 541

х=

5951 : х = 541

х=

х : 47 = 119

х=

х : 47 = 119

х=

х : 47 = 119

х=

41 ∙ х = 4100

х=

41 ∙ х = 4100

х=

41 ∙ х = 4100

х=

х : 11 = 2915

х =

х : 11 = 2915

х=

х : 11 = 2915

х=

187 ∙ х = 2244

х=

187 ∙ х = 2244

х=

187 ∙ х = 2244

х=

Составные уравнения

Ф. И. ___________________ Реши уравнения:	Ф. И. ___________________ Реши уравнения:
х + (273 – 54) = 648 + 254	х + (273 – 54) = 648 + 254
432 + (808 ∙ х) = 4096 : 2	432 + (808 ∙ х) = 4096 : 2
(989 – 154) – х = 142 ∙ 3	(989 – 154) – х = 142 ∙ 3
Х + (296 + 387) = 1737 – 598	Х + (296 + 387) = 1737 – 598
(1671 + 129) : х = 300 ∙ 3	(1671 + 129) : х = 300 ∙ 3
(725 : х) + 125 = 791 – 641	(725 : х) + 125 = 791 – 641

По теме: методические разработки, презентации и конспекты

Карточка “Проверка вычислительных навыков за 1 класс”

Карточка представляет собой раздаточный материал для проверки вычислительных навыков. …

Карточки на отработку навыков счета

Примеры на сложение и вычитание вида: 10 + 2, 12 – 2, 12 – 10…

Карточки для отработки навыка нахождения грамматической основы предложения во 2 классе

Карточки для отработки навыка нахождения грамматической основы предложения (2 класс)…

Карточки для отработки навыка устного счёта в пределах 10

Табличное сложение и вычитание в пределах 10…

Карточки для отработки навыка определения падежа имени существительного.

Индивидуальная карточка для отработки навыка определения падежа имени существительного. В карточке даны словосочетания, а рядом нужно записать падеж…

Карточки для отработки навыков устного счёта на 14 дней (2 класс)

Карточки содержат примеры для отработки навыков устного счёта на 14 полных дней. Первые 3 дня решали в классе с обучающимися, а затем работали самостоятельно дома. Если обучающиеся будут ежедневно отр…

Карточки для отработки навыка чтения по английскому языку

Тренируем навык чтения по английскому языку. Данный материал содержит карточки для отработки навыка чтения и презентация для учителя. Данные карточки нашла на просторах Интернета и решила использовать…

Математика. 4 класс – Справочник

Как решать уравнение в математике

Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают латинской буквой.

Решить уравнение – это значит найти значение неизвестного, при котором равенство будет верным.

Корень уравнения – это значение неизвестного, обозначенного латинской буквой в уравнении.

Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

Обязательная и дополнительная литература по теме урока:

1. Моро М. И. Учебник для 4 класса четырехлетней начальной школы. М. «Просвещение» — 2017.С. 62,63

2. Волкова Е. В. математика Всероссийская проверочная работа за курс начальной школы. Издательство «Экзамен» 2018.С.27

3. Петерсон Л. Г. математика 3 класс. Часть 2. Ювента, 2015.-96с.: ил. С.77-78

Теоретический материал для самостоятельного изучения:

376 + 282; (х — у) : 3

Являются ли эти записи уравнениями?

Это не уравнения, так как в уравнении должен быть знак «=». Это выражения.

Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают латинской буквой.

Рассмотрите другие записи:

24 + х = 49; 24 + х = 79 — 30

Это уравнения, так как это равенства, содержащие переменную.

Попробуем их решить.

Что значит решить уравнение?

Решить уравнение – это значит найти значение неизвестного, при котором равенство будет верным.

Вспомните алгоритм решения уравнений.

Вспомнить компоненты действия данного уравнения. Определить неизвестный компонент. Вспомнить правило нахождения неизвестного компонента. Применить правило и найти неизвестный компонент. Записать ответ. Сделать проверку

Используя алгоритм, решите первое уравнение

Значение неизвестного х = 25. Это корень уравнения.

Корень уравнения – это значение неизвестного, обозначенного латинской буквой в уравнении. В данном случае – это Х.

Можно ли решить второе уравнение, используя этот же алгоритм?

Такие уравнения не рассматривались. Какова же цель нашего урока?

Цель урока: научиться решать уравнения, в которых в ответе не число, а числовое выражение.

Такие уравнения мы будем называть составные. Поэтому тема урока: «Решение составных уравнений»

Чтобы решить это уравнение, нужно упростить правую часть.

24 + х = 79 — 30, после чего получаем уравнение известного вам вида

Ответ: корень уравнения 25

Составим алгоритм решения составных уравнений.

Алгоритм решения составных уравнений

1. Найти значение числового выражения.

2. Вспомнить компоненты действия данного уравнения.

3. Определить неизвестный компонент.

4. Вспомнить правило нахождения неизвестного компонента.

5. Применить правило и найти неизвестный компонент.

6. Записать ответ.

7. Сделать проверку.

Решим еще одно уравнение:

Применяем алгоритм решения составных уравнений:

Найти значение числового выражения: 75 — х = 9 ∙ 7 Вспомнить компоненты действия данного уравнения: 75 — х = 63

3. Определить неизвестный компонент.

4. Вспомнить правило нахождения неизвестного компонента.

5. Применить правило и найти неизвестный компонент.

6. Записать ответ.

7. Сделать проверку.

Ответ: корень уравнения 12

Вывод: чтобы решить составное уравнение, в которых в ответе не число, а числовое выражение, необходимо упростить правую часть ( т. е решить выражение), после чего получаем уравнение известного вам вида и решаем его, используя алгоритм решения уравнений.

Решим задачу, составив уравнение:

Сумма неизвестного числа и числа 390 равна произведению чисел 70 и 6. Найди это число.

1. Сумма неизвестного числа и числа 390 – обозначим неизвестное число переменной х, тогда получим х + 390

Ответ корень уравнения 12.

Resh. edu. ru

06.09.2020 15:14:44

2020-09-06 15:14:44

Источники:

Https://resh. edu. ru/subject/lesson/4580/conspect/

Урок 26. уравнение. решение уравнений подбором неизвестного числа — Математика — 2 класс — Российская электронная школа » /> » /> .keyword { color: red; }

Как решать уравнение в математике

Уравнение – равенство, содержащее неизвестное число, которое надо найти.

Корень уравнения – это значение буквы, при котором из уравнения получается верное равенство.

Решить уравнение, значит найти его корни.

Основная и дополнительная литература по теме урока

1. Моро М. И., Бантова М. А., Бельтюкова Г. В. и др. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1. – 8-е изд. – М.: Просвещение, 2017. – С. 80-81.

2. Моро М. И., Бантова М. А. Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.1. – 6-е изд., дораб. – М.: Просвещение, 2016. – С. 60.

3. Моро М. И., Волкова С. И. Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. 9-е изд. – М.: Просвещение, 2014. – С. 60.

Теоретический материал для самостоятельного изучения

Вы умеете читать буквенные выражения. Например:

Вы уже знаете, что равенства бывают верные и неверные.

Рассмотрим верное равенство с окошком: + 4 = 12

Запишем вместо окошка маленькую латинскую букву, как в буквенное выражение. Какое число надо поместить вместо буквы Х, чтобы равенство стало верным?

Это число 8. Получили верное равенство: сумма чисел 8 и 4 равна 12.

Равенство с буквой, которое мы записали – это Уравнение.

Неизвестное число обозначается маленькими латинскими буквами, как и в буквенном выражении.

Решить уравнение – значит найти все такие значения Х (если они есть), при которых равенство будет верным. Значение буквы, при котором из уравнения получается верное равенство, называется

Корень уравнения.

Решим уравнение 10 – d = 6 способом подбора.

Возьмём число 5. Сейчас проверим, верно ли подобрали число. Заменим D В уравнении числом 5. Получим равенство: 10 – 5 = 6. Оно неверно. Значит, число подобрали неверно.

Попробуем взять другое число. Например, 4. При подстановке его вместо D получили верное равенство: 10 – 4 = 6. Значит, число четыре – корень уравнения, его решение.

Сейчас мы с вами рассмотрим, как по схеме составить уравнение. Перед нами такая схема. Изучим, что обозначает каждое число в схеме. Число 27 обозначает «целое». Оно состоит из двух частей. Первая «часть» – это число 20, вторая «часть» – это число Х.

ЧАСТЬ + ЧАСТЬ = ЦЕЛОЕ

Рассмотрим другой пример. Перед вами другая схема. Изучим, где на схеме целое, а где части: Х — это «целое», а 30 и 6 – это части.

Вывод: Уравнение – это равенство, содержащее неизвестное число, которое надо найти. Когда решение уравнения находится легко, пользуются способом подбора. Нужно подобрать такое число, чтобы получилось верное равенство.

Рассмотрим верное равенство с окошком: + 4 = 12

Теоретический материал для самостоятельного изучения.

Resh. edu. ru

11.04.2018 13:09:09

2018-04-11 13:09:09

Источники:

Https://resh. edu. ru/subject/lesson/5674/conspect/

Как решать линейные уравнения — формулы и примеры решения простейших уравнений » /> » /> .keyword { color: red; }

Как решать уравнение в математике

Сначала мы решаем уравнения в школе в тетрадях, а потом в уме на совещаниях. В статье расскажем, как решать самые простые уравнения быстро и легко.

О чем эта статья:

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядят так: ах + b = 0, где A и B — действительные числа. Вот, что поможет в решении:

Если

А ≠ 0 — уравнение имеет единственный корень: х = — b : а;

Если А = 0 — уравнение корней не имеет;

Если А и B равны нулю, то корнем уравнения является любое число.

Квадратное уравнение выглядит так: ax2 + bx + c = 0, где коэффициенты A, B и C — произвольные числа, a ≠ 0.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

кубические, уравнения четвертой степени, иррациональные и рациональные, и другие.

Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

Для примера рассмотрим простейшее уравнение: x+3=5.

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.

Приведем подобные и завершим решение.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной Х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной X стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: -4x = 12

Разделим обе части на -4, чтобы коэффициент при неизвестной стал равен единице.

-4x = 12 | : (-4)
X = −3

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Раскрываем скобки, если они есть. Группируем члены, которые содержат неизвестную переменную в одну часть уравнения, остальные члены — в другую. Приводим подобные члены в каждой части уравнения. Решаем уравнение, которое получилось: aх = b. Делим обе части на коэффициент при неизвестном.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

ЮПеренести 1 из левой части в правую со знаком минус.

Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.

Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3(х − 4) + 2х − 1.

5х − 15 + 2 = 3х − 12 + 2х − 1

Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.

5х − 3х − 2х = −12 − 1 + 15 − 2

Приведем подобные члены.

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.

Разделим обе части на -4, чтобы коэффициент при неизвестной стал равен единице.

При неизвестной х стоит числовой коэффициент 4.

Skysmart. ru

06.12.2017 19:09:18

2017-12-06 19:09:18

Источники:

Https://skysmart. ru/articles/mathematic/reshenie-prostyh-linejnyh-uravnenij

Линейные уравнения с параметром. Анализ решений

Уравнения с параметром. Задача 18 (С6)

Рассмотрим линейные уравнения с параметром вида: $$p(a)x-q(a)=0,$$ где $p(a)$ и $q(a)$- выражения, которые зависят от параметра. Для того, чтобы решить такое уравнение, нужно найти все $x$ при всех значениях параметра $a$. Приведем наше уравнение к виду: $$p(a)x=q(a),$$ Отсюда единственное решение:

$x=\frac{q(a)}{p(a)}$ при $p(a)≠0.$

Если же $p(a)=0$ и $q(a)=0$, то решением данного уравнения является любое число. И последний случай, когда $p(a)=0$,а $q(a)≠0$, то уравнение не имеет решений. Замечу, что по некоторым уравнениям сразу невозможно определить, являются ли они линейными. Выполнив некоторые преобразования, вдруг обнаружим, что в уравнении отсутствуют члены с $x$ в степени большей, чем 1. Если изначально у нас и были старшие степени, то теперь они сократились. Мы провели анализ линейного уравнения в общем виде, теперь разберем несколько примеров:

Пример 1

Решить уравнение $ax-5a=7x-3$ при всех возможных $a$.

Перенесем все одночлены с $x$ влево, а оставшиеся члены – вправо. И вынесем $x$ за скобку, как общий множитель: $$x(a-7)=5a-3;$$ Первый случай, когда $(a-7)≠0$. Тогда мы можем поделить все уравнение на $a-7$ и выразить: $$x=\frac{5a-3}{a-7}.$$ Второй случай, когда $(a-7)=0$, получим уравнение $$x*0=32,$$ которое не имеет решений. Таким образом, мы нашли решения уравнения для всех значений параметра $а$. Например, $x=\frac{2}{7}$ при $a=0,$ $x=\frac{-1}{3}$ при $a=1$ и т.д.
Ответ: При $a=7$ $x∈∅;$
при $a≠7$ $x=\frac{5a-3}{a-7}.$

Пример 2

Найдите все $a$, при которых корнем уравнения $$ax+5a-2(3x+2)=-5x+a^2$$ будет любое число. 2}{a}=5a.\) Этот корень не будет удовлетворять ОДЗ.

Ответ: При $a=0$ решениями уравнения будут все действительные числа, кроме $x=0.$ Если $a≠0,$ то решений нет.

Показательные и логарифмические уравнения

Решение показательных и логарифмических уравнений с параметром

Неравенства с параметром в задании 18 ЕГЭ

При решении неравенств нужно понимать, какие преобразования будут равносильными, и какие нет. Разберем несколько примеров простейших неравенств с параметром.

Графический метод решения задания с параметром

Применение графического метода для решения задачи с параметром 18(С6) ЕГЭ по профильной математике. Подробно разбираем как решать уравнения и неравенства с параметром при помощи графиков.

Графический метод решения параметра при помощи семейства кривых

В статье подробно разобран второй графический метод решения уравнений и неравенств с параметрами. Детально разобраны несколько примеров.

Симметрия в задачах с параметром

Использование свойств функции при решении заданий с параметром из ЕГЭ по математике профильного уровня. Симметрия функций и приемы решения.

Финансовая математика в ЕГЭ. Экономическая задача в задании 15

Теория для решения заданий 15 по финансовой математике. Аннуитетные и дифференцированные платежи, понятие сложного процента. Основные методы решения задач на проценты.

Метод координат. Задача 14 ЕГЭ

Подробный разбор метода координат в стереометрии. Формулы расстояния и угла между скрещивающимися прямыми. Уравнение плоскости. Координаты вектора. Расстояние от точки до плоскости. Угол между плоскостями. Выбор системы координат.

Как сдать ЕГЭ по математике

Частые ошибки, необходимая краткая теория, статистика прошлых лет во 2й части ЕГЭ по математике профильного уровня.

Простые уравнения и их применение, транспонирование, линейное уравнение, применение простых уравнений, решенные примеры, практические вопросы, часто задаваемые вопросы

LearnPracticeDownload

Уравнения являются одним из наиболее важных аспектов математики. Слово определяет равенство между двумя частями уравнения. Он гарантирует, что оба выражения уравнения равны, используя простой знак «равно» (=). Уравнения помогают сбалансировать выражения с обеих сторон с использованием арифметических операций, таких как сложение, вычитание, деление и умножение. Чтобы полностью понять эту концепцию, нам нужно понять использование констант и переменных.

1.	Введение в простые уравнения
2.	Транспонирование или транспонирование
3.	Применение простых уравнений
4.	Линейное уравнение
5.	Решенные примеры
6.	Практические вопросы
7.	Часто задаваемые вопросы о простых уравнениях и их приложениях

Введение в простые уравнения

Математическое уравнение, представляющее связь между двумя выражениями по обе стороны от знака равенства (=), является простым уравнением. Уравнение состоит из переменных и числовых констант. Например, x + 4 = 10, где x – переменная. Числа 4 и 10 являются постоянными, так как они не меняются. + — оператор, оператор может быть + или —

В приведенном выше уравнении мы стремимся найти значение x. Как только значение определено, уравнение x + 4 должно быть равно 10. Даже если левая сторона (LHS) поменять местами правая сторона (RHS), уравнение останется прежним. Простое уравнение остается неизменным, если одно и то же число прибавляется, вычитается и умножается с каждой стороны уравнения и делится на одно и то же ненулевое число.

Транспонирование или транспонирование

Одним из применений простых уравнений является решение уравнения путем сдвига переменной или числа на другую сторону знака «=». Однако мы должны иметь в виду, что знак перед числом также меняется. Например, «+» становится «-», а «-» становится «+», когда стороны меняются. Но для деления и умножения это другое, переносимое умножение будет идти как деление, а переносимое деление будет идти как умножение.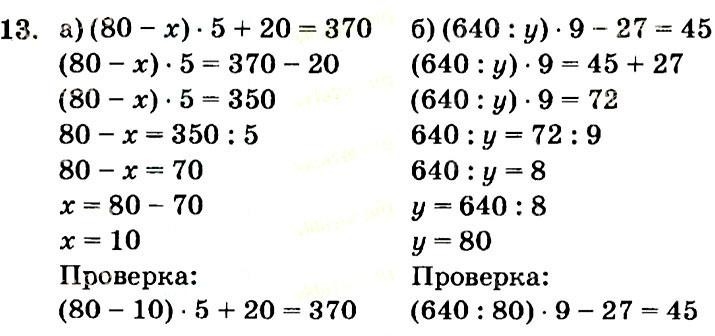

Например: Найдите значение x

3x – 5 = 10
3x = 10 + 5
3x = 15
х = 15/3
х = 5
Следовательно, значение x равно 5

Применение простых уравнений

Простые уравнения можно использовать и для решения задач в реальных жизненных ситуациях. Применение простых уравнений зависит от ситуации, когда нам нужно самим составить уравнение и найти значение неизвестной переменной. Мы сталкиваемся с такими ситуациями, когда покупаем товары в магазине, вычисляем возрастные проблемы, находим пропущенные числа, угадываем неизвестные числа, вычисляем скорость или время поезда и так далее. Переводим ситуации в форму уравнений. Мы разрабатываем стратегии в виде уравнений для решения этих проблем. Например, если ребенок хочет купить 10 карандашей и коробку, которые вместе стоят 35 долларов, стоимость одного карандаша можно принять за х, а стоимость одной коробки можно принять за у, а уравнение можно получить как 10х + у. = 35,

Простые уравнения и их приложения можно увидеть в различных математических концепциях, таких как алгебра, геометрия и дроби. Алгебра и геометрия – одни из самых важных разделов для детей. Простые уравнения и их приложения помогают понять концепцию алгебры на раннем этапе.

Линейное уравнение

Простые уравнения также могут называться линейными уравнениями, в которых имеется более одной переменной, и которые могут быть решены с использованием различных методов, таких как использование графика, уравновешивание уравнения путем преобразования LHS = RHS и транспонирования. Чтобы решить линейное уравнение, полезно знать, как транспонировать или переставлять формулы. При решении линейного уравнения мы пытаемся сделать неизвестную величину предметом уравнения.

Например: 4x + y = 11, где значения x и y равны 2 и 3 соответственно.

4(2) + 3 = 11

8 + 3 = 11

11 = 11

Следовательно, LHS = RHS

Важные моменты

две переменные
9010 решить, уравновешивая уравнение и переставляя числа.
При перестановке чисел предшествующие знаки числа меняются.
При балансировке уравнения число должно быть одинаковым с обеих сторон.
Применение простых уравнений используются в нашей повседневной жизни и могут быть легко решены.
Рекомендации
Переменные, константы и выражения
Линейное уравнение с двумя переменными
Линейные уравнения
Графики линейных уравнений

Пример 1: Докажите, что LHS = RHS в этом уравнении x + 4 = 10
Решение: х + 4 = 10
х + 4 – 4 = 10 – 4
х = 6
Значение X равно 6, и когда X заменяется значением в уравнении, мы получаем
. 6 + 4 = 10
Таким образом, LHS = RHS
Пример 2: В равнобедренном треугольнике угол при вершине равен 40 градусов. Чему равны углы при основании треугольника? (Помните, сумма трех углов треугольника равна 180 градусам)
Решение:
В равнобедренном треугольнике углы при основании равны.
Пусть углы при основании равны x градусов каждый.

Сумма трех углов треугольника равна 180
40 + x + x = 180
40 + 2x = 180
Теперь, переставив 40, получится -40.
2x = 180 – 40
2x = 140
Теперь снова переставим 2, получится /2
x = 140/2
x = 70
Таким образом, углы при основании равны 70 градусов каждый.
Пример 3: Если ваша мать дает вам 100 рупий, чтобы вы купили яблоки, и говорит, что оставьте у нее 40 рупий, чтобы купить шоколад, и вы узнаете, что цена одного килограмма яблок составляет 12 рупий, то сколько яблок нужно вы покупаете для всех?
Предположим, что вам нужно покупать яблоки в килограммах, поэтому общая сумма денег, которую вы потратите, составляет рупий. 12x. Теперь у вас есть 40 рупий для себя. Так уравнение будет?
Решение:
12х + 40 = 100
(перенос 40 на другую сторону, т.е. получается «- 40»)
12x = 100 – 40
12х = 60
х = 60/12
х = 5
Таким образом, вы можете купить 5 кг яблок и купить шоколадные конфеты.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайду

Часто задаваемые вопросы о простых уравнениях и их приложениях
Что такое простое уравнение?
Простое уравнение относится к математическому уравнению, которое уравновешивает взаимосвязь между левой и правой сторонами со знаком «равно». Эта категория уравнений состоит из переменных, обычно в форме x и y.
Зачем нужна транспозиция?
Решение простых уравнений часто требует их перестановки. В таких случаях необходимо ввести переменную «X» на одной стороне уравнения вместе с константами, упомянутыми на другой стороне. Этот метод известен как процесс транспонирования. Любая математическая операция, такая как сложение, вычитание, умножение и деление, выполняемая с одной стороны уравнения, требует выполнения и с другой стороны. Важно сбалансировать уравнение так, чтобы обе части были равны друг другу.
Что такое переменная?
Переменная означает неизвестный фактор в уравнении, который нужно найти в простом уравнении. Уравнение также может иметь несколько переменных, и в этом случае оно будет известно как квадратное уравнение. Переменные играют разные роли в разных математических формулах. Его можно идентифицировать с помощью различных конкретных имен, таких как неопределенная переменная, которая появляется в формальном степенном ряду.
Какой пример простого уравнения?
Примером простого уравнения является 4x – 15 = 25. Буква, которая используется для замены чисел в алгебре, известна как переменная. Однако существуют определенные буквы и символы, которые заменяют фиксированное значение в простом уравнении, и они известны как константы.
Что такое константа?
Константа — это фиксированное число в уравнении, которое преобразуется для нахождения значений переменных x и y. Эти числа не изменяются, но с помощью арифметических операций, таких как сложение, вычитание, умножение и деление, эти константы перестраиваются и вычисляются.
В чем разница между простым уравнением и линейным уравнением?
Математическое уравнение, в котором с обеих сторон есть математическое выражение, хотя бы одна переменная и знак равенства (=), называется простым уравнением. например. 5x+3x = 8x
Принимая во внимание, что математическое уравнение, которое имеет математическое выражение с обеих сторон вместе с двумя переменными и знаком равенства (=), известно как линейное уравнение. например, x = 3y +6
Загрузить БЕСПЛАТНЫЕ учебные материалы
Рабочие листы по линейным уравнениям
Рабочие листы по математике и
наглядный учебный план
Словесные задачи на простые уравнения
Задача 1 :
18 раз отнять от числа 30.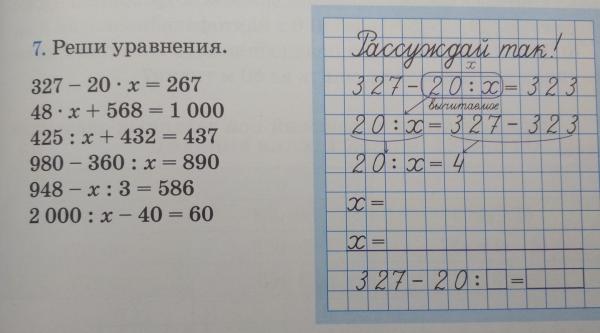 Найдите число.
Решение:
Пусть x будет числом.
Дано: 18 вычитается из 8 умноженных на 30
Тогда у нас есть
8x – 18 = 30
Прибавьте 18 к обеим частям.
8x = 48
Разделите обе части на 8.
x = 6
Следовательно, число равно 6. прибавляя к обоим, дробь становится 3/4. Найдите дробь.
Решение:
Пусть x будет числителем.
Дано : Знаменатель дроби больше числителя на 5.
Из приведенной выше информации
дробь = x/(x + 5) —-(1)
Дано : Если 3 прибавить к оба, дробь становится 3/4.
Из вышеприведенной информации имеем
(x + 3)/(x + 5 + 3) = 3/4
Упростить.
(х + 3)/(х + 8) = 3/4
4(х + 3) = 3(х + 8)
4х + 12 = 3х + 24
x = 12
Замените x =12 в (1).
дробь = 12/(12 + 5)
= 12/17
Задача 3 :
Если из удвоенного его настоящего возраста вычесть трехкратный возраст А 6 лет назад, результат будет равен его нынешнему возрасту. Найдите настоящий возраст А.
Решение:
Пусть x будет настоящим возрастом A.
Возраст А 6 лет назад = x – 6.
Трижды возраст А 6 лет назад = 3(x – 6).
Удвоить его нынешний возраст = 2x.
Дано: трижды возраст А 6 лет назад вычесть из удвоенного его настоящего возраста, результат будет равен его настоящему возрасту.
2x – 3(x – 6) = x
2x – 3x + 18 = x
– x + 18 = x
18 = 2x
Разделите обе части на 2. , Настоящий возраст А – 9 лет.
Задача 4 :
Число состоит из двух цифр. Цифра в разряде десятков в два раза больше цифры в разряде единиц. Если из числа вычесть 18, цифры меняются местами. Найдите число.
Решение :
Пусть x будет разрядом единиц.
Тогда цифра в разряде десятков = 2x.
Итак, число равно (2x)x.
Дано: Если из числа вычесть 18, цифры меняются местами.
(2x)x – 18 = x(2x)
(2x)x – 18 = x(2x)
10(2x) + 1x – 18 = 10x + 1(2x)
Упростить.
20x + x – 18 = 10x + 2x
21x – 18 = 12x
21x – 18 = 12x
9x = 18
Разделите обе части на 9.
x = 2
Цифра в разряде единиц равна 2.
Тогда цифра в разряде десятков равна
= 2 ⋅ 2
= 4
3 90 число равно 42.
Задача 5:
Для определенного товара уравнение спроса, дающее спрос “d” в кг по цене “p” в долларах за кг. d = 100 (10 – р). Уравнение снабжения, дающее запас «s» в кг. для цены “p” в долларах за кг s = 75(p – 3). Найдите равновесную цену.
Решение:
Равновесная цена — это рыночная цена, при которой количество требуемых товаров равно количеству предлагаемых товаров.
D = S
100 (10 – P) = 75 (P – 3)
1000 – 100p = 75p – 225
1225 = 175p
Разделите обе стороны на 175.
7 = P
. Следовательно. , равновесная цена равна 7 долл.
Задача 6 :
Четвертая часть числа больше шестой на 4. Найдите число.
Решение:
Пусть x будет искомым числом.
Четвертая часть числа = x/4
Шестая часть числа = x/6
Дано: Четвертая часть числа больше шестой части на 4.
x/4 – x/6 = 4
L.C.M (4, 6) равно 12.
(3x/12) – (2x/12) = 4
(3x – 2x)/12 = 4
x/12 = 4
Умножить обе части на 12.
x = 48
Следовательно, искомое число равно 48.
Задача 7 :
Ширина прямоугольника составляет 2/3 его длины. Если периметр прямоугольника равен 80 см. Найдите его площадь.
Решение:
Пусть x будет длиной прямоугольника.
Тогда ширина прямоугольника равна 2x/3.
Дано: Периметр равен 80 см.
Периметр = 80 см
2(l + w) = 80
Разделите обе стороны на 2.
l + w = 40
Подставьте l = x и w = 2x/3.
х + 2х/3 = 40
(3x + 2x)/3 = 40
5x/3 = 40
Умножьте обе части на 3/5.
х = 24
Длина 24 см.
Тогда ширина равна
= 2x/3
= (2 ⋅ 24)/3
= 16 см
Формула для нахождения площади прямоугольника:
= l ⋅ l
3 900 24 и w = 16.
= 24 ⋅ 16
= 384 см ²
Задача 8 :
В треугольнике второй угол на 5° больше первого. И третий угол в три раза больше первого угла. Найдите три угла треугольника.
Решение :
Пусть x° – первый угол.
Тогда имеем
второй угол = x° + 5°
третий угол = 3x°
Мы знаем, что сумма трех углов в любом треугольнике равна 180°.
x° + (x° + 5°) + (3x°) = 180°
x + x + 5 + 3x = 180
5x + 5 = 180
Вычтите 5 с обеих сторон.
5x = 175
Разделите обе стороны на 5.
x = 35
Первый угол равен 35°.
Второй угол равен
= 35° + 5°
= 40°
Третий угол равен
= 3 ⋅ 35°
= 105°
Следовательно, три угла треугольника , 40° и 105°.
Пожалуйста, отправьте ваш отзыв на [email protected]
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
Открытые учебники | Siyavula
Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Математика
Читать онлайн
Учебники
Английский
7A PDF (CC-BY-ND)
7B PDF (CC-BY-ND)
Африкаанс
7A PDF (CC-BY-ND)
7B PDF (CC-BY-ND)
Читать онлайн
Учебники
Английский
8A PDF (CC-BY-ND)
8B PDF (CC-BY-ND)
Африкаанс
8A PDF (CC-BY-ND)
8B PDF (CC-BY-ND)
Читать онлайн
Учебники
Английский
9A PDF (CC-BY-ND)
9B PDF (CC-BY-ND)
Африкаанс
9A PDF (CC-BY-ND)
9B PDF (CC-BY-ND)
Читать онлайн
Учебники
Английский
PDF (CC-BY-ND)
ePUB (CC-BY-ND)
ePUB (CC-BY)
Африкаанс
PDF (CC-BY-ND)
ePUB (CC-BY-ND)
ePUB (CC-BY)
Пособия для учителей
Английский
PDF (CC-BY-ND)
Африкаанс
PDF (CC-BY-ND)
Читать онлайн
Учебники
Английский
PDF (CC-BY-ND)
ePUB (CC-BY-ND)
ePUB (CC-BY)
Африкаанс
PDF (CC-BY-ND)
ePUB (CC-BY-ND)
ePUB (CC-BY)
Пособия для учителей
Английский
PDF (CC-BY-ND)
Африкаанс
PDF (CC-BY-ND)
Читать онлайн
Учебники
Английский
PDF (CC-BY-ND)
ePUB (CC-BY-ND)
ePUB (CC-BY)
Африкаанс
PDF (CC-BY-ND)
ePUB (CC-BY-ND)
ePUB (CC-BY)
Пособия для учителей
Английский
PDF (CC-BY-ND)
Африкаанс
PDF (CC-BY-ND)
Читать онлайн
Учебники
Английский
PDF (CC-BY-ND)
ePUB (CC-BY-ND)
ePUB (CC-BY)
Африкаанс
PDF (CC-BY-ND)
ePUB (CC-BY-ND)
ePUB (CC-BY)
Пособия для учителей
Английский
PDF (CC-BY-ND)
Африкаанс
PDF (CC-BY-ND)
Наука
Читать онлайн
Учебники
Английский
PDF (CC-BY-ND)
ePUB (CC-BY-ND)
ePUB (CC-BY)
Африкаанс
PDF (CC-BY-ND)
Пособия для учителей
Английский
PDF (CC-BY-ND)
Африкаанс
PDF (CC-BY-ND)
Читать онлайн
Учебники
Английский
PDF (CC-BY-ND)
ePUB (CC-BY-ND)
ePUB (CC-BY)
Африкаанс
PDF (CC-BY-ND)
ePUB (CC-BY-ND)
ePUB (CC-BY)
Пособия для учителей
Английский
PDF (CC-BY-ND)
Африкаанс
PDF (CC-BY-ND)
Читать онлайн
Учебники
Английский
PDF (CC-BY-ND)
ePUB (CC-BY-ND)
ePUB (CC-BY)
Африкаанс
PDF (CC-BY-ND)
ePUB (CC-BY-ND)
ePUB (CC-BY)
Пособия для учителей
Английский
PDF (CC-BY-ND)
Африкаанс
PDF (CC-BY-ND)
Читать онлайн
Учебники
Английский
PDF (CC-BY-ND)
ePUB (CC-BY-ND)
ePUB (CC-BY)
Африкаанс
PDF (CC-BY-ND)
ePUB (CC-BY-ND)
ePUB (CC-BY)
Пособия для учителей
Английский
PDF (CC-BY-ND)
Африкаанс
PDF (CC-BY-ND)
Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 7А
PDF (CC-BY-ND)
Класс 7Б
PDF (CC-BY-ND)
Африкаанс
Граад 7А
PDF (CC-BY-ND)
Граад 7Б
PDF (CC-BY-ND)
Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 8А
PDF (CC-BY-ND)
Класс 8Б
PDF (CC-BY-ND)
Африкаанс
Граад 8А
PDF (CC-BY-ND)
Граад 8Б
PDF (CC-BY-ND)
Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 9А
PDF (CC-BY-ND)
Класс 9Б
PDF (CC-BY-ND)
Африкаанс
Граад 9А
PDF (CC-BY-ND)
Граад 9Б
PDF (CC-BY-ND)
Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 4А
PDF (CC-BY-ND)
Класс 4Б
PDF (CC-BY-ND)
Африкаанс
Граад 4А
PDF (CC-BY-ND)
Граад 4Б
PDF (CC-BY-ND)
Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 5А
PDF (CC-BY-ND)
Класс 5Б
PDF (CC-BY-ND)
Африкаанс
Граад 5А
PDF (CC-BY-ND)
Граад 5Б
PDF (CC-BY-ND)
Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 6А
PDF (CC-BY-ND)
Класс 6Б
PDF (CC-BY-ND)
Африкаанс
Граад 6А
PDF (CC-BY-ND)
Граад 6Б
PDF (CC-BY-ND)
Лицензирование наших книг
Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.