Прописи по математике 1: ГДЗ рабочая тетрадь по математике 1 класс Моро, Волкова 1 часть

Приёмы работы при изучении словарных слов в первом классе

Приёмы работы при изучении словарных слов в первом классе

Со словами с непроверяемыми написаниями младшие школьники встречаются на каждом уроке. Работая по «Прописи» и учебнику, первоклассники наблюдают над написанием таких слов, как воробей, ворона, сорока, пенал, карандаш и др., запоминают правописание слов Москва, учитель, ученик, собака, корова. В каждом из последующих классов количество таких слов, требующих запоминания и грамотного употребления в устной и письменной речи, увеличивается. Усвоение написания трудных слов требует многократных систематических упражнений, которые связываются со всеми видами письменных работ учащихся.

Чтобы словарная работа была для детей интересна и давала нужный результат, я стараюсь использовать разные виды работ и широко разнообразить дополнительный и наглядный материал. Для того чтобы запомнить непроверяемую букву интересно, с учетом психологической особенности мышления младшего школьника, надо “оживить” букву,  создать  “образ” в конкретном слове. Трудная орфограмма словарного слова связывается с ярким ассоциативным образом, который вспоминается при написании данного словарного слова, помогая правильно написать орфограмму.

Работа над словарными словами проводится ежедневно на каждом уроке русского языка. Все словарные слова объединены в тематические группы, каждая из которых изучается в течение недели. В первый день вводят сами слова, в каждый из последующих дней повторяют и выполняют одно из упражнений. В конце недели слова записывают по памяти или под диктовку и дополняют список словами, пройденными ранее.

Тема «Школа»

Класс, ученик, ученица, учитель, учительница.

Упражнение 1.

Учитель показывает карточки со словарными словами. Задача ребят молча прочитать и запомнить слово. Время предъявления каждой карточки – 5 секунд. Далее учитель предлагает учащимся послушать рассказ, в котором будут встречаться слова. Дети, услышав слово, должны подать сигнал – хлопнуть в ладоши. Затем те слова, которые дети запомнили, увидев и услышав, они записывают в тетрадь.

Тема «Одежда»

Пальто, одежда, платок, сапоги.

Упражнение 1.

На доске записаны словарные слова. Дети читают их по слогам, целыми – словами (быстро, медленно, про себя). Затем слова учитель «закрывает».

Учащимся предлагается вспомнить слова:

– с безударной гласной о;

– с мягким знаком в середине слова;

– состоящие из трех слогов;

– с парным согласным на конце;

– первое слово в списке, последнее слово в списке.

Тема «Деревня»

Деревня, работа, машина, молоко.

Упражнение 1.

Учитель показывает карточки со словарными словами. Задача ребят молча прочитать и запомнить слово. Время предъявления каждой карточки – 5 секунд. Далее учитель предлагает учащимся послушать рассказ, в котором будут встречаться слова. Дети, услышав слово, должны подать сигнал – хлопнуть в ладоши. Затем те слова, которые дети запомнили, увидев и услышав, они записывают в тетрадь.

 Тема «Дикие и домашние животные»

Корова, заяц, лисица, медведь, собака.

Упражнение 1.

Учитель показывает карточки со словарными словами. Задача ребят молча прочитать и запомнить слово. Время предъявления каждой карточки – 5 секунд. Далее учитель предлагает учащимся послушать рассказ, в котором будут встречаться слова. Дети, услышав слово, должны подать сигнал – хлопнуть в ладоши. Затем те слова, которые дети запомнили, увидев и услышав, они записывают в тетрадь.

Тема «Птицы»

Воробей, сорока, ворона, петух.

Упражнение 1.

На доске записаны словарные слова. Дети читают их по слогам, целыми – словами (быстро, медленно, про себя). Затем слова учитель «закрывает».

Учащимся предлагается вспомнить слова:

– с безударной е гласной е;

– которое начинается с глухого согласного твердого звука;

– в которых есть сочетание -оро-;

– состоящее из двух слогов;

– третье слово в списке.

Далее ребята записывают эти слова по памяти. Когда все дети заканчивают писать, учитель открывает запись на доске, каждый ребенок проверяет результат.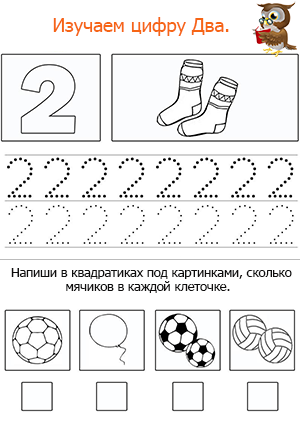

ГДЗ за 1 класс по Математике Кочурова Е.Э. рабочая тетрадь

gdz-bot.ru

Описание решебника

автор: Кочурова Е.Э..

«ГДЗ по Математике 1 класс Рабочая тетрадь Кочурова (Вентана-граф)» станут для маленьких учеников хорошей опорой в освоении такого непростого предмета как математика. Решебник составлен экспертами, и поможет разобраться во всех сложных моментах.

Зачем школьникам нужно изучать дисциплину

Математика – это основной предмет школьной программы. Ее изучение начинается с первого класса, и вплоть до выпускных экзаменов ребята приобретают необходимые знания как для повседневной жизни, так и для дальнейшего профессионального образования. Как учебная дисциплина она преследует следующие цели:

1. Развитие образного, алгоритмического и логического мышления.
2. Воспитание таких качеств личности как целеустремленность, усидчивость, аккуратность.
3. Формирование понимания значимости науки в жизни человека, и общества в целом.

В обычной жизни мы постоянно сталкиваемся с расчетными операциями и цифрами, поэтому, чтобы чувствовать себя уверенно в различных ситуациях, элементарными навыками в математической области должен обладать каждый.

Краткое описание учебного курса за 1 класс

Программа по математике за первый класс познакомит маленьких учеников с основами арифметики. На уроках ребята познакомятся со следующими темами: формы, свойства и признаки предметов, нумерация чисел от 1 до 20, их сравнение, сложение и вычитание, текстовые задачи на разность и сумму, меры длины, сантиметр и дециметр. Для первоклассников материал достаточно сложный и, чтобы его усвоить без проблем, лучше всего иметь всегда под рукой такого помощника как «ГДЗ по Математике 1 класс Рабочая тетрадь Кочурова Е.Э. (Вентана-граф)».

Реальная помощь ГДЗ по Математике 1 класс Рабочая тетрадь Кочурова

Онлайн-сборник имеет в своем составе детально расписанные верные ответы практически ко всем заданиям. С их помощью ученик сможет проработать особо сложный вопрос, заблаговременно осуществить подготовку к текущему опросу учебного материала на уроке, закрепить уже пройденные темы в полном объеме, а также быстро и без ошибок выполнить домашнее задание. Пользоваться решебником удобно и легко, его структура полностью аналогична учебнику и расположение заданий совпадает, поэтому первоклассник без труда отыщет готовое решение по номеру упражнения. ГДЗ существенно облегчат обучение, к тому же используя их регулярно ученик вникнет во все специфические особенности предмета, и избежит многочисленных ошибок и недочётов.

Рекомендуемые решебники

В.Н. Рудницкая, Вентана-граф тетрадь для проверочных работ В.Н. Рудницкая, Вентана-граф

Ответы к урокам

Урок 1 Урок 2 Урок 3 Урок 4 Урок 5 Урок 6 Урок 7 Урок 8 Урок 9 Урок 10 Урок 11 Урок 12 Урок 13 Урок 14 Урок 15 Урок 16 Урок 17 Урок 18 Урок 19 Урок 20 Урок 21 Урок 22 Урок 23 Урок 24 Урок 25 Урок 26 Урок 27 Урок 28 Урок 29 Урок 30 Урок 31 Урок 32 Урок 33 Урок 34 Урок 35 Урок 36 Урок 37 Урок 38 Урок 39 Урок 40 Урок 41 Урок 42 Урок 43 Урок 44 Урок 45 Урок 46 Урок 47 Урок 48 Урок 49 Урок 50 Урок 51 Урок 52 Урок 53 Урок 54 Урок 55 Урок 56 Урок 57 Урок 58 Урок 59 Урок 60 Урок 61 Урок 62 Урок 63 Урок 64 Урок 65 Урок 66 Урок 67 Урок 68 Урок 69 Урок 70 Урок 71 Урок 72 Урок 73 Урок 74 Урок 75 Урок 76 Урок 77 Урок 78 Урок 79 Урок 80 Урок 81

[email protected] gdz-bot. ru © 2022 при поддержке gdz.ru 💙

Расчет дозировки в аптеке | Аптечная математика — это просто!

Аптечные расчеты

Аптечные расчеты | Расчет дозировки

Расчет дозировки

Расчет дозировки является одним из наиболее распространенных вопросов по расчетам в аптеках, задаваемых на тестах. Они также являются одними из самых важных вычислений, которые необходимо знать.

Различия между дозами могут иметь огромные клинические последствия. И технический персонал аптеки , и фармацевты должны иметь четкое, всестороннее и безошибочное понимание и знание расчета дозировки.

Ниже мы рассмотрим восемь различных способов расчета дозировки. Попрактикуйтесь в каждом вопросе расчета аптеки, прежде чем изучать ответ. Таким образом, вы можете выявить любые пробелы в знаниях на этом пути.

Образец задачи 1

Сколько таблеток нужно прописать пациенту, которому требуется 4 таблетки препарата два раза в день в течение 6/7?

• 4 таблетки два раза в день = 8 таблеток
• 6/7 относится к 6 дням из 1 недели = 8 x 6 = 48 таблеток

Ответ : 48 таблеток

Пример задачи 2

В вашу аптеку приходит пациент и просит лекарство от кашля. Его клиницист прописал ему принимать по 15 мл лекарства четыре раза в день в течение 7 дней.

Какое количество доз требуется и какой минимальный объем лекарства от кашля должен быть выдан?

Дозы вводятся каждые 5 мл – это означает, что доза этого пациента в 15 мл состоит из трех ложек по 5 мл.

4 раза в день в течение 7 дней составляет 28 доз – опять же, каждая доза состоит из 5 мл ложки.

28 доз x 15 мл = Необходимо выдать 420 мл лекарства от кашля .

Примечание : Дозы менее 5 мл можно вводить с помощью перорального шприца, который может понадобиться, например, детям или пожилым людям.

Ответ :

• Количество доз: 28
• Минимальный дозируемый объем: 420 мл

Пример задачи 3

Больному прописано 9 мг препарата X два раза в день в течение 5/7. Ей также назначают 7 мг один раз в день (того же препарата) на оставшиеся 2/7. Препарат X доступен только в таблетках по 2 мг и 5 мг.

Сколько таблеток каждой дозировки следует назначить пациенту?

• 9 мг x два раза в день = 18 мг
• 18 мг x 5 дней = 90 мг в течение 5 дней X (5/7)
• 14 мг требуется в течение следующих двух дней (2/7)
• Общая доза : 104 мг препарата X.

Было бы неправильно прописывать двадцать таблеток по 5 мг и две таблетки по 2 мг, хотя в сумме получается 104 мг.

Это потому, что у пациента закончатся таблетки по 2 мг! Только доза 9 мг требует 5 мг + 2 мг + 2 мг. не останется 2 мг для второй дозы в первый день лечения.

Для каждой суточной дозы требуется две таблетки по 5 мг и четыре таблетки по 2 мг, что составляет десять таблеток по 5 мг и двадцать таблеток по 2 мг для 5/7. Еще 7 мг требуется в течение следующих двух дней, то есть две таблетки по 5 мг и две таблетки по 2 мг на 2/7.

В общей сложности пациенту необходимо двенадцать таблеток по 5 мг (60 мг) и двадцать две таблетки по 2 мг (44 мг), что соответствует требуемой дозе 104 мг.

Образец задачи 4

Адреналин доступен в виде инъекций по 100 мкг/мл. Больному требуется внутримышечная инъекция 0,5 мг. Сколько миллилитров инъекции необходимо для получения необходимой дозы?

Во-первых, нам нужно рассмотреть, являются ли наши единицы непротиворечивыми — в этом случае единицы не являются последовательными.

0,5 мг x 1000 = 500 мкг.

Адреналин доступен в виде инъекций по 100 мкг/мл.

Поэтому нам нужно 5мл имеющегося состава адреналина.

Ответ: 5 мл

Пример задачи 5

Рекомендуемая доза флуконазола при кандидозе слизистых оболочек у детей составляет 3 мг/кг в день. Рассчитайте дозу, необходимую для ребенка (3 года). Предложите соответствующую формулировку.

Для такого расчета дозировки вы должны обратиться к справочнику. БНФ (« Британский национальный формуляр » или другое международное руководство по дозированию) ясно, что «ребенок» определяется как лицо в возрасте до 12 лет.

BNF предоставляет таблицу с идеальной массой тела и ростом в зависимости от возраста ребенка. Эти таблицы необходимо учитывать при расчете дозы для детей. Если вес ребенка не указан, нередко можно оценить его значение. Например, 6-летний ребенок имеет предполагаемый вес от 18 до 23 кг, то есть ок. 20 кг .

Учитывая это, 3-летний ребенок имеет идеальную массу тела 14 кг. Таким образом, идеальная доза составляет 14 кг x 3 мг = 42 мг флуконазола.

Какой состав выбрать?

• 50 мг, 150 мг, 200 мг капсулы
• 50 мг/мл и 200 мг/5 мл суспензии

Капсулы исключены. Детям в возрасте до 5 лет предпочтительно назначать жидкие формы.

Наиболее подходящей формой является 50 мг/5 мл суспензии флуконазола.

Если в 5 мл 50 мг, то в 1 мг 0,1 мл.

Нам нужно 42 мг флуконазола – 42 x 0,1 мл = 4,2 мл

Ответ : Ребенку 3 лет следует назначать 4,2 мл суспензии флуконазола (50 мг/5 мл) в день.

Образец Задача 6

Препарат X необходимо принимать по 15 мг/кг в день в два приема. Рассчитайте дозу для 6-месячного ребенка и объем педиатрической инъекции. Препарат X доступен в дозировке 50 мг/мл.

Идеальная масса тела шестимесячного ребенка составляет 7,6 кг.

Учитывая, что доза составляет 15 мг на каждый 1 кг, 7,6 кг эквивалентны 114 мг.

Теперь, когда мы узнали необходимое количество препарата X, теперь нам нужно выяснить, сколько мл имеющегося препарата обеспечивает эту точную дозу.

Если в 1 мл препарата 50 мг, то в 0,02 мл должно содержаться 1 мг.

Если умножить 0,02 мл на 114 мг, получится 2,28 мл.

Однако в вопросе указывалось, что препарат X необходимо давать в два приема.

Ответ: 2,28 мл препарата следует принимать ежедневно в два приема по 1,14 мл.

Пример задачи 7

Какая пероральная доза метотрексата подходит для 5-летнего ребенка весом 18 кг? Пероральная доза метотрексата составляет 15 мг/м2 ² в неделю.

Во-первых, нам нужно узнать, какова идеальная площадь поверхности тела пятилетнего ребенка.

Идеальная площадь поверхности тела пятилетнего ребенка составляет 0,74 м ² .

При наличии 15 мг в каждом 1 м ² , сколько мг в 0,74 м ² ?

Разделить 1 м ² /0,74 м ² , мы узнаем пропорциональную разницу коэффициентов. В данном случае коэффициент равен 1,35.

Ответ : Разделив 15 мг на 1,35, мы узнаем, что недельная доза метотрексата должна составлять 11,1 мг.

Образец задачи 8

Препарат X содержит 9,25 мг витамина А (в виде ретинилацетата) и 400 МЕ эргокальциферола. Препарат Y содержит 2240 МЕ витамина А и 10 мкг витамина D.

Какой препарат содержит наибольшую концентрацию витаминов?

Обратите внимание, что единицы измерения не эквивалентны.

Для витамина А:

• 1 МЕ = 0,344 мкг.
• 9,25 мг витамина А; мы также должны преобразовать это в микрограммы.
• 9,25 мг = 9250 мкг.
• 9250/0,344 = 26 890 МЕ

Следовательно, препарат X содержит 26 890 МЕ витамина А, а препарат Y содержит 2 240 МЕ витамина А.

Когда мы применяем тот же процесс к эргокальциферолу, мы узнаем, что одинаковое количество витамина D содержится в обоих составах .

Ответ : Препарат X содержит большую концентрацию витамина.

Заключительные мысли

Расчет дозировки остается одним из самых фундаментальных вопросов в широкой церкви аптечных расчетов.

Здесь мы рассмотрели основные расчеты, которые вы должны знать, а также некоторые ключевые факторы, которые следует учитывать, такие как масса тела, важность выявления несовместимых единиц и пошаговая методология, которой следует следовать для работы. решать проблемы логично и последовательно.

Желаемый расчет дозы по методу формулы – StatPearls

Тэмми Дж. Тони-Батлер; Самар Николя; Лэнс Уилкокс.

Информация об авторе

Последнее обновление: 23 июня 2022 г.

Введение

Существует 3 основных метода расчета дозировок лекарств; Анализ размеров, соотношение пропорций и формула или желаемый метод. Мы более подробно рассмотрим один из этих трех методов, метод «Желаемое вместо того, чтобы иметь» или «Формула».

Желаемое вместо того, чтобы иметь или метод формулы использует формулу или уравнение для решения для неизвестной величины (x), очень похоже на отношение пропорции.

Для расчета лекарств необходимо использовать коэффициенты преобразования, например, при преобразовании фунтов в килограммы или литров в миллилитры. Упрощенный по дизайну, этот метод позволяет клиницистам работать с различными единицами измерения, конвертируя коэффициенты, чтобы найти ответ. Эти методы полезны для проверки точности других методов расчета, таким образом действуя как двойная или тройная проверка.

Подготовка

Когда клиницисты подготовлены и знают ключевые коэффициенты пересчета, они будут меньше беспокоиться о расчетах. Это жизненно важно для точности, независимо от того, какая формула или метод используются.

Коэффициенты пересчета

• 1 кг = 2,2 фунта

• 1 Галлон = 4 кварта

• 1 TSP = 5 мл

• 1 дюйм = 2,54 См

• 9008 1,1000 мг.0003

• 1 кг = 1000 г

• 1 унция = 30 мл = 2 ст.

• 1 ст. = 16 унций

• 1 столовая ложка = 3 чайные ложки

• 60 минут = 1 час

• 1 CC = 1 мл

• 2 Pints ​​= 1 QT

• 8 OZ = 240 мл = 1 Glass

• 1 TSP = 240 мл = 1 Glass

• 1.

• 1 Pt = 500 мл = 16 унций

• 1 унция = 30 мл

• 4 унции = 120 мл (Кейси, 2018)

Техника

Есть 3 первичных метода для расчета Medication. дозы, указанные выше. К ним относятся метод или формула желательного преобладания, размерный анализ, соотношение и пропорция (цитируется по Boyer, 2002) [Lindow, 2004].

Желательно, а не методом формулы

Desired over Have или Formula Method — это формула или уравнение для решения неизвестной величины (x), очень похожее на пропорцию отношения. Расчеты лекарств требуют использования коэффициентов пересчета, например, при переводе фунтов в килограммы или литров в миллилитры. Упрощенный по дизайну, этот метод позволяет нам работать с различными единицами измерения, конвертируя коэффициенты, чтобы найти ответ. Это полезно для проверки точности других методов расчета, упомянутых выше, таким образом действуя как двойная или тройная проверка.

• Основная формула, решение для x, помогает нам составить уравнение:

• D/H x Q = x, или Желаемая доза (количество) = заказанное количество дозы/количество на руках x количество .

Например, поставщик запрашивает лоразепам 4 мг IV Push для пациента с тяжелой алкогольной абстиненцией. У врача есть флаконы по 2 мг/мл под рукой. Сколько миллилитров он должен набрать в шприц, чтобы ввести желаемую дозу?

Единицы измерения должны совпадать, например, миллилитры и миллилитры, либо необходимо преобразовать в аналогичные единицы измерения. В приведенном выше примере заказанная доза была в миллиграммах, а имеющаяся доза была в миллиграммах, обе из которых компенсируются, оставляя миллилитры (ответ требовал миллилитров), поэтому дальнейшее преобразование не требуется.

Метод размерного анализа

Заказ, размещенный поставщиком на лоразепам 4 мг внутривенно PUSH для оценки CIWA 25 или выше, следует протоколу CAGE для последующих дозировок на основе оценки CIWA.

• У врача есть флаконы по 2 мг/мл в автоматическом дозаторе.

• Сколько миллилитров необходимо для получения заказанной дозы?

• Желаемая доза os помещается в 1 помните, (x мл) = 4 мг/1 x 1 мл/2 мг x (4)(1)/2 x 4/2 x 2/1 = 2 мл, сохраните умножение/деление, пока не будет достигнуто желаемое количество, 2 мл в этом примере.

• Обратите внимание, что дробь была настроена так, чтобы миллиграммы и миллиграммы были размещены стратегически, поэтому единицы могли уравновешивать друг друга, что облегчало решение уравнения для желаемой единицы или миллилитров. Ответ имеет смысл, так что работа сделана.

Нули можно аннулировать так же, как и аналогичные единицы. Например:

• 1000/500 x 10/5 = 2, 2 нуля в числе 1000 и 2 нуля в числе 500 можно вычеркнуть, поскольку единицы в числителе и знаменателе одинаковы, оставив 10/5, дробь для решения которой гораздо проще. , и ответ имеет смысл.

Мы рассмотрели нули, а теперь давайте посмотрим на 1.

• Если число умножить на 1, то число не изменится.

• Напротив, если вы умножаете число на ноль, число становится нулем.

• Ниже перечислены примеры: 18 x 0 = 0 или 20 x 1 = 20.

Метод отношений и пропорций

Метод соотношения и пропорции существует уже много лет и является одним из старейших методов, используемых при расчете лекарств (цитируется по Boyer, 2002) [Lindow, 2004]. Дополнительные принципы — это метод решения проблем, который не имеет отношения к этим отношениям. Только умножение и деление используются для решения задачи соотношения и пропорции, а не сложения. Пример, приведенный ниже, даст лучшее объяснение, используя формат дроби или двоеточия:

Медицинский работник заказывает лоразепам 4 мг внутривенно. Подождите сейчас, чтобы получить 25 баллов по шкале CIWA. В наличии есть флаконы по 2 мг/мл. Сколько миллилитров требуется для выполнения заказанной дозы?

Можно использовать H:V::D:X, а умножение означает DV и Extremes HX в формате двоеточия.

• Hx = DV, x = DV/H, 2:1::4:x, 2x = (4)(1), x = 4/2, x = 2 мл В исследовании 2016 года оценивалась роль уверенности в общей арифметике в навыках расчета лекарств. Участники исследования посещали занятия по коррекционной математике из самых разных областей образования и возрастной динамики, стремясь получить первую степень в области сестринского дела, базовую степень или курсы после регистрации (Шелтон, 2016).

  Исследование показало, что треть учащихся испытывают неуверенность в себе, возникшую на более раннем этапе обучения, еще в начальной школе (Шелтон, 2016). Исследование пришло к выводу, что уверенность играет роль в расчетах доз и общей производительности математических расчетов и может быть улучшена в среде, которая способствует подходу глубокого обучения (Шелтон, 2016).

  Клиническое значение

  Ошибки при лечении могут быть вредными и дорогостоящими для пациентов.[1] Расчет лекарств и базовые математические навыки играют важную роль в безопасном приеме лекарств.

  Согласно исследованию медсестер интенсивной терапии (ОИТ), проведенному в 2016 году, 80 % медсестер считают, что знание расчета дозировки лекарств необходимо для уменьшения ошибок при приеме лекарств во время приготовления внутривенных препаратов.[2]

  Лекарства с высоким риском, такие как гепарин и инсулин, часто требуют повторной проверки дозировки более чем одним поставщиком перед введением препарата. Следуйте установленным правилам и рекомендациям по перепроверке расчетов дозы другим лицензированным поставщиком.

  Опубликованное в 2018 году исследование, проведенное группой медсестер онкологических отделений в 3 швейцарских больницах, посвящено процессу двойной проверки и его ограничениям в текущей среде здравоохранения, а также увеличению рабочей нагрузки медсестер и нехватке времени, отвлекающей обстановке и нехватке ресурсов. Исследование пришло к выводу, что медсестры отделения онкологии твердо верят в эффективность перепроверки лекарств, несмотря на сообщения об ограничениях этой процедуры в клинической практике.[3]

  Улучшение результатов работы команды здравоохранения

  Все члены межпрофессиональной группы несут ответственность за расчет дозы. Врачи, медсестры и фармацевты должны хорошо разбираться в желаемых формулах. Этот метод имеет неоценимое значение для правильного лечения пациентов.

  Контрольные вопросы

  • Доступ к бесплатным вопросам с несколькими вариантами ответов по этой теме.