Прописи цифры 1 и 2: Цифра 1 пропись – Подготовка к школе и развивающие задания для детей Мама7я

Прописи цифр. | Методическая разработка по математике (подготовительная группа):

Прописи цифр

Большое значение при обучении письму цифр имеет определение правильного наклона. При письме в клетке наклон определяется отрезком, соединяющим правый верхний угол клетки с серединой её нижней стороны. Прежде чем приступить к объяснению написания цифры, необходимо показать ребёнку её образец и проанализировать, из каких элементов состоит цифра (палочка, волнистая линия, овал, полуовал). Показ написания цифры должен сопровождаться краткими пояснениями о том, где начинается линия, в каком направлении ведётся, где заканчивается, в каком месте ручка должна быть оторвана от бумаги и какой будет следующая линия. Первые цифры, написанные ребёнком самостоятельно, должны быть просмотрены взрослым, который делает необходимые замечания.

Особенности написания цифр и образцы цифры

Прописная цифра один (1)

Начинают писать маленькую палочку немного выше и правее центра клетки, ведут линию вверх к правому верхнему углу клетки. Затем пишут большую палочку от верхнего правого угла почти до середины нижней стороны клетки.

Прописная цифра два (2)

Начинают писать немного ниже середины верхней стороны клетки. Ведут линию вверх, закругляя в правом верхнем углу клетки. Затем ведут линию вниз к середине нижней стороны клетки. Вдоль нижней стороны клетки. Вдоль нижней стороны клетки пишут волнистую линию, ведя руку к правому нижнему углу клетки.

Прописная цифра три (3)

Начинают писать немного ниже середины верхней стороны клетки. Ведут линию вверх, закругляя в правом верхнем углу клетки. Затем ведут линию вниз, немного не доводят до середины клетки и пишут нижний полуовал.

Прописная цифра четыре (4)

Начинают писать немного правее середины верхней стороны клетки. Ведут прямую линию почти к центру клетки, затем ведут палочку вправо и немного не доводят до правой стороны клетки. Пишут длинную палочку, начиная выше середины правой стороны клетки и доводя её до нижней стороны клетки.

Прописная цифра пять (5)

Начинают писать наклонную палочку немного правее середины верхней стороны клетки и ведут её почти до центра клетки. Затем пишут полуовал. Сверху от палочки пишут вправо волнистую линию.

Прописная цифра шесть (6)

Начинают писать полуовал немного ниже верхнего правого угла клетки, закругляют, касаясь верхней стороны клетки, и ведут руку вниз. Закругляют линию, касаясь нижней стороны клетки и ведут руку вверх. Затем закругляют линию влево немного выше центра клетки.

Прописная цифра семь (7)

Начинают писать волнистую линию немного ниже середины верхней стороны клетки и доводят её до правого верхнего угла клетки. Потом пишут большую палочку, доводя её почти до середины нижней стороны клетки, а затем перечёркивают её маленькой палочкой посередине.

Прописная цифра восемь (8)

Начинают писать немного ниже и правее середины верхней стороны клетки. Ведут линию вверх и вправо, закругляют, касаясь верхней и правой сторон клетки.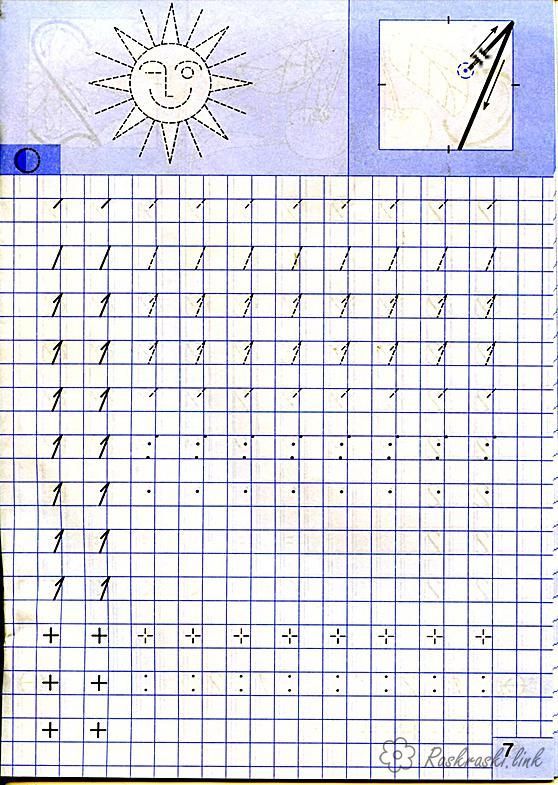 Затем ведут руку вниз, закругляют линию, касаясь нижней стороны клетки. Далее, закругляясь, линия идёт вверх к начальной точке.

Прописная цифра девять (9)

Начинают писать немного ниже правого верхнего угла клетки. В правом верхнем углу клетки линию закругляют и ведут руку вниз, к центру клетки. Здесь линию вновь закругляют и ведут вверх к началу овала. Затем ведут руку вниз, закругляя у середины нижней стороны клетки.

Прописная цифра ноль (0)

Пропись по Математике (Цифры от 1 до 10)

Пропись по Математике (Цифры от 1 до 10)

Пропись по Математике (Цифры от 1 до 10).
Эта пропись по математике для начального знакомства с математикой. Что узнает и чему научится ребенок занимаясь по этим прописям? В круг первоначальных математических сведений войдут числа первого десятка, счет и правильное написание этих чисел.
Цель пропись по математике: выучить числа от 0 до 10, научиться их писать и научить считать.
Эта пропись по математике предназначена для подготовки детей дошкольного возраста к письму в тетради.
Задания в данной прописи по математике помогут развить мелкую моторику и координацию движений руки.
Пропись по математике предназначена для занятий с детьми от 4 лет и старше. Также эти прописи можно использовать в старших и подготовительных группах детских садов и в начальной школе.

Пропись по Математике

Пропись по Математике 

 

Скачиваем пропись по математике бесплатно. Смотрите и скачивайте Пропись с цифрами

Следующее Предыдущее Главная страница

Подписаться на: Комментарии к сообщению (Atom)

• Твердые и мягкие согласные звуки

  Используйте карточки , чтобы научить ребенка определять когда согласные бывают мягкими , когда твердыми. Синим цветом -твердые Зеленым цв…

• Слоги.Составляем слова из слогов

  Слоги.Составляем слова из слогов. Скачайте бесплатно карточки с буквами и слогами. Всего 20 карточек. Буквы и слоги для детей. Разрежьте…

• Русский Алфавит Цветные Карточки

  Русский Алфавит Цветные Карточки. На каждой карточке с буквой изображена картинка начинающаяся на эту букву. С помощью этих карточек можно …

• Картинки с изображением Одежды и Обуви

  Картинки с изображением повседневной одежды и обуви, Одежда, Обувь, карточки одежда, Карточки обувь. Тематические карточки “Одежда&qu…

• Развивающие карточки для Игр с Детьми

  Сегодня познакомимся с оригинальным способом как изготовить без особых затрат развивающие карточки для занятий с детьми от 1 года. Интересн…

• Профессии Карточки

  Уникальные Карточки с Профессиями. Скачайте Бесплатно развивающие карточки с профессиями для Ваших детей. Знакомство детей с профессиями….

• Соедини цифры и Раскрась Рисунок

  Изучаете цифры и счет с ребенком? Как закрепить пройденный материал? Закрепление пройденного материала можно превратить в интересную и р. ..

• Карточки с Цифрами

  Карточки с Цифрами. Карточки помогут ребенку выучить цифры. Карточки можно использовать для занятий дома, в детском саду или в начальной шк…

• Карточки – Учим Ребенка Счету

  Карточки-как научить ребенка счету. Просто распечатайте цветные карточки, которые помогут Вашему ребенку узнать цифры от 1 до 10. Предлаг…

• Карточки СЛОГИ (не цветные)

  Слоги. Скачиваем бесплатно карточки.Скачайте бесплатно карточки (не цветные) с буквами и слогами. Всего карточек: 21. Буквы и слоги для …

Сколько раз цифра 1 встречается в числах от 1 до 1000?

Системы счисления — это значение, используемое для счета и измерения объектов, а также для выполнения арифметических вычислений. Это метод записи для выражения чисел. Он обеспечивает уникальное представление каждого числа и представляет арифметическую и алгебраическую форму числа. Это позволяет нам выполнять арифметические операции, такие как сложение, вычитание, умножение и деление.

Уравнение — это объявление, которое связывает два алгебраических выражения с равными значениями знаком «=». Например: в уравнении 8x + 4 = 7, 8x + 4 — это выражение в левой части, а 7 — это выражение в правой части, связанное знаком «=».

Что такое число?

Слово или символ, обозначающий сумму, называется числом. Числа 4, 6, 8 и т. д. — четные числа, а 3, 5, 7 и т. д. — нечетные числа. Число – это значение, образованное комбинацией цифр. Эти числа используются для выражения алгебраических величин. Целое число представляет собой набор из 10 символов в диапазоне от 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Любое объединение целых чисел представляет собой число. Размер числа зависит от количества цифр, которые используются для его построения. Например: 126, 128, 0,356, -12, 78, 94 и т. д.

Целые числа

Целые числа такие же, как натуральные числа, но они также включают «ноль». Мы можем подарить целые числа символом W. Целые числа включают в себя все натуральные числа и 0 (ноль).

Мы знаем, что числа 1, 2, 3, 4, 5 — натуральные числа. А числа 0, 1, 2, 3, 4, 5, 6 и т. д. — это целые числа, так как они включают в себя и 0. Целые числа представлены как W, а натуральные числа представлены как N. Поэтому правильно сказать,

                                                                       W= {N} + 0

В числовой строке все, что находится справа от 0 (включая .

Сколько раз цифра 1 встречается в числах от 1 до 1000?

Решение:

Подсказка: Самый простой способ – записать числа в диапазоне от 10 до 100, а затем подсчитать количество единиц в них

Шаги, чтобы найти решение:

Сначала возьмем числа в диапазоне 10:

В диапазоне чисел от 0 до 10 цифра 1 появляется 2 раза.

Теперь складываем числа в диапазоне 100

В диапазоне чисел от 0 до 99 цифра 1 появляется 20 раз.

(Они: 1, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 21, 31, 41, 51, 61, 71, 81, 91)

Обратите внимание, что в числе 11, 1 появляется два раза.

Теперь от 100 до 199 цифра 1 появляется 120 раз.

В этом случае цифра на разряде сотен равна 1. Следовательно, имеется 120 единиц от 100 до 199.

Объяснение- мы должны найти единицы из разряда 100, 101, 102……….. 199. На разряде сотен из этих 3 цифра 1 появится 100 раз. На месте десятков 1 появится 10 раз

То есть в случаях 110, 111, 112, 113, 114…… 119. На месте единиц 1 появится 10 раз (101, 111, 121, 131……. 191) 

Итак, добавьте это:

100 + 10 + 10 = 120, поэтому 1 встречается 120 раз.

Теперь с 200 до 299 имеем 201, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 221, 231, 241, 251, 261, 271, 281, 291 цифра 1 встречается 20 раз.

Аналогично,

От 300 до 399 имеем 301,…311,….391. Опять 20 раз

От 400 до 499 имеем 401,…411,…491. Опять 20 раз

От 500 до 599 имеем 501,…511,…591. Опять 20 раз.

От 600 до 699 имеем 601,…611,…691. Опять 20 раз

От 700 до 799 имеем 701,…711,…791. Опять 20 раз

От 800 до 899 имеем 801,…811,…891. Снова 20 раз

От 900 до 999 имеем 901,…911,…991. Снова 20 раз

и тогда у нас есть 1000, в котором цифра 1 появляется 1 раз

Складывая все вышеперечисленное, мы получаем:

Общее количество раз = (20).(9) + 120 + 1

= 180 + 120 + 1

= 301

Следовательно, когда мы перечисляем числа от 1 до 1000, цифра 1 пишется 301 раз.

Примечание: Не забывайте подсчитывать цифру 1 дважды в числах типа 11, а также не забывайте подсчитывать цифру 1 в сотом разряде в числах от 100 до 199, а также в тысячном разряде, например 1000.

Подобные вопросы

Вопрос 1: При перечислении чисел от 1 до 1000 сколько раз встречается цифра 5.

Ответ:

Этапы поиска решения:

Сначала возьмем числа в диапазоне 10:

Из диапазона чисел от 0 до 10 цифра 5 появляется 1 раз.

Теперь складываем числа в диапазоне 100

В диапазоне чисел от 0 до 99 цифра 5 появляется 20 раз.

(Они: 5, 15, 25, 35, 45, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 65, 75, 85, 95)

Обратите внимание, что в числе 55, 5 появляется два раза.

Теперь от 100 до 199 имеем: 105, 115, 125, 135, 145, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 165, 175, 185, 195. Цифра 5 появляется 20 раз.

Аналогично,

От 200 до 299 имеем 205,215…….245, 250,…255,…..,295. Опять 20 раз.

От 300 до 399 имеем 305,…355,…,395. Опять 20 раз

От 400 до 499 имеем 405,…455,…,495. Опять 20 раз

От 600 до 699 имеем 605,…655,…,695. Опять 20 раз

От 700 до 799 имеем 705,…755,…,795. Снова 20 раз

От 800 до 899 имеем 805,…855,…,895. Снова 20 раз

От 900 до 999 имеем 905,…955,…,995. Снова 20 раз

Теперь оставшийся диапазон от 500 до 599:

Теперь от 500 до 599 цифра 5 появляется 120 раз.

В этом случае цифра сотен равна 5. Следовательно, имеется 120 пятерок от 500 до 599.

Объяснение: Нам нужно найти пятерки из 500, 501, 502………. . 599. В сотнях место этих трехзначных чисел, 5 придет 100 раз. На месте десятков 5 будет 10 раз

То есть в случаях 550, 551, 552, 553, 554…… 559. На месте единиц 5 будет 10 раз (505, 555, 525, 535……. 595)

Итак, добавьте это:

100 + 10 + 10 = 120, так что 5 появится 120 раз.

Складывая все вышеперечисленное, мы получаем:

Общее количество раз = (20).(9) + 120 

= 180 + 120

= 300

Следовательно, когда мы перечисляем числа от 1 до 1000, цифра 5 написано 300 раз.

Примечание: Не забудьте дважды подсчитать цифру 5 в числах типа 55, а также не забудьте подсчитать цифру 5 в сотых долях в числах от 500 до 599.

Вопрос 2: Как сколько раз цифра 2 встречается в числах от 1 до 100?

Ответ:

Полное пошаговое решение:

Нужно найти, сколько раз цифра 2 встречается в числах от 1 до 100.

От 1 до 10 цифра 2 появляется только один раз для 2.

От 11 до 20 цифра 2 появляется два раза для чисел от 12 до 20.

От 21 до 30 цифра 2 появляется в числах 21, 22, 23, 24, 25, 26, 27, 28 , 29 и 22

встречается дважды. Итак, оно появляется десять раз.

От 31 до 40 цифра 2 появляется только один раз для 32.

От 41 до 50 цифра 2 появляется только один раз для 42.

От 51 до 60 цифра 2 появляется только один раз для 52.

От 61 до 70 цифра 2 появляется только один раз для 62.

От 71 до 80 цифра 2 появляется только один раз для 72.

От 81 до 90 цифра 2 появляется только один раз для 82.

От 91 до 100 цифра 2 появляется только один раз для 92.

Итак, общее количество повторений 2 равно 1+2+10+1+1+1+1+1+1+1 = 20.

Следовательно, цифра 2 встречается в числах от 1 до 100 20 раз.

Типы чисел — различие и классификация

Можете ли вы представить, какой была бы ваша жизнь, если бы у вас не было способа представить возраст, вес, дни рождения, время, счет, банковские счета и номера телефонов? Десять математических цифр (от 0 до 9) используются для определения всех этих величин.

Числа — это строки цифр, используемые для представления количества. Величина числа указывает на размер количества. Он может быть как большим, так и маленьким. Они существуют в разных формах, таких как 3, 999, 0,351, 2/5 и т. д.

Типы чисел в математике

Точно так же, как разные члены семьи живут в разных домах, разные числа относятся к одной семье, но имеют разные типы. Со временем различные комбинации из десяти цифр были отнесены к различным типам чисел. Эти образцы чисел отличаются друг от друга из-за различных представлений и свойств.

Натуральные числа

Натуральные числа или счетные числа — это самые основные типы чисел, которые вы впервые узнали в детстве. Они начинаются с 1 и идут до бесконечности, т. е. 1, 2, 3, 4, 5, 6 и так далее. Их также называют положительными целыми числами. В установленной форме они могут быть записаны как:

{1, 2, 3, 4, 5, …}

Натуральные числа представлены символом N .

Целые числа

Целые числа — это набор натуральных чисел, включая ноль.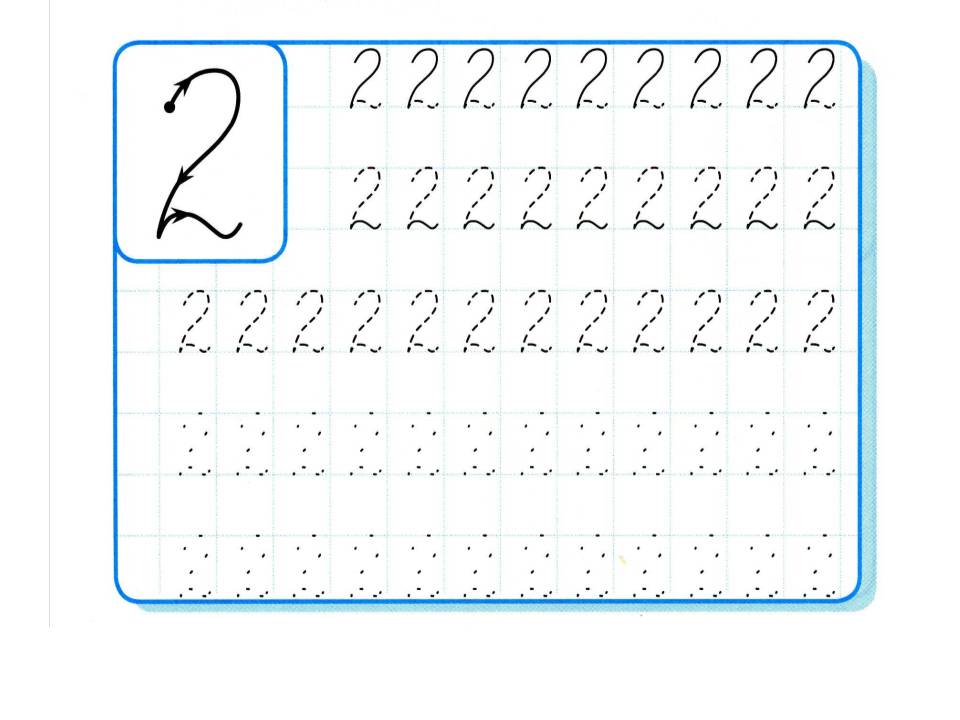 Это означает, что они начинаются с 0 и доходят до 1, 2, 3 и т. д., т. е.

{0, 1, 2, 3, 4, 5, …}

Целые числа представлены символом W .

Целые числа

Целые числа представляют собой множество всех целых чисел и отрицательных чисел натуральных чисел. Они содержат все числа, лежащие между отрицательной бесконечностью и положительной бесконечностью. Они могут быть положительными, нулевыми или отрицательными, но не могут быть записаны в виде десятичной или дробной части. Целые числа могут быть записаны в заданной форме как

{…, -3, -2, -1, 0, 1, 2, 3, …}

Можно сказать, что все целые числа и натуральные числа являются целыми числами, но не все целые числа являются натуральными числами или целыми числами.

Символ Z представляет целые числа.

Дроби

Дробь представляет части целого куска. Его можно записать в виде a/b , где a и b — целые числа, а b никогда не может быть равно 0. Все дроби — рациональные числа, но не все рациональные числа — дроби. .

Далее дроби преобразуются в правильные и неправильные дроби. Неправильные дроби – это те, в которых числитель больше знаменателя, а в правильных функциях верно обратное, то есть знаменатель больше числителя. Примерами правильных дробей являются 3/7 и 99/101, а 7/3 и 101/99 — неправильные дроби. Это означает, что неправильные дроби всегда больше 1.

Все завершающие и повторяющиеся десятичные дроби можно записать в виде дробей. Вы можете записать завершающую десятичную дробь 1,25 как 125/100 = 5/4. Повторяющееся десятичное число 0,3333 можно записать как 1/3.

Рациональные числа

Вы можете записывать рациональные числа в виде дроби. Слово «рациональный» происходит от слова «отношение», поскольку рациональные числа — это отношения двух целых чисел. Например, 0,7 — рациональное число, потому что его можно записать как 7/10. Другими примерами рациональных чисел являются -1/3, 2/5, 99/100, 1,57 и т.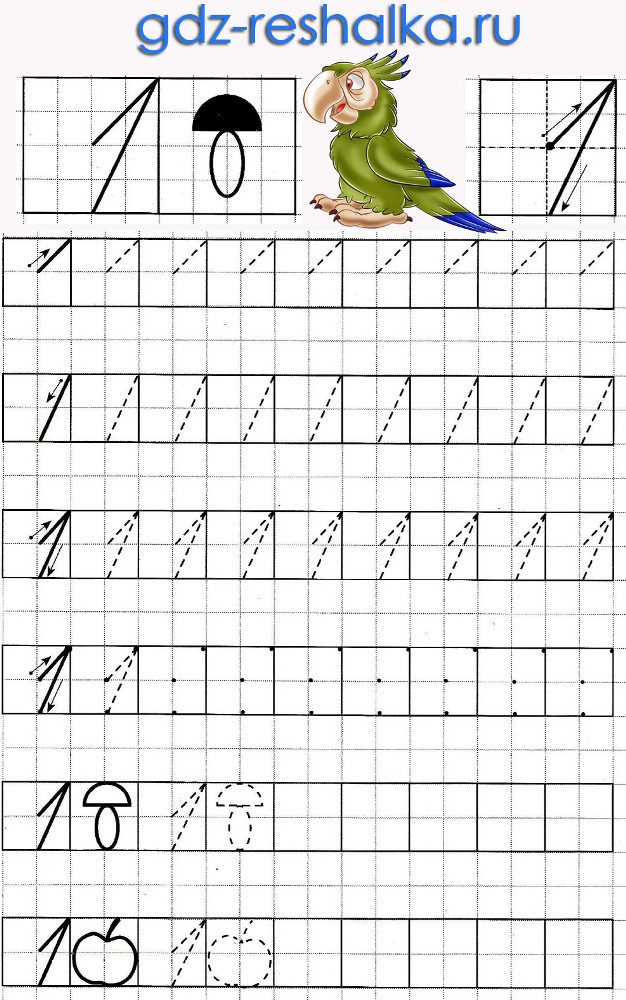 д.

Рассмотрим рациональное число p/q , где p и q — два целых числа. Здесь числитель p может быть любым целым числом (положительным или отрицательным), но знаменатель q никогда не может быть 0, так как дробь не определена. Кроме того, если q = 1, то дробь является целым числом.

Символ Q обозначает рациональные числа.

Иррациональные числа

Иррациональные числа нельзя записать в виде дроби, т. е. их нельзя записать в виде отношения двух целых чисел. Вот несколько примеров иррациональных чисел: √2, √5, 0,353535…, π и так далее. Вы можете видеть, что цифры в иррациональных числах продолжаются до бесконечности без повторяющегося шаблона.

Символ Q обозначает иррациональные числа.

Вещественные числа

Вещественные числа представляют собой совокупность всех рациональных и иррациональных чисел. Сюда входят все числа, которые можно записать в десятичной форме. Все целые числа являются действительными числами, но не все действительные числа являются целыми числами. Действительные числа включают в себя все целые числа, целые числа, дроби, повторяющиеся десятичные дроби, завершающие десятичные дроби и так далее.

Символ R представляет действительные числа.

Воображаемые числа

Числа, отличные от действительных чисел, являются мнимыми или комплексными числами. Когда мы возводим в квадрат мнимое число, он дает отрицательный результат, что означает, что это квадратный корень из отрицательного числа, например, √-2 и √-5. Когда мы возводим эти числа в квадрат, результаты равны -2 и -5. Квадратный корень из отрицательной единицы представлен буквой i , т.е.

i = √-1

Пример 1

Чему равен квадратный корень из -16? Запишите свой ответ в терминах воображаемого числа 9.0229 и .

Решение

• Шаг 1: Запишите форму квадратного корня.

√(-16)

• Шаг 2: Разделить -1.

√(16 × -1)

• Шаг 3: Разделение квадратных корней.

√(16) × √(-1)

• Шаг 4: Извлеките квадратный корень.

4 × √(-1)

• Шаг 5: Запишите в виде i.

4 i

Иногда вы получаете воображаемое решение уравнений.

Пример 2

Решите уравнение,

x ² + 2 = 0

Решение

• Шаг 1: Принимайте константу по другую сторону.

x ² = -2

• Шаг 2: Извлеките квадратный корень с обеих сторон.

√ х ² = +√-2 или -√-2

• Шаг 3: Решить.

x = √ (2) × √ (-1)

x = +√2 I или -√2 I

9
• Шаг 40230
  2
  • Шаг 4: arseging 40230 3
    2
    • . В исходном уравнении и посмотрите, получим ли мы 0.

    x ² + 2

    ( + √2 I ) ² + 2 = -2 + 2 = 0 (как I . = √-1 и квадрат I IS -1)

    (-,2 I ) ² + 2 = -2 + 2 = 0 (AS I = √ -1 и квадрат I IS -1)

    То, что их имя «воображаемое», не означает, что они бесполезны. У них много приложений. Одним из величайших применений мнимых чисел является их использование в электрических цепях. Расчеты тока и напряжения выполняются в терминах мнимых чисел. Эти числа также используются в сложных математических вычислениях. В некоторых местах мнимое число также представлено буквой 9.0229 Дж .

    Комплексные числа

    Мнимое число объединяется с действительным числом для получения комплексного числа. Он представлен как a + bi , где действительная часть и b являются комплексной частью комплексного числа. Действительные числа лежат на числовой прямой, а комплексные — на двумерной плоской плоскости.

    Как и мнимые числа, комплексные числа тоже не бесполезны. Они используются во многих приложениях, таких как «Сигналы и системы» и «Преобразование Фурье».

    Простые и составные числа

    Простые и составные числа противоположны друг другу. Простые числа — это тип целых чисел без делителей, кроме самих себя и 1, например, 2, 3, 5, 7 и так далее. Число 4 не является простым числом, потому что оно делится на 2. Точно так же 12 также не является простым числом, потому что оно делится на 2, 3 и 4. Таким образом, 4 и 12 являются примерами составных чисел.

    Трансцендентные числа

    Числа, которые никогда не могут быть нулем (или корнем) полиномиального уравнения с рациональными коэффициентами, называются трансцендентными числами. Не все иррациональные числа являются трансцендентными числами, но все трансцендентные числа являются иррациональными числами.

    Классификация чисел

    Семейство чисел, которое мы видели выше, также может быть отнесено к разным категориям. Это похоже на то, что в семье 20 человек, но они живут в двух общих семейных домах по 10 человек в каждом, что означает, что 10 человек живут в одном доме. Мы можем сказать, что два или более типов чисел могут подпадать под одну категорию.

    Дискретные и непрерывные числа

    Типы счетных чисел называются дискретными числами, а типы чисел, которые нельзя посчитать, называются непрерывными числами. Все натуральные числа, целые числа, целые числа и рациональные числа дискретны. Это связано с тем, что каждое их множество счетно. Множество действительных чисел слишком велико и не может быть сосчитано, поэтому оно классифицируется как непрерывное число. Если мы случайным образом возьмем два ближайших действительных числа, между ними все равно будет бесконечно больше действительных чисел; следовательно, их нельзя сосчитать.

    Наборы чисел

    Числа также можно классифицировать в виде наборов. Каждый тип числа является подмножеством другого типа числа. Например, натуральные числа являются подмножеством целых чисел. Точно так же целые числа являются подмножеством целых чисел. Множество рациональных чисел содержит все целые числа и дроби.