Примеры в столбик по математике 2 класс: сложение и вычитание чисел до 10, до 20, до 50, до 100, десятков, сотен, однозначных, двузначных и трехзначных чисел в столбик, задачи с ответами. Скачать в pdf, онлайн, бесплатно. Повторение.

Карточки “Решение примеров в столбик” 2 класс

Ф.И._________________________________________________ вариант – 1

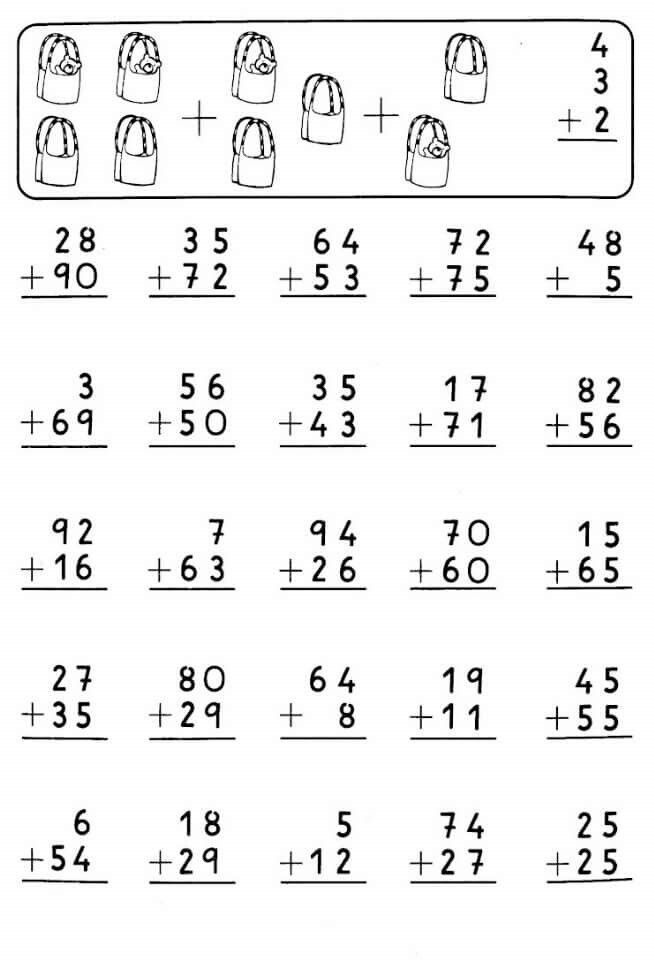
Решите примеры, записывая их столбиком

98 – 43 54 + 25 27 – 4 34 +2

52 +36 67 – 21 26 +70 48 – 24

Ф.И._________________________________________________ вариант – 2

Решите примеры, записывая их столбиком

48 +50 86 – 43 24 + 35 47 – 4

50 + 17 35 – 13 56 + 3 86 – 25

Ф.И._________________________________________________ вариант – 3

Решите примеры, записывая их столбиком

56 + 4 63 + 7 44 +6 75 + 5

31 + 9 52 +8 58 + 2 47 +3

Ф.И._________________________________________________ вариант – 4

Решите примеры, записывая их столбиком

52 +8 57 + 3 25 +5 77 +3

28 +2 64 + 6 36 +4 61 +9

Ф.И._________________________________________________ вариант – 5

Решите примеры, записывая их столбиком

52 +18 57 + 23 25 +65 77 +13

28 +42 64 + 16 36 +54 61 +29

Ф.И._________________________________________________ вариант – 6

Решите примеры, записывая их столбиком

56 + 24 63 + 27 44 +26 75 + 15

31 + 49 52 +38 58 +32 47 + 43

Ф. И._________________________________________________ вариант – 7

Решите примеры, записывая их столбиком

70 – 4 80 – 6 40 – 5 30 – 7

20 – 8 50 – 3 60 – 9 90 – 2

Ф.И._________________________________________________ вариант – 8

Решите примеры, записывая их столбиком

70 – 8 80 – 9 40 – 3 30 – 2

20 – 5 50 – 4 60 – 6 90 – 7

Ф.И._________________________________________________ вариант – 9

Решите примеры, записывая их столбиком

70 – 54 80 – 66 40 – 35 30 – 17

20 – 18 50 – 23 60 – 49 90 –52

Ф.И._________________________________________________ вариант – 10

Решите примеры, записывая их столбиком

70 – 54 80 – 56 40 – 25 30 – 27

20 – 18 50 –33 60 – 39 90 – 62

Ф.И._________________________________________________ вариант – 11

Решите примеры, записывая их столбиком

77 +16 35 + 48 27 + 34 34 +38

43 +29 15 + 29 56 + 37 53 + 17

Ф.И._________________________________________________ вариант – 12

Решите примеры, записывая их столбиком

67 +16 25 + 48 47 + 34 54 +38

53 +29 15 + 49 56 + 27 63 +17

Ф.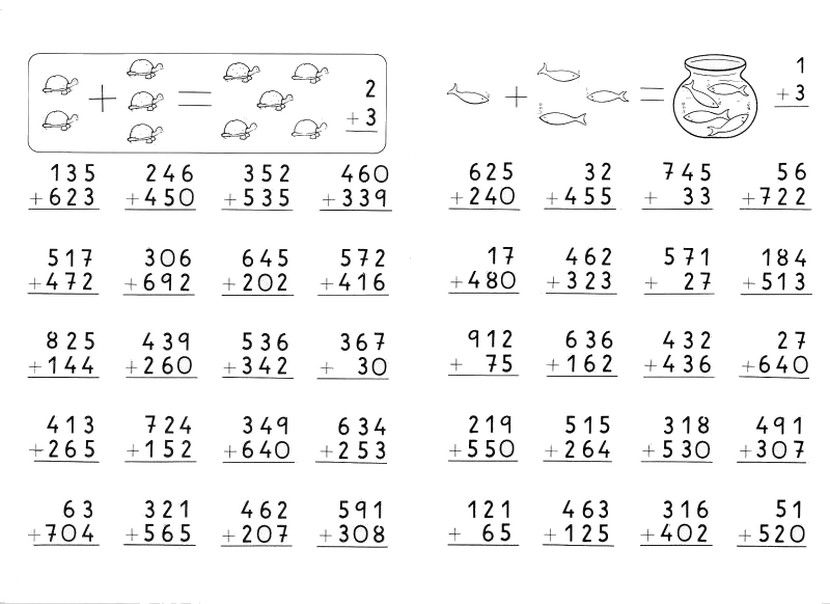 И._________________________________________________ вариант – 13

Решите примеры, записывая их столбиком

54 – 28 84 – 27 65 – 29 45 – 16

53 – 29 67 – 38 56 – 27 63 – 17

Ф.И._________________________________________________ вариант – 14

Решите примеры, записывая их столбиком

38 – 19 95 – 47 53 – 36 44 – 36

63 – 17 42 – 25 87 – 58 61 – 33

Ф.И._________________________________________________ вариант – 15

Решите примеры, записывая их столбиком

45 +31 80 – 24 45 – 37 34 + 57 50 – 4 56 +47 63 +24 60 – 21

54 +28 73 – 64 26 +57 50 – 8 70 – 46 38 +27 70 – 15 45 +57

Ф.И._________________________________________________ вариант – 16

Решите примеры, записывая их столбиком

45 +34 80 – 28 45 – 39 34 + 56 50 – 5 56 +49 63 +24 60 – 23

55 +28 72 – 64 28 +57 50 – 6 70 – 36 39 +27 70 – 17 45 +56

Ф.И._________________________________________________

Решите примеры, записывая их столбиком

50 – 7 +22 70 – 8 +36 76 – 23 +42

38 +12 – 9 84 – 34 – 18 98 – 18 – 15

«3000 примеров по математике с ответами и методическими рекомендациями.

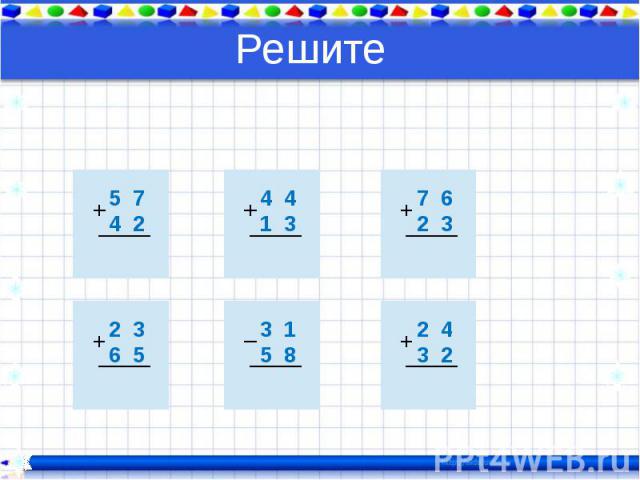Решаем в столбик. 2 класс» Узорова Ольга Васильевна, Нефедова Елена Алексеевна – описание книги | 3000 примеров для начальной школы с ответами

3000 примеров по математике с ответами и методическими рекомендациями. Решаем в столбик. 2 класс

Узорова Ольга Васильевна, Нефедова Елена Алексеевна

Foreign rights >>

ISBN 978-5-17-117070-7
Последний тираж: 20.03.2020 г.

Аннотация

Пособие содержит примеры на сложение и вычитание в столбик. При составлении пособия соблюдалась принятая в классической начальной школе методическая последовательность в отборе и системе расположения заданий. Примеры распределены по работам, каждая из которых дополнена работой над ошибками.
В конце пособия даны ответы.
Книга будет полезна для коллективной и индивидуальной работы на уроке и самостоятельных занятий дома.

Случайная новинка

Отзывы читателей

Характеристики

Автор:

Узорова Ольга Васильевна, Нефедова Елена Алексеевна

Редакция:

Малыш

Серия:

3000 примеров для начальной школы с ответами

ISBN:

978-5-17-117070-7

Ниша:

УЧЕБНАЯ ЛИТЕРАТУРА ДЛЯ НАЧАЛЬНОЙ ШКОЛЫ (1-4 КЛ)

Вес (кг):

0. 065

Переплет:

Мягкий

Страниц:

24

Ширина (мм):

210

Высота (мм):

280

Дата последнего тиража:

20.03.2020 г.

Бумага:

Бумага писчая 60/65

ББК:

22.1я71

УДК:

373:51

Знак информационной продукции:

6+

Смотрите также

Смотрите также

Вы просматривали

Вы просматривали

Мы в социальных сетях

Мы в соцсетях

@izdatelstvoast

---

Новости, новинки,
подборки и рекомендации

Введите вашу почту

* Введите текст жалобы*

Спасибо за обращение!

Ваша жалоба будет рассмотрена в самое ближайшее время.

Введите вашу почту* Как к Вам обращаться* Введите пароль*

Спасибо за регистрацию!

На указанный E-mail придёт запрос на подтверждение регистрации.

Введите вашу почту*

Отлично!

Письмо с информацией о смене пароля было отправлено на ваш E-mail.

Иллюстративная математика

Иллюстративная математика

Класс 2

2 класс

2.ОА. 2 класс – Операции и алгебраическое мышление

2.ОА.А. Представлять и решать задачи на сложение и вычитание.

2.ОА.А.1. Используйте сложение и вычитание в пределах 100 для решения одно- и двухшаговых задач со словами, включающих ситуации сложения, взятия, сложения, разъединения и сравнения с неизвестными во всех позициях, например, с помощью рисунков и уравнений с символом для неизвестного числа, представляющего проблему. См. Глоссарий, Таблица 1.

• Карандаш и наклейка
• Экономия денег 2

2.ОА.Б. Сложите и вычтите в пределах 20.



2.ОА.Б.2. Свободно складывать и вычитать в пределах 20, используя умственные стратегии. Список умственных стратегий см. в стандарте 1.OA.6. К концу 2 класса знать наизусть все суммы двух однозначных чисел.

• Стремление к беглости
• Удар по целевому номеру

2.ОА.С. Работайте с равными группами объектов, чтобы получить основу для умножения.

• Запоздалое признание

2.ОА.С.3. Определите, имеет ли группа объектов (до 20) нечетное или четное количество членов, например, путем объединения объектов в пары или подсчета их по 2; Напишите уравнение, выражающее четное число в виде суммы двух равных слагаемых.

• Кнопки нечетные и четные
• Красные и синие плитки

2.ОА.С.4. Используйте сложение, чтобы найти общее количество объектов, расположенных в прямоугольных массивах до 5 строк и до 5 столбцов; напишите уравнение, выражающее сумму в виде суммы равных слагаемых.


• Подсчет точек в массивах
• Разбиение прямоугольника на единичные квадраты

2.НБТ. 2 класс – Числа и операции с основанием десять

2.НБТ.А. Поймите значение места.

2.НБТ.А.1. Поймите, что три цифры трехзначного числа представляют количество сотен, десятков и единиц; например, 706 равно 7 сотням, 0 десяткам и 6 единицам. Под особыми случаями следует понимать следующее:

• Коробки и коробки карандашей
• Объединение и разделение
• Подсчет марок
• Игра с наибольшим числом
• Глядя на числа в любом направлении
• Изготовление 124
• Один, десять и сто больше и меньше
• Перегруппировка
• Десять 10 долларов составляют 100 долларов.
• Три задачи на композицию/декомпозицию

2.НБТ.А.1.б. Числа 100, 200, 300, 400, 500, 600, 700, 800, 900 относятся к одной, двум, трем, четырем, пяти, шести, семи, восьми или девяти сотням (и 0 десяткам и 0 единицам).


• Пока нет задач, иллюстрирующих этот стандарт.

2.НБТ.А.2. Считать в пределах 1000; пропуск счета на 5, 10 и 100 секунд.

• Экономия денег 2

2.НБТ.А.3. Читать и записывать числа до 1000, используя десятичные числа, имена чисел и расширенную форму.

• Глядя на числа в любом направлении

2.НБТ.А.4. Сравните два трехзначных числа на основе значений цифр сотен, десятков и единиц, используя символы $>$, = и $

<$ для записи результатов сравнения.
• Сравнения 1
• Сравнения 2
• Цифры 2-5-7
• Сравнение числовых строк
• Заказ 3-значных номеров
• Использование изображений для объяснения сравнения чисел

2.НБТ.Б. Используйте понимание значения разряда и свойства операций сложения и вычитания.

2.НБТ.Б.5. Свободно складывать и вычитать в пределах 100, используя стратегии, основанные на разрядности, свойствах операций и/или связи между сложением и вычитанием.


• Форд и Логан Добавляют 45+36
• Банка пенни Джамира
• Экономия денег 1
• Экономия денег 2

2.НБТ.Б.6. Сложите до четырех двузначных чисел, используя стратегии, основанные на разрядности и свойствах операций.

• Головоломка с платным мостом

2.НБТ.Б.7. Складывать и вычитать в пределах 1000, используя конкретные модели или чертежи и стратегии, основанные на позиционном значении, свойствах операций и/или отношениях между сложением и вычитанием; связать стратегию с письменным методом. Поймите, что при сложении или вычитании трехзначных чисел добавляются или вычитаются сотни и сотни, десятки и десятки, единицы и единицы; а иногда надо составить или разложить десятки или сотни.

• Сколько дней до летних каникул?
• Много способов сделать дополнение 2
• Пейтон и Пресли обсуждают дополнение

2.НБТ.Б.8. Мысленно прибавьте 10 или 100 к заданному числу 100–900 и мысленно вычтите 10 или 100 из заданного числа 100–900.


• Хоровой счет

2.НБТ.Б.9. Объясните, почему стратегии сложения и вычитания работают, используя позиционное значение и свойства операций. Объяснения могут быть подкреплены рисунками или предметами.

• Пейтон и Пресли обсуждают дополнение

2.МД. 2 класс – Измерения и данные

2.МД.А. Измерьте и оцените длину в стандартных единицах.

• Насколько велик фут?

2.МД.А.1. Измерьте длину объекта, выбрав и используя соответствующие инструменты, такие как линейки, линейки, измерительные рейки и измерительные ленты.

• Определение длины

2.МД.А.2. Дважды измерьте длину объекта, используя для двух измерений единицы длины разной длины; опишите, как два измерения соотносятся с размером выбранной единицы измерения.

• Пока нет задач, иллюстрирующих этот стандарт.

2.

МД.А.3. Оцените длину, используя единицы измерения: дюймы, футы, сантиметры и метры.
• Определение длины

2.МД.А.4. Измерьте, чтобы определить, насколько длиннее один объект, чем другой, выражая разницу в длине с точки зрения стандартной единицы длины.

• Определение длины

2.МД.Б. Свяжите сложение и вычитание с длиной.

2.МД.Б.5. Используйте сложение и вычитание в пределах 100 для решения текстовых задач с длинами, заданными в одних и тех же единицах, например, с помощью рисунков (например, рисунков линеек) и уравнений с символом неизвестного числа для представления задачи.

• Соревнования по прыжкам в высоту

2.МД.Б.6. Представляйте целые числа как длины от 0 на диаграмме числовых линий с равноотстоящими точками, соответствующими числам 0, 1, 2, …, и представляйте суммы и разности целых чисел в пределах 100 на диаграмме числовых линий.


• Лягушка и жаба на числовой прямой

2.МД.К. Работа со временем и деньгами.

• Запоздалое признание

2.MD.C.7. Говорите и записывайте время по аналоговым и цифровым часам с точностью до ближайших пяти минут, используя время до и после полудня.

• Время заказа

2.MD.C.8. Решайте словесные задачи с участием долларовых банкнот, четвертаков, десятицентовиков, пятицентовых монет и пенни, используя соответствующие символы \$ и $¢$. Пример: Если у вас есть 2 цента и 3 пенни, сколько у вас центов?

• Александр, который был богат в прошлое воскресенье
• Выбор, выбор, выбор
• Банка пенни Джамира
• Зоомагазин
• Экономия денег 1
• Выбор Сьюзен
• Посещение Аркады

2.МД.Д. Представлять и интерпретировать данные.

2.МД.Д.9. Генерируйте данные измерений, измеряя длины нескольких объектов с точностью до целой единицы или выполняя повторные измерения одного и того же объекта.

Покажите измерения, построив линейный график, где горизонтальная шкала отмечена в целых числах.
• Выращивание бобовых растений
• Измерения размаха рук
• Самая длинная прогулка

2.МД.Д.10. Нарисуйте графическое изображение и столбчатую диаграмму (с единичной шкалой), чтобы представить набор данных с четырьмя категориями. Решайте простые задачи на сборку, разборку и сравнение См. Глоссарий, Таблицу 1, используя информацию, представленную в виде гистограммы.

• Любимый вкус мороженого

2.Г. 2 класс – Геометрия

2.Г.А. Рассуждайте о формах и их атрибутах.

2.Г.А.1. Распознавать и рисовать фигуры, имеющие определенные атрибуты, такие как заданное количество углов или заданное количество равных граней. Размеры сравниваются непосредственно или визуально, а не путем измерения. Определите треугольники, четырехугольники, пятиугольники, шестиугольники и кубы.


• Полигоны

2.Г.А.2. Разделите прямоугольник на строки и столбцы квадратов одинакового размера и посчитайте, чтобы найти их общее количество.

• Разбиение прямоугольника на единичные квадраты

2.Г.А.3. Разделите круги и прямоугольники на две, три или четыре равные доли, опишите доли, используя слова

половин , третей , половину , треть и т. д., и опишите целое как две половины, три трети, четыре четверти. Признайте, что равные части одинаковых целых не обязательно должны иметь одинаковую форму.
• Представление половины прямоугольника
• Какие картинки представляют одну половину?

Grade 5, Mr. Porr / Math Vocabulary

 

 

 

 

 

 

Math Glossary

Algorithm – a set of step-by-step instructions for doing something, such as carrying вычисление или решение проблемы.

Угол – фигура, образованная двумя лучами или двумя отрезками, имеющими один конец

Площадь – количество поверхности внутри фигуры. Площадь измеряется в квадратных единицах, таких как квадратные дюймы или квадратные сантиметры.

Массив – расположение объектов в строки и столбцы, образующие прямоугольник. Все строки и столбцы должны быть заполнены. Каждая строка и столбец должны быть заполнены. Каждая строка имеет одинаковое количество объектов, и каждый столбец имеет одинаковое количество объектов.

Гистограмма — диаграмма, в которой для представления данных используются горизонтальные или вертикальные полосы.

Base — имя, используемое для стороны многоугольника или грани трехмерной фигуры.

Вместимость – (1) количество, которое может вместить контейнер. Объем контейнера. Емкость обычно измеряется в таких единицах, как галлоны, пинты, чашки и литры. (2) Максимальный вес, который могут измерить весы.

История количества изменений – история чисел, в которой сумма увеличивается (история изменения на большее количество) или уменьшается (история изменения на меньшее). Диаграмма изменений может использоваться для отслеживания чисел и отсутствующей информации в таких задачах.

Окружность – расстояние по окружности; периметр круга.

История числа сравнения – история числа, в которой сравниваются две величины. Сравнительную диаграмму можно использовать для отслеживания чисел и отсутствующей информации в таких задачах.

Составное число – счетное число, имеющее более двух различных множителей. Например, 4 — составное число, потому что оно имеет три делителя: 1, 2 и 4.

Конус — твердое тело, имеющее круглое основание и криволинейную поверхность, которая заканчивается в точке, называемой вершиной.

Конгруэнтные фигуры – фигуры, имеющие одинаковую форму и одинаковый размер. Две фигуры на плоской поверхности конгруэнтны, если они точно совпадают, когда одна находится поверх другой.

Координатная сетка – сетка, образованная путем рисования двух числовых линий, образующих прямые углы. Числовые линии пересекаются в своих нулевых точках. Вы можете использовать упорядоченные пары чисел, чтобы найти точки на сетке. (Числа в каждой паре называются координатами.) Карты часто основаны на координатных сетках.

Координаты – см. заказанную пару

Счетные числа- числа используемые при счете 1,2,3,4 и так далее. Ноль иногда считают счетным числом.

Цилиндр – твердое тело, имеющее два параллельных основания одинакового размера. Основания соединены криволинейной поверхностью. Суповая банка имеет форму цилиндра.

Данные – информация, которая собирается путем подсчета, измерения, вопросов или наблюдения.

Десятичный — число, например 23,4, содержащее десятичную точку. Денежные суммы, такие как 6,58 долларов США, представляют собой десятичные числа. Десятичная точка в деньгах отделяет доллары от центов.

Десятичная точка – точка, используемая для отделения единиц от десятых в десятичных числах.

Градус – (1) единица измерения углов. (2) Единица измерения температуры. В обоих случаях для обозначения градусов используется небольшой выпуклый кружок.

Знаменатель – число под чертой в дроби. Например, в ¾ знаменатель равен 4.

Диаметр – (1) Отрезок, проходящий через центр окружности и имеющий концы на окружности. (2) Длина этого сегмента линии. Точно так же определяется диаметр шара. Диаметр круга или сферы в два раза больше длины его радиуса.

Цифры – символы 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, которые используются для записи любого числа в нашей системе счисления.

Ребро – отрезок линии или кривая, где сходятся поверхности твердого тела.

Конечная точка – точка в конце отрезка или луча. Отрезок линии именуется с помощью буквенных обозначений его конечных точек. Луч называется с использованием буквенных меток его конечной точки и другой точки на луче.

Равные группы – коллекции или группы вещей, содержащие одинаковое количество вещей. Например, ряды стульев по 6 стульев в ряду представляют собой равные группы.

Равносторонний треугольник – треугольник, у которого все три стороны равны по длине. В равностороннем треугольнике все три угла имеют одинаковую величину.

Эквивалентные имена – разные способы наименования одного и того же числа

Оценка – ответ, который должен быть близок к точному ответу. Оценить — значит дать ответ, который должен быть близок к точному ответу.

Четное число – счетное число, которое можно разделить на 2 без остатка. Четные числа 2,4,6,8 и так далее.

Событие — то, что происходит. Подбрасывание монеты орлом – событие. Выпадение на кубике числа меньше 5 является событием. Вероятность события – это вероятность того, что событие произойдет.

Исследования – В повседневных занятиях по математике с первого по третий класс независимые занятия или занятия в малых группах, направленные на одно или несколько из следующих действий: разработка концепций, манипуляции, сбор данных, решение задач, игры и проверка навыков.

Грань – плоская поверхность снаружи твердого тела.

Семейство фактов – (1) набор связанных фактов сложения и вычитания. Например, 5+6=11, 6+5=11, 11-5=6 и 11-6=5 являются семейством фактов. (2) Набор связанных граней умножения и деления.

Треугольники фактов – карточки в форме треугольника, на которых показаны семейства фактов. Треугольники фактов используются как карточки для запоминания основных фактов сложения, вычитания, умножения и деления.

Фактор – (1) любое из чисел, умноженных для получения произведения. (2) Число, которое делится нацело на другое число.

Таблица фактов — диаграмма со строками и столбцами, которая показывает все основные факты сложения и вычитания или все основные факты умножения и деления.

Дробь – число в виде ½. Число 1 называется числителем и может быть любым счетным числом или 0, а число 2 называется знаменателем и может быть любым счетным числом, кроме 0. Дроби можно использовать для обозначения части целого или части набора.

Рамки и стрелки — Диаграмма, используемая в математике на каждый день для отображения последовательности числовых шаблонов.

Функциональная машина — воображаемая машина, используемая в повседневной математике для изменения чисел в соответствии с заданным правилом.

Решечный метод – один из методов решения задач на умножение.

Линейный график — график, использующий линейные сегменты для соединения точек данных. Линейные графики часто используются, чтобы показать, как что-то изменилось за определенный период времени.

Линейный график — эскиз данных, в котором используются крестики, галочки или другие метки над числовой линией, чтобы показать, сколько раз каждое значение появляется в наборе данных.

Отрезок – прямой путь, соединяющий две точки. Две точки называются конечными точками отрезка.

Линейная симметрия – фигура имеет линейную симметрию, если линия может разделить ее на две части, которые выглядят как зеркальные отражения друг друга. Две части выглядят одинаково, но обращены в противоположные стороны. Линия раздела называется линией симметрии.

Математические ящики – Сборник задач по математике на каждый день для отработки навыков. Математические ящики для каждого урока находятся в математическом журнале.

Математическое сообщение — вводное задание по математике на каждый день, которое дети выполняют перед началом урока.

Максимум – наибольшая сумма. Самое большое число в наборе данных.

Среднее – среднее число в наборе данных. Среднее значение находится путем сложения всех значений данных и последующего деления на количество чисел в наборе данных.

Медиана – среднее число в наборе данных, когда числа расположены в порядке от наименьшего к наибольшему или от наибольшего к наименьшему. Медиана также известна как среднее число или среднее значение.

Метрическая система – система измерения, которая используется учеными повсеместно, причем в большинстве стран мира, кроме США. Метрическая система – это десятичная система. Он основан на кратности 10.

Минимум – наименьшая сумма. Наименьшее число в наборе данных.

Режим — число или значение, которое чаще всего встречается в наборе данных.

Ящик для сбора имен — в программе Everyday Mathematics, место для написания эквивалентных имен для одного и того же числа.

Отрицательное число – число меньше нуля. Число слева от нуля на горизонтальной числовой прямой. Число ниже нуля на вертикальной числовой прямой. Символ- может использоваться для записи отрицательного числа. Например, «минус 5» обычно записывается как -5.

Числовая сетка — таблица со строками и столбцами, в которой числа перечислены по порядку. Ежемесячный календарь представляет собой числовую сетку.

Номерная строка – строка с нанесенными на ней по порядку номерами.

Модель числа – группа чисел и символов, показывающая, как можно решить числовую историю. Например, 10-6=4 и 10-6 являются числовыми моделями для следующей истории: У меня было 10 печенек. Я отдал 6. Сколько у меня осталось?

Числитель – число над чертой в дроби. Например, в ¾ числитель 3.

Нечетное число — счетное число, которое нельзя точно разделить на 2. При делении нечетного числа на 2 в остатке 1. Нечетные числа — это 1, 3, 5 и т. д.

Упорядоченная пара – пара чисел, например (5, 3) или (1, 4), используемая для поиска местоположения на координатной сетке. Числа в упорядоченной паре называются координатами.

Параллельный – Всегда на одинаковом расстоянии друг от друга и никогда не встречаются и не пересекаются друг с другом, независимо от того, насколько далеко они простираются. Отрезки параллельны, если они являются частями параллельных прямых. Основания призмы параллельны. Основания цилиндра параллельны.

Параллелограмм – 4-сторонний многоугольник, противоположные стороны которого параллельны. Противоположные стороны параллелограмма также имеют одинаковую длину. И наоборот такой же длины. А противоположные углы в параллелограмме имеют одинаковую величину.

Метод частных произведений – один из методов решения задач на умножение.

Метод частных сумм – один метод решения задач на сложение

Рассказ о частях и сумме – Рассказ о числах, в котором две части объединяются для нахождения суммы. Диаграмма частей и общего может использоваться для отслеживания чисел и недостающей информации в таких задачах.

Шаблон для выкройки — Математика на каждый день с первого по третий класс, лист пластика с вырезанными геометрическими фигурами, используемый для рисования узоров и дизайна.

Процент – за сотню, за каждую сотню или из сотни.

Периметр – расстояние вокруг многоугольника или другой формы. Периметр круга называется окружностью.

Пиктограмма — график, использующий изображения или символы для отображения чисел. Ключ для пиктограммы говорит, сколько стоит каждое изображение или символ.

Разрядное значение – система записи чисел, в которой значение цифры зависит от ее места в числе

Многоугольник – замкнутая фигура на плоской поверхности, состоящая из отрезков, соединенных встык. Отрезки составляют один замкнутый путь и не могут пересекаться.

Многогранник – твердое тело, все поверхности (называемые гранями) плоские и образованные многоугольниками. Многогранник не имеет искривленных поверхностей

Положительное число – число больше нуля. Число справа от нуля на горизонтальной числовой строке. Число выше нуля на вертикальной числовой прямой. Положительное число может быть записано с помощью символа +, но обычно пишется без него

Простое число – счетное число, которое имеет ровно два различных делителя, являющихся счетными числами: само себя и 1. Например, 5 является простым числом, потому что его единственными делителями являются 5 и 1. Число 1 не является простым числом. потому что это число имеет только один делитель, само число 1.

Призма – многогранник, имеющий два параллельных основания, образованных многоугольниками одинакового размера и формы. Остальные грани соединяют основания и имеют форму параллелограмма. Эти другие грани часто представляют собой прямоугольники. Призмы получили свое название из-за формы основания.

Вероятность – число от 0 до 1, указывающее вероятность того, что событие произойдет. Чем ближе вероятность к 1; тем более вероятно, что произойдет событие

Произведение – результат умножения двух чисел, называемых множителями.

Пирамида – многогранник, одна грань которого, основание, может иметь любую форму многоугольника. Все остальные грани имеют треугольную форму и сходятся в вершине, называемой вершиной. Пирамида получила свое название из-за формы основания.

Четырехугольник – многоугольник, имеющий четыре угла. То же, что четырехугольник.

Четырехугольник – многоугольник, имеющий четыре стороны. То же, что четырехугольник.

Частное – результат деления одного числа на другое число.

Радиус (множественное число: радиусы ) – (1) Отрезок прямой от центра круга до любой точки на круге. (2) Длина этого сегмента линии. Точно так же определяется радиус сферы. Радиус круга или сферы равен половине длины его диаметра.

Диапазон – разница между наибольшим (максимальным) и наименьшим (минимальным) числом в наборе данных.

Луч – прямой путь, который имеет одну конечную точку и продолжается вечно в одном направлении.

Правильный многоугольник – многоугольник, все стороны которого имеют одинаковую длину и все углы (внутри многоугольника) имеют одинаковый размер

Остаток – сумма, оставшаяся после деления или деления вещей поровну. Иногда остатка нет.

Ромб – параллелограмм, у которого все четыре стороны одинаковой длины. Каждый квадрат является ромбом, но не все ромбы являются квадратами.

Прямые углы – угол 90 градусов. Стороны прямого угла из прямоугольного угла.

Прямоугольный треугольник – треугольник, у которого один угол равен 90 градусов.

Round – для корректировки числа, чтобы с ним было удобнее работать. Часто числа округляются до ближайших 10, 100, 1000 и так далее. Например, 864, округленное до ближайшей сотни, равно 9.00

Чертеж в масштабе — рисунок, представляющий реальный объект или область, но другого размера. Карты представляют собой чертежи в масштабе. Архитекторы и строители используют чертежи в масштабе.

Сторона – (1) Один из лучей или сегментов, составляющих угол. (2) Один из отрезков многоугольника. (3) Одна из граней объемной фигуры.

Твердые тела – трехмерные формы, такие как призмы, пирамиды, цилиндры, конусы и сферы.

Стандартные блоки- единицы измерения, которые имеют одинаковый размер независимо от того, кто их использует, когда и где они используются.

3-мерный (3-D) – имеющий длину, ширину и толщину. Твердые объекты, занимающие пространство, такие как мячи, камни, коробки и книги, являются трехмерными.

Метод Trade-first – один из методов решения задач на вычитание

Трапеция – 4-сторонний многоугольник, имеющий ровно одну пару параллельных сторон.

Оборотные факты — числа можно складывать или умножать в любом порядке. 3+5=8 и 5+3=8 являются фактами сложения с оборотом. 4×5=20 и 5×5=20 – факты обратного умножения. Обратных фактов для вычитания и деления нет, если числа разные.

2-мерный (2-D)- Имеющий длину и ширину, но не толщину.