Примеры уравнения 4 класс: Сложные уравнения. 4 класс
Решаем примеры и уравнения. 4 класс (Елизавета Коротяева)
180 ₽
+ до 27 баллов
Бонусная программа
Итоговая сумма бонусов может отличаться от указанной, если к заказу будут применены скидки.
Офлайн
Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.
В наличии в 9 магазинах. Смотреть на карте
Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.
Пособие «Решаем примеры и уравнения. 4 класс» предназначено для самостоятельной работы учащихся. Каждый раздел четко структурирован: он содержит правила, образцы выполненных заданий различных типов, предусмотренных программой по математике для начальной школы, и упражнения для отработки практических навыков. В книге размещены ключи ко всем заданиям. .
.Издание предназначено для учеников младших классов, их родителей и учителей.
.
.Издание предназначено для учеников младших классов, их родителей и учителей.
Описание
Характеристики
Пособие «Решаем примеры и уравнения. 4 класс» предназначено для самостоятельной работы учащихся. Каждый раздел четко структурирован: он содержит правила, образцы выполненных заданий различных типов, предусмотренных программой по математике для начальной школы, и упражнения для отработки практических навыков. В книге размещены ключи ко всем заданиям. . .Издание предназначено для учеников младших классов, их родителей и учителей.
Феникс
На товар пока нет отзывов
Поделитесь своим мнением раньше всех
Как получить бонусы за отзыв о товаре
1
Сделайте заказ в интернет-магазине
2
Напишите развёрнутый отзыв от 300 символов только на то, что вы купили
3
Дождитесь, пока отзыв опубликуют.
Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.
Правила начисления бонусов
Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.
Правила начисления бонусов
Книга «Решаем примеры и уравнения. 4 класс» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене.
Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом
другом регионе России, вы можете оформить заказ на книгу
Елизавета Коротяева
«Решаем примеры и уравнения.
Решение уравнений 6 класс онлайн-подготовка на Ростелеком Лицей
Решение уравнений
Уравнение, которое можно привести к виду ax = b, где a и b − некоторые числа
(a≠0), называется линейным уравнением с одним неизвестным.
Рассмотрим решение уравнения:
4·(х-5) = 16 (1)
х-5 = 16:4
х-5 = 4 (2)
х = 9
Уравнение (2) можно получить из уравнения (1), разделив обе части уравнения на 4.
4(х-5)=16 |:4 (1) 9 – корень уравнения (1), так как
4(x-5)4=164 4(9-5) = 16 – верное равенство.
х-5 = 4 (2) 9 – корень уравнения (2), так как
9-5 = 4 – верное равенство.
Число 9 – это корень уравнения (1) и корень уравнения (2).
Сформулируем первое свойство уравнения.
Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю, и корни уравнения не изменятся.
Применим первое свойство к решению уравнения.
Пример 1. Решим уравнение 34x-98x=54-18.
Умножим обе части уравнения на 8. Тогда коэффициент перед x станет целым.
34x-98x = 54-18 |·8
3∙84x-9∙88x = 5∙84-1∙88
6x-9x = 10-1
-3x = 9
x = 9:(-3)
x = -3.
Пример 2. Решим уравнение 0,7x-0,2x = 5,5.
Умножим обе части уравнения на 10. Тогда коэффициенты перед x станут целыми.
0,7х-0,2х = 5,5 |·10
7х-2х = 55
5х = 55
x = 55:5
x = 11.
Пример 3. Решим уравнение -20x-50∙2 = 100.
Разделим обе части этого уравнения на 2.
(-20х-50)·2 = 10 |:2
-20х-50 = 50
-20х = 50+50
-20х = 100
x = 100:(-20)
x = -5.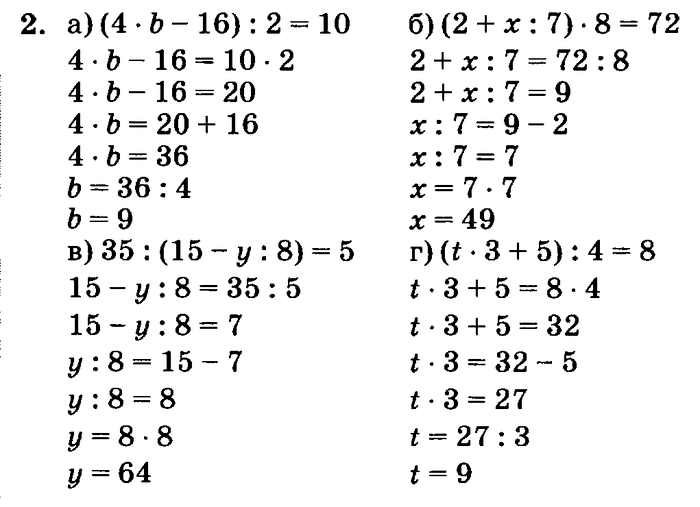
Пример 4. Решим уравнение 2,1∙4-6y = -42.
Разделим обе части равенства на 2,1.
2,1·(4-6у) = -4 |:2,1
4-6у = -20
-6у = -24
y = -24:(-6)
y = 4.
Пример 5. Решим уравнение 2х+5 = 17.
По правилу отыскания неизвестного слагаемого имеем 2х = 17-5; 2х = 12. Уравнения 2х+5 = 17 и 2х = 17-5 имеют один и тот же корень 6, т.к. 2·6+5 = 17 и 2·6 = 17-5.
Уравнение 2х = 17-5 можно записать так: 2х = 17+(-5).
Видим, что корень уравнения 2х+5 = 17 не изменяется, если перенести слагаемое 5 из левой части уравнения в правую, изменив его знак на противоположный.
Пример 6. Решим уравнение 5х = 2х+6.
Вычтем из правой и левой части равенства 2х.
5х-2х = 2х-2х+6
Или 5х-2х = 6
3х = 6
x = 2.
Уравнение 5х-2х = 6 можно получить из исходного, если слагаемое 2х перенести из правой части в левую, изменив его знак на противоположный.
Таким образом выполняется второе свойство уравнения:
Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом знак.
Пример 7. Решим уравнение 13x+12 = x.
Умножим левую и правую часть равенства на 3.
13x+12 = x |·3
x+36 = 3x
Перенесем с противоположными знаками слагаемое 36 из левой части в правую, а слагаемое 3х из правой части в левую.
x-3x = -36
-2x = -36
x = -36:(-2)
x = 18
Рассмотрим сложные примеры.
Пример 8. Решим уравнение 12∙8x-4-5 = 6∙13x+12.
Сначала раскроем скобки.
12∙8x-12∙4-5 = 6∙13x+6∙12
4x-2-5 = 2x+3
Перенесем слагаемые, которые содержат неизвестное, в левую часть, а известные слагаемые в правую часть.
4х-2х = 3+2+5
2х = 10
x = 5
Пример 9. Решим уравнение 7-x6 = 19x-118.
Воспользуемся основным свойством пропорции: произведение средних равно произведению крайних.
8·(7-х) = 6·(19х-11)
Раскроем скобки в левой и в правой части уравнения.
8·7-8·х = 6·19х-6·11
56-8х = 114х-66
Перенесем неизвестное влево, а известное вправо.
-8х-114х = -66-56
-122х = -122
x = 1
Решение уравнений — 9 класс
Представлены примеры для 9 класса с подробным пошаговым подходом к решению простых уравнений и уравнений со скобками и дробями. Также обсуждается проверка решений уравнения. Также включены дополнительные вопросы и их решения с подробными объяснениями.
Что такое уравнение и его решение?
Сначала мы рассмотрим концепцию уравнений и решение уравнения.
Уравнение — это выражение, выражающее равенство двух математических выражений. Уравнение имеет знак равенства, правостороннее выражение и левостороннее выражение.
Уравнение имеет знак равенства, правостороннее выражение и левостороннее выражение.
Пример 1
Это примеры уравнений с неизвестным \( x \)
\( \quad 2 x = – 6 \) , \( \quad x + 3 = 7 \) , \( \quad 2(x + 3) = – (2x+4) \)
В каждом уравнении есть знак равенства, разделяющий левую и правую части уравнения.
Левая часть уравнения \( \quad \color{red}{2 x – 6} = x + 5 \) равна \( \quad \color{red}{2 x – 6} \).
Правая часть уравнения \( \quad 2 x – 6 = \color{red}{x + 5} \) равна \( \quad \color{red}{x + 5} \).
Решением уравнения с неизвестным \(x\) является набор всех значений \(x\), которые делают уравнение верным утверждением.
Пример 2
Какое из следующих значений \( x \): \( – 4, 2\) является(ются) решением(ями) уравнения \( 2 x + 2 = x + 4 \)?
Решение примера 2
Замените \( x \) его числовым значением в левой и правой частях уравнения
а) Проверить \( \color{red}{x = – 4} \)
Оценить левую часть: \( 2 \color{red}x + 2 = 2 \color{red}{( – 4 )} + 2 = – 8 + 2 = – 6 \) ,
Оцените правую часть: \( \color{red}x + 4 = \color{red}{( – 4)} + 4 = 0 \)
Числовые значения левой и правой частей не равны, поэтому \( x = – 4 \) НЕ является решением уравнения \( 2 x + 2 = x + 4 \).
а) Проверить \( \color{red}{x = 2} \)
Оцените левую часть: \( 2 x + 2 = 2 \color{red}{(2 )} + 2 = 4 + 2 = 6 \) ,
Оцените правую часть: \( \color{red}x + 4 = \color{red}{(2)} + 4 = 6 \)
Числовые значения левой и правой сторон равны, поэтому \( x = 2 \) равно
Важные свойства для решения уравнений
Чтобы решить уравнение, нам нужны математические шаги, которые помогут получить все члены с неизвестными с одной стороны и постоянными с другой стороны.
Некоторые из наиболее важных свойств, используемых для решения уравнений, перечислены ниже.
1) Если мы прибавим или вычтем одну и ту же величину к обеим частям уравнения, мы получим уравнение, имеющее то же решение, что и исходное.
1) Если мы умножим или разделим обе части уравнения на одну и ту же величину, НЕ равную нулю, мы получим уравнение, имеющее то же решение, что и исходное.
Решение простых уравнений
Пример 3
Решите уравнение \( 2x + 1 = – 5 \) и проверьте полученное решение.
Решение примера 3
Основная идея состоит в том, чтобы все члены с неизвестным \( x \) с одной стороны и все постоянные члены с другой стороны уравнения
Оставим члены \( 2x \) слева, а постоянные члены – справа. Это можно сделать, вычитая \( 1 \) из обеих частей уравнения
Это можно сделать, вычитая \( 1 \) из обеих частей уравнения
Упростите, чтобы получить
\( \четверка \четверка 2x = – 6 \)
Чтобы получить \( x \) из \( 2x \), мы разделим обе части приведенного выше уравнения на 2
\( \quad \quad \dfrac{2 x}{\color{red}2} = \dfrac{-6}{\color{red}2} \)
Упростить
\( \квадратный \четверный х = -3 \)
Проверить решение, полученное в исходном (заданном) уравнении
Оценить левую часть уравнения для \( x = – 3 \) : \( \quad 2x + 1 = 2(-3) + 1 = – 5 \)
Оценить левую часть уравнения для \( x = – 3 \) : \( \quad – 5 \)
Левая и правая части равны \( – 5 \) для \( x = – 3 \), поэтому \( x = – 3 \) является решением данного уравнения.
Пример 4
Решите уравнение \( x – 2 – 3x = – 7 – x \) и проверьте полученное решение.
Решение примера 4
Сгруппируйте одинаковые члены в двух частях уравнения.
 \( x \) и \( – 3x \) подобны терминам в левой части и могут быть сгруппированы, чтобы дать
\( x \) и \( – 3x \) подобны терминам в левой части и могут быть сгруппированы, чтобы дать \( \четверка \четверка – 2х – 2 = – 7 – х \)
Добавьте \( 2 \) к обеим частям уравнения, чтобы исключить постоянные члены из левой части.
\( \quad \quad – 2x – 2 \color{red}{+ 2} = – 7 – x \color{red}{+ 2} \)
Упростить
\( \четверка \четверка – 2x = – x – 5 \)
Добавьте \( x \) к обеим частям уравнения, чтобы исключить члены с \( x \) из правой части.
\( \quad \quad – 2x \color{red}{+x } = – x – 5 \color{red}{+x }\)
Упростите, чтобы получить
\( \четверка \четверка – х = – 5 \)
Если мы знаем \( – x \) и нам нужно \( x \), мы умножаем обе части уравнения на \( – 1 \)
\( \quad \quad \color{red}{(-1)}(- x) = \color{red}{(-1)}(- 5) \)
Упростить
Проверить решение, полученное в исходном (заданном) уравнении
Левая часть уравнения для \( x = 5 \) : \( \quad x – 2 – 3x = 5 – 2 -3(5) = – 12 \)
Правая часть уравнения для \( x = 5 \) : \( \quad – 7 – x = – 7 – (5) = – 12 \)
Левая и правая части равны \( – 12 \) для \( x = 5 \), поэтому \( x = – 3 \) является решением данного уравнения.
Решение уравнений со скобками
Пример 5
Решите уравнение \( – 2 (x – 2) + 3 = 3 (-x + 4) – 3 \) и проверьте полученное решение.
Решение примера 5
Данное уравнение
\( \quad \quad \color{red}{- 2} (x – 2) + 3 = \color{red}3 (-x + 4) – 3 \)
Используйте распределительный закон: \( \quad a(b+c) = ab + ac \quad \), который является одним из основных правил алгебры, чтобы убрать скобки.
Распределите \(\color{red}{-2} \) и \(\color{red}3 \).
\( \quad \quad \color{red}{- 2} (x ) \color{red}{- 2} (- 2) + 3 = \color{red}3 (-x) + \color{red }3 (4) – 3 \)
Упростить
\( \quad \quad – 2 х + 4 + 3 = – 3 х + 12 – 3 \)
Сгруппируйте одинаковые члены в обеих частях уравнения.
\( \quad \quad – 2 x + 7 = – 3 x + 9 \)
Вычтите \( 7 \) из обеих частей уравнения, чтобы исключить постоянные члены из левой части уравнения.
\( \quad \quad – 2 x + 7 – 7 = – 3 x + 9 – 7 \)
Групповые термины
\( \квадратный \четверный – 2x = – 3x + 2 \)
Добавьте \( 3x \) к обеим частям уравнения, чтобы исключить члены в \( x \) из левой правой части уравнения.
\( \quad \quad – 2x + 3 x = – 3x + 2 + 3x \)
Сгруппируйте похожие термины и упростите
\( \квадрат \квадрат х = 2 \)
Проверить решение, полученное в исходном (заданном) уравнении
Оцените левую часть уравнения для \( x = 2 \) : \( \quad – 2 (x – 2) + 3 = – 2 ((2) – 2) + 3 = 3 \)
Оцените правую часть уравнения для \( x = 2 \) : \( \quad 3 (-x + 4) – 3 = 3 (-(2) + 4) – 3 = 3 \)
Левая и правая стороны равны 3 для \( x = 2 \), поэтому \( x = 2 \) является решением данного уравнения.
Решение уравнений с дробями
Принятый здесь метод решения уравнений с дробями заключается в том, что мы сначала избавляемся от дробей (чтобы не иметь дело с дробями) путем умножения, а затем решаем уравнение.
Пример 6
Решите уравнение \( \quad \dfrac{x}{2} = – 3 \) и проверьте полученное решение.
Решение примера 6
Чтобы исключить знаменатель \( 2 \) в \( \dfrac{x}{2} \), мы умножаем две части уравнения на знаменатель \( 2 \)
\( \quad \color{red}2 \left(\dfrac{x}{2} \right) = \color{red}2 (- 3) \)
Упростить
\( \quad x = – 6 \)
Проверить решение, полученное в исходном (заданном) уравнении
Левая часть уравнения для \( x = -6 \) : \( \quad \dfrac{x}{2} = \dfrac{-6}{2} = – 3 \)
Левая и правая стороны равны \( – 3 \) для \( x = – 6 \), поэтому \( x = – 6 \) является решением данного уравнения.
Пример 7
Решите уравнение \( \quad \dfrac{x}{3} – \dfrac{1}{2} = \dfrac{1}{3} \) и проверьте полученное решение.
Решение примера 7
Теперь у нас есть две дроби со знаменателями \( 2 \) и \( 3 \) в данном уравнении. Чтобы избавиться от дробей, нам нужно умножить обе части уравнения на НОК (наименьшее общее кратное) двух разных знаменателей \(2\) и \(3\).
Найдите НОК \( 2 \) и \( 3 \), который равен \( 6 \).
Умножьте обе части уравнения на НОК, который равен \( 6 \)
\( \quad\quad \color{red}6 \left( \dfrac{x}{3} – \dfrac{1}{2} \right) = \color{red}6 \left(\dfrac{1 {3}\справа) \)
Распределить коэффициент \( 6 \)
\( \quad\quad 6 \left(\dfrac{x}{3} \right) – 6 \left(\dfrac{1}{2} \right) = 6 \left(\dfrac{1}{3) } \верно) \)
Переставить как
\( \quad\quad \left(\dfrac{6}{3} \right) x – \left(\dfrac{6}{2} \right) = \left(\dfrac{6}{3} \ верно) \)
Упростить
\( \четверка\четверка 2x – 3 = 2 \)
ПРИМЕЧАНИЕ. Чтобы избавиться от дробей, необходим один шаг, который представляет собой умножение обеих частей уравнения на НОК знаменателей, поскольку НОК кратен каждому знаменателю.
Чтобы избавиться от дробей, необходим один шаг, который представляет собой умножение обеих частей уравнения на НОК знаменателей, поскольку НОК кратен каждому знаменателю.
Решите приведенное выше уравнение, добавив \( 3 \) к обеим частям, и упростите, чтобы получить
\( \четверка\четверка 2 х = 5 \)
Разделить обе части на \( 2 \)
\( \quad\quad x = \dfrac{5}{2} \)
Проверить решение, полученное в исходном (заданном) уравнении
Левая часть уравнения для \( x = \dfrac{5}{2} \) : \( \quad \dfrac{x}{3} – \dfrac{1}{2} = \dfrac{1}{3 } x – \dfrac{1}{2} = \dfrac{1}{3} \left(\dfrac{5}{2}\right) – \dfrac{1}{2} = \dfrac{1}{ 3} \)
Левая и правая стороны равны \( \dfrac{1}{3} \) для \( x = \dfrac{5}{2} \), поэтому \( x = \dfrac{5}{2} } \) является решением данного уравнения.
Пример 8
Решите уравнение \( \quad \dfrac{2x + 1}{5} + 2 = – \dfrac{x}{3} \) и проверьте полученное решение.
Решение примера 8
Теперь у нас есть дроби со знаменателями \( 5 \) и \( 3 \) в данном уравнении. Нам нужно умножить обе части уравнения на НОК (наименьшее общее кратное) двух разных знаменателей \(5\) и \(3\).
Нам нужно умножить обе части уравнения на НОК (наименьшее общее кратное) двух разных знаменателей \(5\) и \(3\).
Найдите LCM \( 5 \) и \( 3 \), которое равно \( 15 \).
ПРИМЕЧАНИЕ. Один шаг, который представляет собой умножение обеих частей уравнения на НОК знаменателей, необходим, чтобы избавиться от дробей, потому что НОК кратен каждому знаменателю.
Умножить обе части уравнения на НОК \( 15 \)
\( \quad\quad \color{red}{15} \left( \dfrac{2x + 1}{5} + 2 \right) = \color{red}{15} \left(\ – \dfrac{ х}{3} \справа) \)
Коэффициент распределения \( 15 \)
\( \quad\quad 15 \left(\dfrac{2x+1}{5} \right) + 15 (2) = 15 \left( – \dfrac{x}{3} \right) \)
Переставить как
\( \quad\quad \dfrac{15}{5}(2x+1) + 15 (2) = \dfrac{15}{3}(-x) \)
Упростить
\( \четверка\четверка 3 (2x+1) + 30 = – 5x \)
Распределить множитель \(3 \) в левой части и сгруппировать подобные термины
\( \quad\quad 6 x + 3 + 30 = – 5x \)
\( \quad\quad 6x + 33 = – 5 x \)
Вычтите \( 33 \) с обеих сторон и прибавьте \( 5x \) к обеим сторонам. (ПРИМЕЧАНИЕ: мы выполнили две операции за один шаг.)
(ПРИМЕЧАНИЕ: мы выполнили две операции за один шаг.)
\( \quad\quad 6x + 33 \color{red}{- 33 + 5x } = – 5 x \color{red}{- 33 + 5x } \)
Групповые термины
\( \quad\quad 11 x = – 33 \)
Разделите обе части на \( 11 \)
\( \quad\quad \dfrac{ 11 x} {11} = \dfrac{-33}{11} \)
Упростить
\( \четверка\четверка х = – 3 \)
Проверить решение, полученное в исходном (данном) уравнении
Левая часть уравнения для \( x = – 3 \) : \( \quad \dfrac{2x + 1}{5} + 2 = \dfrac{2( -3)+1}{5}+2=1\)
Правая часть уравнения для \( x = -3 \) : \( \quad – \dfrac{x}{3} = – \dfrac{-3}{3} = 1 \) Левая и правая части равны \( 1 \) для \( x = -3 \), поэтому \( x = – 3 \) является решением данного уравнения.
Вопросы
- Решите следующие уравнения и проверьте найденное решение.

- ) \( 2x + 2 = 6 \)
- ) \( 5у – 2 = 7у – 8 \)
- ) \( -2x + 4 + 5x = 7 + 4x – 3 \)
- ) \( 0,2 д + 4 = – 0,1 д – 2 \)
- ) \(-2(2х-6) = -(х-4) \)
- ) \( -(х+2)+4 = 2(х+3) + х \)
- ) \( \dfrac{x}{5} = – 6 \)
- ) \( – \dfrac{x}{3} = \dfrac{1}{2} \)
- ) \( – \dfrac{x}{4} = \dfrac{1}{2} – x \)
- ) \( – \dfrac{x-3}{7} = \dfrac{1}{2} (- 2x + 6) \)
- ) \( – \dfrac{1}{2} – x + 5 = \dfrac{1}{5} + 2(x-2) \)
Включены ответы на вышеуказанные вопросы.
Дополнительные справочные материалы и ссылки
Решить уравнения, системы уравнений и неравенства
Найти наименьшее общее кратное
Математика средней школы (6, 7, 8, 9 классы) — бесплатные вопросы и задачи с ответами
Математика средней школы (10 классы, 11 и 12) – Бесплатные вопросы и задачи с ответами
Начальная математика (4 и 5 классы) с бесплатными вопросами и задачами с ответами
4.OA.1, 4.OA.2 — Массачусетс, 4 класс Математика Уравнения умножения и сравнения
Уравнения умножения и сравнения
Описание
4. 0A.1 Интерпретируйте уравнение умножения как сравнение, например, интерпретируйте 35 = 5 × 7 как утверждение, что 35 в 5 раз больше, чем 7, и в 7 раз больше, чем 5. Представьте вербальные утверждения мультипликативных сравнений в виде уравнений умножения.
4.OA.2 Умножение или деление для решения текстовых задач, связанных с мультипликативным сравнением, например, с использованием рисунков и уравнений с символом неизвестного числа для представления задачи, отличающей мультипликативное сравнение от аддитивного сравнения.
0A.1 Интерпретируйте уравнение умножения как сравнение, например, интерпретируйте 35 = 5 × 7 как утверждение, что 35 в 5 раз больше, чем 7, и в 7 раз больше, чем 5. Представьте вербальные утверждения мультипликативных сравнений в виде уравнений умножения.
4.OA.2 Умножение или деление для решения текстовых задач, связанных с мультипликативным сравнением, например, с использованием рисунков и уравнений с символом неизвестного числа для представления задачи, отличающей мультипликативное сравнение от аддитивного сравнения.
Дополнительная информация
Ключевые слова
Больше тем о Массачусетсе
- 4.НБТ.1
Знайте, что в многозначном целом числе цифра на одном месте в десять раз больше, чем на месте справа от нее. Например, осознайте, что 700 ÷ 70 = 10, применяя концепции позиционного значения и деления.
- 4.НБТ.6
Находите целые числа в частных и остатках с до четырехзначными делителями и однозначными делителями, используя стратегии, основанные на разрядном значении, свойствах операций и/или взаимосвязи между умножением и делением. Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.
Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.
- 4.NF.1
Объясните, почему дробь a/b эквивалентна дроби (n × a)/(n × b), используя визуальные модели дробей, обращая внимание на то, как количество и размер частей различаются, даже если сами две дроби одинаковы. размер. Используйте этот принцип для распознавания и создания эквивалентных дробей.
- 4.NF.7
Сравните два десятичных знака с сотыми, рассуждая об их размере. Признайте, что сравнения действительны только тогда, когда два десятичных знака относятся к одному и тому же целому. Запишите результаты сравнений символами >, = или < и обоснуйте выводы, например, с помощью визуальной модели.
- 4.МД.5
Распознавать углы как геометрические фигуры, которые образуются там, где два луча имеют общую конечную точку, и понимать принципы измерения углов.
Вот навык, которым Массачусетс требует от вас овладеть
- Уровень образования 4
- Государственный тест MCAS следующего поколения
- ГОСТы Структуры учебного плана штата Массачусетс
- Предмет Математика
- Название темы Уравнения умножения и сравнения
- Стандартный идентификатор 4.
 ОА.1, 4.ОА.2
ОА.1, 4.ОА.2 - Описание
4.0A.1 Интерпретировать уравнение умножения как сравнение, например, интерпретировать 35 = 5 × 7 как утверждение, что 35 в 5 раз больше, чем 7, и в 7 раз больше, чем 5. Представлять вербальные утверждения мультипликативных сравнений в виде уравнений умножения . 4.OA.2 Умножение или деление для решения текстовых задач, связанных с мультипликативным сравнением, например, с использованием рисунков и уравнений с символом неизвестного числа для представления задачи, отличающей мультипликативное сравнение от аддитивного сравнения.
Определение темы
Уравнения умножения в качестве сравнения могут быть представлены фразой «умножить на столько, сколько».
a × b → a раз больше, чем b
ИЛИ
a × b → b раз больше, чем a
Текстовый урок
Пример 1:
Переведите уравнение
8 = 2 × 4
Знак равенства можно перевести как «есть».
Знак умножения можно перевести как «умножить на столько, сколько».
Уравнение можно перевести как:
8 в 2 раза больше 4, или 8 в 4 раза больше 2.
Пример 2:
В понедельник Аманда решила 5 задач по математике. Во вторник она решила в 4 раза больше математических задач. Сколько математических задач решила Аманда во вторник?
Интерпретируйте фразу «в разы больше», составьте уравнение и решите его.
4 × 5 = ?
Решение уравнения равно 20.
Итак, во вторник Аманда решила 20 математических задач.
Массачусетс полностью внедрил Массачусетские учебные программы.
Массачусетс полностью внедрил Массачусетскую учебную программу, основанную на Массачусетской учебной программе. Школы Массачусетса будут проводить оценки MCAS Next-Gen для оценки уровня знаний учащихся в соответствии со стандартами штата. Программа подготовки к экзаменам Next-Gen MCAS от Education Galaxy обеспечивает онлайн-оценку и практику для учащихся классов K-5, чтобы помочь им освоить основы учебного плана штата Массачусетс.