Примеры столбиком для 3 класса по математике умножение и деление: примеры на сложение, вычитание, умножение и деление
Деление в столбик – объяснение (3 класс)
Сегодня мы рассмотрим деление в столбик — объяснение (3 класс).
Бывают небольшие числа, и с ними можно работать в уме. Бывают очень большие числа, для таких чисел люди нашли разные способы умножения и деления. Есть умножение в столбик. Это замечательно, там сразу видно что куда необходимо переносить и куда добавлять. Конечно, если аккуратно записывать. Но если есть умножение в столбик, тогда должно быть и деление в столбик.
Люди нашли удобный способ представления деления больших чисел, чтобы ничего не забыть.
Пример:
Это удобно, но почему так?
Сегодня в этом разбираются Бом, Бим и ребята.
Содержание статьи:
Деление — это действие обратное умножениюДеление двух чисел — это действие обратное к умножению. Используется для нахождения одного из неизвестных (первого или второго множителя) в операции умножения. Делить на ноль — нельзя.
Деление в столбик — это удобный способ представления деления одного числа на другое.
Сегодня ребята пришли раньше на представление и пошли осматривать цирк. По дороге им встретился Бим, который вез тележку с тремя коробками.
— Здравствуйте, ребята! — обрадовался. Бим. — Пойдемте за кулисы, поможете мне и Бому!
Бим и ребята пошли к Бому. В трех коробках находились бананы: в первой большой коробке лежали два больших пакета, в каждом большом пакете лежало по 100 бананов. Во второй, средней коробке, лежали два средних пакета; и здесь в каждом среднем пакете лежало по 10 бананов. В третьей маленькой коробке лежало четыре банана.
— Давайте посчитаем сколько всего бананов получается, — предложил Бим. — В большом пакете 100 бананов. Всего 2 больших пакета. В двух больших пакетах будет:
2 х 100 = 200 бананов.
Всего в большой коробке лежит 200 бананов.
Теперь считаем сколько бананов в средней коробке: два пакета по 10 бананов,
2 х 10 = 20 бананов.
В маленькой коробке 4 банана. Получается, что во всех трех коробках будет:
200 + 20 + 4 = 224 банана.
Мне буфетчица сказала, что надо поделить эти бананы на 14 представлений и дать тебе, Бом, для твоих подопечных. Вот, что я придумал. Давайте все бананы высыплем в одну коробку и будем раскладывать по одному банану на 14 подносов пока все бананы не закончатся.
Бим начал высыпать все бананы в маленькую коробку.
— Здесь, конечно, бананов немного, а если бы бананов была тонна, то ты тоже по одному банану раскладывал бы? — поинтересовался Бом. — Очень легко запутаться. Давай придумаем другой способ.
— Ребята, — обратился Бом к школьникам, — помогите Биму все бананы сложить на место. В большой коробке должно быть два больших пакета по 100 бананов, всего в большой коробке будет 200 бананов. В средней коробке два средних пакета по 10 бананов в каждом пакете, всего в средней коробке будет 20 бананов.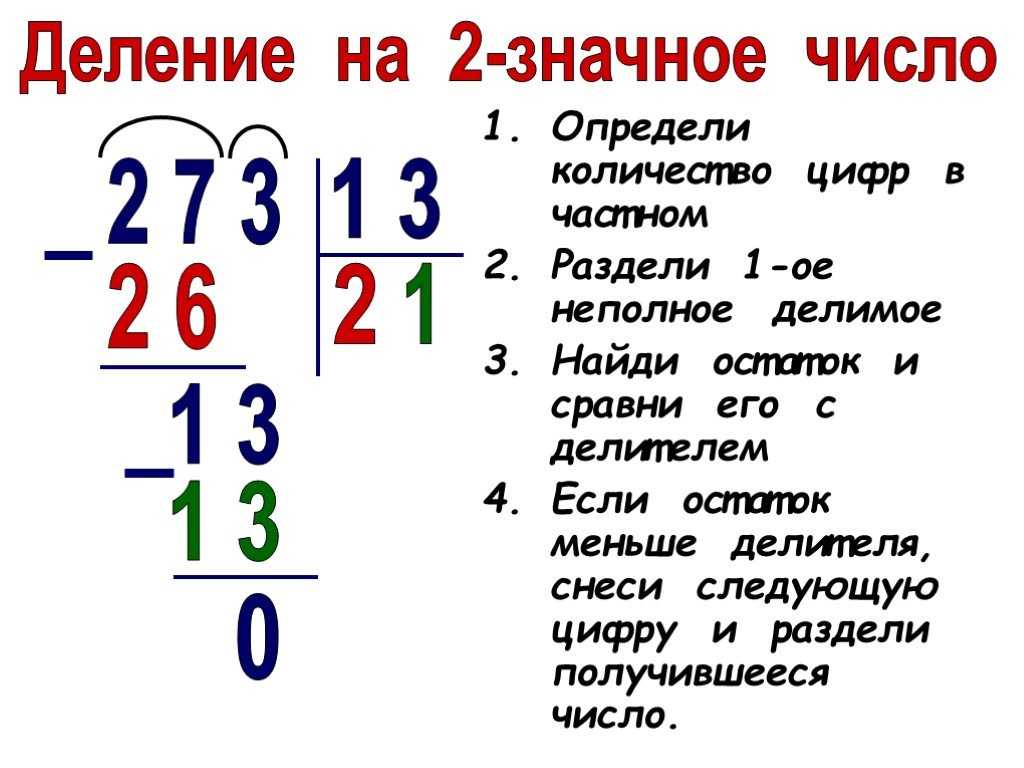
В маленькой коробке будет четыре банана.
И давай, Бим, договоримся, что в большой коробке будут лежать только большие пакеты по 100 бананов, в средней только средние пакеты по 10 бананов, в маленькой коробке только оставшиеся бананы без никаких пакетиков.
Ребята быстро помогли Бому и Биму.
— Вот теперь всё на месте, — подытожил Бом. — Давайте теперь будем делить так, чтобы бананов хватило на 14 представлений. В большой коробке два больших пакета, два на 14 не делится. А что, если мы бананы переложим из большой коробки в среднюю? Но для этого нужно достать каждый большой пакет и выложить из него бананы по 10 штук в средние пакети, и тогда мы можем бананы из большой коробки переложить в среднюю коробку.
Бом достал большой пакет из большой коробки. Ребята переложили бананы в средние пакеты и начали считать:
— Из одного большого пакета получается 10 средних пакетов по 10 бананов.
— У нас два больших пакета, значит из двух больших пакетов у нас получается 20 средних пакетов по 10 бананов, продолжил Бом.
— Мы все средние пакеты помещаем в среднюю коробку.
Ого! В средней коробке уже 22 средних пакета. Такое количество уже делится на 14, это у нас неполное деление с остатком. Получается, на каждое представление будет по одному среднему пакету.
Бом взял 14 подносов и разложил по 1 среднему пакетику на каждый поднос:
— У нас было 22 средних пакетика, 14 мы разложили по местам, остаток 8 средних пакетиков в средней коробке и 4 банана в маленькой. Восемь на четырнадцать не делится. Но если мы оставшиеся в средней коробке бананы в восьми средних пакетах высыплем в маленькую коробочку, то получится в маленькой коробочке 84 банана:
8 х 10 + 4 = 84.
84 банана делятся на 14, получается по 6 бананов, то есть мы на каждый поднос должны добавить еще по 6 бананов. У нас всего 14 подносов, и на каждом подносе лежит одинаковое количество бананов. Значит мы поделили поровну все бананы, которые у нас были. На каждом подносе 1 средний пакет и 6 бананов. Выходит, что всего на каждом подносе по 16 бананов.
— Неужели всякий раз придется по разным пакетикам раскладывать, чтобы правильно поделить? — озадаченно спросил Бим.
— Совсем не обязательно, — ответил Коля. — Люди вместо коробок и пакетиков договорились, как будет называться каждая из цифр в числе. Цифра, которая стоит в числе самой правой, называется разрядом единиц. У нас в маленькой коробке 4 банана, значит число единиц — 4.
— Следующая цифра, которая находится левее разряда единиц называется разрядом десятков, — продолжила Оля. — У нас в средней коробке 2 пакета, значит число десятков равно 2. И мы знаем, что 2 десятка — это 20, и у нас в средней коробке как раз 2 пакетика по 10 бананов, всего 20 бананов.
— Следующая цифра, которая находится левее разряда десятков называется разрядом сотен. У нас это самая большая коробка, в ней два больших пакета, значит число бананов 200, — закончил Вася. — И мы знаем, что 2 сотни — это число 200.
— А какие еще числа могут стоять … в разрядах? — поинтересовался Бим.
— Число в каждом из разрядов может быть любой цифрой от 0 до 9, — ответил Биму Коля. — Еще левее от разряда сотен стоит разряд тысяч. У нас нет еще большей коробки, в которой лежали бы пакеты с количеством бананов по 1000 в каждом, поэтому мы ничего не пишем.
— Мы разложили бананы, у нас общее число бананов 224: 4 банана в маленькой коробке, 2 средних пакета по 10 бананов в средней коробке, — всего 20, и 2 больших пакета из 100 бананов в большой коробке, — подытожил Бом. — Число единиц у нас 4, число десятков 2, число сотен 2. Записываем: 4 стоит справа, левее стоит число десятков 2, еще левее число сотен 2. Теперь это число 224 будем делить на 14.
— Давайте теперь запишем деление 224 на 14 в столбик, — предложил Коля. — Делимое у нас 224, делитель 14. Смотрим: первая цифра слева 2 (число сотен) на 14 не делится, значит надо к ней справа приписать следующую за “2” цифру 2. Читаем число, которое получилось — 22. Число 22 уже делится на 14. Число 14 помещается в числе 22 по одному (1) разу, вот это число “1” и записываем в ответ для частного первым, потом надо из 22 вычесть 14 х 1:
22
—
14
____
8
Мы при делении 22 на 14 находим неполное частное 1 и остаток 8.
Неполное частное записываем в частное результата, остаток пишем как при обычном вычитании чисел в столбик.
Теперь смотрим, есть ли еще цифры справа, в делимом 224. Да такая цифра есть, после 22 стоит цифра 4, мы её записываем справа от остатка 8. Эта четверка будет стоять на том же месте в строке, где стоит 4 в числе 224, но только ниже возле “8”. У нас внизу получается число “84”. Смотрим, делится ли оно на делитель “14”. Делится. В результате деления 84 на 14 получаем “6”, его записываем справа от “1” в частном. А внизу после того, как умножим 14 х 6 = 84 мы пишем опять обыкновенное вычитание в столбик:
84
—
84
___
0
Ура! Еще и остаток в конце равен 0. В числе 224 нет справа больше цифр, сносить на более нижние строки нечего. Значит, мы закончили деление. Частное — 16.
— Смотрите, получилось такое же число, как и количество бананов на каждом подносе, — обрадовалась Оля.
— Проверка, что деление выполнено правильно, делается также как и для обычного деления: частное умножается на делитель, должно получиться делимое, — добавил Вася.
— Сейчас каждый из нас еще по одному примеру деления в столбик запишет, — продолжил Коля.
Коля 1000 : 25 = 40. Оля 1025 : 25 = 41. Вася 10025 : 25 =401.
— Жалко, что у нас нет бананов в остатке, я бы его съел, огорчился Бим.
— Делаем вывод, — продолжил Коля. — Все деление в столбик состоит из неполных делений чисел, пока в числе не окончатся все разряды, но если после того, как мы снесли последний разряд (число единиц) остался остаток, то все деление у нас неполное, и результат будет состоять из частного-результата и остатка-результата. Если в конце деления остаток 0, то так и говорят, что делимое делится на делитель без остатка.
Можно и так определить деление в столбик, — подытожил Бом:
Деление в столбик — это ряд неполных делений чисел (неполных делимых), составленных из остатков от деления и цифр делимого, на делитель.
В результате деления в столбик должны быть использованы все цифры делимого.
Вначале в делимом выделяем первое неполное делимое из цифр делимого, начиная с левой цифры делимого, пока неполное делимое не будет делиться не делитель. Частное от неполного деления записываем первой цифрой в частном.
К остатку от неполного деления сносим следующие цифры из делимого, пока новое неполное делимое не будет делится на делитель. При этом, если после снесенной цифры, неполное делимое не делится на делитель, то в частное ставится справа 0. После деления нового неполного делителя на делимое неполное частное записывается справа от уже найденных цифр частного, а к полученному неполному остатку опять сносятся последующие цифры из делимого. Действия повторяются, пока не будут снесены все цифры делимого.
Неполное частное при делении в столбик — это частное от деления в столбик, при котором имеется остаток после использования последнего разряда в операции деления в столбик.
— Получается, — подхватил Вася, — что при делении в столбик тоже может быть неполное деление, когда есть остаток в самом конце деления. И результат тогда пишут, как при обычном неполном делении: частное-результат или как обычно говорят “частное”, а в конце в скобочке пишут остаток.
Пример:
— Спасибо ребята, что помогли нам сегодня разобраться с делением в столбик, — поблагодарил зрителей Бом. — Вот вам 315 конфет. Поделите в столбик 315 на 15 и разложите по 15 конфет в каждый кулечек. Три пакетика заберите себе, а остальные я раздам другим ребятам. Сколько всего получится пакетиков и сколько пакетиков мне останется раздать ребятам пусть посчитают ребята, которые научились делению в столбик.
— Подсказка. В ответе должен быть 21 кулечек, три из которых получили Коля, Оля и Вася, — добавил Бим. — Теперь напишите, пожалуйста, вопросы и ответы для ребят с Бомом, а я побежал одеваться, мой выход в самом начале представления, а выход Бома с обезьянками будет позже.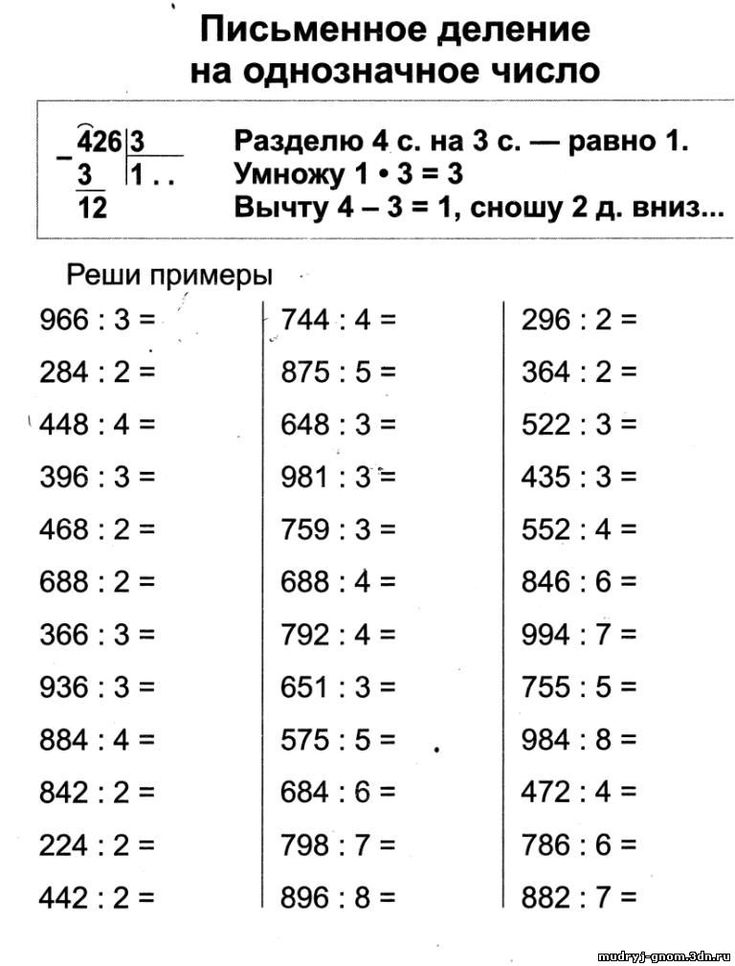
Бим убежал.
— До начала представления еще есть время, — посмотрел на часы Бом. — Ребята, давайте запишем вопросы:
- Что такое деление?
- Деление в столбик — это …
- Деление в столбик с остатком — это …
И как обычно, ответы:
- Деление двух чисел — это действие обратное к умножению, используется для нахождения одного из неизвестных (первого или второго множителя) в операции умножения. Делить на ноль — нельзя.
- Деление в столбик — это удобный способ представления обыкновенного деления. Деление — это действие обратное к умножению.
- Неполное частное при делении в столбик — это частное от деления в столбик, при котором имеется остаток после использования последнего разряда в операции деления в столбик
— Спасибо, ребята! — обрадовался Бом. — Вы очень помогли нам с Бимом. А теперь бегите на представление.
Сегодня мы постарались в игровой форме рассмотреть тему: «Деление в столбик — объяснение (3 класс)».
Надеемся, что ребята выучат деление в столбик и оно им еще не один раз пригодится.
Оригинальная идея подачи материала принадлежит Стуловой Лилии Валериевне (преподаватель математики от 5 лет и старше).
Не забудьте оценить наши старания! Комментарии приветствуются. По желанию подписывайтесь на нас в Яндекс.Дзен и в других социальных сетях!!!)))
3 класс. Моро. Учебник №2. Ответы к стр. 106
Что узнали. Чему научились в 3 классе?
Умножение и делениеОтветы к стр. 106
1. Проверь, хорошо ли ты знаешь таблицы умножения и деления:
1) Вспомни, какие числа получаются при умножении 2, 3, 4 и т. д. на числа от 1 до 9, и продолжи ряды чисел.
5, 10, 15, 20, 25, 30, 35, 40, 45.
3, 6, 9, 12, 15, 18, 21, 24, 27.
6, 12, 18, 24, 30, 36, 42, 48, 54.
2, 4, 6, 8, 10, 12, 14, 16, 18.
7, 14, 21, 28, 35, 42, 56, 63.
9, 18, 27, 36, 45, 54, 63, 72, 81.
8, 16, 24, 32, 40, 48, 56, 64, 72.
4, 8, 12, 16, 20, 24, 28, 32, 36.
2) Объясни, как можно, используя таблицу умножения, найти частное.
54 : 9 = 6 32 : 8 = 4 56 : 7 = 8 18 : 2 = 9
3) Произведением каких двух однозначных множителей можно заменить числа: 64, 32, 63, 48, 27, 18, 24, 36, 56, 81?
8 • 8 = 64
4 • 8 = 32
7 • 9 = 63
6 • 8 = 48
3 • 9 = 27
2 • 9 = 18 3 • 6 = 18
4 • 6 = 24 3 • 8 = 24
6 • 6 = 36 4 • 9 = 36
7 • 8 = 56
9 • 9 = 81
4) Проверь, можешь ли ты правильно решить примеры каждого столбика за 2 мин (записывай только ответы).
4 • 3 = 12 6 : 2 = 3 7 • 8 = 56 27 : 3 = 9
6 • 5 = 30 12 : 4 = 3 3 • 6 = 18 56 : 8 = 7
9 • 7 = 63 36 : 9 = 4 7 • 7 = 49 15 : 5 = 3
6 • 8 = 48 42 : 6 = 7 8 • 9 = 72 64 : 8 = 8
2 • 9 = 18 25 : 5 = 5 4 • 5 = 20 36 : 6 = 6
8 • 4 = 32 24 : 3 = 8 9 • 3 = 27 81 : 9 = 9
9 • 5 = 45 32 : 4 = 8 5 • 8 = 40 12 : 3 = 4
7.
Вспомни, как можно умножить сумму на число, и реши с устным объяснением.
27 • 4 = 20 • 4 + 7 • 4 = 108 32 • 3 = 30 • 3 + 2 • 3 = 96
18 • 5 = 10 • 5 + 8 • 5 = 90 17 • 4 = 10 • 4 + 7 • 4 = 68
8. Вспомни, как можно разделить сумму на число, и реши с устным объяснением.
46 : 2 = 40 : 2 + 6 : 2 = 23 84 : 7 = 70 : 7 + 14 : 7 = 12
96 : 3 = 90 : 3 + 6 : 3 = 32 96 : 4 = 80 : 4 + 16 : 4 = 24
ЗАДАНИЕ НА ПОЛЯХ:
Головоломка:
36 = 6 • 6
36 = 2 • 3 • 6
48 = 6 • 2 • 2 • 2
ГДЗ по математике. Учебник. 3 класс. Часть 2. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С.
И., Степанова С. В.
Математика. 3 класс
Когда дети изучают умножение и деление
Из всех математических операций умножение и деление могут быть самыми трудными для изучения детьми. Овладение этими навыками — логичный следующий шаг после сложения и вычитания. Но на самом деле это скорее скачок для большинства детей. Узнайте, когда дети учатся умножать и делить.
Изучите связанные темы
Математика
Когда дети обычно изучают умножение
Обучение умножению может начаться уже во втором классе. Дети обычно начинают с объединения равных групп (3 + 3 + 3 = 9)., что соответствует 3 × 3 = 9). Это называется повторным добавлением.
Вот как и когда дети учатся умножать:
- Во втором классе дети учатся визуализировать повторяющееся сложение. (Это как нарисовать квадрат с пятью строками и пятью столбцами, чтобы представить 5 × 5 = 25.
) - В третьем классе дети начинают понимать связь между умножением и делением. (Это как знать, что 3 × 4 = 12, а 12 ÷ 4 = 3.)
- В четвертом классе, Дети начинают умножать двузначные числа на двузначные числа.
)Чтобы научиться умножению, дети используют практические материалы и наглядные модели для разложения чисел и построения концепции.
К концу пятого класса большинство детей знают, как использовать распространенную процедуру умножения больших чисел. Некоторым нужно немного больше времени и практики, чтобы полностью понять концепцию.
Когда дети обычно изучают деление
Деление обычно является самым сложным математическим понятием для детей. Уравнение деления состоит из трех частей:
- Делимое — это число, которое нужно разделить (первое число в задаче).
- Делитель — это число, на которое делится делимое (второе число в задаче).
Обучение делению начинается в третьем классе.
Дети знакомятся с понятием, выполняя многократное вычитание. (Например, 20 – 5, затем еще 5, и еще 5, и еще один 5. Это то же самое, что 20 ÷ 4.)
Вот как и когда дети учатся делить:
- В третьем классе детей начинают делить путем многократного вычитания. Они учатся делить две цифры на однозначные числа с решениями больше 10.
- В четвертом классе дети начинают учиться делить четырехзначные числа на однозначные числа. (Например, 4000 ÷ 2.)
- В пятом классе ребенка начинают делить четырехзначные числа на четырехзначные числа. (Например, 8 000 ÷ 4 000.) Кроме того, большинство детей знакомятся с десятичными дробями в пятом классе.
Дети должны полностью понимать, как умножать и делить, прежде чем перейти в среднюю школу. Но это не значит, что каждый ребенок это поймет. Некоторым детям нужно больше времени и практики.
Почему у некоторых детей возникают проблемы с умножением и делением
У детей нередко возникают проблемы с математикой, особенно с умножением и делением.
Для этого есть много причин и много способов помочь. Поддержка, такая как отдельное обучение или обучение в небольшой группе, может со временем иметь большое значение.
Например, у некоторых детей возникают проблемы с пониманием основных математических понятий, известных как чувство числа. Проблемы с концентрацией внимания или памятью могут повлиять на изучение математики. Так может тревога.
Узнайте больше о том, почему у детей проблемы с математикой.
Основные выводы
Дети должны понимать, как умножать и делить до поступления в среднюю школу.
Дети, у которых проблемы с пониманием чисел или пониманием основных математических понятий, могут иметь проблемы с умножением и делением.
С дополнительной поддержкой и практикой дети могут улучшить навыки умножения и деления.
Связанные темы
Математика
Дополнение, вычитание, умножение и обзор дивизии – математика 3 -го класса
В математике 4 Основные : Дополнение , .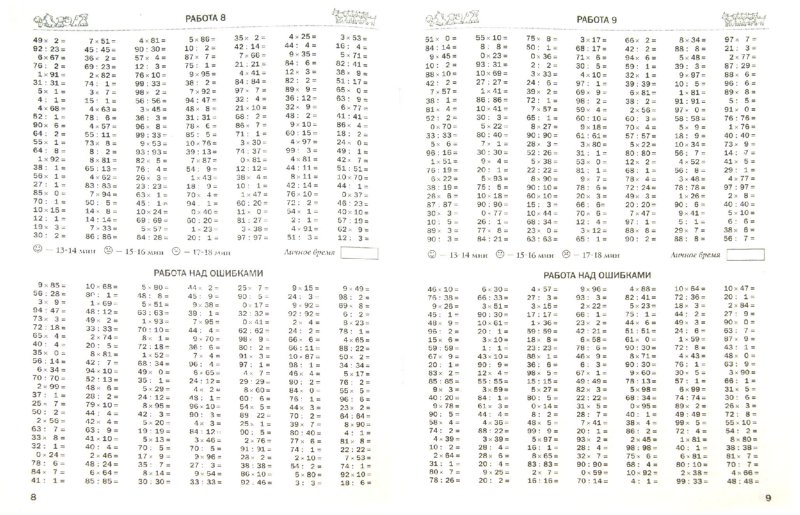
умножение и деление .
Давайте вспомним, что вы узнали о каждом из них.
Что такое сложение?
Объединение двух или более чисел называется сложением .
Сложение Уравнение состоит из двух или более сложений , символа плюс (+), символа равенства (=) и суммы .
Попробуем сложить числа.
Дополнение Пример 1
4,255 + 3,104 = ?
Давайте добавим числа, используя форму столбца .
Начните с места единиц справа (👉) и решайте столбец за столбцом.
Итак, каков ответ?
Верно! Это 7359.
Дополнение Пример 2
675 + 198 = ?
Запишите задачу в виде столбца.
На этот раз нам пришлось перегруппироваться!
Совет: Когда сумма в столбце больше 9, вам нужно перегруппировать !
Отлично!
Теперь приступим к вычитанию.
Обзор вычитания
Вычитание — это вычитание части числа.
Попробуем вычесть несколько чисел.
Пример вычитания 1
497 – 251 = ?
Давайте вычтем, используя столбец формы.
Как и в случае сложения, начните со столбца «Единицы».
Какая разница?
497 – 251 = 246
Отличная работа! 👏
Пример вычитания 2
7 301 – 6 361 = ?
Вычитаем! На этот раз нам нужно перегруппировать .
Какая тебе разница?
7 301 – 6 361 = 940
Вперед! 🤗
Давайте теперь рассмотрим умножение и деление.
Обзор умножения
Повторное добавление одинаковых групп называется умножением .
Например, когда мы умножаем 2 круги 5 раз, получаем 10 кругов.
5 × 2 = 10
Уравнения умножения состоят из множителей и произведения.
Давайте рассмотрим несколько примеров умножения.
Пример умножения 1
9 × 8 = ?
Умножение — это сокращение для повторного сложения .
Это означает добавить 9 к самому 8 раз, или добавить 7 8 0116 до сам 9 раз.
9 × 8 =
9 + 9 + 9 + 9 + 9 + 9 + 9 + 9 = 72
Итак,
9 × 8 = 72
Пример умножения 2
× 3 256116?
Давайте умножим эти большие числа, используя форму столбца .
Сначала умножаем цифру Единицы разряда на 3.
Затем умножаем цифру Десятки разряд на 3 и добавить перенос.
Получаем 16, значит, надо переносить на сотни.
Наконец, мы умножаем цифру в разряде Сотни на 3 и добавляем перенос.
Отличная работа! 👏
Подразделение Обзор
Подразделение разбивает число на равные группы.
Например, когда мы разделим 10 кругов на 5 равные группы, мы получим 2 круга в каждой группе.
10 ÷ 5 = 2
деление уравнение имеет делимое , делитель , символ деления (÷ или ⟌) и частное .
Давайте рассмотрим некоторые задачи на деление.
Раздел Пример 1
30 ÷ 6 = ?
Давайте решим это с помощью повторного вычитания.
✅ Начнем с 30 и вычтем 6 из и , , пока не достигнем 0. Количество раз, которое мы вычитаем, и есть наш ответ.
Итак,
30 ÷ 6 = 5
Отлично!
Совет: Думайте о делении как о противоположности умножения.
Если вы видите 30 ÷ 6 = ? только подумайте: какое число умножить на 6 будет 30?
6 х ? = 30
И вы получите тот же ответ: 5!
Раздел Пример 2
882 ÷ 7 = ?
Давайте решим этот вопрос, используя длинное деление .
Начнем с расстановки чисел в форме деления.
Теперь посмотрите на первую цифру, 8.
Можете ли вы сказать, сколько семерок поместится в 8?
Очень хорошо! 1.