Примеры со скобками по математике для 2 класса: Выражения со скобками – 2 класс, примеры, порядок действия
Урок матемтаики 2 класс “Порядок действий. Скобки” | План-конспект урока по математике (2 класс):
Конспект урока по математике.
Класс: 2
Программа: Школа России.
Тема: Порядок выполнения действий. Скобки.
Тип урока: урок изучения и первичного закрепления новых знаний
Цели: познакомить с порядком выполнения действий при вычислениях; учить находить значения выражений со скобками; развивать умение решать текстовые задачи и задачи логического характера; совершенствовать вычислительные навыки.
Планируемые результаты:
Регулятивные:
– определять цель деятельности на уроке с помощью учителя;
– находить и формулировать проблему совместно с учителем;
– планировать учебную деятельность на уроке;
-оценивать полученный результат.
Познавательные:
-добывать новые знания в учебнике;
-перерабатывать полученную информацию, наблюдать и делать выводы.
Коммуникативные:
-слушать и понимать речь других;
– участвовать в беседе на уроке.
Предметные:
– использовать в своей речи название компонентов действий сложения и вычитания;
-осознанно следовать алгоритму выполнения действий в выражениях со скобками;
-находить значение выражений в двух действиях;
-уметь читать числовые выражения.
Этапы урока:
Оборудование: учебник «Математика» 2 класс, М.И. Моро, М.А.Бантова, проектор, экран, презентация.
Ход урока:
1. Организационный момент.
– Здравствуйте, дети. Давайте проверим, все ли необходимые предметы у вас на партах.
2. Актуализация знаний.
1) Каллиграфическая минутка.
– Начнём работу с каллиграфической минутки:
– Запишите число, в котором 7 десятков и 6 единиц. Пропиши его до конца строки. Ниже представьте это число в виде суммы разрядных слагаемых.
2) Устный счет.
– Решите примеры. (на доске)
5+8 | 56-5 56-50 |
3 3+5 | 4+3 4+34 |
15 15-5 | 78-8 78-8 |
5+8=13 56-50=6
3+5=8 4+34=38
15-5=10 78-8=70
-Я задумала число, и прибавила к нему 2, получила 19. Какое число я задумала? (17)
Какое число я задумала? (17)
– Я задумала число, и прибавила 3, получила 35.
Какое число я задумала? (32)
– Я задумала число, и вычла 3, получила 40.
Какое число я задумала? (43)
-Запишите число, следующее за числом 49. (50)
– Запишите число, предшествующее числу 25. (24)
3.Самоопределение к деятельности.
(На доске записаны примеры.)
20-9+8=19
20-9+8=3
-Рассмотрите примеры. Сравните. Чем они похожи? Чем отличаются?
-Какое равенство верно? (Первое.)
– Как выполняли действия? (Сначала выполнили вычитание, а потом сложение.)
– В каком порядке нужно выполнить действия во втором равенстве, чтобы оно стало верным? (Сначала сложить 9 и 3, а затем из 20 вычесть их сумму.)
Для чего нам нужно знать порядок действий? Правильно выполнять вычисления в длинных выражениях.
-Сформулируйте тему урока. Тема урока: Порядок действий.
– Мы поняли, как нужно решать эти примеры. А как показать это другим?
– Чего мы не знаем? (Как показать, в каком порядке нужно выполнять действия в некоторых примерах. )
)
– О чём сейчас говорили? (О порядке выполнения действий.)
– Какая тема урока? (Порядок выполнения действий.)
-Какова цель нашего урока? (Научиться обозначать в записи порядок действий.)
– Откройте учебник на странице 38 и проверьте, правильно ли вы догадались.
4.Работа по теме урока.
Учитель вместе с учащимися формулируют правило: «Действия, записанные в скобках, выполняются первыми.» (на слайд)
На слайде два примера:
10-(5+2)
(10-5) +2
-Чем похожи эти выражения, а чем различаются? (Похожи-набором чисел и знаков, различаются-порядком скобок)
Учащиеся составляют алгоритм решения выражении со скобками с помощью учителя.
Алгоритм: (на слайде по порядку)
- Выполняется действия, записанные в скобках.
- Выполняется сложение и вычитание, действие по порядку слева направо.
-Одинаковое ли значение получилось в этих выражениях? (нет)
После данной работы учащиеся формулируют вывод: «Скобки изменяют порядок действий в выражениях и их значения. » (На слайд)
» (На слайд)
5.Физминутка.
6. Закрепление изученного материла.
1) Работа по учебнику.
– Мы получили новое знание. Проверим, правильно ли мы сделали выводы.
Сравним наше новое знание с научным в учебнике. Прочитайте на с.38 выделенное в рамочку.
– выполним задание №1 на стр.38. Что нужно сделать? (Коллективное выполнение с комментированием. Выходят к доске.)
2) Работа с карточками.
– для закрепления полученных знаний поработаем парами с карточками.
– прочитайте задание. (приложение №1)
ЗАДАНИЕ: Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой.
10-6+3 10 –(2+3)
5+3+2 4+(8-2)
9-9+5 5+(4-2)
– Проверьте ответы. (слайд)
10-6+3 10 –(2+3)
5+3+2 4+(8-2)
9-9+5 5+(4-2)
– Оцените свою работу в парах. Если выполнили всё правильно-то весёлый смайлик, если допустили ошибки- то серьёзный, не улыбающийся, а если ничего не получилось – грустный.
7. Повторение пройденного материала.
– Обратимся к задаче на стр.39 №5.
– Прочитайте. (Дети читают задачу сначала про себя, а затем один ученик читает её вслух).
– О ком говорится в задаче?
– Чем занимался Коля?
– Какую пользу приносит людям посещение бассейна? ( Укрепляет здоровье человека.)
– Вы тоже должны укреплять своё здоровье, заниматься спортом.
– Что известно в задаче?
– Что нужно найти в задаче?
– Давайте обратимся к чертежу задачи.
– Что обозначают числа 100? 60?
– Как ответить на вопрос задачи?
– Запишите решение и ответ. (Один ученик работает у доски).
– Молодцы, справились с заданием.
8.Рефлексия.
«Проверь себя», стр. 39
9. Итог урока.
– что нового вы узнали на уроке? (о порядке выполнения действий в выражении со скобками и без скобок)
– что запомнили? (действия, записанные в скобках, выполняют первыми)
– чему научились? (решать примеры со скобками)
– оцените свою работу на уроке с помощью сигнальных карточек (зелёный-всё понял; жёлтый- некоторые моменты остались мне непонятны; красный- ничего не понял, мне нужна помощь)
9. Домашнее задание.
Домашнее задание.
– дома предлагаю ещё раз повторить правило о порядке выполнения действий и потренироваться в решении выражений со скобками. Стр. 38 № 1, №6
Приложение 1
Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3 10 –(2+3) 5+3+2 4+(8-2) 9-9+5 5+(4-2) | Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3 10 –(2+3) 5+3+2 4+(8-2) 9-9+5 5+(4-2) |
Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3 10 –(2+3) 5+3+2 4+(8-2) 9-9+5 5+(4-2) | Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3 10 –(2+3) 5+3+2 4+(8-2) 9-9+5 5+(4-2) |
Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3 10 –(2+3) 5+3+2 4+(8-2) 9-9+5 5+(4-2) | Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3 10 –(2+3) 5+3+2 4+(8-2) 9-9+5 5+(4-2) |
Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3 10 –(2+3) 5+3+2 4+(8-2) 9-9+5 5+(4-2) | Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3 10 –(2+3) 5+3+2 4+(8-2) 9-9+5 5+(4-2) |
Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3 10 –(2+3) 5+3+2 4+(8-2) 9-9+5 5+(4-2) | Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3 10 –(2+3) 5+3+2 4+(8-2) 9-9+5 5+(4-2) |
Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3 10 –(2+3) 5+3+2 4+(8-2) 9-9+5 5+(4-2) | Найдите значение данных выражений и соедините выражения левой части с равными по значению в правой. 10-6+3 10 –(2+3) 5+3+2 4+(8-2) 9-9+5 5+(4-2) |
Математика 2 класс “Порядок выполнения действий. Скобки” конспект
Просмотр содержимого документа
«Математика 2 класс “Порядок выполнения действий. Скобки” конспект»
Открытый урок по математике во 2 классе («Школа России» М.И. Моро)
Тема: Порядок выполнения действий. Скобки
Скобки
Дата проведения:23.10.2019 г
Учитель начальных классов: Киселева Инна
Александровна.
2019 г
Методическая разработка урока
(в соответствии с требованиями ФГОС)
Тема урока:Порядок выполнения действий. Скобки
Класс: 2
УМК: «Школа России» М.И. Моро
Цель урока: познакомить с порядком выполнения действий при вычислениях.
Задачи:
Образовательная:
– учить находить значения выражений со скобками;
– развивать умения решения текстовых задач;
– отрабатывать навыки устного и письменного счёта.
Развивающая: способствовать развитию логического мышления.
Воспитательная: воспитывать интерес к математике, ответственность за выполнение работы в паре.
Тип урока: Урок открытия новых знаний.
Планируемые результаты:
Личностные: готовность и способность к саморазвитию; воспитание чувства само- и взаимоуважения; развитие сотрудничества при работе в паре; способность к самооценке на основе критерия успешности учебной деятельности, положительное отношение к изучению математики.
Метапредметные: развитие речи; формирование умений сравнивать, обобщать факты и понятия; развитие у учащихся умения организовывать учебное сотрудничество, самостоятельность; устанавливать соответствие полученного результата поставленной цели.
Предметные: умение ориентироваться в своей системе знаний: отличать новое от уже известного; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт.
Методы обучения: проблемно – поисковый, побуждающий диалог, проблемный диалог.
Формы организации познавательной деятельности обучающихся:
фронтальная, индивидуальная, работа в парах.
Средства обучения: интерактивная доска, ПК, презентация, учебник М.И. Моро 2 класс УМК «Школа России», тетради, индивидуальные карточки с заданием для самостоятельной работы, таблица «Знаю. Хочу знать. Умею»
Технологическая карта
№ п/п | Этап | УУД | Деятельность | ЭОР | Время (в мину- тах) | |
учителя | учащихся | |||||
1 | Орг. | Познавательные: Осознанное и произвольное построение речевого высказывания. Регулятивные: Прогнозирование своей деятельности. Коммуникативные: Умение слушать. | Ребята, доброе утро. Присаживайтесь, пожалуйста. В начале урока давайте поприветствуем другу друга. Партеру по плечу пожмите руку, партнеру парте улыбнитесь. Пожелайте друг другу удачи и хорошего настроения. Ну что, приступим к работе! Запишите число, классная работа. С чего мы, как правило, начинаем уроки математики. | Приветствуют учителя. Готовят рабочее место. С математической разминки. | 1 мин. | |
2 | Актуализация знаний | Познавательные: Ориентироваться в своей системе знаний Регулятивные: Умение обрабатывать информацию, выбирать действие в соответствии с поставленной задачей Коммуникативные: Доносить свою позицию до других: высказывать свою точку зрения и пытаться её обосновать, приводя аргументы. | Начинаем математическую разминку. – найдите значения выражения . 1. Уменьшаемое 12, вычитаемое 3, найдите разность. (9) 2. Первое слагаемое 16, второе слагаемое 4, найдите сумму. (20) 3. Чему равна сумма чисел 8 и 5.(13) 4.Найдите разность чисел 19 и 8.(11) 5.На столе 4 яблока, а груш на 2 больше. Сколько на столе груш? (6) 6.На сколько 15 больше 6 (9) 7.Из 48 вычтите число 20. (28) 8.20 уменьшите на 5 (25) А теперь, ребята, обменяйтесь ответами с партнером по парте и сверьте полученные результат с эталоном. Слайд 3 Оцените работу партнера по шкале оценивания. Верните тетради друг другу. Полученные данные занесите в таблицу в графу ЗНАЮ. | Отвечают на вопросы учителя, выполняют задания устного счёта. Выставляют оценку в листы самооценивания. Заполняют в таблице « Знаю. Хочу знать. Слайд 4 | Презентация | 7 мин. |
3 | Изучение нового материала. Формулирование темы и целей урока. | Познавательные: Добывать новые знания Регулятивные: Самостоятельно формулировать цель урока после предварительного обсуждения. Совместно с учителем обнаруживать и формулировать учебную проблему. Коммуникативные: Умение с достаточной полнотой и точностью выражать свои мысли, находить ответы на поставленные вопросы, учиться грамотно, использовать в речи новые термины | Двигаемся дальше На доске записаны выражения. 12-2+8=18 12-2+8=2 – Рассмотрите выражения. Сравните. Чем они похожи? Чем отличаются? Какое равенство верно? Как выполняли действия? А кто уже знает, в каком порядке нужно выполнить действия во втором равенстве, чтобы оно стало верным? Мы поняли , как нужно решить этот пример. Понять мы поняли. А чего мы не знаем? . – На слайде написана китайская мудрость: «Расскажи – и я забуду, покажи – и я запомню, дай попробовать и я пойму» Проанализируйте эти слова? Как вы понимаете их? (если не ответят: – нам интереснее кататься с горки самим или смотреть?) Ребята если вернуться к нашим выражениям. О чем мы сейчас говорили? Какова тема нашего урока? Какую цель поставим перед собой? Учитель выставляет карточку с примером 10-5+2 Прочитайте выражение. Какое действие надо выполнить первым? Почему? Как называется то, что выделено? Из числа вычитаем сумму. Для того, чтобы показать, что первым действием будет сложение, в математике используют скобки. По другому наш пример можно записать так: 10- (5+2) вывешиваю на доску. Что показывают скобки? Давайте вычислим. Расставляем порядок действий 10-(5+2) 5+2=7 10-7=3 Можно не указывать порядок действий и укоротить запись, записав результат, полученный в скобках, карандашом. Какие действия выполняются первыми, если в выражениях присутствуют скобки? – Посмотрите, чем отличаются столбики примеров? (слайд) 8-3+4=9 8-(3+4)=1 18-8+9=19 18-(8+9)=1 Зачем нужны скобки? Как выполняли действия в первом столбике? Как будем выполнять действия во втором столбике, чтобы получить эти значения выражений? Сравните порядок выполнения действий в первом и во втором столбиках. Что вы можете сказать? Что нам поможет указать на порядок выполнения действий? Мы свами получили новое знание. Проверим, правильно ли мы сделали выводы. Сравним наше новое значение с научным в учебнике. Откройте учебник на странице 38. Прочитайте выделенное в рамочку. Кто уже может рассказать правило? После этого коллективное выполнение № 1 стр.38 (1 столбик –я) 2 и 3 ребята у доски Ребята, вы очень любознательные, в нашей таблице какую графу мы можем заполнить? | Похожи числами и знаками действий. Отличаются результатом Первое Сначала выполнили вычитание, а потом сложение. Сначала сложить 2 и 8 , а затем из 12 вычесть их сумму. Да Как показать в каком порядке нужно выполнять действия в некоторых выражениях. Лучше и быстрее понимаешь и запоминаешь, если сам ищешь ответы на вопросы, а не когда тебе просто говорят. О порядке выполнения действий. Порядок выполнения действий Надо научиться обозначать в записи порядок действий и показать эти умения. От 10 отнять сумму чисел 5 и 2 Сложение Оно выделено Что данное действие нужно выполнять первым Действия в скобках В первом столбике нет скобок, а во втором есть. Чтобы показать какое действие будем выполнять первым По порядку Сначала выполним действие в скобках. В первом столбике мы выполняли действия по порядку, а во втором сначала в скобках. Скобки. По одному выходят к доске и проговаривая порядок действий и решают. | презентация | 15 мин |
5 | Физкультминутка | Формирование ответственного отношения к своему здоровью | Организация комплекса упражнений для снятия нагрузки. Спасибо! Присаживайтесь на свои места. | Выполняют движения под руководством учителя: | 2 мин. | |
6 | Закрепление изученного | Регулятивные: Умение применять полученные знания, осуществлять пошаговый контроль | Учебник открыт на стр. Что нужно сделать? Выполняем первый столбик. Вызываю одного к доске. Записываем первый пример. Проверяем , получим ли мы нужный результат, если вычисления будем выполнять по порядку. Измени порядок действий. Какое действие выполним первым? Вычислите. Получился ли у вас нужный результат? Поставьте скобки. Так аналогично с остальными примерами. Обратите внимание что, если скобки не меняют порядок действий, их можно не ставить. Поработаем устно. Рассмотрите рисунок. Составьте задачу по первому решению. Составьте задачу по второму решению. Можно ли задачи назвать обратными? | Один ученик читает задание. Не получим Сложение Да В лодке плыли пять детей и 1 взрослый. Сколько всего человек плыло в лодке? В лодке было 6 человек. На берег вышли два человека. Сколько человек осталось в лодке? Нет , у них разные искомые данные. | 10 мин | |
Первичное применение новых знаний | Познавательные: Регулятивные: Умение применять полученные знания, осуществлять пошаговый контроль. Коммуникативные: Организовывать учебное сотрудничество, умение работать в группе, оценивать результаты, оказывать и принимать помощь. | Продолжаем работу по теме урока. Ребята, предлагаю вам поработать индивидуально. Каждому из вас необходимо произвести вычисления, записав их в тетрадь. По завершению вычислений – покажите готовность. Сверьте с эталоном. В конверте. Подводим итоги. Встаньте те, у кого результаты вычислений получились верными. Молодцы. А теперь встаньте те, у кого вычисления вызвали затруднения. Ребята, это 1-ый урок по такой сложной теме. | Учащиеся работают, выставление оценки в лист самооценивания. | 6 мин. | ||
7 | Итог урока. Рефлексия | Познавательные: Оценка процесса и результата деятельности. Регулятивные: Волевая саморегуляция, осознание учащимися того, что уже усвоено. Коммуникативные: Уметь выражать свои мысли. | Подводится итог по заполнению таблицы «Знаю. Хочу знать. Умею» – Назовите тему урока. – Какие цели вы сегодня перед собой ставили? Где полученные новые знания нам могут пригодиться? Вы абсолютно правы. В конце урока предлагаю вам оценить полученные знания. Заполните графу умею в таблице по шкале знаний. Если вы считаете, что все то, что вы сегодня узнали на уроке вам пригодится в жизни, то храните их в чемодане, если полученные знания для вас оказались бесполезны, выбросьте их в корзину, а если те знания, которые вы получили на уроке, усвоены не до конца, отправьте их в мясорубку, мы их доработаем. Ребята , а вот теперь встаньте и приклейте стикер к выбранному предмету. Да ребята , те знания которые мы получили оказались полезными и нужными, но а некоторым из нас нужна помощь, и на следующих уроках мы обязательно восполним пробелы. За продуктивную работу на уроке ….. получают отличную оценку. | Заполняют графу «Умею». Порядок выполнения действий Надо научиться обозначать в записи порядок действий и показать эти умения. На уроках математики в 3,4 классе, в средней школе, при выполнении олимпиадных заданий. Оценивают свою работу при помощи шкалы самооценки. | Слайд презентации | 3 мин |
9 | Инструктаж домашнего задания | Ребята домашнее задание на слайде. 1 ур.Учебник с.39 № 0,№ 6. 2 ур. Учебник с. 39 № 5. | Записывают задание. | 1 мин | ||
Скобки в математике: они имеют большое значение
Каждый символ, каждая строка, каждая точка с запятой имеют значение, когда дело доходит до математики. Одна точка в неправильном месте может изменить смысл математического предложения и, следовательно, всего решения задачи.
Сколько раз учащиеся теряют баллы по математике просто потому, что пропускают знак минус или неправильно возводят число в квадрат, или из-за того, что неправильно соблюдают порядок действий или… забывают о скобках там, где они необходимы. Однако скобки в математике важны, и их нельзя упускать из виду.
Кронштейны. Давайте обсудим их важность в математике и то, как помочь учащимся запомнить наиболее распространенные случаи, когда скобки абсолютно необходимы.
Порядок операций
Учащиеся начинают по-настоящему понимать важность квадратных скобок в математике, когда начинают изучать порядок операций. Откуда же взялся порядок действий и кто его придумал? Многие современные математики согласны с тем, что она была разработана одновременно с открытием и введением алгебраических обозначений, то есть в 1600-х годах. Однако даже во времена символической алгебры большинству было ясно, что умножение должно предшествовать сложению, чтобы получить правильное решение.
Сегодня мы изучаем и со временем используем порядок операций довольно естественно. В 20 веке была создана аббревиатура для обозначения порядка операций – BEDMAS: скобки, экспоненты, деление, умножение, сложение, вычитание.
Как мы видим, всякий раз, когда алгебраическое выражение содержит скобки, операция в скобках должна выполняться до любых других операций. Это, конечно, если операция в скобках возможна. Например, в выражении 2 + (2x – 1) хотя и есть скобки и внутри них есть операция, мы не можем ее реально выполнить, так как добавляемые термы не похожи на термы, так как содержат переменную и другой – просто константа. Таким образом, в этом выражении можно «опустить» скобки и тогда упростить:
Это, конечно, если операция в скобках возможна. Например, в выражении 2 + (2x – 1) хотя и есть скобки и внутри них есть операция, мы не можем ее реально выполнить, так как добавляемые термы не похожи на термы, так как содержат переменную и другой – просто константа. Таким образом, в этом выражении можно «опустить» скобки и тогда упростить:
2x + 2 – 1 = 2x + 1.
Очень важно практиковаться и действительно хорошо разбираться в BEDMAS, поскольку он служит основой для многих-многих других понятий, как простых, так и сложных.
Скобки и отрицательные числа
Скобки очень важны при выполнении операций с отрицательными числами.
Одна из самых распространенных ошибок, которую допускают учащиеся, заключается в том, что они забывают поставить отрицательное число в скобки, когда возводят его в степень четного числа .
Вот почему это так важно:
(-2) 5 означает, что (-2) было умножено на себя 5 раз
(-2) × (-2) × (-2) × (- 2) × (-2), что равно +32
, тогда как
-2 5 означает -(2 5 ), поэтому только 2 (без отрицательного значения) было умножено само на себя 5 раз, и тогда результат умножить на (-1)
– (2 × 2 × 2 × 2 × 2), что равно -31
Еще одна ситуация, когда важно поставить в скобках отрицательное число, — это когда стоит двойной знак минус. Например, такие выражения, как 242-(-12), означают, что мы вычитаем отрицательное значение 12 (что означает добавление 12) из произведения 24 и 2.
Например, такие выражения, как 242-(-12), означают, что мы вычитаем отрицательное значение 12 (что означает добавление 12) из произведения 24 и 2.
После вычисления этого выражения ответ будет 48 + 12 = 60.
Описанная выше ситуация очень распространена при умножении, делении, сложении и вычитании положительных и отрицательных целых чисел, дробей и десятичных дробей. Он также применяется к ситуациям, когда отрицательный знак распределяется по выражению в скобках, например: (3x+1) = -3x – 1
Распределительное свойство умножения
Скобки несут еще одно важное значение, когда учащиеся начинают работать с алгебраическими выражениями и уравнениями с переменными.
Фермер строит забор вокруг прямоугольного поля. Длина забора на 100 м больше ширины. Общая площадь поля составляет 600 квадратных метров. Каковы фактические размеры поля и сколько всего необходимо ограждения?
Мы не знаем, какова ширина или длина поля, но мы можем использовать переменную для представления ширины, и тогда выражение, представляющее длину, будет еще на 100 метров (дополнение).
Пусть х будет шириной, тогда длина будет (х+10) — обратите внимание, как все выражение представляет длину, поэтому мы поместили его в скобки, чтобы показать, что это все одно измерение.
Теперь, если мы применим площадь прямоугольника к A = lw
Итак, используя имеющуюся информацию, наше уравнение будет выглядеть так:
600 = x(x+100)
большая разница в том, как устроено это уравнение и как мы в конечном итоге придем к решению. При правильной настройке, как указано выше, переменная x должна быть распределена по каждому члену внутри скобки.
Если бы он был установлен без скобок, 100 осталось бы константой.
Как и в программировании, каждый символ имеет значение, и одна лишняя или отсутствующая скобка может привести к тому, что код перестанет работать, то же самое и с математикой в целом. Правильные обозначения, форма и соответствующие символы чрезвычайно важны для получения желаемого результата. Вот почему скобки в математике требуют особого внимания. Обучение детей тому, как систематизировать математические понятия и почему это важно, поможет им быть более успешными и уверенными в математике на долгие годы.
Обучение детей тому, как систематизировать математические понятия и почему это важно, поможет им быть более успешными и уверенными в математике на долгие годы.
Скобки: использование, типы, правило BODMAS, примеры
- Автор Мадхурима дас
- Последнее изменение 11-11-2022
Скобки подразумевают своего рода группировку, операторы в подвыражении имеют приоритет над операторами в окружающем выражении. Использование квадратных скобок обычно встречается в математических функциях. Мы видели такие выражения, как (3×2)–1. (3×2)–1. Мы можем рассмотреть две части выражения: часть в скобках и часть вне скобок.
Помните, если мы ошибемся в расчетах, мы можем получить неверный ответ. Как мы пойдем, если там больше одной скобки? Мы используем арифметические операции в соответствии с их приоритетом. Точно так же мы используем скобки в соответствии с их приоритетом. Давайте обсудим здесь различные типы скобок и их использование.
В математике скобки – это символы, которые часто используются для создания групп или для объяснения порядка выполнения операций в выражении. Некоторые скобки имеют несколько конкретных применений в математике.
Некоторые скобки имеют несколько конкретных применений в математике.
Обычно мы используем квадратные скобки для группировки в математике. Мы обычно используем следующие типы кронштейнов:
1. \(\left({} \right)\) назвал скобку
2. \(\left\{{} \right\}\) назвал фигурные скобки
3. \(\left[{} \right ]\) называется квадратными скобками
Мы всегда используем пару скобок, которые имеют открывающую и закрывающую часть. Скобки используются для прозрачности порядка операций.
Например, предположим, что у вас есть выражение \(2 + 5 \times 7 – 2). Мы знаем, что порядок математических операций – деление, умножение, сложение и вычитание. Итак, мы будем двигаться вправо, начиная с умножения до выполнения сложений и вычитаний, и мы получим \(2 + 35 – 2 = 35.\)
Что мы будем делать, если мы хотим сначала выполнить сложение и вычитание и умножить результаты? Этого можно добиться, правильно используя скобки.
Если мы используем скобки, то проблема становится такой: \(\left({2 + 5} \right) \times \left({7 – 2} \right).\) Здесь круглые скобки или скобки говорят нам делать что-то отличное от порядка обычных операций. Иногда мы также используем их для визуальной ясности.
Изучите концепции BODMAS
BODMAS Правило
BODMAS — это краткая форма, используемая для скобок, порядка, деления, умножения, сложения и вычитания. Иногда люди используют PEMDAS (круглые скобки, экспоненты, умножение, деление, сложение и вычитание), похожие на BODMAS.
Описывает порядок выполнения математических операций при решении математического выражения. В соответствии с этим правилом, если в выражении присутствует несколько квадратных скобок, сначала начните упрощать самую внутреннюю круглую скобку или круглую скобку, затем квадратную скобку и фигурную скобку, а затем решите в соответствии с арифметическими операциями приоритета.
Другими словами, согласно правилу BODMAS, чтобы решить любое математическое выражение, сначала решите члены, написанные в скобках, а затем упростите экспоненциальные члены. После этого решаем операции деления и умножения, затем, наконец, сложения и вычитания. Таким образом, правило BODMAS оценивает математические выражения и справляется со сложными вычислениями намного проще и правильнее.
Шаги для запоминания правила BODMAS
Упростите выражение внутри скобок. Помните о приоритете скобок. Начните решение внутри \(\left({} \right),\), затем \(\left\{{}\right\}\) и после этого следует \(\left[{} \right].\)
Затем выполните деление или умножение (слева направо).
Затем выполните сложение или вычитание (слева направо).
Использование скобок
Согласно правилу BODMAS, чтобы решить любое математическое выражение, сначала решите члены, написанные в скобках, упростите экспоненциальные члены и перейдите к операциям деления и умножения, затем, наконец, к сложению и вычитанию.
Если в выражении есть какие-либо скобки, откройте скобки и добавьте или вычтите члены.
\(a + \left({b + c} \right) = a + b + c,\quad a + \left({b – c} \right) = a + b – c\)
Если есть знак минус, открываем скобку, умножаем знак минус на каждое слагаемое внутри скобки. \ (а – \ влево ({b + c} \ вправо) = а – б – с \)
Если есть какой-либо член вне скобок, умножьте этот внешний член на каждый член в скобках. \(a\left({b + c} \right) = ab + ac\)
Пример, \(11 – \left({3 – 2} \right) = 11 – 3 + 2 = 11 – 1 = 10 \)
Пример, \(3\влево({5 – 2} \вправо) = 15 – 6 = 9\)
Реальный пример использования скобок
Давайте разберемся на примере. Во время вчерашней бури с дерева в нашем саду упало несколько гуав. Моя мама подобрала его в сумке. Я посчитал, что в пакете \(40\) гуавы. Оттуда я взял \(5\) гуавы, а моя сестра взяла \(6). Через некоторое время моя тетя нашла в саду еще \(10\) гуавы. Она разделила их всех поровну между \(13\) девочками и мальчиками по соседству. Сколько гуавы получил каждый? Давайте узнаем.
Сколько гуавы получил каждый? Давайте узнаем.
- Шаг 1 : Сколько гуавы было изначально? \(40\) гуавы.
- Шаг 2 : Сколько гуавы мы с сестрой взяли?
\(\left({5 + 6} \right)\) Поместим это в первую скобку \(\left({} \right).\) - Шаг 3 : После того, как мы взяли гуаву, как много осталось в мешке?
\(\left\{{40 – \left({5 + 6} \right)} \right\}\) Помещаем во вторую скобку \(\left\{{} \right\}.\)
Если тетя нашла \(10\) больше гуавы, общее количество гуавы будет \(\слева\{{40 – \слева({5 + 6} \справа)} \справа\} + 10\)
У нас осталось больше заданий. Итак, нам нужен еще один кронштейн. Мы будем называть эту скобку квадратной скобкой. - Шаг 4 : Разделите поровну между \(13\) людьми. Каждый получит, \(\left[{\left\{{40 – \left({5 + 6} \right)} \right\} + 10} \right] \div 13\)
\(\left[ {\left\{{40 – \left({5 + 6} \right)} \right\} + 10} \right] \div 13\)
\( = \left[{\left\{{40 – 11} \right\} + 10} \right] \div 13\) (Упростить внутри круглой скобки)
\( = \left[{29 + 10} \right] \div 13\) (Упростить внутри фигурной скобки)
\( = 39 \div 13\) (Упростить в квадратных скобках)
\( = 3\) (Разделить)
Следовательно, каждый получит \(3\) гуавы.
Вот как скобки помогают нам в решении экземпляра.
Когда требуется больше вычислений и необходимо изменить порядок математических операций, мы прибегаем к помощи скобок.
10 математических приемов для быстрого расчета
Решенные примеры в скобках
Q.1. Решите \(8 + 9 \дел 9 + 5 \умножить на 2 – 7\).
Ответ: Данное выражение равно \(8 + 9 \div 9 + 5 \times 2 – 7.\)
Поскольку здесь нет скобок, порядок математических операций будет деление, умножение, сложение и затем вычитание .
Сначала выполним операцию деления, т.е. \(9 \div 9 = 1\)
Таким образом, выражение станет \(8 + 1 + 5 \times 2 – 7\)
Затем мы выполним умножение, т.е. (5 \times 2 = 10\)
Теперь выражение принимает вид \(8 + 1 + 10 – 7\)
Затем выполните сложение, т.е. \(8 + 1 + 10 = 19\)
Наконец-то сделаем вычитание.
Теперь \(19 – 7 = 12\)
Следовательно, требуемый ответ равен \(12.\)
Q. 2. Упростите \(\left\{ {25 – 3\left( {6 + 1} \right)} \right\} \div 4 + 9\).
2. Упростите \(\left\{ {25 – 3\left( {6 + 1} \right)} \right\} \div 4 + 9\).
Ответ: Данное выражение равно \(\left\{{25 – 3\left({6 + 1} \right)} \right\} \div 4 + 9.\)
Начнем решать внутри круглая скобка или круглая скобка, т. е. \(\left({6 + 1} \right) = 7\)
Затем умножьте \(3\left( 7 \right)\) или \(3 \times 7 = 21 \)
Теперь выражение принимает вид \(\left\{{25 – 21} \right\} \div 4 + 9\)
Операция с фигурными скобками, т. е. \(\left\{{25 – 21} \right\ } = 4\)
Итак, выражение принимает вид \(4 \div 4 +9\)
Следовательно, \(4 \div 4 = 1\)
Наконец, \(1 + 9 = 10\)
Следовательно, требуется ответ \(10\) после упрощения выражения.
Q.3. Решите \(\left( {1/4 + 1/8} \right)\) из 32.
Ответ: Здесь нам нужно решить выражение \(\left({\frac{1}{4} + \frac{1}{8}} \right)\) из \(32.\)
Во-первых, нам нужно обработать выражение внутри скобки, т. е. \(\left({\frac{1}{4} + \frac{1}{8}} \right) = \frac{{2 + 1 }}{8} = \frac{3}{8}\)
Теперь выражение принимает вид \(\frac{3}{8}\) of \(32\)
‘Of’ означает умножение. Итак, \(\frac{3}{8} \times 32 = 12\)
Итак, \(\frac{3}{8} \times 32 = 12\)
Следовательно, требуемый ответ равен \(12.\)
Q.4. Упростите \(150 \div 15\left\{ {\left( {12 – 6} \right) – \left( {14 – 12} \right)} \right\}\).
Ответ: Данное выражение равно \(150 \div 15\left\{{\left({12 – 6} \right) – \left({14 – 12} \right)} \right\}\ )
Во-первых, мы должны оперировать и упростить термины внутри \(\left({} \right)\), а затем \(\left\{{} \right\}.\)
Теперь, \(150 \div 15 \left\{{\left({12 – 6} \right) – \left({14 – 12} \right)} \right\}\)
\( = 150 \div 15\left\{{6 – 2} \right\}\) (Решение внутри круглой скобки)
\( = 150 \div 15\left\{ 4 \right\}\) (Решение внутри фигурной скобки)
\( = 10\left\{ 4 \right\}\) (Делить \(150\) на \(15\),т. е. \(12\))
\( = 10 \times 4\) (если перед скобкой нет оператора, считать как есть оператор умножения) \( = 40\) (Умножить \(10\) и \(4\))
Следовательно, требуется ответ \(40.\)
Q.5. Решите \(16\left[ {8 – \left\{ {5 – 2\left( {2 – 1 + 1} \right)} \right\}} \right]\), используя правило BODMAS.
Ответ: Данное выражение равно \(16\left[{8 – \left\{{5 – 2\left({2 – 1 + 1} \right)} \right\}} \right.] \)
Сначала разгадайте скобки.
Теперь \(16\влево[{8 – \влево\{{5 – 2\влево({1 + 1} \вправо)} \вправо\}} \вправо]\)
\( = 16\влево[ {8 – \left\{{5 – 2 \times 2} \right\}} \right]\)(решается внутри изогнутой скобки)
\( = 16\left[{8 – \left\{{5 – 4} \right\}} \right]\) (умноженное внутри фигурной скобки)
\( = 16\left[{8 – 1} \right]\)(Решение внутри фигурной скобки)
\( = 16 \times 7\) (Решение внутри квадратных скобок)
\( = 112\) (умножение)
Следовательно, искомый ответ равен \(112. \)
Часто задаваемые вопросы о кронштейнах
Q.1. Когда использовать скобки?
Ответ: В математике скобки — это символы, которые часто используются для создания групп или для объяснения порядка выполнения операций в выражении. Некоторые скобки имеют несколько конкретных применений в математике.
Q.2. Как использовать скобочную формулу в математике?
Ответ: Обычно мы используем скобки для группировки в математике. Эти символы скобок:
1. \(\left({} \right)\)
2. \(\left\{{} \right\}\)
3. \(\left[{} \right] \)
Мы всегда используем пару скобок, которые имеют открывающую и закрывающую часть. Скобки используются для прозрачности порядка операций. Порядок скобок следующий: \(\left({} \right),\left\{{} \right\}\) и \(\left[{} \right].\)
В.3. Что вы подразумеваете под БОДМАС?
Ответ: BODMAS — это краткая форма, используемая для скобок, порядка, деления, умножения, сложения и вычитания. Он описывает математические операции, которые необходимо выполнить при решении математического выражения. Согласно этому правилу, если в выражении присутствует несколько скобок, начните упрощение внутри круглой скобки, затем фигурной скобки, затем квадратной скобки, а затем решите вопрос о приоритете арифметических операций.
Q.4. Вы умножаете сначала, если нет скобок?
Ответ: Согласно правилу BODMAS, скобка должна быть решена первой. Если скобки нет, то следующим приоритетом будет деление или умножение (поскольку и деление, и умножение имеют одинаковый порядок предпочтения), и если умножение идет первым в математическом выражении слева направо. Таким образом, мы сначала умножаем, если нет скобок, так как умножение идет первым в выражении слева направо.
Q.5. Используете ли вы БОДМАС, когда нет брекетов?
Ответ: Да, мы используем правило BODMAS, чтобы получить правильный ответ, даже если нет скобок. Если скобок нет, начните решение с «порядка» или «из», затем следует деление или умножение (в зависимости от того, что идет первым слева направо), а затем сложение или вычитание (что наступит раньше).
Последние обновления. Но ежегодные экзамены для учащихся 7-го класса проводятся внутри соответствующих школ в.


 момент
момент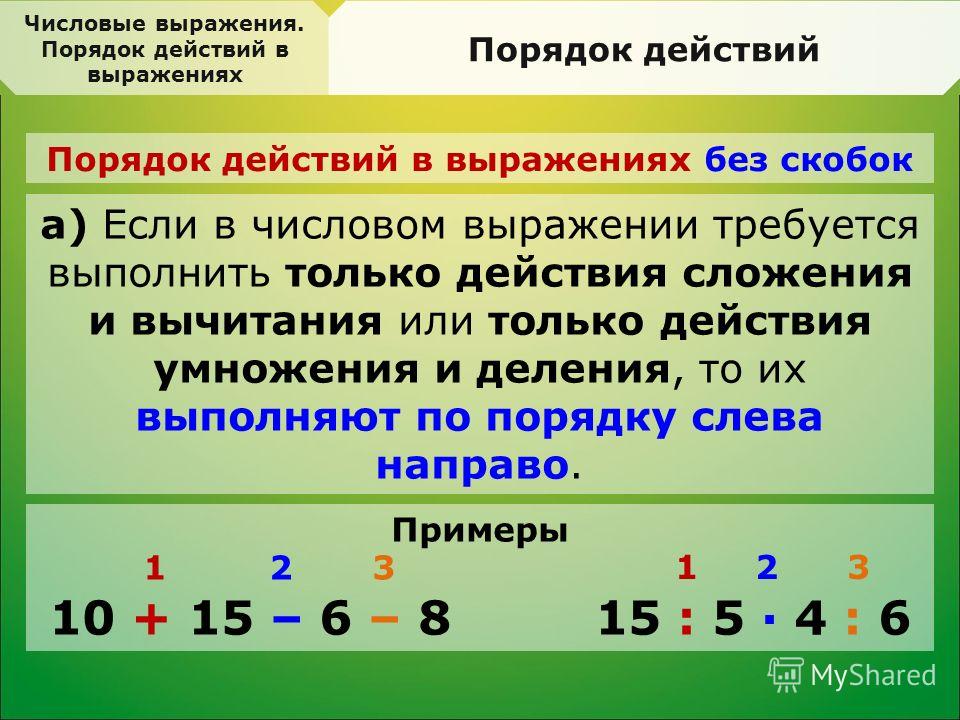
 Узнал.» графу «Знаю»
Узнал.» графу «Знаю»


 38 . Отступив две клетки вниз , записываем номер 2.
38 . Отступив две клетки вниз , записываем номер 2.
 Мы продолжим тренироваться в решении таких выражений.
Мы продолжим тренироваться в решении таких выражений.
