Примеры сложение в столбик: Онлайн калькулятор. Сложение и вычитание столбиком
Сложение натуральных чисел в столбик: правила, примеры
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Арифметика Сложение двузначных, трехзначных и многозначных чисел столбиком
В данной публикации мы рассмотрим правила и практические примеры того, каким образом можно складывать столбиком натуральные числа (двузначные, трехзначные и многозначные).
- Правила сложения в столбик
- Примеры сложения в столбик
Правила сложения в столбик
Два и более числа с любым количеством разрядов можно сложить в столбик. Для этого:
- Пишем первое число (для удобства начинаем с того, у которого больше разрядов).
- Под ним записываем второе число так, чтобы цифры одного и того же разряда обоих чисел располагались строго друг под другом (т.
 е. десятки под десятками, сотни под сотнями и т.д.).
е. десятки под десятками, сотни под сотнями и т.д.). - Аналогичным образом записываем третье и последующие числа, если они есть.
- Чертим горизонтальную линию, которая будет отделять слагаемые от суммы.
- Приступаем к сложению цифр – отдельно для каждого разряда суммируемых чисел (справа налево), записываем результат под чертой в том же столбце. При этом, если сумма столбца оказалась двузначной, в нем пишем последнюю цифру, а первую переносим в следующий разряд (слева), т.е. прибавляем к цифрам, содержащимся в нем (см. пример 2). Иногда в результате такого действия в сумме появляется еще один более старший разряд, которого изначально не было (см. пример 4). В редких случаях, когда слагаемых много, может потребоваться перенос не на один, а на несколько разрядов.
Примеры сложения в столбик
Пример 1
Сложим двузначные числа: 41 и 57.
Пример 2
Найдем сумму чисел: 37 и 28.
Пример 3
Вычислим сумму двузначного и трехзначного чисел: 56 и 147.
Пример 4
Просуммируем трехзначные числа: 485 и 743.
Пример 5
Сложим двузначные, трехзначные и четырехзначные числа: 62, 341, 578 и 1209.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Посмотрите, перед вами карта нашего путешествия. Вы готовы? Тогда в путь. Покажите, с каким настроением вы отправляетесь в путь. (СМАЙЛИКИ) Зеленый – хорошее Желтый – не очень хорошее Красный – плохое 1 .Первый остров на пути «ТИХИЙ». Откройте тетради, запишите число. Классная работа. 1 задание Запиши числа, которые на 2 десятка больше данных… 225, 600, 308,471,708,780. Проверяем, поменяйтесь тетрадями с соседом. За правильный ответ, ставим (+), за неправильный(-). Поднимите руки, у кого нет ни одной ошибки.. 2 задание Запиши числа в порядке увеличения: 210,853,358,609,725,201,906,440. Проверяем. (201 210 358 440 609 725 853 906) Встаньте те, у кого нет ни одной ошибки. 3 задание Реши цепочку примеров. Кто решит правильно, первым узнает тему нашего урока. Посчитайте.. 507+3….+90….+200…+70…+8…+22=880 Проверим, по цепочке. 808- вычитание 900- сложение 888-сравнение Итак, тема нашего урока сложение…. Давайте вспомним, что изучали на прошлом уроке? Кто правильно назовет тему урока? Какую цель поставим на уроке? Чтобы достигнуть нашей цели, давайте составим план действий … У вас на столах есть примерный план, возьмите карандаши и проставьте числа, в какой последовательности будем работать… 1) (3 )Самостоятельное решение примеров; 2) (2 )Коллективно потренироваться в решении примеров; 3) (1 )Вспомнить алгоритм (порядок) решения примеров 4)(4 )Проверка полученных знаний (План вывешивается на доску) 2. Кто догадался, что будем делать на этом острове?… Вспомним наш план.. (1)Вспомнить алгоритм (порядок) решения примеров. Алгоритм сложения трёхзначных чисел. Складываю единицы… Результат пишу под единицами. Складываю десятки… Результат пишу под десятками. Складываю сотни… Результат пишу под сотнями. Читаю ответ… Что теперь будем делать? (2)Коллективно потренироваться в решении примеров; (на доске) 1.Реши примеры, записывая их в столбик. (с объяснением у доски) (по цепочке) 347+214= 805+79= 434+256= 48+361= 57+128= 714+95= 2.Найди и исправь ошибки. Определи, кто прав Маша, или Миша? Маша: Миша: 346 +346 99 99 445 1336 Вернемся к нашему плану… 3)Самостоятельное решение примеров; У вас на партах лежат карточки с заданиями. Задания трех уровней: уровень «А»- легкий, уровень «Б»- средний по трудности и уровень «В» – сложный.
Проверьте, правильно ли вы выполнили. (Даются ответы к заданиям.) 3 . «ВЕСЕЛЫЙ»остров. Ребята, мы с вами причаливаем к берегу. Давайте сойдем на берег, отдохнем, погреемся на солнышке.. Наш игровик, пожалуйста, организуй нам отдых.. Как вы думаете, какое задание нам предстоит выполнить на этом острове? Правильно… Откройте учебник на Стр.63, прочитайте задачу №5.. Поднимите руки, кто может ее решить? Решаем самостоятельно.. Остальные решают с карточкой помощницей. 183р. Р. 209р. Проверяем. 1)209 +183=392(р) Ответ: мама брала 392р. 2.Работа в паре Стр. Послушайте задачу.. Обсудите, какое вы выбираете решение и почему? (Проверка, запишите правильное решение в тетрадь ) Продолжим путь. Нас ждет следующий остров 5.«ПРОВЕРОЧНЫЙ» 1.Работа в парах. 1.Придумать для соседа 3 примера по нашей теме…. (Взаимопроверка) 2.Проверочный тест. Получите карточки для тестовой работы. Запишите своё имя. 1.Найди число, которое меньше 700 на 1. а) 600 б) 699 в) 690 2.Сколько надо прибавить к числу 800, чтобы получилось 870? а) 7 б) 70 в) 700 3. Если 700 увеличить на 250, то получится: а) 750 б) 725 в) 950 4. Прибавьте числа 395 и 143. а) 583 б) 538 в) 539 5. Найдите сумму чисел 726 и 159. а) 858 б)884 в) 885 Проверьте Наш корабль вернулся в порт. Какую цель мы ставили на уроке? Как вы думаете, достигли мы ее? Продолжите высказывание: Сегодня на уроке я узнал… Мне показалось трудным… Я могу использовать эти знания… «Смайлик улыбается»- Урок прошел удачно. Я доволен собой! «Смайлик строгий»- Мне было трудно, но я Справлялся с заданиями. Я вполне доволен собой! «Смайлик грустный» – Мне было очень трудно. Мне нужна помощь! И мне бы особенно хотелось выделить работу на уроке….. Более активным надо быть… Сдайте пожалуйста ваши карты. Ребята, мы славно потрудились. Спасибо за работу! Нет, т.к на выходной не задается… |
Сложение десятичных знаков в столбце – Математика с мамой
Сложение десятичных знаков в столбцеExampleVideoQuestionsLesson
Отправить в Google Classroom
ExampleVideoQuestionsLesson
Отправить в Google Classroom
- Сначала выровняйте десятичные точки каждого числа.
- Выровняйте цифры чисел, стоящих на одном месте в столбцах значений.
- Добавьте цифры в каждом столбце справа налево.
- Если ответ на это дополнение содержит 2 цифры, то перенесите цифру десятков в следующий столбец.
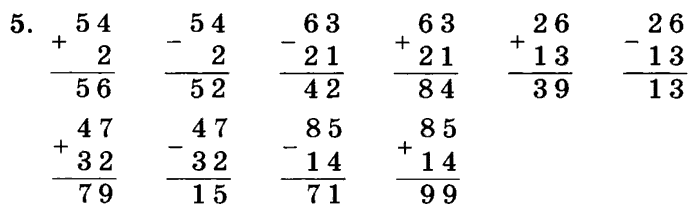
- 7 + 5 = 12, поэтому мы записываем 2 ниже и переносим 1.
- Теперь мы добавляем цифры в следующем столбце, включая 1, которую мы перенесли.
- 1 + 2 + 1, которую мы несли = 4.
- 1,7 + 2,5 = 4,2.
Выровняйте десятичные точки и цифры в каждом столбце разряда.
Добавьте каждую цифру к цифре выше.
Как складывать десятичные дроби
Чтобы сложить десятичные дроби, сначала выровняйте десятичные точки каждого числа, а затем выровняйте цифры в каждом столбце разряда. Добавляйте цифры отдельно справа налево.
Запишите ответы на каждое дополнение под цифрами. Напишите только одну цифру в каждом столбце разряда. Если ответ представляет собой двузначное число, перенесите десятку, чтобы добавить к цифрам в следующем столбце.
Мы рассмотрим пример сложения десятичных чисел 1,7 + 2,5.
Первый шаг заключается в том, чтобы написать одну десятичную дробь над другой. Важно сначала выровнять десятичные точки чисел.
Важно сначала выровнять десятичные точки чисел.
Затем выровняйте цифры в каждом столбце разряда.
Далее мы добавляем цифры справа налево.
Складывая цифры в десятом столбце, получаем 7 + 5 = 12.
Мы пишем только 1 цифру в каждом столбце разряда. Это означает, что мы записываем «2» из «12» ниже и переносим «1» в следующий столбец слева.
Запишите переносимую цифру под строками ответов.
Теперь мы добавляем цифры в столбце единиц. У нас есть 1 + 2 + 1, который мы несли ранее.
1 + 2 + 1 = 4
Теперь все цифры добавлены, читаем наш ответ между строк ответа.
1,7 + 2,5 = 4,2
В следующем примере мы добавляем десятичные дроби 0,52 + 0,67.
Первым шагом при сложении двух десятичных чисел является выравнивание десятичных знаков.
Затем мы выстраиваем цифры в столбцах с одинаковыми разрядами.
Выстраиваем 2 и 7 в столбце сотых, 5 и 6 в столбце десятых и нули в столбце единиц.
Начнем с добавления цифр справа налево, начиная с столбца сотых.
2 + 7 = 9 и так, мы пишем 9 в строках ответа ниже.
Теперь складываем цифры в десятом столбце.
5 + 6 = 11 и так, мы пишем 1 ниже и переносим другую 1 цифру в следующий столбец слева.
Наконец, мы добавляем цифры в столбце единиц. У нас есть 0 + 0 + 1, которую мы несли. 0 + 0 + 1 = 1. Мы пишем эту 1 в пространстве ответов.
Сложение десятичных знаков с разными разрядными значениями
Чтобы сложить десятичные дроби с разными разрядными значениями, выровняйте десятичные точки. Затем выровняйте цифры слева направо. Пишите нули в конце десятичных чисел, в которых меньше цифр, чем в других числах, пока числа не будут иметь одинаковое количество цифр.
Затем добавьте цифры в каждый столбец разряда отдельно, работая справа налево.
Например, мы добавим два десятичных знака 3,4 и 1,58.
Десятичное число 3,4 состоит всего из 2 цифр, тогда как десятичное число 1,58 состоит из 3 цифр.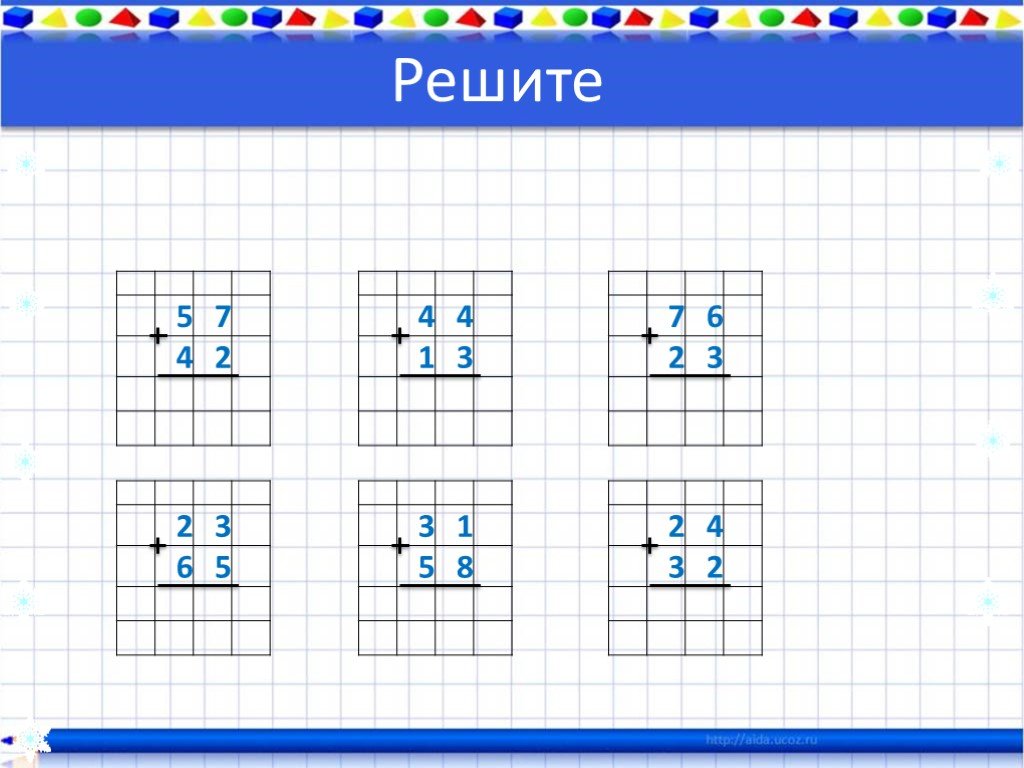
Сначала мы пишем два числа, выстраивая десятичные точки, а затем цифры слева направо.
Ставим цифру 0 в конце числа 3,4 в столбце сотых, чтобы получилось 3,40.
Два десятичных числа теперь имеют одинаковое количество столбцов разряда.
Складываем цифры справа налево, начиная с сотого столбца.
0 + 8 = 8
4 + 5 = 9
3 + 1 = 4
3,4 + 1,58 = 4,98
Вот еще один пример сложения десятичных знаков с разными разрядными значениями. У нас 5.07+7.4.
5.07 имеет 3 цифры с последней цифрой в столбце сотых.
7.4 имеет 2 цифры с последней цифрой в десятом столбце.
мы добавляем ноль после 7,4, чтобы получить 7,40.
Складывая цифры в столбце сотых, 7 + 0 = 7.
Складывая цифры в десятом столбце, 0 + 4 = 4.
Складывая цифры в столбце единиц, 5 + 7 = 12.
5,07 + 7,4 = 12,47
Сложение с перегруппировкой – Математика с мамой
В этом уроке мы используем метод сложения столбцов для сложения трехзначных чисел.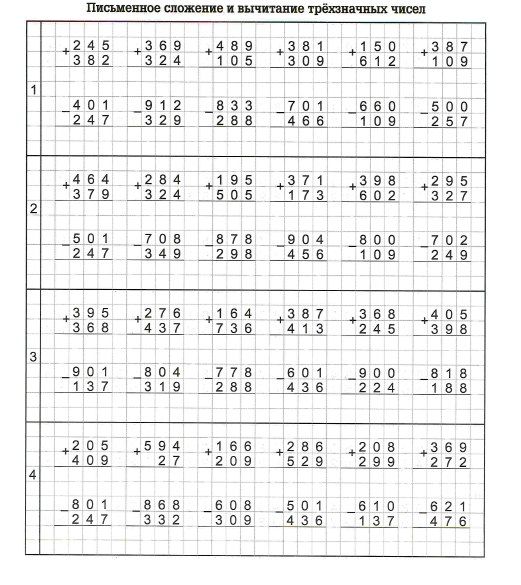
Чтобы добавить числа, используя метод сложения столбцов, выровняйте цифры каждого числа друг над другом и добавьте их отдельно. Сумма каждой цифры написана ниже, по одной цифре в ячейке.
Мы используем метод перегруппировки, когда после сложения цифр в столбце разряда получается более одной цифры.
В математике перегруппировка — это процесс перемещения значений между столбцами позиционных значений. При выполнении сложения часто используется перегруппировка, чтобы переместить группу из десяти в следующий столбец разряда вверх. Некоторые примеры перегруппировки: замена 10 единиц на 1 группу из десяти или 10 десятков на 1 группу из сотни.
При обучении сложению некоторые учителя используют слово 9.0031 «перенос» , а также слово «перегруппировка» .
Перенос и перегруппировка означают одно и то же вдобавок. Перенос — это перемещение десятки в следующую колонку разряда. Перегруппировка также используется при вычитании, где ее иногда называют заимствованием.
В этом уроке мы узнаем о перегруппировке, рассмотрев несколько примеров сложения, включающих перегруппировку.
Вот пример 246 + 173:
В числе 246 6 шт. (или один). Они показаны шестью фиолетовыми счетчиками в столбце единиц измерения.
У него 4 десятка . Они показаны четырьмя группами из десяти фиолетовых счетчиков в столбце десятков.
Он также имеет >2 сотни , которые показаны двумя группами сто фиолетовых счетчиков в столбце сотен.
Мы хотим добавить 173.
Число 173 имеет 3 единицы , которые показаны тремя зелеными счетчиками в столбце единиц измерения.
У него 7 десятков . Они показаны семью группами из десяти зеленых счетчиков в столбце десятков.
У него также есть 1 сотня . Это показано одной группой из ста зеленых счетчиков в столбце сотен.
Теперь, когда мы выровняли цифры каждого числа в столбцах разряда, мы можем сложить цифры в каждом столбце.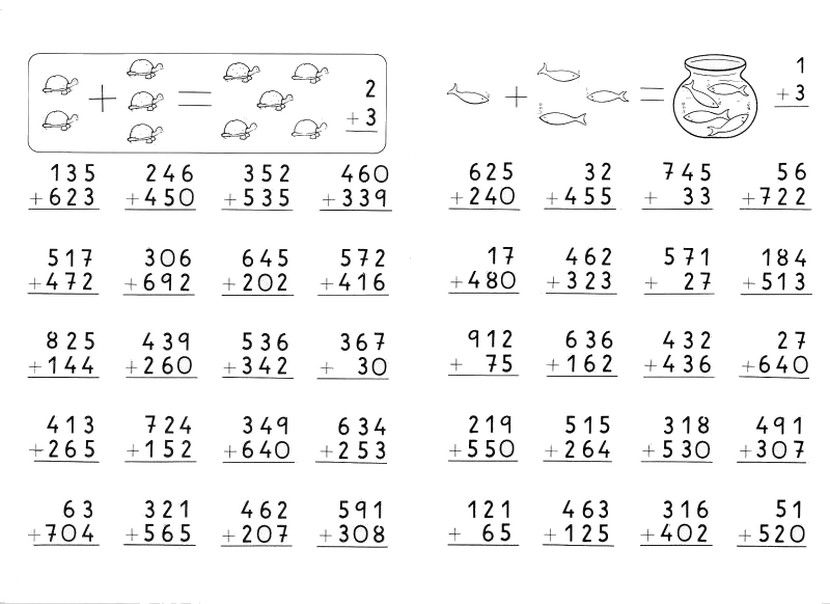
У нас есть всего 9 счетчиков в столбце единиц.
Далее смотрим на столбец десятков. Всего у нас 11 десятков.
Число 11 состоит из двух цифр .
У нас не может быть более одной цифры в каждом столбце разряда .
Поэтому нам нужно перегруппировать 100 счетчиков, чтобы перенести их в столбец сотен.
В столбце сотен у нас может быть групп по сотне 9.0034 . Следовательно, мы можем перегруппировать сто счетчиков из столбца десятков и перенести их в столбец сотен .
Теперь, когда мы перенесли 1 сотню в столбец сотен , у нас остался 1 десяток в столбце десятков.
Наконец, мы смотрим на столбец сотен. У нас есть 4 группы сто счетчиков.
Следовательно,
246 + 173 = 419
При обучении перегруппировке полезно представить концепцию визуально, как указано выше. Вы можете использовать жетоны или блоки Dienes, чтобы научить этому.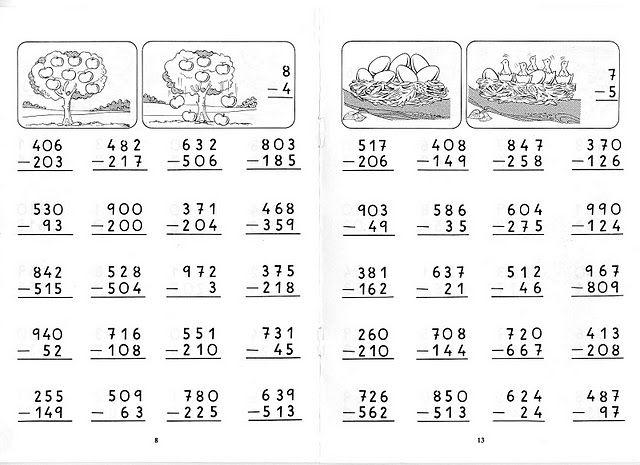 Как только идея перегруппировки понята, сложение столбцов лучше всего обучать методически с помощью письменных цифр.
Как только идея перегруппировки понята, сложение столбцов лучше всего обучать методически с помощью письменных цифр.
Мы используем перегруппировку всякий раз, когда сумма цифр в каждом столбце сложения столбца больше 9. Мы перегруппируем десять единиц, чтобы получить 1 группу из десяти, или мы можем перегруппировать десять групп из десяти, чтобы сделать одну группу из сотни.
При использовании добавления столбцов процесс перегруппировки часто называется , содержащим , поскольку дополнительная цифра переносится для добавления к следующему столбцу цифр.
Мы еще раз посмотрим на этот пример, но на этот раз мы будем использовать числа для представления каждой цифры и изложим расчет с использованием метода сложения столбцов.
Мы выстраиваем цифры каждого числа в соответствии с их разрядными значениями.
Начнем с добавления цифр в столбце единиц .
6 + 3 = 9
Мы пишем 9 в колонке единиц под 6 и 3.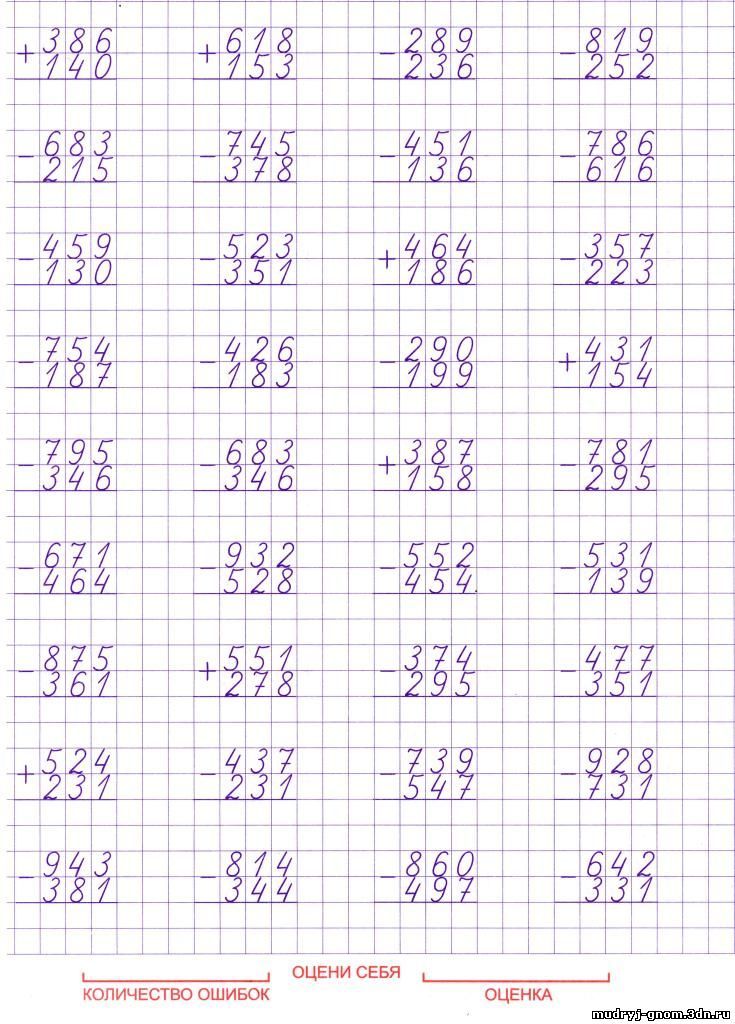
Далее мы добавляем цифры в столбце десятков .
4 + 7 = 11
В числе 11 есть 1 единица, которую мы сохраняем в столбце десятков, и 1 десяток, который мы переносим в столбец сотен и пишем под чертой.
Наконец, мы добавляем цифры в столбце сотен . Мы также должны не забыть добавить 1, которую мы перенесли.
2 + 1 + 1 = 4
Следовательно,
246 + 173 = 419
Мы рассмотрим еще несколько примеров добавления столбцов с перегруппировкой.
Здесь у нас есть 3-значные числа 417 + 235.
Мы устанавливаем числа с помощью метода сложения столбцов, с одной цифрой в ячейке и одним числом над другим.
Сначала мы добавим единицы.
7 + 5 = 12
У нас не может быть двух цифр, записанных в одном поле или в одном столбце разрядности, поэтому мы знаем, что нам нужно перегруппироваться.
Мы записываем цифру единиц «12», которая равна «2».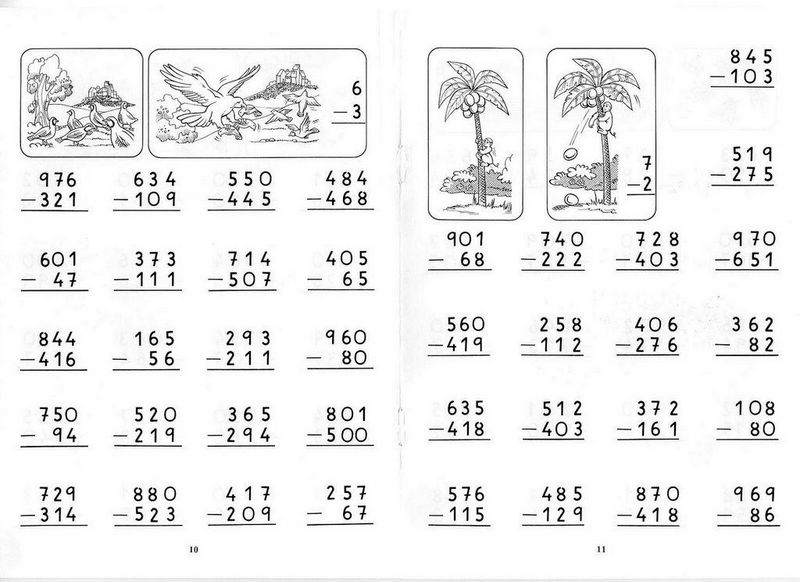.jpg)
Десятка «1» переносится в столбец десятков. Мы не пишем это между строк. Вместо этого мы можем написать это ниже строки.
Нам нужно добавить эту «1», которая была перенесена в столбец десятков.
1 + 3 + ‘1’, который был перенесен = 5
Складывая цифры в столбце сотен, мы получаем 4 + 2 = 6.
В этом примере сложения трехзначных чисел у нас есть 863 + 524.
Мы устанавливаем числа в методе сложения столбцов с первым числом над вторым.
Мы можем легко добавить цифры столбца единиц измерения, так как 3 + 4 = 7.
В столбце десятков у нас 6 + 2 = 8.
Складывая цифры сотен, мы получаем 8 + 5 = 13.
13 содержит две цифры, поэтому мы должны перенести «1» в следующий столбец.
Десять сотен составляют 1 тысячу.
Мы пишем «3» в столбце сотен, а «1» переносим в столбец тысяч слева.
Добавление 3-значного столбца с двойной перегруппировкой
После обучения процессу перегруппировки его можно применять несколько раз в рамках одного и того же вопроса. Некоторые задачи на сложение трехзначных чисел включают перегруппировку дважды в пределах одной суммы.
Некоторые задачи на сложение трехзначных чисел включают перегруппировку дважды в пределах одной суммы.
Вот пример 365 + 187.
Начиная с 5 + 7 в столбце единиц, мы получаем 12.
12 содержит две цифры, поэтому мы переносим «1» в столбец десятков.
Затем мы добавляем цифры столбца десятков.
Складывая цифры в столбце десятков, мы получаем 6 + 8 из двух заданных чисел плюс «1», которую мы перенесли в процессе перегруппировки.
6 + 8 + 1 = 15.
Снова 15 содержит две цифры, поэтому нам нужно перегруппироваться.
Мы переносим «1» из столбца десятков в столбец сотен, оставляя «5» в столбце десятков.
Наконец, мы добавляем цифры столбца сотен. У нас есть 3 + 1 в двух данных числах, и нам нужно добавить «1», который был перенесен.
3 + 1 + 1 = 5.
У нас есть 365 + 187 = 552.
В этой сумме мы перенесли дважды, перегруппировав из столбца единиц в столбец десятков, а также из столбца десятков в столбец сотен.
Вот еще пример с двойной перегруппировкой.
Мы складываем трехзначные числа 728 + 644.
Мы устанавливаем цифры друг над другом в соответствии с методом добавления столбцов и добавляем цифры в столбец единиц (единиц).
8 + 4 = 12, это двузначное число. Нам нужно перенести «1» в столбец десятков, оставив «2» в столбце единиц.
Теперь мы добавляем цифры столбца десятков плюс переносимую «1».
В столбце десятков у нас 2+4 плюс тот, который мы несли.
2 + 4 + 1 = 7, которое содержит только одну цифру. Мы можем просто написать «7» в столбце десятков.
Теперь мы добавляем сотни цифр.
У нас есть 7 + 6, что равно 13.
Мы не можем написать «13» только в столбце сотен, потому что он содержит 2 цифры.
Мы переносим «1» в столбец тысяч.
Мы можем перегруппировать десять сотен, чтобы получить одну тысячу.
Поскольку в столбце тысяч нет другой цифры, мы просто пишем здесь «1».
 е. десятки под десятками, сотни под сотнями и т.д.).
е. десятки под десятками, сотни под сотнями и т.д.).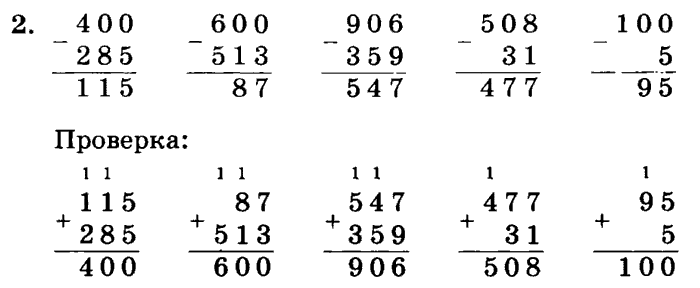 Сложение натуральных чисел столбиком, примеры, решения
Сложение натуральных чисел столбиком, примеры, решения (слайд 10)
(слайд 10) 
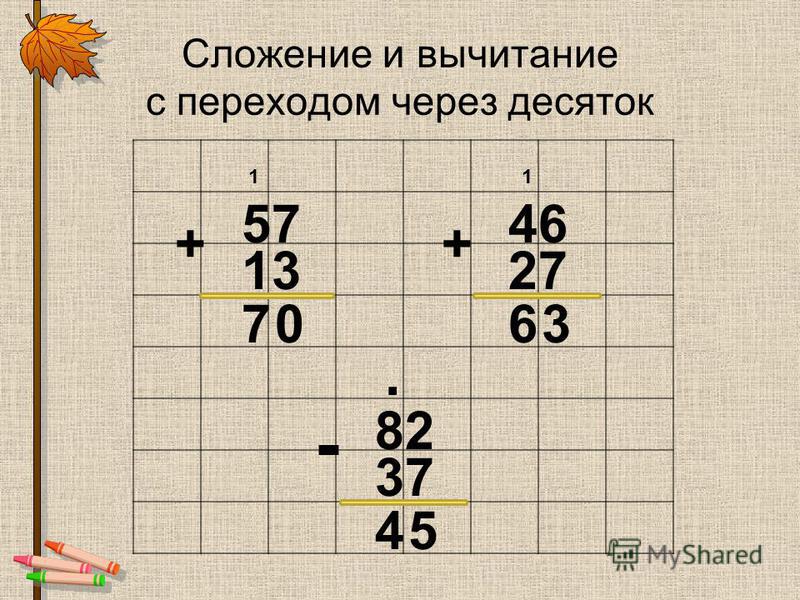
 Зелёный цвет показывает, что ваша работа была успешной и дорога к следующим знаниям для вас открыта. Если у вас ещё есть небольшие затруднения и вам нужно немного поработать над новым алгоритмом – покажите жёлтую карточку. Красный покажет, что путь к новым знаниям пока закрыт.
Зелёный цвет показывает, что ваша работа была успешной и дорога к следующим знаниям для вас открыта. Если у вас ещё есть небольшие затруднения и вам нужно немного поработать над новым алгоритмом – покажите жёлтую карточку. Красный покажет, что путь к новым знаниям пока закрыт.
 На горизонте новый остров
«ПРИМЕРНЫЙ
».
На горизонте новый остров
«ПРИМЕРНЫЙ
». Вы можете выбрать, задания какого уровня вы будете выполнять.
Вы можете выбрать, задания какого уровня вы будете выполнять.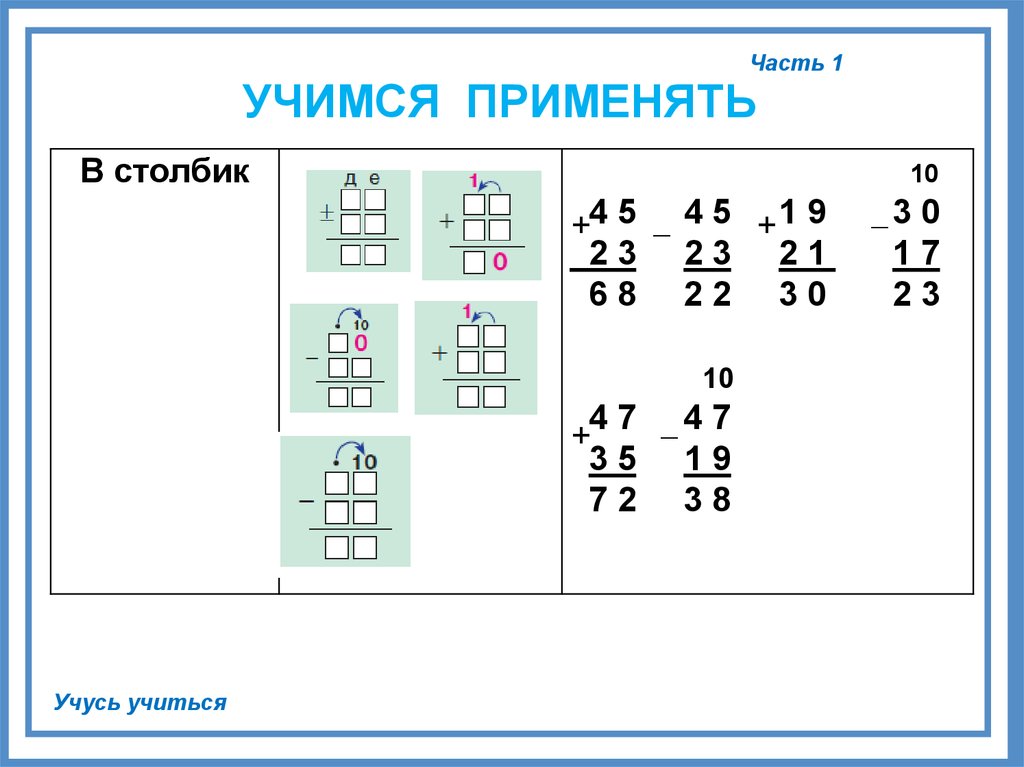 66, задача №17.
66, задача №17.


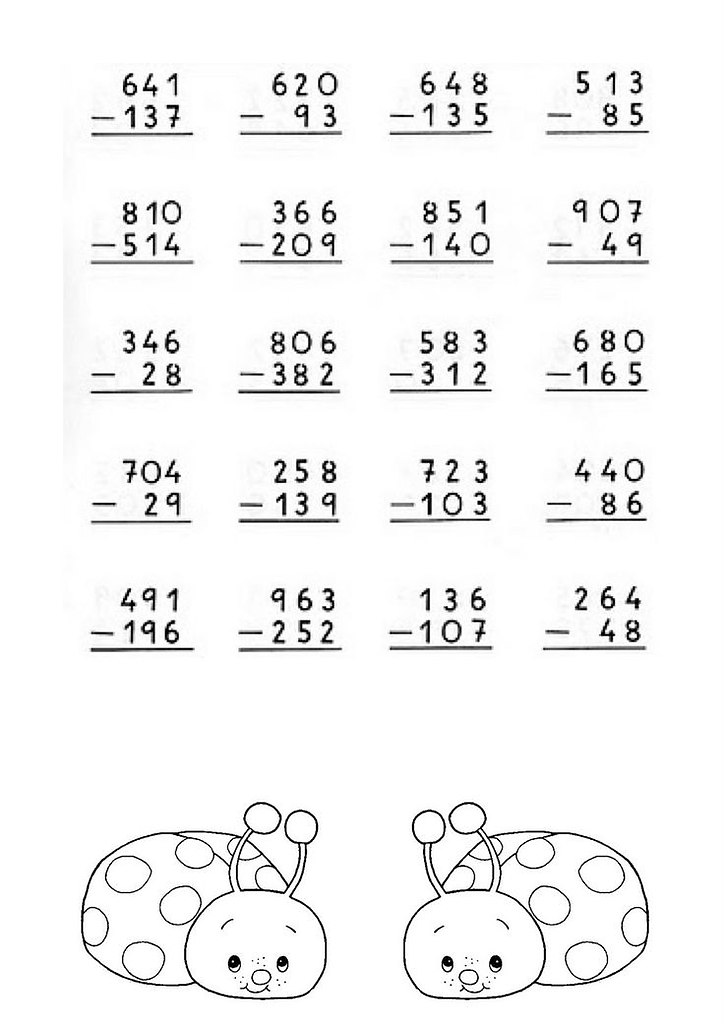 После этого происходит продвижение на один столбец влево и все действия повторяются в той лишь разницей, что к сумме еще прибавляется запомненное число. Процесс продолжается до тех пор, пока столбцы не закончатся.
После этого происходит продвижение на один столбец влево и все действия повторяются в той лишь разницей, что к сумме еще прибавляется запомненное число. Процесс продолжается до тех пор, пока столбцы не закончатся. В результате имеем число 7 . Так как 7 меньше, чем 10 , то записываем это число под горизонтальной линией, а запоминать нам никакое число не нужно. Получаем:
В результате имеем число 7 . Так как 7 меньше, чем 10 , то записываем это число под горизонтальной линией, а запоминать нам никакое число не нужно. Получаем: Чтобы не забыть о запомненном числе, его будем записывать сверху в соседнем слева столбце, причем будем использовать другой цвет. Запись примет вид:
Чтобы не забыть о запомненном числе, его будем записывать сверху в соседнем слева столбце, причем будем использовать другой цвет. Запись примет вид: Получаем 9+1=10 . Поэтому записываем под линией число 0 и запоминаем число 1 :
Получаем 9+1=10 . Поэтому записываем под линией число 0 и запоминаем число 1 :
 Прибавляем к полученному значению запомненную единицу: 7+1=8 . Записываем число 8 под чертой в соответствующем столбце:
Прибавляем к полученному значению запомненную единицу: 7+1=8 . Записываем число 8 под чертой в соответствующем столбце:
 Этот пример можно рассматривать как некоторый образец записи сложения двух натуральных чисел столбиком.
Этот пример можно рассматривать как некоторый образец записи сложения двух натуральных чисел столбиком.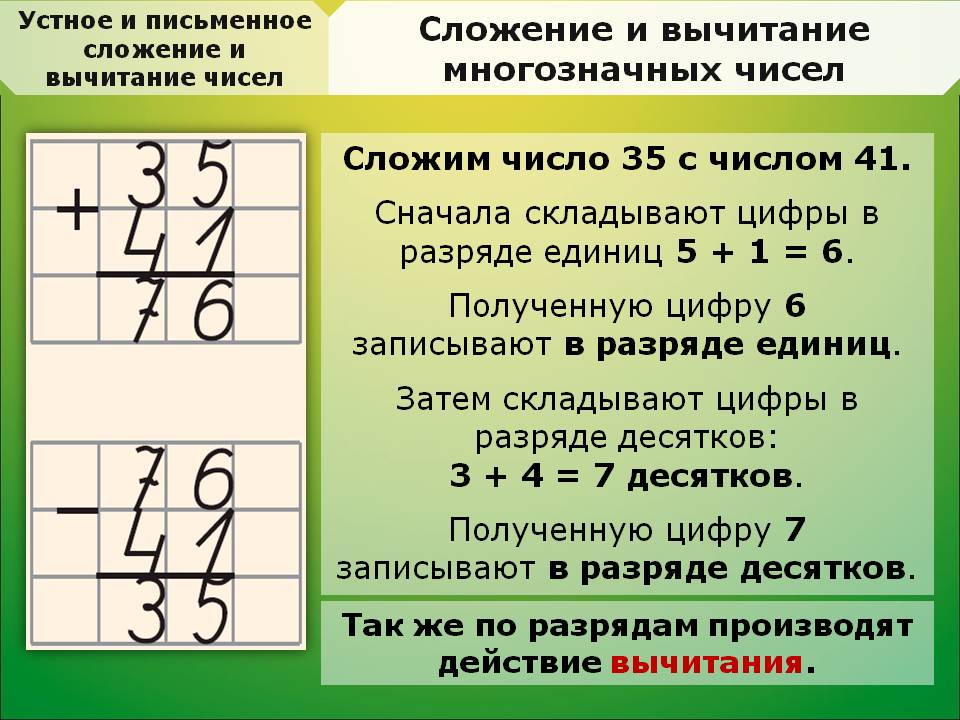 В результате получим ответ:
В результате получим ответ: В результате получили:
В результате получили: