Примеры с остатком для 3 класса по математике: Индивидуальные карточки по теме “Примеры на табличное деление с остатком” | Материал по математике (3 класс) по теме:
Индивидуальные карточки по теме “Примеры на табличное деление с остатком” | Материал по математике (3 класс) по теме:
Опубликовано 14.05.2012 – 11:22 – Тихонова Ольга Ивановна
Индивидуальные карточки содержат уже готовые примеры, достаточно записать ответ. Данный вид работы можно использовать на этапах повторения и закрепления.
Скачать:
Предварительный просмотр:
Примеры на табличное деление с остатком
65 : 8 = (ост. ) | 34 : 8 = (ост. ) | 76 : 8 = (ост. ) | 51 : 7 = (ост. ) |
44 : 7 = (ост. ) | 41 : 8 = (ост. ) | 76 : 8 = (ост. ) | 58 : 8 = (ост. ) |
22 : 8 = (ост. ) | 25 : 7 = (ост. ) | 66 : 7 = (ост. ) | 62 : 7 = (ост. ) |
1 : 7 = (ост. | 46 : 8 = (ост. ) | 55 : 8 = (ост. ) | 79 : 8 = (ост. ) |
34 : 8 = (ост. ) | 18 : 7 = (ост. ) | 65 : 7 = (ост. ) | 14 : 8 = (ост. ) |
23 : 7 = (ост. ) | 29 : 8 = (ост. ) | 77 : 8 = (ост. ) | 78 : 8 = (ост. ) |
57 : 8 = (ост. ) | 4 : 8 = (ост. ) | 42 : 8 = (ост. ) | 64 : 7 = (ост. ) |
22 : 7 = (ост. ) | 30 : 7 = (ост. ) | 68 : 7 = (ост. ) | 39 : 8 = (ост. ) |
35 : 8 = (ост. ) | 1 : 8 = (ост. ) | 44 : 8 = (ост. ) | 67 : 7 = (ост. ) |
8 : 7 = (ост. ) | 54 : 8 = (ост. | 61 : 7 = (ост. ) | 43 : 8 = (ост. ) |
15 : 8 = (ост. ) | 31 : 7 = (ост. ) | 17 : 8 = (ост. ) | 69 : 7 = (ост. ) |
19 : 7 = (ост. ) | 59 : 8 = (ост. ) | 73 : 8 = (ост. ) | 49 : 8 = (ост. ) |
37 : 8 = (ост. ) | 71 : 8 = (ост. ) | 30 : 8 = (ост. ) | 3 : 8 = (ост. ) |
43 : 7 = (ост. ) | 29 : 8 = (ост. ) | 16 : 7 = (ост. ) | 29 : 7 = (ост. ) |
36 : 8 = (ост. ) | 59 : 7 = (ост. ) | 57 : 7 = (ост. ) | 45 : 7 = (ост. ) |
20 : 7 = (ост. ) | 15 : 7 = (ост. ) | 52 : 8 = (ост. | 68 : 7 = (ост. ) |
38 : 8 = (ост. ) | 27 : 7 = (ост. ) | 18 : 8 = (ост. ) | 31 : 8 = (ост. ) |
24 : 7 = (ост. ) | 2 : 7 = (ост. ) | 8 : 8 = (ост. ) | 60 : 7 = (ост. ) |
45 : 8 = (ост. ) | 75 : 8 = (ост. ) | 19 : 8 = (ост. ) | 13 : 7 = (ост. ) |
25 : 7 = (ост. ) | 33 : 8 = (ост. ) | 27 : 8 = (ост. ) | 51 : 8 = (ост. ) |
47 : 8 = (ост. ) | 17 : 7 = (ост. ) | 12 : 8 = (ост. ) | 46 : 7 = (ост. ) |
2 : 8 = (ост. ) | 58 : 7 = (ост. ) | 7 : 8 = (ост. ) | 33 : 7 = (ост. ) |
53 : 8 = (ост. | 50 : 8 = (ост. ) | 47 : 7 = (ост. ) | 67 : 8 = (ост. ) |
60 : 8 = (ост. ) | 3 : 7 = (ост. ) | 55 : 7 = (ост. ) | 40 : 7 = (ост. ) |
9 : 8 = (ост. ) | 5 : 8 = (ост. ) | 11 : 8 = (ост. ) | 62 : 8 = (ост. ) |
61 : 8 = (ост. ) | 4 : 7 = (ост. ) | 34 : 7 = (ост. ) | 9 : 7 = (ост. ) |
69 : 8 = (ост. ) | 12 : 7 = (ост. ) | 68 : 8 = (ост. ) | 26 : 8 = (ост. ) |
13 : 8 = (ост. ) | 10 : 8 = (ост. ) | 39 : 7 = (ост. ) | 23 : 8 = (ост. ) |
36 : 7 = (ост. ) | 32 : 7 = (ост. ) | 63 : 8 = (ост. | 48 : 7 = (ост. ) |
66 : 8 = (ост. ) | 70 : 8 = (ост. ) | 53 : 7 = (ост. ) | 25 : 8 = (ост. ) |
38 : 7 = (ост. ) | 41 : 7 = (ост. ) | 10 : 7 = (ост. ) | 5 : 8 = (ост. ) |
28 : 8 = (ост. ) | 47 : 7 = (ост. ) | 52 : 7 = (ост. ) | 37 : 7 = (ост. ) |
6 : 7 = (ост. ) | 2 : 8 = (ост. ) | 21 : 8 = (ост. ) | 38 : 7 = (ост. ) |
25 : 8 = (ост. ) | 26 : 8 = (ост. ) | 66 : 8 = (ост. ) | 36 : 7 = (ост. ) |
74 : 8 = (ост. ) | 8 : 8 = (ост. ) | 50 : 8 = (ост. ) | 7 : 8 = (ост. ) |
20 : 8 = (ост. | 46 : 7 = (ост. ) | 13 : 7 = (ост. ) | 2 : 7 = (ост. ) |
37 : 7 = (ост. ) | 13 : 8 = (ост. ) | 61 : 8 = (ост. ) | 70 : 8 = (ост. ) |
11 : 7 = (ост. ) | 51 : 8 = (ост. ) | 25 : 7 = (ост. ) | 10 : 8 = (ост. ) |
54 : 7 = (ост. ) | 45 : 8 = (ост. ) | 3 : 7 = (ост. ) | 75 : 8 = (ост. ) |
5 : 7 = (ост. ) | 19 : 8 = (ост. ) | 62 : 8 = (ост. ) | 2 : 8 = (ост. ) |
50 : 7 = (ост. ) | 39 : 7 = (ост. ) | 60 : 8 = (ост. ) | 3 : 7 = (ост. ) |
5 : 8 = (ост. ) | 40 : 7 = (ост. ) | 38 : 8 = (ост. | 27 : 7 = (ост. ) |
)
)
)
)
)
)
)Предварительный просмотр:
Примеры на табличное деление с остатком
26 : 5 = (ост. ) | 39 : 4 = (ост. ) | 13 : 6 = (ост. ) | 57 : 6 = (ост. ) |
29 : 4 = (ост. ) | 1 : 5 = (ост. ) | 1 : 4 = (ост. ) | 9 : 5 = (ост. ) |
13 : 3 = (ост. ) | 26 : 3 = (ост. ) | 6 : 5 = (ост. ) | 2 : 6 = (ост. ) |
9 : 2 = (ост. ) | 30 : 4 = (ост. ) | 37 : 5 = (ост. ) | 32 : 6 = (ост. ) |
19 : 6 = (ост. ) | 13 : 2 = (ост. ) | 18 : 4 = (ост. ) | 2 : 5 = (ост. ) |
22 : 3 = (ост. | 7 : 3 = (ост. ) | 48 : 5 = (ост. ) | 43 : 6 = (ост. ) |
3 : 4 = (ост. ) | 12 : 5 = (ост. ) | 8 : 6 = (ост. ) | 25 : 4 = (ост. ) |
34 : 5 = (ост. ) | 29 : 6 = (ост. ) | 31 : 5 = (ост. ) | 27 : 6 = (ост. ) |
21 : 6 = (ост. ) | 8 : 3 = (ост. ) | 52 : 6 = (ост. ) | 20 : 3 = (ост. ) |
15 : 4 = (ост. ) | 23 : 5 = (ост. ) | 1 : 2 = (ост. ) | 10 : 4 = (ост. ) |
28 : 3 = (ост. ) | 7 : 5 = (ост. ) | 29 : 3 = (ост. ) | 8 : 5 = (ост. ) |
3 : 6 = (ост. ) | 47 : 6 = (ост. ) | 4 : 6 = (ост. | 49 : 6 = (ост. ) |
7 : 4 = (ост. ) | 16 : 5 = (ост. ) | 11 : 6 = (ост. ) | 56 : 6 = (ост. ) |
16 : 3 = (ост. ) | 37 : 4 = (ост. ) | 43 : 5 = (ост. ) | 38 : 6 = (ост. ) |
15 : 2 = (ост. ) | 19 : 4 = (ост. ) | 27 : 5 = (ост. ) | 22 : 6 = (ост. ) |
36 : 5 = (ост. ) | 31 : 6 = (ост. ) | 5 : 2 = (ост. ) | 13 : 4 = (ост. ) |
3 : 2 = (ост. ) | 11 : 4 = (ост. ) | 19 : 5 = (ост. ) | 15 : 6 = (ост. ) |
18 : 5 = (ост. ) | 14 : 6 = (ост. ) | 5 : 3 = (ост. ) | 27 : 4 = (ост. ) |
7 : 2 = (ост. | 14 : 4 = (ост. ) | 47 : 5 = (ост. ) | 41 : 6 = (ост. ) |
46 : 6 = (ост. ) | 9 : 4 = (ост. ) | 17 : 5 = (ост. ) | 2 : 3 = (ост. ) |
19 : 3 = (ост. ) | 17 : 3 = (ост. ) | 37 : 4 = (ост. ) | 21 : 5 = (ост. ) |
19 : 2 = (ост. ) | 22 : 4 = (ост. ) | 29 : 5 = (ост. ) | 25 : 6 = (ост. ) |
2 : 4 = (ост. ) | 11 : 5 = (ост. ) | 7 : 6 = (ост. ) | 51 : 6 = (ост. ) |
41 : 5 = (ост. ) | 35 : 6 = (ост. ) | 23 : 3 = (ост. ) | 3 : 5 = (ост. ) |
1 : 6 = (ост. ) | 34 : 4 = (ост. ) | 6 : 4 = (ост. | 14 : 5 = (ост. ) |
5 : 4 = (ост. ) | 13 : 5 = (ост. ) | 11 : 2 = (ост. ) | 17 : 4 = (ост. ) |
44 : 5 = (ост. ) | 39 : 6 = (ост. ) | 4 : 3 = (ост. ) | 26 : 4 = (ост. ) |
10 : 3 = (ост. ) | 31 : 4 = (ост. ) | 38 : 5 = (ост. ) | 33 : 6 = (ост. ) |
17 : 2 = (ост. ) | 21 : 4 = (ост. ) | 28 : 5 = (ост. ) | 23 : 6 = (ост. ) |
14 : 3 = (ост. ) | 35 : 4 = (ост. ) | 42 : 5 = (ост. ) | 37 : 6 = (ост. ) |
5 : 6 = (ост. ) | 50 : 6 = (ост. ) | 24 : 5 = (ост. ) | 20 : 6 = (ост. |
49 : 5 = (ост. ) | 44 : 6 = (ост. ) | 10 : 6 = (ост. ) | 55 : 6 = (ост. ) |
33 : 5 = (ост. ) | 28 : 6 = (ост. ) | 25 : 3 = (ост. ) | 4 : 5 = (ост. ) |
22 : 5 = (ост. ) | 17 : 6 = (ост. ) | 46 : 5 = (ост. ) | 40 : 6 = (ост. ) |
9 : 6 = (ост. ) | 53 : 6 = (ост. ) | 45 : 6 = (ост. ) | 16 : 6 = (ост. ) |
11 : 3 = (ост. ) | 33 : 4 = (ост. ) | 39 : 5 = (ост. ) | 34 : 6 = (ост. ) |
1 : 3 = (ост. ) | 23 : 4 = (ост. ) | 31 : 5 = (ост. ) | 26 : 6 = (ост. ) |
29 : 5 = (ост. | 41 : 5 = (ост. ) | 19 : 2 = (ост. ) | 22 : 4 = (ост. ) |
25 : 6 = (ост. ) | 9 : 4 = (ост. ) | 14 : 3 = (ост. ) | 46 : 6 = (ост. ) |
25 : 6 = (ост. ) | 28 : 3 = (ост. ) | 36 : 5 = (ост. ) | 11 : 4 = (ост. ) |
2 : 3 = (ост. ) | 27 : 5 = (ост. ) | 31 : 6 = (ост. ) | 19 : 5 = (ост. ) |
)
)
)
)
)
)По теме: методические разработки, презентации и конспекты
Индивидуальная карточка по теме “Случаи табличного деления”
Индивидуальная карточка содержит уже готовые примеры для 2-3 класса, достаточно записать ответ. Данный вид работы можно использовать на этапах повторения и закрепления….
карточки для проверки знаний табличных случаев умножения и деления
Карточки используют на уроках математики для проверки усвоения детьми табличных случаев умножения и деления в 3 классе.
использование карточек позволяет экономить время на уроке….
Индивидуальные карточки по математике на тему “Деление с остатком”
Индивидуальные карточки по математике на тему “Деление с остатком” разработаны для учащихся 3 класса для тренировки навыков вычисления, закрепления знаний таблицы умножения и деления….
Раздаточный материал – карточки примеров по математике на деление с остатком для 3 класса
Раздаточный материал представляет собой карточки (4 варианта) примеров на деление с остатком, которые позволяют проверить вычислительные навыки учащихся….
Индивидуальные карточки по таблице умножения и деления 2 -3 класс УМК Перспектива
Индивидуальные карточки для отработки и проверки таблицы умножения и деления 2 -3 класс УМК Перспектива…
Карточки для индивидуальной работы “Деление с остатком”, 3 класс
Карточки предназначены для индивидуальной работы на этапе закрепления вычислительных навыков по теме “Деление с остатком” с каждым обучающимся.
..
Карточки по математике 3 класс “Деление с остатком”.
Карточки по математике 3 класс “Деление с остатком”….
Поделиться:
«Деление с остатком », 3 класс
Муниципальное бюджетное образовательное учреждение
«Средняя общеобразовательная школа № 9 им. В.К Демидова»
ТВОРЧЕСКАЯ РАЗРАБОТКА УРОКА
Тема: Системно-деятельностный подход
на уроке математики «Деление с остатком »
(УМК «ПНШ», 3 класс)
Выполнила:
Скупченко Марина Вадимовна
учитель начальных классов
Новокузнецк, 2018
I. Введение.
В основе ФГОС лежит системно-деятельностный подход, который предполагает совокупность приёмов, способов организации рассмотрении объекта, как целостного множества элементов в совокупности отношений и связи между ними.
Сущность системно-деятельностного подхода проявляется в формировании личности ученика и продвижении его в развитии не тогда, когда он воспринимает знания в готовом виде, а в процессе его собственной деятельности, направленной на «открытие нового знания».
Системно – деятельностный подход к обучению предполагает наличие у детей познавательного мотива (желания узнать, открыть, научиться) и конкретной учебной цели (понимания того, что именно нужно выяснить, освоить). Из пассивного потребителя знаний учащийся становится активным субъектом образовательной деятельности. Категория деятельности при таком подходе к обучению является фундаментальной и смыслообразующей всего процесса обучения.
На уроках учитель организует поиски учащимися знаний,
решений; управляет этими поисками, развивая познавательную деятельность учащихся; учит учиться. Учитель призван осуществлять скрытое управление процессом обучения, быть вдохновителем учащихся.
Для построения образовательного процесса, отвечающим всем данным требованиям, педагогу крайне необходимы конкретные, знания ФГОС и умения их реализовать в практике.
Принцип деятельности заключается в том, что ученик, получает знания не в готовом виде, а добывает их сам в процессе собственной учебно-познавательной деятельности.
Курс математики в начальной школе призван решать следующие задачи:
• создать условия для формирования логического и абстрактного мышления у младших школьников на входе в основную школу как основы их дальнейшего эффективного обучения;
• сформировать набор необходимых для дальнейшего обучения предметных и общеучебных умений на основе решения как предметных, так и интегрированных жизненных задач;
• обеспечить прочное и сознательное овладение системой математических знаний и умений, необходимых для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования; обеспечить интеллектуальное развитие, сформировать качества мышления, характерные для математической деятельности и необходимые для полноценной жизни в обществе;
• сформировать устойчивый интерес к математике на основе дифференцированного подхода к учащимся;
• выявить и развить математические и творческие способности на основе
заданий, носящих нестандартный, занимательный характер.
В творческой разработке представлена работа по реализации системно – деятельностного подхода.
«Математика» (3 класс) по УМК «Перспективная начальная школа», А.Л Чекин
II.Творческая разработка урока по математике
Урок математики в 3 классе по УМК «Перспективная начальная школа»
Тема урока: «Деление с остатком»
Цели урока:
Обучающая – создание условий для самостоятельного «открытия» учащимися нового способа деления- с остатком;
Развивающая – развитие умения наблюдать, сравнивать, делать выводы.
Воспитательная – воспитание культуры общения в малых группах.
Ход урока:
I.Организационный момент
Мы пришли сюда учиться,
Не лениться, а трудиться,
Только тот, кто много знает-
В жизни что-то достигает!
II. Актуализация знаний
Повторение табличных случаев деления
2.
1Создание «ситуации успеха»
1.Математическая эстафета
Решить примеры, записанные на доске (устно)
35:7 36:6 32:4
42:6 48:8 49:7
54:9 56:7 63:7
-Давайте вспомним, как называются компоненты при делении?
(делимое, делитель, частное)
-Как найти неизвестное делимое? Делитель? Частное?
-Какие вы молодцы, значит следующее задание вы выполните с таким же успехом!
2.2. Задача на слайде
Маша и Миша ждут в гости четырёх друзей. Мама сказала, чтобы они угостили их конфетами. Миша решил заранее разделить конфеты между 6 детьми поровну. В вазе было 12 «Васильков», 15 «Ромашек» и 18 «Юбилейных».
-Найдите способ, который поможет Мише разделить конфеты.
12:6=2 18:6=3 15:6-?
III.Постановка учебной задачи
-В чем затруднение?
-Что у вас не получается выполнить? (15:6)
-Вы так легко решали предыдущие задания. Почему возникло затруднение? ( Не знаем способа деления чисел, которые не делятся нацело.
Раньше не встречались с таким делением.)
(формулирование проблемы).
-Значит, что вы не смогли выполнить? (деление 15 на 6)
-Какие конфеты вы не можете разделить на 6 частей? ( Конфеты «Ромашка» – ? (На доске фиксируется знак ?)
-Чему вы должны научиться на уроке? (Нам нужно найти новый способ деления)
-Вы можете открыть сами этот способ!
Для этого поработаем в группах
IV.Открытие новового знания
4.1 Организация групповой работы
Задание для групп
1.Обсудите в группе и предложите свой способ деления 15 конфет «Ромашка» на 6 равных частей, используя счетные палочки.
-Сделайте запись в виде выражения .
(вспоминаем правила работы в группе)
4.2.Обсуждение результатов групповой работы
-одна группа выступает, остальные сравнивают результаты
15:6=2 (осталось еще 3 палочки)
4.3.Что означает каждое число в записи деления с остатком?
Делимое – 15, делитель – 6, значение частного-2, означает, что каждому гостю досталось по 2 конфеты, а число 3- это палочки, которые остались
-Число конфет «Ромашка» 15 разделили на число 6 ( с остатком)
-У какой группы другой способ?
-Давайте выведем алгоритм этого способа деления:
4.
4.Составление алгоритма:
– ищем число близкое к делимому – неполное делимое, которое делится без остатка (12)
-делим неполное делимое 12 на 6, получается 2
-находим разницу между делимым и неполным делимым (15-12=3)
-записываем остаток (остаток 3)
Давайте заменим числа буквенной символикой
а : в = с (ост. d) – ? где d<в
-Проговорите этот алгоритм своему соседу по парте, а он вам!
4.5 -Назовите из предложенных те выражения, где деление нацело, а где деление с остатком:
49, 50, 51, 56, 60, 63, 65, 70 выбери то, что делится на 7 нацело, а что с остатком
V. Первичное закрепление
-Пользуясь алгоритмом, решите примеры по вариантам:
18:7 19:5
17:4 21:5
31:3 42:4
-Сейчас каждый решит сам примеры.
Куда будете смотреть?(алгоритм) Получилось?
-Давайте проверим результаты ( взаимопроверка – у соседа карточка с правильными ответами)
-У кого все получилось?
-Кому было легко? Почему? (хорошо знаю таблицу умножения и соответствующие случаи деления, понял и применил новый способ деления)
-Кому было трудно? Почему?
VI. Физминутка
Гимнастика для глаз
Дети двигают глазами за указкой учителя (вверх, вниз, по прямой).
Обводят прямоугольник, круг по часовой и против часовой стрелки.
Представьте, что у вас вырос нос, как у Буратино. Закройте глаза.
Обведите носом эти фигуры.
Используется гимнастика для глаз.
-снятие мышечного напряжения;
– охрана здоровья ребенка;
– соблюдение гигиенических требований.
VII. Самостоятельная работа с самопроверкой по эталону.
а : в = с (ост. d) – ?
На карточках – задания трёх уровней ( дети сами делают выбор, какое задание им решить)
1 уровень
Проверить, правильно ли решены выражения на деление с остатком.
68 : 9 = 7 (ост. 5) 53 : 6 = 8 (ост. 4)
83 : 9 = 9 (ост. 2)
2 уровень
Вставьте пропущенные цифры, чтобы получились верные записи 4… : 7 = 5 (ост. 6)
2… : 3 = 9(ост. 2)
5… : 7 = 7 (ост. 5)
3 уровень
Из чисел 16, 24, 45, 37, 65 выбери те, при делении которых на 7 в остатке получается 2.
Выполните запись деления с остатком.
Самопроверка результатов работы по эталону, выданному учителем.
Итог урока
9.1 Рефлексия учебной деятельности
-Чему вы должны были научиться?(Нам нужно было найти новый способ деления)
-Как можете проговорить новый способ деления ?(Это способ деления с остатком)
– Кто освоил новый способ деления?
9.2 Заполните карты самооценки и выразите оценку своей учебной деятельности через «светофор»:
Зеленый – я понимаю достаточно хорошо, чтобы еще кому-нибудь объяснить.
Желтый – я кое-что понимаю, но не все.
Красный – я ничего не понимаю.
X. Домашнее задание
10.1
Обязательная часть – стр. 53, выполнить № 154- выполняют все.
По желанию – № 155.
III. Список литературы
1. Асмолов А. Г. Системно-деятельностный подход к построению образовательных стандартов / А.Г. Асмолов .- М.: Просвещение, 2008.- №2.
2. Гревцова И. Системно-деятельностный подход в технологии школьного обучения / И. Гревцова // Школьные технологии, 2003. – № 6.
3. Дмитриев С. В. Системно-деятельностный подход в технологии школьного обучения / С. В. Дмитриев // Школьные технологии, 2003.- N 6. – 30 с.
4.Урок в современной начальной школе: лучшие педагогические практики под редакцией кандидата педагогических наук Т. О. Автайкиной/Новокузнецк МАОУ ДПО ИПК-2013
Что такое остаток? Определение, формула, свойства, пример
Что такое остаток в математике?
Остаток — это то, что «осталось» или «осталось».
Итак, что означает остаток в задаче на деление? Значение остатка остаточное значение или оставшаяся часть после задачи деления называется остатком.
В задаче на деление есть два случая.
- Когда одно число полностью делится на другое число: В этом случае у нас ничего не остается в конце деления.
- Когда число не делится на другое число: В этом случае у нас остается некоторое значение в конце деления. Мы называем это «остатком» от деления.
Определение остатка
Определение остатка в математике может быть дано как остаточное число в задаче на деление . Если число не делится полностью на другое число, то у нас остается значение, которое называется остатком. Остаток всегда меньше делителя.
Родственные игры
Части деления
Четыре важные части любой задачи на деление:
- Дивиденд
- Делитель
- Частное
- Остаток
В задаче на деление делимое число называется делимым. Число, на которое делится делимое, называется делителем. Результат деления называется «частным». Когда делимое не полностью делится на делитель, остаточное значение называется «остатком».
Пример: разделить 25 на 6.
Мы знаем, что $6\times4 = 24$
Таким образом, частное $= 4$ и остаток от 1.
Мы можем записать это как $25 \ div 6 \rightarrow 4 R 1$, где 4 — частное, а 1 — остаток.
Связанные рабочие листы
Остаток в делении: примеры
Давайте обсудим несколько примеров.
Пример 1: Предположим, у вас есть 9 цветов (9 — делимое). Вы хотите разделить цветы поровну на 2 группы (2 — это делитель). В каждой группе будет по 4 цветка (4 — частное). Таким образом, 8 цветков распределяются поровну, а 1 цветок остается.
Пример 2: Число 16 не делится точно на 5. Ближайшее значение к 16, которое мы можем получить, равно $5\times3 = 15$
Следовательно, $16 \div 5$ дает частное 3, а остаток равен $16\;-\;(5\times3)= 1$
Следовательно, $R = 1$
Пример 3: Задача деления с остатком 0.
$27\div9 = 3$
27 полностью делится на 3.
Таким образом, остаток равен 0.
Формула остатка
В задаче на деление делимое, делитель, частное и остаток связаны следующим уравнением
$Дивиденд = (Делитель \Частное) + Остаток$
Таким образом, мы можем выразить остаток как
$Остаток = Делимое\;-\;(Делитель\Дробное)$
Как найти остаток
Как найти остаток в задаче на деление? Давайте разберем шаги на примере. Этот метод удобен для использования, когда задействованные числа невелики и просты в использовании для вычислений.
Пример: Найдите остаток от деления 69 на 6.
Шаг 1: Определите части раздела.
Здесь делимое $= 69$, делитель $= 6$
Шаг 2: Проверить, есть ли делимое в таблице делителей. Если нет, найдите кратное делителя, ближайшего к делимому.
Здесь 69 не входит в таблицу 6. Оно не делится на 6 полностью.
Ближайшее кратное $6 = 6\times11 = 66$
и частное $= 6$
Шаг 3: Вычесть это множитель от дивиденда.
$69\;-\;66 = 3$
Вы также можете использовать формулу, которую мы обсуждали ранее.
$Остаток = Дивиденд\;-\;(Делитель \множество Частное)$
Здесь остаток $= 69 – (6\times11) = 3$
| $18\дел 7$ | $130 Частное= 2$ | Остаток $= 4$ | ||
| $15 \дел 10$ | Частное $= 1$ | Остаток $=2 5$ | Частное $= 3$ | Остаток $= 5$ |
| $46 \дел 9$ | Частное $= 5$ | Остаток $= 1$ | 8 19013 9013 div 5$Частное $= 3$ | Остаток $= 0$ |
Метод деления в длину
Лучший способ найти остаток — метод деления в длину. Когда делимое большое число, лучше использовать метод длинного деления. Это метод деления больших чисел на более мелкие группы или части. Это помогает разбить проблему на простые и легкие шаги.
Обратите внимание, что остаток всегда должен быть меньше делителя. Если он больше делителя, значит, деление неполное.
Пример: Разделите 75 на 4. Найдите остаток.
Свойства остатка
- Остаток всегда меньше делителя.
- Если одно число (делитель) полностью делит другое число (делимое), то остаток равен 0. Это называется полным делением.
- Если делимое кратно делителю, то остаток равен 0,
Узнайте об остатке с помощью действия
Длинное деление — это метод, который позволяет нам делить большие числа на несколько меньших групп или частей. Когда мы делим делимое на делитель, полученное частное представляет собой количество групп, которые можно составить, а остаток определяет, сколько элементов или чисел останется несгруппированным.
Давайте проведем веселое занятие и познакомимся с понятиями деления и остатка.
Рассмотрим группу предметов, которую нужно разделить на равные группы.
- Количество объектов: Дивиденд
- Количество групп: Делитель
- Количество элементов в каждой малой группе: Частное
- Осталось: Остаток
Пример 1: Как мы можем разделить 12 цветов между 3 детьми?
Если 12 цветов разделить между 3 детьми, то каждый ребенок получит по 4 цветка и ни одного цветка не останется.
Пример 2: Разделите 9 книг на 2 равные группы. Сколько книг осталось?
Когда 9 книг делятся на две группы, каждая группа получает по 4 книги и остается 1 книга.
Когда мы не можем составить равные группы или распределить поровну по всем группам, число, оставшееся неразделенным, называется остатком.
Как представить остаток
Мы можем представить части задачи деления, используя одно уравнение.
Пример 1: Если у вас есть 9 ирисок, и вы делите их поровну со своими четырьмя друзьями. Сколько ирисок у вас будет?
Если вы дадите по две ириски своим друзьям, вы разделите 8 ирисок. У вас останется только 1 ириска, и этот остаток от 1 ириски называется остатком.
Математически это выражение можно записать так:
$9 \div 4 = 2 \;R\; 1$
9 — делимое, 4 — делитель, 2 — частное, 1 — остаток.
Пример 2: Делим 22 на 3.
Получаем 3 равные части от 7, которые в сумме дают 21.
$3\times7 = 21$
У нас осталось 1. Это 1 — остаток.
Представим это как: $21 \div 7 = 3$
Пример 3: Другой способ представить остаток — представить его в виде смешанных дробей. Число 19, деленное на 2, можно записать как $\frac{19}{2} = 9\frac{1}{2}$.
Факты об остатке
- Когда одно число полностью делится на другое число, остаток равен 0, и такое деление называется полным делением.
- Слово «остаток» происходит от латинского слова «remanere», что означает «остаться».
Заключение
В этой статье мы узнали об остатке в задаче на деление, методах нахождения остатка, методе деления в длину, свойствах остатка. Давайте решим несколько примеров, чтобы лучше понять концепцию.
Решенные примеры остатка
1. Найдите остаток от деления 23 на 4.
Решение:
Здесь, divisor $ = 4 $, дивиденд $ = 23 $
Остальная $= 3$, делимое $= 87$
87 полностью делится на 3.
Таким образом, остаток равен 0.
3. Какой член отсутствует?
Решение:
Здесь делитель равен 7, а делимое равно 456.
Недостающий член $= 7\times6 = 42$
4. Найдите делимое, делитель, частное и остаток при делении 100 на 9?
Решение :
Здесь делитель $= 9$ и делимое $= 100$
Ближайшее к 100$ кратное 9 = 9\times11 = 99$
$= 100\;-\;99 = 1$
Практические задачи на остаток
1
Найдите делимое, если делитель равен 8, частное равно 71, а остаток равен 4.
125
458
582
158
Правильный ответ: 582
$Дивиденд = (делитель х частное) + остаток$
$Дивиденд = (71\times8) + 4$ 0 9 0 015 $2Дивиденд 3 2
40 шоколадок и 10 детских. Если мы разделим конфеты поровну между всеми учениками, сколько останется?
1
3
5
Правильный ответ: 0
$40 = 10\times4$
40 кратно 10.
Таким образом, оно полностью делится на 10.
Остаток $= 0$
3
Остаток всегда меньше ____.
делимое
делитель
частное
Правильный ответ: делитель
Остаток всегда меньше делителя.
4
У Беллы $\$31$. Она делит его поровну между 4 друзьями. Какая сумма у нее осталась?
$\$2$
$\$4$
$\$3$
$\$1$
Правильный ответ: $\$3$
$31div4 = 7$ с остатком 3
Таким образом, у Беллы осталось $\$3$.
Часто задаваемые вопросы об остатке
Всегда ли остаток равен 0?
Если одно число делится на другое число без остатка, то остаток равен 0. Если число не делится на другое число полностью, то остаток не равен 0.
Каково правило для остатков?
Остаток всегда меньше или равен делителю. Если остаток больше делителя, то длинное деление неполное или содержит ошибку.
Каковы недостатки метода деления в длину при нахождении остатка?
Он довольно длинный и усложняется при использовании с большими цифрами.
Существуют ли быстрые приемы, чтобы найти остаток или какую-нибудь короткую формулу?
Если вы хотите ускорить расчет, вы можете использовать эту формулу вместо метода деления: $Remainder = Dividend \;-\; (Делитель\умножить на частное)$
Что значит, когда остаток равен нулю?
Когда остаток равен 0, это означает, что и частное, и делитель являются множителями делимого.
Что такое деление с остатком? Объяснение для начальной школы
Деление с остатком и деление в целом является ключевым навыком, которому обучают по математике в старших классах начальной школы в течение первого года обучения в средней школе. Учащиеся старших классов познакомятся с расчетами деления с остатками, когда остается определенное количество.
В этой статье мы объясним деление с остатком и предоставим рабочие примеры, в том числе текстовые задачи, чтобы помочь вам в обучении делению с остатком ваших учеников начальной школы.
Четыре операции (сложение, вычитание, умножение и деление) являются ключевой частью математической программы в начальной школе. Обучение делению начинается в 3-м классе, где детей учат только делению, где ответы точные, без остатка. Начиная с 4-го класса учащиеся должны уметь работать с задачами на деление с остатками.
Контрольные работы по математике на конец года для 4 и 5 классов
Оцените успеваемость по математике к концу 4 и 5 классов или подготовьтесь к контрольным работам штата с помощью этого пакета контрольных работ по математике
Что такое деление с остатком?
Деление с остатком — это вычисление деления без точного ответа — в ответе будет определенная сумма остатка.
- Первое число (сумма, которую нужно разделить) называется дивидендом ;
- Второе число (на которое делится делимое) называется 9.0007 делитель ;
- Ответ называется частным .
При вычислении деления с остатками мы поэтому говорим, что частное будет иметь определенное количество остатка.
Этот остаток может быть выражен в виде стандартного остатка (записывается буквой «r», а затем остатком) или дробью (остаток становится числителем, а делитель становится знаменателем).
Например, при делении с использованием прямоугольных массивов или моделей площадей 432 ÷ 5 = 86 r2 (стандартный остаток) и 496 ÷ 11 = 45 \frac{1}{11} (остаток дроби).
Начиная с 6-го класса учащиеся начинают деление с деления в большую сторону или по стандартному алгоритму. Задача 432 ÷ 15 может быть выражена как 28 r12, 28 \frac{4}{5} или 28,8, как в приведенных ниже примерах.
См. также: Что такое деление?
Как выполнить деление с остатками
При делении с остатками остаток всегда будет меньше делителя. Если он больше, то была допущена ошибка, так как это означает, что из этого остатка можно сделать другую «группу».
Например, возьмем 14 ÷ 3. Есть 4 группы по 3 в 14 с 2 оставшимися – это выражается как 4 r2. Технически, как и во втором примере ниже, это также можно записать как 3 r5, однако мы можем сделать еще одну группу делителя (3) из остатка (5), что затем превратит его в 4 r2 как исходный ответ.
.
Точно так же технически это можно записать как 2 r8 (хотя мы могли бы сделать еще 2 группы делителя из остатка здесь) или 1 r11 (мы могли бы сделать еще 3 группы делителя из этого остатка), но исходное ответ 4 r2 является математически правильным.
Эта концепция аналогична длинному делению и всем методам деления. Помните, что остаток может быть выражен одним из трех способов.
- В качестве остатка (например, r1 в приведенном ниже примере)
- В виде дроби (например, \frac{1}{5} в приведенном ниже примере – остаток от 1 становится числителем дроби, а делитель 5 становится знаменателем).
- Десятичный
Метод такой же, как и выше, но после завершения деления разряда единиц добавьте десятичную точку и ноль в конец делимого, чтобы по существу «продолжить» деление (продолжайте, чтобы убедиться, что разрядные разряды равны выровнен правильно).
В этом случае, после подсчета, что 21 единица, разделенная на 5, равна 4 единицам с 1 оставшейся единицей, 1 оставшаяся единица может рассматриваться как 10 десятых вместо этого.
Затем мы можем разделить 10 десятых на 5, что равно 2 десятым, следовательно, частное равно 134,2.
Это то же самое, что 134 r1 или 134 \frac{1}{5}, так как при делении на 5 остаток от 1 совпадает с \frac{1}{5}, что эквивалентно 2 десятым.
Если десятичный остаток длиннее одного знака после запятой, продолжайте добавлять 0 к делимому до тех пор, пока деление не завершится, или если десятичные дроби продолжаются долго, как в приведенном ниже примере 425 ÷ 7, просто округляйте до требуемая степень точности – в данном случае 60,7 до 1 знака после запятой (или 60,7143 до 3 знаков после запятой).
Задачи на деление с остатком длиннее 2 знаков после запятой вряд ли будут задавать детям в начальной школе.
Однако полезно знать, как интерпретировать эти ответы, особенно как округлять десятичные знаки, поскольку деление, выполненное на калькуляторе, может давать ответы с большим количеством десятичных знаков, и дети должны понимать, что это значит.
Этот процесс аналогичен методу длинного деления.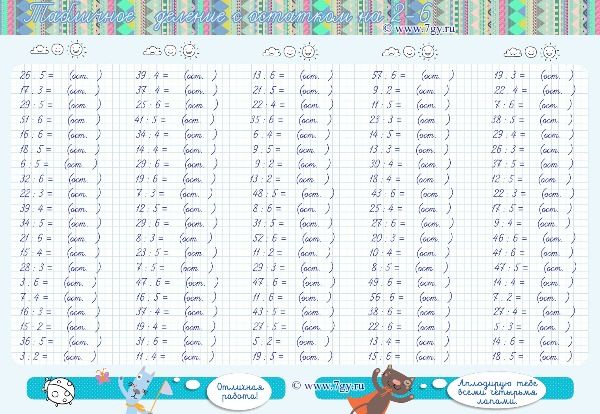
Например, 9 139 ÷ 21 можно выразить как 435 r4, 435 \frac{4}{21} или 435,19.(округлено до 2 знаков после запятой).
Примеры деления с остатками
См. ниже примеры моделей коротких областей с остатками, выраженными всеми тремя способами.
Третий пример четырехзначного деления ниже является примером повторяющегося десятичного остатка — в этом случае цифра 3 будет продолжаться вечно, поэтому лучше выразить этот остаток в виде дроби ( \frac{1} {3} в этом случае).
Оставшуюся часть этих задач на длинное деление также можно выразить тремя различными способами (метод тот же самый даже с большими числами в качестве делителей).
Когда дети узнают о делении с остатком в школе?
Общая основная учебная программа гласит, что 4-классников следует учить делить числа до 4 цифр на однозначное число, используя стратегии, основанные на разрядном значении, свойствах операций и/или связи между умножением и делением. . Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.
Пятиклассников следует научить находить целочисленные частные целых чисел с делимыми до четырех цифр и двузначными делителями, используя стратегии, основанные на разрядном значении, свойствах операций и/или взаимосвязи между умножением и деление.
Учащиеся должны уметь иллюстрировать и объяснять вычисления, используя уравнения, прямоугольные массивы и/или модели площадей.
Пятиклассники также могут связать эквивалентные дроби > 1, которые упрощаются до целых чисел с делением, и другие дроби > 1 с делением с остатком, используя числовую прямую и другие модели, и, следовательно, перейти от них к неправильным и смешанным дробям.
Шестиклассники знакомятся с делением по стандартному алгоритму, или делением в длину. К концу 6 класса учащиеся будут свободно делить многозначные числа по стандартному алгоритму.
Подробнее о том, как учить деление, читайте в нашей статье.
Как деление с остатком связано с другими областями математики?
В 5-м классе, поскольку дети должны вычислять эквиваленты десятичных дробей для простой дроби, им может потребоваться завершить деление с десятичным остатком.
Например, чтобы вычислить десятичный эквивалент \frac{5}{8}, детям нужно будет разделить 5 на 8, что в данном случае можно превратить в 5,000 ÷ 8, поскольку ответ (0,625) имеет 3 знака после запятой. .
Как деление с остатком связано с реальной жизнью?
Всякий раз, когда что-то нужно разделить между двумя или более группами, требуется разделение с остатком или без остатка. Подходящий «тип» остатка зависит от контекста проблемы.
«Стандартный» или дробный остаток подходит в тех случаях, когда точный ответ не требуется. Например, в автобусной поездке 267 человек нуждаются в транспорте, а автобусы вмещают по 42 человека. 267 ÷ 42 = 6 r15, или 6 \frac{15}{42} , или 6,36 (округлено до 2 знаков после запятой).
У нас не может быть части автобуса, поэтому здесь нам понадобится 7 автобусов (округляем до ближайшего целого числа). Десятичный остаток было бы сложнее интерпретировать (что такое 0,36 автобуса?), но другие остатки говорят нам, что в 7-м автобусе останется 15 человек, а остальные будут заполнены.
Десятичные остатки были бы более уместны в таких контекстах, как деньги. Например, купюра в 188 долларов, разделенная между пятью людьми, равна 188 ÷ 5, что составляет 37 r3, или 37 \frac{3}{5} , или 37,6. Десятичный остаток здесь соответствует денежному контексту — в этом случае каждый человек должен был бы 37,60 долларов.
Деление с остатком Примеры работы
1. 96 учеников и учителей едут на микроавтобусе на футбольный турнир. Сколько потребуется 15-местных микроавтобусов?
96 ÷ 15 = 6 r6 (это можно сделать с помощью метода письменного деления, но в этом случае легче считать по 15, чтобы увидеть, сколько вписывается в 96 – 15, 30, 45, 60, 75, 90 = 6 групп). Остается 6, что означает, что 6 человек остались без автобуса, поэтому потребуется 7 микроавтобусов.
2. Завершите числовые предложения:
a) 340 ÷ 7 = ___ остаток ___
b) ___ ÷ 3 = 295 остаток 2
a) Используйте площадную модель, чтобы получить ответ 48 остаток 0 4 9057
б) Поскольку делимое здесь отсутствует, нам нужно использовать обратное, чтобы вычислить его.
Представьте, что вопрос был __ ÷ 2 = 3 остаток 1. Мы можем вычислить делимое, умножив делитель на частное и добавив остаток: 3 x 2 + 1 = 7, поэтому 7 ÷ 2 = 3 остатка 1.
Здесь применяется тот же метод – умножьте делитель (3) на частное (295) и добавьте остаток (2) – это дает нам 887, поэтому ответ 887 ÷ 3 = 295 остаток 2.
3. Бакалейщик упаковывает яйца. В каждой коробке по 6 яиц. Бакалейщику нужно упаковать 980 яиц. Сколько коробок она может заполнить и сколько яиц останется?
Используя модель площади, мы можем вычислить, что бакалейщик может заполнить 163 коробки, и останется 2 яйца.
Практические вопросы по делению с остатком
- В школе Блокли учатся 275 детей. Они объединяются в группы по восемь человек. Какое наибольшее количество групп по восемь человек они могут составить?
Ответ: 34 группы - Какие два выражения деления имеют ответ 5 r2?
а) 17 ÷ 5
б) 17 ÷ 3
в) 22 ÷ 4
г) 22 ÷ 5
Ответы: б) и в) - Марта хочет купить игрушку стоимостью 18,49 долларов.
. Она экономит 1,50 доллара в неделю. Сколько недель ей нужно накопить, прежде чем она сможет купить книгу?
Ответ: 13 недель - В каждом вычислении впишите пропущенное число:
а) 25 ÷___ = 3r4
б) 35 ÷ ___ = 4r3
Ответы: а) 7; б) 8 - В мешочке 90 шариков. 4 ребенка берут по 20 шариков. Сколько шариков осталось в мешке?
Ответ: 10 шариков
. Она экономит 1,50 доллара в неделю. Сколько недель ей нужно накопить, прежде чем она сможет купить книгу? Ищете дополнительные ресурсы для учебного отдела? Почему бы не ознакомиться со всеми нашими статьями о вопросах на деление и рабочими листами по делению.
Подробнее:
- Как преподавать дивизию
- Объяснение разделения для начальной школы
- Чему мы научились, проводя урок длинного деления 2968 раз
Как ответить на деление с остатком?
Разделите всю сумму на равные группы, как при обычном делении.
Как остатки работают в математике?
Остатки — это «остатки» в делении — когда число было разделено и ответ не является точным числом. Они могут быть выражены в виде числа, дроби или десятичной дроби.
Есть ли у вас ученики, которым нужна дополнительная помощь по математике?
Предоставьте учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью персонализированного обучения элементарной математике с их собственным онлайн-репетитором по математике.
Каждый учащийся получает дифференцированное обучение, предназначенное для устранения индивидуальных пробелов в обучении, а система обучения гарантирует, что каждый учащийся учится в нужном темпе. Уроки соответствуют стандартам и оценкам вашего штата, плюс вы будете получать регулярные отчеты о каждом шаге.
Программы доступны для четвертого и пятого классов, и вы можете попробовать 6 уроков абсолютно бесплатно.