Примеры с делением для 4 класса: 4 класс, деление, задачи на деление многозначных чисел столбиком, свойство

Как объяснить ребенку деление столбиком: легко и доступно

Суть и принцип деления можно объяснить двумя способами: дошкольникам рассказать простыми словами, а младшим школьникам — математически. Обычно ребёнку сложно разобраться в операции деления, если он не понимает, как умножать числа, и путается в понятиях состава примера: «множитель», «сумма», произведение». В статье рассказываем, как родитель может объяснить деление доступно в зависимости от возраста ребёнка.

Как объяснить деление дошкольнику

Дети впервые сталкиваются с делением в раннем детстве, когда ещё не понимают, что значит «число». Малыш в песочнице слышит: «Поделись игрушкой», и он понимает, что ведёрко нужно отдать другу, а лопатку оставить себе. 

Основное правило для объяснения любого понятия малышам — показывать на жизненных примерах, при этом они должны соответствовать возрасту ребёнка. Поэтому дошкольникам лучше рассказывать, как делить игрушки и бананы, а не деньги и почтовые конверты.

Шаг 1.

Делить без остатка

Есть десять конфет для мамы, папы, ребёнка, бабушки и дедушки. Нужно поделить конфеты так, чтобы у всех было одинаковое количество. Ребёнок будет раздавать всем по одной, пока они не закончатся. Становясь старше, он будет учиться раздавать сразу по две, три и более.

Шаг 2. Делить с остатком

Есть десять конфет для мамы, папы, ребёнка и бабушки. Дедушка отказался от сладкого. Ребёнок может раздать каждому по две конфеты, и  две останутся.

Шаг 3. Делить с остатком, который делится

Ребёнок может раздать всем членам семьи, кроме дедушки, по половинке конфеты, разделив две конфеты, от которых дедушка отказался. Тогда у каждого будет по две с половиной конфеты.

Шаг 4. Делить с остатком, который не делится

На двоих детей нужно разделить три мяча. Один невозможно разделить, и он просто останется.

Последние два шага помогут ребёнку разобраться с дробями в будущем.

<<Форма демодоступа>>

Как объяснить деление школьнику

Чтобы ребёнок освоил деление, ему нужно знать несколько понятий:

• «числа» и «разряды»;
• «делимое», «делитель», «частное»;
• «множитель», «произведение»;
• «обратное действие».

Шаг 1. Повторить, как делить поровну и с остатком

Если ребёнок не освоил простое деление, стоит повторить его.

Шаг 2. Объяснить обратное действие

До знакомства с делением дети осваивают операции сложения, вычитания и умножения. Младшие школьники уже понимают, что вычитание — это действие, обратное сложению: если к двум прибавить два, получим четыре; и наоборот, если из четырёх вычесть два, получим два.  Объясните ребёнку, что деление — это действие, обратное умножению. Произведение чисел можно разделить на один из множителей и получить второй множитель: например, если два умножить на два, получится четыре, и наоборот, при делении четырёх на два получится два. Чтобы умножать и делить числа, нужно знать таблицу умножения.

Шаг 3. Делить двузначное число на однозначное без остатка

Стоит брать числа бо́льшие, чем в таблице умножения. Например, последнее число, на которое умножается пять в таблице умножения, — это десять, и их произведение — 50. Значит, можно начинать с 55 и выше.

Если взять 55, то легко разделить каждый разряд числа на пять. Если взять, например, 60, то ситуация становится сложнее. Здесь на помощь могут прийти деление в столбик или строчку.

Как разделить 60 на 5:

1. Сначала делим число из разряда десятков, то есть шесть делим на пять. Важно, чтобы число в этом разряде было больше числа, на которое делим. То есть если нам необходимо 30 разделить на пять, не нужно делить десятки отдельно от единиц. Так как шесть не делится на пять без остатка, нужно найти ближайшее к шестёрке меньшее число, которое делится на пять без остатка, — это пять. При делении пятёрки на пять получаем единицу. Результат этого деления записываем после знака равенства: 60 : 5 = 1_.
2. Шестёрку раскладываем по составу на пятёрку, которую взяли для деления, и единицу. Эту единицу записываем над шестёркой или просто держим в уме.
3. Соединяем единицу, которую держали в уме, и цифру из разряда единиц в числе 60, то есть единицу и ноль. 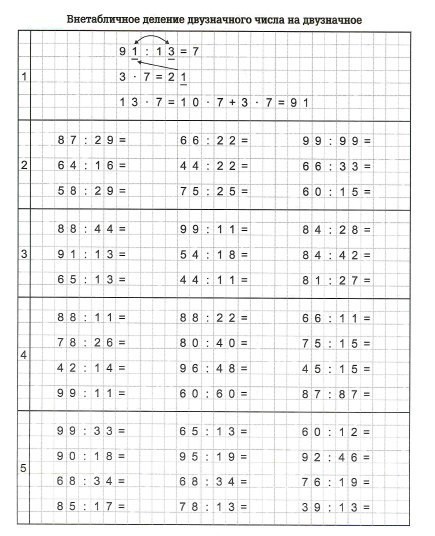Получаем десять. При делении десяти на пятёрку получаем двойку, результат этого деления записываем после знака равенства за разрядом десятков.
4. Получаем: 60 : 5 = 12.

Шаг 4. Делить двузначное число на однозначное с остатком

Здесь принцип такой же, как и в предыдущем шаге: число делим в столбик или в строчку.

Как разделить 88 на 5:

1. Сначала делим число из разряда десятков, то есть восемь делим на пять. Важно, чтобы число в этом разряде было больше числа, на которое делим. Так как восемь не делится на пять без остатка, нужно найти ближайшее к восьмёрке меньшее число, которое делится на пять без остатка, — это пять. При делении пятёрки на пять получаем единицу. Результат этого деления записываем после знака равенства: 88 : 5 = 1_.
2. Восемь раскладываем по составу на пятёрку, которую взяли для деления, и тройку. Эту тройку записываем над восьмёркой или просто держим в уме.
3. Соединяем тройку, которую держали в уме, и цифру из разряда единиц в числе 88, то есть три и восемь. 38 на пять не делится, ищем меньшее ближайшее число, делимое на пять без остатка, — это число 35. 35 : 5 = 7, результат записываем после знака равенства после разряда десятков: 88 : 5 = 17.
4. 38 раскладываем по составу, то есть на 35 и три. Так как три не делится на пять, берём взаймы ноль и ставим запятую в частном: 17,_. Соединяем три и ноль, получаем 30. При делении тридцати на пятёрку получаем шесть. Результат этого деления записываем после знака равенства после запятой.
5. Получаем: 88 : 5 = 17,6.

Как только ребёнок освоит навык, можно усложнять задания: делить трёх-, четырёхзначные числа на однозначное с остатком и без него.

Шаг 5. Делить трёхзначное число на двузначное с остатком и без него

Принцип деления такой же, как и выше, но нужно делить уже на двузначное число.

Как разделить 100 на 20:

Число в разряде сотен меньше делителя. Смотрим на число, составляющее разряды сотен и десятков, оно тоже меньше делителя, поэтому берём всё число сразу. Подбором находим частное: 100 : 20 = 5.

Как разделить 104 на 32:

1. В этом примере нам нужно взять всё число целиком. Оно делится с остатком, поэтому подбираем ближайшее к 104 меньшее число. 96 : 32 = 3, результат записываем после знака равенства: 104 : 32 = 3_.
2. 104 раскладываем по составу, то есть на 96, которую взяли для деления, и восемь. Восемь на 32 не делится, поэтому берём взаймы ноль и ставим запятую в частном: 3,_. Соединяем восемь и ноль, получаем: 80 : 32. Число 80 не делится на 32 без остатка, поэтому подбираем ближайшее к 80 меньшее число, делимое на 32 без остатка, — это 64. 64 : 32 = 2, результат записываем после знака равенства после запятой: 104 : 32 = 3,2_.
3. 80 раскладываем по составу, то есть на 64, которую взяли для деления, и 16. 16 на 32 не делится, и оно меньше делителя, поэтому берём взаймы к 16 ноль. Получаем: 160 : 32 = 5,  результат записываем после знака равенства после запятой в разряде сотых.
4. Получаем: 104 : 32 = 3,25.

Альтернативные варианты

Группировка

Чтобы разделить 30 на три, можно представить 30 мистеров Фоксов и считать тройками, то есть тем числом, на которое будем делить. В группе из 30 мистеров Фоксов получится десять групп по три мистера Фокса. Значит, 30 : 3 = 10.

30 мистеров Фоксов, где обведено по три мистера.

<<Форма аттестации>>

Разложение

Чтобы разделить 90 на три, можно представить 90 в виде суммы чисел, каждое из которых точно делится на три.

Подбор

Чтобы разделить 96 на 12, нужно подбирать числа, пока не получим восемь: 96 : 12 = 8.

Иллюстрация: justyna stasik / Dribbble

3000 примеров по математике с ответами и методическими рекомендациями. 4 класс. Решаем в столбик (Елена Нефёдова, Ольга Узорова)

Читать отрывок

139 ₽

100 ₽

+ до 20 баллов

Бонусная программа

Итоговая сумма бонусов может отличаться от указанной, если к заказу будут применены скидки.

Офлайн

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

В наличии в 141 магазине. Смотреть на карте

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

Пособие содержит примеры на умножение и деление в столбик. При составлении пособия соблюдалась принятая в классической начальной школе методическая последовательность в отборе и системе расположения заданий. Примеры распределены по работам, каждая из которых дополнена работой над ошибками. В конце пособия даны ответы. На второй и третьей сторонке обложки приведены алгоритмы решения примеров на различные действия, на четвертой сторонке – методические указания по работе с пособием.

Книга будет полезна для коллективной и индивидуальной работы на уроке и самостоятельных занятий дома.

Описание

Характеристики

Пособие содержит примеры на умножение и деление в столбик.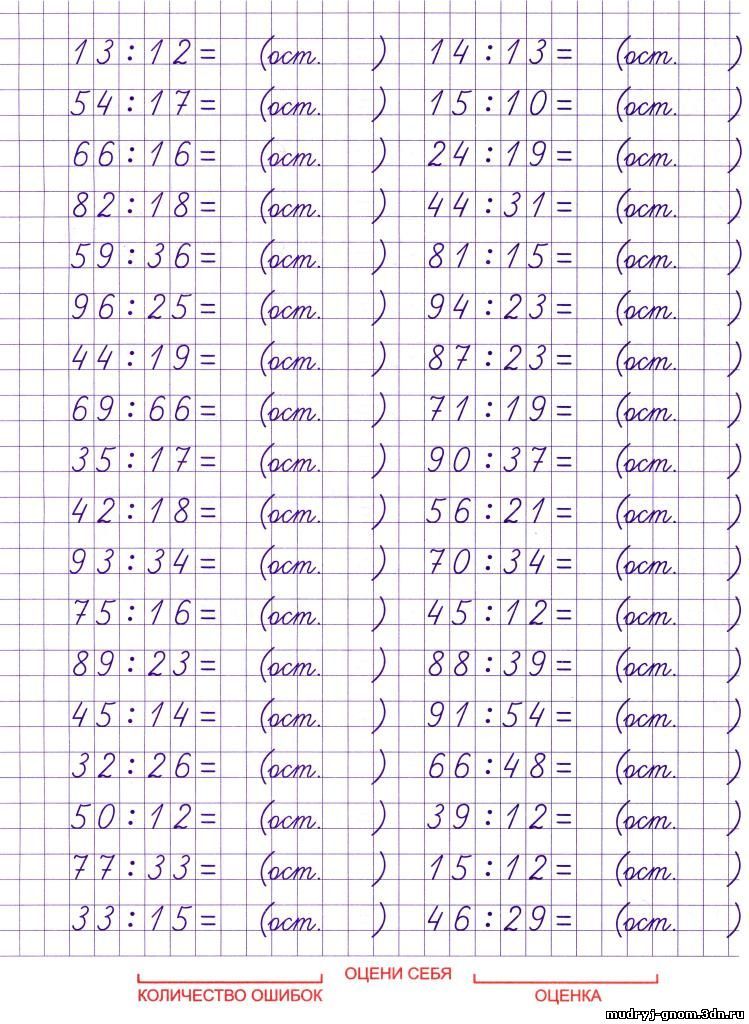 При составлении пособия соблюдалась принятая в классической начальной школе методическая последовательность в отборе и системе расположения заданий. Примеры распределены по работам, каждая из которых дополнена работой над ошибками. В конце пособия даны ответы. На второй и третьей сторонке обложки приведены алгоритмы решения примеров на различные действия, на четвертой сторонке – методические указания по работе с пособием.

Книга будет полезна для коллективной и индивидуальной работы на уроке и самостоятельных занятий дома.

АСТ

Как получить бонусы за отзыв о товаре

1

Сделайте заказ в интернет-магазине

2

Напишите развёрнутый отзыв от 300 символов только на то, что вы купили

3

Дождитесь, пока отзыв опубликуют.

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

умножение и деление многозначных чисел

Плюсы

Пособие снабжено подробным описанием решения примеров, а также информация почему возникают трудности, и как их устранить. Мне как раз помог этот материал. Советую.

Минусы

тонкая

Книга «3000 примеров по математике с ответами и методическими рекомендациями. 4 класс. Решаем в столбик» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене. Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом другом регионе России, вы можете оформить заказ на книгу Елена Нефёдова, Ольга Узорова «3000 примеров по математике с ответами и методическими рекомендациями. 4 класс. Решаем в столбик» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.

Умножение и деление: Введение в деление

Урок 4: Введение в деление

/en/multiplicationdivision/video-multiplication/content/

Что такое деление?

Подразделение делит что-то поровну. Например, допустим, у вас есть 10 лотерейных билетов, и вы хотите поделиться ими с 5 друзьями.

Вы делите билетов между друзьями. Каждый друг получает равное количество билетов.

Видите, у каждого из них по 2 билета? Когда вы делите 10 билетов между пятью друзьями, вы создаете 5 равных групп по 2 билета.

В реальной жизни часто случаются деления. Например, рассмотрим ситуацию ниже.

• Представьте, что у нас есть 6 кексов…

• Представьте, что у нас есть 6 кексов… и 2 пустых лотка.

• На каждый поднос мы положим равное количество кексов. Другими словами, мы разделим кексов между двумя подносами.

• На каждый поднос мы положим равное количество кексов. Другими словами, мы будем делить кексы между двумя лотками.

• На каждый поднос мы положим равное количество кексов. Другими словами, мы разделим кексов между двумя подносами.

• На каждый поднос мы положим равное количество кексов. Другими словами, мы разделим кексов между двумя подносами.

• На каждый поднос мы положим равное количество кексов. Другими словами, мы разделим кексов между двумя подносами.

• На каждый поднос мы положим одинаковое количество кексов. Другими словами, мы разделим кексов между двумя подносами.

• На каждый поднос мы положим равное количество кексов. Другими словами, мы разделим кексов между двумя подносами.

• Шесть кексов были разделены на 2 равные группы.

• Давайте посчитаем кексы, чтобы узнать, сколько кексов в каждой группе.

• Давайте посчитаем кексы, чтобы узнать, сколько кексов в каждой группе.

• Давайте посчитаем кексы, чтобы узнать, сколько кексов в каждой группе.

• Давайте посчитаем кексы, чтобы узнать, сколько кексов в каждой группе.

• Давайте посчитаем кексы, чтобы узнать, сколько кексов в каждой группе.

• Давайте посчитаем кексы, чтобы узнать, сколько кексов в каждой группе.

• Давайте посчитаем кексы, чтобы узнать, сколько кексов в каждой группе.

• На каждом подносе по 3 кекса. Если вы начнете с шести кексов и разделите их на две равные группы, то в каждой группе будет по три кекса.

Написание выражений деления

В слайд-шоу вы видели, что мы разделили шесть кексов на две равные группы. Чтобы вычислить количество кексов в каждой группе, вы можете написать выражение деления следующим образом:

6 / 2

Вы также можете написать выражение следующим образом:

6 ÷ 2

Любое выражение можно прочитать как шесть разделить на два . Знак деления (/ или ÷) означает, что что-то делится. Поэтому мы всегда ставили после первого числа — было 6 кексов, и мы разделили их на 2 группы.

Многие жизненные ситуации можно выразить с помощью деления. Например, представьте, что вы расставляете 15 банок на 3 полках. Вы можете разделить, чтобы убедиться, что вы поставили одинаковое количество банок на каждой полке. Другими словами, 15 банок, разделенных тремя полками, или 15/3.

Попробуйте это!

Попробуйте настроить эти ситуации как выражения деления. Пока не пытайтесь их решить.

У учительницы есть 16 карандашей, которые она распределяет поровну между 4 учениками.

У флориста есть 18 роз, и он делит их поровну между 3 вазами.

У вас есть 6 угощений, которыми вы поровну делитесь с 3 собаками.

Решение задач на деление

Вы можете использовать , считая , для решения простых задач на деление. Например, допустим, у нас есть 12 саженцев. Решаем посадить их в два ровных ряда. Сколько растений в каждом ряду? Мы могли бы написать этот вопрос так:

12 / 2

Помните, что это выражение означает 12 разделить на два , или 12 саженцев разделить на 2 ряда. Это простая проблема. Чтобы решить ее, вы можете разделить саженцы на две группы, а затем подсчитать , сколько растений в каждой группе. Ответ: 6. Мы знаем, что 12/2 = 6.

В то время как подсчет работает для задач, которые начинаются с маленьких чисел, задача, которая начинается с большого числа , может занять много времени, чтобы решить ее с помощью подсчета. По этой причине большинство людей запомнить простых задач на деление, чтобы быстро их решать. Если это звучит сложно, не волнуйтесь. С некоторой практикой вы сможете быстро запомнить ответы.

В разделе «Введение в умножение» вы познакомились с таблицей умножения на . На этом уроке вы использовали его для решения задач на умножение. Вы также можете использовать таблицу умножения для решения задач на деление.

Давайте начнем с проблемы, с которой мы уже знакомы. Как бы мы решили задачу о ростке с таблицей умножения?

Нажмите на слайд-шоу ниже, чтобы узнать, как это сделать.

• Помните, что каждое число в верхней части таблицы умножения находится в начале столбца .

• Например, это столбец, который идет с 7.

• Каждое число в левой части таблицы умножения является началом строки . Этот ряд идет с 9.

• Давайте попробуем решить задачу о ростке: 12 / 2.

• Сначала найдите число, на которое вы делите, справа от знака деления. В 12/2 мы делим на 2.

• Найдите столбец 2.

• Затем найдите число, которое вы делите, слева от знака деления. В 12/2 это 12.

• Найдите 12 в колонке 2.

• Найдите число в начале ряда, которое перекрывает 12. В данном случае это 6-й ряд.

• Итак, ответ или частное для 12/2 равно 6.

• Попробуем еще раз. На этот раз мы решим 15 / 5.

• Сначала мы найдем 5-й столбец, так как мы делим на 5.

• Затем мы найдем 15 в 5-м столбце, так как это число, которое мы делим.

• Наконец, мы найдем число в начале строки, которое перекрывает 15. Это 3. Итак, 15/5 = 3.

Попробуйте!

Решите эти задачи на деление. Если вам нужна помощь, вы можете использовать таблицу умножения.

42 ÷ 7 =

5 ÷ 1 =

33 ÷ 3 =

Остатки

На предыдущих страницах мы делили числа поровну. Например, в начале урока мы разделили 10 билетов поровну между 5 людьми. Каждый получил по 2 билета. Что происходит, когда число нельзя разделить поровну?

Например, рассмотрим ситуацию ниже.

• Допустим, у нас есть 10 билетов…

• Допустим, у нас есть 10 билетов… которые мы делим между 3 друзьями.

• Попробуем решить задачу 10 / 3.

• Посмотрим, сколько билетов мы сможем дать каждому из наших друзей…

• Посмотрим, сколько билетов мы сможем дать каждому из наши друзья…

• Посмотрим, сколько билетов мы можем подарить каждому из наших друзей… Один…

• Посмотрим, сколько билетов мы сможем подарить каждому из наших друзей. .. Один …

• Посмотрим, сколько билетов мы сможем подарить каждому из наших друзей… Один…

• Давайте посмотрим, сколько билетов мы можем дать каждому из наших друзей… Один… Два…

• Давайте посмотрим, сколько билетов мы можем дать каждому из наших друзей… Один. .. Два…

• Давайте посмотрим, сколько билетов мы можем дать каждому из наших друзей… Один… Два…

• Давайте посмотрим, сколько билетов мы можем дать каждому из наших друзья… Раз… Два… Три.

• Что теперь? У нас 3 друга и остался только 1 билет.

• Это означает, что 1 — это остаток или оставшаяся сумма.

• Мы готовы написать наше частное.

• У каждого друга по три билета, поэтому запишем 3.

• Затем запишем остаток. Это 1. Видите, как мы написали это рядом со строчной буквой r ?

• Итак, 10/3 = 3 r1. Мы можем прочитать это частное как три остатка один . 10 билетов, разделенных на 3 друзей, означает, что каждый друг получает 3 билета, а 1 билет остается.

Из слайд-шоу видно, что остаток (1) меньше, чем число, на которое мы делим (3). Так будет всегда, когда у проблемы есть остаток. Например, взгляните на каждую из этих задач ниже:

21/5 = 4 r1

Остаток от 1 меньше 5.

76/6 = 12 r4

Остаток от 4 меньше 6.

Если остаток больше, это означает, что остаток слишком велик. Вам нужно будет попробовать разделить еще раз. Например, если у вас 4 друга и осталось 7 билетов, вы знаете, что каждый друг может получить как минимум еще один билет.

Практика!

Практика разделения с этими проблемами. Если хотите, можете воспользоваться таблицей умножить на . Есть 3 наборов задач по 5 задач в каждом.

Установите 1

72 ÷ 9 =

64 ÷ 8 =

70 ÷ 10 =

55 ÷ 11 =

21 ÷ 3 =

Установка 2

35 ÷ 5 =

322. 322. 322. 322. 322. 322. =

72 ÷ 6 =

12 ÷ 2 =

28 ÷ 7 =

Набор 3

6 ÷ 1 =

81 ÷ 9 =

24 ÷ 3 =

49 ÷ 7 =

144 ÷ 12 =

Продолжать

Предыдущий: Видео: Умножение

Далее:Длинная дивизия

/en/multiplicationdivision/long-division/content/

Стратегии разделения для учащихся старших классов

3-й класс

Купить сейчас

4 класс

Купить сейчас

5-й класс

Купить сейчас

2-й класс

Купить сейчас

15 января 2020 г. 4 комментария

На прошлой неделе я помог вам познакомить ваших третьеклассников с делением. Щелкните здесь , чтобы просмотреть эту запись в блоге. Сегодня давайте рассмотрим стратегии разделения для ваших четверо-пятиклассников.

1. Используйте манипуляции!

У вас может возникнуть соблазн пропустить этот шаг, но учащимся крайне важно начать с конкретного этапа, чтобы развить концептуальное понимание деления. Ниже приведены несколько примеров того, как вы можете использовать десятичные блоки для моделирования деления. Один из способов модели  68 ÷ 4 показано ниже.

2. Использование модели площади для частных частных

Учащиеся знают, что они могут найти площадь прямоугольника, умножив длину x ширину .

В приведенной ниже модели мы знаем ширину и общую площадь прямоугольника. Нам нужно найти длину.

3. Неполные частные

В этом примере учащиеся должны выяснить, сколько групп по 6 содержится в числе 1428. Потребовалось бы очень много времени, чтобы использовать стратегию повторного вычитания, изученную в третьем классе.

Вместо этого учащиеся могут вынимать куски в группах по 6 , используя стратегию частичного частного.

Ниже приведен еще один пример разделения фрагментов на группы по 7 штук. После того, как вы подтвердите подписку, бесплатные ресурсы, перечисленные в этом сообщении блога, будут отправлены на ваш почтовый ящик!

Загрузите халяву!

Введите адрес электронной почты и ресурс будет отправлен на ваш почтовый ящик!

Имя

Адрес электронной почты

Мы используем это поле для обнаружения спам-ботов. Если вы заполните это, вы будете отмечены как спамер.

Работает на ConvertKit

Что дальше?

Если ваши 4- или 5-классники борются с этими стратегиями, возможно, им придется вернуться и повторить основы деления.

Щелкните здесь , чтобы прочитать сообщение в блоге, посвященное введению деления в третьеклассники.

Нужны ресурсы для ваших математических центров?

Нажмите на изображения ниже, чтобы просмотреть бумажные и безбумажные математические центры четвертого и пятого классов.

 

    

---

Сохранить на потом

Рубрики: Math Workshop, Multiplication & Division

Скачать бесплатно!

3-й класс Распечатка + цифровая математика

Получите доступ к ТРЕМ печатным и цифровым математическим играм, чтобы повторять дроби!

Я хочу эту халяву!

Вам также могут понравиться эти публикации

Взаимодействие с читателями

Math Tech All Access

Получите мгновенный доступ ко всем ресурсам Math Tech Connections!

Вступай в Клуб!

Интерактивные цифровые математические слайды

Все ресурсы

Привет, друзья!

Меня зовут Мариэла! Я преподаватель и основатель Math Tech Connections. Я начал создавать ресурсы для своих учеников, когда увидел, что обучение по учебнику не работает. Студентам нужны увлекательные, практические занятия! Моя цель — сэкономить ваше время с помощью качественных, соответствующих стандартам ресурсов, которые делают математику увлекательной.