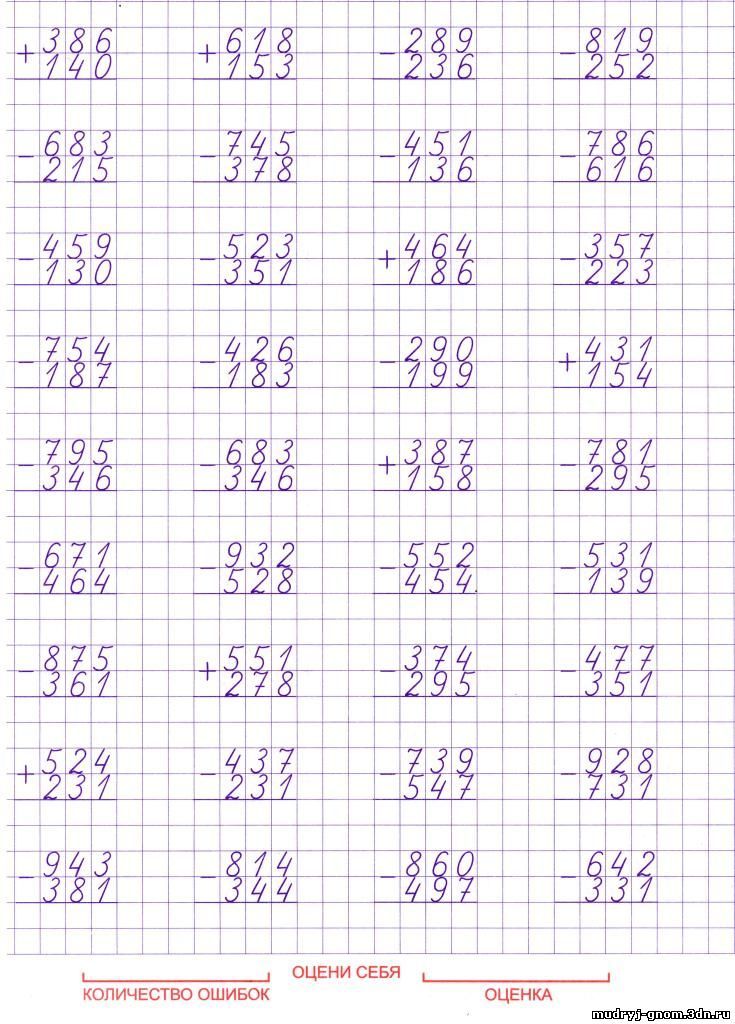
Примеры по математике в столбик: примеры столбиком 2 класс | Картотека по математике (2 класс):
примеры столбиком 2 класс | Картотека по математике (2 класс):
2 класс
Письменное сложение двузначных чисел без перехода через десяток.
В-1 +34 +42 +76 +84 +52 +27 + 63 23 37 12 14 35 52 26 + 26 +57 +88 +65 + 75 +44 +36 31 22 11 23 23 35 53 |
В-2 +25 + 46 +51 +34 +62 +77 + 84 +14 34 22 36 54 27 21 13 73 +32 +64 +15 +43 +26 + 12 + 48 +37 43 24 63 45 72 84 31 41 |
В-3 +45 + 36 +24 +13 +51 +62 +72 +84 53 42 65 76 28 27 25 13 +35 + 63 +56 +67 +82 + 72 +53 +31 23 36 22 12 17 26 34 58 |
2 класс
Письменное сложение двузначных чисел без перехода через десяток.
В-1 _98 _65 _74 _86 _59 _48 _34 _48 35 34 51 63 47 26 13 25 _89 _56 _47 _68 _95 _84 _43 _97 76 23 36 45 73 53 22 64 |
В-2 _85 _76 _65 _98 _54 _49 _63 _96 54 43 33 75 32 27 41 64 _58 _67 _56 _89 _45 _94 _36 _69 37 46 35 67 34 72 14 37 |
В-3 _74 _96 _85 _69 _48 _37 _58 _99 43 65 52 36 24 15 36 78 _47 _69 _58 _96 _84 _73 _85 _98 36 46 26 63 61 52 64 74 |
2 класс
Письменное сложение и вычитание двузначных чисел без перехода через десяток.
В1 +24 _56 +75 _98 + 32 _87 +15 54 23 12 76 56 75 73 _97 +32 _78 +47 _ 69 +53 _88 +64 85 24 56 52 37 36 56 23
|
В-2 +45 _42 +57 _89 + 65 _78 _37 +37 42 21 32 77 34 56 16 31 +47 _87 +31 _98 +56 _87 +26 _75 32 45 48 76 32 43 43 51 |
В-3 +36 _86 +31 _93 +32 _56 +75 _64 43 52 37 62 47 33 22 42 +77 _25 +52 _48 +43 _76 +53 _86 21 13 36 27 56 44 26 63 |
2 класс
Письменное сложение и вычитание двузначных чисел без перехода через десяток.
В-4 +36 _85 _97 +54 _48 +73 _84 +37 52 63 74 42 16 24 53 62
_67 +63 _96 +45 _83 +27 _69 +13 25 16 53 22 41 41 36 84 |
В-5 +45 _94 +32 _86 +63 _78 +41 -57 33 73 57 52 31 26 38 34 +62 _85 +41 _97 +36 _76 +54 _95 23 54 37 75 33 32 15 63 |
В-6 +31 _67 +54 _97 +45 _86 +23 _76 24 34 35 64 34 53 46 33 +64 _ 75 +31 _68 +23 _96 +14 23 43 37 27 56 74 84 |
2 класс
Письменное сложение двузначных чисел с переходом через десяток.
В-1 +25 + 46 +53 +34 +62 +77 + 74 +14 47 39 28 57 19 14 18 79 + 26 +57 +78 +65 + 65 +44 +36 37 24 15 28 27 38 56 |
В-2 +45 +36 +24 +16 +53 +68 +69 +74 46 48 69 76 28 27 25 17 +35 + 58 +56 +67 +77 + 66 +59 +34 29 36 29 16 17 26 34 58 |
В-3 +34 +44 +76 +79 +56 +27 + 67 29 37 15 14 35 56 26 + 26 +57 +78 +65 + 65 +49 +36 38 24 13 29 28 35 57 |
2 класс
Письменное вычитание двузначных чисел с переходом через десяток.
В-1 _93 _61 _74 _86 _51 _48 _32 _44 35 34 57 68 37 29 13 25 _81 _56 _47 _63 _95 _84 _43 _97 76 29 19 45 77 58 25 69 |
В-2 _85 _76 _65 _91 _54 _41 _63 _96 57 49 36 75 36 27 34 69 _58 _67 _53 _84 _45 _94 _36 _63 39 48 25 57 18 66 18 37 |
В-3 _74 _96 _85 _61 _48 _32 _54 _91 48 69 57 36 29 15 36 78 _47 _63 _58 _96 _84 _73 _85 _93 18 36 29 68 57 2 8 57 74 |
2 класс
Письменное сложение двузначных чисел вида 37+53
В-1 +34 +42 +76 +84 +52 +27 +63 26 38 14 16 38 53 27 + 26 +57 +88 +65 + 75 +44 +36 34 23 12 25 25 36 54 |
В-2 +25 + 46 +51 +34 +62 +77 + 84 +14 35 24 39 56 28 23 16 76 +32 +64 +15 +43 +26 + 12 + 48 +37 48 26 65 47 74 88 32 43 |
В-3 +45 + 36 +24 +13 +51 +62 +72 +84 55 44 66 77 29 28 28 16 +35 + 63 +56 +67 +82 + 72 +53 +31 25 37 24 13 18 28 37 59 |
2 класс
Вычитание из круглого числа двузначного.
В-1 _40 _60 _80 _90 _30 _100 _70 23 17 46 58 13 89 35 _50 _90 _60 _80 _100 _70 _30 32 48 25 41 57 38 16 |
В-2 _50 _90 _60 _100 _40 _80 _30 27 74 38 69 22 56 17 _70 _60 _80 _40 _100 _50 _90 43 19 48 24 79 36 67
|
В-3
_90 _40 _80 _30 _100 _60 _50 67 18 39 19 48 32 27 _70 _90 _60 _100 _80 _50 _40 24 53 48 75 39 21 19 |
2 класс
Письменные случаи сложения и вычитания двузначных чисел в пределах ста.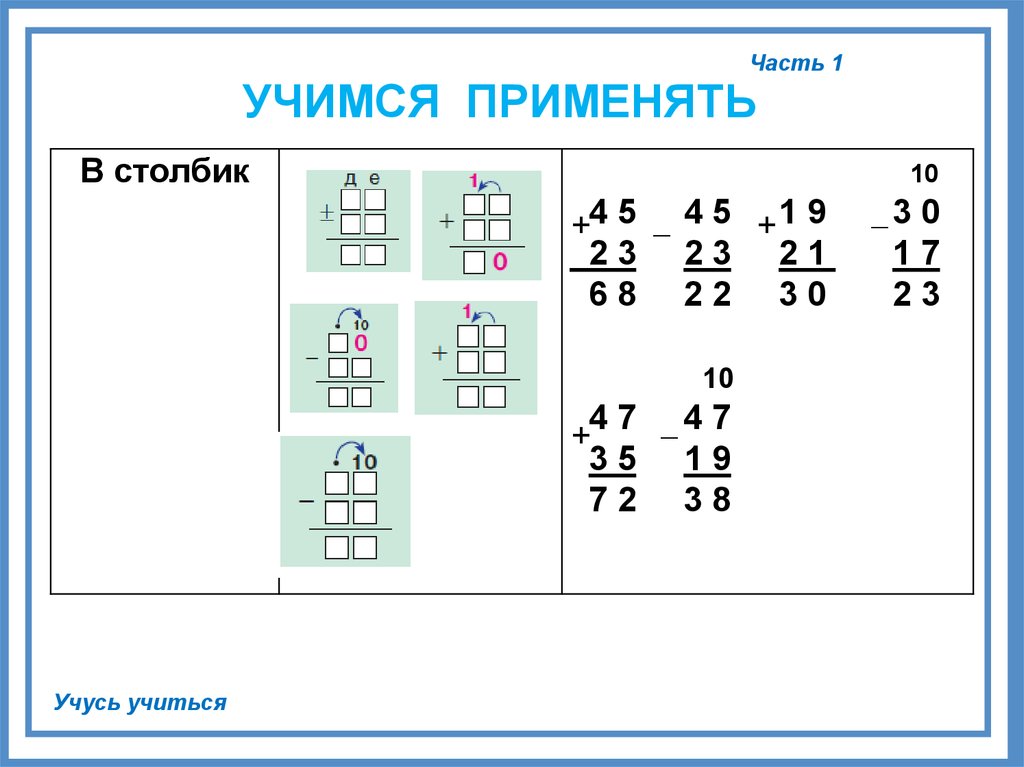
В-1 +34 _45 +67 +72 +54 _90 -72 23 14 23 28 27 67 45 +42 _95 +54 +63 +75 _60 _85 44 62 16 37 18 31 58 |
В-2 +56 _66 +47 +53 +27 _80 _61 23 24 33 47 64 56 18 +63 _78 +27 +86 +65 _70 _45 25 43 53 14 26 34 27 |
В-3 +36 _87 + 58 +49 +66 _60 _84 52 36 22 51 17 25 48
+47 _89 +68 +77 +56 -90 _85 52 36 12 23 36 43 58 |
3000 примеров по математике с ответами и метод.
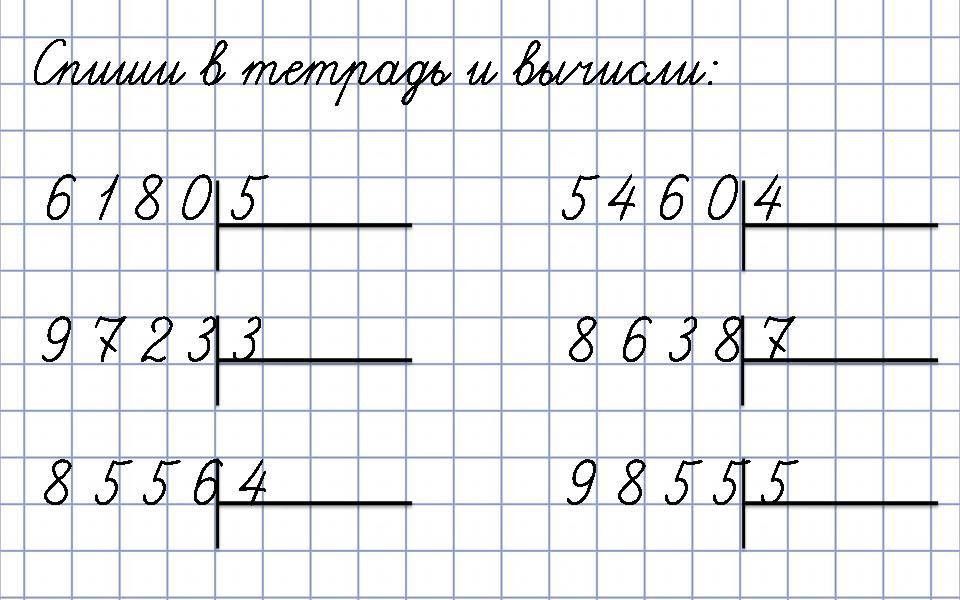 рекомендац.Решаем в столбик 3000 примеров по математике с ответами и метод.рекомендац.Решаем в столбик
рекомендац.Решаем в столбик 3000 примеров по математике с ответами и метод.рекомендац.Решаем в столбикКаталог/ Учебная литература/ Для начальной школы/ Математика/3000 примеров по математике с ответами и метод.рекомендац.Решаем в столбик
Аннотация к книге «3000 примеров по математике с ответами и метод.рекомендац.Решаем в столбик»
Пособие содержит примеры на умножение и деление в столбик. При составлении пособия соблюдалась принятая в классической начальной школе методическая последовательность в отборе и системе расположения заданий. Примеры распределены по работам, каждая из которых дополнена работой над ошибками. В конце пособия даны ответы. На второй и третьей сторонке обложки приведены алгоритмы решения примеров на различные действия, на четвертой сторонке – методические указания по работе с пособием. Книга будет полезна для коллективной и индивидуальной работы на уроке и самостоятельных занятий дома.
Отзывов пока что нет
Возможно, вам понравится
73
62.05 Р
219
186.15 Р
184
156.4 Р
-
135
114.
 75 Р
75 Р 233
198.05 Р
197
167.45 Р
175.95 Р
131
111.
 35 Р
35 Р88
74.8 Р
46
39.1 Р
-
497
422.45 Р
89
75.
 65 Р
65 Р183
155.55 Р
72
61.2 Р
108
91.8 Р
153
130.
 05 Р
05 Р- 249
211.65 Р
114
96.9 Р
346
294.1 Р
© 2000–2021, ООО «Гемера-Плюс»
Моя книга | Сеть книжных магазинов в Саратове
Вектор столбца – математика GCSE
Введение
Что такое вектор-столбец?
Как написать вектор-столбец
Рабочий лист вектора столбца
Как нарисовать вектор, используя вектор-столбец
Распространенные заблуждения
Практические вопросы вектора столбца
Вектор-столбец GCSE вопросы
Контрольный список обучения
Следующие уроки
Вы знали?
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Что такое вектор-столбец?
Как написать вектор-столбец
Рабочий лист вектора столбца
Как нарисовать вектор, используя вектор-столбец
Распространенные заблуждения
Практические вопросы вектора столбца
Вектор-столбец GCSE вопросы
Контрольный список обучения
Следующие уроки
Вы знали?
Все еще застряли?
Здесь мы узнаем о векторах-столбцах, в том числе о том, как написать вектор-столбец и как нарисовать диаграмму вектора-столбца.
Существуют также векторные рабочие листы на основе экзаменационных вопросов Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое вектор-столбец?
Вектор-столбец — это способ записи вектора, который дает информацию о векторе. Он разделен на горизонтальную составляющую и вертикальную составляющую.
Существует горизонтальный компонент , также известный как \textbf{x} компонент Это верхнее число в векторе-столбце и говорит нам, на сколько пробелов вправо или влево нужно переместиться.
Если число положительное , направление к правильно .
Если число отрицательное , то направление слева .
Существует вертикальный компонент 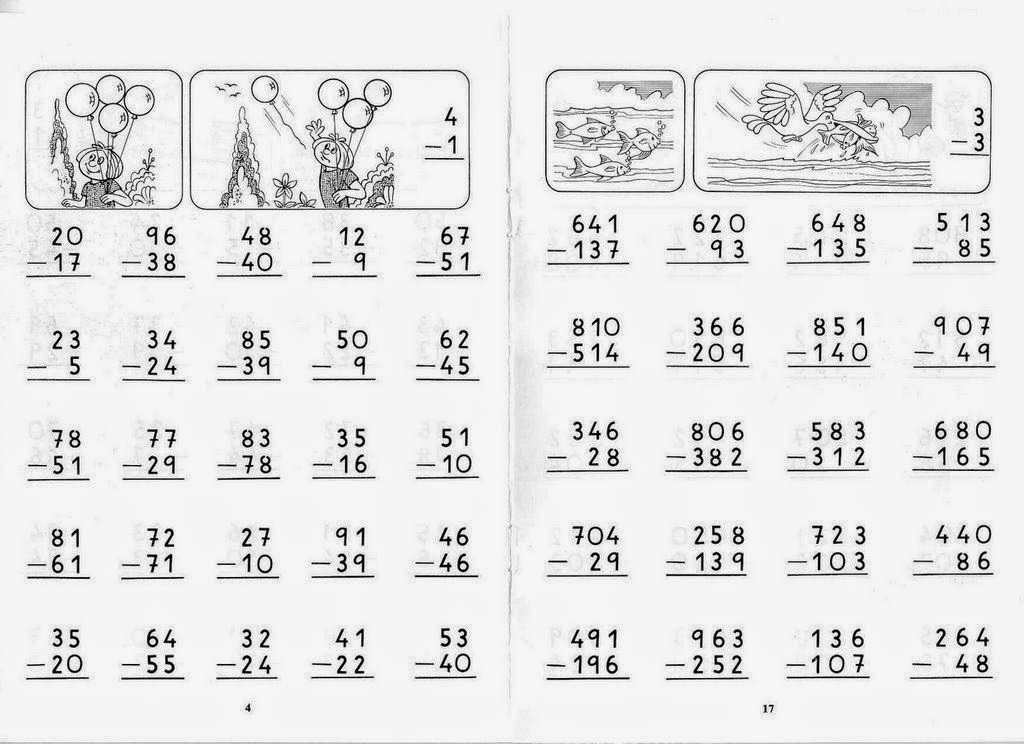
Если число положительное , направление вверх .
Если число отрицательное , направление равно вниз .
Вектор \textbf{a} может быть записан как вектор-столбец \begin{pmatrix} \; 3 \;\\ \; 2\; \end{pmatrix}
\textbf{a}= \begin{pmatrix} \; 3 \;\\ \; 2\; \end{pmatrix} \text{is} \begin{pmatrix} 3 \ \text{right}\\ 2 \ \text{up}\\ \end{pmatrix}
Обратите внимание, что горизонтальная и вертикальная составляющие образуют прямоугольный треугольник.
Вектор \textbf{b} может быть записан как вектор-столбец \begin{pmatrix} \; 3 \;\\ \; -4\; \end{pматрица}
\textbf{b}= \begin{pmatrix} \; 3 \;\\ \; -4\; \end{pmatrix} \text{is} \begin{pmatrix} 3 \ \text{right}\\ -4 \ \text{down}\\ \end{pmatrix}
Обратите внимание, что горизонтальная и вертикальная составляющие образуют прямоугольный треугольник.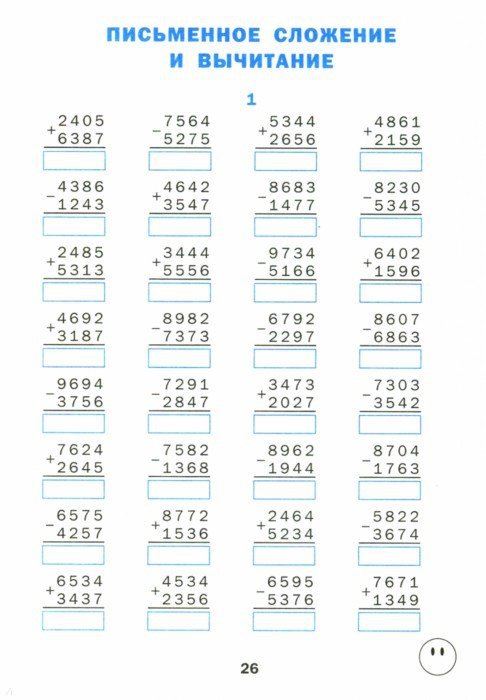
Что такое вектор-столбец?
Как записать вектор-столбец
Чтобы записать вектор как вектор-столбец:
- Вычислить горизонтальную составляющую ( \textbf{х} компонент ).
- Разработайте вертикальную составляющую ( \textbf{y} составляющая).
- Запишите вектор-столбец.
Как записать вектор-столбец
Рабочий лист с векторными столбцами
Получите бесплатный рабочий лист с более чем 20 вопросами и ответами. Включает рассуждения и прикладные вопросы.
СКОРО
ИксРабочий лист вектора столбца
Получите бесплатный векторный лист из 20+ вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКОРО
Примеры векторов-столбцов
Пример 1: запись вектора-столбца
Запись вектора \textbf{a} в виде вектора-столбца.
- Разработайте горизонтальную составляющую ( \textbf{x} составляющая).
Из начальной точки вектора проведите горизонтальную линию.
Эта линия на 4 клетки вправо.
2 Разработать вертикальную составляющую ( \textbf{y} составляющую).
От конца горизонтального компонента проведите вертикальную линию до конца вектора.
Эта линия на 3 клетки вверх.
3 Запишите вектор-столбец.
Запишите горизонтальную и вертикальную составляющие в вектор-столбец.
Вектор \textbf{a} как вектор-столбец:
\textbf{а}= \begin{pматрица} \; 4 \;\\ \; 3 \; \end{pматрица}
Пример 2: записать вектор-столбец
Записать вектор \textbf{b} как вектор-столбец.
Разработать горизонтальную составляющую ( \textbf{x} составляющая).
Из начальной точки вектора проведите горизонтальную линию.
Эта линия на 4 клетки вправо.
Разработайте вертикальную составляющую ( \textbf{y} составляющая).
От конца горизонтального компонента проведите вертикальную линию до конца вектора.
Эта линия находится на 1 клетку ниже.
Запишите вектор-столбец.
Запишите горизонтальную и вертикальную составляющие в вектор-столбец.
Вектор \textbf{b} как вектор-столбец:
\textbf{b}=
\begin{pматрица}
\; 4 \;\\
\; -1\;
\end{pматрица}
Пример 3: записать вектор-столбец
Записать вектор \textbf{v} как вектор-столбец.
Разработать горизонтальную составляющую ( \textbf{x} компонент).
Из начальной точки вектора проведите горизонтальную линию. Мы пытаемся построить прямоугольный треугольник.
Эта линия на 2 клетки левее.
Разработайте вертикальную составляющую ( \textbf{y} составляющая).
От конца горизонтального компонента проведите вертикальную линию до конца вектора.
Эта линия находится на 1 клетку ниже.
Запишите вектор-столбец.
Запишите горизонтальную и вертикальную составляющие в вектор-столбец.
Вектор \textbf{v} как вектор-столбец:
\textbf{v}=
\begin{pматрица}
\; -2 \;\\
\; -1\;
\end{pматрица}
Как нарисовать вектор, используя вектор-столбец
Чтобы нарисовать диаграмму вектора-столбца:
- Нарисуйте горизонтальную составляющую ( \textbf{x} компонент).
- Нарисуйте вертикальный компонент ( \textbf{y} компонент ).
- Нарисуйте вектор.
Как нарисовать вектор с помощью вектор-столбца
Рисование диаграммы вектор-столбца примеров
Пример 4.
 Нарисуйте диаграмму вектор-столбца
Нарисуйте диаграмму вектор-столбцаНарисуйте диаграмму вектор-столбца \begin{pmatrix} \; 2 \;\\ \; 5 \; \end{pmatrix}
Нарисуйте горизонтальный компонент ( \textbf{x} компонент ).
На сетке выберите начальную точку и нарисуйте горизонтальную составляющую
Верхнее число равно 2, поэтому мы проводим линию на 2 клетки вправо.
Нарисуйте вертикальный компонент ( \textbf{y} компонент ).
От конца горизонтального компонента нарисуйте вертикальный компонент.
Нижнее число равно 5, поэтому мы рисуем линию на 5 клеток вверх.
Нарисовать вектор.
Соедините начальную и конечную точки и не забудьте поставить стрелку направления на линию.
Пример 5: нарисовать диаграмму вектор-столбца
Нарисовать диаграмму вектор-столбца \begin{pmatrix} \; -3 \;\\\; 1 \; \end{pmatrix}
Нарисуйте горизонтальный компонент ( \textbf{x} компонент ).
На сетке выберите начальную точку и нарисуйте горизонтальную составляющую
Верхнее число равно -3, поэтому мы рисуем линию на 3 клетки левее.
Нарисуйте вертикальный компонент ( \textbf{y} компонент ).
От конца горизонтального компонента нарисуйте вертикальный компонент.
Нижнее число равно 1, поэтому мы рисуем линию на 1 клетку вверх.
Нарисуйте вектор.
Соедините начальную и конечную точки и не забудьте поставить стрелку направления на линию.
Пример 6: нарисовать диаграмму вектор-столбца
Нарисовать диаграмму вектор-столбца \begin{pmatrix} \; -6 \;\\\; -1\; \end{pmatrix}
Нарисуйте горизонтальный компонент ( \textbf{x} компонент ).
На сетке выберите начальную точку и нарисуйте горизонтальную составляющую
Верхнее число равно -6, поэтому мы рисуем линию на 6 клеток левее.
Нарисуйте вертикальную составляющую ( \textbf{y} компонент).
От конца горизонтального компонента нарисуйте вертикальный компонент.
Нижнее число равно -1, поэтому мы рисуем линию на 1 клетку вниз.
Нарисуйте вектор.
Соедините начальную и конечную точки и не забудьте поставить стрелку направления на линию.
Распространенные заблуждения
- Убедитесь, что знаки правильные
Помните:
Если верхнее число положительное, направление вправо.
Если верхнее число отрицательное, направление влево.
Если нижнее число положительное, направление вверх.
Если нижнее число отрицательное, направление вниз.
- Обозначение векторов-столбцов
Векторы-столбцы имеют только 2 числа в скобках; верхний номер и нижний номер. Нет необходимости в каких-либо других знаках препинания, таких как запятые или точки с запятой, и нет необходимости в строке для разделения чисел.
Нет необходимости в каких-либо других знаках препинания, таких как запятые или точки с запятой, и нет необходимости в строке для разделения чисел.
Практические вопросы по вектору-столбцу
\begin{pmatrix} \; -4 \;\\ \; 1 \; \end{pmatrix}
\begin{pmatrix} \; 4 \;\\ \; 1 \; \end{pmatrix}
\begin{pmatrix} \; 1 \;\\ \; 4\; \end{pmatrix}
\begin{pmatrix} \; -1 \;\\ \; 4\; \end{pmatrix}
Нарисуйте горизонтальную линию и вертикальную линию и посчитайте квадраты.
\begin{pmatrix} \; 4 \;\\\; 1 \; \end{pmatrix}
\begin{pmatrix} \; 2 \;\\ \; -4\; \end{pматрица}
\begin{pmatrix} \; 4 \;\\ \; -2\; \end{pmatrix}
\begin{pmatrix} \; -4 \;\\ \; -2\; \end{pmatrix}
\begin{pmatrix} \; -2 \;\\ \; 4\; \end{pmatrix}
Нарисуйте горизонтальную линию и вертикальную линию и посчитайте квадраты.
\begin{pmatrix} \; -2 \;\\\; 4\; \end{pmatrix}
\begin{pmatrix} \; 1 \;\\ \; 3 \; \end{pmatrix}
\begin{pmatrix} \; -1 \;\\ \; 3 \; \end{pmatrix}
\begin{pmatrix} \; 1 \;\\ \; -3\; \end{pматрица}
\begin{pmatrix} \; -1 \;\\ \; -3\; \end{pmatrix}
Нарисуйте горизонтальную линию и вертикальную линию и посчитайте квадраты.
Вектор-столбец для \textbf{x} равен
\begin{pматрица} \; 1 \;\\ \; -3\; \end{pматрица}
Верхнее число вектора-столбца равно 1 . Это горизонтальная составляющая. Используйте это, чтобы провести горизонтальную линию вправо. Нижнее число вектора-столбца равно 4 . Это вертикальная составляющая. Используйте это, чтобы нарисовать вертикальную линию вверх.
Верхнее число вектора-столбца равно -3 . Это горизонтальная составляющая. Используйте это, чтобы нарисовать горизонтальную линию слева. Нижнее число вектора-столбца равно -2 . Это вертикальная составляющая. Используйте это, чтобы нарисовать вертикальную линию вниз.
Верхнее число вектора-столбца равно -5 . Это горизонтальная составляющая. Используйте это, чтобы нарисовать горизонтальную линию слева. Нижнее число вектора-столбца равно 2 . Это вертикальная составляющая. Используйте это, чтобы нарисовать вертикальную линию вверх.
Нижнее число вектора-столбца равно 2 . Это вертикальная составляющая. Используйте это, чтобы нарисовать вертикальную линию вверх.
Вектор-столбец Вопросы GCSE
1. Какой вектор-столбец является правильным для этого вектора?
\begin{выровнено} &\quad \text{A} \quad \quad\quad \quad \;\; \text{B} \quad \quad \quad \quad \text{C} \quad \quad \quad \quad \text{D} \\\\ &\begin{pmatrix} \; 4 \;\\ \; 0 \; \end{pmatrix} \quad \quad \begin{pmatrix} \; -4 \;\\ \; 0 \; \end{pmatrix} \quad \quad \begin{pматрица} \; 0 \;\\ \; 4\; \end{pmatrix} \quad \quad \begin{pматрица} \; 0 \;\\ \; -4\; \end{pматрица} \end{выровнено}
(1 балл)
Показать ответ
\begin{align} &\quad \text{B} \\\\ &\begin{pmatrix} \; -4 \;\\ \; 0 \; \end{pматрица} \end{выровнено}
(1)
2. Вектор-столбец \begin{pmatrix} \; 4 \;\\\; а \; \end{pmatrix} представляет:
Каково значение ?
(1 балл)
Показать ответ
a=-3
(1)
3. Напишите вектор столбца для этого вектора
Напишите вектор столбца для этого вектора
(2 оценки)
Показать ответ
\ Begin {PMATRIX} \; 2 \;\\ \; -5 \; \end{pматрица}
(для правильной горизонтальной составляющей)
(1)
(для правильной вертикальной составляющей)
(1)
0003
- Как записать вектор в виде вектор-столбца
- Как нарисовать диаграмму вектор-столбца
Знаете ли вы?
Не входит в GCSE: мы можем транспонировать вектор-столбец, чтобы записать его как вектор-строку (и наоборот). Они выглядят как координаты, но без запятых.
Векторы также можно расширить до математики уровня A и высшей математики, научившись умножать два вектора вместе с помощью скалярного произведения.
Векторы-столбцы являются простым примером матриц. В математике GCSE у нас есть один столбец. Матрицы изучаются на уровне A Level Additional Maths..jpg) T\). 9T \]
T\). 9T \]
Чтобы выполнить сложение матрицы с , две матрицы должны иметь одинаковые размеры. Это означает, что они должны иметь одинаковое количество строк и столбцов. В этом случае просто добавьте каждый отдельный компонент, как показано ниже.
Например
\[A + B = \begin{pmatrix} 1 & -5 & 4 \\ 2 & 5 & 3 \end{pmatrix} + \begin{pmatrix} 8 & -3 & -4 \\ 4 & -2 & 9 \end{pmatrix} = \begin{pmatrix} 1 + 8 & -5 – 3 & 4 – 4 \\ 2 + 4 & 5 -2 & 3 + 9Т \]
Матричное скалярное умножение Раздел
Чтобы умножить матрицу на скаляр, также известное как скалярное умножение , умножьте каждый элемент матрицы на скаляр.
Например…
\[ 6*A = 6 * \begin{pmatrix} 1 & -5 & 4\\ 2 & 5 & 3 \end{pmatrix} = \begin{pmatrix} 6 * 1 & 6 * -5 & 6 * 4\\ 6 * 2 и 6 *5 и 6 * 3 \end{pmatrix} = \begin{pmatrix} 6 & -30 & 24 \\ 12 & 30 & 18 \end{pmatrix}\]
Чтобы умножить два вектора одинаковой длины, нужно взять скалярное произведение , также называемое внутренним произведением . Это делается путем умножения каждой записи в двух векторах вместе, а затем сложения всех произведений.
Это делается путем умножения каждой записи в двух векторах вместе, а затем сложения всех произведений.
Например, для векторов x и y скалярное произведение рассчитывается ниже
\[ x \cdot y = \begin{pmatrix} 1 & -5 & 4 \end{pmatrix} * \begin{pmatrix} 4 & -2 & 5 \end{pmatrix} = 1*4 + (-5 )*(-2) + 4*5 = 4+10+20 = 34\]
Умножение матриц Раздел
Чтобы выполнить умножение матриц , первая матрица должна иметь такое же количество столбцов, сколько строк во второй матрице. Количество строк полученной матрицы равно количеству строк первой матрицы, а количество столбцов полученной матрицы равно количеству столбцов второй матрицы. Таким образом, матрицу 3 × 5 можно умножить на матрицу 5 × 7, получив матрицу 3 × 7, но нельзя умножить матрицу 2 × 8 на матрицу 4 × 2. Чтобы найти элементы в результирующей матрице, просто возьмите скалярное произведение соответствующей строки первой матрицы и соответствующего столбца второй матрицы.