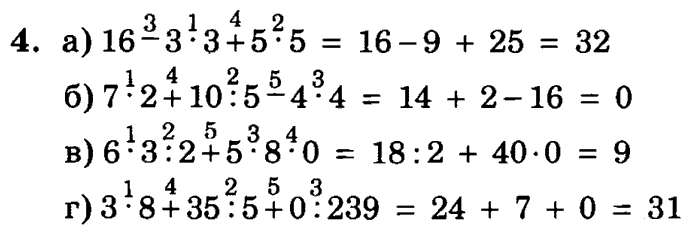Примеры по математике 4 класс на порядок действий со скобками: Математика :”Порядок выполнения действий в примерах без скобок и со скобками.” (4 класс)

Выполнение действий со скобками, примеры по математике со скобками от Skills4u

Зарегистрируйся и получи 7 дней бесплатного доступа к тренажерам и персональный план прокачки знаний до 100%!

Вопросов в тесте: 25

Среднее время прохождения: ~10:00

Зарегистрируйся и получи персональный план прокачки знаний до 100%!

Как работает платформа Skills4u

Тестирование по предмету за класс

Платформа определит, какие темы сформированы слабо и составит индивидуальный план обучения

Персональный план обучения

План обучения и повторений поможет ученику в закреплении всех необходимых тем по предмету

Закрепление темы на 100%

Платформа напомнит и проконтролирует все повторения для закрепления каждой темы на 100%

Проработка слабых тем с предыдущих классов

Чтобы идеально овладеть предметом, рекомендуем закрепить пробелы, начиная с самых простых тем

Почему нужно пройти общее тестирование по математике за 3 класс, а не по отдельной теме «Порядок выполнения действий (сложение, вычитание, умножение, деление) со скобками»

Пройдя тестирование за класс вы получите ПОЛНУЮ КАРТИНУ ЗНАНИЙ ПО ВСЕМ ТЕМАМ.
Такой подход позволит глубинно проанализировать знания, вывести успеваемость и понимание предмета на качественно новый уровень.

Пройдя тестирование по одной теме вы получите РЕЗУЛЬТАТ ЗНАНИЙ ТОЛЬКО ЭТОЙ ТЕМЫ, которая, возможно, плохо изучена. Такой метод не является комплексным и дает лишь точечное понимание знаний по предмету.

Зарегистрироваться и пройти тестирование

В начальной школе действия со скобками изучают в 3 классе на уроках математики. Для некоторых учеников они представляют затруднение, поэтому мы рекомендуем пройти проверочный тест, чтобы определить, насколько ваш ребенок усвоил эту тему.

Наш интерактивный тест на выполнение действий со скобками состоит из 25 заданий, в каждом из которых вам предстоит выполнить несложные вычисления и записать ответ в отведенную графу. Если ответ указан верно, загорается зеленый свет, и сразу появляется очередной вопрос. Если же допущена ошибка, результат вычислений подсвечивается красным, но обязательно указывается и правильное решение.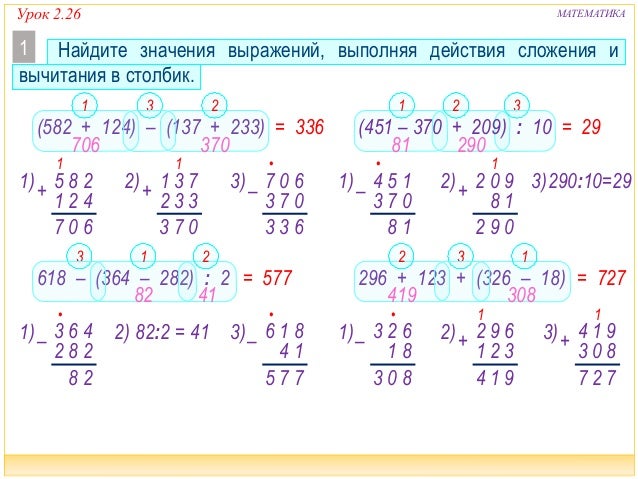

Это позволяет понять, где допущена ошибка.

Самое главное, когда вы решаете примеры, это соблюдать правильный порядок действий со скобками. Для этого необходимо определить, что выполнять сначала: умножение или вычитание. Если вы хорошо изучили правила, сомнений не возникнет. В начальной школе порядок действий в математике со скобками изучают уже в 3 классе. Наш тест будет полезен как третьеклассникам, так и ученикам старших классов, которые хотят проверить, насколько хорошо они запомнили правила. Мы рекомендуем проверить знания перед важной контрольной или проверочной работой, в начале учебного года после каникул.

Немного интересной статистики, или почему важно проходить общее тестирование и закрывать пробелы в знаниях за текущие и предыдущие классы

• 60% пятиклассников не могут быстро выполнять базовые математические действия, такие как вычитание и сложение.
• 70% пятиклассников часто делают ошибки в таких действиях как умножение и деление.
• Более 75% девятиклассников не могут решить системы из двух уравнений.
• До 20% выпускников школы реально обладают математическими познаниями на уровне 6-8 класса. До 40% — не выше 9 класса.
• От 5 к 7 классу возникает четко выраженная тенденция ухудшения математической подготовки, а доля троечников увеличивается с 20-25% до 40-45%.

Основано на результатах учеников нашей платформы и исследованиях журнала “Коммерсант”

Каждый желающий может пройти тест на действия со скобками за 3 класс совершенно бесплатно. По итогам тестирования формируется рейтинг ученика и даются рекомендации по дальнейшему продолжению занятий. Система сама напомнит, когда пора приступить к упражнениям.

Для того чтобы получить устойчивый учебный навык по указанной теме и всегда выбирать правильный порядок действий в примерах со скобками, нужно зарегистрироваться на сайте образовательной платформы Skills4u и оформить доступ к тренажерам по различным предметам школьной программы. Существуют варианты доступа на месяц, полугодие и полный учебный год.

Вы также можете выбирать, какой навык нужно прокачать в данный момент: нужна ли вся математика, действие со скобками или другие темы за 3 класс начальной школы. Стоимость подписки варьируется в зависимости от выбранного уровня доступа, но всегда остается чисто символической. Это один из самых выгодных способов подтянуть успеваемость и получить индивидуальный подход к изучению и независимую оценку знаний.

Как растут результаты учеников
после занятий на тренажерах Skills4u

Занятия
на Skills4u

Занятия
с учебником

Успеваемость

Мотивация

Внимательность

Скорость

Самостоятельность

Запоминание

Первичный Тест «Порядок выполнения действий (сложение, вычитание, умножение, деление) со скобками» по математике за 3 класс онлайн и бесплатно предоставляется всем желающим.

Советуем пройти тестирование за весь 3 класс по математике, чтобы узнать пробелы в знаниях по всем темам и получить индивидуальный план обучения.

После регистрации вы получите 7 дней бесплатного доступа, чтобы увидеть первые результаты занятий и оценить эффективность тренажеров.

Зарегистрироваться и пройти тестирование

Регистрируйтесь на сайте образовательной платформы Skills4u и решайте примеры действий со скобками в удобное для вас время. Родители могут быть спокойны – им не понадобится листать учебник. Достаточно будет только напомнить ребенку, что наступило время занятий. Система сама пришлет напоминание и познакомит с результатом. Желаем успеха!

А для комплексного результата пройдите общее тестирование за
класс! Узнайте пробелы в знаниях по всем темам

Ученик

Занимайся 20 минут в день и прокачай знания по школьной программе за месяц!

Родитель

Наслаждайтесь прогрессом вашего ребенка в школе и на платформе

Учитель/
репетитор

Задавайте и проверяйте домашние задания прямо на платформе

Зарегистрироваться и пройти тестирование

65145

---

учеников уже занимаются с нами

Калькулятор со скобками

0
AC		+/-	÷
7	8	9	×
4	5	6	–
1	2	3	+
0	00	,	=

Данный математический калькулятор может вычислить математическое выражение со скобками, определить порядок действий в выражении без скобок и произвести такие математические операции как: сложение, вычитание, умножение, деление, возведение в степень

Вы так же можете воспользоваться калькулятором выражений. Данный математический калькулятор сможет вычислить выражение, содержащее множество математических операций и функций, в том числе вложенных.

sin

cos

tan

cot

sec

csc

asin

acos

atan

acot

asec

acsc

x^y

x²

x³

ln

lg

lb

(

7

4

1

√x

)

8

5

2

.

³√x

C

9

6

3

e

π

+

−

×

÷

←

=

Порядок действий в выражениях без скобок

1. Умножение, деление
2. Сложение вычитание

Например:
25 – 15 ∙ 2 + 8 : 2 = -1

1) 15 ∙ 2 = 30
2) 8 : 2 = 4
3) 25 – 30 = -5
4) -5 + 4 = -1

Порядок действий в выражениях со скобками

1. Действия в скобках
1. Умножение, деление
2. Сложение вычитание

Например:
(14 + 7) : 7 + 3 ∙ 2 = 9
1) 14 + 7 = 21
2) 21 : 7 = 3
3) 3 ∙ 2 = 6
4) 3 + 6 = 9

Вам могут также быть полезны следующие сервисы

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор упрощения выражений

Калькулятор со скобками

Калькулятор уравнений

Калькулятор суммы

Калькулятор пределов функций

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Калькулятор делителей числа

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Калькулятор свойств корней и степеней

Калькулятор комплексных чисел

Калькулятор среднего арифметического

Калькулятор арифметической прогрессии

Калькулятор геометрической прогрессии

Калькулятор модуля числа

Калькулятор абсолютной погрешности приближения

Калькулятор абсолютной погрешности

Калькулятор относительной погрешности

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькулятор нахождения наименьшего угла

Калькулятор определения вида угла

Калькулятор смежных углов

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N2 | Двоичная система счисления

N3 | Троичная система счисления

N4 | Четырехичная система счисления

N5 | Пятеричная система счисления

N6 | Шестеричная система счисления

N7 | Семеричная система счисления

N8 | Восьмеричная система счисления

N9 | Девятеричная система счисления

N11 | Одиннадцатиричная система счисления

N12 | Двенадцатеричная система счисления

N13 | Тринадцатеричная система счисления

N14 | Четырнадцатеричная система счисления

N15 | Пятнадцатеричная система счисления

N16 | Шестнадцатеричная система счисления

N17 | Семнадцатеричная система счисления

N18 | Восемнадцатеричная система счисления

N19 | Девятнадцатеричная система счисления

N20 | Двадцатеричная система счисления

N21 | Двадцатиодноричная система счисления

N22 | Двадцатидвухричная система счисления

N23 | Двадцатитрехричная система счисления

N24 | Двадцатичетырехричная система счисления

N25 | Двадцатипятеричная система счисления

N26 | Двадцатишестеричная система счисления

N27 | Двадцатисемеричная система счисления

N28 | Двадцативосьмеричная система счисления

N29 | Двадцатидевятиричная система счисления

N30 | Тридцатиричная система счисления

N31 | Тридцатиодноричная система счисления

N32 | Тридцатидвухричная система счисления

N33 | Тридцатитрехричная система счисления

N34 | Тридцатичетырехричная система счисления

N35 | Тридцатипятиричная система счисления

N36 | Тридцатишестиричная система счисления

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка. Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Генератор Pdf с примерами

Тренажёры решения примеров

Тренажёр таблицы умножения

Тренажер счета для дошкольников

Тренажер счета на внимательность для дошкольников

Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ.

Тренажер решения примеров с разными действиями

Тренажёры решения столбиком

Тренажёр сложения столбиком

Тренажёр вычитания столбиком

Тренажёр умножения столбиком

Тренажёр деления столбиком с остатком

Калькуляторы решения столбиком

Калькулятор сложения, вычитания, умножения и деления столбиком

Калькулятор деления столбиком с остатком

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Цифры в текст

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

Что такое порядок операций? – определение, правила и примеры

Порядок операций – это набор правил, которым необходимо следовать в определенном порядке при решении уравнения.

Все мы хорошо знаем четыре основных математических действия: сложение, умножение, деление и вычитание. С детства мы постоянно репетируем задачи, связанные с этими четырьмя операциями. Эти операции используются, от добавления счета за вашу покупку в торговом центре до разделения пиццы на четыре равные части. Но до сих пор мы решали проблемы, связанные с каждой операцией в отдельности.

Что, если у нас есть выражение, в котором все четыре операции работают вместе? Мы сначала умножаем или сначала вычитаем? Это может быть проблематично, если вы будете следовать неправильному подходу. Это может привести к неправильным ответам. Поэтому порядок действий вступил в действие.

Анализ любого математического утверждения с использованием арифметических операций, таких как деление, умножение, сложение и вычитание, в математике называется операциями. Давайте посмотрим на законы порядка операций и посмотрим, насколько хорошо мы можем их вспомнить, используя простые стратегии. В этой статье вы узнаете порядок операций, правила порядка операций, математический порядок операций и решите задачи на порядок операций.

Почему выполняется Порядок операций?

При оценке уравнений в арифметике может потребоваться выполнение множества операций, и упрощение, в конце концов, дает разные результаты. Однако на каждую фразу может быть только один правильный ответ. Мы используем принципы, чтобы упростить любое данное математическое выражение, чтобы найти правильный ответ. Эти принципы основаны на всех основных математических операторах.

С единственной целью всегда получать правильные ответы на любое математическое уравнение, был реализован порядок операций.

Каков порядок действий?

В математике такие операторы, как сложение (+), вычитание (-), умножение (×) и деление (÷), имеют приоритет друг над другом. Мы не можем самостоятельно решить выражение, содержащее любой из двух операторов. Мы должны следовать правилам порядка операций, которые гласят, что в любом выражении, как арифметическом, так и алгебраическом, первыми будут оцениваться скобки. Заказ будет рассчитываться во вторую очередь. Умножение и деление будут оцениваться третьими и, наконец, сложение и вычитание будут упрощены.

Приоритет решения любого выражения упоминается в таблице ниже:

Приоритет	Операция
Первые	Брэкиров	Порядки (Экспоненты, Квадратный корень, Кубический корень, Логарифмический и т. д.)
Третьи	Деление или умножение (Операция, расположенная слева от выражения, будет оцениваться первой)
Четвертая	Сложение или вычитание (в зависимости от того, какая операция находится в левой части выражения, будет оцениваться первой)

Определение порядка операций принципы приоритета, которые мы используем при решении любого математического уравнения, включающего множество операций. Когда между двумя операторами существует подвыражение, должен быть реализован оператор, который появляется первым в таблице, упомянутой в предыдущем разделе.

Давайте теперь разберемся с порядком операций, правило за правилом, в соответствии с установленным приоритетом: операторы, применяемые к выражению. При решении любого выражения всегда двигайтесь от левой стороны к правой. Это поможет вам облегчить упрощение этого выражения. Теперь прочитайте правила, упомянутые ниже, чтобы полностью понять концепцию порядка операций:

Правило 1: Необходимо всегда проверять наличие скобок или круглых скобок в выражении. Чаще всего в математических выражениях встречаются скобки «()», «{}» и «[]». Когда терм содержит все три скобки, решите уравнение следующим образом:

• Сначала решите термины внутри круглой скобки «()» или круглых скобок.
• Решите условия внутри фигурных скобок «{}» секунды.
• Наконец, решите условия в квадратных скобках «[ ]».

Кроме того, помните, что если в любой из скобок есть несколько операций, обязательно используйте порядок операций для их решения.

Правило 2: После того, как вы решите числа в скобках, найдите любые термины в следующем порядке, такие как возведенные в степень термины, корневые термины, логарифмические термины, тригонометрические термины и т. д., и решите их.

Правило 3: Осталось расставить четыре основных оператора в правильном порядке. Вы можете выполнять умножение или деление в зависимости от того, какой оператор стоит первым с левой стороны выражения.

Правило 4: Последним шагом является добавление или вычитание элементов в том же порядке слева направо.

Если вы помните эти пять правил, значит, вы усвоили порядок действий. Каким бы длинным ни было выражение, вы легко сможете решить его, не задумываясь. Если вы не уверены, что запомните эти правила, есть два простых способа их запомнить. Они известны как BODMAS и PEMDAS. В следующих разделах вы узнаете об этих двух аббревиатурах для порядка операций.

Способы запоминания порядка операций – BODMAS и PEMDAS

Существует два очень важных способа запоминания порядка действий. Они сокращенно называются правилом PEMDAS и правилом BODMAS. Буквы в этих аббревиатурах определяют математические операции. Буква, которая присутствует первой, применяется первой к любому уравнению.

Давайте теперь узнаем, что означает каждая из букв в этих аббревиатурах:

Порядок операций BODMAS

BODMAS — наиболее распространенная аббревиатура для порядка операций. Многие из вас наверняка слышали об этом где-то в своей жизни. В развернутом виде это означает:

• B – Скобки ( ), { }, [ ]
• О – Заказ
• D – Отдел (÷)
• M – Умножение (×)
• А – Дополнение (+)
• S – Вычитание (-)

Порядок работы PEMDAS

PEMDAS также является аббревиатурой от порядка работы. Тем не менее, его меньше слышно в нашей повседневной жизни, но он столь же эффективен, как и БОДМАС.

• P – Скобки (), {}, [].
• E – Показатель степени (a2) (Например, здесь a – это число с показателем степени 2 )
• М – Умножение (×)
• Д – Отдел (÷)
• A – означает Дополнение (+)
• S – означает вычитание (-)

Это самый эффективный метод запоминания последовательности событий. Забавная фраза « Пожалуйста, извините, моя дорогая тетя Салли »- хороший способ запомнить PEMDAS.

Оба эти метода используются для упрощения нашего понимания порядка операций. Мы увидим пример порядка операций, чтобы прояснить эту тему.

Каков порядок операций в математике?

Порядок операций — это правило, определяющее правильную последовательность шагов для вычисления математического выражения. Если у вас есть выражение только с одной операцией (например, только сложение, только вычитание, только умножение или только деление), правильный способ его решения — слева направо. Однако для выражений с несколькими операциями необходимо соблюдать порядок операций.

Пример порядка операций

Давайте рассмотрим различные примеры, упомянутые ниже, чтобы понять точность правил, используемых в порядке операций.

1. Для вычисления арифметических операторов

Выражение 1: 2 + 3 x 5 

• Правильный способ: Правильный способ решить это выражение — сначала умножить 3 x 5 = 15, а затем добавить 2 к результату. 15 + 2 = 17.
• Неверный путь: Если сначала добавить 2 + 3. Получаем 6 х 5 = 30, что неверно при решении этого выражения.

Выражение 2: 15 ÷ 3 x 2 – 6

• Правильный способ: Правильный способ решить это выражение – сначала разделить 15 и 3 = 5, потому что оно ближе к левой части выражения. Затем умножьте 5 на 2 = 10 и вычтите из этого 6, что дает 10 – 6 = 4. 
• Неверный способ: Если умножить 3 х 2 = 6, то вычесть из него 6, то получим 15 ÷ 0 = не определено. Это неправильный способ решения этого выражения.

2. Для оценки заказов

Выражение 1: 6 x 32

• Правильный способ: Правильный способ решить это выражение – сначала решить порядок, то есть 32 = 9. Теперь умножьте это на 6. 9 x 6 = 54
• Неверный путь: Если умножить 6 х 3 = 18, то возведем в квадрат ответ, получим 182 = 324, что неверно.

Выражение 2: 2 x sin 30

• Правильный способ: Сначала оцените порядок sin 30 = ½. Теперь умножаем 2 на ответ. 2 х ½ = 1
• Неверный способ: Если умножить 30 на 2 = 60 и решить порядок, то получим sin 60 = 3/2. Какой ответ неверный

3. Для оценки кронштейнов

Выражение 1: (12 + 3) x 4

Решение: В этом выражении мы видим, что скобки присутствуют; следовательно, мы сначала решим содержимое в скобках. Следовательно, 12 + 3 = 15. Теперь умножаем 15 на 4 = 60.

Выражение 2: 4 – 32 ÷ 8 

4 – 32 ÷ 8 = 8 – 8 = 0 – это решение. (Это правильно. Это правильный способ.) 

Рассмотрим другой подход к тому же выражению.

4 – 32 ÷ 8 = (-28) ÷ 8 = -3,5 (Неверно (это неправильный метод).

Выражение 3: 8 x (6 + 6) 

8 x (12) = 96 (Это правильный способ решения скобок. ) 

Рассмотрим другой метод для того же выражения. 

8 x (6 + 6) = 48 + 6 = 54 (Это неправильный способ решения скобок.)

Примечание: Мы должны соблюдать шаблон операторов при выполнении порядка операций над любой данной фразой.

Из вышеупомянутых правил мы узнаем, как выполнять несколько операций, если они входят в одно уравнение. Очень важно изучить эти понятия, чтобы исключить все возможные ошибки при выполнении расчетов. Более того, освоение порядка действий поможет получить больше баллов на экзаменах.

Что такое правило БОДМАС и как оно применяется в математике

• Дом
• >
• Блог
• >
• Что такое правило БОДМАСА и как оно применяется в математике

Джессика Камински

5 минут чтения

20 мая 2022 г.

Что такое БОДМАС в математике? В математике правило BODMAS или Bodmas определяет порядок операций, которым необходимо следовать при выполнении вычислений. Ребенку необходимо знать, в каком порядке выполнять действия, чтобы получить правильный ответ. Это руководство поможет вам понять, как применять правило к математическим задачам.

Что такое БОДМАС?

Что означает БОДМАС? BODMAS означает скобки, порядки (степени и корни), деление, умножение, сложение и вычитание. Интерпретация правила такова: сначала нужно решать скобки, затем порядки (степени, квадратные корни), деление и умножение, и, наконец, сложение и вычитание.

Порядок операций BODMAS важен, потому что все мы можем по-разному интерпретировать арифметические выражения. Один человек может первым складывать, а другой может первым умножать. Использование BODMAS гарантирует, что все производят вычисления в заданном математическом выражении по одному и тому же шаблону.

БОДМАС помогает нам узнать правильный порядок операций для решения математических задач. Кроме того, правило говорит нам, что мы должны найти ответ на любую сумму в определенном порядке. Вот краткое изложение того, как мы можем прийти к правильному ответу при работе с BODMAS:

Числа

Числа — это объекты, которые позволяют нам считать вещи, сравнивать суммы и производить вычисления. Мы не отдаем приоритет числам в BODMAS. Мы относимся к ним как к равным, независимо от того, маленькие они или большие.

Операторы

Операторы — это символы, которые выполняют математические операции со значением. Они применимы в выражениях, которые представляют собой группы символов, оценивающие одно значение. Кроме того, математические операторы — это символы, представляющие действия, такие как сложение или умножение. Операторы выполняют определенные действия при использовании в математических уравнениях. Это:

• Дополнение (+)
• Вычитание (-)
• Отдел (/)
• Умножение (*)

BODMAS Пример

Порядок операций всегда важен. Например, возьмем выражение

3 + 2 x 5 =

. Поскольку в нем нет скобок и порядков, перед сложением чисел необходимо выполнить умножение. Это потому, что умножение имеет более высокий приоритет, чем сложение.

BODMAS Значение

Полная форма BODMAS: Скобки, Порядок, Деление, Умножение, Сложение и Вычитание. Вам необходимо следовать этому порядку при выполнении вычислений, включающих более одной операции. Если вы не будете следовать ему, вы получите неправильный ответ.

Как использовать правило БОДМАС

Правило БОДМАС в математике:

• Если есть скобки, то сначала решить скобки.
• Если скобок нет, то сначала решить Приказы.
• Если порядок не очевиден, решите Умножение и Деление.
• Если нет ни умножения, ни деления, решите сложение и вычитание.
• Сложение и вычитание слева направо.

Порядок, в котором вы выполняете операции, важен, потому что он определяет, как вычислить окончательный ответ. Например, вам нужно вычислить ответ на это уравнение:

2 + 3 x 4

Вы получите ответ 20, если сначала выполните сложение, а затем умножение. Однако, если вы сначала выполнили умножение, а затем сложение, вы получите ответ 14. Другими словами, порядок, в котором вы выполняете операции, может изменить окончательный ответ.

BODMAS против PEMDAS

BODMAS и PEMDAS — это аббревиатуры, призванные помочь вам запомнить порядок операций в математике. Их также можно использовать при решении уравнений, поскольку оба обозначают порядок операций.

Разница между этими двумя правилами в том, что они работают по-разному. Мы используем BODMAS, когда в скобках или квадратных скобках есть несколько операций. Мы применяем PEMDAS в случае нескольких операций вне круглых или квадратных скобок.

PEMDAS означает Скобки, Экспоненты, Умножение, Деление, Сложение и Вычитание, тогда как BODMAS означает Скобки, Порядки (или экспоненты), Деление, Умножение, Сложение и Вычитание.

Эти два метода имеют одинаковые шаги для решения проблемы. Разница в том, как вы их применяете. В BODMAS операционные приказы следуют слева направо, а в PEMDAS — справа налево.

Как и когда преподается БОДМАС?

BODMAS следует преподавать после того, как дети изучили четыре действия с числами: сложение, вычитание, умножение и деление. Правило БОДМАСа обычно изучают в начальной школе учащиеся в возрасте 9-12 лет и используют для выполнения математических операций в правильном порядке.

Заключение

Если вы не уверены в последовательности операций, используйте BODMAS, чтобы определиться с выбором.

Как только учитель убедится, что дети понимают концепцию БОДМАС и могут применять ее для решения простых задач, он может продолжить использовать правило в более сложных задачах.

Джессика Камински

Джессика — опытный репетитор по математике с десятилетним опытом работы в этой области. Имея степень бакалавра и магистра математики, ей нравится воспитывать математических гениев, независимо от их возраста, уровня и навыков.