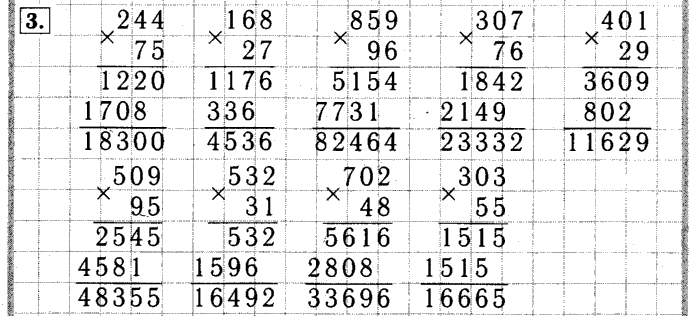
Примеры на умножение 4: 4 класс. Примеры на умножение многозначных чисел в столбик. Примеры с ответами. Скачать pdf или jpg.

Умножение на 4 | Таблица умножения

    На этой странице представлены примеры, описывающие умножение на 4 и умножение числа 4, деление, некоторые способы произношения и записи, таблица умножения на 4 без ответов, в конце статьи – картинки для скачивания, с помощью которых можно распечатать часть таблицы. Умножение на 4:
1 x 4 = 4
2 x 4 = 8
3 x 4 = 12
4 x 4 = 16
5 x 4 = 20
6 x 4 = 24
7 x 4 = 28
8 x 4 = 32
9 x 4 = 36
10 x 4 = 40

Первый вариант произношения:
1 x 4 = 4 (1 умножить на 4, равно 4)
2 x 4 = 8 (2 умножить на 4, равно 8)
3 x 4 = 12 (3 умножить на 4, равно 12)
4 x 4 = 16 (4 умножить на 4, равно 16)
5 x 4 = 20 (5 умножить на 4, равно 20)
6 x 4 = 24 (6 умножить на 4, равно 24)
7 x 4 = 28 (7 умножить на 4, равно 28)
8 x 4 = 32 (8 умножить на 4, равно 32)
9 x 4 = 36 (9 умножить на 4, равно 36)
10 x 4 = 40 (10 умножить на 4, равно 40)

Второй вариант произношения:
1 x 4 = 4 ( по 1 взять 4 раза, получится 4)

2 x 4 = 8 ( по 2 взять 4 раза, получится 8)
3 x 4 = 12 ( по 3 взять 4 раза, получится 12)
4 x 4 = 16 ( по 4 взять 4 раза, получится 16)
5 x 4 = 20 ( по 5 взять 4 раза, получится 20)
6 x 4 = 24 ( по 6 взять 4 раза, получится 24)
7 x 4 = 28 ( по 7 взять 4 раза, получится 28)
8 x 4 = 32 ( по 8 взять 4 раза, получится 32)
9 x 4 = 36 ( по 9 взять 4 раза, получится 36)
10 x 4 = 40 ( по 10 взять 4 раза, получится 40)

От перемены мест множителей значение произведения не меняется, поэтому, зная результаты умножения на 4, можно легко найти результаты умножения числа 4. В качестве знака умножения в разных источниках используют разные символы. Выше был показан пример с (x), в этот раз сделаем запись с помощью приподнятой точки ( ∙ )

Умножение числа 4:

4 ∙ 1 = 4
4 ∙ 2 = 8
4 ∙ 3 = 12
4 ∙ 4 = 16
4 ∙ 5 = 20
4 ∙ 6 = 24
4 ∙ 7 = 28
4 ∙ 8 = 32
4 ∙ 9 = 36
4 ∙ 10 = 40

Варианты произношения:
4 ∙ 1 = 4 (по 4 взять 1 раз, получится 4)
4 ∙ 2 = 8 (по 4 взять 2 раза, получится 8)
4 ∙ 3 = 12 (по 4 взять 3 раза, получится 12)
4 ∙ 4 = 16 (по 4 взять 4 раза, получится 16)
4 ∙ 5 = 20 (по 4 взять 5 раз, получится 20)
4 ∙ 6 = 24 (по 4 взять 6 раз, получится 24)
4 ∙ 7 = 28 (по 4 взять 7 раз, получится 28)
4 ∙ 8 = 32 (по 4 взять 8 раз, получится 32)
4 ∙ 9 = 36 (по 4 взять 9 раз, получится 36)
4 ∙ 10 = 40 (по 4 взять 10 раз, получится 40)

4 ∙ 1 = 4 (4 умножить на 1, равно 4)
4 ∙ 2 = 8 (4 умножить на 2, равно 8)
4 ∙ 3 = 12 (4 умножить на 3, равно 12)
4 ∙ 4 = 16 (4 умножить на 4, равно 16)
4 ∙ 5 = 20 (4 умножить на 5, равно 20)
4 ∙ 6 = 24 (4 умножить на 6, равно 24)
4 ∙ 7 = 28 (4 умножить на 7, равно 28)
4 ∙ 8 = 32 (4 умножить на 8, равно 32)
4 ∙ 9 = 36 (4 умножить на 9, равно 36)
4 ∙ 10 = 40 (4 умножить на 10, равно 40)

Деление на 4:

4 ÷ 4 = 1
8 ÷ 4 = 2

12 ÷ 4 = 3
16 ÷ 4 = 4
20 ÷ 4 = 5
24 ÷ 4 = 6
28 ÷ 4 = 7
32 ÷ 4 = 8
36 ÷ 4 = 9
40 ÷ 4 = 10

4 ÷ 4 = 1 (4 разделить на 4, равно 1)
8 ÷ 4 = 2 (8 разделить на 4, равно 2)
12 ÷ 4 = 3 (12 разделить на 4, равно 3)
16 ÷ 4 = 4 (16 разделить на 4, равно 4)
20 ÷ 4 = 5 (20 разделить на 4, равно 5)
24 ÷ 4 = 6 (24 разделить на 4, равно 6)
28 ÷ 4 = 7 (28 разделить на 4, равно 7)
32 ÷ 4 = 8 (32 разделить на 4, равно 8)
36 ÷ 4 = 9 (36 разделить на 4, равно 9)
40 ÷ 4 = 10 (40 разделить на 4, равно 10)

Картинка: 

Деление. Картинка: 

Таблица умножения и деления на 4 без ответов (по порядку и вразброс):

1 ∙ 4 =	3 ∙ 4 =	4 ÷ 4 =	36 ÷ 4 =
2 ∙ 4 =	6 ∙ 4 =	8 ÷ 4 =	32 ÷ 4 =
3 ∙ 4 =	1 ∙ 4 =	12 ÷ 4 =	28 ÷ 4 =
4 ∙ 4 =	4 ∙ 4 =	16 ÷ 4 =	24 ÷ 4 =
5 ∙ 4 =	2 ∙ 4 =	20 ÷ 4 =	16 ÷ 4 =
6 ∙ 4 =	7 ∙ 4 =	24 ÷ 4 =	20 ÷ 4 =
7 ∙ 4 =	10 ∙ 4 =	28 ÷ 4 =	12 ÷ 4 =
8 ∙ 4 =	5 ∙ 4 =	32 ÷ 4 =	8 ÷ 4 =
9 ∙ 4 =	9 ∙ 4 =	36 ÷ 4 =	4 ÷ 4 =
10 ∙ 4 =	8 ∙ 4 =	40 ÷ 4 =	40 ÷ 4 =

Способы записи таблицы умножения на 4:

x	Приподнятая точка	*	Знак не указан
1 x 4 = 4	1 ∙ 4 = 4	1 * 4 = 4	1 __ 4 = 4
2 x 4 = 8	2 ∙ 4 = 8	2 * 4 = 8	2 __ 4 = 8
3 x 4 = 12	3 ∙ 4 = 12	3 * 4 = 12	3 __ 4 = 12
4 x 4 = 16	4 ∙ 4 = 16	4 * 4 = 16	4 __ 4 = 16
5 x 4 = 20	5 ∙ 4 = 20	5 * 4 = 20	5 __ 4 = 20
6 x 4 = 24	6 ∙ 4 = 24	6 * 4 = 24	6 __ 4 = 24
7 x 4 = 28	7 ∙ 4 = 28	7 * 4 = 28	7 __ 4 = 28
8 x 4 = 32	8 ∙ 4 = 32	8 * 4 = 32	8 __ 4 = 32
9 x 4 = 36	9 ∙ 4 = 36	9 * 4 = 36	9 __ 4 = 36
10 x 4 = 40	10 ∙ 4 = 40	10 * 4 = 40	10 __ 4 = 40

Способы записи таблицы деления на 4:

/	:	÷	Знак не указан
4 / 4 = 1	4 : 4 = 1	4 ÷ 4 = 1	4 __ 4 = 1
8 / 4 = 2	8 : 4 = 2	8 ÷ 4 = 2	8 __ 4 = 2
12 / 4 = 3	12 : 4 = 3	12 ÷ 4 = 3	12 __ 4 = 3
16 / 4 = 4	16 : 4 = 4	16 ÷ 4 = 4	16 __ 4 = 4
20 / 4 = 5	20 : 4 = 5	20 ÷ 4 = 5	20 __ 4 = 5
24 / 4 = 6	24 : 4 = 6	24 ÷ 4 = 6	24 __ 4 = 6
28 / 4 = 7	28 : 4 = 7	28 ÷ 4 = 7	28 __ 4 = 7
32 / 4 = 8	32 : 4 = 8	32 ÷ 4 = 8	32 __ 4 = 8
36 / 4 = 9	36 : 4 = 9	36 ÷ 4 = 9	36 __ 4 = 9
40 / 4 = 10	40 : 4 = 10	40 ÷ 4 = 10	40 __ 4 = 10

Умножение на:

‹ Умножение на 3 Вверх Умножение на 5 ›

3000 примеров по математике.

4 класс. Цепочки примеров. Умножение и деление круглых чисел (Елена Нефёдова, Ольга Узорова) Читать отрывок

134 ₽

97 ₽

+ до 20 баллов

Бонусная программа

Итоговая сумма бонусов может отличаться от указанной, если к заказу будут применены скидки.

Офлайн

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

В наличии в 119 магазинах. Смотреть на карте

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

В пособии представлен материал, который поможет сформировать навыки устного счета по базовым темам 4 класса. Отвечая на вопросы учителя к каждому из приведенных примеров, учащиеся выполняют несколько математических заданий – всего более 3000 примеров.
Последовательное выполнение заданий пособия поможет ученикам овладеть навыками устного счёта всех форм: беглым слуховым счётом (учитель вслух читает цепочку примеров, делая небольшие остановки для подсчёта, и ученик через несколько секунд отвечает), зрительным счётом (цепочки примеров записаны, а ответы ученик либо сообщает устно, либо записывает), комбинированным счетом (учитель диктует цепочки примеров, а ученик записывает ответы).

Систематическое выполнение этих заданий развивает логическое и математическое мышление, сообразительность, укрепляет память и внимание. По усмотрению учителя цепочки примеров можно использовать как для олимпиадных работ и заданий повышенной сложности, так и для повторения и закрепления изученной темы. Для лучшего усвоения материала рекомендуется решать по десять примеров в день.
Пособие можно использовать на уроках математики и для самостоятельной работы дома.

Описание

Характеристики

В пособии представлен материал, который поможет сформировать навыки устного счета по базовым темам 4 класса.

Отвечая на вопросы учителя к каждому из приведенных примеров, учащиеся выполняют несколько математических заданий – всего более 3000 примеров.
Последовательное выполнение заданий пособия поможет ученикам овладеть навыками устного счёта всех форм: беглым слуховым счётом (учитель вслух читает цепочку примеров, делая небольшие остановки для подсчёта, и ученик через несколько секунд отвечает), зрительным счётом (цепочки примеров записаны, а ответы ученик либо сообщает устно, либо записывает), комбинированным счетом (учитель диктует цепочки примеров, а ученик записывает ответы).
Систематическое выполнение этих заданий развивает логическое и математическое мышление, сообразительность, укрепляет память и внимание. По усмотрению учителя цепочки примеров можно использовать как для олимпиадных работ и заданий повышенной сложности, так и для повторения и закрепления изученной темы. Для лучшего усвоения материала рекомендуется решать по десять примеров в день.
Пособие можно использовать на уроках математики и для самостоятельной работы дома.

АСТ

На товар пока нет отзывов

Поделитесь своим мнением раньше всех

Как получить бонусы за отзыв о товаре

1

Сделайте заказ в интернет-магазине

2

Напишите развёрнутый отзыв от 300 символов только на то, что вы купили

3

Дождитесь, пока отзыв опубликуют.

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Книга «3000 примеров по математике. 4 класс. Цепочки примеров. Умножение и деление круглых чисел» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене. Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом другом регионе России, вы можете оформить заказ на книгу Елена Нефёдова, Ольга Узорова «3000 примеров по математике. 4 класс. Цепочки примеров. Умножение и деление круглых чисел» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.

Что такое длинное умножение? Объяснение для начальной школы

Длинное умножение — это метод, используемый для умножения с использованием стандартного алгоритма. Старшее элементарное умножение включает в себя умножение числа с двумя или более цифрами на двузначное число, например. 34 x 27, 851 x 82 или 4274 x 93. В этой статье объясняется процесс умножения этих чисел с помощью длинного умножения, также известного как умножение по стандартному алгоритму.

Когда мы используем длинное умножение?

Длинное умножение — это метод, используемый для умножения нескольких цифр. В начальной учебной программе преподается стандартный алгоритм умножения двух-, трех- и четырехзначных чисел, множимого, на двузначные числа.

Метод длинного умножения

Ниже приведены три примера длинного умножения, демонстрирующие стандартный алгоритм умножения или формальный метод, используемый при умножении больших чисел:

Первое и третье умножение демонстрируют наиболее распространенные методы умножения.

Пример 1: 24 x 16

Это пример двузначного умножения. 26 делится на 20 и 6. Сначала 124 умножается на 6, что равно 744; Затем 126 умножается на 20 и получается 2480; 2480 и 744 складываются вместе, чтобы получить 3224. Чтобы преуспеть в использовании стандартного алгоритма при умножении, важно, чтобы дети свободно владели фактами умножения или таблицами умножения. Если ваши ученики изо всех сил пытаются стать уверенными в своих фактах умножения, то мы рекомендуем попробовать эти игры на умножение в качестве отличного следующего шага. Вы также можете помочь учащимся с помощью таблицы умножения. Также важно, чтобы учащиеся знали и были уверены в значении места, чтобы избежать ошибок.

Пример 3: 124 x 26

Здесь у вас есть пошаговое руководство по длинному умножению для третьего примера:

1. Задайте вопрос формальным методом, обычно с большими числами в качестве верхнего числа и меньшего номер как нижний номер. Убедитесь, что столбцы единиц и десятков (и т. д.) обоих чисел совпадают.
2. Не забудьте начать процесс умножения с единиц, также известных как разряд единиц, поэтому умножьте 6 на 4
3. Запишите ответ правильно в разряде единиц. Помните, что вы можете написать только одну цифру, поэтому перегруппируйтесь в разряд десятков
4. Умножить 6 на 2
5. Добавьте все, что вы перенесли из предыдущего умножения.
6. Умножить 6 на 1; Добавьте все, что вы перенесли из предыдущего умножения.
7. Запишите ответ правильно
8. Отбросьте ноль, так как теперь мы умножаем на 10 с
9. Умножить 2 на 4
10. Напиши ответ правильно
11. Умножить 2 на 2
12. Запишите ответ
13. Умножить 2 на 1
14. Напиши ответ правильно
15. Правильно сложите два ответа, чтобы получить окончательный ответ

Теперь все, что вам нужно сделать, это следовать этому пошаговому руководству для любых других подобных вопросов на умножение, где будет использоваться стандартный алгоритм.

Когда мои ученики узнают о длинном умножении на в начальной школе?

Сначала дети узнают, как выполнять стандартный алгоритм для решения задач на умножение, в 5-м классе, где они должны умножать трехзначные и четырехзначные числа на одно- или двузначное число, используя стандартный алгоритм, включая длинные умножение двузначных чисел. Также ожидается, что учащиеся 5-го класса будут использовать свои знания для решения текстовых задач и использования стандартного алгоритма для умножения с десятичными числами и дробями, а также развивать свои знания о взаимосвязи между стандартным алгоритмом при умножении и делении.

• В соответствии с базовыми знаниями и навыками Техаса (TEKS) в 4-м классе учащиеся должны использовать стратегии, включая стандартный алгоритм, для умножения до четырехзначного числа на однозначное число и для умножения 2 -значное число на двузначное число.
• Согласно стандарту Texas Essential Knowledge and Skills (TEKS), учащиеся 5-го класса должны бегло умножать трехзначное число на двузначное, используя стандартный алгоритм. Учащиеся также будут решать произведения десятичных дробей с точностью до сотых.

Длинные вопросы на умножение

1. 746 x 23 =

(ответ: 17 158)

2. В коробке лежат подносы с дынями. На подносе 15 дынь. В коробке 3 лотка. Супермаркет продает 40 коробок дынь. Сколько дынь продается в супермаркете?

(Ответ: 15 x 3 x 40 = 1800)

3. Впишите две недостающие цифры, чтобы это длинное умножение было правильным.

(Ответ: 4 1 x 2 6)

4. Магазин игрушек заказывает 11 ящиков шариков. В каждой коробке по 6 мешков с шариками. В каждом мешочке 45 шариков. Сколько всего шариков заказывает магазин?

(Ответ: 11 x 6 x 45 = 2970)

5. В магазине продаются листы самоклеящихся этикеток. На каждом листе 36 строк и 18 столбцов надписей. Сколько всего наклеек на 45 листах?

(Ответ: 36 х 18 х 45 = 29 160)

Что означает длинное умножение?

Длинное умножение, также называемое стандартным алгоритмом умножения, представляет собой метод умножения, обычно используемый для трехзначных и более крупных чисел.

В каком году школьники изучают длинное умножение?

Согласно Common Core State Standards умножение по стандартному алгоритму чаще всего вводится в 5-м классе. Однако школы и округа, которые следуют стандартам штата Техас, начнут использовать стандартный алгоритм, начиная с 4-го класса.

Читать дальше

• Что такое квадратное число: разъяснение для родителей и детей
• Что такое наименьшее общее кратное: объяснение для основных родителей и детей
• Что такое число в кубе: объяснение для основных родителей и детей

Есть ли у вас ученики, которым нужна дополнительная помощь по математике?
Предоставьте учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью персонализированного обучения элементарной математике с их собственным онлайн-репетитором по математике.

Каждый учащийся получает дифференцированное обучение, предназначенное для устранения индивидуальных пробелов в обучении, а организованное обучение гарантирует, что каждый учащийся учится в нужном темпе. Уроки соответствуют стандартам и оценкам вашего штата, плюс вы будете получать регулярные отчеты о каждом шаге.

Программы доступны для четвертого и пятого классов, и вы можете попробовать 6 уроков абсолютно бесплатно.

Стратегии умножения для 4 и 5 классов

Прослушать эту статью

Оценить этот пост

---

В этой статье обсуждаются три стратегии умножения. Кроме того, вы найдете решенные примеры с пояснениями и ссылками на рабочие листы для дополнительной практики или оценки.

Что такое умножение?

Умножение — одно из четырех основных арифметических действий, наряду со сложением, вычитанием и делением.

Процесс умножения представляет собой многократное сложение одинаковых групп, при котором одно число добавляется к самому себе несколько раз.

Части умножения

В умножении 10 x 4 = 40 первое число ( 10 ) называется множимым , а второе число ( 4 ) называется множителем .

Множитель и множитель известны как множителя , а ответ ( 40 ) известен как произведение .

Типы умножения

Существует множество доступных методов умножения.

Учителя могут требовать, чтобы ученики практиковались и использовали определенные методы в классе, но каждый ученик должен найти тот метод, который подходит ему больше всего.

Хотя мы можем использовать все методы умножения для решения любой задачи на умножение, некоторые методы больше подходят для решения определенного типа задач.

Метод многократного сложения

Обычно мы используем повторное сложение для решения задач на умножение в классах ниже 4-го и 5-го . Этот метод умножения просто многократно прибавляет одно и то же число к самому себе.

Например, мы можем решить 10 x 4, прибавив 10 к самой себе 4 раза. Таким образом, 10 + 10 + 10 + 10 = 40 .

Это хорошая стратегия для небольших чисел или нескольких групп больших чисел. Мысленно относительно легко складывать числа, кратные десяти, и поэтому этот метод также хорошо работает.

Использование этого подхода для умножения больших чисел становится утомительным и подверженным ошибкам.

Например, если вы хотите решить 83 x 64, вам придется прибавить 83 к самому себе 64 раза. Это займет много времени и велика вероятность ошибиться.

Присоединяйтесь к моему списку адресов электронной почты и загружайте бесплатные материалы из моей бесплатной библиотеки ресурсов .

Имя *

Адрес электронной почты *

Как мы умножаем большие числа?

В четвертом и пятом классах некоторые из стратегий умножения больших многозначных чисел включают: 

1. частичное произведение
2. зональная модель
3. длинное умножение

Что такое частичный продукт?

Частичное произведение — это произведение, полученное при умножении многозначного множимого на одну цифру многозначного множителя.

Частичные произведения — отличный способ научиться умножать многозначные числа.

Стратегия умножения частичным произведением

Метод частичного произведения применяется для умножения чисел, превышающих 10. Этот метод позволяет учащимся использовать концепцию разрядных значений для умножения чисел.

Это хорошая стратегия умножения для улучшения понимания чисел.

В этом методе мы

1. ставим задачу вертикально
2. разбить числа на части по разрядному значению
3. найти продукты частей отдельно
4. добавить отдельные продукты, чтобы найти конечный продукт

Примеры частичного умножения произведения

Следующие примеры помогут понять концепцию частичного умножения произведения.

Умножение частичного произведения на однозначный множитель (54 x 2):

Чтобы умножить двузначное число на однозначное число с помощью частичного произведения, выполните следующие действия:

Напишите числа вертикально, одно над другим. Множимое должно идти сверху.

Нарисуйте горизонтальную линию под уравнением.

Разбейте каждое число на части в зависимости от его разрядности. Следовательно, 54 = 50 + 4 и 2 = 2·9.0030

Умножьте разряд единиц множителя на разряд единиц множимого и запишите произведение (2 x 4 = 8)

Затем умножьте разряд единиц множителя на разряд десятков множимого и запишите произведение под первым произведением (2 x 50 = 100).

Наконец, сложите два частичных произведения, чтобы получить окончательный ответ (8 + 100 = 108).

Если множимое имеет более двух цифр , умножьте цифру единиц множителя на оставшиеся цифры множимого в порядке (сотни, тысячи и т. д.) перед добавлением частичных произведений.

Частичное произведение умножения на двузначный множитель (65 x 23):

Чтобы умножить два двузначных числа с помощью частичного произведения, выполните следующие действия: один над другим.

Нарисуйте горизонтальную линию под уравнением.

Разбейте каждое число на части в зависимости от его разрядности. Следовательно, 65 = 60 + 5 и 23 = 20 + 3 

.

Умножьте разряд единиц множителя на разряд единиц множимого и запишите произведение (3 x 5 = 15).

Затем умножьте разряд единиц множителя на разряд десятков множимого и запишите произведение под первым произведением (3 x 60 = 180).

Затем умножьте разряд десятков множителя на разряд единиц множимого и запишите произведение под двумя произведениями (20 x 5 = 100).

Наконец, умножьте разряд десятков множителя на разряд десятков множимого и запишите его под тремя предыдущими произведениями (20 x 60 = 1200).

Сложите четыре частичных произведения, чтобы получить окончательный ответ (15 + 180 + 100 + 1200 = 1495).

Присоединяйтесь к моему списку адресов электронной почты и загружайте бесплатные материалы из моей бесплатной библиотеки ресурсов .

Имя *

Адрес электронной почты *

Что такое модель площади?

Модель площади — это тип прямоугольной диаграммы или модели, используемой в математике для решения задач на умножение и деление.

Множители или частное и делитель определяют длину и ширину прямоугольника. Модель площади также известна как коробка модель .

Если прямоугольник имеет длину 25 единиц и ширину 18 единиц, то эту площадь можно вычислить, найдя произведение 25 х 18.

Для упрощения вычислений мы можем дополнительно разделить этот прямоугольник на меньшие прямоугольники, а затем добавьте площади этих меньших прямоугольников, чтобы определить общую площадь прямоугольника.

Мы можем сделать это, разбив длины сторон на меньшие числа, используя расширенные формы.

Примеры умножения модели площади

Следующие примеры помогут понять концепцию умножения модели площади.

Умножение модели площади с одноразрядным множителем (54 x 2):

Чтобы умножить двузначное число на однозначное t число с использованием модели площади, выполните указанные шаги. : 

1. Запишите числа в развернутом виде в виде десятков и единиц. (54 = 50 + 4), (2 = 2)
2. Нарисуйте прямоугольник или коробку с двумя столбцами.
3. Напишите термины двузначного числа в верхней части прямоугольника, по одному в верхней части каждой ячейки.
4. Слева от прямоугольника напишите член однозначного числа сбоку от ячейки.
5. Запишите произведение десятков и единиц в первой ячейке (2 x 50 = 100 ).
6. Затем запишите произведение единиц во второй ячейке (2 x 4 = 8 ).
7. Наконец, сложите все частичные произведения, чтобы получить конечный продукт (100 + 8 = 108 ).

Модель площади Умножение с двузначным множителем (65 x 23):

Чтобы умножить два двузначных числа с помощью модели площади, выполните следующие действия: образуют десятки и единицы. (65 = 60 + 5), (23 = 20 + 3)

Нарисуйте прямоугольник или коробку с 2 рядами и 2 столбцами.

Напишите условия одного из чисел в верхней части прямоугольника, по одному в верхней части каждой клетки.

Слева от прямоугольника напишите члены другого числа, по одному на стороне каждой клетки.

Запишите произведение десятков в первой ячейке. Затем запишите произведение десятков и единиц во вторую и третью клетки. Запишите произведение единиц в четвертой ячейке.

Наконец, сложите все частичные продукты, чтобы получить конечный продукт.

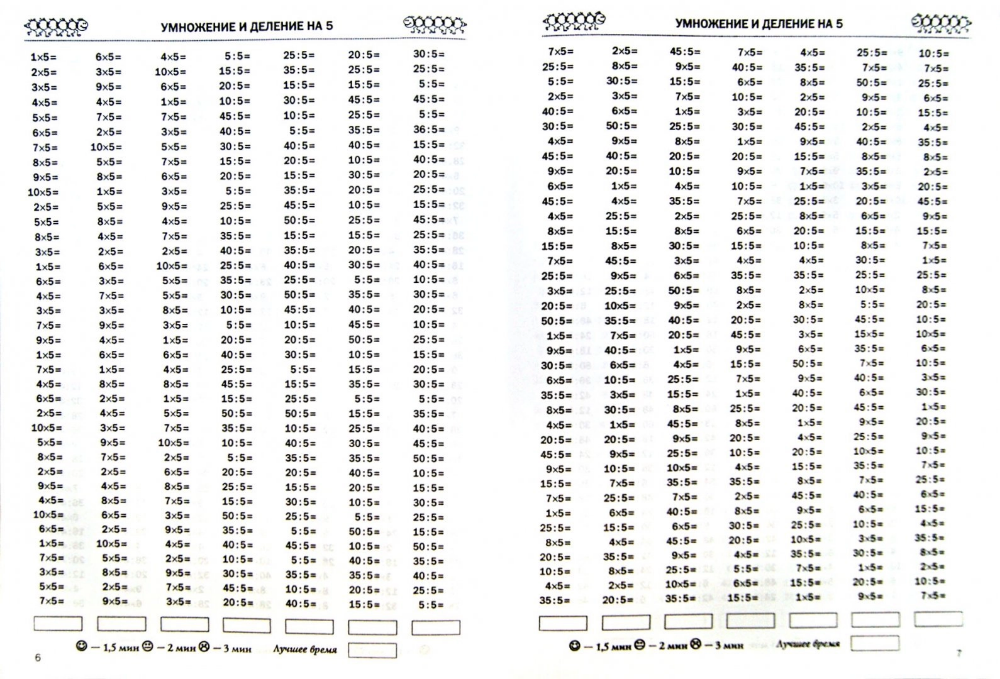
Стратегия длинного умножения

Длинное умножение также известно как стандартный или традиционный алгоритм.

Этот метод обычно считается лучшим.

Однако этот метод подвержен ошибкам, когда учащиеся не полностью понимают этапы.

Примеры длинного умножения

Следующие примеры помогут понять концепцию длинного умножения.

Длинное умножение с однозначной цифрой Множитель (54 x 2):

Чтобы умножить двузначное число на однозначное число с помощью длинного умножения, выполните следующие действия:0005

1. Пишите числа вертикально, одно над другим. Убедитесь, что значения мест выровнены. Номер с наибольшим количеством цифр должен идти сверху.
2. Нарисуйте горизонтальную линию под уравнением.
3. Умножьте цифру единиц нижнего числа на цифру единиц верхнего числа (2 x 8 = 8). Продукт идет в те места ниже линии.
4. Умножьте цифру единиц нижнего числа на цифру десятков верхнего числа (2 x 5 = 10). Поскольку 10 — двузначное число, 1 нужно «перенести» в разряд сотен.
5. Нет цифры в разряде сотен верхнего числа, которую можно умножить на цифру в разряде единиц нижнего числа. Поэтому 1, «перенесенная» в разряд сотен, записывается в разряде сотен произведения.
6. Теперь верхнее число полностью умножается на нижнее число (54 x 2 = 108 ).

Если в верхнем числе больше двух цифр, умножьте цифру в разряде единиц нижнего числа на оставшиеся цифры верхнего числа по порядку (сотни, тысячи, десять тысяч и т. д.).

Если продукт имеет две цифры, первая цифра должна быть «перенесена» на начало следующего разряда.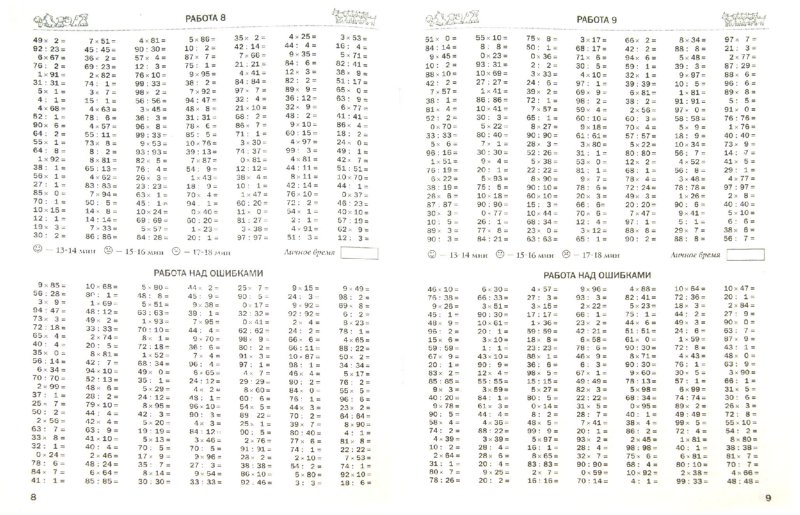

Длинное умножение с двузначным множителем (65 x 23):

Чтобы умножить два двузначных числа с помощью длинного умножения, выполните следующие действия:

1. Напишите числа вертикально, одно сверху другой. Убедитесь, что значения мест выровнены.
2. Нарисуйте горизонтальную линию под уравнением.
3. Умножьте цифру единиц нижнего числа на цифру единиц верхнего числа (3 x 5 = 15). Продукт идет в те места ниже линии. Поскольку 15 — двузначное число, 1 нужно «перенести» на разряд десятков.
4. Умножьте цифру в разряде единиц нижнего числа на цифру разряда десятков верхнего числа (3 x 6 = 18). Поскольку 1 была «перенесена» в разряд десятков, ее нужно прибавить, чтобы получить 19. Кроме того, поскольку 19 — двузначное число, 1 необходимо «перенести» в разряд сотен.
5. Нет цифры в разряде сотен верхнего числа, которую можно умножить на цифру в разряде единиц нижнего числа. 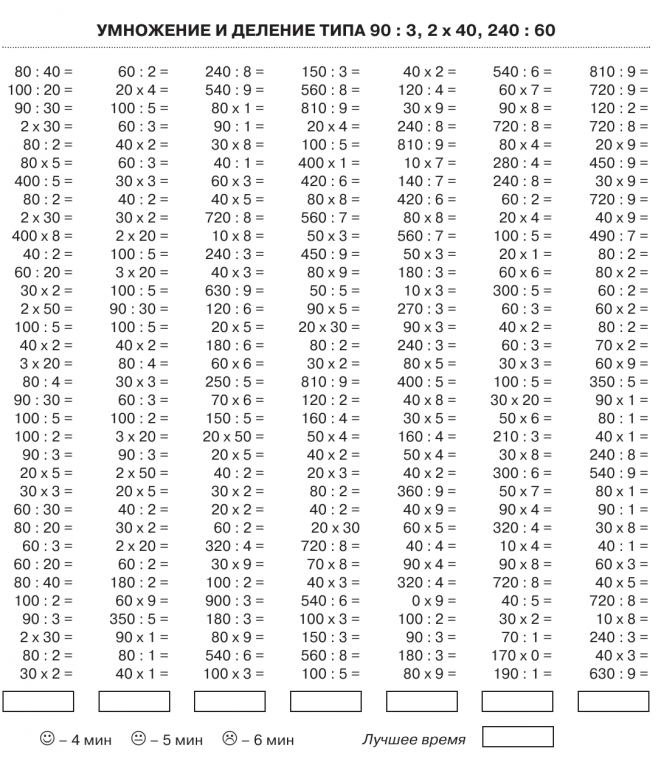Поэтому 1, «перенесенная» в разряд сотен, записывается в разряде сотен произведения.
6. Теперь верхнее число полностью умножается на нижнее (65 x 3 = 195 ).
7. Повторите шаги, используя цифру в разряде десятков нижнего числа. Единственная разница в том, что, поскольку мы сейчас работаем с разрядом десятков, продукт будет начинаться с разряда десятков. Обычно 0 записывается как в качестве заполнителя на месте единиц второго продукта .
8. Запишите произведение 65 x 20 ( 1,300 ) под первым произведением.
9. Сложите два произведения, чтобы получить ответ (195 + 1300 = 1495 ).
.

Другая распространенная ошибка заключается в том, что учащиеся начинают записывать второе произведение в разряд единиц , когда множитель имеет более одной цифры.

Заключение

Способность к умножению — это жизненный навык, который дети должны развивать в раннем возрасте, чтобы справляться с трудностями в реальном мире, как и другие математические операции.