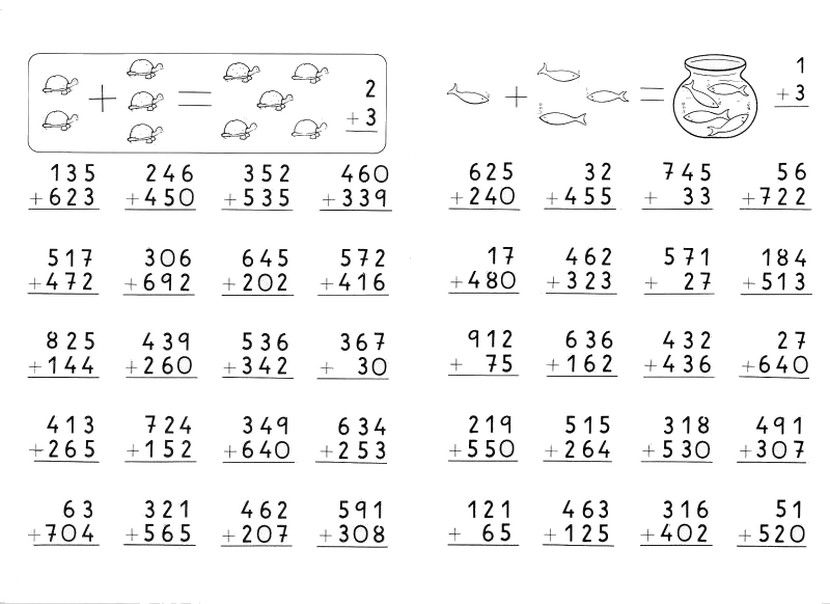
Примеры на сложение 4 класс в столбик: Примеры на сложения и вычитания чисел в столбик. Скачать pdf или jpg.

Примеры на сложение. Математика 4 класс.



Примеры на сложение. Математика 4 класс. 

Задачи по математике 4 класс

MAT-ZADACHI.RU





Математика 4 класс

• Математические диктанты
• Тесты
• Нестандартные задачи
• Логические задачи
• Задачи с ответами
• Примеры

Контрольные работы

1 четверть
• Числа, которые больше 1000. Нумерация
• Итоговая контрольная работа за 1 четверть

2 четверть
• Итоговая контрольная работа 1

Итоговая контрольная работа 2

3 четверть
• Контрольная работа 1

Контрольная работа 2

Итоговая контрольная работа

4 четверть
• Деление на двузначное число

Итоговые контрольные работы за курс начальной школы
• Контрольная работа 1

Контрольная работа 2





Математика 4 класс ->> Примеры

Чтобы увидеть решение, наведите на пример курсор мыши.

526 + 179 = 705	470 + 398 = 868	52 + 391 = 443	506 + 466 = 972	229 + 56 = 285
550 + 371 = 921	97 + 597 = 694	263 + 631 = 894	208 + 167 = 375	347 + 412 = 759
163 + 833 = 996	375 + 299 = 674	60 + 141 = 741	95 + 121 = 216	637 + 24 = 661
94 + 784 = 878	75 + 363 = 438	503 + 58 = 561	365 + 162 = 527	291 + 643 = 934
461 + 163 = 624	141 + 753 = 894	256 + 638 = 894	352 + 263 = 615	60 + 437 = 497
710 + 40 = 750	397 + 235 = 632	118 + 407 = 525	551 + 130 = 681	274 + 583 = 857
342 + 264 = 606	961 + 18 = 979	237 + 254 = 491	551 + 348 = 899	653 + 148 = 801
2 + 396 = 398	208 + 716 = 924	130 + 156 = 286	120 + 166 = 286	165 + 205 = 370
567 + 173 = 740	873 + 68 = 941	130 + 156 = 286	837 + 68 = 905	285 + 287 = 572
480 + 441 = 921	614 + 28 = 642	306 + 175 = 481	17 + 328 = 345	608 + 391 = 999
108 + 631 = 739	318 + 583 = 901	300 + 476 = 776	753 + 105 = 858	339 + 499 = 838
141 + 419 = 560	92 + 692 = 784	418 + 517 = 935	110 + 49 = 159	177 + 807 = 984
295 + 681 = 976	81 + 415 = 496	700 + 173 = 873	0 + 973 = 973	750 + 112 = 862
50 + 98 = 148	14 + 616 = 630	725 + 67 = 792	894 + 70 = 964	14 + 616 = 630
725 + 57 = 782	894 + 70 = 964	40 + 227 = 267	236 + 236 = 472	236 + 751 = 987
488 + 466 = 954	211 + 709 = 920	87 + 550 = 637	250 + 415 = 665	862 + 135 = 997
376 + 422 = 798	301 + 332 = 633	823 + 6 = 829	642 + 289 = 931	269 + 53 = 322
404 + 463 = 867	172 + 728 = 900	43 + 371 = 414	46 + 213 = 259	125 + 873 = 998
294 + 173 = 467	44 + 44 = 88	138 + 353 = 491	399 + 425 = 824	364 + 446 = 810
370 + 279 = 649	450 + 55 = 505	65 + 369 = 434	357 + 222 = 579	198 + 262 = 460
741 + 148 = 889	644 + 341 = 985	589 + 250 = 839	527 + 282 = 809	10 + 555 = 565
71 + 30 = 101	731 + 141 = 872	653 + 345 = 998	23 + 70 = 93	557 + 316 = 873
203 + 701 = 904	95 + 818 = 913	346 + 153 = 499	331 + 395 = 726	928 + 51 = 979
632 + 110 = 742	46 + 500 = 546	445 + 31 = 476	401 + 59 = 460	277 + 551 = 828
259 + 737 = 996	635 + 271 = 806	377 + 581 = 958	72 + 252 = 324	54 + 601 = 660
30 + 561 = 591	612 + 332 = 944	183 + 237 = 420	89 + 441 = 530	462 + 83 = 545
51 + 613 = 664	114 + 749 = 863	96 + 286 = 382	624 + 110 = 734	689 + 137 = 826
507 + 415 = 922	300 + 162 = 462	158 + 319 = 477	390 + 252 = 642	470 + 436 = 906
9 + 237 = 246	663 + 241 = 904	192 + 372 = 564	127 + 523 = 650	90 + 832 = 922
384 + 610 = 994	82 + 369 = 4511	342 + 358 = 700	73 + 852 = 925	597 + 307 = 904
____________________	____________________	____________________	____________________	____________________





Простые задачи

• Простые задачи на движение

Составные задачи

• Задачи на встречное движение
• Задачи на движение в одном направлении
• Задачи на противоположное движение
• Задачи на нахождение неизвестного по двум разностям
• Задачи на нахождение числа по доле и доли по числу
• Задачи на нахождение площади
• Задачи на сложение и вычитание многозначных чисел
• Задачи на умножение и деление многозначных чисел
• Задачи на приведение к единице и пропорциональное деление
• Задачи на определение цены, количества, стоимости



Примеры на вычитание.

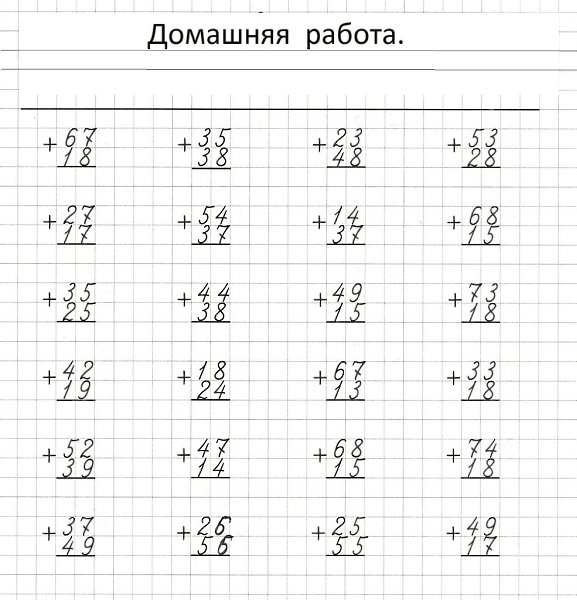Математика 4 класс.



Примеры на вычитание. Математика 4 класс. 

Задачи по математике 4 класс

MAT-ZADACHI.RU





Математика 4 класс

• Математические диктанты
• Тесты
• Нестандартные задачи
• Логические задачи
• Задачи с ответами
• Примеры

Контрольные работы

1 четверть
• Числа, которые больше 1000. Нумерация
• Итоговая контрольная работа за 1 четверть

2 четверть
• Итоговая контрольная работа 1

Итоговая контрольная работа 2

3 четверть
• Контрольная работа 1

Контрольная работа 2

Итоговая контрольная работа

4 четверть
• Деление на двузначное число

Итоговые контрольные работы за курс начальной школы
• Контрольная работа 1

Контрольная работа 2





Математика 4 класс ->> Примеры

Чтобы увидеть решение, наведите на пример курсор мыши.

849 – 238 = 611	562 – 218 = 344	552 – 141 = 411	805 – 512 = 293	800 – 390 = 410
552 – 550 = 2	812 – 274 = 538	986 – 432 = 554	110 – 90 = 20	368 – 135 = 233
700 – 3 = 697	989 – 132 = 857	988 – 99 = 889	686 – 173 = 513	829 – 186 = 643
735 – 326 = 409	866 – 714 = 152	93 – 40 = 53	826 – 413 = 413	909 – 256 = 653
946 – 847 = 99	98 – 50 = 48	532 – 129 = 403	589 – 516 = 73	398 – 218 = 180
652 – 607 = 45	236 – 236 = 0	805 – 697 = 108	419 – 202 = 217	152 -139 = 13
622 – 414 = 208	350 – 30 = 320	264 – 29 = 235	941 – 727 = 214	751 – 723 = 28
779 – 564 = 215	130 – 2 = 128	495 – 384 = 111	840 – 351 = 489	735 – 380 = 355
95 – 80 = 15	985 – 766 = 219	946 – 110 = 836	70 – 64 = 6	780 – 176 = 604
883 – 813 = 70	765 – 431 = 334	630 – 50 = 580	943 – 891 = 52	200 – 2 = 198
330 – 7 = 323	353 – 291 = 62	917 – 885 = 32	652 – 249 = 403	370 – 279 = 91
830 – 431 = 399	847 – 263 = 584	680 – 463 = 217	717 – 383 = 334	972 – 166 = 806
834 – 785 = 49	368 – 345 = 23	835 – 525 = 310	345 – 281 = 64	834 – 299 = 535
853 – 229 = 624	666 – 127 = 539	651 – 469 = 182	405 – 366 = 39	814 – 761 = 53
688 – 6 = 682	976 – 545 = 431	771 – 384 = 387	764 – 482 = 282	968 – 92 = 876
308 – 214 = 94	990 – 18 = 972	869 – 102 = 767	989 – 313 = 676	954 – 417 = 537
759 – 104 = 655	751 – 531 = 220	743 – 662 = 81	575 – 110 = 465	751 – 639 = 112
900 – 545 = 355	300 – 162 = 138	663 – 263 = 400	715 – 441 = 274	820 – 407 = 413
839 – 249 = 590	66 – 24 = 42	245 – 216 = 29	577 – 473 = 104	886 – 421 = 465
379 – 322 = 57	912 – 80 = 832	408 – 91 = 317	978 – 165 = 813	524 – 510 = 14
778 – 555 = 223	893 – 44 = 849	955 – 623 = 332	984 – 649 = 335	357 – 262 = 95
501 – 306 = 195	363 – 188 = 175	939 – 484 = 455	318 – 198 = 120	127 – 94 = 33
272 – 90 = 182	379 – 143 = 236	825 – 642 = 183	170 – 107 = 63	252 – 53 = 199
727 – 617 = 110	575 – 509 = 66	554 – 40 = 514	78 – 67 = 11	185 – 68 = 117
725 – 79 = 646	347 – 152 = 195	798 – 460 = 338	973 – 210 = 763	151 – 37 = 114
655 – 33 = 622	834 – 405 = 429	737 – 215 = 522	355 – 294 = 61	853 – 53 = 800
640 – 20 = 620	961 – 315 = 646	602 – 88 = 514	960 – 90 = 870	848 – 658 = 190
620 – 153 = 467	763 – 108 = 655	246 – 119 = 127	577 – 239 = 338	751 – 135 = 616
853 – 73 = 780	200 – 180 = 20	390 – 272 = 118	428 – 3 = 425	490 – 285 = 205
436 – 104 = 332	810 – 267 = 543	525 – 210 = 315	786 – 293 = 493	933 – 861 = 72
____________________	____________________	____________________	____________________	____________________





Простые задачи

• Простые задачи на движение

Составные задачи

• Задачи на встречное движение
• Задачи на движение в одном направлении
• Задачи на противоположное движение
• Задачи на нахождение неизвестного по двум разностям
• Задачи на нахождение числа по доле и доли по числу
• Задачи на нахождение площади
• Задачи на сложение и вычитание многозначных чисел
• Задачи на умножение и деление многозначных чисел
• Задачи на приведение к единице и пропорциональное деление
• Задачи на определение цены, количества, стоимости



Каковы различные типы стратегий и методов сложения? (Примеры)

• Введение в сложение
• Стратегии операции сложения
• Сложение с использованием открытой числовой строки
• Сложение с использованием частичной суммы
• Сложение с использованием перегруппировки
• Сложение моделей с использованием метода компенсации
• Сложение моделей с использованием метода компенсации
• 4 90 Примеры решений
• Часто задаваемые вопросы

Введение в сложение

Сложение — это метод соединения вещей. Когда вы складываете два числа вместе, вы считаете их одним большим числом. В реальной жизни сложение происходит часто.

Что, если бы, например, было еще три яблока?

Как видите, если вы начнете с двух яблок и добавите еще три, у вас будет пять яблок. Вы можете выразить это так:

Сложение можно представить в виде уравнения: 2 + 3 = 5. Его можно записать как два плюс три равно пяти. Математическое уравнение — это математическое предложение. Вместо слов используются цифры и символы. При записи уравнений сложения мы используем два символа: «+» и «=». Знак плюс (+) обозначает добавление двух элементов. Вот почему мы поместили его в середину яблок. Мы начали с двух яблок, а затем добавили еще три.

Знак равенства (=) является другим символом в уравнении. В уравнении знак равенства указывает на то, что два или более элемента равны или эквивалентны. Эквивалентные вещи не всегда выглядят или звучат одинаково, но означают одно и то же. Знак равенства в математике указывает на то, что два числа или выражения означают одно и то же, несмотря на их внешний вид.

Любая операция сложения может быть выражена письменно. Допустим, вы пригласили 12 друзей на празднование дня рождения. Вы приглашаете еще четырех человек в последнюю минуту. Вы можете написать что-то вроде этого, чтобы получить общее количество гостей, пришедших в ваш дом:

Это выражение просто еще один способ продемонстрировать ситуацию: вечеринка по случаю дня рождения будет проводиться для 12 друзей плюс еще четверо.

Стратегии для операции сложения

Определенные стратегии используются для фиксированного выполнения операций. Используя эти стратегии, мы можем легко и эффективно выполнять математические операции. Существует пять основных стратегий сложения. Давайте взглянем на эти стратегии:

1. Дополнение с использованием линии с открытым номером

2. Дополнение с использованием частичной суммы

3. С помощью перегруппировки

4. С помощью метода компенсации

5. . Дополнение с использованием метода компенсации

5. 8888888 гг. модели

Сложение с использованием открытой числовой строки

На открытой числовой строке нет цифр или маркировки. Открытые числовые строки удобны для работы с разрядными значениями при добавлении чисел.

 

Давайте рассмотрим несколько способов применения этой стратегии.

Рассмотрим 17 + 38 для следующих случаев:

Например,

• Номерная линия 1:

999

. , за которыми следуют единицы (7 + 8). Числовой ряд начинается с 10 (десятки от первого числа) и продолжается до 40 путем добавления трех десятков от второго числа. Затем мы сложили 7 + 8, чтобы получить 15. Затем два результата суммировались, чтобы получить 55.

 

• Числовая строка 2:  

 

Мы должны оставить 17 в целом и добавить три десятка из второго числа. Затем 8 единиц были разбиты на 3 + 5. Затем из 3 единиц было получено 47 + 3 = 50. Наконец, мы добавили последние пять, чтобы получить 50 + 5 = 55. :  

 

Мы знаем, что 38 можно разбить на 30 + 8. Кроме того, 8 можно разбить на 3 + 5, так что 38, наконец, равно 30 + 3 + 5. Теперь мы взяли три единицы из 8 в 38. Затем к 17 прибавляется три, чтобы получить 20 (17 + 3 = 20). Затем мы взяли три десятка из 30, чтобы получить 50. Наконец, мы добавили оставшиеся 5 к общему количеству 55.

Сложение с использованием частичной суммы

По сравнению со всеми другими методами сложения метод частичной суммы является самым простым. Метод частичной суммы, как следует из названия, одновременно вычисляет частичные суммы для разных столбцов разряда. Затем мы складываем все частичные суммы, чтобы найти общую сумму.

 

Частично добавленные суммы можно добавлять в любом порядке, но наиболее распространенный способ — слева направо. Поскольку мы читаем слева направо, такой порядок кажется естественным, и он также отдает приоритет наиболее важному разряду, с которого следует начинать в сложениях, например, тысячи перед сотнями, сотни перед десятками и так далее.

 

Для ментальной арифметики можно легко адаптировать метод сложения частичных сумм.

 

Например, сложение 7701 и 243.

 

 

Он используется с методом сложения столбцов, при котором суммы располагаются вертикально и числа складываются по одному. Перегруппировку иногда называют «переносом». Когда вы складываете все числа в столбце вместе, и в сумме получается десять или более, число в разряде десятков переносится в следующий столбец разряда.

 

Например, если столбец единиц содержит 2 и 9, общее количество будет 11. Вы должны поместить 1 в столбец единиц, а затем перенести 1 в столбец десятков.

 

Когда сумма значений в одном столбце разряда превышает девять, применяется перегруппировка.

 

Нет необходимости использовать метод перегруппировки, если сумма значений в каждом столбце разряда равна девяти или меньше.

 

Например, рассмотрим уравнение сложения 28 + 14,9.0025

 

Как и в случае любого сложения с помощью метода столбцов, мы можем выстроить эти числа вертикально в столбцах их позиционных значений.

Затем числа в столбце единиц можно добавить. Это крайний правый столбец, который содержит 8 и 4. Эти два числа в сумме дают 12. Мы напишем 2 в столбце единиц под чертой и перенесем 1 в столбец десятков, написав его над цифрой. два других числа, следуя методу перегруппировки. После этого этапа у вас должно получиться что-то похожее на это:

 

 

 

После этого вы можете сложить вместе цифры из столбца десятков – 2 и 1 из исходных чисел, а также 1, которую вы только что перенесли. Тогда вы получите 4 как ответ из суммы 1 + 2 + 1. Это должно быть записано в колонке десятков вашего ответа.

 

 

Так работает метод перегруппировки. Ответ на этот вопрос: 42.

Дополнение методом компенсации

Округление числа в большую сторону (для упрощения сложения) и последующее вычитание лишнего числа после завершения вычисления называется «компенсацией».

Например,

Добавление 29 и 16.

Написание в качестве выражения, 29 + 16

Это простые. что превратило 29 в 30, чтобы получить 45.

 

Например,

 

Складываем 695 и 116. 

В виде выражения имеем 695 + 116

. получите 811.

Полезные ресурсы для детей

Повторите математические формулы и важные понятия, используя наши рабочие листы по математике! Эти рабочие листы помогают учащимся развивать математические навыки в увлекательной и интересной форме. Нажмите на ссылку ниже, чтобы получить все простые для понимания математические калькуляторы и рабочие листы.

Сложение с использованием блочных моделей

Блоки с основанием 10 — это визуальные представления, которые помогают нам понять систему с основанием 10, представляя разрядное значение чисел. Мы используем эти блоки для визуализации процесса перегруппировки, чтобы мы могли полностью понять распространенные способы сложения чисел. Этот метод также помогает нам выявлять ошибки в дополнение.

 

Давайте разберемся в этом, используя модели. Каждый куб является единицей. Этот стек содержит десять единиц.

 

 

Предположим, что всего имеется десять стопок.

 

 

Десять стопок по десять штук в каждой равно ста.

1 сотня = 10 десятков = 100.

Например, Добавление 44 и 37.

Решанные примеры из различных методов добавления

Решающие примеры из различных методов добавления

2

. , группа детей бросает монету. У них 13 орлов и 32 решки. Сколько раз они подбросили монету?

 

Решение: Добавьте 13 и 32, чтобы узнать, сколько раз была подброшена монета. Используйте открытую числовую строку для работы над сложением чисел 13 и 32. Когда числа в операции сложения более простые, мы можем использовать метод числовой строки для сложения.

 

 

Сначала были добавлены десятки (10 + 30), а затем единицы (3 + 2). Числовая строка начинается с 10 (десятки от первого числа) и продолжается до 40, добавляя три десятка от второго числа. Затем мы добавили 3 + 2, чтобы получить 5, а затем добавили к 40, чтобы получить 45.

 

Следовательно, они подбросили монету 45 раз.

 

2) В одном озере 1525 лягушек, а в другом озере 251. Сколько всего лягушек?

 

Решение: Добавление 1525 и 251 лягушек, чтобы найти всех лягушек. Для этого вопроса можно использовать метод частичной суммы, поскольку он упрощает расчеты за счет использования частичных сумм по одному столбцу разряда за раз. Затем он складывает все частичные суммы, чтобы найти общую сумму. Когда нам нужно разделить большие числа, мы должны использовать метод частичной суммы.

 

 

Таким образом, общее количество лягушек в обоих озерах равно 1776.

 

деревьев, которые он посадил?

 

Решение: Добавьте 16 и 18, чтобы найти общее количество деревьев, посаженных Джозефом. Когда сумма значений в одном столбце разряда превышает девять, используется перегруппировка.

 

Здесь сумма значений в одном разряде = 6 + 8 = 14, что превышает девять. Поэтому используется метод перегруппировки.

 

Как и в случае любой операции сложения, включающей метод столбцов, мы можем выстроить эти числа вертикально в соответствии со столбцами их позиционных значений.

Затем числа в столбце единиц можно добавить. Это крайний правый столбец, который содержит 6 и 8. Эти два числа в сумме дают 14. Мы напишем 4 в столбце единиц под чертой, а 1 перенесем в столбец десятков, написав его над цифрой. два других числа, следуя методу перегруппировки. После этого этапа у вас должно получиться что-то похожее на это:

 

 

Теперь вы можете сложить вместе цифры из столбца десятков – 1 и 1 из исходных чисел, а также 1, которую вы только что перенесли. Вы получите 3 как ответ из суммы 1 + 1 + 1. Это должно быть записано в колонке десятков вашего ответа.

 

 

 

Таким образом, всего Иосиф посадил 34 дерева.

Учебная программа по математике для всех классов

Наши онлайн-уроки по математике специально разработаны с учетом возраста и академического уровня вашего ребенка. Нажмите на ссылки ниже, чтобы узнать больше о наших онлайн-классах по математике для 1–8 классов.

Часто задаваемые вопросы о методах и стратегиях сложения

Какие стратегии можно использовать для сложения двух чисел?

• Счет от однозначного числа
• Техника прыжков
• Счет до десяти
• Сколько длятся десятки? (разбить большие числа на десятки и единицы, добавить единицы, затем добавить десятки)
• Поставьте цель десять (когда число близко к десяти, мы можем «позаимствовать» у другого числа, чтобы оно достигло десяти)
• Стратегия компенсации
• Когда числа совпадают, удвойте их.
• Если числа близки, удвойте их, а затем зафиксируйте.

 

Как компенсация упрощает сложение?

С некоторыми числами работать легче, чем с другими. Может быть, проще прибавить или вычесть десять, чем девять или одиннадцать. Компенсация — это метод упрощения сложения или вычитания чисел. Если вы добавляете или вычитаете слишком много или слишком мало, вы также должны добавить или вычесть это в результате в качестве компенсации.

Ознакомьтесь с другими нашими курсами

Сложение – формула, определение, примеры

Сложение – это процесс сложения двух или более элементов вместе. В математике сложение — это метод вычисления суммы двух или более чисел. Это основная арифметическая операция, которая обычно используется в нашей повседневной жизни. Одно из наиболее распространенных применений сложения — когда мы работаем с деньгами, рассчитываем счета за продукты или рассчитываем время.

1.	Что такое сложение?
2.	Части дополнения
3.	Дополнительные проблемы Word
4.	Часто задаваемые вопросы по дополнению

Что такое сложение?

Сложение — это операция, используемая в математике для сложения чисел. Результат, который получается после сложения, известен как сумма заданных чисел. Например, если мы сложим 2 и 3, (2 + 3) получим сумму 5. Здесь мы выполнили операцию сложения двух чисел 2 и 3, чтобы получить сумму, т. е. 5

Символ сложения

В математике используются разные символы. Символ сложения является одним из широко используемых математических символов. В приведенном выше определении сложения мы читаем о сложении двух чисел 2 и 3. Если мы наблюдаем закономерность сложения (2 + 3 = 5), символ (+) соединяет два числа и завершает данное выражение. Символ сложения состоит из одной горизонтальной и одной вертикальной линий. Он также известен как знак сложения или знак плюса (+) 9.0025

Части дополнения

Оператор добавления можно разделить на следующие части.

• Addend: Добавляемые числа называются addends.
• Символ сложения: Символ сложения (+) помещается между сложениями. Если оператор написан горизонтально, как показано ниже, то мы ставим знак равенства (=) непосредственно перед записью суммы.
• Сумма: Окончательный результат, полученный после сложения слагаемых, называется суммой.

Формула сложения

Формула сложения представляет собой утверждение, которое показывает факт сложения и выражается как сложение + сложение = сумма . Это можно понять с помощью примера, показанного на рисунке ниже. Базовую формулу сложения или математическое уравнение сложения можно объяснить следующим образом.

Здесь 5 и 3 — слагаемые, а 8 — сумма. Следует отметить, что в факте сложения может быть несколько дополнений. Например, 5 + 7 + 9+ 3 = 24.

Как решить задачи на сложение?

При решении задач на сложение однозначные числа можно складывать простым способом, но для больших чисел мы разбиваем числа на столбцы, используя соответствующие разрядные значения, такие как единицы, десятки, сотни, тысячи и т. д. Мы всегда начинаем делать сложение с правой стороны в соответствии с позиционной системой. Это означает, что мы начинаем со столбца единиц, затем переходим к столбцу десятков, затем к столбцу сотен и так далее. При решении таких задач могут встречаться случаи с переносами и случаи без переносов. Давайте разберемся с добавлением с перегруппировкой и сложением без перегруппировки в следующих разделах.

Сложение без перегруппировки

Сложение, при котором сумма цифр меньше или равна 9 в каждом столбце, называется сложением без перегруппировки. Разберемся, как сложить два и более числа без перегруппировки на примере.

Пример: Добавьте 11234 и 21123

Решение: Мы воспользуемся приведенными ниже шагами и попытаемся связать их со следующим рисунком.

• Шаг 1: Начните с цифр в столбце единиц. (4 + 3 = 7)
• Шаг 2: Перейти к цифрам в столбце десятков. (3 + 2 = 5)
• Шаг 3: Теперь добавьте цифры в столбце сотен. (2 + 1 = 3)
• Шаг 4: После этого добавьте цифры в столбце тысяч. (1 + 1 = 2)
• Шаг 5: Наконец, добавьте цифры в столбец «Десять тысяч». (1 + 2 = 3)
• Шаг 6: 11234 + 21123 = 32357.

Кроме того, без перегруппировки мы просто добавляем цифры в каждом столбце разряда и объединяем соответствующие суммы вместе, чтобы получить ответ. Теперь давайте разберемся с добавлением с перегруппировкой.

Сложение с перегруппировкой

При сложении чисел, если сумма слагаемых в любом из столбцов больше 9, перегруппируем эту сумму на десятки и единицы. Затем мы переносим разряд десятков суммы в предыдущий столбец и записываем разряд единиц суммы в этот конкретный столбец. Другими словами, мы пишем только число в «цифре разряда единиц» в этом конкретном столбце, а «цифру разряда десятков» переносим в столбец непосредственно слева. Давайте разберемся, как добавить два или более числа путем перегруппировки с помощью примера.

Пример: Сложите 3475 и 2865.

Решение: Давайте выполним указанные шаги и попробуем связать их со следующим рисунком.

• Шаг 1: Начните с разряда единиц. (5 + 5 = 10). Здесь сумма равна 10. Десятки суммы, то есть 1, будут перенесены в предыдущий столбец.
• Шаг 2: Добавьте цифры из столбца десятков вместе с переносом 1. Это означает, 1 (перенос) + 7 + 6 = 14. Здесь сумма равна 14. Десятки суммы, то есть 1, перенесутся в разряд сотен.
• Шаг 3: Теперь добавьте цифры сотен вместе с цифрой переноса 1. Это означает, что 1 (перенос) + 4 + 8 = 13. Здесь сумма равна 13. Цифра десятков суммы , то есть 1, будет перенесено в разряд тысяч.
• Шаг 4: Теперь добавьте цифры разряда тысяч вместе с цифрой переноса 1, то есть 1 (перенос) + 3 + 2 = 6
• Шаг 5: Следовательно, сумма 3475 + 2865 = 6340

Примечание: Существует важное свойство сложения, которое гласит, что изменение порядка чисел не меняет ответ. Например, если мы перевернем слагаемые на приведенном выше рисунке, мы получим в результате ту же сумму (2865 + 3475 = 6340). Это известно как коммутативное свойство сложения.

Сложение в числовой строке

Другой способ сложения чисел — с помощью числовых строк. Давайте разберемся с добавлением в числовой строке с помощью примера и числовой строки, приведенной ниже. Если нам нужно решить 10 + 3, мы начинаем с того, что отмечаем число 10 на числовой прямой. Когда мы складываем с помощью числовой строки, мы считаем, перемещая одно число за раз вправо от числа. Так как мы добавляем 10 и 3, мы переместимся на 3 шага вправо. Это приводит нас к 13. Следовательно, 10 + 3 = 13,9.0025

Свойства сложения

При выполнении сложения обычно используются свойства, перечисленные ниже:

• Коммутативное свойство: В соответствии с этим свойством сумма двух или более слагаемых остается неизменной независимо от порядка слагаемых. Например, 8 + 7 = 7 + 8 = 15 
.
• Ассоциативное свойство: В соответствии с этим свойством сумма трех или более слагаемых остается неизменной независимо от группировки слагаемых. Например, 5 + (7 + 3) = (5 + 7) + 3 = 15
• Свойство аддитивной идентичности: в соответствии с этим свойством сложения, если мы добавляем 0 к любому числу, результирующая сумма всегда является фактическим числом. Например, 0 + 7 = 7,
.

Проблемы с дополнительными словами

Концепция операции сложения используется в нашей повседневной деятельности. Мы должны внимательно наблюдать за ситуацией и находить решение, используя советы и рекомендации, которые следуют за дополнением. Давайте поймем, как решить задач на сложение слов с помощью интересного примера.

Пример: На футбольном матче присутствовало 4535 зрителей в первом ряду и 2332 зрителя во втором ряду. Используя понятие сложения, найдите общее количество зрителей, присутствующих на матче.

Решение:

Количество зрителей в первом ряду = 4535; количество зрителей во втором ряду = 2332. Мы можем получить общее количество зрителей, если сложим заданное количество зрителей в двух рядах.
Здесь 4535 и 2332 — слагаемые. Давайте найдем общее количество зрителей, добавив эти два числа, используя следующие шаги.

• Шаг 1: Добавьте цифры вместо единиц. (5 + 2 = 7)
• Шаг 2: Сложите цифры в разряде десятков. (3 + 3 = 6)
• Шаг 3: Сложите цифры в разряде сотен. (5 + 3 = 8)
• Шаг 4: Теперь добавьте цифры разряда тысяч. (4 + 2 = 6)
• Шаг 5: 4535 + 2332 = 6867

Следовательно, общее количество зрителей, присутствующих на матче = 6867

Вот несколько советов и приемов, которым вы можете следовать, выполняя сложение в своей повседневной жизни.

Советы и рекомендации по сложению

• Такие слова, как «собрать вместе», «всего», «в целом», «всего» подсказывают, что вам нужно сложить данные числа.
• Начните с большего числа и добавьте к нему меньшее. Например, прибавить 12 к 43 проще, чем прибавить 43 к 12.
• Разбейте числа в соответствии с их разрядностью, чтобы упростить сложение. Например, 22 + 64 можно разделить как 20 + 2 + 60 + 4. Хотя это выглядит сложно, сложение в уме упрощается.
• При добавлении различных цифр убедитесь, что числа размещены одно под другим в правильном столбце их разряда.
• Добавление нуля к любому числу дает само число.
• Когда 1 добавляется к любому числу, сумма является преемником этого числа.
• Знак, используемый для обозначения добавления: «+»
• Порядок, в котором вы добавляете набор чисел, не имеет значения, сумма остается прежней. Например, 2+5+3=10; и 5 + 3 + 2 = 10. Это называется ассоциативным свойством сложения.

☛Ссылки по теме

• Что такое перегруппировка в математическом сложении?
• Калькулятор сложения
• Сложение алгебраических выражений
• Сложение дробей
• Сложение десятичных знаков

Часто задаваемые вопросы по дополнению

Что такое сложение в математике?

Сложение — это процесс сложения двух или более чисел для получения их суммы. Сложение в математике — это основная арифметическая операция, используемая для вычисления суммы двух или более чисел. Например, 7 + 7 = 14.

Где мы используем сложение?

В повседневных ситуациях мы используем сложение. Например, если мы хотим знать, сколько денег мы потратили на купленные предметы, или мы хотим рассчитать время, которое нам потребуется, чтобы закончить задачу, или мы хотим узнать количество ингредиентов, используемых при приготовлении чего-либо, нам нужно для выполнения операции сложения.

Какие существуют типы сложения?

Типы добавления означают различные используемые методы добавления. Например, сложение по вертикали, сложение с использованием числовых таблиц, сложение маленьких чисел с помощью пальцев, сложение с использованием числовой строки и так далее.

Что такое стратегии сложения?

Стратегии сложения — это различные способы обучения сложению. Например, с помощью числовой строки, с помощью таблицы разрядности, разделения десятков и единиц и последующего их сложения по отдельности и многие другие.

Каковы реальные примеры сложения?

Есть много примеров сложения, с которыми мы сталкиваемся в повседневной жизни. Допустим, у вас есть 5 яблок, а ваш друг дал вам еще 3, после сложения 5+3 получаем 8. Итак, всего у вас 8 яблок. Точно так же предположим, что в классе 16 девочек и 13 мальчиков. Если мы сложим числа 16 + 13, мы получим общее количество учеников в классе, равное 29.

Каковы свойства сложения?

Основные свойства сложения приведены ниже. Каждое свойство имеет свое индивидуальное значение, основанное на сложении.

• Коммутативное свойство: В соответствии с этим свойством сумма двух или более слагаемых остается неизменной, даже если изменяется порядок слагаемых. Например, 3 + 7 = 7 + 3 = 10 
.
• Ассоциативное свойство: В соответствии с этим свойством сумма трех или более слагаемых остается неизменной независимо от группировки слагаемых. Например, (8 + 7) + 2 = 8 + (7 + 2) = 17
• Свойство аддитивной идентичности: в соответствии с этим свойством сложения, если мы добавляем 0 к любому числу, результирующая сумма всегда является фактическим числом. Например, 0 + 16 = 16,

Какие части дополнения?

Различные части дополнения приведены ниже. Давайте разберемся в этих частях с помощью примера. Например, возьмем 4 + 7 + 2 = 13

• Сложение: Кроме того, числа или термины, которые складываются вместе, называются слагаемыми. В данном случае 4, 7 и 2 являются слагаемыми.
• Символ сложения (+) и знак равенства (=) : Символ сложения используется между слагаемыми, а знак равенства ставится непосредственно перед суммой.
• Сумма: Окончательный результат, полученный после выполнения сложения, называется суммой. Здесь сумма равна 13.

Что такое свойство идентичности сложения?

В соответствии со свойством идентичности сложения, если к любому числу добавить 0, результирующая сумма всегда будет фактическим числом. Например, 0 + 16 = 16.

В чем разница между сложением и вычитанием?

Сложение — это математическая операция, в которой мы складываем числа, чтобы получить их сумму.