Примеры на деление с ответами в столбик 4 класс: Примеры деления на однозначное число столбиком ( 4 класс)
Серии товаров – 3000 примеров | 32 SKU в наличии
Все основные правила русского языка. 3 класс. Узорова О. В., Нефёдова Е. А.
98 ₽ / опт
Детские товары
Без скидок
Арт.: 3653917; Издательство «АСТ»3000 примеровРоссияВ боксе 60 шт.
Вид
3 класс
1 класс
2 класс
Товар партнёра
На складе 18 шт.
3000 примеров по русскому языку. 2 класс. Узорова О. В., Нефёдова Е. А.
94 ₽ / опт
Детские товары
Без скидок
Арт.: 3653902; Издательство «АСТ»3000 примеровРоссияВ боксе 80 шт.
Вид
2 класс
1 класс
Товар партнёра
300 задач по математике. 3 класс. Узорова О. В., Нефёдова Е. А.
100 ₽ / опт
Детские товары
Без скидок
Арт.
: 3653856; Издательство «АСТ»3000 примеровРоссияВ боксе 60 шт.
Вид
3 класс
1 класс
Товар партнёра
3000 примеров по математике. 1 класс. Счёт от 1 до 5. Узорова О. В., Нефёдова Е. А.
100 ₽ / опт
Детские товары
Без скидок
Арт.: 3653898; Издательство «АСТ»3000 примеровРоссияВ боксе 60 шт.
Товар партнёра
3000 заданий по русскому языку. 1 класс. Контрольное списывание. Узорова О. В., Нефёдова Е. А.
100 ₽ / опт
Детские товары
Без скидок
Арт.: 3653860; Издательство «АСТ»3000 примеровРоссияВ боксе 50 шт.
Товар партнёра
3000 примеров по математике. 3-4 класс. Внетабличное умножение и деление. Крупный шрифт. Узорова О. В., Нефёдова Е. А.
100 ₽ / опт
Детские товары
Без скидок
Арт.
: 3653875; Издательство «АСТ»3000 примеровРоссияБумага, картонВ боксе 49 шт.
Товар партнёра
3000 примеров по математике. 2 класс. Устный счёт. Счёт в пределах 100. Узорова О. В., Нефёдова Е. А.
100 ₽ / опт
Детские товары
Без скидок
Арт.: 3653892; Издательство «АСТ»3000 примеровРоссияВ боксе 60 шт.
Товар партнёра
3000 примеров по математике. 2 класс. Часть 2. Счёт в пределах 100. Узорова О. В., Нефёдова Е. А.
100 ₽ / опт
Детские товары
Без скидок
Арт.: 3653899; Издательство «АСТ»3000 примеровРоссияВ боксе 60 шт.
Товар партнёра
3000 примеров по математике. 3 класс. Табличное умножение и деление. Узорова О. В., Нефёдова Е. А.
100 ₽ / опт
Детские товары
Без скидок
Арт.: 3653900; Издательство «АСТ»3000 примеровРоссияВ боксе 60 шт.
Товар партнёра
3000 примеров по русскому языку. 3 класс. Крупный шрифт. Узорова О. В., Нефёдова Е. А.
100 ₽ / опт
Детские товары
Без скидок
Арт.: 3653904; Издательство «АСТ»3000 примеровРоссияВ боксе 40 шт.
Вид
3 класс
4 класс
Товар партнёра
4 простых способа научить ребенка делить столбиком — без слез и скандалов
Кажется, математика в начальной школе — это очень просто. Но есть темы, с которыми дети (и даже некоторые взрослые) не справляются. Одна из них — деление столбиком. Наш блогер, учитель начальных классов Ольга Катаева, рассказывает, как помочь ребенку освоить этот навык.
Одна из сложнейших тем по математике в начальной школе — деление столбиком. Поэтому материал в учебнике выстраивается от простого к сложному. Подготовка к делению столбиком начинается во втором классе. Основа — знание таблицы умножения, ведь деление — обратное умножению действие.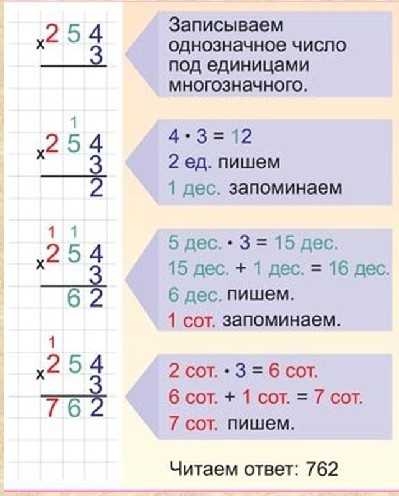
Что делать, если у ребёнка не получается делить столбиком? Для начала надо понять, в чем причина:
- знает ли ребенок таблицу умножения?
- умеет делить с остатком?
- умеет вычитать столбиком?
- понимает ли, что такое «метод подбора»?
- правильно ли оформляет запись (цифра под цифрой, единицы под единицами, десятки под десятками)?
- достаточно ли тренировался делить столбиком?
«Деление столбиком» нужно объяснять индивидуально: конечно, учитель в школе расскажет, но и родителям важно повторить дома еще раз, чтобы у ребенка была возможность задать вопросы. Вот несколько советов родителям.
1. Замените математические термины на понятные ребёнку
Например, термин «первое неполное делимое» можно заменить на «деление по частям», «метод подбора» — сколько раз число помещается в неполном делимом — части.
2. Научите пользоваться таблицей умножения
Объясните, как пользоваться таблицей умножения при подборе числа
3.
Разбирайте разные примерыЕсть разные случаи деления столбиком: деление на однозначное число, на двузначное, трёхзначное, деление чисел, в записи которых есть нули, деление чисел с нулями в конце, деление, когда в значении есть нули в середине и другие. Каждый отдельный случай лучше разбирать вместе с ребёнком (после объяснения учителем на уроке). Подобрать примеры на деление столбиком на каждый случай поможет учебник. Прорешивайте предыдущие номера.
Если примеров на деление столбиком мало в учебнике, составьте сами: перемножьте разные числа, поменяйте местами значение и один из множителей и запишите примеры на листочек.
4. Уточните с ребёнком понятия «число» и «цифра»
Давайте попробуем: разделим 2788 на 82. Начнём с оформления записи. Чтобы исключить ошибки в вычислениях, пишем по принципу «цифра под цифрой». Далее: первая часть — 2 (в разряде тысяч) — не подходит, 2 меньше 82. Следующая часть — 27 (сотен) — тоже не подходит, так как 27 меньше 82.
Тогда берём 278.
При этом определяем сколько цифр будет в ответе. В данном примере — 2. Подбираем число: мысленно прикрываем последние цифры в делимом и делителе, получается, нужно поделить 27 на 8 — деление с остатком. В таблице умножения на 8 ищем близкий ответ — это 24, поэтому попробуем взять по 3. Умножаем 82 на 3, получается 246 — подходит.
Записываем 246 под первой частью — 278 — единицы под единицами, десятки под десятками, сотни под сотнями. Находим остаток, вычитанием (нужно уметь вычитать столбиком). Получается 32. 32 меньше 82, значит, первую цифру ответа подобрали правильно.
Осталась ещё часть — 8. Переносим 8 в строчку с остатком — 328. Следим, чтобы в записи соблюдался принцип «цифра под цифрой». Подбираем цифру ответа. При подборе последней цифры ответа ориентируемся, в том числе, на последние цифры остатка и делителя — это 8 и 2. Прикрываем последние цифры остатка и делителя, получаем, что 32 нужно делить на 8. В таблице умножения на 8 находим число 4. Проверяем, подходит ли 4.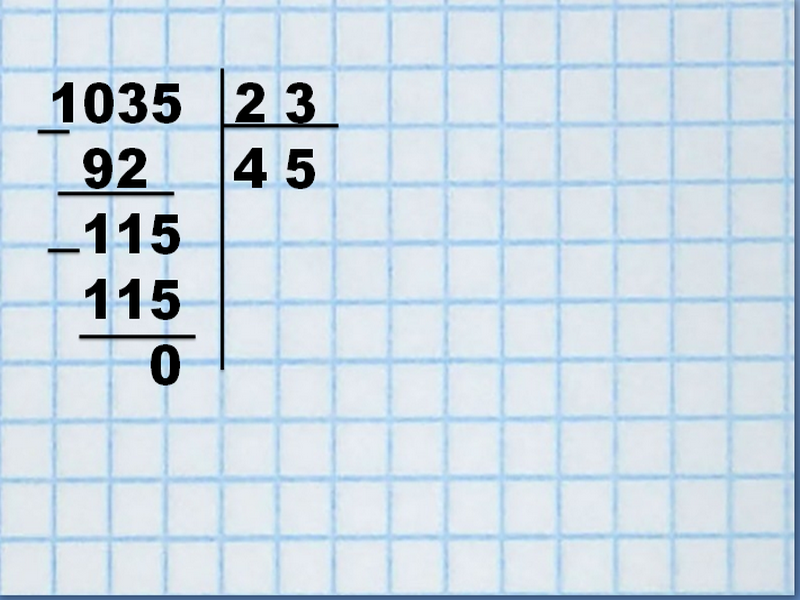
Умножаем 82 на 4, получаем 328.
Записываем результат умножения под остатком, соблюдая принцип «цифра под цифрой», находим вычитанием остаток — это 0. Записываем 0. Деление выполнено. Результат (ответ) — 34.
Воспринимать инструкцию на слух очень сложно, особенно детям. Читать инструкцию тоже трудно — нужно вчитываться, вникать в смысл, следить, как связаны предыдущий и следующий шаги. Длинную инструкцию надо делить на смысловые части. Есть ученики, которым нужно «показать пальцем», куда какую цифру вписать, где какое число найти. Приём «покажи пальцем» отлично срабатывает при индивидуальном объяснении.
Не дожидайтесь, когда ребёнок перестанет справляться с вычислениями в теме «Деление столбиком», поддерживайте его и, главное, выучите таблицу умножения после окончания 1-го класса. Практика показывает, что потом запомнить ее становится всё труднее и труднее.
Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.
Фото: k_samurkas / Shutterstock / Fotodom
Что такое коммутативная собственность? Определение, формула, примеры
Коммутативное свойство
Коммутативное свойство утверждает, что числа, с которыми мы работаем, можно перемещать или менять местами с их позиции без какого-либо изменения ответа.
Это свойство справедливо для сложения и умножения, но не для вычитания и деления. Давайте посмотрим.
Приведенные выше примеры ясно показывают, что свойство коммутативности верно для сложения и умножения, но не для вычитания и деления. Итак, если мы поменяем местами числа в операторах вычитания или деления, это изменит всю проблему.
Итак, математически коммутативное свойство сложения и умножения выглядит так:
Родственные игры
Коммутативное свойство сложения:
a + b = b + a; где a и b — любые 2 целых числа
Связанные рабочие листы
Коммутативное свойство умножения:
a × b = b × a; где a и b — любые 2 ненулевых целых числа
Варианты использования коммутативного свойства
- У Майры 6 яблок и 2 персика. У Ким 2 яблока и 6 персиков. У кого больше фруктов?
Даже если у обоих разное количество яблок и персиков, у них равное количество фруктов, потому что 2 + 6 = 6 + 2.
- Сара покупает 3 упаковки булочек. В каждой упаковке по 4 булочки. Мила покупает 4 упаковки булочек, в каждой по 3 булочки. Кто купил больше булочек?
Даже если у обоих разное количество упаковок булочек, причем у каждого из них разное количество булочек, они оба купили одинаковое количество булочек, потому что 3 × 4 = 4 × 3.
Решенные примеры по свойству переместимости
Пример 1: Заполните пропущенные числа, используя свойство переместимости.
- _________ + 27 = 27 + 11
- 45 + 89 = 89 + _________
- 84 × ______ = 77 × 84
- 118 × 36 = ________ × 118
Решение:
- 11; по коммутативному свойству сложения
- 45; по коммутативному свойству сложения
- 77; по коммутативному свойству умножения
- 36; по коммутативному свойству умножения
Пример 2: Используйте 14 × 15 = 210, чтобы найти 15 × 14.
Решение:
Согласно свойству перестановочности умножения 15 × 14 = 14 × 15. 5
9 = 210, поэтому 15 × 14 также равно 210.
Пример 3: Используйте 827 + 389 = 1,216, чтобы найти 389 + 827.
Решение:
= 389 + 827.Поскольку 827 + 389 = 1216, значит, 389 + 827 также равно 1216.
Пример 4: Используйте свойство коммутативности сложения, чтобы записать уравнение 3 + 5 + 9 = 17 в другой последовательности слагаемых.
Решение:
3 + 9 + 5 = 17 (поскольку 5 + 9 = 9 + 5)
5 + 3 + 9 = 17 (поскольку 3 + 5 = 5 + 3)
5 + 9 + 3 = 17 (потому что 3 + 9 = 9 + 3)
Точно так же мы можем переставить слагаемые и написать:
9 + 3 + 5 = 17
9 + 5 + 3 = 17
Пример 4: Бен купил 3 упаковки по 6 ручек в каждой. Миа купила 6 упаковок по 3 ручки в каждой. Они купили одинаковое количество ручек или нет?
Решение:
Бен купил 3 упаковки по 6 ручек в каждой.
Итак, общее количество ручек, которые купил Бен = 3 × 6
Миа купила 6 упаковок по 3 ручки в каждой.
Итак, общее количество ручек, которые купил Бен = 6 × 3
По свойству перестановочности умножения 3 × 6 = 6 × 3.
Итак, Бен и Миа купили одинаковое количество ручек.
Пример 5: У Лизы 78 красных и 6 синих шариков. У Бет есть 6 упаковок по 78 шариков в каждой. У них одинаковое количество шариков?
Решение:
Так как у Лизы 78 красных и 6 синих шариков.
Итак, общее количество шариков у Лизы = 78 + 6
У Бет 6 пакетов по 78 шариков в каждом.
Итак, общее количество шариков с Бет = 6 × 78
Очевидно, что сложение и умножение двух чисел дает разные результаты. (Кроме 2 + 2 и 2 × 2.
То есть 78 + 6 ≠ 6 × 78
Значит, у Лизы и Бет не одинаковое количество шариков.
Что из нижеперечисленного представляет коммутативное свойство сложения?0005
8 + 5 = 5 × 8
Правильный ответ: 8 + 5 = 5 + 8
Согласно свойству коммутативности сложения сумма не меняется при перестановке слагаемых.
То есть а + b = b + а.
2
Что из следующего представляет коммутативное свойство умножения?
7 × $\frac{1}{7}$ = 1
7 × 1 = 7
7 × 3 = 3 × 7
7 × 0 = 0
Правильный ответ: 7 × 3 = 3 × 7
Согласно коммутативному свойству умножения, произведение остается тем же самым при замене местами множимого и множителя. То есть а × b = b × а.
3
Какое из следующих выражений будет следовать свойству коммутативности?
15 ÷ 3
15 × 3
15 – 3
3 ÷ 15
Правильный ответ: 15 × 3
Коммутативное свойство не выполняется для деления и вычитания.
4
Выберите набор чисел, чтобы утверждение было верным.
5 + _____ = 4 + ______
5, 5
4, 4
5, 4
4, 5
Правильный ответ: 4, 5
5 + 4 = 4 + 5
(по коммутативности сложения)
Часто задаваемые вопросы о коммутативности
Можно ли применить коммутативность сложения/умножения к трем числам?
Да.
По определению коммутативность применяется к 2 числам, но результат остается тем же и для 3 чисел. Это потому, что мы можем применить это свойство к двум числам из 3 в различных комбинациях.
Какие операции не следуют коммутативному свойству?
Коммутативное свойство не применимо к вычитанию и делению.
Что такое ассоциативное свойство сложения (или умножения)?
Это свойство указывает, что при сложении (или умножении) трех или более чисел сумма (или произведение) остается одинаковой независимо от группировки слагаемых (или множимых). То есть
(a + b) + c = a + (b + c)
(a × b) × c = a × (b × c), где a, b и c — целые числа.
Для каких операций выполняется свойство ассоциативности?
Ассоциативное свойство верно для сложения и умножения.
Какое распределительное свойство умножения?
Под распределительным свойством умножения над сложением мы подразумеваем, что умножение суммы двух или более слагаемых на число даст тот же результат, что и умножение каждого слагаемого по отдельности на число, а затем сложение произведений вместе.
То есть
a × (b + c) = (a × b) + (a × c), где a, b и c — целые числа.
Умножение × | Основы арифметики
На этой странице рассматриваются основы умножения (×) .
См. другие наши арифметические страницы для обсуждения и примеров: сложение (+), вычитание (-) и деление ( ÷ ).
Умножение
При записи общий знак умножения — « × ». В электронных таблицах и некоторых других компьютерных приложенияхСимвол 0023 * ’ (или звездочка) используется для обозначения операции умножения.
Чтобы выполнять расчеты по умножению без калькулятора или электронной таблицы, вам нужно знать, как складывать числа. См. нашу страницу «Добавление» для помощи в добавлении.
Когда вы «умножаете» или «умножаете» число, вы добавляете его само к себе несколько раз, например, 4 умножить на 3 — это то же самое, что сказать 4 + 4 + 4 = 12. Таким образом, умножение — это более быстрый способ сложения.
одно и то же число много раз, например 3 × 4 = 12. Этот расчет аналогичен утверждению, если у меня есть 3 мешка с 4 яблоками, сколько яблок у меня всего?
Основные правила умножения:
- Любое число, умноженное на 0, равно 0. 200 × 0 = 0
- Любое число, умноженное на 1, остается прежним. 200 × 1 = 200,
- Когда число умножается на два, мы удваиваем число. 200 × 2 = 400,
- Когда целое число умножается на 10, мы можем просто написать 0 в конце (в 10 один ноль, потому что это 1 × 10). 200 × 10 = 2000.
- При умножении на 100 пишем два нуля в конце, на тысячу пишем три нуля в конце и так далее. 4 × 2000 например 4 × 2 = 8 с 3 нулями: 8000.
Для простого и быстрого умножения полезно запомнить умножение или «таблицу умножения на », как показано ниже. Эта таблица дает ответы на все умножения до 10 × 10. Чтобы получить ответ на 4 × 6, например, найдите 4 в верхней (заштрихованной красным) строке и найдите 6 в левом (заштрихованном красным) столбце – точка пересечения двух прямых и есть ответ: 24 .
Не имеет значения, с какой стороны вы ищете номера; если вы найдете 4 в первом столбце и 6 в первой строке, вы получите тот же ответ, 24.
Таблица умножения
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Приведенная выше таблица может помочь нам быстро вычислить ответ на следующую задачу.
Меган ведет трех своих братьев в кино, всего ей нужно купить 4 билета, и каждый билет стоит 8 фунтов стерлингов. Сколько будет полная стоимость поездки? Нам нужно рассчитать 4 лота по £8, что записывается 4 × 8.
Найдите 4 в вертикальном красном столбце и 8 в горизонтальном красном столбце, ответ находится в ячейке, где две линии пересекаются: 32 . Таким образом, стоимость похода в кино составит £32 .
Часто бывает необходимо умножить числа больше 10. В этом случае приведенная выше таблица умножения не может дать немедленный ответ. Тем не менее, мы все еще можем использовать его, чтобы упростить вычисления.
Лиза занимается ресторанным бизнесом. Ей приходится доставлять бутерброды на 23 предприятия, в каждом из которых работает по 14 сотрудников. Если предположить, что каждый сотрудник съедает один бутерброд, сколько бутербродов должна приготовить Лиза?
Каждому из 23 предприятий нужно по 14 бутербродов, что составляет 23 лота из 14 или, другими словами, 23, умноженное на 14.
Нам нужно найти ответ на вычисление 23 × 14.
Сначала запишите свои числа в столбцах, представляющих сотни, десятки и единицы (см. нашу страницу Числа ).
| Сотни | Десятки | Единицы |
| 2 | 3 | |
| 1 | 4 |
Шаг 1: Начиная с правого столбца (единицы), умножьте 4 и 3. При необходимости вы можете обратиться к приведенной выше таблице умножения. Запишите ответ (12) под своим расчетом, поставив 1 в столбце десятков и 2 в столбце единиц.
Синие числа — это те, над которыми мы сейчас работаем, а розовые числа — это первая часть нашего ответа.
| Сотни | Единицы | |
| 2 | 3 | |
| 1 | 4 | |
| 1 | 2 |
Шаг 2: Затем мы умножаем 4 на следующее число, которое равно 2 (или 20, потому что оно находится в столбце десятков).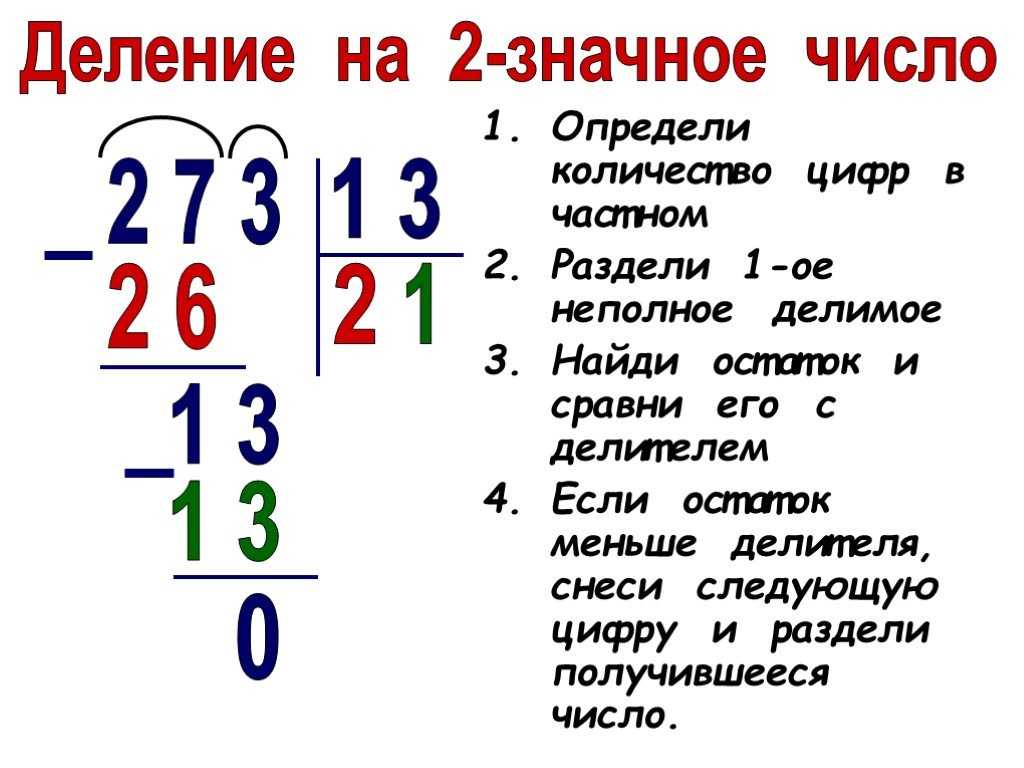
Запишите свой ответ внизу в столбце десятков: Мы пишем 8 в столбце десятков (4 умножить на 2 десятка) и ноль в столбце единиц (4 умножить на 2 десятка равно 4 × 20 = 80).
| Сотни | Десятки | Единицы |
| 2 | 3 | |
| 1 | 4 | |
| 1 | 2 | |
| 8 | 0 |
Шаг 3: В предыдущих шагах мы умножили единицы нижнего числа (4) на верхнее число (23). Далее нам нужно умножить десятки в нижнем числе (1) на верхнее число (23). Теперь мы работаем с цифрой в столбце десятков нижнего числа и повторяем шаги, описанные выше. Оглядываясь назад на наши основные правила умножения выше, мы знаем, что когда мы умножаем число на 10, мы пишем ноль в конце. На этом шаге, поскольку мы перешли столбец и работаем с десятками, мы должны не забыть записать нули в первом столбце (единицы).
Решите 1 × 3. Как и выше, мы записываем наш ответ (3) в столбце десятков и (0) в столбце единиц.
| Сотни | Десятки | Единицы |
| 2 | 3 | |
| 1 | 4 | |
| 1 | 2 | |
| 8 | 0 | |
| 3 | 0 |
Шаг 4: Последнее умножение, которое нам нужно выполнить, это 1 × 2. Оба числа находятся в столбце десятков, поэтому мы умножаем один набор из 10 на два набора из 10. Используя правила, которые мы изучили в предыдущие шаги, нам нужно написать ноль в столбце единиц и ноль в столбце десятков. Наш ответ (1 × 2 = 2) записан в столбце сотен, потому что мы фактически вычислили 10 × 20 = 200.
| Сотни | Десятки | Единицы |
| 2 | 3 | |
| 1 | 4 | |
| 1 | 2 | |
| 8 | 0 | |
| 3 | 0 | |
| 2 | 0 | 0 |
Этап 5: На этом этапе мы закончили умножение; осталось только сложить все наши ответы (розовые числа), чтобы найти общее количество необходимых бутербродов.
См. нашу Дополнение страницу, если вам нужна помощь в сложении чисел.
| Сотни | Десятки | Единицы | |
| 2 | 3 | ||
| 1 | 4 | ||
| 1 | 2 | ||
| 8 | 0 | ||
| 3 | 0 | ||
| 2 | 0 | 0 | |
| Итого: | 3 | 2 | 2 |
12 + 80 + 30 + 200 = 322. Мы подсчитали, что Лизе нужно сделать всего 322 бутерброды.
В приведенном выше примере показано, как выполнить умножение, разделенное на все возможные части, но по мере повышения уверенности шаги можно пропускать.
Мы могли бы, например, умножить 4 на 23, разбив сумму на части:
4 × 20 = 80
4 × 3 = 12
80 + 12 = 92
| Сотни | Десятки | Единицы |
| 2 | 3 | |
| 1 | 4 | |
| 9 | 2 |
То же самое для второго столбца:
10 × 23 = 230
| Сотни | Десятки | Единицы |
| 2 | 3 | |
| 1 | 4 | |
| 9 | 2 | |
| 2 | 3 | 0 |
Наконец, мы добавляем два наших ответа:
| Сотни | Десятки | Единицы | |
| 2 | 3 | ||
| 1 | 4 | ||
| 9 | 2 | ||
| 2 | 3 | 0 | |
| Итого: | 3 | 2 | 2 |
92 + 230 = 322.
Умножение более двух чисел умножьте следующее число на первую сумму. Например, если бы Джо хотел подсчитать, сколько часов он проработал за четыре недели, расчет будет выглядеть так:
Джо работает 7 часов в день, 5 дней в неделю в течение четырех недель.
Шаг первый:
7 × 5 = 35 (количество часов, которые Джо работает в неделю).
Шаг второй:
Чтобы найти, сколько часов Джо работает за четыре недели, мы можем умножить этот ответ (35) на 4. 35 × 4 = 140.
Если мы знаем, что Джо получает 12 фунтов стерлингов в час. , мы можем подсчитать, сколько денег он заработал за четыре недели: 12 × 140.
Быстрый способ вычислить это — вычислить:
10 × 140 = 1400 (помните, что если мы умножим на 10, то получим просто добавьте ноль в конец числа, на которое мы умножаем).
2 × 140 = 280 то же, что 2 × 14 (с нулем на конце) или 140 + 140.
Складываем наши ответы вместе: 1400 + 280 = 1680.