Примеры круги эйлера логика: круги Эйлера – Основы логики и логические основы компьютера
круги Эйлера – Основы логики и логические основы компьютера
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.Какое количество страниц (в тысячах) будет найдено по запросу Крейсер & Линкор?Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
При помощи кругов Эйлера изобразим условия задачи. При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.
Опираясь на условия задачи, составим уравнения:
Чтобы найти Крейсер & Линкор (обозначенный на чертеже как область 2), подставим уравнение (2) в уравнение (1) и выясним, что:
4800 + 3 = 7000, откуда получаем 3 = 2200.
Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:
2 + 2200 = 4500, откуда 2 = 2300.
Ответ: 2300 – количество страниц, найденных по запросу Крейсер & Линкор.
В языке запросов поискового сервера для обозначения логической операции “ИЛИ” используется символ “|”, а для логической операции “И” – символ “&”.
Решение
Для решения задачи отобразим множества Тортов и Пирогов в виде кругов Эйлера.
Обозначим каждый сектор отдельной буквой (А, Б, В).
Из условия задачи следует:
Торты │Пироги = А+Б+В = 12000
Торты & Пироги = Б = 6500
Пироги = Б+В = 7700
Чтобы найти количество Тортов (Торты = А+Б), надо найти сектор А, для этого из общего множества (Торты│Пироги) отнимем множество Пироги.
Торты│Пироги – Пироги = А+Б+В-(Б+В) = А = 1200 – 7700 = 4300
Сектор А равен 4300, следовательно
Торты = А+Б = 4300+6500 = 10800
Задача 3
В языке запросов поискового сервера для обозначения логической операции “ИЛИ” используется символ “|”, а для логической операции “И” – символ “&”.
| Запрос | Найдено страниц (в тысячах) |
| Пироженое & Выпечка | 5100 |
| Пироженое | 9700 |
| Пироженое | Выпечка | 14200 |
Какое количество страниц (в тысячах) будет найдено по запросуВыпечка?
Для решения задачи отобразим множестваПироженых и Выпечек в виде кругов Эйлера.
Обозначим каждый сектор отдельной буквой (А, Б, В).
Из условия задачи следует:
Пироженое & Выпечка = Б = 5100
Пироженое = А+Б = 9700
Пироженое │ Выпечка = А+Б+В = 14200
Чтобы найти количество Выпечки (Выпечка = Б+В), надо найти секторВ, для этого из общего множества (Пироженое │ Выпечка ) отнимем множество Пироженое.
Пироженое │ Выпечка – Пироженное = А+Б+В-(А+Б) = В = 14200–9700 = 4500Сектор В равен 4500, следовательно Выпечка = Б + В = 4500+5100 =9600
Задача 4В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции “ИЛИ” используется символ “|”, а для логической операции “И” – символ “&”.
| 1 | спаниели | (терьеры & овчарки) |
| 2 | спаниели | овчарки |
| 3 | спаниели | терьеры | овчарки |
| 4 | терьеры & овчарки |
Решение
Представим множества овчарок, терьеров и спаниелей в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).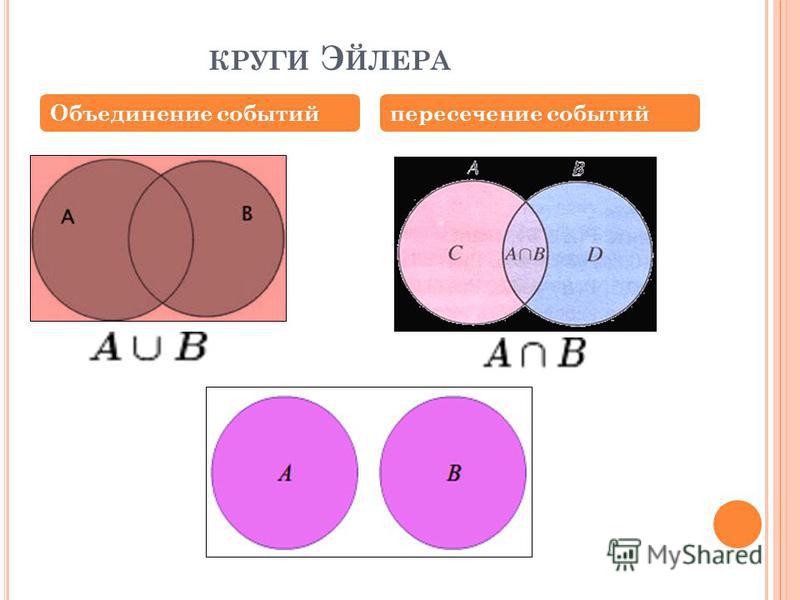
Преобразим условие задачи в виде суммы секторов:
спаниели │(терьеры & овчарки) = Г + Б
спаниели│овчарки = Г + Б + В
спаниели│терьеры│овчарки = А + Б + В + Г
терьеры & овчарки = Б
Из сумм секторов мы видим какой запрос выдал больше количества страниц.
Расположим номера запросов в порядке убывания количества страниц: 3 2 1 4
Задача 5
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции “ИЛИ” используется символ “|”, а для логической операции “И” – символ “&”.
| 1 | барокко | классицизм | ампир |
| 2 | барокко | (классицизм & ампир) |
| 3 | классицизм & ампир |
| 4 | барокко | классицизм |
Решение
Представим множества классицизм, ампир и классицизм в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).
Преобразим условие задачи в виде суммы секторов:
барокко│ классицизм │ампир = А + Б + В + Гбарокко │(классицизм & ампир) = Г + Б
классицизм & ампир = Б
барокко│ классицизм = Г + Б + А
Из сумм секторов мы видим какой запрос выдал больше количества страниц.
Расположим номера запросов в порядке возрастания количества страниц: 3 2 4 1
Задача 6
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции “ИЛИ” используется символ “|”, а для логической операции “И” – символ “&”.
| 1 | канарейки | щеглы | содержание |
| 2 | канарейки & содержание |
| 3 | канарейки & щеглы & содержание |
| 4 | разведение & содержание & канарейки & щеглы |
Решение
Для решения задачи представим запросы в виде кругов Эйлера.
K – канарейки,
Щ – щеглы,
С – содержание,
Р – разведение.
Далее будем закрашивать красным цветом сектора согласно запросам, наибольший по величине сектор даст большее количество страниц на запрос.
| канарейки | терьеры | содержание | канарейки & содержание | канарейки & щеглы & содержание | разведение & содержание & канарейки & щеглы |
Самая большая область закрашенных секторов у первого запроса, затем у второго, затем у третьего, а у четвертого запроса самый маленький.
В порядке возрастания по количеству страниц запросы будут представлены в следующем порядке: 4 3 2 1
Обратите внимание что в первом запросе закрашенные сектора кругов Эйлера содержат в себе закрашенные сектора второго запроса, а закрашенные сектора второго запроса содержат закрашенные сектора третьего запроса, закрашенные сектора третьего запроса содержат закрашенный сектор четвертого запроса.
Только при таких условиях мы можем быть уверены, что правильно решили задачу.
Задача 7 (ЕГЭ 2013)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Фрегат | Эсминец | 3400 |
| Фрегат & Эсминец | 900 |
| Фрегат | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Эсминец?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Ответ: 2200
Решение: Запрос “Фрегат” обозначим символом “Ф”, “Эсминец” – символом “Э”.
Э=(Ф|Э)-Ф+(Ф&Э)=3400-2100+900=2200.
Разбор задачи B12 (демо ЕГЭ 2012)
Время выполнения-2 мин, уровень сложности-повышенныйВ языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Шахматы | Теннис | 7770 |
| Теннис | 5500 |
| Шахматы & Теннис | 1000 |
Какое количество страниц (в тысячах) будет найдено по запросу Шахматы?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Ответ: 3270
Решение: Изобразим запросы в виде диаграмм Эйлера-Венна.Запрос “Шахматы” обозначим символом “Ш”, “Теннис” – символом “Т”.
Ш=(Ш|Т)-Т+(Ш&Т)=7770-5500+1000=3270.
Задачи для самостоятельного решения
Задача 1
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции “ИЛИ” используется символ “|”, а для логической операции “И” – символ “&”.
| 1 | принтеры & сканеры & продажа |
| 2 | принтеры & продажа |
| 3 | принтеры | продажа |
| 4 | принтеры | сканеры | продажа |
Задача 2
В таблице приведены запросы к поисковому серверу.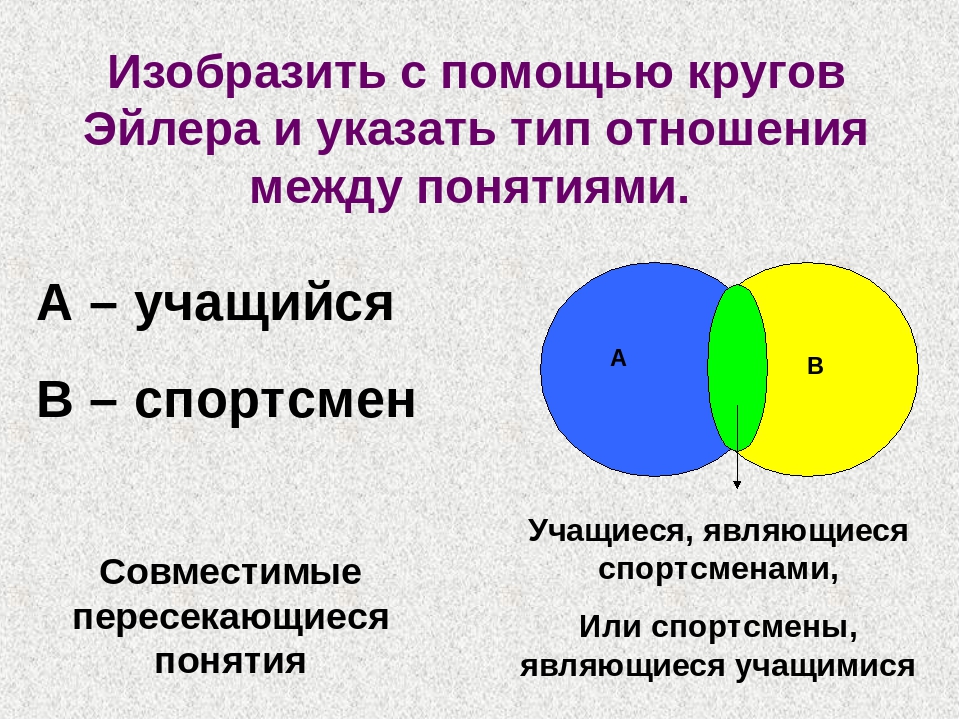 Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции “ИЛИ” используется символ “|”, а для логической операции “И” – символ “&”.
| 1 | физкультура |
| 2 | физкультура & подтягивания & отжимания |
| 3 | физкультура & подтягивания |
| 4 | физкультура | фитнесс |
1.6. Круговые схемы Эйлера. Логика. Учебное пособие
1.6. Круговые схемы Эйлера
Как мы уже знаем, в логике выделяется шесть вариантов отношений между понятиями. Два любых сравнимых понятия обязательно находятся в одном из этих отношений. Например, понятия писатель и россиянин находятся в отношении пересечения, писатель и человек – подчинения, Москва и столица России – равнозначности, Москва и Петербург – соподчинения, мокрая дорога и сухая дорога – противоположности, Антарктида и материк – подчинения, Антарктида и Африка – соподчинения и т. д. и т. п.
Надо обратить внимание на то, что если два понятия обозначают часть и целое, например месяц и год, то они находятся в отношении соподчинения, хотя может показаться, что между ними отношение подчинения, ведь месяц входит в год. Однако, если бы понятия месяц и год были подчиненными, то тогда надо было бы утверждать, что месяц – это обязательно год, а год – это не обязательно месяц (вспомним отношение подчинения на примере понятий 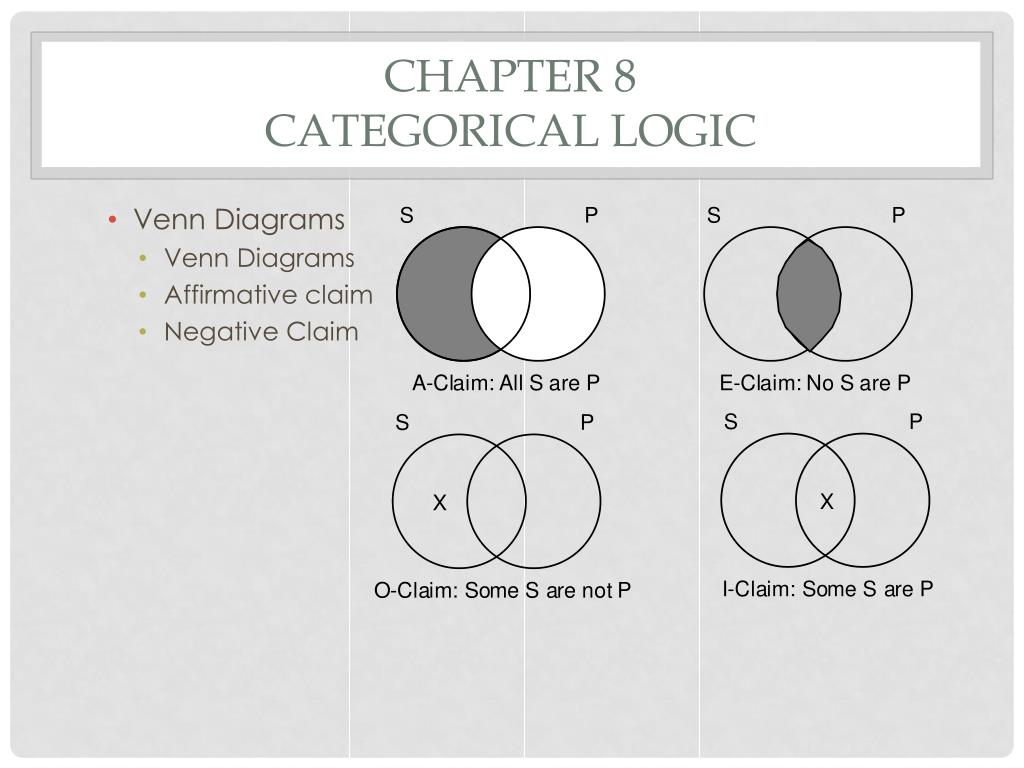 п., находятся в отношении соподчинения, т. к. часть и целое – не то же самое, что вид и род.
п., находятся в отношении соподчинения, т. к. часть и целое – не то же самое, что вид и род.
В начале говорилось о том, что понятия бывают сравнимыми и несравнимыми. Считается, что рассмотренные шесть вариантов отношений применимы только к сравнимым понятиям. Однако возможно утверждать, что все несравнимые понятия находятся между собой в отношении соподчинения. Например, такие несравнимые понятия, как пингвин
и небесное тело возможно рассматривать как соподчиненные, ведь пингвин – это не небесное тело и наоборот, но в то же время объемы понятий пингвин и небесное тело входят в более широкий объем третьего понятия, родового по отношению к ним: это может быть понятие объект окружающего мира или форма материи (ведь и пингвин и небесное тело – это различные объекты окружающего мира или различные формы материи). Если же одно понятие обозначает что-то материальное, а другое – нематериальное (например, дерево и мысль), то родовым для этих (как возможно утверждать) соподчиненных понятий является понятие форма бытия, т. к. и дерево, и мысль, и что угодно еще – это различные формы бытия.Как нам уже известно, отношения между понятиями изображаются круговыми схемами Эйлера. Причем до сих пор мы изображали схематично отношения между двумя понятиями, а это можно сделать и с большим количеством понятий. Например, отношения между понятиями
Взаимное расположение кругов показывает, что понятия боксер и негр находятся в отношении пересечения (боксер может быть негром и может им не быть, а также негр может быть боксером и может им не быть), а понятия боксер и человек, так же как и понятия негр и человек находятся в отношении подчинения (ведь любой боксер и любой негр – это обязательно человек, но человек может не быть ни боксером, ни негром).
Рассмотрим отношения между понятиями дедушка, отец, мужчина, человек с помощью круговой схемы:
Как видим, указанные четыре понятия находятся в отношении последовательного подчинения: дедушка – это обязательно отец, а отец – не обязательно дедушка; любой отец – это обязательно мужчина, однако не всякий мужчина является отцом; и, наконец, мужчина – это обязательно человек, но человеком может быть не только мужчина.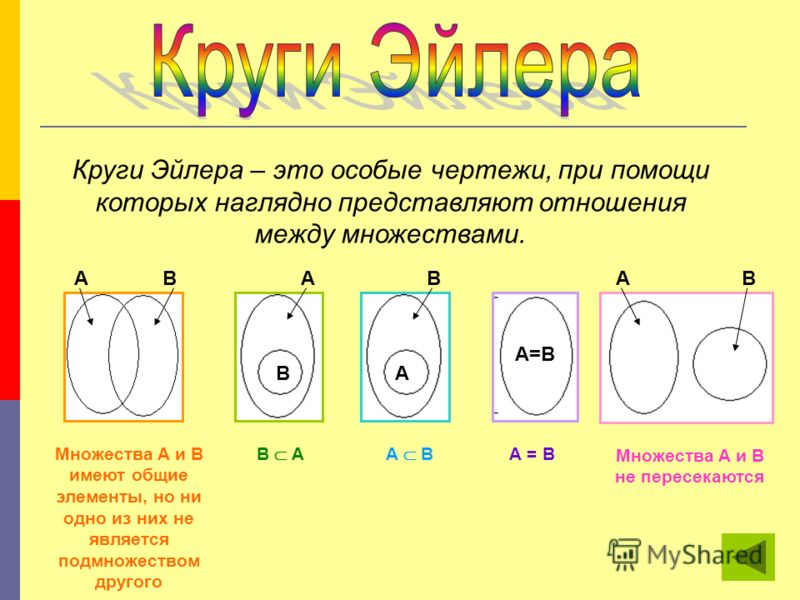
Попробуйте самостоятельно прокомментировать эту схему, установив все имеющиеся на ней виды отношений между понятиями.
Подытоживая сказанное, отметим, что отношения между понятиями – это отношения между их объемами. Значит, для того, чтобы было возможно установить отношения между понятиями, их объем должен быть резким, а содержание, соответственно, ясным, т. е. эти понятия должны быть определенными. Что касается неопределенных понятий, о которых шла речь выше, то установить точные отношения между ними достаточно сложно, фактически невозможно, ведь из-за неясности их содержания и нерезкости объема два каких-нибудь неопределенных понятия можно будет характеризовать как равнозначные или как пересекающиеся, или как подчиняющиеся и т. д. Например, возможно ли установить отношения между неопределенными понятиями
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРеспочему один раз увидеть лучше, чем сто раз услышать
Если вы думаете, что ничего не знаете о кругах Эйлера, вы ошибаетесь. На самом деле вы наверняка не раз с ними сталкивались, просто не знали, как это называется. Где именно? Схемы в виде кругов Эйлера легли в основу многих популярных интернет-мемов (растиражированных в сети изображений на определенную тему).
Давайте вместе разберемся, что же это за круги, почему они так называются и почему ими так удобно пользоваться для решения многих задач.
Происхождение термина
Круги Эйлера – это геометрическая схема, которая помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью.
Пока не очень понятно, верно? Посмотрите на этот рисунок:
На рисунке представлено множество – все возможные игрушки. Некоторые из игрушек являются конструкторами – они выделены в отдельный овал. Это часть большого множества «игрушки» и одновременно отдельное множество (ведь конструктором может быть и «Лего», и примитивные конструкторы из кубиков для малышей). Какая-то часть большого множества «игрушки» может быть заводными игрушками. Они не конструкторы, поэтому мы рисуем для них отдельный овал. Желтый овал «заводной автомобиль» относится одновременно к множеству «игрушки» и является частью меньшего множества «заводная игрушка». Поэтому и изображается внутри обоих овалов сразу.
Ну что, так стало понятнее? Именно поэтому круги Эйлера – это тот метод, который наглядно демонстрирует: лучше один раз увидеть, чем сто раз услышать. Его заслуга в том, что наглядность упрощает рассуждения и помогает быстрее и проще получить ответ.
Автор метода – ученый Леонард Эйлер (1707-1783). Он так и говорил о названных его именем схемах: «круги подходят для того, чтобы облегчить наши размышления». Эйлер считается немецким, швейцарским и даже российским математиком, механиком и физиком. Дело в том, что он много лет проработал в Петербургской академии наук и внес существенный вклад в развитие российской науки.
До него подобным принципом при построении своих умозаключений руководствовался немецкий математик и философ Готфрид Лейбниц.
Метод Эйлера получил заслуженное признание и популярность. И после него немало ученых использовали его в своей работе, а также видоизменяли на свой лад. Например, чешский математик Бернард Больцано использовал тот же метод, но с прямоугольными схемами.
Например, чешский математик Бернард Больцано использовал тот же метод, но с прямоугольными схемами.
Свою лепту внес также немецкий математике Эрнест Шредер. Но главные заслуги принадлежат англичанину Джону Венну. Он был специалистом в логике и издал книгу «Символическая логика», в которой подробно изложил свой вариант метода (использовал преимущественно изображения пересечений множеств).
Благодаря вкладу Венна метод даже называют диаграммами Венна или еще Эйлера-Венна.
Зачем нужны круги Эйлера?
Круги Эйлера имеют прикладное назначение, то есть с их помощью на практике решаются задачи на объединение или пересечение множеств в математике, логике, менеджменте и не только.
Если говорить о видах кругов Эйлера, то можно разделить их на те, что описывают объединение каких-то понятий (например, соотношение рода и вида) – мы их рассмотрели на примере в начале статьи.
А также на те, что описывают пересечение множеств по какому-то признаку. Таким принципом руководствовался Джон Венн в своих схемах. И именно он лежит в основе многих популярных в интернете мемов. Вот вам один из примеров таких кругов Эйлера:
Забавно, правда? И главное, все сразу становится понятно. Можно потратить много слов, объясняя свою точку зрения, а можно просто нарисовать простую схему, которая сразу расставит все по местам.
Кстати, если вы не можете определиться, какую профессию выбрать, попробуйте нарисовать схему в виде кругов Эйлера. Возможно, чертеж вроде этого поможет вам определиться с выбором:
Те варианты, которые окажутся на пересечении всех трех кругов, и есть профессия, которая не только сможет вас прокормить, но и будет вам нравиться.
Решение задач с помощью кругов Эйлера
Давайте рассмотрим несколько примеров задач, которые можно решить с помощью кругов Эйлера.
Вот на этом сайте – http://logika.vobrazovanie.ru/index.php?link=kr_e.html Елена Сергеевна Саженина предлагает интересные и несложные задачи, для решения которых потребуется метод Эйлера.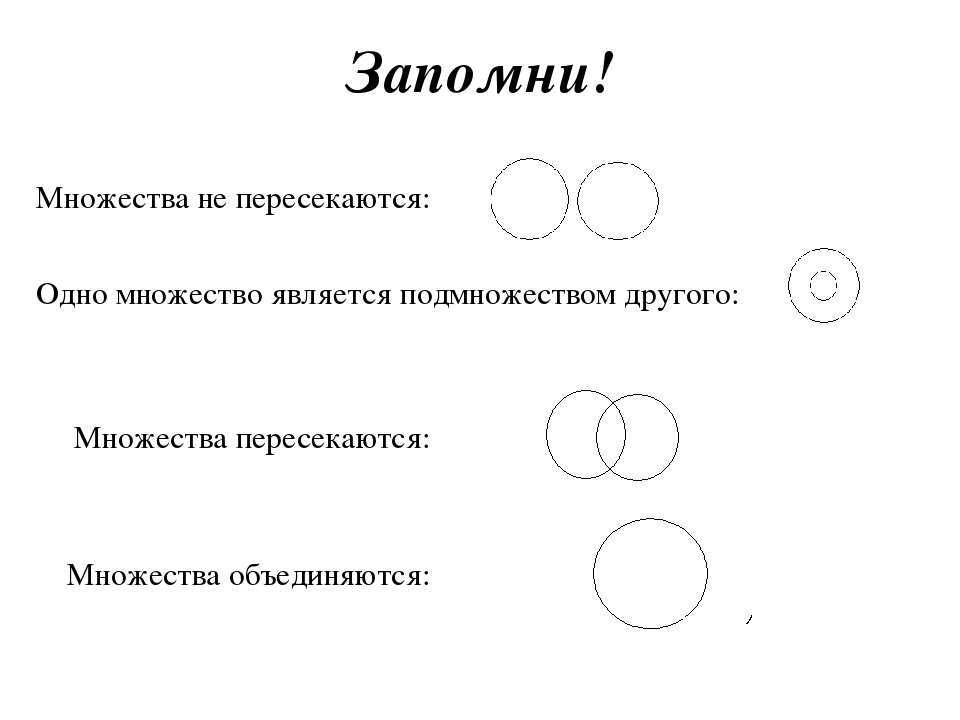 Используя логику и математику, разберем одну из них.
Используя логику и математику, разберем одну из них.
Задача про любимые мультфильмы
Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым – «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».
Решение:
Так как по условиям задачи у нас даны три множества, чертим три круга. А так как по ответам ребят выходит, что множества пересекаются друг с другом, чертеж будет выглядеть так:
Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу:
Выходит, что:
21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».
13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».
Осталось только разобраться, сколько шестиклассников двум другим вариантам предпочитает мультфильм «Губка Боб Квадратные Штаны». От всего количества учеников отнимаем всех тех, кто любит два других мультфильма или выбрал несколько вариантов:
38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».
Теперь смело можем сложить все полученные цифры и выяснить, что:
мультфильм «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек. Это и есть ответ на поставленный в задаче вопрос.
А еще давайте рассмотрим задачу, которая в 2011 году была вынесена на демонстрационный тест ЕГЭ по информатике и ИКТ (источник – http://eileracrugi.narod.ru/index/0-6).
Условия задачи:
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.
| Запрос | Найдено страниц (в тысячах) |
| Крейсер | Линкор | 7000 |
| Крейсер | 4800 |
| Линкор | 4500 |
Какое количество страниц (в тысячах) будет найдено по запросу Крейсер & Линкор?
Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
При помощи кругов Эйлера изобразим условия задачи. При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.
Опираясь на условия задачи, составим уравнения:
- Крейсер | Линкор: 1 + 2 + 3 = 7000
- Крейсер: 1 + 2 = 4800
- Линкор: 2 + 3 = 4500
Чтобы найти Крейсер & Линкор (обозначенный на чертеже как область 2), подставим уравнение (2) в уравнение (1) и выясним, что:
4800 + 3 = 7000, откуда получаем 3 = 2200.
Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:
2 + 2200 = 4500, откуда 2 = 2300.
Ответ: 2300 – количество страниц, найденных по запросу Крейсер & Линкор.
Как видите, круги Эйлера помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.
Заключение
Полагаю, нам удалось убедить вас, что круги Эйлера – не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Причем не только абстрактных задач на школьный уроках, но и вполне себе житейских проблем. Выбора будущей профессии, например.
Вам еще наверняка будет любопытно узнать, что в современной массовой культуре круги Эйлера нашли отражение не только в виде мемов, но и в популярных сериалах. Таких, как «Теория большого взрыва» и «4исла».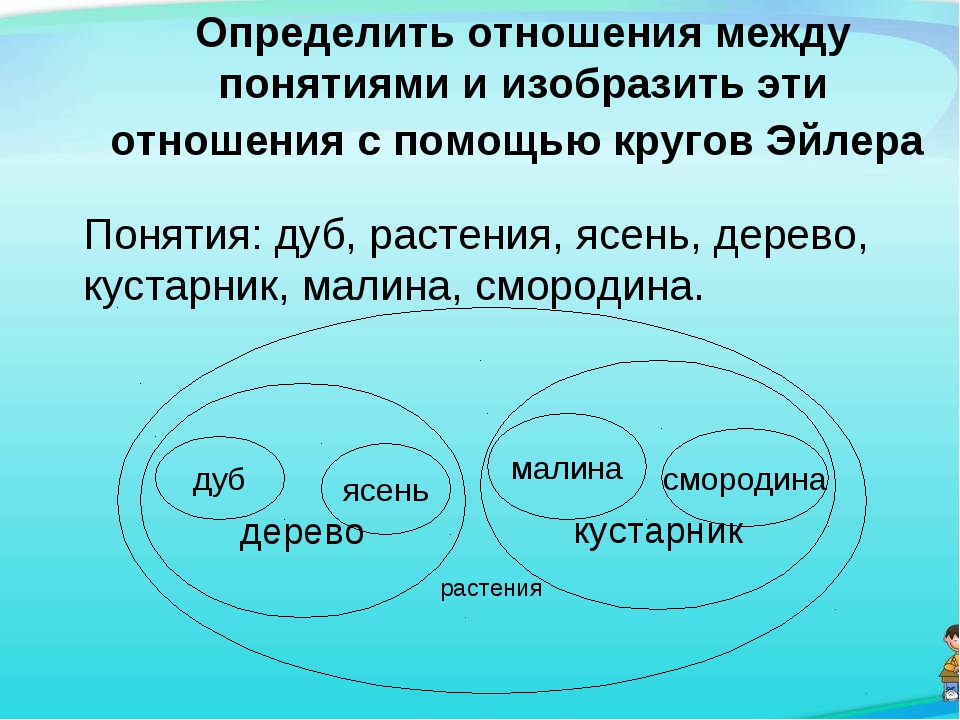
Используйте это полезный и наглядный метод для решения задач. И обязательно расскажите о нем друзьям и одноклассникам. Для этого под статьей есть специальные кнопки.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
В кругах Эйлера | SKVOT
Работа креатора — это не только генерить идеи. Но и вовремя включить критическое мышление — чтобы найти в концепциях противоречия и отбросить то, что не выживет.
Инструменты есть не только для креативного, но и для логического мышления. И круги Эйлера — как раз из этого списка. Рассказываем, что это, и на примере креативных проектах показываем принцип работы кругов.
Рисовать, чтобы думать
Круги Эйлера — это шесть простых геометрических схем, которые помогают разобраться в соотношении понятий. Математик Леонард Эйлер придумал их еще в XVIII веке и предположил, что этот инструмент упростит размышления любому, кто мыслит.
Эйлер предложил шесть типов отношений: равнозначность, подчинение, соподчинение, пересечение, противоречие, противоположность. Вот как они объясняются с помощью окружностей:
По сути, круги Эйлера — способ визуализировать отношения между любыми объектами, группами объектов и даже абстрактными понятиями. Например, чтобы искать точки пересечения между любителями «Звездных войн», жителями швейцарских горных сел и посетителями музыкального фестиваля Sziget.
Чем больше понятий, тем сложнее представить их связи мысленно, цифрами, списками — и тем эффективнее делать схему. Например, в сериале «Теория большого взрыва» Говард при помощи кругов Эйлера объясняет Леонарду, почему ему стоит забить на поиски идеальной женщины:
Круги Эйлера используют для решения логических задач уже в средней школе.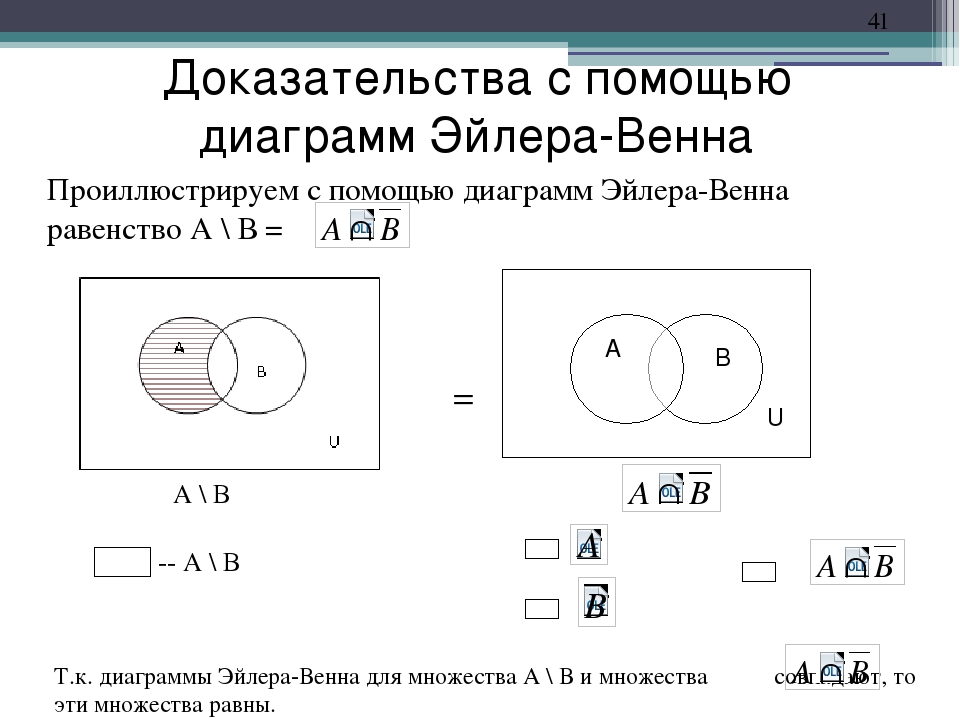 Но схемы универсальны — и действительно пригодятся любому, кто размышляет.
Но схемы универсальны — и действительно пригодятся любому, кто размышляет.
Нарисуй, распечатай, запомни круги Эйлера — и используй, если нужно:
- — Разработать стратегию и проверять, как идея/проект с ней соотносятся.
- — Анализировать контент конкурентов, кампании каннских победителей, рекламу Superbowl — и понять ключевые схемы.
- — Выбрать tone of voice, героя истории, стиль вижуала, маскот для бренда, месседж для слогана.
- — Найти противоречия и логические ямы в брифе, сценарии, посте для соцсетей.
- — Освоить новый скил, но с направлением определиться трудно.
Эйлер на кейсах
Самый надежный способ разобраться в механизме системы, которую придумал Эйлер, — найти примеры в готовых кейсах. Увидишь, как работает равнозначность в стратегии бренда или пересечение в поисках героя для рекламного ролика, — поймешь, как использовать этот подход в своих целях.
#1. Равнозначность
У Эйлера этот тип взаимодействия понятий выглядит как два круга, которые полностью совпадают. Одно равно другому, как ни назови. Стивен Хокинг = автор книги «Краткая история времени». Или «Пираты Карибского моря: на странных берегах» = самый дорогой фильм в истории (пока).
Один рекламный ролик не сможет за минуту убедить пользователей, что пиво = Guinness, мыло = Dove, а детское масло = Johnson’s Baby. Нужна эффективная (часто многолетняя) маркетинговая стратегия, которая приведет к этому убеждению.
В идеале название бренда будет однозначно ассоциироваться с целой индустрией или продуктом. Слышишь «мебель для самостоятельной сборки» — сразу понимаешь, что это IKEA. Видишь пошаговый гайд по сборке — точно IKEA. А с помощью этих прочных связей бренд может говорить на самые разные темы: экологичность, ресайклинг, домашний уют и социальная ответственность.
instagram.com/p/CIllzy6Fahf/?utm_source=ig_embed&utm_campaign=loading” data-instgrm-version=”13″>
#2. Подчинение
Допустим, общее понятие — это большой круг. Внутри него находится другой, маленький, и это — частность большого. Зимних олимпийских видов спорта много, и бобслей, например, один из них.
Такой тип отношений — мощный инструмент для рекламного месседжа. Особенно если его целью оказывается инклюзия: включение незаметной, неожиданной, уязвимой группы в сообщество. Nike на протяжении нескольких лет топит за спорт как удовольствие, независимо от телосложения, опыта, целей и происхождения. И на уровне продукта, и на уровне рекламных кампаний.
Коллекцию Victory Swim разработали для спортсменок-мусульманок — и Nike промит ее идеальным роликом, где женщины в хиджабах участвуют в соревнованиях, серфят, занимаются дайвингом и учат дочек плавать. И становятся частью сообщества Nike:
#3. Соподчинение
Графический ключ к этому соотношению — большой круг, внутри которого помещаются несколько маленьких. Маленькие понятия на равных и полностью включены в какое-то общее. Например, актеры, получившие Оскар, — Хоакин Феникс, Гэри Олдман, Леонардо Ди Каприо.
Если поместишь ключевое понятие в не самую очевидную область и будешь искать соподчинение в ней, выйдет крутой экспириенс. Например, очевидно было с началом пандемии находить параллели в прошлом — в частности, с эпидемией «испанки».
Креаторы латвийского агентства Nord DDB во время весеннего локдауна разработали серию принтов о бедах, которые мы уже пережили (а значит, есть все шансы пережить и жесткий карантин). Среди самых страшных событий прошлого: шлепанцы на носки и кроксы с платформой. Реально страшно:
#4. Пересечение
Пересечение
Эта диаграмма Эйлера — самая культовая и попсовая: ее растащили в коуч-пособия и мемы. Суть в том, что объем одного понятия частично совпадает с объемом другого — у них есть что-то общее.
Это крутой визуальный инструмент для поиска инсайта. Если представить бренд как исходный круг и строить вокруг него пересечения с ценностями и потребностями ЦА, попадешь в область, где совпадение будет максимальным.
Например, у Starbucks есть фишка: писать имя посетителя на кофейном стаканчике. Этот факт даже не про кофе, он — маленькая деталь в общем объеме информации о бренде. Но среди посетителей кофеен точно есть те, кто хочет сказать свое имя — и услышать его от бариста. Значит, нужно найти героя, который только в Starbucks может назвать себя как угодно, а не так, как написано в паспорте.
#5. Противоречие
В отличие от противоположности, противоречие держится на конфликте. Круг разделен пополам. Одна его часть утверждает, что не является второй частью. И наоборот.
На этом принципе строятся самые остроумные рекламные войны между брендами: Audi vs BMW, Pepsi vs Coca Cola, Old Spice vs Axe. Чаще это противостояние скрытое — борьба стратегий, разделение целевых аудиторий, — но иногда начинается прямой троллинг конкурента.
Рекламная борьба между McDonald’s и Burger King — самая долгая и зрелищная. Клоун, маскот Мака, шифруется и приходит в Burger King за воппером. Потом Burger King показывает, что весь год снимал рекламу вопперов, заслоняя ими бигмаки. Конкуренты меряются вкусом и размером бургеров, близостью ресторанов уже больше 20 лет.
А зарывают топор войны только ради социально важных поступков, но и тогда это соревнование в благородстве. В начале осеннего локдауна французский Burger King опубликовал в медиа призыв покупать в McDonald’s и других сетях фастфуда — чтобы индустрия выжила. Конечно, воппер будет лучшим решением, но и бигмак сойдет.
Конечно, воппер будет лучшим решением, но и бигмак сойдет.
#6. Противоположность
Понятия с противоположными характеристиками Эйлер представляет как две части круга, между которыми остается свободное пространство — это все остальное. Проза и поэзия — две противоположности, а между ними: верлибр и ритмическая проза, например.
Противоположности — это мирные антонимы, которые не вступают в конфликт и не строят свою идентичность на отрицании друг друга. Это холодное, а это горячее. Это промышленное, а это DIY.
Wunderman Thompson построили на противоположности крутую кампанию для West Australian Ballet. В качестве промо новой постановки «Дракула» на стенах общественных туалетов разместили необычные принты. Изображение вампира в зеркале не отражается — постер пустой. Тут Дракула есть — там нет:
Логический вывод
В системе Эйлера — шесть простых геометрических схем, которые нарисует от руки даже ребенок. По отдельности каждая из них определяет только одно взаимодействие. Но если берешься за большую тему, в твоей схеме могут сочетаться сразу несколько типов соотношений.
Например, целевая аудитория бренда — подростки от 13 до 18. Среди них есть те, кто использует инстаграм, и те, кто использует тикток. Тиктокеры и инста-teens входят в целевую по принципу соподчинения. Но есть небольшая группа, которая зависает в обеих соцсетях — и между собой они взаимодействуют по принципу пересечения.
Тестить мир на противоречия и связи — суперполезно и суперувлекательно. Хорошие новости: ты не сможешь остановиться. Плохие новости: ты не сможешь остановиться.
Решение логических задач с помощью кругов эйлера
Муниципальное общеобразовательное учреждение
лицей № 8 «Олимпия»
Дзержинского района г.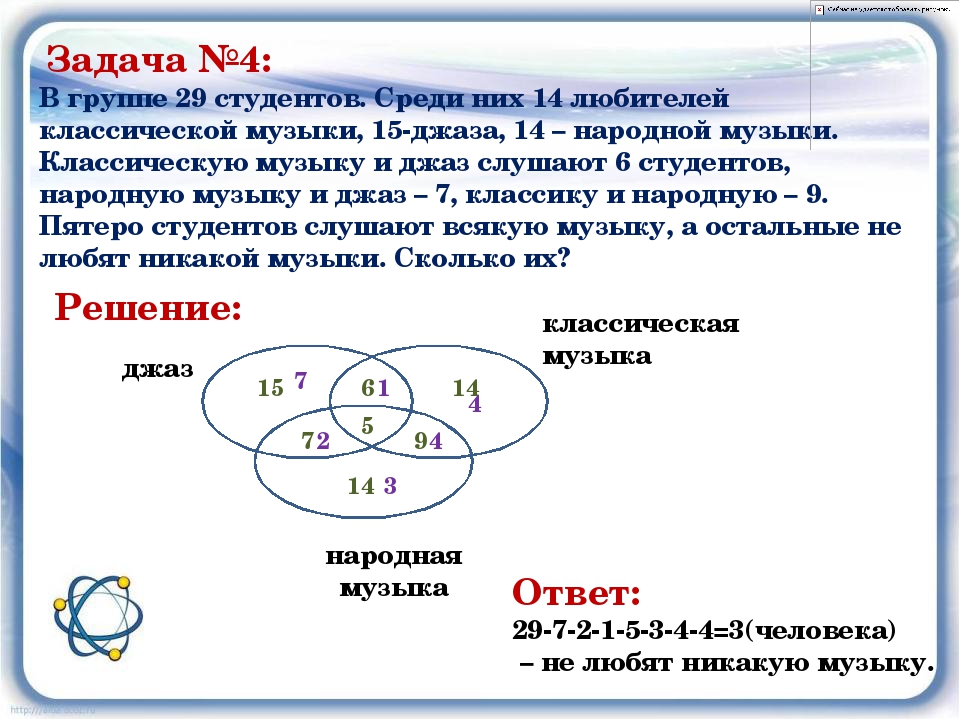 Волгограда
Волгограда
Телефоны (8442) 58-80-83, 51-81-31 адрес электронной почты lyceum8@mail.ru
Решение логических задач с помощью кругов Эйлера
Выполнил:
Назаретян Сюзана Горовна,
ученица 5 Б класса
Учитель:
Кокиева Лилия Диляверовна, учитель
математики высшей категории
Волгоград, 2011
Оглавление | С. |
Введение…………………………………………………………………………………… | 3 — 4 |
Глава I. Логические задачи и круги Эйлера ……………..…….…… | 5 — 9 |
1.1. Трудно решать логические задачи? …..……………………. | 5 — 6 |
1.2. Немного о множествах ………..…………………………… | 6 — 8 |
1.3. Из истории кругов Эйлера …….……..……………………. | 8 — 9 |
Глава II. Решение логических задач с помощью кругов Эйлера….. | 7 — 14 |
2.1. Задачи на пересечение и объединение двух множеств……. | 9 —12 |
2.2. Задачи на пересечение и объединение трёх множеств …… | 12 — 14 |
Заключение……………………………………………………………………………….. | 15 |
Список источников и литературы………………………………………………. | 16 |
Приложения . | 17—20 |
Введение.
Сколько гостей Вам встречать, если собираются друзья с 15 угощениями и 20 украшениями? Может ли хватить всем места за столом, вмещающем 22 человека? Первое, что приходит на ум, это 35 человек. А причём здесь 22 человека? Есть подвох? Конечно! Ведь надо рассмотреть несколько вариантов.
Как узнать количество учащихся класса, посещающих одновременно две или три секции, если известны количества участников каждой секции отдельно? Можно ли научиться решать такие задачи, планируя результат? Хочется ответить положительно.
А как решить такую задачу: «Министерство послало в один из лицеев инспектора для проверки, как в нём ведётся преподавание иностранных языков. Сотрудник министерства в отчёте записал, что в лицее учатся 100 детей. Каждый изучает по крайней мере один из трёх языков: французский, немецкий и испанский. Причём все три языка изучают 5 человек; немецкий и испанский 10;французский и испанский 8; немецкий и французский 20; испанский 30, немецкий 23, французский 50. Инспектор, представивший отчёт, был уволен. Почему?»? Такое длинное условие: пока дочитали до конца – забыли начало. Что делать?
Оказывается, такие задачи решаются с помощью кругов Эйлера. Изображение условий задачи в виде кругов Эйлера, как правило, упрощает и облегчает путь к её решению.
Актуальность нашей работы заключается в том, чтобы такие задачи не ставили нас «в тупик» и мы могли их решать.
С учетом этого и была выбрана темаисследования: «Решение логических задач с помощью кругов Эйлера».
Объект исследования — логические задачи.
Предмет исследования —использование кругов Эйлера для решения логических задач .
Гипотеза исследования. Можно решать логические задачи определённого вида специальными способами и в 5 – 6 классах.
Можно решать логические задачи определённого вида специальными способами и в 5 – 6 классах.
Целью нашего исследования является исследование механизма решения определённых логических задач при помощи кругов Эйлера.
Для достижения цели исследования и обоснования гипотезы нам необходимо решить ряд задач:
Найти необходимые сведения о пересечении и объединении множеств, о кругах Эйлера.
Рассмотреть способы решения логических задач на пересечение и объединение двух и трёх множеств.
Вывести в общем виде способ решения логических задач определённого вида с помощью кругов Эйлера.
Научиться решать конкретные логические задачи с помощью кругов Эйлера.
Создать модели «Круги Эйлера» для решения задач с двумя и тремя множествами в помощь учащимся.
Методы исследования:
1. Поиск, анализ и синтез различных источников информации.
2. Интервьюирование, беседы.
Практическая значимость заключается в расширении аппарата для решения логических задач. Данный материал можно будет использовать на некоторых уроках, для проведения кружков, факультативных занятий по математике. Применение кругов Эйлера придает задачам наглядность и простоту.
Теоретическая значимость заключается в разработке способа действий при решении логических задач с помощью кругов Эйлера в общем виде.
Здесь будет выводиться история переписки.
Глава I. Логические задачи и круги Эйлера
1.1. Трудно решать логические задачи?
Логика – это искусство рассуждать, умение делать правильные выводы. Это не всегда легко, потому что очень часто необходимая информация «замаскирована», представлена неявно, и надо уметь её извлечь.

Решение логических задач – одно из важнейших средств развития мыслительных способностей.
Логические задачи обладают рядом достоинств, позволяющих использовать их для развития соображения и улучшения логического мышления детей, начиная с детского сада и заканчивая старшими классами средней школы. Логические задачи допускают изложение в занимательной, игровой форме. С другой стороны, такие задачи труднее, для их решения часто не требуется глубоких знаний, а следует применить смекалку.
Вдоль овражка
Шла фуражка,
Две косынки,
Три корзинки
И от них не отставала
Белоснежная панама.
Посчитай поскорей
Сколько было детей?
Задача предполагает несколько решений. Потому что мы точно не знаем, носил ли кто – нибудь и головной убор, и корзинку.
1 Решение. Предполагается, что каждый ребёнок носил 1 предмет. Значит, детей было 7.
2 Решение. Предполагается, что 1 из детей нёс корзинку и головной убор. Следовательно, детей было 6.
3 Решение. Предполагается, что 2 из детей носили и корзинку, и головной убор. Следовательно, детей было 5 .
4 Решение. Предполагается, что 3 из детей носили и корзинку, и головной убор. Следовательно, детей было 4.
1.2. Немного о множествах
Множество – одно из основных понятий математики. Его смысл выражается словами: совокупность, собрание, класс, набор, команда и т.д. Этот смысл поясняется многочисленными примерами. Так, можно говорить о множестве всех учащихся 5-го класса, о множестве всех жителей Волгограда, о множестве всех натуральных чисел, о множестве корней данного уравнения. Основатель теории множеств немецкий математик Георг Кантор (1845–1918) так определил множество – «многое, мыслимое как единое, целое».
Множества обозначаются прописными буквами латинского алфавита А, В, С, …
О предметах, составляющих множество, говорят, что они принадлежат этому множеству или являются его элементами. Множества, элементами которых являются числа, называются числовыми множествами.
Множества, элементами которых являются числа, называются числовыми множествами.
Множество может быть задано перечислением всех его элементов в произвольном порядке. Такое множество называют конечным. Мы будем рассматривать только конечные множества.
Множество, в котором нуль элементов, называют пустым.
Над множествами, как и над числами, производят операции. Рассмотрим некоторые из них: пересечение, объединение и разность.
Пересечение множеств
Возьмем множество X, состоящее из букв а, б, в, г, д, и множество Y, состоящее из букв г, д, е, ж:
X = {а, б, в, г, д}, Y= {г, д, е, ж}.
Эти множества имеют общие элементы гид. Множества X и Y называются пересекающимися множествами. Множество общих элементов X и Y называют пересечением множеств X и Y и обозначают с помощью знака :Х Y={г, д} (рис. 1).
Пусть множество А = {1, 3, 5}. Множества А и X не имеют ни одного общего элемента. В таком случае множества А и X называются непересекающимися множествами. Пересечением множеств А и X является пустое множество: А Х= (рис. 2).
Пересечением множеств называется новое множество, состоящее
из элементов, принадлежащих одновременно нескольким множествам
Рис. 1
Рис. 2
Объединение множеств
Если из элементов множеств X и Y составить новое множество, состоящее из всех элементов этих множеств и не содержащее других элементов, то получится объединение множеств Х и Y, которое обозначают с помощью знака :
X и Y= {а, б, в, г, д, е, ж) (рис. 4).
Объединение множеств А и X не является пустым:
А X = {1, 3, 5, а, б, в, г, д) (рис. 5).
5).
Объединением множеств называется новое множество, состоящее
из элементов, принадлежащих хотя бы одному из множеств.
Рис. 3
Рис. 4
Рис. 4Разность
Разность множеств X и Y — это множество всех элементов из X, не являющихся элементами из Y.Разность обозначают Х\Y = {а, б, в} (рис. 5).
Рис. 5
1.3. Из истории кругов Эйлера
Часто множество изображают кругами, эти круги обычно называют «кругами Эйлера» по имени величайшего математика Леонарда Эйлера.
Леонард Эйлер (Euler) (1707 – 1783 г.г.) – математик, механик, физик и астроном. По происхождению швейцарец, а работал в основном в Росси и в Германии. В 1726 году был приглашен в Петербургскую АН и в 1727 году переехал в Россию. В 1741 – 1766 годах работал в Берлине, член Берлинской АН. Эйлер – ученый необычайной широты интересов и творческой продуктивности. Автор свыше 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др., оказавших значительное влияние на развитие науки.
Одним из первых, кто разрабатывал метод решения задач с помощью кругов Эйлера, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646 – 1716). В его черновых набросках были обнаружены рисунки с такими кругами. Затем этот метод довольно основательно развил швейцарский математик Леонард Эйлер (1707 – 1783). Он долгие годы работал в Петербургской Академии наук. К этому времени относятся его знаменитые «Письма к немецкой принцессе», написанные в период с 1761 по 1768 год. В некоторых из этих «Писем…» Эйлер как раз и рассказывает о кругах, которые «очень подходят для того, чтобы облегчить наши размышления». После Эйлера этот же метод разрабатывал чешский математик Бернард Больцано (1781 – 1848).
После Эйлера этот же метод разрабатывал чешский математик Бернард Больцано (1781 – 1848).
Только в отличие от Эйлера он рисовал не круговые, а прямоугольные схемы. Методом кругов пользовался и немецкий математик Эрнест Шредер (1841 – 1902). Этот метод широко используется в книге «Алгебра логики». Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843 – 1923). С наибольшей полнотой этот метод изложен им в книге «Символическая логика», изданной в Лондоне в 1881 году. В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами (или кругами) Эйлера – Венна.
Глава II. Решение логических задач с помощью кругов Эйлера
2.1. Задачи на пересечение и объединение двух множеств
К Лене на День Рождения пришли гости с подарками. Получилось так, что подарили только букеты цветов и воздушные шарики. Шесть гостей подарили букеты цветов, четыре – воздушные шарики. Сколько было гостей?
Задача предполагает несколько решений. Потому что мы точно не знаем, брал ли кто – нибудь из гостей два подарка.
1 Решение. Предполагается, что каждый гость с одним подарком. Следовательно, гостей 10.
2 Решение. Предполагается, что 1 из гостей пришел и с шариком, и с букетом цветов. Следовательно, 6 + 3 = 9 гостей.
3 Решение. Предполагается, что 2 из гостей пришли с двумя подарками. Следовательно, гостей 8.
4 Решение. Предполагается, что 3 из гостей пришли и с шариком, и с букетом цветов. Следовательно, 6 + 1 = 7.
5 Решение. Предполагается, 4 из гостей пришли с 2 подарками. Следовательно, 4 + 2 = 6 гостей.
1
Ц
)2)Ш
Ш
4
5
1
3
Ш
Ц
Ш
Ц
) 4)4
2
2
3
3
Ш
Ц
5)2
В одном множестве 40 элементов, а в другом 30. Сколько элементов может быть в их:
Сколько элементов может быть в их:
а) пересечении; б) объединении?
Ответ: а) от 0 до 30; б) от 40 до 70.
“;Ёлки”; и “;Неудержимый”;: Некоторые ребята из нашего класса любят ходить в кино. Известно, что 12 ребят смотрели фильм «Ёлки», 9 человек – фильм «Неудержимый», из них 6 смотрели и «Ёлки», и «Неудержимый». Сколько человек смотрели только фильм «Неудержимый»?
Сначала заполняем пересечение. Это будет число 6. Потом заполняем множество ребят, смотревших фильм «Ёлки». Это будет число 6. Так как 6 из двенадцати к тому же ещё смотрели фильм «Неудержимый». После заполняем множество ребят, смотревших фильм «Неудержимый». Это будет число 3. Так как 6 из 9 к тому же ещё смотрели фильм «Ёлки».
Ответ: 3 человека смотрели только фильм «Неудержимый».
20 человек знают английский и 10 – немецкий, из них 5 знают и английский, и немецкий. Сколько человек всего?
Способ 1. С помощью модели «Круги Эйлера» (Приложение 1).
10+20 – 5=25 человек.
Способ 2.
1) 20 – 5 = 15(чел.) – знают только английский язык;
2) 10 – 5 = 5 (чел.) – знают только немецкий язык;
3) 15+5+5 = 25 (чел.) – всего.
15
5
10
А
Можно решать и короче:
20 – 5 = 15(чел.) – знают только английский язык;
10+15 = 25 (чел.) – знают немецкий и только английский
2.2. Задачи на пересечение и объединение трёх множеств
В классе всего 36 человек. Учащиеся посещают математический, физический и химический кружки, причем, математический кружок посещают 18 человек, физический – 14 человек, химический – 10 человек. Кроме того, известно, что все три кружка посещают 2 человека, математический и физический -8,математический и химический – 5, физический и химический – 3.
Кроме того, известно, что все три кружка посещают 2 человека, математический и физический -8,математический и химический – 5, физический и химический – 3.
Сколько учеников класса не посещают никаких кружков?
Способ 1. На рисунке большой круг изображает множество всех учеников класса. Внутри этого круга расположены три пересекающихся круга меньшего диаметра: эти круги изображают соответственно множества членов математического, физического и химического кружков. Эти круги обозначены буквами М, Ф, Х.
Общей части всех трех кругов соответствует множество ребят, посещающих все три кружка, поэтому она обозначена МФХ.
Через обозначено множество ребят, посещающих математический и физический кружки, но не посещающих химический кружок. Аналогичным образом обозначены и все остальные области. Здесь для удобства обозначений мы будем отсутствие отмечать чертой над символом.
Теперь обратимся к числовым данным (см. Приложение 2).
В область МФХ впишем число 2, т.к. все три кружка посещают 2 ученика. Далее известно, что ребят, посещающих математический и физический кружки, было 8. Значит, в область МФ надо вписать число 8. Но область МФ состоит из двух частей: и МФХ, причем в МФХ входят 2 человека. Значит, на долю остается 6 человек.
Теперь рассмотрим множество МХ, на которое приходится 5 человек. Эта область также состоит из двух частей. На МФХ приходится 2 человека, значит, на приходится 3.
Рассмотрим теперь множество М, в которое входят 18 учеников. Оно состоит из 4 частей. Количественный состав трех подмножеств мы уже нашли: это 2, 6 и 3. Значит, в четвертое подмножество входит 18 – (2+3+6) = 7 человек.
Рассмотрим множество ФХ, на которое приходится 3 человека. Эта область также состоит из двух частей. На МФХ приходится 2 человека, значит, на приходится 1.
Рассмотрим множество Ф, в которое входят 14 учеников. Оно состоит из 4 частей. Количественный состав трех подмножеств мы уже нашли: это 2, 6 и 1. Значит, в четвертое подмножество входит 14 – (2+1+6) = 5 человек.
36 – (10+7+6+5) = 8 человек. Таким образом, в классе 8 ребят, не посещающих никаких кружков.
М
6
5
7
2
3
1
4
? 8
Способ 2. С помощью модели «Круги Эйлера» (Приложение 1).
Представим множества учащихся, посещающих математический, физический и химический кружки, в виде кругов, вырезанных из плотной бумаги. Будем считать, что площадь каждого из этих кругов равна числу учащихся, посещающих соответствующий кружок. Наложим круги друг на друга так, чтобы было понятно, что есть учащиеся, посещающие один, два или три кружка. Вычислим площадь получившейся фигуры:
14 + 18 + 10 – ((8 + 5 + 3) 2) – 2 = 8 (чел.)— не посещают кружки.
Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским – 28, французским – 42. Английским и немецким одновременно владеют 8 человек, английским и французским – 10, немецким и французским – 5, всеми тремя языками – 3. Сколько туристов не владеют ни одним языком?
Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3. Английским и французским языком владеют 10 человек, а 3 из них владеют еще и немецким. Следовательно, только английским и французским владеют 10-3=7 человек.
Аналогично получаем, что только английским и немецким владеют 8-3=5 человек, а немецким и французским 5-3=2 туриста.
Немецкий знают 30 человек, но 5+3+2=10 из них владеют и другими языками, следовательно, только немецкий знают 20 человек. Аналогично получаем, что одним английским владеют 13 человек,а одним французским – 30.
Всего 100 туристов. 20+13+30+5+7+2+3=80 туристов знают хотя бы один язык, следовательно, 20 человек не владеют ни одним из данных языков.
Заключение
Существует множество приемов, которые используются при решении текстовых логических задач (Приложение 3). Очень часто решение задачи помогает найти рисунок, он делает решение простым и наглядным. Задачи, решаемые с помощью кругов Эйлера, предлагаются на математических олимпиадах, но в школьной программе не отводятся часы на изучение данной темы. Ценность использования кругов Эйлера состоит в том, что решения задач с громоздкими условиями и со многими данными становятся проще.
Подобные задачи часто имеют практический характер, что немаловажно в современной жизни. Они заставляют задумываться, подходить к решению какой-либо проблемы с разных сторон, уметь выбирать из множества способов решения наиболее простой, легкий путь.
Нами созданы модели «Круги Эйлера» для решения логических задач на пересечение двух и трёх множеств, которыми можно пользоваться как на месте (за партой), так и у доски (Приложение 4).
Поиск готовых способов решения выделенных логических задач, самостоятельное описание способа действий при использовании кругов Эйлера для их решения, а также попытки рассмотрения другой формы представления данных условия позволили нам решить поставленные задачи.
Цель была достигнута. С результатами работы были ознакомлены наши одноклассники, что позволило решать логические задачи этого вида не только нам.
Теперь наши одноклассники решают такие задачи, используя не только модели, но и памятку со способом действий, написанных нами.
Теперь мы точно будем знать, сколько друзей нам надо встречать в гости. От 20 до 35! А значит, и за стол всех всё же можно будет посадить.
Данная тема, безусловно, расширяет математический кругозор учащихся, обогащает арсенал средств, используемых в решении разнообразных задач.
Литература
Задачи для внеклассной работы по математике в V – VI классах: Пособие для учителей Текст/ Сост. В.Ю. Сафонова. Под ред. Д.Б. Фукса, А. Л. Гавронского. М.: МИРОС, 1993. с. 42. – ISBN 5-7084-0023-4
Занимательная математика. 5 – 11 классы. Текст: (Как сделать уроки нескучными) / Авт. – сост. Т.Д. Гаврилова. Волгоград: Учитель, 2005. с.32-38. – 10000 экз. –5-7057-0482-8
Депман,И.Я., Виленкин, Н.Я. За страницами учебника математики Пособие для учащихся 5 – 6 кл. Текст/ И.Я Депман. М.: Просвещение, 1999. с. 189 – 191, 231. – 10000 экз. – ISBN 5-09-007107-1
Смыкалова, Е.В. Дополнительные главы по математике для учащихся 5 класса. Текст: СПб: СМИО Пресс, 2009. с.14-20. – 2000 экз. – ISBN 5-7704-0055-2
Фарков, А.В. Математические олимпиады в школе.5–11 классы.Текст / А.В. Фарков. М.: Айрис–пресс, 2007. с. 27, 34, 61. – 7000 экз. – ISBN 978-5-8112-2394-7
Энциклопедия для детей. Т. 11. Математика Текст/ Глав.ред. М.Д. Аксёнова. М.: Аванта +,2001. с. 537 – 542. – 20000экз. – ISBN 5-8483-0015-1
Иванищев, Д. М. Поляна загадок – математика царица.
/
Дистанционная обучающая олимпиада по математике (ДООМ)
/
Сопова, С. С. Диаграмма Эйлера-Вена и “;дерево”;. Взаимодополнение.
/
Приложение 1
Модель «Круги Эйлера» на пересечение двух множеств
На листе бумаги нарисовать два круга.
Разрезать по пунктирным линиям и получить детали.
На бумаге цвета 1 обвести и вырезать детали № 1 () (), № 2 ().
На бумаге цвета 2 обвести и вырезать детали № 2, № 3 () ().
– окошко для названия множества, – окошко для числа
Модель «Круги Эйлера» на пересечение трёх множеств
На листе бумаги нарисовать три круга.
Разрезать по пунктирным линиям и получить детали.
На бумаге цвета 1 обвести и вырезать детали № 5 () (), № 2, № 1, № 4.
На бумаге цвета 2 обвести и вырезать детали № 6 (), (), № 2, № 1, № 3.
На бумаге цвета 3 обвести и вырезать детали № 7 (), (), № 4 (), № 1 (),
№ 3 ().
Приложение 2.
Способ действий при решении задач
на пересечение и объединение трёх множеств с помощью кругов Эйлера
Начертить три пересекающихся круга. Обозначить множества: A, B, C.
Начертить большой круг, в котором окажутся три маленьких. Это общее количество объектов – множество Е.
Начертить отдельное множество D – подмножество множества E Это те, кто не является элементом множеств А, В и С.
Найти часть круга, являющуюся общей для всех трёх множеств (№1) и записать данные.
Найти часть круга, являющуюся общей для двух множеств (№1 и №2) и записать данные в №2.
Найти часть круга, являющуюся общей для двух множеств (№1 и №3) и записать данные в №3.
Найти часть круга, являющуюся общей для двух множеств (№1 и №4) и записать данные в №4.
Найти часть круга, отвечающую за каждое множество в отдельности:
5 = А – (1 + 2 + 4), 6 = В – (1 + 2 + 3), 7 = С – (1 + 3 + 4).
Должно выполняться: 1 + 2 + 3 + 4 + 5 + 6 + 7 + D = E/
Записываем ответ на вопрос задачи.
Приложение 3.
Задача (/). а)На 3 курсе факультета обучается 81 студент. Многие из них выбрали одинаковые дисциплины, посещают одни и те же лекции и хорошо знают друг друга. б) 43 студента посещают лекции по философии, в)32 – по логике и г)41 – по естествознанию. д) Философию и логику выбрали 11 человек. е) Философию и естествознание посещает 21 студент, ж)а логику и естествознание – 16. з) 4 человека выбрали только философию и логику.
Сколько студентов посещают лекции:
1) по всем трём предметам,
2)только по философии и естествознанию,
3)только по логике и естествознанию,
4)только по философии,
5)только по естествознанию,
6)только по логике,
7)не выбрали ни одну из этих дисциплин.
Каждое высказывание из условия записать в виде логического выражения, строго подписывая друг под другом элементы. Решать систему будем с тех уравнений, где меньше всего неизвестных, попарно вычитая уравнения. При решении стремимся убрать как можно больше неизвестных.
1) Возможные варианты перебираем с учетом
а) + + + + + + + = 81
б) + 0 + 0 + + + 0 + + 0 = 43
в) 0 + + 0 + + 0 + + + 0 = 32
г) 0 + 0 + + 0 + + + + 0 = 41
д) 0 + 0 + 0 + + 0 + 0 + + 0 = 11
е) 0 + 0 + 0 + 0 + + 0 + + 0 = 21
ж) 0 + 0 + 0 + 0 + 0 + + + 0 = 16
з) 0 + 0 + 0 + + 0 + 0 + 0 + 0 = 4
2) Четко видно, что = 4. Подписываем под чертой вычисленные значения и убираем использованные уравнения. Ниже приведен подробный ход решения.
а) + + + + + + + = 81
б) + 0 + 0 + + + 0 + + 0 = 43
в) 0 + + 0 + + 0 + + + 0 = 32
г) 0 + 0 + + 0 + + + + 0 = 41
д) 0 + 0 + 0 + + 0 + 0 + + 0 = 11
е) 0 + 0 + 0 + 0 + + 0 + + 0 = 21
ж) 0 + 0 + 0 + 0 + 0 + + + 0 = 16
и) 4
а) + + + + + + + = 81
б) + 0 + 0 + + + 0 + + 0 = 43
в) 0 + + 0 + + 0 + + + 0 = 32
г) 0 + 0 + + 0 + + + + 0 = 41
е) 0 + 0 + 0 + 0 + + 0 + + 0 = 21
ж) 0 + 0 + 0 + 0 + 0 + + + 0 = 16
и) 4 7
а) + + + + + + + = 81
б) + 0 + 0 + + + 0 + + 0 = 43
в) 0 + + 0 + + 0 + + + 0 = 32
г) 0 + 0 + + 0 + + + + 0 = 41
и) 4 14 9 7
а) + + + + + + + = 81
и) 18 12 11 4 14 9 7
0) + + ++ + + + = 81
и) 18 12 11 4 14 9 7 6
Ответ:1) по всем трём предметам, , 7
2)только по философии и естествознанию, , 14
3)только по логике и естествознанию, , 9
4)только по философии, , 18
5)только по естествознанию, , 11
6)только по логике, , 12
7)не выбрали ни одну из этих дисциплин, , 6
Приложение 4
Отчёт о проделанной работе перед коллегами
Использование метода кругов Эйлера (диаграмм Эйлера–Венна) при решении задач в курсе информатики и ИКТ
1. Введение
В курсе Информатики и ИКТ основной и старшей школы рассматриваются такие важные темы как “Основы логики” и “Поиск информации в Интернет”. При решении определенного типа задач удобно использовать круги Эйлера (диаграммы Эйлера-Венна).
Математическая справка. Диаграммы Эйлера-Венна используются прежде всего в теории множеств как схематичное изображение всех возможных пересечений нескольких множеств. В общем случае они изображают все 2n комбинаций n свойств. Например, при n=3 диаграмма Эйлера-Венна обычно изображается в виде трех кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.
2. Представление логических связок в поисковых запросах
При изучении темы “Поиск информации в Интернет” рассматриваются примеры поисковых запросов с использованием логических связок, аналогичным по смыслу союзам “и”, “или” русского языка. Смысл логических связок становится более понятным, если проиллюстрировать их с помощью графической схемы – кругов Эйлера (диаграмм Эйлера-Венна).
| Логическая связка | Пример запроса | Пояснение | Круги Эйлера |
| & – “И” | Париж & университет | Будут отобраны все страницы, где упоминаются оба слова: Париж и университет | Рис.1 |
| | – “ИЛИ” | Париж | университет | Будут отобраны все страницы, где упоминаются слова Париж и/или университет | Рис.2 |
3. Связь логических операций с теорией множеств
С помощью диаграмм Эйлера-Венна можно наглядно представить связь логических операций с теорией множеств. Для демонстрации можно воспользоваться слайдами в Приложение 1.
Логические операции задаются своими таблицами истинности. В Приложении 2 подробно рассматриваются графические иллюстрации логических операций вместе с их таблицами истинности. Поясним принцип построения диаграммы в общем случае. На диаграмме – область круга с именем А отображает истинность высказывания А (в теории множеств круг А – обозначение всех элементов, входящих в данное множество). Соответственно, область вне круга отображает значение “ложь” соответствующего высказывания. Что бы понять какая область диаграммы будет отображением логической операции нужно заштриховать только те области, в которых значения логической операции на наборах A и B равны “истина”.
Например, значение импликации равно “истина” в трех случаях (00, 01 и 11). Заштрихуем последовательно: 1) область вне двух пересекающихся кругов, которая соответствует значениям А=0, В=0; 2) область, относящуюся только к кругу В (полумесяц), которая соответствует значениям А=0, В=1; 3) область, относящуюся и к кругу А и к кругу В (пересечение) – соответствует значениям А=1, В=1. Объединение этих трех областей и будет графическим представлением логической операции импликации.
4. Использование кругов Эйлера при доказательстве логических равенств (законов)
Для того, чтобы доказать логические равенства можно применить метод диаграмм Эйлера-Венна. Докажем следующее равенство ¬(АvВ) = ¬А&¬В (закон де Моргана).
Для наглядного представления левой части равенства выполним последовательно: заштрихуем оба круга (применим дизъюнкцию) серым цветом, затем для отображения инверсии заштрихуем область за пределами кругов черным цветом:
Рис.3 Рис.4
Для визуального представления правой части равенства выполним последовательно: заштрихуем область для отображения инверсии (¬А) серым цветом и аналогично область ¬В также серым цветом; затем для отображения конъюнкции нужно взять пересечение этих серых областей (результат наложения представлен черным цветом):
Рис.5 Рис.6 Рис.7
Видим, что области для отображения левой и правой части равны. Что и требовалось доказать.
5. Задачи в формате ГИА и ЕГЭ по теме: “Поиск информации в Интернет”
Задача №18 из демо-версии ГИА 2013.
В таблице приведены запросы к поисковому серверу. Для каждого запроса указан его код – соответствующая буква от А до Г. Расположите коды запросов слева направо в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.
| Код | Запрос |
| А | (Муха & Денежка) | Самовар |
| Б | Муха & Денежка & Базар & Самовар |
| В | Муха | Денежка | Самовар |
| Г | Муха & Денежка & Самовар |
Решение:
Для каждого запроса построим диаграмму Эйлера-Венна:
| Запрос А Рис.8 |
Запрос Б Рис. 9 |
Запрос В Рис. 10 |
Запрос Г Рис. 11 |
Ответ: ВАГБ.
Задача В12 из демо-версии ЕГЭ-2013.
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысяч) |
| Фрегат | Эсминец | 3400 |
| Фрегат & Эсминец | 900 |
| Фрегат | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Эсминец?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
Пусть
Ф – количество страниц (в тысячах) по запросу Фрегат;
Э – количество страниц (в тысячах) по запросу Эсминец;
Х – количество страниц (в тысячах) по запросу, в котором упоминается Фрегат и не упоминается Эсминец;
У – количество страниц (в тысячах) по запросу, в котором упоминается Эсминец и не упоминается Фрегат.
Построим диаграммы Эйлера-Венна для каждого запроса:
| Запрос | Диаграмма Эйлера-Венна | Количество страниц |
| Фрегат | Эсминец | Рис.12 | 3400 |
| Фрегат & Эсминец | Рис.13 | 900 |
| Фрегат | Рис.14 | 2100 |
| Эсминец | Рис.15 | ? |
Согласно диаграммам имеем:
- Х+900+У = Ф+У = 2100+У = 3400. Отсюда находим У = 3400-2100 = 1300.
- Э = 900+У = 900+1300= 2200.
Ответ: 2200.
6. Решение логических содержательных задач методом диаграмм Эйлера-Венна
Задача 1.
В классе 36 человек. Ученики этого класса посещают математический, физический и химический кружки, причем математический кружок посещают 18 человек, физический – 14 человек, химический – 10. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек – и математический и физический, 5 и математический и химический, 3 – и физический и химический.
Сколько учеников класса не посещают никаких кружков?
Решение:
Для решения данной задачи очень удобным и наглядным является использование кругов Эйлера.
Самый большой круг – множество всех учеников класса. Внутри круга три пересекающихся множества: членов математического (М), физического (Ф), химического (Х) кружков.
Пусть МФХ – множество ребят, каждый из которых посещает все три кружка. МФ¬Х – множество ребят, каждый из которых посещает математический и физический кружки и не посещает химический. ¬М¬ФХ – множество ребят, каждый из которых посещает химический кружок и не посещает физический и математический кружки.
Аналогично введем множества: ¬МФХ, М¬ФХ, М¬Ф¬Х, ¬МФ¬Х, ¬М¬Ф¬Х.
Известно, что все три кружка посещают 2 человека, следовательно, в область МФХ впишем число 2. Т.к. 8 человек посещают и математический и физический кружки и среди них уже есть 2 человека, посещающих все три кружка, то в область МФ¬Х впишем 6 человек (8-2). Аналогично определим количество учащихся в остальных множествах:
| Круги Эйлера с названиями
непересекающихся множеств: Рис. 16 |
Круги Эйлера с количественной
информацией: Рис. 17 Например, количество человек, которые посещают физический кружок 2+6+1+5=14 |
Просуммируем количество человек по всем областям: 7+6+3+2+4+1+5=28. Следовательно, 28 человек из класса посещают кружки.
Значит, 36-28 = 8 учеников не посещают кружки.
Ответ: 8.
Задача 2.
После зимних каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников класса двое не были ни в кино. ни в театре, ни в цирке. В кино побывало 25 человек, в театре – 11, в цирке 17 человек; и в кино, и в театре – 6; и в кино и в цирке – 10; и в театре и в цирке – 4.
Сколько человек побывало и в кино, и в театре, и в цирке?
Решение:
Пусть х – количество ребят, которые побывали и в кино, и в театре, и в цирке.
Тогда можно построить следующую диаграмму и посчитать количество ребят в каждой области:
Рис.18. |
В кино и театре побывало 6 чел., значит,
только в кино и театре (6-х) чел. Аналогично, только в кино и цирке (10-х) чел. Только в театре и цирке (4-х) чел. В кино побывало 25 чел., значит, из них только в кино были 25 – (10-х) – (6-х) – х = (9+х). Аналогично, только в театре были (1+х) чел. Только в цирке были (3+х) чел. Не были в театре, кино и цирке – 2 чел. Значит, 36-2=34 чел. побывали на мероприятиях. С другой стороны можем просуммировать количество человек, которые были в театре, кино и цирке: (9+х)+(1+х)+(3+х)+(10-х)+(6-х)+(4-х)+х = 34 33+х = 34. Отсюда следует, что только один человек побывал на всех трех мероприятиях. |
Ответ: 1.
Таким образом, круги Эйлера (диаграммы Эйлера-Венна) находят практическое применение при решении задач в формате ЕГЭ и ГИА и при решении содержательных логических задач.
Литература
- В.Ю. Лыскова, Е.А. Ракитина. Логика в информатике. М.: Информатика и Образование, 2006. 155 с.
- Л.Л. Босова. Арифметические и логические основы ЭВМ. М.: Информатика и образование, 2000. 207 с.
- Л.Л. Босова, А.Ю. Босова. Учебник. Информатика и ИКТ для 8 класса: БИНОМ. Лаборатория знаний, 2012. 220 с.
- Л.Л. Босова, А.Ю. Босова. Учебник. Информатика и ИКТ для 9 класса: БИНОМ. Лаборатория знаний, 2012. 244 с.
- Сайт ФИПИ: http://www.fipi.ru/
Диаграмма Эйлера. Диаграммы Эйлера – геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Перв
Пользователи также искали:
круги эйлера 4 круга, круги эйлера числа, круги эйлера дискретная математика, круги эйлера для дошкольников, круги эйлера мать дочь бабушка внучка, круги эйлера примеры множества, круги эйлера реферат, сложные задачи на круги эйлера, эйлера, круги, диаграммы, диаграммой, диаграммах, диаграмму, диаграмме, сложные задачи на круги, логики, диаграмм, диаграммы эйлера, сложные, диаграмма, задачи, диаграмм эйлера, круги эйлера реферат, логика, диаграмма эйлера, круги эйлера круга, круги эйлера числа, логике, круги эйлера для дошкольников, diagram, эйлер, диаграмме эйлера, внучка, дочь, мать, математика, дискретная,
| Прикладная логика. Круги Эйлера примеры. 24.02.2014, 19:17. 0. 30292. Усложняйте развитие логического мышления с кругами Эйлера! Решение этих Теги: логика.. .. диаграмма венна с русского на все языки. Круги Эйлера хорошо известная графическая модель, используемая в логике для Так, согласно Б. Расселу, логика не может оперировать пустыми понятиями и терминами Диаграмма Кэрролла аналог круга Эйлера.. .. Диаграммы Эйлера Венна Логика и множества Киберфорум. Круги Эйлера геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.. .. Теория множеств Информатика Алгебра логики, теория. Решено: Диаграммы Эйлера Венна Логика и множества Ответ.. .. Глава 2 математиЧесКаЯ ЛОГиКа. Круги Эйлера: Отношения между понятиями: Пособие для преподавателей и студентов вузов по курсу Логика. Составитель А.И.Синюк.. .. Диаграмматический способ рассуждения и решения логических. Построение диаграмм Эйлера Венна. Алгебра логики Диаграммы Эйлера Венна Диаграмма Эйлера Венна наглядное средство для работы со. .. Диаграммы Эйлера Венна. Введение. В курсе Информатики и ИКТ основной и старшей школы рассматриваются такие важные темы как Основы логики и Поиск. .. КРУГИ ЭЙЛЕРА:. Как выбирать свойства для придумывания задачи на пересечение множеств? Как решить задачу с тремя кругами. Если не знать алгоритма, то на. .. Диаграмма Венна. Диаграмма Венна также используется название диаграмма Эйлера Они появились в сочинениях английского логика Джона Венна 1834 1923,. .. Диаграмма Эйлера с видео 2. Диаграмма Эйлера. Совершенно та же. Только лучше. Используется в математике, логике, менеджменте и других прикладных. | Использование метода кругов Эйлера диаграмм Эйлера–Венна. Диаграммы Венна по аналогии с кругами Эйлера – это схематическое. ибо на очереди основы математической логики, а не философия Спасибо. .. ДИАГРАММЫ ВЕННА. получил название алгебры логики, или алгебры высказываний. Ещё его На диаграмме Эйлера–Венна дополнение множества A это все точки за. .. Диаграмма Эйлера это Что такое Диаграмма Эйлера?. диаграмма Эйлера Венна обычно изображается в виде трёх кругов с в сочинениях английского логика Джона Венна, подробно изложившего их в. .. Множества. Операции над множествами. Отображение. Решено: Диаграмма Эйлера Венна Логика и множества Ответ.. .. Круги Эйлера. Изучаем множества с кругами Эйлера Венна. Выбор блоков по одному признаку. Круги Эйлера Венна с цифрами из набора Логика и цифры.. .. Круги Эйлера это Что такое Круги Эйлера?. ДИАГРАММЫ ВЕННА – графический способ задания и анализа Напр., в случае классической логики высказываний для формул, составленных из квадрат, круги Эйлера и оригинальные диаграммы Л.Кэрролла. Однако метод. .. Применение диаграмм Эйлера Венна при решении логических. в алгебре логики Venn diagram мат. Диаграмма Эйлера Пример диаграммы Эйлера. B живое существо, A человек, C неживая вещь.. .. Круги Эйлера примеры. Пример диаграммы Эйлера. B живое существо, A человек, C неживая вещь. достигли в сочинениях английского логика Джона Венна 1843 1923,. .. Диаграмма Эйлера Венна Логика и множества Киберфорум. Учитывая, что по сути своей логика не является математической наукой и поэтому имеет дело с понятиями, а не с терминами, часто диаграммы Эйлера. .. Круги Эйлера Венна с цифрами из набора Логика и цифры. Использование диаграмм Эйлера Венна для доказательства логических например, в теории множеств, теории вероятности, логике, статистике и. |
Обзор диаграмм Эйлера
| Диаграммы Эйлера
2004 Брайтон, Великобритания Сентябрь
22-23 |
Дом | Требуют документов | Представления | Регистрация | Программа | Местный аранжировки | Диаграммы Эйлера | Брайтон
Что такое диаграммы Эйлера?
Леонард Эйлер (произносится как «Масленка») был одним из величайших математиков всех времен. время.Многие утверждают, что он был величайшим. Одно из его малоизвестных изобретений это диаграммы Эйлера, которые он использовал для иллюстрации рассуждений.
Диаграмма Эйлера показана выше. Одна из распространенных интерпретаций Эйлера диаграммы – это то, что пересечение множеств. При такой интерпретации вышеупомянутое На диаграмме используются области для представления наборов A, B и C. Диаграмма также включает площади для перекрестков AB, AC и ABC. Никакая область не представляет набор (не A) C, поэтому множество C целиком содержится в A.
Визуально диаграммы Эйлера состоят из контуров , нарисованных как простые замкнутые кривые. Контуры разделяют плоскость на зоны . Зона можно определить по содержащим контурам. На диаграмме выше контуры помечены A, B и C, а зоны A, B, AB, AC и ABC присутствуют в диаграмма (а также внешняя зона, не содержащая контуров). Мы тут свяжите с каждой зоной метку, образованную контурами, внутри которых она находится содержится.
Диаграммы Венна, диаграммы Эйлера и Лейбница
Термины диаграмма Эйлера и диаграмма Венна часто путают. Диаграммы Венна можно рассматривать как частный случай диаграмм Эйлера, поскольку диаграммы Венна должны содержать все возможные зоны, тогда как диаграммы Эйлера могут содержать подмножество всех возможных зон. На диаграммах Венна заштрихованная зона представляет собой пустое множество, тогда как на диаграмме Эйлера соответствующая зона может отсутствовать на диаграмме. Этот означает, что по мере увеличения числа контуров диаграммы Эйлера обычно меньше визуально сложнее, чем эквивалентная диаграмма Венна, особенно если количество непустой пересечений мало.
Барон [Bar69] отмечает, что Лейбниц произвел аналогичные диаграмм до Эйлера, однако, многие из них не были опубликованы. Она также наблюдает еще более ранние диаграммы типа Эйлера Рамона Лулля в 13 веке.
Примечания к конкурирующим типам диаграмм можно найти по адресу: Wikipedia, Interactive Сборник математики и головоломок и Венн Фрэнка Рски Диаграмма обзора.
Области применения
В этом разделе показано несколько примеров использования диаграмм Эйлера.Часто, Диаграммы Эйлера дополняются дополнительными структурами, такими как точки, метки или графики, показывающие информацию о том, что содержится в различных зонах.
Одной из важных особенностей диаграмм Эйлера является их способность визуализировать сложные иерархии. На изображении выше показано, что некоторые животные относятся к более чем одной классификации, например «собака» и «кошка», которые являются домашними животными. и млекопитающие. Нелегко показать такие отношения с более обычными людьми. древовидная иерархическая визуализация классификаций.VENNFS [CES03] использует этот подход диаграммы Эйлера для визуализации организации файловой системы. Это позволяет файлам располагаться более чем в одном каталоге файловой системы компьютера. [VV04] предлагают использовать диаграммы Эйлера для визуализации больших баз данных с использованием нескольких классификации.
Оригинальное приложение диаграмм Эйлера, как способ схематического представления демонстрируя логику, широко используются в школах, где они являются большим подспорьем для теория обучающих множеств.Другие академические работы включают Hammer [Ham95], который представил здоровую и законченную логическую систему, основанную на диаграммах Эйлера. Более выразительных рассуждений можно добиться, дополнив диаграммы графиками. Шин [Shi94] разработал первую такую формальную систему. Это было расширено до Spider [HMTKG01] и диаграммы ограничений [GHK01] группой визуального моделирования Университета Брайтона и другими. Пример диаграммы ограничений показан выше. Эти расширенные диаграммы Эйлера можно рассматривать как гиперграфы, и как таковые должна быть возможность применить методы визуализации для улучшенного Эйлера диаграммы в более общем плане для приложений, использующих гиперграфы.
Построение диаграмм Эйлера
Большая часть недавних исследований посвящена встраиванию Эйлера диаграммы в плоскости из текстового описания зон, которые должны появиться в диаграмма. Эту работу делает более интересной наличие хорошего воспитания. условия. Хорошая форма ограничивает внешний вид диаграмм Эйлера, и поэтому в некоторой степени, чем лучше построена, тем лучше понимается диаграмма. Однако некоторые диаграммы Эйлера невозможно нарисовать при некоторой хорошей форме. условия.Общие условия оздоровления:
- Форма контуров может быть ограничена определенными формами, такими как круглая, овальная, прямоугольная или выпуклая.
- Тройные точки не могут быть разрешены, поэтому только два контура могут пересекаться в любой заданной точке.
- Допускаются только поперечные пересечения контуров, так что линии не могут касаться без пересечения.
- Параллельные контуры не могут быть разрешены, поэтому сегмент линии не может представлять границу 2 или более контуров.
- Отключенные зоны не могут быть разрешены, поэтому зоны не могут появляться более одного раза на диаграмме
- Контуры должны быть простыми кривыми, чтобы контуры не пересекались сами собой.
Ослабление этих ограничений позволяет рисовать все диаграммы Эйлера. Сам Эйлер рисовал только диаграммы с кружками, не нарушая ни одной из схем. условия благополучия.
Некоторые примеры хорошего самочувствия:
| 1.Эта диаграмма Венна 4 (Диаграмма Венна с 4 контуры), нарисованные с невыпуклыми контурами. Эту диаграмму можно нарисовать с помощью выпуклые формы. | |
| 2. На этой диаграмме представлены зоны A, B, C, AB, AC и BC (но не ABC) получил тройную точку. Эту диаграмму невозможно нарисовать без нарушение правил благополучия 2, 5 или 6. | |
| 3.Это пример непересечной диаграммы. представляющие зоны A и B. | |
| 4. Это диаграмма, представляющая зоны AB, AC. В для визуализации требуются общие сегменты кривой. | |
| 5. На этих диаграммах области одного цвета представляют та же зона. На диаграмме слева есть отключенные зоны. Диаграмма справа имеет ту же семантику, что и слева, но хорошо сформирован.Отключенные зоны особенно неприятны там, где предназначены предметы. группироваться по зонам. Если бы использовались диаграммы, подобные приведенным слева, тогда два элемента, которые должны были быть сгруппированы вместе, могли появиться в различные разделы диаграммы, даже если семантика диаграмма будет правильной. | |
| 6. Это диаграмма зон A и B, представленная непростые кривые. |
Первой работой по автоматическому построению диаграмм Эйлера выступили Флауэр и Howse [FH02], кто предложил и реализовал метод рисования подмножества диаграмм поддержание всех условий благополучия, кроме 1, внизу слева диаграмма, созданная этим методом. Дальнейшая работа Чоу и Руски [CR03], описал реализованный метод встраивания небольших диаграмм с ограничениями по форме контуров, включая фигуры, построенные из прямоугольников.Verroust и Виуд [VV04] предложили систему рисования всех диаграмм Эйлера до 8 контуров, расслабляющую правила оздоровления 1,2,3 и 4.
Схема диаграмм Эйлера
Это относится к рисованию диаграмм Эйлера с учетом их эстетичный вид. Методы генерации, описанные в предыдущем разделе часто создают сложные для понимания диаграммы Эйлера. Наше недавнее исследование [FRM03] взял диаграммы Эйлера, порожденные [FH02] и применил эстетические метрики к контурам, пытаясь сделать диаграммы более понятным, см. выше изображения до и после.Это было тогда расширен для рисования графиков в диаграммах Эйлера [MRF04].
Контакт
Если вы заметили ошибку или хотите что-то добавить на эту страницу, свяжитесь с Питером Роджерсом.
Ссылки
Стэнфорд
Энциклопедия философии имеет подробное резюме и сравнение диаграммы.
типы
Примеры
использование диаграмм Эйлера в логических рассуждениях
Статья в Википедии о Венне и Эйлере
диаграммы
Venn
Сравнение Эйлера
Диаграмма Венна
Обзор Фрэнка Руски
Список литературы
[Bar69] M.Э. Барон. Примечание о
Историческое развитие логических диаграмм. Математический вестник: Журнал
математической ассоциации. Том LIII, вып. 383 May 1969.
[CES03] Р. Де Кьяра, У Эрра и В. Скарано.
VENNFS: файловый менеджер диаграммы Венна. Proc. Визуализация информации IEEE
(IV03). С. 120-126. 2003.
[CR03] С. Чоу и Ф.
Руски. Построение пропорциональных площадей диаграмм Венна и Эйлера. Proc. GD2003. LNCS
2912. Springer Verlag.
[Eul61] L. Euler. Lettres a Une Princesse d’Allemagne, vol 2. 1761. Letters No.
102–108.
[FH02] J. Flower and J. Howse. Создание
Диаграммы Эйлера, Proc. Диаграммы 2002, Springer Verlag, 61-75.
[FRM03] Дж. Флауэр, П. Роджерс и П. Маттон. Показатели макета
для диаграмм Эйлера. Proc. Визуализация информации IEEE (IV03). С. 272-280.
2003.
[GHK01] Дж. Гил, Дж. Хоуз и С. Кент.
К формализации диаграмм ограничений, Труды человекоцентрических
Вычислительная техника (HCC 2001) Стреза, Италия, IEEE Computer Society Press, 72-79.2001.
[Ham95] E. M. Hammer. Логика и Визуализация
Информация, публикации CSLI. 1995.
[HMTKG01] Дж. Хоуз, Ф. Молина, Дж. Тейлор, С. Кент и Дж. Гил. Диаграммы паука: A
Диаграммная система рассуждений, Журнал визуальных языков и вычислений 12,
299-324. 2001
[MRF04] П. Маттон, П. Роджерс и Дж.
Цветок. Рисование графиков в диаграммах Эйлера. Proc. Диаграммы 2004. LNAI 2980.
Springer Verlag. 66-81.
[Shi94] S-J Shin.В
Логический статус диаграмм. ЧАШКА. 1994.
[Ven80] J.
Венн, О схематическом и механическом представлении предложений и
рассуждения, Лондонский, Эдинбургский и Дублинский философский журнал и журнал
наук, 9 (1880) 1-18.
[VV04] А. Верруст и
М.-Л. Viaud. Обеспечение возможности рисования расширенных диаграмм Эйлера до 8
Наборы. Proc. Диаграммы 2004. LNAI 2980. Springer Verlag. 128-141.
12.2: Использование диаграмм Венна-Эйлера для проверки на недействительность
В логике классов мы можем создавать диаграммы, которые помогают нам проверять аргументы на достоверность. Однако, прежде чем мы это сделаем, давайте улучшим наши навыки рассуждений с помощью дополнения классов, то есть набора всего, что не входит в класс. Если вы американец, то как нас зовут неамериканцы? Это «иностранец». Чем больше путешествуют американцы, тем чаще они встречаются с неамериканцами.
Предполагая, что никто не может быть одновременно евреем и христианином, было бы верно сказать, что все евреи не христиане, и верно сказать, что некоторые неевреи не являются христианами, но было бы неверно утверждать, что все нехристиане. -Христиане – евреи, и ложно говорить, что все нехристиане неевреи.Ух! Поздравления и комплименты, если вы смогли понять всю сложность этих дополнений к занятиям. Если бы вы могли, вы можете правильно выполнить эту проверку концепции.
Упражнение \ (\ PageIndex {1} \)
Мартин (на фото выше) не белый мужчина, если Мартину
а. белый не мужчина.
г. небелого цвета кобель,
г. не белый, не мужчина.
г. любой из вышеперечисленных.
- Ответ
Ответ (d).Ответить на подобные вопросы было бы намного проще, если бы у нас был какой-то метод изображения или диаграммы, который бы показал нам, что происходит. Может быть, вы сможете изобрести такой Эйлер пытался сделать это еще в XVIII веке в Швейцарии.
Умение отрицать члены необходимо для построения диаграмм Венна-Эйлера. Этот метод построения диаграмм – полезный способ быстро оценить дедуктивную достоверность аргументов в логике класса. Он может подсказать вам правильную оценку, когда аргумент слишком сложен для анализа в вашей голове.Представляя этот метод, мы сначала представим диаграммы для классов, затем обобщим метод, чтобы его можно было использовать для отображения того, являются ли предложения о классах истинными или ложными, а затем снова обобщим метод, чтобы его можно было использовать, чтобы показать, являются ли предложения о классах истинными или ложными. аргументы, использующие эти предложения, дедуктивно верны.
Круг ниже представляет собой диаграмму Эйлера для класса яблок.
r
На этой двумерной диаграмме любая точка внутри круга представляет яблоко, а любая точка за пределами круга представляет собой не яблоко, например мусульманина или карандаш.Обычно для маркировки используется заглавная буква для начала имени региона (класса) и строчная буква для имени конкретного члена региона (класса). Маленькая буква «r» обозначает точку справа от круга, которая представляет конкретное не яблоко, скажем, Томаса Эдисона, американского изобретателя и основателя General Electric Corporation. В форме региона нет ничего важного. Эллипс или прямоугольник подойдут, если ясно, что находится в области, а что нет, то есть что входит в класс, а что нет.Размер круга тоже не важен. Мы также не обращаем внимания на перемещение диаграммы влево, вправо, вверх или вниз. Все эти изменения приведут к одной и той же диаграмме с точки зрения логики классов.
Ниже приводится более сложная диаграмма, которая представляет как класс яблок, так и класс фруктов. В реальном мире класс яблок полностью входит в более крупный класс фруктов. На диаграмме представлена картина этих отношений в реальном мире:
Приведенная выше диаграмма отражает истинность предложения «Все яблоки – плоды», но вы можете рисовать диаграммы, которые не представляют того, каков мир.
Любая метка для региона может находиться внутри или за ее пределами, при условии, что нет двусмысленности в том, какая метка соответствует какому региону. Иногда мы будем называть овальные области «кругами», поскольку не обращаем внимания на разницу между кругом и эллипсом.
Вот диаграмма Эйлера, в которой верны утверждения вида «Нет А есть Б»:
Что важно в этой диаграмме, так это то, что две окружности не пересекаются (перекрываются). Круги также не должны касаться друг друга, потому что это затруднит определение того, есть ли у двух классов общий член.
Вот диаграмма Венна, показывающая ту же информацию, но менее интуитивно:
На диаграмме Венна все круги должны взаимно перекрываться. Для диаграмм Эйлера этого не требуется. Рассмотрим точки x, y и z на следующей диаграмме. Классы A и B пересекаются, то есть у них есть общие члены. Один из этих участников – y.
Пункт x не входит ни в класс A, ни в класс B. Он входит в дополнение к каждому из них. Точка y находится как в A, так и в B.Точка z находится в B, но не в A. Просматривая диаграмму, вы можете видеть, что некоторые члены B находятся в A, а некоторые нет. Однако вы не можете сказать, имеет ли A больше членов, чем B. Если область A больше, чем B на диаграмме, вы не можете сказать, имеет ли A больше членов, чем B. есть вообще какие-либо участники. Однако на всех диаграммах с этого момента мы будем предполагать, что мы начинаем с классов, которые не пусты.
Вот диаграмма, представляющая реальные отношения между яблоками, фруктами, апельсинами, яблоками в Париже, яблоками в ресторанах в Париже и фруктами, принадлежащими нашему другу Хуану:
Для ясности, мы всегда будем использовать заглавные буквы или прописные слова для классов вещей.Если мы хотим добавить информацию о том, что какой-то конкретный объект является членом одного из классов, мы будем использовать строчную букву для представления члена. На предыдущей диаграмме строчная буква a представляет одно яблоко в моем холодильнике. Вы можете видеть, что буква а находится за пределами круга P; это показывает, что яблоко в моем холодильнике не в Париже. Обратите внимание, что сам Хуан не входит ни в один из классов на приведенной выше диаграмме; информация о Хуане заложена в определение Дж.Изучив диаграмму, вы можете сказать, что Хуану не принадлежат парижские яблоки (потому что J и P не пересекаются), но он владеет яблоками (потому что J пересекает A), владеет апельсинами (потому что J пересекает O) и имеет владеть каким-то другим неуказанным фруктом (потому что J находится в F, но не все J в A или O).
Пусть A = граждане США, проживающие в Нью-Йорке, B = горожане, C = американцы. Вот диаграмма Эйлера, отображающая их отношения в реальном мире.
Вот как отобразить те же отношения с диаграммой Венна:
На диаграммах Венна заштрихованные области представляют собой пустое множество; они ничего не содержат.При применении техники Венна к трем множествам, три окружности должны пересекаться друг с другом, в отличие от диаграмм Эйлера.
Как бы вы нарисовали диаграмму, на которой утверждение, что некоторые яблоки из Канады, а некоторые нет, верно? Это поможет:
C = класс вещей из Канады
А = сорт яблок
Шаблон предложения «Все А не Б» верен на следующей диаграмме:
Обратите внимание, что это та же диаграмма, которую вы нарисовали для «Нет А есть Б.«Логически эквивалентные предложения имеют одинаковые виды диаграмм. Это ключевая идея классовой логики.
Приведенная выше диаграмма представляла бы ложное предложение «Техасцы не американцы», если бы использовался следующий словарь:
A = техасцы
B = американцы
Хотя это предложение неверно в реальном мире, диаграмма показывает, каким был бы мир, если бы предложение было истинным. То же самое можно сказать и о том, что диаграмма – это картина того, что истинно в определенном «возможном мире», который не является реальным миром.
Упражнение \ (\ PageIndex {1} \)
Сделайте утверждение «Все техасцы не американцы» верным на диаграмме, используя приведенный выше словарь для A и B.
- Ответ
Обратите внимание, что на этой диаграмме каждый техасец A находится за пределами Америки B и, следовательно, не является американцем. Итак, этот возможный мир – не реальный мир.
Пусть A будет классом яблок. На двух диаграммах ниже предложение «Все яблоки – бананы» верно (даже если это предложение неверно в реальном мире):
Но обратите внимание на разницу в двух диаграммах.В том, что слева, несколько бананов не могут быть яблоками. На диаграмме справа это не так. На второй диаграмме класс яблок и класс бананов – это один и тот же класс. Диаграмма реальных отношений между яблоками и бананами будет выглядеть так:
Упражнение \ (\ PageIndex {1} \)
Нарисуйте диаграмму для яблок и фруктов, в которой следующее предложение на диаграмме неверно: «Все яблоки – плоды». Предложение верно в реальном мире, но его не будет в возможном мире, представленном на вашей диаграмме.
- Ответ
Есть несколько типов диаграмм, которые будут работать.
С таким предложением, как «Все яблоки – плоды», аналитик может рассматривать его в логике классов или в логике предложений. В логике классов это логически эквивалентно «Все вещи в классе яблок являются также вещами в классе фруктов». Это устанавливает отношения между двумя классами. В сентенциальной логике это предложение логически эквивалентно «Если это яблоко, то это фрукт.”Это устанавливает условную связь между двумя вложенными предложениями.
Теперь мы можем обобщить метод диаграмм до метода оценки дедуктивной достоверности аргументов при условии, что предложения, составляющие аргумент, описывают, как классы объектов связаны друг с другом. Диаграмма Венна-Эйлера метод оценки аргументов работает только для дедуктивных аргументов в логике классов. Он показывает, что аргумент действителен, если нет диаграммы контрпримера к аргументу. По определению, контрпример к аргументу – это возможная ситуация или интерпретация аргумента, показывающая, как у него могут быть истинные посылки и ложное заключение.
Более конкретно, вот , как применить метод проверки действительности в логике класса:
Переведите посылки и заключение аргумента в соответствующие предложения классовой логики. Найдите контрпример. То есть попытайтесь изобразить эти предложения в логике классов так, чтобы посылки оказались верными на диаграмме, а вывод на диаграмме оказался ложным. Если есть такая диаграмма, то эта диаграмма контрпримера показывает, что аргумент дедуктивно неверен.Однако, если все возможные диаграммы не дают контрпримера, аргумент объявляется дедуктивно действительным.
Этот метод никогда не даст неправильного ответа, если вы действительно правильно изучили все возможные схемы. Аргумент действителен, если контрпримера не существует, а не только в том случае, если вы не можете его найти. Может быть, вы не можете его найти, потому что не присмотрелись. Таким образом, применение метода диаграмм Венна-Эйлера рискованно, поскольку его ответ зависит от того, правильно ли вы говорите, что смотрели, и уверены, что контрпример не существует.
Чтобы увидеть эту технику в действии, давайте опробуем ее на следующем шаблоне аргумента:
Нет A – B.
Нет C – B.
Итак, нет A – C.
Вот диаграмма, которая подтверждает все предпосылки:
Ни один из кругов не пересекается и не содержится внутри другого. На этой диаграмме вывод верный. Можем ли мы сделать вывод, что шаблон аргумента действителен? Нет, не из этой информации. Вместо этого нам следовало бы поискать, чтобы убедиться, что нет диаграммы, которая делает предположения истинными, а вывод ложным.На самом деле есть такая диаграмма:
Здесь вывод неверен, когда посылки верны, что является явным признаком недействительности. Поэтому метод диаграммы объявляет шаблон аргумента недопустимым.
Упражнение \ (\ PageIndex {1} \)
Используйте метод диаграммы, чтобы показать действительность этого шаблона аргумента:
Все A – B.
Все B – C.
Итак, все A – C.
- Ответ
Вот способ нарисовать схему, на которой оба предположения верны
Могут быть и другие схемы помещений: разрешить окружность A равной окружности B, или для B равной C.Однако на всех возможных схемах помещений вывод на схеме оказывается верным. Итак, контрпример не может быть приведен. Следовательно, метод Венна-Эйлера объявляет этот шаблон аргумента действительным.
Упражнение \ (\ PageIndex {1} \)
Используйте технику диаграмм, чтобы оценить достоверность или несостоятельность этого аргумента. Некоторые интерпретируйте как «хотя бы один, а может быть, и все».
Некоторые кошки относятся к кошачьим.
Некоторые животные относятся к кошачьим.
Итак, некоторые животные – кошки.
- Ответ
Аргумент недействителен; следующая диаграмма служит контрпримером:
Некоторые C являются F.
Некоторые A являются F.
Некоторые A являются C
Пытаясь найти логическую форму аргумента, не всегда можно сказать, следует ли искать его форму в логике класса или в логике предложений. Поэкспериментируйте, чтобы увидеть, что сработает.Некоторые аргументы имеют логические формы, которые не могут быть адекватно выражены в любом случае, и тогда для аргументации необходимо задействовать более мощные логики, такие как логика предикатов.
Кроме того, некоторые аргументы являются дедуктивно действительными, хотя их достоверность не зависит от логической формы с использованием какой-либо формальной логики. Вот пример:
Джон – холостяк.
Значит, он не женат.
Действительность обусловлена не только формой, но и содержанием – в частности, тем фактом, что определение холостяка подразумевает, что все холостяки не состоят в браке.Мы могли бы заставить этот аргумент быть действительным из-за его логической формы в логике класса, если бы мы могли закодировать идею о том, что все холостяки не связаны с логикой класса, и мы можем. Просто добавьте предпосылку: все холостяки не женаты. Допустимые аргументы, для которых не требуется вставка определений, называются формально действительными. Все формально верные аргументы дедуктивно действительны, но обратное неверно. Однако в нашем курсе мы не будем обращать внимания на это тонкое различие. Если вы видите, что для того, чтобы аргумент был действительным, необходимо определение, вставьте его и не беспокойтесь о том, что это показывает, что ваш аргумент дедуктивно действителен, но не формально.
ДиаграммыВенна-Эйлера используются не только для проверки достоверности. Если два предложения могут иметь одну и ту же диаграмму, то они являются логически эквивалентными в логике классов. Диаграммы также можно использовать для проверки согласованности. Если есть диаграмма, на которой каждое предложение в наборе предложений оказывается истинным, тогда набор будет логически непротиворечивым .
Диаграммы Веннаи диаграммы Эйлера, объясненные на примерах
ДиаграммыВенна и диаграммы Эйлера выглядят очень похожими, поэтому понятно, что многих людей смущает понимание разницы.Хотя оба типа диаграмм основаны на теории множеств, есть некоторые тонкие различия, которые делают их уникальными. Надеюсь, эта статья развеет ваши сомнения относительно диаграмм Венна и диаграмм Эйлера, и я приведу несколько примеров, чтобы сделать ее более ясной.
Венн против Эйлера: определение
Как я упоминал ранее, оба набора диаграмм основаны на теории множеств. Диаграмма Венна показывает все возможные логические отношения между набором наборов. Но диаграмма Эйлера показывает только отношения, существующие в реальном мире.
Диаграммы Венна и
Диаграммы Эйлера ПримерыНачнем с очень простого примера. Давайте рассмотрим надмножество животных с млекопитающими и птицами как подмножества. Диаграмма Венна показывает пересечение двух множеств, хотя такой возможности не существует в реальном мире. Диаграмма Эйлера, с другой стороны, не показывает пересечения.
Диаграммы Венна показывают все возможные комбинации, даже если они не существуют в реальном сценарии.Теперь давайте рассмотрим более сложный пример с колодой карт.Опять же, важно помнить о различии между двумя типами диаграмм: все возможные комбинации против реальных комбинаций . Давайте возьмем карты в качестве расширенного набора, а черные карты, красные карты и ромбы – в качестве подмножества.
Как одни и те же данные представлены по-разному с использованием диаграмм Венна и диаграмм ЭйлераКак показано в приведенном выше примере, диаграммы Венна показывают четыре пересечения, для которых нет данных, потому что они должны отображать все возможные комбинации.
Существуют различные методы преобразования диаграмм Венна в диаграммы Эйлера , и наоборот.Ознакомьтесь с этой замечательной вики-статьей о диаграммах Эйлера, в которой объясняются некоторые методы, которые вы можете использовать для преобразования диаграмм Венна в диаграммы Эйлера. Я надеюсь, что приведенные выше примеры помогли вам развеять ваши сомнения относительно диаграмм Венна и диаграмм Эйлера. Если у вас есть какие-либо вопросы, не стесняйтесь задавать их в разделе комментариев.
Рисуете ли вы диаграммы Венна или диаграммы Эйлера, Creately предоставит вам все необходимые инструменты. Вы можете быстро начать работу, используя шаблоны диаграмм Венна, доступные нашим пользователям, или начать с нуля в области рисования.Если вы хотите добавить значки и изображения на диаграмму Венна, это можно легко сделать с помощью встроенного поиска изображений Google, доступного на левой боковой панели. Благодаря такому количеству супер крутых функций вы не ошибетесь с Creately.
Диаграммы Венна и Эйлера | Давайте поговорим о науке
Диаграммы Венна
Иногда мы используем картинки для рисования наборов. Один тип изображения называется диаграммой Венна . Диаграммы Венна помогают визуально показать отношения между наборами.Обычно диаграммы Венна имеют два перекрывающихся круга. Но вы можете нарисовать диаграммы Венна с тремя или более перекрывающимися замкнутыми кривыми. Диаграммы Венна не всегда показывают, что конкретно входит в набор. Например, на картинке ниже показаны наборы K и L:
. Диаграмма Венна множеств K и L (© 2021 Let’s Talk Science).Каждый кружок представляет все элементы набора. Имея только изображение, вы можете задать вопросы о подмножествах , пересечении и соединении .
Является ли K ⊆ L (находится ли K внутри L)? НЕТ.
Является ли L ⊆ K (находится ли L внутри K)? НЕТ.
Вопросы 1: Что такое K ∩ L? (Какая область внутри обоих наборов?) Нарисуйте изображение, а затем закрасьте его. Ответы даны внизу страницы.
Диаграмма Венна множеств K и L (© 2021 Let’s Talk Science).Вопросы 2: Что такое K ∪ L? (Какова общая площадь набора K, набора L или обоих?) Закрасьте картинку, чтобы показать свой ответ.
Диаграмма Венна множеств K и L (© 2021 Let’s Talk Science).Попробуйте это с наборами:
E = {1, 3, 8, 9, 14, 17}
F = {0, 14, 3, 5, 10, 20}
Вопросы 3: Используйте диаграмму Венна, чтобы показать наборы E и F .
Что такое E ∩ F ?
Что такое E ∪ F ?
Кем был Венн?
Джон Венн (1834-1923) был английским логиком .Логик – это тот, кто изучает способы логического мышления. Его помнят за изобретение диаграммы, названной в его честь – диаграммы Венна.
Венн был воспитан его отцом, который был преподобным англиканской церкви. Его мать умерла, когда он был очень молод. Он поступил в Кембриджский университет, где на втором курсе получил стипендию по математике. Несмотря на то, что в школе он действительно хорошо разбирался в математике, после ее окончания он стал преподобным, как его отец и дед.
Венн никогда не переставал думать о математике. После нескольких лет религиозной работы он вернулся в Кембридж, где преподавал логику и вероятность. В 1867 году он женился, и у него родился сын – Джон. Его сын Джон в конце концов стал президентом Королевского колледжа Кембриджского университета, где вместе со своим отцом выполнял важные исследовательские проекты.
Диаграммы Венна были впервые опубликованы в 1880 году в статье под названием «О схематическом и механическом представлении предложений и рассуждений.”в” Философском журнале и научном журнале “.
Диаграммы Эйлера
Другой способ показать множества и их отношения – использовать диаграмму Эйлера . Эти диаграммы похожи на диаграммы Венна, но имеют тенденцию быть более сложными. Они часто показывают подмножества, а также пересечение и объединение. В диаграмме Эйлера размер и форма кругов / овалов не важны. Важно то, как они перекрываются или не перекрываются.
Пример диаграммы Эйлера для множеств M, N, P, Q и R (© 2021 Let’s Talk Science).Вопрос 4:
Является ли какой-либо набор подмножеством (⊆) другого?
Если да, то какой?
Вопрос 5:
A) Цвет в N ∪ Q
Пример диаграммы Эйлера для множеств M, N, P, Q и R (© 2021 Let’s Talk Science).B) Цвет M ∩ R
Пример диаграммы Эйлера для множеств M, N, P, Q и R (© 2021 Let’s Talk Science).C) Цвет в P ∩ N ∩ Q
Пример диаграммы Эйлера для множеств M, N, P, Q и R (© 2021 Let’s Talk Science).D) Тень в M ∪ P ∪ R
Пример диаграммы Эйлера для множеств M, N, P, Q и R (© 2021 Let’s Talk Science).
Возможен ли N ∩ R ? Нет! N и R не перекрываются. В теории множеств мы называем это пустым набором или пустым набором , потому что он ничего не содержит. Символ для нулевого набора – ∅ . Вот еще один пример нулевого набора:
G – количество жирафов в классе миссис Браун.B = {} = ∅
Приложения диаграмм Венна и Эйлера
Диаграммы Венна и Эйлера полезны в самых разных контекстах. Оба типа диаграмм помогают нам визуализировать концепции и отношения. Это может помочь нам легче понять сложную информацию. Эти диаграммы используют одну и ту же структуру для представления множества различных типов контента.
Например, диаграммы Венна часто используются для решения математических задач. Представление вопроса в виде диаграммы Венна часто упрощает понимание и решение.Компании часто используют диаграммы Венна для сравнения продуктов, анализа конкурентов и принятия решений. Диаграммы Венна представляют собой множество других видов практической информации, от химии до географии. Их можно использовать даже для юмора или для представления сложных философских вопросов. Диаграммы Венна и Эйлера – простой способ представить все виды информации.
ОТВЕТОВВопрос 1:
Что такое K ∩ L? (Какая область внутри обоих наборов?) Закрасьте картинку, чтобы показать свой ответ.
Пересечение множеств K и L (© 2021 Let’s Talk Science).Вопрос 2:
Что такое K ∪ L? (Какова общая площадь набора K, набора L или обоих?) Закрасьте картинку, чтобы показать свой ответ.
Объединение множеств K и L (© 2021 Let’s Talk Science).Вопрос 3:
Используйте диаграмму Венна, чтобы показать наборы E и F .
Пересечение и объединение множеств E и F (© 2021 Let’s Talk Science).E ∩ F = {3, 14}
E ∪ F = {0, 1, 3, 5, 8, 9, 10, 14, 17, 20}
Вопрос 4:
Является ли какой-либо набор подмножеством (⊆) другого?
Если да, то какой?
Да, R является подмножеством P ( R ⊆ P )
Вопрос 5:
A) Цвет в N ∪ Q
N ∪ Q (© 2021 Давайте поговорим о науке).B) Цвет M ∩ R
M ∩ R (© 2021 Давайте поговорим о науке).C) Цвет в P ∩ N ∩ Q
P ∩ N ∩ Q (© 2021 Let’s Talk Science).D) Тень в M ∪ P ∪ R
M ∪ P ∪ R (© 2021 Let’s Talk Science).Математика для гуманитарных наук Corequisite
Результаты обучения
- Различение индуктивного аргумента и дедуктивного аргумента
- Вычислить дедуктивные аргументы
- Анализируйте аргументы с помощью диаграмм Венна или таблиц истинности
- Использовать логический вывод, чтобы сделать вывод о том, верно ли утверждение
Логический аргумент – это утверждение, что набор предпосылок поддерживает заключение.Есть два основных типа аргументов: индуктивные и дедуктивные.
стратегия успеха
Практикуйтесь в примерах и ПОПРОБУЙТЕ ИТ-проблемы из этого раздела как можно больше. Идеи логики сильны и помогают сделать нас сильнее в этом мире.
Как всегда, практика и повторение помогут вам освоиться. Выполнение как можно большего количества различных задач даст вам более широкий доступ к логическим ситуациям и поможет вам получить более глубокое понимание в целом.
Типы аргументов
Индуктивный аргумент использует набор конкретных примеров в качестве предпосылок и использует их, чтобы предложить общий вывод.
Дедуктивный аргумент использует набор общих утверждений в качестве предпосылок и использует их, чтобы предложить конкретную ситуацию в качестве заключения.
Пример
Аргумент «когда я ходил в магазин на прошлой неделе, я забыл свой кошелек, а когда я пошел сегодня, я забыл свой кошелек.Я всегда забываю свою сумочку, когда иду в магазин », – это индуктивный аргумент.
Помещения:
Я забыл свой кошелек на прошлой неделе
Я забыл свой кошелек сегодня
Вывод:
Я всегда забываю свой кошелек
Обратите внимание, что посылки – это конкретные ситуации, а заключение – это общее утверждение. В данном случае это довольно слабый аргумент, поскольку он основан всего на двух примерах.
Пример
Аргумент «каждый день в течение последнего года над моим домом в 14:00 пролетает самолет.Самолет будет летать над моим домом каждый день в 2 часа дня », – это более сильный индуктивный аргумент, поскольку он основан на большем количестве доказательств.
Вычисление индуктивных аргументов
Индуктивный аргумент никогда не может доказать истинность вывода, но он может предоставить либо слабые, либо убедительные доказательства того, что он может быть правдой.
Многие научные теории, такие как теория большого взрыва, никогда не могут быть доказаны. Напротив, это индуктивные аргументы, подкрепленные множеством свидетельств.Обычно в науке идея считается гипотезой до тех пор, пока она не будет хорошо проверена, после чего она становится теорией. Общеизвестные научные теории, такие как теория гравитации Ньютона, выдержали годы испытаний и доказательств, хотя иногда их нужно корректировать на основе новых данных. Что касается гравитации, это произошло, когда Эйнштейн предложил общую теорию относительности.
Дедуктивный аргумент является более достоверным или нет, что упрощает их оценку.
Оценка дедуктивных аргументов
Дедуктивный аргумент считается действительным, если все посылки верны, и вывод логически следует из этих посылок. Другими словами, посылки верны, и вывод обязательно следует из этих посылок.
Пример
Аргумент «Все кошки – млекопитающие, а тигр – это кошка, значит, тигр – это млекопитающее» – это действительный дедуктивный аргумент.
Помещения:
Все кошки – млекопитающие
Тигр – это кошка
Вывод:
Тигр – млекопитающее
Оба предположения верны.Чтобы увидеть, что посылки должны логически вести к заключению, можно использовать диаграмму Венна. Исходя из первой предпосылки, мы можем заключить, что набор кошек является подмножеством множества млекопитающих. Из второй посылки нам говорят, что тигр находится внутри множества кошек. Исходя из этого, мы можем видеть на диаграмме Венна, что тигр также находится внутри группы млекопитающих, так что вывод верен.
Анализ аргументов с помощью диаграмм Венна / Эйлера
Для анализа аргумента с помощью диаграммы Венна / Эйлера
- Постройте диаграмму Венна / Эйлера, основанную на предпосылках аргумента
- Если помещения недостаточно, чтобы определить, что определяет расположение элемента, укажите это.
- Аргумент действителен, если ясно, что заключение должно быть верным
Пример
| Помещение: | Все пожарные знают КПП |
| Помещение: | Джилл знает CPR |
| Заключение: | Джилл – пожарный |
Исходя из первой предпосылки, мы знаем, что все пожарные находятся внутри группы тех, кто знает СЛР. Из второй посылки мы знаем, что Джилл является членом этого большего набора, но у нас недостаточно информации, чтобы знать, является ли она также членом меньшего подмножества, то есть пожарных.
Поскольку вывод не обязательно следует из предпосылок, это неверный аргумент, независимо от того, действительно ли Джилл является пожарным.
Важно отметить, что то, действительно ли Джилл – пожарный, не имеет значения для оценки обоснованности аргумента; нас интересует только то, достаточно ли предпосылок, чтобы доказать вывод.
В дополнение к этим предпосылкам категориального стиля в форме «все ___», «некоторые ____» и «нет ____» также часто можно увидеть посылки, являющиеся имплицитными.
Пример
| Помещение: | Если вы живете в Сиэтле, вы живете в Вашингтоне. |
| Помещение: | Маркус не живет в Сиэтле. |
| Заключение: | Маркус не живет в Вашингтоне. |
Из первой предпосылки мы знаем, что совокупность людей, живущих в Сиэтле, находится внутри совокупности тех, кто живет в Вашингтоне. Из второй посылки мы знаем, что Маркус не находится в множестве Сиэтла, но у нас недостаточно информации, чтобы знать, живет ли Маркус в Вашингтоне или нет.Это недопустимый аргумент.
Пример
Рассмотрим аргумент «Вы женатый мужчина, значит, у вас должна быть жена».
Показать решениеЭто неверный аргумент, поскольку есть, по крайней мере, в некоторых частях мира, мужчины, состоящие в браке с другими мужчинами, поэтому посылка не является недостаточной, чтобы сделать вывод.
Некоторые аргументы лучше анализировать с помощью таблиц истинности.
Пример
Рассмотрим аргумент:
| Помещение: | Если вы купили хлеб, значит вы пошли в магазин |
| Помещение: | Вы купили хлеб |
| Заключение: | Вы зашли в магазин |
Хотя мы надеемся, что этот пример является довольно очевидным аргументом, мы можем проанализировать его с помощью таблицы истинности, представив каждую из посылок символически.Затем мы можем взглянуть на импликацию, что все предпосылки вместе подразумевают заключение. Если таблица истинности является тавтологией (всегда верно), то аргумент действителен.
Мы получим, что B означает «вы купили хлеб», а S – «вы пошли в магазин». Тогда аргумент принимает вид:
| Помещение: | [латекс] B {\ rightarrow} S [/ латекс] |
| Помещение: | [латекс] B [/ латекс] |
| Заключение: | [латекс] S [/ латекс] |
Чтобы проверить достоверность, мы смотрим, подразумевает ли комбинация обоих посылов заключение; правда ли, что [латекс] \ left [\ left (B {\ rightarrow} S \ right) {\ wedge} B \ right] {\ rightarrow} S [/ latex]?
| [латекс] B [/ латекс] | [латекс] S [/ латекс] | [латекс] B {\ rightarrow} S [/ латекс] | [латекс] \ влево (B {\ rightarrow} S \ right) {\ wedge} B [/ латекс] | [латекс] \ left [\ left (B {\ rightarrow} S \ right) {\ wedge} B \ right] {\ rightarrow} S [/ latex] |
| т | т | т | т | т |
| т | F | F | F | т |
| ф | т | т | F | т |
| ф | F | т | F | т |
Поскольку таблица истинности для [латекса] \ left [\ left (B {\ rightarrow} S \ right) {\ wedge} B \ right] {\ rightarrow} S [/ latex] всегда истинна, это веский аргумент.
Анализ аргументов с использованием таблиц истинности
Чтобы проанализировать аргумент с помощью таблицы истинности:
- Символически обозначить каждое из помещений
- Создайте условное утверждение, объединив все посылки с антецедентом и образуя его, и используя заключение как следствие.
- Создайте таблицу истинности для этого утверждения. Если это всегда правда, то аргумент действителен.
Пример
| Помещение: | Если я пойду в торговый центр, то куплю новые джинсы. |
| Помещение: | Если я куплю новые джинсы, я куплю к ним рубашку. |
| Заключение: | Если я приду в торговый центр, куплю рубашку. |
Пусть M = я иду в торговый центр, J = я покупаю джинсы и S = я покупаю рубашку.
Предпосылки и заключение можно сформулировать как:
| Помещение: | [латекс] M {\ rightarrow} J [/ латекс] |
| Помещение: | [латекс] J {\ rightarrow} S [/ латекс] |
| Заключение: | [латекс] M {\ rightarrow} S [/ латекс] |
Мы можем построить таблицу истинности для [латекса] \ left [\ left (M {\ rightarrow} J \ right) \ wedge \ left (J {\ rightarrow} S \ right) \ right] {\ rightarrow} \ left (M {\ rightarrow} S \ right) [/ латекс]
| [латекс] M [/ латекс] | [латекс] J [/ латекс] | [латекс] S [/ латекс] | [латекс] M {\ rightarrow} J [/ латекс] | [латекс] J {\ rightarrow} S [/ латекс] | [латекс] \ влево (M {\ rightarrow} J \ вправо) \ клин \ влево (J {\ rightarrow} S \ вправо) [/ латекс] | [латекс] M {\ rightarrow} S [/ латекс] | [латекс] \ left [\ left (M {\ rightarrow} J \ right) \ клин \ left (J {\ rightarrow} S \ right) \ right] {\ rightarrow} \ left (M {\ rightarrow} S \ справа) [/ латекс] |
| т | т | т | т | т | т | т | т |
| т | т | F | т | F | F | F | т |
| т | F | т | F | т | F | т | т |
| т | F | F | F | т | F | F | т |
| ф | т | т | т | т | т | т | т |
| ф | т | F | т | F | F | т | т |
| ф | F | т | т | т | т | т | т |
| ф | F | F | т | т | т | т | т |
Из таблицы истинности мы видим, что это действительный аргумент.
Предыдущая задача является примером силлогизма.
Силлогизм
Силлогизм – это импликация, производная от двух других, где следствие одного предшествует другому. Общая форма силлогизма:
| Помещение: | [латекс] p {\ rightarrow} q [/ латекс] |
| Помещение: | [латекс] q {\ rightarrow} r [/ латекс] |
| Заключение: | [латекс] p {\ rightarrow} r [/ латекс] |
Иногда это называют транзитивным свойством импликации.
подробнее о переходном свойстве
Переходное свойство регулярно появляется в различных областях математических исследований. Например, транзитивное свойство равенства утверждает
если [латекс] a = b [/ латекс] и [латекс] b = c [/ латекс], то [латекс] a = c [/ латекс].
Пример
| Помещение: | Если я буду много работать, я получу прибавку. |
| Помещение: | Если я получу прибавку, я куплю лодку. |
| Заключение: | Если я не куплю лодку, значит, я не много работал. |
Если мы допустим W = усердно трудиться, R = получать прибавку и B = покупать лодку, то мы можем представить наш аргумент символически:
| Помещение: | [латекс] H {\ rightarrow} R [/ латекс] |
| Помещение: | [латекс] R {\ rightarrow} B [/ латекс] |
| Заключение: | [латекс] \ sim {B} {\ rightarrow} {\ sim} H [/ латекс] |
Мы могли бы построить таблицу истинности для этого аргумента, но вместо этого мы будем использовать обозначение контрапозитива, которое мы узнали ранее, чтобы отметить, что импликация [латекс] {\ sim} B {\ rightarrow} {\ sim} H [/ latex] эквивалентно импликации [latex] H {\ rightarrow} B [/ latex].Перефразируя, мы видим, что этот вывод действительно является логическим силлогизмом, выведенным из посылок.
Попробуй
Верен ли этот аргумент?
| Помещение: | Если я пойду на вечеринку, завтра я очень устану. |
| Помещение: | Если я пойду на вечеринку, я увижу друзей. |
| Заключение: | Если не увижу друзей, завтра не устану. |
Льюис Кэрролл, автор книги Алиса в стране чудес , был учителем математики и логики и написал две книги по логике.В них он предлагал посылки как загадку, соединяемую силлогизмами.
Пример
Решите головоломку. Другими словами, сделайте логический вывод из этих посылок.
Все младенцы нелогичны.
Никого, кто умеет управлять крокодилом, не презирают.
Нелогичных людей презирают.
Показать решениеПусть B = младенец, D = презираемый, I = нелогичный, а M = может управлять крокодилом.
Тогда мы можем записать помещение как:
[латекс] B {\ rightarrow} I \\ M {\ rightarrow} {\ sim} D \\ I {\ rightarrow} D [/ латекс]
Из первого и третьего посылок мы можем заключить, что [латекс] B {\ rightarrow} D [/ латекс]; что младенцев презирают.
Используя контрапозитив второй посылки, [латекс] D {\ rightarrow} {\ sim} M [/ latex], мы можем заключить, что [latex] B \ rightarrow \ sim {M} [/ latex]; что младенцы не могут справиться с крокодилами.
Хотя это и глупо, но это логический вывод из данной посылки.
Логический вывод
Предположим, мы знаем, что утверждение формы [latex] P {\ rightarrow} Q [/ latex] верно. Это говорит нам, что всякий раз, когда P истинно, Q также будет истинным. Само по себе [latex] P {\ rightarrow} Q [/ latex] истинное значение не говорит нам, что либо P , либо Q истинно (они оба могут быть ложными, либо P может быть ложным и Q правда).Однако, если вдобавок мы знаем, что P истинно, то должно быть, что Q истинно. Это называется логическим выводом . : Имея два истинных утверждения, мы можем сделать вывод, что третье утверждение истинно. В этом случае истинные утверждения [латекс] P {\ rightarrow} Q [/ latex] и P «складываются вместе», чтобы получить Q . Это описано ниже, когда [latex] P {\ rightarrow} Q [/ latex] уложены друг на друга с линией, отделяющей их от Q .Предполагаемое значение состоит в том, что [латекс] P {\ rightarrow} Q [/ latex] в сочетании с P дает Q .
| [латекс] P {\ rightarrow} Q \\\ подчеркивание {P \, \, \, \, \, \, \, \, \, \, \, \,} \\ Q [/ латекс ] | [латекс] \, \, P {\ rightarrow} Q \\\ подчеркивание {{\ sim} Q \, \, \, \, \, \, \, \, \, \, \, \,} \ \ {\ sim} P [/ latex] | [латекс] \, \, P {\ vee} Q \\\ подчеркивание {{\ sim} P \, \, \, \, \, \, \, \, \, \, \, \,} \ \ Q [/ латекс] |
Два других логических вывода перечислены выше. В каждом случае вы должны убедить себя (основываясь на вашем знании соответствующих таблиц истинности), что истинность утверждений над линией заставляет утверждение под линией быть истинным.
Ниже приведены некоторые дополнительные полезные логические выводы. Первый выражает очевидный факт, что если P и Q оба верны, то утверждение [latex] P {\ wedge} Q [/ latex] будет истинным. С другой стороны, истинность [latex] P {\ wedge} Q [/ latex] заставляет P (также Q ) быть истинным. Наконец, если P истинно, то [latex] P {\ vee} Q [/ latex] должно быть истинным, независимо от того, какое утверждение Q .
| [латекс] \, \, P \\\ подчеркивание {\, \, Q \, \, \, \, \,} \\ P {\ wedge} Q [/ латекс] | [латекс] \ underline {P {\ wedge} Q} \\ P [/ латекс] | [латекс] \ underline {\, P \, \, \, \, \, \, \, \, \,} \\\, P {\ vee} Q [/ латекс] |
Первые два утверждения в каждом случае называются «предпосылками», а последнее утверждение – «заключением.Совмещаем жилки с [латексом] {\ wedge} [/ латексом] («а»). Посылки вместе подразумевают заключение. Таким образом, первый аргумент будет иметь [латекс] \ left (\ left (P {\ rightarrow} Q \ right) {\ wedge} P \ right) {\ rightarrow} Q [/ latex]
Важное примечание
Важно знать причины, по которым мы изучаем логику. Есть три очень веских причины. Во-первых, таблицы истинности, которые мы изучали, сообщают нам точные значения таких слов, как «и», «или», «не» и так далее. Например, всякий раз, когда мы используем или читаем конструкцию «Если…, то» в математическом контексте, логика сообщает нам, что именно имеется в виду.Во-вторых, правила вывода обеспечивают систему, в которой мы можем производить новую информацию (утверждения) из известной информации. Наконец, логические правила, такие как законы ДеМоргана, помогают нам правильно преобразовывать определенные утверждения в (потенциально более полезные) утверждения с тем же значением. Таким образом, логика помогает нам понять значение утверждений, а также порождает новые значимые утверждения.
Logic – это клей, который скрепляет цепочки утверждений и фиксирует точное значение определенных ключевых фраз, таких как конструкции «Если…, то» или «Для всех».Логика – это общий язык, которым пользуются все математики, поэтому мы должны твердо владеть им, чтобы писать и понимать математику.
Диаграмма Эйлера: как нарисовать ее простыми шагами
Вероятность и статистика> Вероятность> Как создать диаграмму Эйлера
Диаграмма Эйлера: обзор
Диаграмма Эйлера похожа, но не идентична диаграмме Венна. Хотя оба они используют круги для создания диаграмм, есть существенное различие: диаграммы Венна представляют весь набор , а диаграммы Эйлера могут представлять часть набора. На диаграмме Венна может быть заштрихованная область для отображения пустого множества. Эта область на диаграмме Эйлера могла просто отсутствовать на диаграмме вообще. Диаграммы Эйлера сложно нарисовать вручную (простая схема описана ниже). Вам, вероятно, лучше использовать программное обеспечение для его создания, например Smart Draw или Venn Master.
Диаграмма Эйлера: шаги
Пример вопроса: Нарисуйте диаграмму Эйлера для представления следующих утверждений:
Все волшебники могут творить магию.
Ящерицы не умеют колдовать.
Никакой волшебник не ящерица.
Шаг 1: Нарисуйте три круга, представляющих три категории (волшебник, ящерица, магия). Совместите их все (используйте карандаш или программное обеспечение, чтобы потом можно было перемещать круги):
Шаг 2: Прочтите первое утверждение и переместите соответствующий кружок на . «Все волшебники могут творить магию» должно означать, что весь волшебный круг должен находиться внутри магического круга.
Шаг 2: Прочтите второй оператор и переместите соответствующий круг на .«Никакие ящерицы не могут творить магию» должно означать, что весь круг ящерицы должен находиться на за пределами магического круга.
Шаг 3: Прочтите третье утверждение и переместите соответствующий круг на . «Волшебники не являются ящерицами» должно означать, что весь круг ящерицы должен быть на за пределами круга волшебника. В этом случае на графике круг ящерицы уже есть за пределами круга волшебника, так что мы закончили!
Ссылка:
Кентский университет. Проверено 19 октября 2015 года.
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
Все о диаграмме Венна
Определение диаграммы Венна
Диаграмма Венна (также известная как диаграмма набора или логика ) может отображать различия, сходства и перекрывающиеся отношения между наборами, т.е.е., группы данных. Чаще всего его используют для описания общих черт между противоборствующими фракциями – например, в приведенном ниже примере диаграммы Венна мы можем увидеть общие характеристики клеток растений и животных.
Исходные клетки растений против клеток животных – https://owlcation.com/stem/Plant-Cells-vs-Animal-Cells-With-DiagramsНабор данных визуализируется как совокупность фиксированных точек внутри замкнутой окружности (обычно кругов, но иногда эллипсов, сфер или даже треугольников): визуально описывает одну категорию, которую имеют все включенные данные.В приведенном выше примере окружность, содержащая характеристики клеток животных, имеет точки данных: неправильная / круглая, центросомы, центриоли, лизосомы, ядро, клеточная мембрана, цитоплазма, митохондрии, аппарат Гольджи и рибосомы. Только , около из этих точек данных / характеристик являются общими для растительных клеток, визуализированных в синем пересечении.
Нравится, как выглядит этот пример диаграммы Венна? Начни и создай свой собственный!
Главный интерес к диаграммам Венна – это пересечение – данные, которые попадают в более чем одну категорию (в приведенном выше примере это поясняется меткой «обе», хотя следует помнить, что пересечение – это , а не . собственный, отдельный набор данных).Диаграммы Венна могут состоять из нескольких пересечений и наборов кругов, но наиболее часто используются трехкружные или тройные диаграммы Венна.
Одним из факторов популярности тройного Венна является то, что он создает в центре изогнутый треугольник идеальной и постоянной ширины, известный как «треугольник Рело». Эта форма очаровала инженеров, математиков, архитекторов и графических дизайнеров как своими математическими возможностями, так и своей визуальной красотой, и использовалась эрудитами от немецкого инженера Франца Рёло (в честь которого они теперь названы) для производства кинетических машин и Леонардо Да. Винчи за проектирование карты.
Начните создавать свои собственные диаграммы и бизнес-графику.
Попробуйте Vizzlo бесплатноРазвитие и история диаграммы Венна
В той или иной форме диаграммы в стиле Венна существуют еще со средневековья. Абстрактное визуальное представление соединений и пересечений различных множеств – невероятно старая концепция, поскольку существует глубокое человеческое стремление показать, что принадлежит, а что нет. Как и большинство логических сред, с годами он рос и органически изменялся, уточнялся, перефокусировался и перенаправлялся в круговую диаграмму, с которой мы так хорошо знакомы сегодня.
Первым математиком, напрямую связавшимся с этим стилем диаграмм, был немецкий эрудит и философ Готфрид Вильгельм Лейбниц примерно в конце 1600-х годов. Лейбниц был, по сути, одним из первых приверженцев многих концепций визуализации данных: он верил в символическое представление сложных мыслей, чтобы не только лучше передавать эти идеи, но и оставлять меньше места для человеческих ошибок, неверной интерпретации и возникающих споров. Для Лейбница этого удалось добиться путем вычисления и визуализации разногласий в формализованных логических диаграммах.
Диаграмма Эйлера
Примерно сто лет спустя известный швейцарский математик Леонард Эйлер стал широко известен тем, что использовал перекрывающиеся круги для представления логических выводов (или силлогистических рассуждений). Эти круги используются для изображения четырех категоричных положений силлогизма:
- Универсальное подтверждение «Все графики Vizzlo выглядят красиво»
- Универсальный отрицательный «Ни один из графиков Vizzlo не является трудным для создания»
- Особо утвердительное «Некоторые из Vizzard Vizzlo включают диаграммы Венна»
- Особо отрицательный «Некоторые из Vizzard Vizzlo не являются диаграммами Венна»
Замечание на полях: Знаете ли вы, что в соответствии с логической семантикой в английском языке до конца XVI века было четыре слова «да» и «нет» ?! Универсальное Утверждение было бы сказано как «Да», Универсальное Отрицательное как «Нет», Частное Утверждение как «Да» и Частное Отрицательное как «Нет».”
Чтобы было ясно, стало обычной практикой данных, а именно – группировать диаграммы Эйлера и Венна под более известным названием «диаграмма Венна», чтобы избежать путаницы – только в очень технических математических ситуациях может потребоваться разграничение между ними.
Современная диаграмма Венна
Диаграмма Венна, известная нам сегодня, была разработана английским математиком Джоном Венном.В 1880 году он опубликовал статью под названием «О схематическом и механическом представлении суждений и рассуждений». В нем Венн предложил изменить диаграмму Эйлера, чтобы она стала более полной визуализацией вероятности, потребовав отображения всех возможностей. Однако название «диаграмма Венна» было придумано американским философом Кларенсом Ирвингом лишь несколько лет спустя, в 1918 году.
С тех пор диаграмма Венна стала центром обширных исследований многих других известных ученых, в том числе А.W.F. Эдвардс, Бранко Грунбаум и Генри Джон Стивен Смит. Они стали важной визуализацией для математических исследований, будь то традиционная трехкружная диаграмма или более сложные версии, включая сферы и эллипсы, для таких областей, как теория множеств, теория логики, вращательная симметрия и изучение сложных форм и чисел, таких как тессеракт.
Что НЕ является диаграммой Венна?
Для такой простой диаграммы Венна с годами неправильно обозначали. Фактически, сейчас мы чаще всего обращаемся почти исключительно к диаграммам Эйлера, когда обсуждаем «Венн.”
ДиаграммыВенна, по сути, являются более специфическим типом диаграмм Эйлера. Вот удобная диаграмма Эйлера, наглядно описывающая, что все диаграммы Венна являются диаграммами Эйлера, но не все диаграммы Эйлера являются диаграммами Венна:
Золотое правило Венна состоит в том, что он всегда визуализирует все возможности , даже если ни один из данных не укладывается в эти пересечения, тогда как диаграмма Эйлера визуализирует только категории, для которых есть данные. Если бы мы заставили приведенную выше диаграмму соответствовать параметрам диаграммы Венна, мы должны были бы представить себе, что существуют некоторые диаграммы Венна, которые не являются диаграммами Эйлера.Чтобы поместить это в контекст, это все равно что заявить, что некоторые животные не пингвины и, следовательно, некоторые пингвины не являются животными.
Чтобы продемонстрировать это различие на практике, представим, что трое друзей сравнивают свои домашние задания. Люси подготовила два домашних задания: одно по теме «Прокариоты и эукариоты» по естествознанию и одно по теме «Вероятность и статистика» по математике. Анвар также подготовил домашнее задание по математике на тему «Вероятность и статистика», но выбрал для науки тему «Клетки животных и клетки растений».Янс написал отличное эссе на тему «Митоз и мейоз» для Science, но совершенно забыл, что его домашняя работа по математике вообще должна была быть.
Если оранжевый набор данных представляет Янса, розовый набор данных представляет Анвара, а синий набор данных представляет Люси, мы можем организовать эту информацию двумя разными способами.
Диаграмма Эйлера показывает только возможностей, по которым у нас уже есть фактические данные. Мы знаем, что Анвар и Люси выполнили домашнее задание по математике на тему «Вероятность и статистика», и пересечение показывает это.Мы знаем, что Янс не создавал никаких домашних заданий по математике, как Анвар и Люси, и что они не выбрали ту же тему, что и он, для науки, поэтому набор данных Янса не пересекается с другими.
Диаграмма Венна показывает ту же информацию – темы, которые трое друзей делали индивидуально, и математическую тему, которую выбрали Анвар и Люси. Однако у нас также есть пересечения, которые не содержат данных, но представляют всех других возможностей.
Оранжевое пересечение слева представляет собой случай, когда Янс вместе с Анваром помнит свою домашнюю работу по математике, а также науку, но в этом гипотетическом результате Люси забывает завершить работу по математике.Зеленый перекресток справа олицетворяет ту же судьбу Анвара. Центральное пересечение показывает вероятность того, что все трое друзей не забудут работать над «Вероятностью и статистикой» для математики, а также над различными темами для естествознания, и никто не получит наказания…
Готовы создать свою собственную диаграмму Венна? Вот небольшой ярлык для страницы Vizzard специально для вас.
Для построения диаграммы Венна между двумя наборами данных должны быть как общие черты, так и различия.Если вся информация по категориям идентична, ваша диаграмма будет выглядеть так:
Даже с двумя наборами данных, если содержащаяся информация не имеет различий, две кривые будут полностью перекрываться, создавая только один круг.
Противоположная проблема, два набора данных без общих черт, также не будут создавать диаграмму Венна (но вполне приемлемую диаграмму Эйлера, показывающую непересекающихся множеств ).
Удивительно, но то, что выглядит столь же знакомым, как приведенный ниже пример, также математически не считается диаграммой Венна.
Как объяснялось ранее, одним из ключевых требований диаграммы Венна является то, что она должна отображать все возможные логические результаты. Поскольку в приведенном выше примере нет пересечения, в котором встречаются только желтый и красный или только синий и оранжевый, это не может считаться полным отображением универсальной логики.
Сводка
Подводя итог, диаграмма Венна:
- Тип диаграммы Эйлера
- Диаграмма с двумя или более наборами данных, изображенными в пределах окружности
- Используется для визуализации различий и общих черт между этими наборами данных
- Используется для выработки всех логических выводов
- Невероятно быстрое изготовление с использованием диаграммы Венна Vizzlo Vizzard
Vizzlo очень проста, и вы можете попробовать ее бесплатно.
 ……………………………………………………………………………..
……………………………………………………………………………..