Примеры для дошкольников больше меньше или равно: Знаки больше меньше равно для дошкольников

Наша математика – Сравнение множеств (больше, меньше, равно) — 24 ответов на Babyblog

Поскольку счет в пределах десяти дочка уже освоила хорошо, я решила попробовать перейти с ней к следующей теме – “Сравнение множеств”. Когда мы только начали заниматься, Даша хорошо понимала, где много, а где мало, но смысл сравнения ей был не совсем понятен. Зато сейчас она уже хорошо сравнивает и расставляет правильные знаки. Даже, когда нет наглядного примера, я иногда спрашиваю ее между делом, что больше/меньше из двух чисел, например 2 или 7, честно говоря, к моему удивлению, Даша всегда отвечает правильно.

Наверное, ни для кого не секрет, что знак сравнения « >» традиционно сравнивают с ротиком птички (а в американских школах, с ротиком крокодильчика).

Поэтому мы тоже не стали ничего придумывать нового и называем между собой знак «>, <» – математической птичкой. При первом знакомстве со знаком «>/<» мы договорились с дочкой, что наша птичка очень хочет кушать.

И поэтому ротиком будет поворачиваться только в ту сторону, где фигурок изображено больше (много), там же где фигурок меньше (мало) птичка просто понюхает своим острым носиком.

Таким образом, когда Даше нужно сравнить два множества (разное количество фигурок на наших карточках) мы зовем нашу птичку. Птичка вылетает из-за шторы, каркает (эффект появления Дашу забавляет) и я ей говорю (не знаю правда насколько это педагогично, но нам помогло…): «Птичка прилетела, понюхала и съела…» И по ходу разбирались, что же она съест и что же понюхает. Дочке эта игра нравится, обычно очень эмоционально на нее реагирует – кормит птичку, потом показывает, где и как она будет нюхать…

А вот собственно и наши карточки, с которыми мы занимается сравнением (всего 31 шт. в разными числовыми комбинациями):

Со знаком равенства мне не пришлось долго объяснять, Даша очень быстро поняла, что если предметов 2 и 2, 3 и 3…., то это значит одинаково или равно «=».

А еще, когда мы занимаемся зарядкой и разминаем ступни ног, Даша разводит и сводит свои ножки в стороны и это очень напоминает знаки «>» и «=» (так очень легко запомнить сами знаки).

2. Еще для разнообразия играем с такими карточками, во время игры я пытаюсь делать акцент на том, что число становится больше предыдущего на единицу. (Например, играл на улице один слоник, к нему прибежала еще одна коровка, детей стало больше, им теперь не скучно, потому что их стало двое и т.д.) Ну и просто сравниваем две карточки с разным количеством животных.

3. Также для того, чтобы ребенок, так сказать, прочувствовал разницу и смысл понятий «больше, меньше, равно» рекомендуют игры по принципу наложения. Мы раскладываем зайчиков и морковки, а еще соотносим крыши с домиками. Вот так:

4. А еще нам нравится такая игра: сделали мы с Дашей предварительно парные карточки с разным количеством одинаковых предметов (на карточки наклеивали наклейки из альбомов «400 наклеек) и раздаем эти карточки между одинаковыми игрушками разного размера: большому тигренку – отдаем больше, маленькому тигренку – меньше (ведь он маленький и много не съест).

5.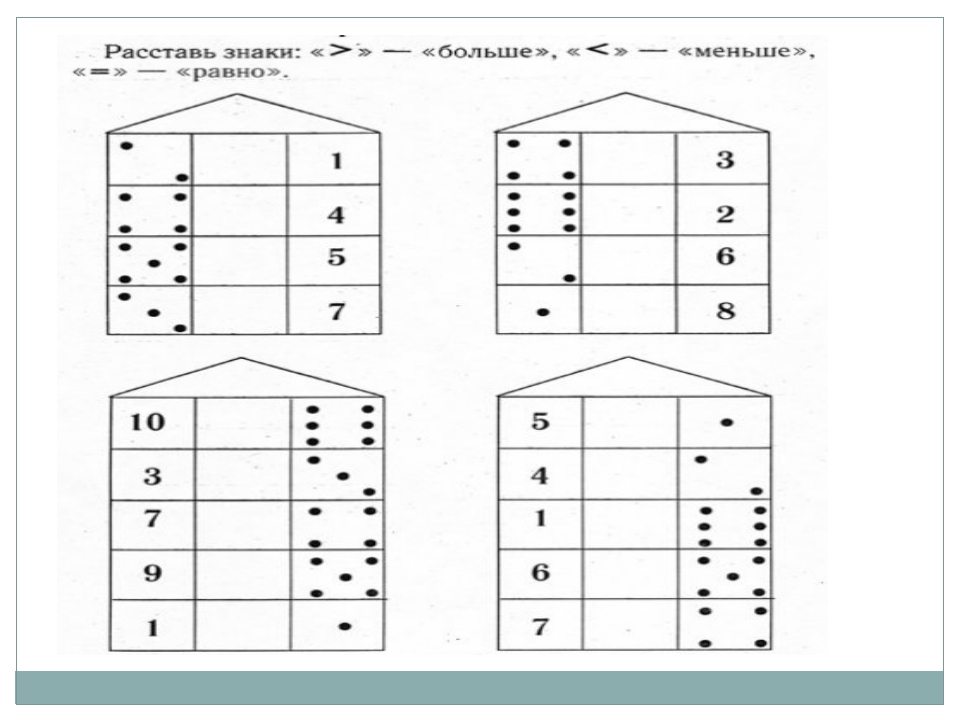 Ну и играем с карточками, которых, я думаю, у каждого уже масса: расставляем по росту картинки и раздаем угощения самой большой – больше всего, потом – меньше, меньше и еще меньше…

6.А еще творчеством понемногу занимаемся (альбом «500 наклеек. Цифры» ) в таком ключе:

7. Расставляем по порядку карточки: от большего к меньшему в соответствии с количеством:

8. Ну и, конечно, в повседневной жизни много сравниваем и куклам дни рождения устраиваем – тарелки, ложки раздаем, сравниваем, делаем выводы, что кукол и тарелочек равно, когда тарелочек столько же, сколько и кукол.

Будем рады, если кому-то наши карточки окажутся также полезными. Все, что у нас есть по этой теме разместила здесь http://zalil.ru/34472581 , пароль 2013. Все можно скачать совершенно бесплатно.

Разработка урока по математике 1 класс по теме: «Знаки (больше), (меньше), = (равно)».

 Тема: «Знаки: > (больше), < (меньше), = (равно)».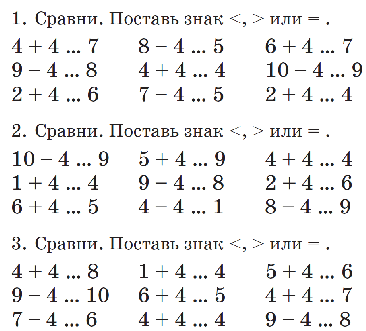

Цели: познакомить со знаками “<”, “>”, “=” и записями вида 2 < 3, 3 = 3, 4 > 2;

совершенствовать знания о составе чисел 3, 4, 5.

ХОД УРОКА

I. Организационный момент.

II. Актуализация раннее изученного.

Устный счет.

– Мы сегодня отправимся с вами на прогулку в сказочный лес.

По тропинке в лесок

Покатился колобок.

Встретил серого зайчишку,

Встретил волка, встретил мишку

Да плутовку – лису

Повстречал еще в лесу.

Отвечай поскорей,

Сколько встретил он зверей?

– Назовите соседей числа 4.

– Какое число следует за числом 5?

– Какое число стоит перед числом 10?

– Какое число стоит между числами 6 и 8?

– Молодцы! Продолжаем свой путь.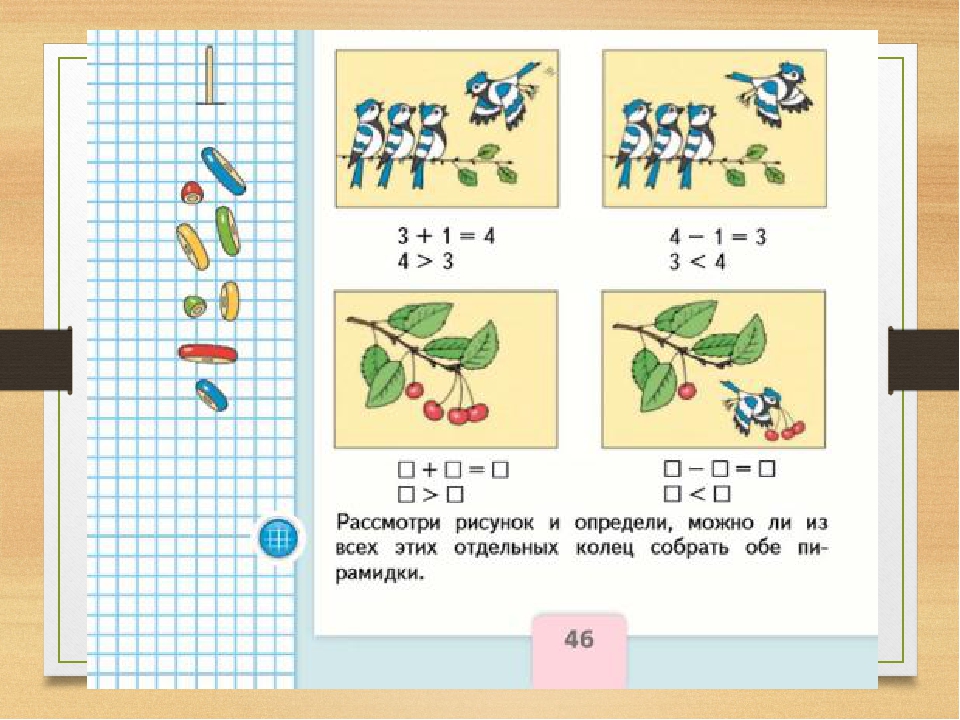

– Посмотрите, какие чудесные елочки повстречались нам на пути. Давайте нарядим их.

 

 

 

 

 

– С каждого ряда один ученик выходит и вставляет нужные числа. (Числа записаны на шишках.)

– Проверка.

– Значит, 3 – это 2 и 1, 1 и 2; 4 – это 2 и 2,3 и 1, 1 и 3, 5 – это 2 и 3, 3 и 2, 4 и 1, 1 и 4.

Физкультминутка.

В небе плавает луна,

В облака зашла она.

1, 2, 3, 4, 5 можем мы луну достать,

6, 7, 8, 9, 10 и пониже перевесить.

III. Объяснение нового материала.

– Мы вышли на полянку. Какие грибы вы видите? (Белые и мухоморы)

 

– На какие другие две группы их можно разбить? (Съедобные и несъедобные)

– Передо мной две корзины.

В одну положите съедобные грибы, в другую несъедобные грибы.

 

– Какие еще съедобные грибы знаете? Помните об этом, когда собираетесь в лес за грибами.

– Посчитаем, сколько тех и других грибов (3 и 2)

– В какой корзине больше грибов? Почему?

– Как вы сравнивали? (Поставили парами, друг под другом)

– Какой вывод делаем? (Белому грибу не хватило пары, значит белых грибов больше)

– Сколько белых грибов? (3)

– Какой цифрой обозначим? (3)

– Сколько мухоморов? (2)

– Какой цифрой обозначим? (2)

– Сравните количество грибов?

– Какое число при счете называют раньше: 3 или 2?

– Сравнили числа вы верно, но как это записать? (Ответы детей).

– Для того чтобы не писать слова «больше», «меньше», «равно» математики договорились обозначать их специальными знаками. Так слово «больше» мы будем обозначать знаком «>». Посмотрите. На, что он похож? (На клювик птички).  

Вы должны запомнить, что острие знака всегда показывает на меньшее число.

– Прочитаем запись (три больше двух): 3 > 2.

-Что мы можем сказать про число мухоморов? (Их два).

– Сколько белых? (3).

– Сделаем вывод: 2 < 3.

– Читаем вслух (два меньше трёх).

– О чём должны помнить при записи неравенства? (Что остриё всегда показывает на меньшее число).

– Как сделать, чтобы грибов стало поровну? (Надо прибавить один мухомор). (работа у доски).

– Сколько белых грибов? (3).

– Сколько мухоморов? (3)

– Что можно сказать про их количество?

– 3=3.

– Прочитаем запись (три равно трём).

– Как по-другому можно сделать одинаковое количество грибов, уравнять их? (Один белый гриб убрать).

– Сколько стало белых грибов?(2).

– Сколько мухоморов?(2).

– Что мы можем сказать про их количество? (Одинаковое)

– Как записать?

– 2=2.

– Прочитаем запись (два равно двум).

– Хорошо! Посмотрите, какая у нас получилась запись. Скажите, с какими знаками вы сегодня познакомились?

Физкультминутка.

Буратино потянулся,

Раз – нагнулся, два – нагнулся

Руки в стороны развел –

Видно ключик не нашел.

Чтобы ключик нам достать,

Надо на носочки встать.

– Закройте, ребята, глаза. Посмотрите вверх, вниз, вправо, влево, прислушайтесь. Слышите, как в нашем волшебном лесу поют птички.

– Молодцы! Открываем глазки, садимся.

– Волшебные птицы приглашают нас к учебнику.

IV. Закрепление

 – Сколько и какие фигуры изображены наверху страницы? Давайте внимательно прочитаем математические записи под фигурами.

– Составьте рассказ о птицах по левому рисунку. Прочитайте записи. Поработаем также по правому рисунку.

– Придумайте рассказ о вишнях и восстановите записи.

Физминутка.

– Найдите задание под первым кругом. Кто может прочитать, что надо сделать?

Самостоятельное составление примеров.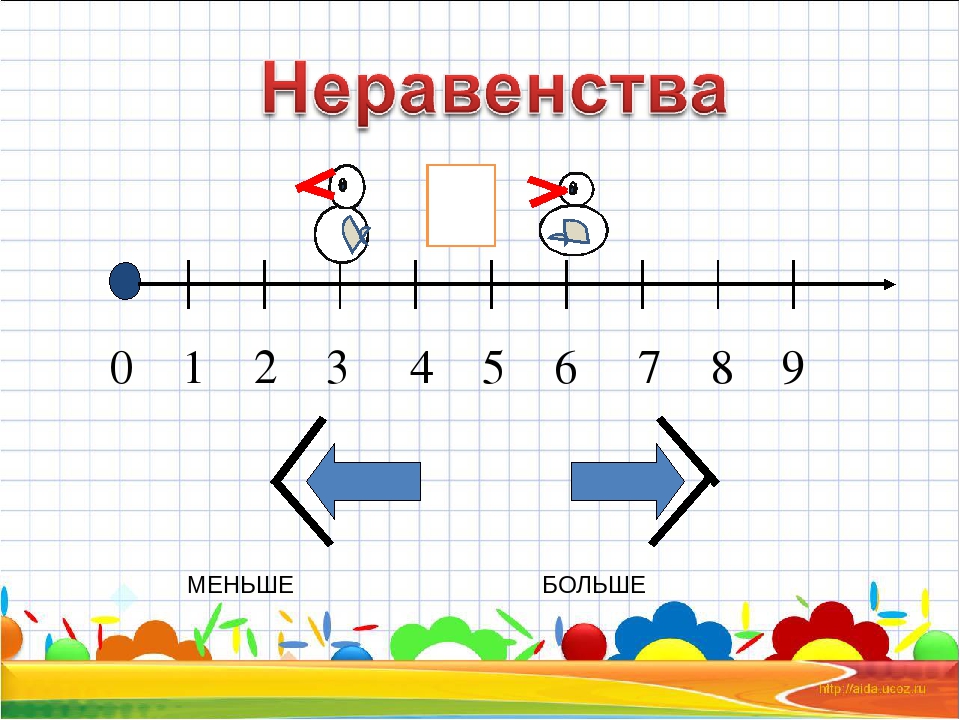 Один ученик работает у доски.

– посмотрите, что случилось с часами внизу страницы? Надо восстановить пропавшие цифры.

– Переходим к последнему заданию. Как называется знак в верхней строке? В нижней? Закончите строки знаков.

V. Итог урока.

-Что нового узнали на уроке?

– О чем должны помнить, когда ставим знаки сравнения?

VI. Домашнее задание:карточки- сравнить числа и выражения.

VII. Рефлексия:

– Кто остался доволен своей работой на уроке?

– Кто считает, что мог работать лучше?

 

 

Конспект по ФЭМП по теме “Решение задач.Знаки больше,меньше,равно”

Конспект НОД по ФЭМП в подготовительной группе «Решение задач.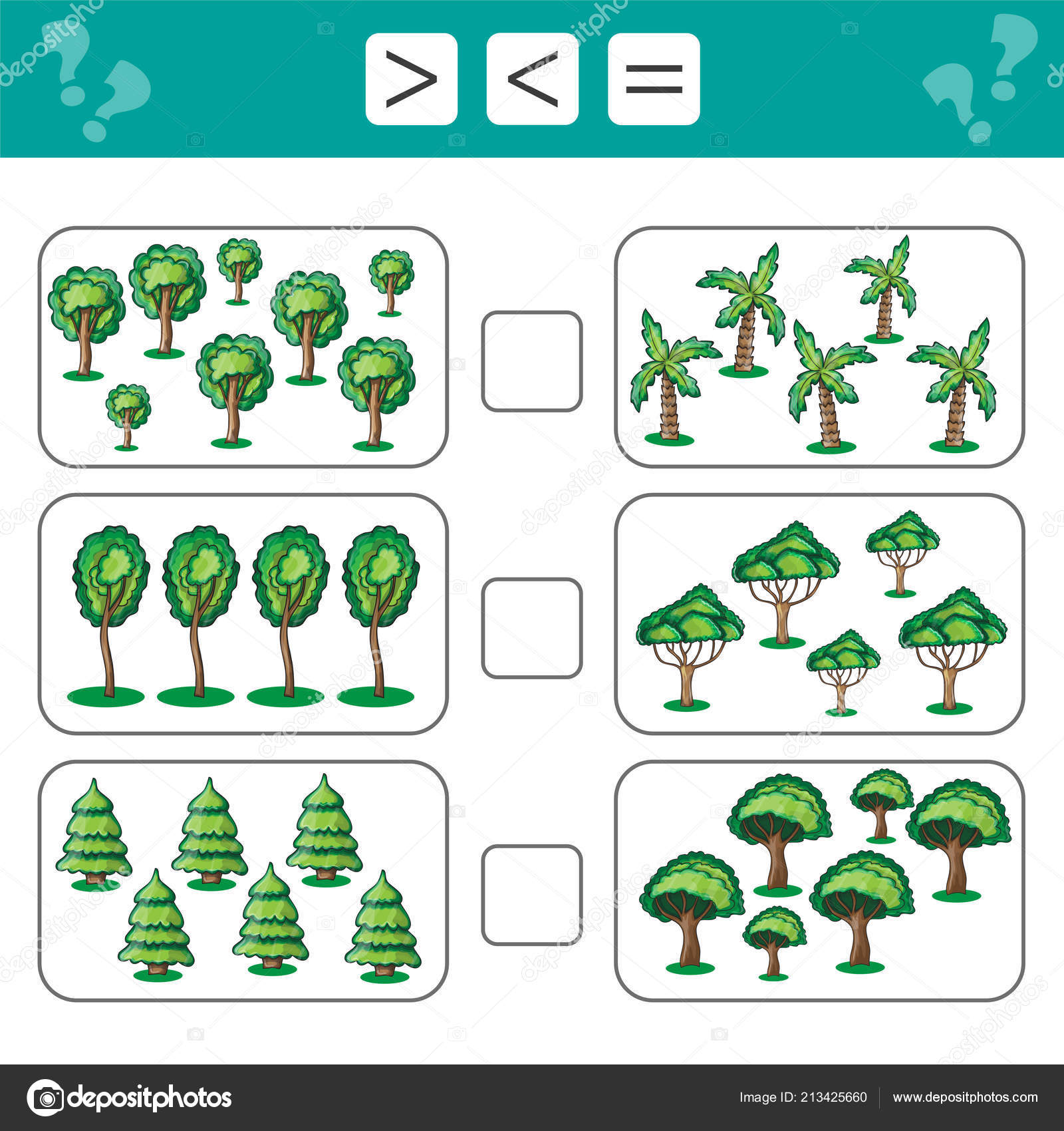 Знаки больше, меньше, равно»

Конспект НОД по ФЭМП в подготовительной группе «Решение задач. Знаки больше, меньше, равно»

Конспект проведения нод по ФЭМП

в подготовительной к школе группе

Цель: развитие интереса к предмету математики, на основе познавательной активности и любознательности.

Задачи:

– упражнять в умении детей составлять и записывать решения задачи с помощью

цифр и арифметических знаков;

– закрепить знание детей о знаках, «», « и «=», умение читать записи;

– уточнить умение детей называть дни недели, их последовательность.

– упражнять в умении оценивать работу друг друга.

Материал: телеграмма от Феи из волшебной Страны Математики; набор цифр от 0 до 10; счетные палочки; карточки с числовыми неравенствами; простой карандаш; карточки с названиями дней недели; схемы для составления задач; солнышко и тучки (картинки).

Место проведения: групповая комната.

Предварительная работа:

1. Выполнение заданий по составлению и решению задач.

2. Знакомство с днями недели.

3. Знакомство со знаками «+», «-», «=»

Ход НОД

1 часть. Психологический настрой:

Для начала встанем в круг,

Сколько здесь друзей вокруг.

Мы друг к другу повернемся

И друг другу улыбнемся.

Воспитатель: Ребята, сегодня утром, почтальон вручил мне телеграмму, адресованную нашей группе. Давайте ее прочитаем

Телеграмма: «Здравствуйте дорогие ребята, пишет вам Фея из Страны Математики. Я приглашаю вас в Страну Математики. Но путь в эту страну будет нелегким. Чтобы в нее попасть, нужно показать свои знания. А чтобы показать свои знания, вам нужно выполнить задания.

2 часть – выполнение заданий

Задание 1 – Разминка

Воспитатель: Ребята, вы хотите попасть в Страну Математики?

Дети: Да.

Воспитатель: Тогда давайте подготовимся к путешествию и проведем математическую разминку. Вы готовы? (Да)

1. Если стол ВЫШЕ стула, то стул … НИЖЕ стола.

2. Если веревка ТОЛЩЕ нитки, то нитка …ТОНЬШЕ веревки.

3. Если линейка ДЛИННЕЕ карандаша, то карандаш … КОРОЧЕ линейки.

4. Если брат СТАРШЕ сестры, то сестра… МЛАДШЕ брата.

5. Что длится дольше: ДЕНЬ или МЕСЯЦ?

6. Что длится меньше: СЕКУНДА или МИНУТА?

7. Что больше: НЕДЕЛЯ или 7 ДНЕЙ?

Задание 2 – отгадывание загадки

Воспитатель: Молодцы ребята, вы очень хорошо подготовились к путешествию. На чём же мы отправимся?

– Чтобы узнать какой транспорт нам понадобиться, нужно отгадать загадку.

Загадка: До Луны не может птица

Долететь и прилуниться,

Но зато умеет это

Делать быстрая (ракета)

(дети проходят за столы и на доске вызванный ребенок выполняет задание)

Воспитатель: Молодцы вы справились с заданием, но что бы ракета взлетела, нам нужно выполнить следующие задание:

На листочках записаны числовые выражения, среди этих чисел есть одно лишнее.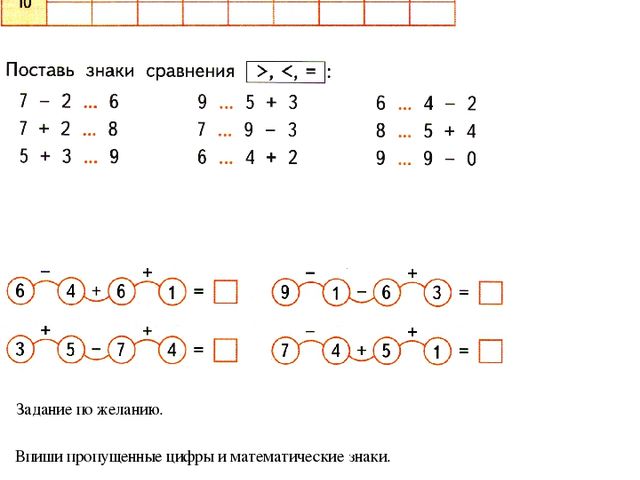 Как его найти? Как вы будете выполнять задание?

Дети: Сначала нужно решить числовые выражения, а потом найти лишнее число.

8+1= 7+2= 4+5= 2+7= 6+3= 8 – 4=

Воспитатель: Молодцы, ребята. Наша ракета готова к взлёту. Полетели.

Воспитатель: Мы приземляемся в «Город знаков».

Задание 3. – «Знаки»

Для выполнения задания нужно сравнить, поставить знаки «», « или «=».

3 5 6 8 4 4 1 7

6 6 2 5 2 3 9 10

7 4 8 8 6 0 8 6

4 0 5 6 2 2 7 5

Взаимопроверка: дети проверяют выполнение заданий друг у друга, если у соседа по столу задание выполнено правильно – поднимают солнышко, если есть ошибки – поднимают тучку.

Задание 4 – Постройка геометрических фигур из счетных палочек

Воспитатель: Следующее остановка: Геометрическая.

Составление геометрических фигур с помощью счётных палочек:

– составить 2 равных треугольника из 5 палочек.

– составить 2 равных квадрата из 7 палочек.

– составить 3 равных треугольника из 7 палочек

– составить 4 равных треугольника из 9 палочек.

Воспитатель: А прежде чем приступить к следующему заданию в «стране Математики» нам нужно немножко отдохнуть и набраться сил для дальнейшего путешествия.

Физминутка:

Хорошо, что солнце светит? (изображают солнце)

Хорошо! (хлопают в ладоши)

Хорошо, что дует ветер? (изображают ветер)

Хорошо! (хлопают в ладоши)

Хорошо идти с друзьями? (шагают)

Хорошо! (хлопают в ладоши)

Хорошо прижаться к маме? (обнимают себя)

Хорошо! (хлопают в ладоши)

Хорошо в краю родном? (разводят руки в стороны)

Хорошо! (хлопают в ладоши)

Хорошо там, где наш дом? (изображают дом)

Хорошо! (хлопают в ладоши)

Хорошо кружиться в танце? (кружатся)

Хорошо! (хлопают в ладоши)

Хорошо что все мы вмести (выставляют большие пальцы

Хорошо! (хлопают в ладоши)

Задание 5 – составление и решение задач по схеме

Воспитатель: Следующая остановка «задачная»

Воспитатель показывает схему для составления задачи и предлагает составить задачу.

Дети составляют задачу, самостоятельно записывают решение задач и объясняют, почему поставили знак «плюс» или «минус».

Задание 6 – д/игра «Живая неделька»

Ну, а теперь последнее задание, которое нам приготовила Фея Математика.

– Мне нужны 7 помощников.

На карточках написаны названия дней недели. Вы под музыку будете ходить по комнате в разных направлениях. При остановке музыки вы должны встать по порядку так, как следуют дни недели.

(Выполнение задания детьми)

Воспитатель: (обратиться к сидящим детям)

– Проверьте, правильно построилась «живая неделька».

– Вадим, какой день недели находится между средой и пятницей?

– На каком месте стоит вторник?

Воспитатель: (обратиться к «Живой недельке»)

-Вы отлично справились с заданием, а теперь поверните свои карточки и мы узнаем какое слово спрятала Фея Математика.  (М-О-Л-О-Д-Ц-Ы)

(Обратиться к сидящим детям)

– Какое слово спрятала Фея?

Дети: МОЛОДЦЫ

Итог занятия. Ребята, вам понравилось наше путешествие в страну

«Математика»?

– Какие задания выполняли?

– Какие были затруднения?

Дом и семья. Общество. Мир женщины. Ждем ребенка. Гороскопы. Грудное вскармливание

Задачи:

• Дать представления о знаках «больше», «меньше», учить детей пользоваться ими, закреплять представления о порядковом и обратном счете, использовании цифр, об отношениях смежных чисел, о составе числа из двух меньших.
• Упражнять в умении составлять и решать задачи, формулировать арифметическое действие, ориентироваться в пространстве по отношению к себе, работать в тетради в клетку.
• Продолжать формировать представления о длине и ширине предметов, об их измерении.
• Воспитывать у детей навыки учебной деятельности, стремление помочь товарищу, участвовать в осуществлении общей цели.

Материал:

• У детей: карточки с точками и цифрами, под которыми зашифрованы разные виды транспорта, тетради в клетку, простые карандаши, ножницы, чистые листы бумаги (формат А4), карточки с наклеенными квадратами разного цвета (на порядковый счет), объемные цифры, карточки с задачами-иллюстрациями, маленькие машины.
• У воспитателя:таблицы с цифровыми рядами, знаки «больше», «меньше»; таблица «Узнай путь белочки к дуплу», «Узнай путь ежика к норе»; аудиозапись «Голос волшебника».

Ход занятия:

До занятия воспитатель вместе с детьми строит из мелкого строительного материала, городок с улицами и площадями, замком, парком. Во дворики домов помещаю мелкие игрушки зверюшек и домашних животных. Дети рассаживаются за столы вокруг этого городка.

«Ребята, какой интересный городок мы с вами построили, но оказывается в нем хозяйничает злой волшебник по имени – Ноль, А город называется Магнитофон. (Голос «волшебника») «Здравствуйте ребята! Я волшебник по имени Ноль, хозяин города математических загадок, приветствую Вас! В моем городе живут звери и животные, но я их запер в ломах и не пускаю повеселиться на теплом весеннем солнышке и зеленой травке, потому, что еще не нашелся никто, кто бы отгадал мои загадки! (Выключается магнитофон)
Ребята, жалко вам зверюшек? Давайте освободим их, выпустим из домов погулять на травке? Но для этого надо решить задачки волшебника Ноля.

1. На чем мы можем поехать в город математических загадок? (Дети перечисляют: на автобусе, на поезде, на самолете, и т.д.) каждый из вас поедет на своем транспорте. Он зашифрован на вашем листочке. Вы видите на листе точки. Все точки надо соединить линиями по порядку, который подскажут цифры. От цифры один проводим линию к цифре два, от цифры два проводим линию к цифре три. И т. д. (После выполнения задания опросить детей: «На чем ты поедешь в город математических загадок?»)

2. Представим, что мы подъехали к городу и остановились у ворот. А в город нас не пускает стража. Стражники приказывают нам отгадать их трудные задачки (берет лежащий у ворот листок и читает) :

а) На поляне у реки
Жили майские жуки.
Дочка, сын, отец и мать
Кто успел их сосчитать? (Четыре жука)

б)На полянке у дубка
Крот увидел два дубка.
А подальше у сосны,
Он нашел еще один.
Ну-ка, кто считать готов?
Сколько крот нашел грибов? (Три грибка)

в) Расставил Андрюшка в два ряда игрушки,
Рядом с мартышкой – плюшевый мишка.
Вместе с лисой – зайка косой.
Следом за ними еж и лягушка.
Сколько игрушек расставил Андрюшка? (Шесть игрушек)

г) Подарил утятам ежик
Восемь кожаных сапожек
Кто ответит из ребят:
Сколько было всех утят? (Четыре утенка)

д) В снег упал Сережка
А за ним Алешка
А за ним Маринка
А за ней Иринка
А потом упал Игнат
Сколько на снегу ребят? (Пять ребят)

– Ну, молодцы, ребята, отгадали все загадки и стражники, наверное, пропустят нас в город.

3. Представим себе, что мы зашли в город математических загадок и сразу попали на числовую улицу. Вот вы, на какой улице живете? (Спросить 2-3 детей) А в этом волшебном городе есть улица Числовая. На ней живет мальчик Гаврюша со своими питомцами (показывает указкой на зверюшек и выставляет их на мольберт таблицу «Гаврюша». Затем показывает картинки лопаты и лейки) Куда пойдет Гаврюша? Что он хочет делать на огороде? Дайте ему в правую руку лейку, а в левую лопатку (показывает тетрадку с неоконченной работой) Гаврюша оставил недоделанную работу по математике. Давайте решим за Гаврюшу его задачи. Что же он тут писал? (Выставляет крупный образец) Посмотрите и скажите, сколько фигур должно быть на третьей строчке? Почему? Докажите. Если ваш товарищ ошибется, поможем ему, т.к. мы вместе должны путешествовать по городу Математических загадок. Откроем тетради и напишем всего пять строчек геометрических фигур, но количество фигур в каждой строчке должно быть разное. Догадайтесь, какое? (Напомнить правило написания в строке)

4. Ребята, как еще долго придется путешествовать по городу. Давайте отдохнем. Поиграем в игру «Чье звено быстрее соберется?» У вас есть карточки, на которых квадраты разного цвета. Все зеленые квадраты соберутся к окну, фиолетовые – к мольберту, а коричневые – к уголку природы. В звеньях постройтесь по порядку и посчитайтесь: 1, 2, 3… Под бубен маршируйте по группе, а по сигналу стройтесь в звенья. Чье звено быстрее соберется? (Играть 2, 3 раза)

5. Продолжаем наше путешествие. Сейчас мы попали на улицу Смекалистых. Есть среди вас Смекалистые? Ну, посмотрим!

а) умеете ли вы считать обратно. Я буду бросать мяч, и называть число, а вы от этого числа считайте обратно (4-5 раз)
б) посмотрите на эту таблицу: Какое число здесь самое большее? А какое число здесь самое меньшее? А число 2 меньше, каких чисел? А число 8 больше, каких чисел?
в) А умеете ли вы отгадывать неизвестные числа? Откройте тетрадки, на которых нарисован утенок из мультиков Диснея, на странице, где Чипполино предлагает нам свои загадки.

В каждой строчке найдите неизвестные числа, поставьте цифру в нужную клетку. Какое неизвестное число в первой строчке? Прочитай всю строчку. Какое неизвестное число во второй строчке? Читай ее. Третью строчку прочитаем все хором. Какое здесь было неизвестное число? Молодцы ребята и эти загадки волшебника Ноля вы отгадали.

6. А сейчас мы с вами попали на улицу знаков (показывает узкий указкой улицу и выставляет на мольберт две цифры: 3 и 3) Какой знак можно поставить между этими цифрами? Правильно (+), (ставит знак) Три плюс три чему равно? А еще, какой знак можно поставить? Дети: минус (–) Три минус три, чему равно? Правильно, нулю. Это любимая цифра волшебника Нуля. А можно между этими цифрами поставить вот такой знак? (Ставит знак равенства) . (Выслушать ответы детей, предложить доказать правильность своего ответа) А если я вместо цифры три поставлю другую цифру? (Ставит цифру 4) Можно ли между ними оставить знак равенства? Нет? Почему же? А я думаю что можно? Докажите. Конечно ребята, 4 больше трех, если какое то число больше или меньше другого, то ставятся вот такие знаки (показывает, выставляет на мольберт два примера: 4 больше 6; 3 и 5 меньше 6), Этот знак называется «больше» и читается так: 4 больше трех, а этот знак называется «меньше» и читается так: 5 меньше 6. Похожи эти знаки друг на друга? Чем они похожи? (Они одинаковые, только острие направлено в разные стороны) Эти знаки можно распознавать по рукам, на правой руке знак «больше» (показывает) , на левой – знак «меньше». Покажите на своей руке знак «больше» (показывает) , покажите – знак «меньше».
Какой знак надо здесь поставить? (Ставит цифры 8 и 3)
А здесь? Ставит цифры (6 и 10) . Ну ребята волшебник Ноль и не думал, что вы запомните эти знаки! Их не трудно запоминать, да?

7. Ребята, на улице знаков протекает река быстрых ответов. Как нам перейти на ту сторону реки? Да нужен мост. Как называется мост, по которому идут пешеходы? А если мы поедем на машине по мосту? Как он будет называться? Давайте из бумаги сделаем пешеходный и автомобильный мосты. Мост у вас должен быть в идее полоски бумаги (показывае т) . С чего начинаем изготовление моста? Какой ширины будет пешеходный мост: узкий или широкий? А автомобильный? Как узнать, какой длинны надо делать мост? Как измерить длину моста? Помогайте друг другу.

8. Перешли мы на ту сторону реки, и попали в замок нерешенных задач. Давайте их решим и выпустим на волю гусят, которые живут в замке. Придумайте задачки по своим картинкам. (Спросить 3-4 ребенка) Какие части есть у задачи? Давайте решим Сашину задачку (повторить ее) Это задача на сложение или вычитание? Как вы ее решили? Придумайте задачку вот по этому примеру (6 + 2 = ?)
А кто решит вот такую задачу: «На озере плавали гуси, Когда один вышел на берег, то в воде осталось 7 гусей. Сколько гусей плавало в озере? Помогайте товарищу решать, решайте вместе».

– Молодцы ребята, у волшебника Ноля совсем испортилось настроение, придется ему выпускать своих пленников.

9. В конце города, ребята парк. И он называется парком Неизвестных чисел. Кто живет в этом парке? (Выставляется таблица «Укажи путь белочки к дуплу» и «Укажи путь ежику к норе») Где спит белочка? (Показывает на дупло) . Где спит ежик? Белочка может пройти к дуплу вот по этим дорожкам, но не по всем, а по какой-то одной, на которой два числа составляют третье в дупле (в каждой из трех дорожек ставит числа и только на одной ставит числа, которые составляют сумму числа, находящегося в дупле) По какой дорожке должна прыгать белочка,? По какой дорожке бежит ежик? Почему?

– Ребята, мы выполнили все задания волшебника Ноля. И мы можем выпустить всех животных, а по улицам повести машины. Возьмите животных и машины, поиграйте в городке.

Данилович Вера Александровна

Фэмп тема : «два мороза» знаки , и отношение =

Цель : создание социальной ситуации развития в процессе ознакомления со знаками &lt ;, >, =.

Задачи :

Сформировать условия для ознакомления со знаками больше , меньше и отношение равно .

Учить формулировать своё высказывание, правильно использовать знаки , и отношение =

Сформировать условия для сравнения количества предметов, используя знаки , и определять на сколько больше , меньше .

Способствовать развитию у детей внимания и наблюдательности.

Воспитывать самостоятельность и уверенность в решении заданий.

Развивать логическое, образное мышление, сообразительность, речь детей.

Предварительная работа : Чтение сказки «Два мороза» , загадки-отгадки (цифры, логические задачки, д/и «математическое лото » , «размышляйка» ,

Материал к занятию : Доска, набор демонстрационного материала к сказке «два мороза» ,набор карточек с предметными картинками на каждого ребенка, простые карандаши, для физминутки :снежинки на ленточках. Карточки для проверки задания на снежинках с № 1, 2, 3. Маркер. Книга «волшебные сказки»

Вводная часть. (Организационный и мотивационный момент.)

Подарок новогодний в нем флешка видио обращение. Доска. Демонстрационный материал разложен на столе возле доски.

Воспитатель : -Ребята подойдите ко мне. (дети возле воспитателя в кругу)

Скажите, чей это Новогодний подарок? Кто из вас его вчера забыл (ответы детей)

Тогда давайте его откроем и посмотрим что же в нем? Сережа помоги мне пожалуйста. (ребенок открывает коробку подарочную)

Воспитатель достает флешку, включает видио – запись письмо, прослушиваем : «Здравствуйте ребята, мы два мороза – Красный нос и Синий нос, прийти к вам мы не можем, так как мы поссорились. Подскажите, кто же из нас лучше подготовился к празднику , решите нашу задачку. Два мороза.

Придется нам их выручать, а то скоро праздник, а какой праздник без Д. Мороза?

Основная часть

На столах карточки, простые карандаши. Снежинки на ленточках.

Воспитатель :

Ребята проходите за столы,

Вы готовы, помочь мне?

Мне нужны помощники. (выбираю двух детей)

Гуляли по лесу два мороза : мороз красный нос и мороз Синий нос. (дети выставляют 2мороза)

Гуляют и каждый себя хвалит, кто же лучше подготовился к празднику .

Мороз К. нос говорит :- У меня снега в лесу больше чем у тебя , нет у меня снега больше , сказал мороз С. нос. (дети в произвольном порядке расклеивают снежинки возле дедов морозов)

А у меня на елке игрушек больше чем у тебя , сказал мороз К. нос,

А ты посмотри, какая у меня елка, и высока и нарядна, и игрушек много (дети выставляют елочки и приклеивают игрушки на неё)

Хорошо, сказал, мороз К. нос -полюбуйся сколько я приготовил подарков для детей.

И у меня подарки есть вот посмотри, сказал мороз С. нос. (подарки расклеивают возле дедов морозов)

Воспитатель : -так долго они спорили и решили обратиться к нам за помощью.

Мы им поможем, а пока ребята взяли снежинки, встали в кружок, нам пора размяться перед важным заданием.

Физминутка «Снежинка» (дети выполняют согласно текста)

Ребята давайте посмотрим, что же за задачка у нас получилась на доске.

У кого снега больше ? Меньше ? На сколько? (ответы детей)

На чьей елке игрушек больше , меньше ? На сколько (ответы детей)

У какого д. мороза подарков больше , меньше ? (ответы детей)

А как же мы им это объясним? (ответы детей)

Ребята, а в математике есть знаки . С помощью которых и можно решить вот такой спор или любую другую задачку, или сравнить предметы где больше или меньше . Это знак больше , меньше , равно (показываю знаки ) . На что похоже эти знаки ? (ответы детей)

Воспитатель объясняет, как определить больше , меньше , равно .

Давайте расставим знаки в нашей задачке (вызываю детей к доске)

Определяем на сколько меньше , больше игрушек , снежинок, подарков.

А что бы наши Д. Морозы не ссорились что нам нужно сделать? (убрать одну снежинку, игрушку новогодней елки)

Это мы решили задачку морозов, а теперь решим свои задачки.

Воспитатель предлагает выполнить задание в карточках.

Заключительная часть.

На доске выполненная детьми картина-задачка.

На снежинках карточки с правильными ответами.

Книга «Волшебные сказки»

-Воспитатель : на снежинках карточки с правильным ответом. -Кто выполнил задание, подойдите с карточкой с №1 к снежинке с №1, №2, №3, Проверьте, справились ли вы с заданием (дети самостоятельно оценивают свою работу)

С какими знаками сегодня познакомились ? А как определить какой знак &lt ;, >,=.

Ребята. За то что мы помогли помириться Д. Морозам они нам подарили книгу «волшебные сказки» . (передаю книгу детям) Всем спасибо, Вы сегодня были молодцы!

Публикации по теме:

Конспект ООД по ФЭМП «Знаки больше, меньше, равно» Задачи: Образовательные: – сформировать представление о знаках меньше «», умение использовать их для записи результата.

Конспект открытого занятия по РЭМП во второй младшей группе «Столько же, больше, меньше» Тема: «Столько же, больше, меньше». Цели: -закреплять представления о сохранении количества, о сравнении групп предметов на основе составления.

Конспект по ФЭМП «Больше, меньше, столько же» Цель: Формировать представления детей о таких понятиях, как “больше, меньше, только же”. Задачи: Знакомить с множествами предметов, сравнивать.

Конспект занятия: Формирование элементарных математических представлений Овощи. Игра больше, меньше. Формирование элементарных математических представлений ОВОЩИ. ИГРА “БОЛЬШЕ, МЕНЬШЕ” Реализация содержания программы в образовательных областях:.

Занятие по ФЭМП (подготовительная группа)

«Морская арифметика»

Цель: формировать умение производить арифметические действия в пределах 10; сравнивать числа, расставляя знаки «больше», «меньше» или «равно». Упражнять в деление целого круга на четыре равные части.

Материал к занятию:

Демонстрационный материал – картинка с изображением морского дворца с девятью окнами; картинка с изображением трёх белых и трёх розовых кругов; шесть картинок с изображением Морского конька на каждой; вырезанные из жёлтого и красного картона звёзды с цифрами.

Раздаточный материал – (из расчёта на одного ребёнка) картинка с изображением морского дворца с девятью окнами; счётный материал; числовые карточки; простой карандаш; бумажный круг.

Ход занятия

В группу входит очень грустная Русалочка.

Воспитатель: Здравствуй, Русалочка! Почему ты такая грустная?

Русалочка: Сегодня я должна сдать своему учителю экзамен по Морской арифметике! Сначала я думала, что нужно будет просто сосчитать все ступеньки нашего дворца, написать все цифры до 10 – это так легко! И я вместо того, чтобы учить Арифметику, отправилась путешествовать. Мой отец – Морской царь – страшно рассердился на меня и придумал мне на экзамен очень трудные задания! Я никак не могу в них разобраться. А если я не сдам экзамен по Морской арифметике, то мне будет запрещено подниматься на поверхность моря целых 10 лет!

Воспитатель: Не надо так расстраиваться! Сейчас мы с ребятами, попробуем разобраться в этих заданиях!

Русалочка: Ах, большое спасибо! Я обещаю, что теперь постараюсь внимательно изучать арифметику!

Задание 1

Русалочка выставляет на фланелеграфе картинку с изображением подводного дворца с девятью окнами. (3 окна на первом этаже и 6 окон на втором этаже)

Воспитатель: Русалочка, это не такое уж и сложное задание. Я уверена, наши ребята с ним справятся. Ребята, что бы вам было удобнее считать, возьмите каждый себе маленькую карточку с изображением подводного дворца.

Дети выполняют задание, используя индивидуальные карточки. Тот, кто справляется с заданием первым, выходит к фланелеграфу и записывает ответ. Остальные проверяют.

Задание 2

Русалочка: Во втором задание мне нужно собрать жемчужное ожерелье из трёх белых и трёх розовых жемчужин.

Воспитатель: Ребята, помогите Русалочке, и скажите, сколько всего жемчужин должно быть в ожерелье.

Воспитатель выставляет на фланелеграф картинку с изображением трёх белых и трёх розовых кружков.

Используя счётный материал, дети составляют математическое выражение.

Задание 3

Русалочка: Морской царь решил прокатиться по своим огромным морским владениям. Нужно сосчитать, сколько Морских коньков запряг в свою повозку Морской царь, если получилось три пары Морских коньков.

Выставляет на фланелеграф шесть картинок с изображением Морского конька на каждой.

Вызванный ребёнок выкладывает три пары картинок с изображением Морских коньков и объясняет свои действия.

Воспитатель: Молодцы, вы справились с этим действительно трудным заданием!

Задание 4

Русалочка: Морской царь заколдовал морских звезд, и они окаменели, а чтобы они вновь ожили, нужно правильно расставить знаки сравнения.

Воспитатель выставляет на фланелеграфе вырезанные из жёлтого и красного картона звёзды. На каждой звезде написана пара цифр: 6 и 8, 7 и 4, 2 и 5, и т.д. Дети поочерёдно вписывают простым карандашом знаки «больше», «меньше» или «равно» между цифрами.

Задание 5

Русалочка: В честь моего дня рождения Морской царь устраивает бал. На балу гостей будут угощать очень вкусным тортом. Я должна разделить торт на равные части между Морским царём, Морской царицей, рыбкой Флаундером и мной.

Воспитатель: Ребята, сколько частей торта получится? (Четыре) Докажите это.

Дети сгибают бумажные круги пополам, затем ещё раз пополам. Разворачивают круг и объясняют, что получилось четыре равные части.

Воспитатель: Вот мы и решили все задания! Теперь, Русалочка, ты наверняка сможешь сдать экзамен по Морской арифметике. Только пообещай нам с ребятами, что теперь ты будешь очень стараться и выучишь арифметику?!

Русалочка: Спасибо вам, ребята за помощь! Я обещаю, что теперь Морская арифметика будет моим самым любимым предметом!

ДС № 193 «Земляничка» АНО ДО «Планета детства «Лада» г. о.Тольятти

Конспект

занятия по ФЭМП

с детьми старшей группы

Тема «Больше. Меньше. Знаки « »

с использованием технологии проблемного обучения

Подготовила:

воспитатель И.Р. Орешкина

2015г.

Цель: Научить самостоятельно добывать знания о знаках «и «>», использовать их при сравнении групп предметов.

Задачи:

Обучающие:

Познакомить со знаками «и «>».

Учить детей сравнивать группы предметов с помощью знаков.

Развивающие:

Развивать пространственное воображение, образное, логическое мышление.

Развивать память, внимание, речь.

Воспитывающие:

Воспитывать интерес к математике, умение работать сообща, умение правильно строить отношения со сверстниками. Материал к занятию:

Демонстрационный:

Раздаточный:

Ход занятия:

Вводная часть.

Ребята какие времена годы мы с вами знаем? А какое у вас любимое время года? А вот мне нравится осень, ее золотая пора, когда идешь по лесу или по дороге усланной золотыми листочками, как по золотому ковру.

Ребята, я приглашаю вас на нашу поляну, где лежат листочки, красивые, яркие! С каких деревьев опали наши листочки? Давайте объединим их в две группы. (Одни большие – кленовые, другие маленькие – дубовые)

Давайте посчитаем, сколько кленовых листочков? Возьмите нужную цифру (4)

А сколько дубовых? Отметим количество нужной цифрой. (4)

Основная часть:

– Сравните количество кленовых и дубовых листочков. (Их равное количество).

Как вы это узнали? (пересчитали, составили пары).

Давайте мы с вами составим равенство: (4=4) Молодцы! Все верно!

Но, пока мы с вами рассуждали, на полянке появились вредные гусеницы,

– Сколько гусениц приползло к кленовым листьям? (3)

А к дубовым? (2)

Давайте мы сравним количество гусениц на кленовых листочках и на дубовых. Какой знак мы поставим между цифрами 3 и 2? (Неравно)

Да, можно поставить этот знак. Но, может ли знак «не равно» рассказать нам, на каких листьях гусениц больше? А какой знак нам поможет это сделать? Вы знаете?

ЭТАПЫ

ДЕЯТЕЛЬНОСТЬ ВОСПИТАТЕЛЯ

ДЕЯТЕЛЬНОСТЬ ДЕТЕЙ

I

Постановка проблемы

Воспитатель фиксирует внимание детей на обнаружении противоречий:

Мы хотим узнать, существует ли знак, который может рассказать какое число больше или меньше? Но не знаем, возможно ли это?

Итак, на какой вопрос мы хотим с вами получить ответ? Что мы хотим с вами узнать?

Дети осознают создавшееся противоречие: – Нужно узнать какой коврик больше, но мы не знаем, как их сравнить

Дети «осознают» цель поиска.

Дети «присваивают» проблему, участвуют в ее формулировке.

II

Актуализация знаний

Для того чтобы решить нашу проблему, в ней нужно сначала разобраться. Пройдите, пожалуйста, на свои места

У вас, у каждого на столах есть по две палочки. С помощью палочек изобразите знак равно. Когда мы можем поставить равно?

Мы с вами считали гусениц и узнали, что на кленовых их 3, а на дубовых-2. У вас на столах есть цифры, возьмите их и положите перед собой. Какой мы можем поставить между ними знак? Почему

Изобразите с помощью этих же палочек знак «неравно».

Когда две части одинаковые.

Дети изображают знак с помощью палочек.

Неравно, потому что две части разные.

Дети пытаются, но понимают, что им не хватает еще по одной палочки.

III

Выдвижение гипотез, предположений

Давайте подумаем, что же нам делать? Ведь больше палочек нет?

А можно ли изобразить какой-нибудь знак с помощью двух палочек, но какой?

А почему именно так?

Действительно, 3 больше, чем 2, поэтому мы поставили знак больше.

А если я цифры поменяю местами, то, что произойдет со знаком?

Правильно, теперь мы получили знак «меньше»

Мы с вами подумали и предположили, что если число маленькое то палочки нужно соединить, а если большое – раскрыть.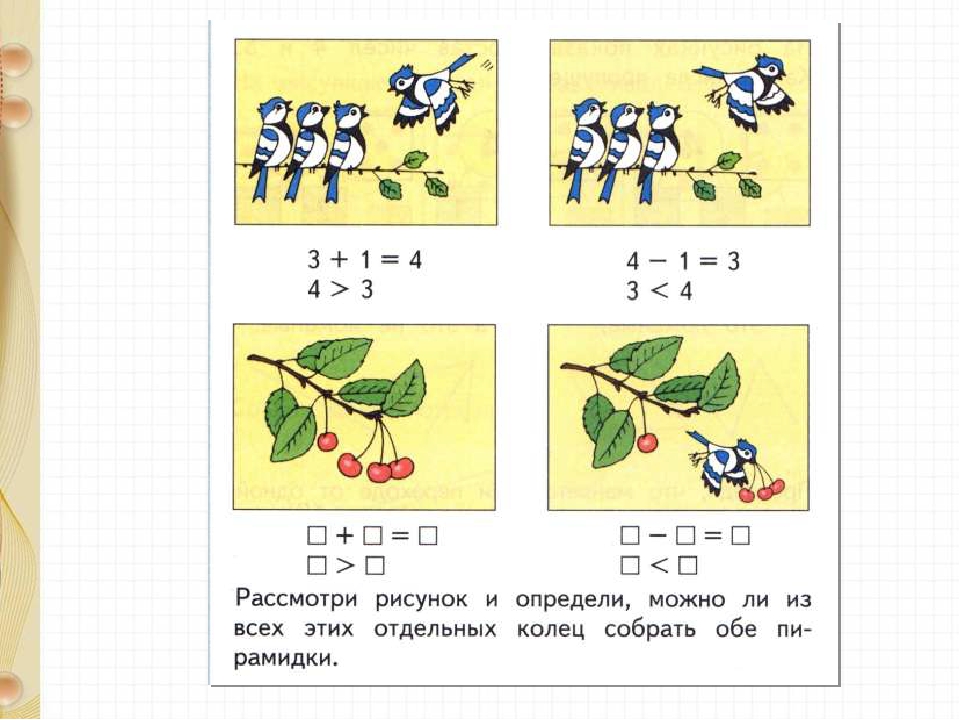

Дети высказывают свои мнения.

Попробовать изобразить с помощью двух палочек.

Дети участвуют в размышлении

У маленького числа палочки соединить, а у большого раскрыть.

3 больше, чем 2, поэтому раскрываем мы палочки около числа3, закрываем возле числа 2.

Знак нужно будет поменять, т.к. 2 меньше, чем три.

IV

Проверка решения

Давайте проверим наше предположение.

Где мы можем посмотреть и проверить его?

Посмотрите, я принесла вам энциклопедию, в которой мы можем посмотреть, верное ли наше предположение? У меня есть закладка.

Что мы с вами видим?

В энциклопедии, у родителей…

Дети рассматривают и делают вывод, что их предположение верно.

V

Введение в систему знаний

А теперь, для того, чтобы закрепить наши новые знания, мы с вами разделимся на две группы.

Каждой паре предлагаю пройти к столам. Вы видите на них таблицы, где уже расставлены знаки. Вам нужно в соответствии со знаками расставить правильно цифры.

Предлагаю поменяться и произвести проверку.

Что вы можете сказать?

Молодцы, вы справились с заданием.

Так какое же мы сделали с вами открытие? С какими новыми знаками познакомились?

Программное содержание:
Продолжать учить детей работать с цифрами от 1 до 10, выстраивать их в ряд по порядку, раскладывать на два меньших числа.
1. Совершенствовать умение решать арифметические задачи, записывать решение с помощью цифр, выделять в задачах – условие, вопрос, решение, ответ.
2. Закреплять знание детей о математических знаках: =, и правильно их использовать.
3. Развивать зрительно — пространственное восприятие и ориентировку при работе в тетради в клетку.
4. Способствовать развитию мыслительной деятельности при решении логической задачи.
5. Воспитывать интерес к математике.

Материал:
Демонстрационный: набор цифр для математического панно, мел, две карточки с нарисованными задачами на сложение и вычитание.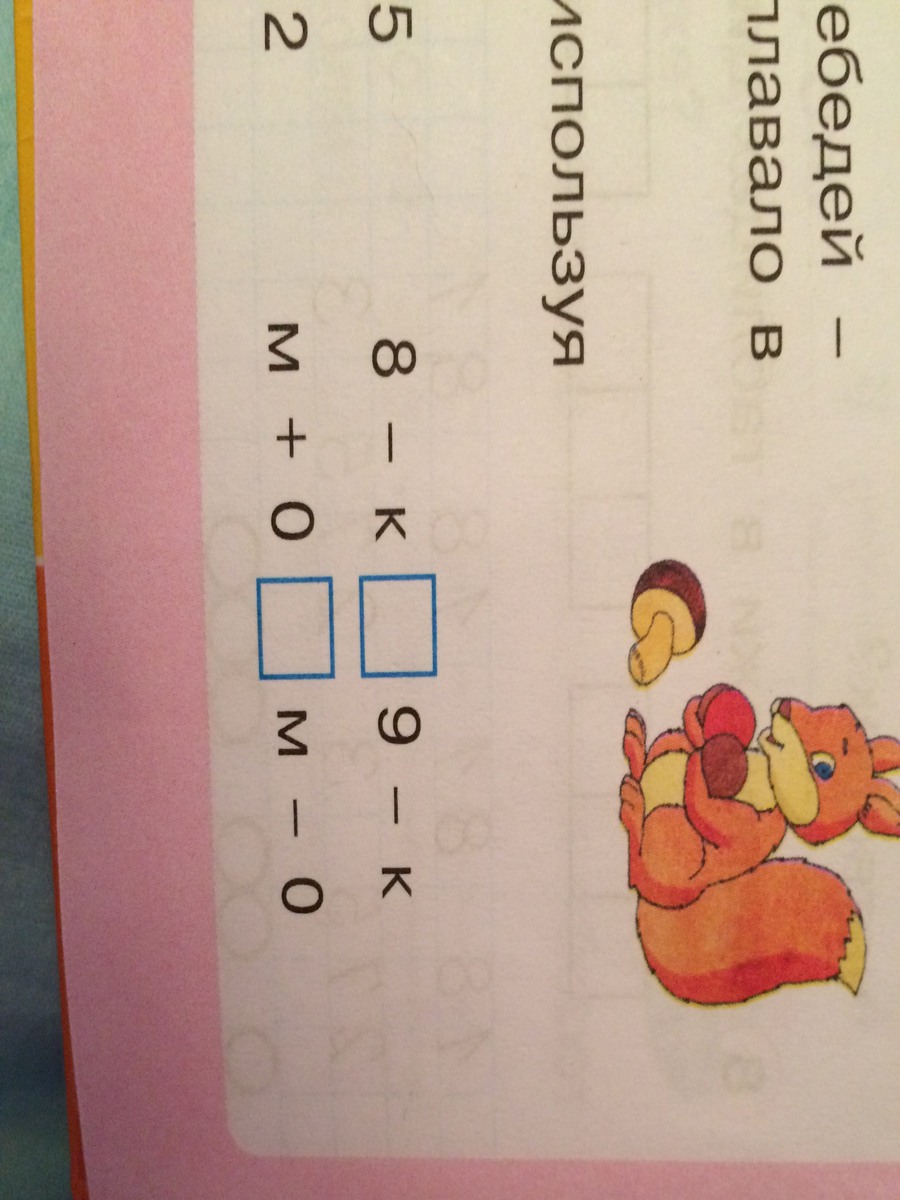
Раздаточный: наборы цифр; наборы математических знаков +,-,=; тетради в клетку; простые карандаши – на каждого ребенка.
Словарная работа:
Активизировать в речи детей слова: цифра, число, знаки – больше, меньше, равно, выражение – два меньше десяти и так далее.

Предварительная работа:
Игры дидактические и настольно-печатные: «Дни недели», «Правда, это или нет», «Убери по заданию», «Живые числа», «Ворота», «В какой руке сколько», «Какой это знак». Решение задач на логику.

Ход:
Звенит колокольчик, дети рассаживаются по местам, воспитатель обращает внимание на осанку детей.
-Сегодня в группу принесли необычное письмо (показывает кассету), давайте его послушаем (включает запись).

«Здравствуйте, дорогие ребята. В нашей математической стране случилась неприятная история: перессорились все цифры, выясняя какая из них самая главная. Спорили долго, но так и ничего не решили, только обиделись друг на друга и разбежались. Помогите вернуть их домой. Вы же знаете, что без цифр не обойтись не взрослым, ни детям. Царица Математики».

— Ну, что поможем! (да).
— Тогда нам необходим транспорт. А вот на чём мы отправимся, сейчас вы узнаете. Для этого нам необходимо приготовить пальчики.

Пальчиковая игра: «Сороконожки».
— Открываем тетради, берем карандаши, покажите как вы, их держите (в правой руке, тремя пальцами «щепотью»).

Проводиться математический диктант: «Самолет».
— Занимаем места, отправляемся на поиски цифр. Посмотрите, посмотрите, на полянке отдыхают цифры, но они вернуться домой, только если мы с вами сравним их, правильно расставив знаки. Какие знаки вы знаете (=,)
— Давайте расставим (дети выходят к доске и расставляют знаки).

2 10 __________ 6 2
6 4 __________ 3 3
1 1 __________ 4 10
(По окончанию работы дети хором читают полученные выражения: «два меньше десяти» и так далее).

— Несколько цифр нам удалось вернуть (просит детей разместить на математическом панно). Отправляемся дальше (звучит музыка).
— Я вижу еще одну цифру одну цифру, она спряталась на воротах, вернётся только тогда, когда вы составите её из двух меньших чисел (состав числа 8).

Игра «Ворота» (вспомнить правила: разделиться на пары и решить каким числом они будут в паре). Игра проводиться на ковре.
— Молодцы, мы вернули ещё одну цифру. Маша, поставь ее на панно.
— Цифры мы искали и немножечко устали, так давайте отдохнем.

Физкультурная минутка:
Мы топаем ногами,
Мы хлопаем руками,
Киваем головой.
Мы руки поднимаем,
Мы руки опускаем,
И бегаем кругом (3 раза).

— Ребята, а я знаю, где ещё могут прятаться цифры, конечно в задачах (дети садятся зав столы).
— Давайте вспомним, из каких частей состоит задача (условие, вопрос, решение, ответ). Воспитатель размещает на доске нарисованную задачу.
— Составьте условие к задаче, задайте вопрос (дети выполняют задание).
— А теперь используя цифры и знаки, запишите задачу и решите её.
8+1=9

Воспитатель с детьми проверяют правильность решения. Так же решают и вторую задачу.
6-1=5
— Какие цифры мы с вами ещё разыскали (9, 5). Мне кажется, мы все цифры собрали, давайте проверим. Ира поставь 9 и 5 на свои места (дети считают, проверяют).
— Какой цифры не достает (7).
— А найти нам ее поможет решение логической задачи.

«В вазе стояли 3 ромашки, 7 васильков и 5 пионов. Сколько в вазе было васильков (7 васильков).
— Ну, вот все цифры в сборе. Звучит голос.

«Спасибо ребята, что помогли вернуть цифры домой. Все вы хорошо поработали, но подумайте сами и оцените свою работу с помощью фишек (дети сами оценивают свою работу, объясняя свой выбор).

Название: Конспект занятия по математике в подготовительной группе «Пропавшие цифры»

Должность: воспитатель
Место работы: МКДОУ «ДСПО №13 «Тюльпан»
Месторасположение: Челябинская область, г. Трехгорный

Примеры на больше меньше или равно по матем для 1 класса :: verconsleta

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

По. Больше, меньше и равно. Сравнение чисел1 класс. Математика.1 класс 2 класс 3 класс 4 класс 5 класс 6 класс 7 класс 8 класс 9 класс класс 11 класс. Музыка. Дети закрепляют счёт предметов в пределах и производят сравнение двух предметных совокупностей по количеству предметов. У р о к 2. Карточки с примерами, 1 класс. Предварительный просмотр: Сложение и вычитание чисел в пределах 20.

1 кл. Учитель Мельникова. Начальные классы. Сравнение чисел: больше, меньше, равно, 1 класс, математика,. Больше, меньше, столько же. Класс: 1. Тип урока: урок изучения нового материала. Материалы для скачивания для 1 класса Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Развивающие онлайн игры для детей. И конечно, если число слева, равно. Категории. Название. Значение. Пример. Произношение. План конспект урока по математике 1 класс на тему: Урок математики в 1.

Описание недоступно из за ограничений в файле Подробнее. Можно использовать после знакомства с числами первого десятка. Решаем задачи по математике 2 класс. Все равно столько же, одинаково. Приведите примеры. Александрова Л. А., Мордкович А. Г. Математика.1 класс. Отношение порядка. Развивающие онлайн игры для детей. Поиск. Играем и. Конспект урока математики в 1 классе. Занимательная математика1 класс. Математика, 52. Цель урока: познакомить учащихся со знаками больше и меньше. Данный урок предназначен для учеников 1 классов,. Задачи.

 

Вместе с Примеры на больше меньше или равно по матем для 1 класса часто ищут

 

знаки больше меньше примеры.

знаки больше меньше равно картинки.

знаки больше меньше для дошкольников.

больше меньше игра.

больше меньше знаки.

знаки больше меньше равно презентация 1 класс.

больше меньше играть онлайн.

больше меньше что гуглят больше

 

Читайте также:

 

Готовые домашние задания по физике илекса в задачнике

 

Гдз 5 класс английский язык friends 1 carol skinner

 

Гдз ответы на билеты по биологии 11 класс

 

математик Эдвард Торп обыграл казино и заработал $800 млн на Уолл-стрит — Истории на vc.ru

Учёный хотел решать реальные задачи с помощью науки. Сначала он использовал физику и математику в азартных играх. Потом переключился на финансовые рынки, применил количественный метод анализа и открыл два хедж-фонда.

{“id”:172206,”url”:”https:\/\/vc.ru\/story\/172206-esli-vy-takie-umnye-pochemu-takie-bednye-matematik-edvard-torp-obygral-kazino-i-zarabotal-800-mln-na-uoll-strit”,”title”:”\u00ab\u0415\u0441\u043b\u0438 \u0432\u044b \u0442\u0430\u043a\u0438\u0435 \u0443\u043c\u043d\u044b\u0435, \u043f\u043e\u0447\u0435\u043c\u0443 \u0442\u0430\u043a\u0438\u0435 \u0431\u0435\u0434\u043d\u044b\u0435\u00bb: \u043c\u0430\u0442\u0435\u043c\u0430\u0442\u0438\u043a \u042d\u0434\u0432\u0430\u0440\u0434 \u0422\u043e\u0440\u043f \u043e\u0431\u044b\u0433\u0440\u0430\u043b \u043a\u0430\u0437\u0438\u043d\u043e \u0438 \u0437\u0430\u0440\u0430\u0431\u043e\u0442\u0430\u043b $800 \u043c\u043b\u043d \u043d\u0430 \u0423\u043e\u043b\u043b-\u0441\u0442\u0440\u0438\u0442″,”services”:{“facebook”:{“url”:”https:\/\/www.facebook.com\/sharer\/sharer.php?u=https:\/\/vc.ru\/story\/172206-esli-vy-takie-umnye-pochemu-takie-bednye-matematik-edvard-torp-obygral-kazino-i-zarabotal-800-mln-na-uoll-strit”,”short_name”:”FB”,”title”:”Facebook”,”width”:600,”height”:450},”vkontakte”:{“url”:”https:\/\/vk.com\/share.php?url=https:\/\/vc.ru\/story\/172206-esli-vy-takie-umnye-pochemu-takie-bednye-matematik-edvard-torp-obygral-kazino-i-zarabotal-800-mln-na-uoll-strit&title=\u00ab\u0415\u0441\u043b\u0438 \u0432\u044b \u0442\u0430\u043a\u0438\u0435 \u0443\u043c\u043d\u044b\u0435, \u043f\u043e\u0447\u0435\u043c\u0443 \u0442\u0430\u043a\u0438\u0435 \u0431\u0435\u0434\u043d\u044b\u0435\u00bb: \u043c\u0430\u0442\u0435\u043c\u0430\u0442\u0438\u043a \u042d\u0434\u0432\u0430\u0440\u0434 \u0422\u043e\u0440\u043f \u043e\u0431\u044b\u0433\u0440\u0430\u043b \u043a\u0430\u0437\u0438\u043d\u043e \u0438 \u0437\u0430\u0440\u0430\u0431\u043e\u0442\u0430\u043b $800 \u043c\u043b\u043d \u043d\u0430 \u0423\u043e\u043b\u043b-\u0441\u0442\u0440\u0438\u0442″,”short_name”:”VK”,”title”:”\u0412\u041a\u043e\u043d\u0442\u0430\u043a\u0442\u0435″,”width”:600,”height”:450},”twitter”:{“url”:”https:\/\/twitter.com\/intent\/tweet?url=https:\/\/vc.ru\/story\/172206-esli-vy-takie-umnye-pochemu-takie-bednye-matematik-edvard-torp-obygral-kazino-i-zarabotal-800-mln-na-uoll-strit&text=\u00ab\u0415\u0441\u043b\u0438 \u0432\u044b \u0442\u0430\u043a\u0438\u0435 \u0443\u043c\u043d\u044b\u0435, \u043f\u043e\u0447\u0435\u043c\u0443 \u0442\u0430\u043a\u0438\u0435 \u0431\u0435\u0434\u043d\u044b\u0435\u00bb: \u043c\u0430\u0442\u0435\u043c\u0430\u0442\u0438\u043a \u042d\u0434\u0432\u0430\u0440\u0434 \u0422\u043e\u0440\u043f \u043e\u0431\u044b\u0433\u0440\u0430\u043b \u043a\u0430\u0437\u0438\u043d\u043e \u0438 \u0437\u0430\u0440\u0430\u0431\u043e\u0442\u0430\u043b $800 \u043c\u043b\u043d \u043d\u0430 \u0423\u043e\u043b\u043b-\u0441\u0442\u0440\u0438\u0442″,”short_name”:”TW”,”title”:”Twitter”,”width”:600,”height”:450},”telegram”:{“url”:”tg:\/\/msg_url?url=https:\/\/vc.ru\/story\/172206-esli-vy-takie-umnye-pochemu-takie-bednye-matematik-edvard-torp-obygral-kazino-i-zarabotal-800-mln-na-uoll-strit&text=\u00ab\u0415\u0441\u043b\u0438 \u0432\u044b \u0442\u0430\u043a\u0438\u0435 \u0443\u043c\u043d\u044b\u0435, \u043f\u043e\u0447\u0435\u043c\u0443 \u0442\u0430\u043a\u0438\u0435 \u0431\u0435\u0434\u043d\u044b\u0435\u00bb: \u043c\u0430\u0442\u0435\u043c\u0430\u0442\u0438\u043a \u042d\u0434\u0432\u0430\u0440\u0434 \u0422\u043e\u0440\u043f \u043e\u0431\u044b\u0433\u0440\u0430\u043b \u043a\u0430\u0437\u0438\u043d\u043e \u0438 \u0437\u0430\u0440\u0430\u0431\u043e\u0442\u0430\u043b $800 \u043c\u043b\u043d \u043d\u0430 \u0423\u043e\u043b\u043b-\u0441\u0442\u0440\u0438\u0442″,”short_name”:”TG”,”title”:”Telegram”,”width”:600,”height”:450},”odnoklassniki”:{“url”:”http:\/\/connect.ok.ru\/dk?st.cmd=WidgetSharePreview&service=odnoklassniki&st.shareUrl=https:\/\/vc.ru\/story\/172206-esli-vy-takie-umnye-pochemu-takie-bednye-matematik-edvard-torp-obygral-kazino-i-zarabotal-800-mln-na-uoll-strit”,”short_name”:”OK”,”title”:”\u041e\u0434\u043d\u043e\u043a\u043b\u0430\u0441\u0441\u043d\u0438\u043a\u0438″,”width”:600,”height”:450},”email”:{“url”:”mailto:?subject=\u00ab\u0415\u0441\u043b\u0438 \u0432\u044b \u0442\u0430\u043a\u0438\u0435 \u0443\u043c\u043d\u044b\u0435, \u043f\u043e\u0447\u0435\u043c\u0443 \u0442\u0430\u043a\u0438\u0435 \u0431\u0435\u0434\u043d\u044b\u0435\u00bb: \u043c\u0430\u0442\u0435\u043c\u0430\u0442\u0438\u043a \u042d\u0434\u0432\u0430\u0440\u0434 \u0422\u043e\u0440\u043f \u043e\u0431\u044b\u0433\u0440\u0430\u043b \u043a\u0430\u0437\u0438\u043d\u043e \u0438 \u0437\u0430\u0440\u0430\u0431\u043e\u0442\u0430\u043b $800 \u043c\u043b\u043d \u043d\u0430 \u0423\u043e\u043b\u043b-\u0441\u0442\u0440\u0438\u0442&body=https:\/\/vc.ru\/story\/172206-esli-vy-takie-umnye-pochemu-takie-bednye-matematik-edvard-torp-obygral-kazino-i-zarabotal-800-mln-na-uoll-strit”,”short_name”:”Email”,”title”:”\u041e\u0442\u043f\u0440\u0430\u0432\u0438\u0442\u044c \u043d\u0430 \u043f\u043e\u0447\u0442\u0443″,”width”:600,”height”:450}},”isFavorited”:false}

301 325 просмотров

Книга Торпа «Обыграй дилера» о выигрышных стратегиях в блэкджеке взволновала мир казино. С математиком и основателем теории информации Клодом Шенноном Торп изобрел первый портативный компьютер, который позволял выиграть в рулетку. Ещё Торп придумал стратегию подсчёта карт в карточной игре баккаре.

Торп — «ветеран» Уолл-стрит с 50-летним опытом. Он разработал и усовершенствовал стратегии торговли конвертируемыми ценными бумагами и основал два фонда: Princeton Newport Partners и Ridgeline Partners. Они приносили ему 20% годовой прибыли.

Детство, увлечение наукой и любовь к экспериментам

Эдвард Торп родился в Чикаго в 1932 году в семье военного Оукли Гленна Торпа. В раннем детстве Торп освоил арифметику: считал в уме и вычислял квадратный и кубический корни. Однажды он решил досчитать до миллиона и заснул на числе 32 576. А когда проснулся, продолжил с того места, на котором остановился, вспоминала его мать.

С началом Второй Мировой войны семья перебралась в Калифорнию, в городок Ломита недалеко от Лос-Анджелеса. В средней школе Торп больше всего увлекался практическими занятиями по радиотехнике и электронике, химии и физике. Он любил ставить эксперименты и узнавать, как всё устроено.

Розыгрыши и эксперименты были частью моего метода изучения наук. Поняв какую-то теорию, я проверял её на самостоятельно придуманных опытах, многие из которых доставили мне массу удовольствия.

Я учился самостоятельно разбираться в различных вопросах, не ограничиваясь тем, чего требовали учителя, родители или школьная программа.

Например, Торп сделал радиоприемник, чтобы понять, как невидимые волны передают звуки через пространство. Дома он устроил химическую лабораторию, где проводил эксперименты: вырабатывал водород, сам готовил порох.

Он создавал и тестировал другие взрывчатые вещества: пироксилин и нитроглицерин. Мастерил бомбы из кусков водопроводных труб, заправлял их порохом и взрывал на холмах недалеко от дома.

В выпускном классе Торп начал думать, как предсказать исход игры в рулетку. Он не увлекался азартными играми. Для него задача лежала в области физики: он видел сходство между вращающейся рулеткой и планетой, вращающейся по орбите.

Когда его учитель английского Джек Чессон приехал из Лас-Вегаса и сказал, что казино обыграть невозможно, Торп заявил, что однажды сделает это — и ему удалось.

Научная карьера и азартные игры

Ключ к рулетке и блэкджеку

В 1958 году Торп получил степень по математике в Калифорнийском университете в Лос-Анджелесе (UCLA) и начал преподавать. В аспирантуре он женился на Вивиан Синетар, она училась на отделении английской литературы. Они прожили вместе всю жизнь и воспитали троих детей.

В 1959 году Торп перешёл преподавать математику в MIT. Одновременно с научными исследованиями Торп получил ответы на интересовавшие его вопросы — как выиграть в рулетку и в блэкджек.

В 1960–1961 годах Торп и профессор MIT Клод Шеннон вместе работали над выигрышной стратегией игры в рулетку. Они купили списанное рулеточное колесо и в ходе опытов создали первый портативный компьютер.

Устройство размером с пачку сигарет один участник клал в ботинок. Первый раз он нажимал пальцем ноги на кнопку, когда рулетку запускали. Второй раз, когда колесо делало один оборот. Компьютер вычислял будущее положение шарика и посылал радиосигнал игроку. У него под одеждой был радиоприемник, от которого тонкий стальной провод шел к динамику в ухе, куда поступал сигнал.

После испытаний в казино Торп и Шеннон убедились, что система работает. Но компьютер был технически несовершенным: динамик иногда вылезал из уха, а провода рвались, из-за чего приходилось выходить из игры. Торп и Шеннон перестали его использовать.

Торп думал над тем, как выиграть в карточную игру блэкджек (или «двадцать одно») с 1958 года. Исследователь заметил, что даже опытные игроки не понимают математику, которая лежит в её основе. Он решил, что сможет найти способ систематически выигрывать в блэкджек.

В блэкджеке меня привлекали не деньги. Меня занимала возможность найти способ выигрывать силой мысли, не выходя из собственной комнаты. Мне также было любопытно исследовать мир азартных игр, о котором я тогда ничего не знал.

Во время игры состав колоды меняется. Какие карты выбывают, а какие остаются, влияет на преимущество игрока или казино. Чтобы вывести выгодные для игрока закономерности, нужно просчитать миллионы карточных комбинаций. Если бы Торп делал это вручную, на калькуляторе, ему не хватило бы жизни. Но в MIT он мог использовать университетский IBM 704.

Торп выяснил, что чем больше в колоде остается девяток, десяток (это также дамы, короли и валеты) и тузов, тем лучше для игрока. Он разработал несколько стратегий подсчёта карт. В 1960 году наконец вывел оптимальную выигрышную стратегию — подсчёт десяток.

Чтобы понять, есть ли у него преимущество, игрок следит за отношением числа других карт к десяткам. В полной колоде 16 десяток и 36 других карт. 36 : 16 = 2,25. Если на момент выставления ставок отношение меньше 2,25, то в колоде много десяток — и игрок в выигрышном положении. Чем соотношение меньше 2,25, тем выше преимущество.

Для ставок Торп применил «критерий Келли», который предлагает делать более крупные ставки, когда у игрока преимущество, и маленькие ставки, когда преимущество на стороне казино.

По этой системе игрок обычно выигрывает большинство крупных ставок и в итоге получает прибыль, хотя он может проиграть большинство мелких ставок в невыгодных ситуациях по ходу игры.

Торп и миллионеры против казино

В 1961 в газете The Boston Globe вышла статья о Торпе — математике, который знает, как выиграть в блэкджек. Торпа завалили письмами и предложениями финансовой поддержки, чтобы испытать стратегию в казино. Предложения доходили до $100 тысяч. Торп отобрал двух кандидатов — мультимиллионеров из Нью-Йорка.

Первый, Эмануэль «Мэнни» Киммел, владел сетью парковок Kinney Parking и раньше занимался контрабандой алкоголя, нелегальными лотереями и был связан с преступными группировками. Второй, Эдди Хенд, был деловым партнером Киммела и занимался автоперевозками.

В ответ на скептические выпады прессы в его сторону Торп решил доказать, что его теория работает,

Я решил отправиться в Неваду отчасти для того, чтобы заткнуть рот любителям распространенных и довольно раздражающих издёвок над учеными: «Если вы такие умные, почему же вы такие бедные?”

После живых встреч и тренировочных игр Торп, Киммел и Хенд отправились в казино в Рино. Там Торп проверил стратегию подсчёта десяток.

Киммел и Хэнд готовы были выделить банкролл — общий капитал для игры — в $100 тысяч. Но Торп договорился на $10 тысяч. Он не хотел рисковать, потому что ещё не очень разбирался в игровом мире.

Тур по разным казино показал, что стратегия работала. В одной из игр за два часа Торп и Киммел на двоих вывели банк стола — $17 тысяч. Из них $6 тысяч выиграл Торп, а $11 тысяч — Киммел. Торп понял, что теряет концентрацию, вышел из игры и обналичил свои фишки. Киммел продолжил и проиграл свою долю.

Для меня блэкджек был игрой математики, а не везения.

После этого партнёры сыграли ещё несколько раз. В итоге поездка по казино закончилась победой. За 30 часов капитал игроков вырос с $10 тысяч до $21 тысячи.

Эдвард Торп в казино

Дон Крэвенс, The LIFE Images Collection, Getty

Паника в казино

Летом 1961 года контракт Торпа с MIT истёк. Ему предлагали продолжить работу, но он ушёл. Большую часть времени учёный проводил над стратегиями для выигрыша в рулетку и блэкджек, а не над научными проектами.

В конечном счёте Торп перевёлся в Университет штата Нью-Мексико. Там он получил постоянный контракт и время для исследований.

Торп продолжал проверять свою стратегию в казино. Выигрышные стратегии игры в блэкджек и способы вычислить шулеров он обобщил в книге «Обыграй дилера», вышедшей в 1962 году.

Книга произвела панику в мире казино. Сначала в прессе выходили язвительные статьи в адрес Торпа, которые отрицали возможность обыграть казино в блэкджек. Но одновременно с этим казино вычисляли игроков, которые считали карты, и запрещали им играть.

Торп даже был вынужден переодеваться и маскироваться, чтобы не стать жертвой местных воротил. В 1964 году впервые в истории казино даже поменяли правила игры в блэкджек. Правда, ненадолго, так как постоянные игроки, которые не считали карты, были недовольны.

Математическая идея, возникшая в моей голове, породила систему, позволяющую победить. Я рассчитывал на честную игру и думал использовать тайное оружие — свой разум — в спортивном состязании.

Вместо этого я столкнулся с запретами на игру, шулерством, стал персоной нон грата за большинством карточных столов. При виде паники, в которую впало это чудовище, я с удовлетворением чувствовал себя отомщённым. Приятно было сознавать, что я сумел изменить окружающий мир одной лишь силой математической мысли.

Баккара, угроза жизни и отход от азартных игр

После рулетки и блэкджека Торп приступил к другой карточной игре — баккаре, известной сейчас по фильму «Казино “Рояль”» о Джеймсе Бонде. В 1962 году совместно с математиком Биллом Уолденом он разработал стратегию подсчёта карт для баккары, в 1963-м — поехал в Лас-Вегас, чтобы проверить её.

Торп и его спутники играли в казино Dunes пять дней. Там их выигрыши не нравились администрации, Торпу два раза сделали «предупреждение»: добавляли наркотики в напитки. В последний, шестой, вечер они играли в казино Sands, откуда Торп ушел с выигрышем в $2500 — но совладелец казино лично запретил Торпу играть в заведении, вспоминал Торп в книге «Человек на все рынки».

Эдвард Торп в 1964 году Журнал Life, выпуск 27 марта 1964 года

По дороге из Лас-Вегаса обратно в Лас-Крусес у игроков возникла проблема с тормозами в автомобиле. Оказалось, что одна деталь была откручена. Играть в казино, где Торпа уже узнавали, становилось опасно. Он решил сменить площадку своей деятельности и обратился к миру инвестиций.

Могут ли мои методы выигрыша в азартных играх дать мне преимущество на величайшей в мире игровой арене, на Уолл-стрит?

Первые неудачные инвестиции

Торп инвестировал гонорары от книг и выигранные деньги, но неудачно. В первый раз он купил 100 акций компании Electric Autolite на $4000, потому что компании прочили рост в будущем. В течение двух лет стоимость акций упала в два раза, и Торп ждал ещё четыре года, пока не вернул вложения.

В другой раз он послушал двух человек, которые, как они говорили, разбогатели на инвестициях в компании по страхованию жизни. Они посоветовали Торпу вложиться в агентство A. M. Best, её индекс рос последние 24 года. Торп послушал, вложил деньги — и всё потерял.

Математик понял, что было ошибкой полагаться на инерцию рынка — на то, что долговременный рост продлится и дальше. Он решил изучить проблему и понять, как устроен рынок, как оценивать риск и прогнозировать стоимость ценных бумаг в будущем.

Торп был уверен, что, как и азартные игры, финансовые рынки можно проанализировать с помощью математики, статистики и компьютера.

Потери нескольких тысяч долларов было достаточно, чтобы правильное управление рисками стало важной для меня темой на следующие пять с лишним десятков лет.

Что такое варранты и как на них заработать

Летом 1965 года Торп прочитал брошюру об инвестиционных варрантах. Варрант — ценная бумага, по которой можно купить обыкновенные акции компании по указанной цене в обозначенный срок или раньше. Чтобы получить выгоду, нужно понимать, правильно ли оценён варрант. Но его стоимость зависит от предполагаемой стоимости обыкновенной акции в будущем.

Представьте, что у вас есть варрант IBM. В настоящий момент акция компании стоит $100. Варрант, срок действия которого истечёт через 12 месяцев, будет иметь ценность, только если акции за это время в какои-то момент вырастут до $110.

Если вы можете определить, насколько они волатильны (какова вероятность того, что они дорастут до отметки в $110 за указанный временной отрезок), вы знаете, какова на самом деле цена варранта.

Скотт Паттерсон

В это время Торп перевёлся на работу в Калифорнийский университет в Ирвайне (UCI). Там профессор Шин Кассуф уже написал диссертацию о варрантах и даже зарабатывал на них деньги.

Торп и Кассуф вместе улучшили метод инвестирования в варранты. В его основе лежало хеджирование рисков. Они приблизительно определяли справедливую цену варрантов.

Чтобы заработать, продавали переоцененные варранты без покрытия (короткая продажа), то есть не покупая их на самом деле. Для этого они одалживали необходимое количество варрантов у брокера, продавали их и получали выручку. Потом, чтобы вернуть брокеру долг, они покупали эти же варранты по текущей цене.

Если текущая цена была ниже цены продажи, была прибыль. Если выше — убыток. Чтобы нейтрализовать риск, Торп и Кассуф хеджировали варранты — покупали связанные с ними обыкновенные акции. Если расчёт был верный, прибыль одной операции компенсировала потери другой.

Торп и Кассуф инвестировали по своей модели, и это приносило им 25% годовых. О своей методике и результатах сделок они рассказали в книге «Обыграй рынок», которая вышла в 1967 году. Торп хотел делиться результатами своих открытий. Будучи человеком из мира науки, он считал, что научные открытия — всеобщее достояние. К тому же это мотивировало его на поиск новых идей.

После выхода книги Торп продолжил работать над теорией и в том же 1967 году вывел формулу, которая позволяла точнее определять, насколько завышена или занижена цена варранта. Торп продолжал инвестировать, и заработок рос.

Глядя на успехи Торпа, коллеги и знакомые доверили ему свои деньги. Он управлял их инвестиционными портфелями. Было ясно, что эффективнее создать пул активов и через одну учётную запись управлять большим количеством с меньшими усилиями. Но Торп ещё не понимал, как это сделать.

Торп открывает хедж-фонд

Встреча с Баффетом

В 1968 году Уоррен Баффет распускал свой инвестиционный фонд Buffett Limited Partnerships. Одним из его инвесторов был Ральф Джерард, декан в UCI, где работал Торп. Джерард хотел снова вложить деньги и подумывал обратиться к Торпу, но сначала попросил опытного инвестора Баффета оценить его.

Так Баффет и Торп встретились: они играли в бридж и обсуждали подходы к инвестициям. Баффет рассказал об устройстве его товарищества инвесторов — по сути, хедж-фонда. После этого Торп понял, как действовать.

Работа фонда: конвертируемый арбитраж

В 1969 году Торпу позвонил брокер Джей Риган, который прочёл «Обыграй рынок» и хотел открыть хедж-фонд по системе Торпа.

В том же году они открыли Convertible Hedge Associates, который позже переименовали в Princeton Newport Partners (PNP). Капитал составил $1,4 млн. Это были деньги Торпа, Ригана и нескольких инвесторов.

Риган в офисе в Нью-Йорке занимался покупкой и продажей ценных бумаг, налогами, учетом и документацией. Торп в Ньюпорт-Бич (в Калифорнии) сосредоточился на разработках и исследовании рынка.

Как и в блэкджеке, я мог оценить предполагаемую прибыль, представить возможный риск и решить, какую часть капитала следует поставить на карту. Но вместо банкролла в $100 тысяч у меня было теперь $1,4 млн, а вместо игорного дома с предельной ставкой $500 я играл на Уолл-стрит — казино без ограничения ставок.

PNP специализировался на хеджировании конвертируемых ценных бумаг: варрантов, опционов, конвертируемых облигаций и привилегированных акций. Постепенно к ним добавлялись другие типы деривативов и производных ценных бумаг по мере их появления.

Фонд работал по принципу конвертируемого арбитража. Это стратегия сделок с конвертируемыми ценными бумагами, когда риски в достаточной мере нейтрализованы, а прибыль вероятна, а зачастую и гарантирована.

Защиту обеспечивал «хедж» — пакет акций и связанных с ними конвертируемых ценных бумаг одной компании. Чтобы создать хедж, нужно было купить недооцененные ценные бумаги и сделать короткую продажу переоцененных. Так минимизировались риски при неблагоприятном изменении цены.

В основе конвертируемого арбитража лежит количественный метод анализа, математические формулы. Торп создал алгоритм, при помощи которого компьютер создавал диаграммы: они показывали «справедливое» соотношение между ценой конвертируемой ценной бумаги и ценой акции той же компании.

Так Торп находил выгодные сделки. Каждый день после закрытия рынка он звонил Ригану в Нью-Йорк с инструкциями по торговле на следующий день.

Так выглядела одна из сделок по модели Торпа. В 1972 компания Resorts International, которая создавала курорты и казино на Багамах, продавала варранты по 27 центов. Модель Торпа говорила, что варранты были недооценены и на самом деле стоили $4. Поэтому PNP купил 10 800 варрантов общей стоимостью $3200 после вычета комиссионных и хеджировали риск потерь, продав 800 обыкновенных акций по цене $8.

Через 6 лет акция преодолела отметку в $100. В итоге фонд продал варранты по цене более $100 и заработал $1 млн.

Система Торпа шла в разрез с принятыми видением рынка — так называемой «гипотезой эффективного рынка». Она гласила, что рынок развивается случайно и нельзя предсказать рост или падение ценных бумаг. И что фактические цены дают исчерпывающую информацию о рынке. Наиболее надежным считали инвестирование в индексные фонды.

Но PNP доказал, что его стратегия устойчива даже при глубоких кризисах. Например, во время «медвежьего рынка» 1973–1974 годов фондовый рынок упал на 48,2%. Такого не было со времен Великой депрессии. В 1974 году индекс S&P 500 упал на 29,7%, а PNP получил прибыль 9%.

Торп стал миллионером: инвестиции или наука

В первые два месяца работы PNP в 1969 году комиссия Торпа составила $5600 — больше университетской зарплаты.

Было ясно, что я стою на распутье. Я мог использовать математические умения для разработки стратегий хеджирования и, возможно, разбогатеть. Или же я мог остаться в мире науки, продолжая борьбу за продвижение по карьерной лестнице и ученые звания.

Торп решил продолжить научную карьеру, потому что любил исследования и преподавание. Одновременно он развивал количественные методы финансирования, но эта информация оставалась только в кругу вкладчиков.

К 1975 году Торп стал миллионером. Постепенно по образу жизни помимо его воли он отдалялся от привычного круга общения — образованных интеллектуалов из университетской среды. Одновременно он расходился и с коллегами по математическому факультету в UCI. Они сосредоточивались на чистой математике, а Торпа всё больше интересовала прикладная математика для решения реальных задач.

В 1982 году Торп отказался от должности профессора в UCI. Последние несколько лет он был главой математического факультета, а затем факультета управления, и разочаровался в том, как устроена университетская система изнутри.

После ухода из университета Торп сосредоточился на конкуренции с математиками, физиками и финансистами, которые теперь стекались на Уолл-стрит из академических кругов. Их прозвали квантами, и Скотт Паттерсон посвятил им одноименную книгу.

Второй хедж-фонд Ridgeline Partners: покупай дёшево, продавай дорого

В 1988 году хедж-фонд PNP закрылся. Главная причина — расследование против нескольких сотрудников принстонского отделения фонда, которые были замешаны в махинациях, неуплате налогов и мошенничестве. Торпа ни в чем не обвиняли, но фонд значительно ослаб после судебных издержек.

Кроме того, отделение в Принстоне тратило большую часть времени на защиту в суде, и прибыль фонда за 1988 год составила всего 4%. Торп вышел, а за ним и вкладчики.

Второй фонд Ridgeline Partners математик открыл в 1994 году с партнёром по прошлому фонду и другом Стивеном Мидзусава. Новый фонд работал по методу статистического арбитража, который Торп опробовал еще во времена PNP.

Торп и Мидзусава наблюдали за двумя группами акций — с наивысшим уровнем роста и падения. В течение следующего периода те акции, которые резко выросли, замедляли свой рост или падали, а упавшие акции росли. Торп и Мидзусава покупали падающие акции, которые затем вырастут (длинная позиция), и продавали растущие акции, которые потеряют в цене (короткая позиция).

Идея статистического арбитража Торпа — уравновесить длинную и короткую позиции. То есть провести длинную покупку и короткую продажу на одну сумму. Это позволяет создать приблизительно рыночно-нейтральный портфель, на который мало влияют колебания рынка.

Весь наш пакет акций, участвующих как в длинных, так и в коротких сделках, обновляется приблизительно раз в две недели. Мы продаем каждый раз на $540 млн акции, полученные в результате длинных покупок, и покупаем взамен новые акции ещё на $540 млн. Так что суммарный торговый оборот составляет $1,08 млрд.

То же происходит и с короткими продажами, сделки по которым прибавляют к обороту еще $1,08 млрд. Поскольку этот цикл повторяется двадцать пять раз в год, за год мы проводим сделок на $54 млрд, или 1,5 млрд акций.

Торп о работе Ridgeline Partners в 2000 году

Фонд работал до 2002 года. За время работы его доходность в среднем составляла 20% годовых, но в 2001–2002 годах она стала снижаться. Торп объяснял это ситуацией на рынке: ростом активов хедж-фондов и распространением статистического арбитража. Решение закрыть фонд подкреплялось и личными причинами.

Время было для меня ценнее, чем получение лишних денег. Мы с Вивиан хотели общаться с детьми, их семьями, путешествовать, читать и получать новые знания.

Жизнь Торпа после фондов

После закрытия Ridgeline Partners Торп инвестирует в другие хедж-фонды. Он говорит, что сейчас его единственная инвестиция в фондовый рынок — акции фонда Уоррена Баффета Berkshire Hathaway. Торп купил их в 1983 году, когда акция стоила $982,50, а сейчас она стоит $315 206.

Торп — президент компании Thorp & Associates, которая занимается консалтингом в области финансов.

Хотя он закончил работу в UCI в 1982 году, учёный продолжал принимать участие в жизни университета. В 2003 году он с женой Вивиан учредил кафедру и должность профессора математики на математическом факультете. Целью Торпа было привлечь выдающегося ученого на должность профессора и поддерживать его исследования. Но он не хотел просто передать средства, он хотел выстроить эффективную финансовую систему кафедры.

Поэтому Торп пожертвовал университету часть акций компании Berkshire Hathaway, проценты от которых следовало реинвестировать. У Торпа было условие — использовать деньги только для поддержки исследовательской работы профессора кафедры, и лишь 5% выделять на ненаучные расходы.

В 2004 году Торп пожертвовал деньги на исследование стволовых клеток. Тогда администрация Джорджа Буша-младшего резко сократила финансирование этой области. Благодаря вкладу Торпа и других спонсоров при UCI заработал Центр исследования стволовых клеток Сью и Билла Гросс.

В 2018-м Торп подарил университетской библиотеке UCI свой архив: научные документы и неопубликованные исследования. За год до этого вышла книга «Человек на все рынки», где Торп рассказал о личной жизни, приключениях в казино и работе в сфере инвестиций.

Торпу 88 лет, его состояние составляет $800 млн.

Лучшим было то время, которое я провел с небезразличными мне людьми — женой, родными, друзьями и сотрудниками. Что бы вы ни делали, радуйтесь жизни и тем людям, с которыми вы ее разделяете, и оставьте после себя что-нибудь, что поможет следующим поколениям.

Страница 83 – ГДЗ Математика 2 класс. Моро, Бантова, Бельтюкова, Волкова, Степанова. Учебник часть 2

Вернуться к содержанию учебника

Табличное умножение и деление

Вопрос

1. Рассмотри записи под каждым рисунком.
Спиши, заполняя пропуски, и объясни, как получено каждое следующее равенство из первого.

Подсказка

Повтори принцип деления на однозначное число.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

2.

12 : 6	18 : 2	16 : 8	14 : 7	8 : 2
12 : 2	18 : 9	16 : 2	14 : 2	8 : 4

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

3. За партами сидели 18 учеников, по 2 ученика за каждой партой. Сколько парт заняли эти ученики?

Подсказка

Если к задаче есть схематический рисунок или чертёж, краткую запись писать не нужно.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

4. Саша купил ручку за 8 р., ластик за 5 р., и у него осталось 2 р. Что узнаешь, вычислив:

8 – 5?               

8  + 5?               

8  + 5 + 2?

Подсказка

Повтори, из каких частей состоит задача.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

5. Какое число больше на 9, чем 25? 36? 47?

Какое число меньше на 8, чем 51? 62? 73?

Подсказка

Если в задаче есть слова «на… больше», то задача решается сложением, а если « на… меньше», то задача решается вычитанием.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

6. 1) Измерь каждое звено ломаной и найди её длину.

2) Начерти квадрат, периметр которого равен длине этой ломаной.

Подсказка

Чтобы найти длину ломаной линии, нужно сложить длины всех её звеньев.

Периметр многоугольника – это сумма длин всех его сторон. У квадрата все стороны равны, поэтому мы можем длину умножить на 4 и вычислить периметр.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

Для игры 12 детей разделились на 2 команды поровну. Сколько детей в каждой команде?

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

Ребусы:

Ответ

Поделись с друзьями в социальных сетях:

Вернуться к содержанию учебника

---

© budu5.com, 2021

Пользовательское соглашение

Copyright

Больше, чем меньше, чем математическое действие

Это, казалось бы, простая концепция: больше, чем меньше. Мы помним, как делали это в детстве и говорили о том, какое число ест «аллигатор». Но как нам довести наших детей до этого уровня? Как мы представляем эту концепцию? Как научить его без рабочего листа?

СВЯЗАННЫЙ: Рабочие листы НЕ мое. Я не фанат, и вы можете прочитать мои мысли здесь.

Почему «больше, чем меньше» – это удивительно сложный навык

На первый взгляд кажется простым: какое число больше? Какое число меньше?

Но чтобы довести ребенка до этого уровня, нужно проделать большую внутреннюю работу.

Во-первых, я собираюсь объяснить все знания, необходимые моему 5,5-летнему ребенку для выполнения этого задания.

Это умение не возникло в одночасье.

Легко слышать, как наши дети считают и думают: «ДА! Мой ребенок знает их количество! » На самом деле то, что знает ваш ребенок, – это первый шаг в очень долгом, пожизненном марафоне с числами.

Первый большой шаг в «знании чисел» – это понимание значения числа. Идея, что символ / цифра 5 означает пять чего-то.Это ОГРОМНО.

СВЯЗАННЫЙ: Хотите знать, как я учил своих детей числам и ценности? Узнайте больше о моей простой программе домашнего дошкольного образования.

Итак, во-первых, потратьте много времени – месяцы, даже годы – просто говоря о значении числа. Прививайте ребенку, что числа что-то означают, что-то представляют и служат не только для запоминания счета.

Что делать дальше?

Затем ваш ребенок должен понять, что некоторые числа больше или меньше других чисел.

Вы делаете это с физическими объектами .

Составьте группы и сравните их. «В какой группе больше?» «В какой группе меньше?»

Опять же, над этим навыком можно потратить годы.

А потом – попробуйте эту игру с ними.

Война.

Помните войну? Война – отличная карточная игра для отработки ценности и более или менее.

Как только ребенок освоил эту игру – , теперь он готов к этому занятию.

Вот и все говорят о том, что больше, чем меньше, чем настроено.

Это действие является процедурным действием , что означает, что ребенок уже знает концепцию и имеет ее. Если ваш ребенок еще не понимает значения чисел, ПОЖАЛУЙСТА, НЕ ПЫТАЙТЕСЬ ДАННЫМ ДЕЙСТВИЕМ.

Нет приза за самое быстрое выполнение процедуры. Вместо этого вы хотите, чтобы ваш ребенок усвоил концепцию наилучшим образом.

Материалы:

Этот пост содержит партнерские ссылки.Занятый малыш – участник партнерской рекламной программы Amazon Services LLC. Как партнер Amazon, я зарабатываю на соответствующих покупках. Подробнее об этих ссылках читайте в моей политике раскрытия информации.

Как ни странно – эти три припаса управляют моей жизнью. Я не могу насытиться ими! Три самых лучших расходных материала.

Как начать это занятие

Я развернул свою бумагу и нанес на нее наборы чисел. Я поставил маленькую точку между каждым числом, чтобы указать, куда мой сын будет ставить наклейку больше или меньше.

Некоторые числа я написал точками вместо чисел.

Некоторые пары равны.

На листе наклеек я поставил традиционный символ «больше чем меньше» вместе с некоторыми знаками равенства.

Помните – это процедурная деятельность…

У моего сына понятий числовых значений и более или менее вниз. Это упражнение было направлено на понимание традиционных символов и процедур для этого.

Мы начали с того, что вспомнили, в какую сторону должна смотреть пасть «аллигатора» (он всегда хочет «съесть» большее число).

И он пошел искать больше, чем меньше.

Это простое занятие, но оно имеет глубокие корни в очень сложном числовом смысле.

Что значит «знать их количество»?

Путь к пониманию чисел долог, извилист и сложен. Когда наши дети впервые учатся запоминать порядок счета, это только первый и самый маленький кусочек этой головоломки.

Стоимость.

Понимание значения чисел, которые больше или меньше других – это шаг в математическом путешествии, который легко помочь нашим детям.

Что вы думаете об этом больше, чем меньше активности?

Больше, меньше и равно – eXtension Alliance for Better Child Care

Одна важная часть обучения маленьких детей математике – помочь им усвоить понятия «больше чем», «меньше чем» и «равно». Эти концепции являются ключевыми для понимания сложения и вычитания. По мере того как общество уделяет все больше внимания важности чтения, письма и арифметики, мы начинаем видеть все больше рекламы, призывающей к использованию флеш-карт, даже начиная с младенчества.Хотя это популярная тенденция, использование флеш-карточек, чтобы помочь маленьким детям запоминать математику и другие факты, неуместно, потому что это не имеет никакого реального значения для ребенка. Маленькие дети получают больше от счета в реальных жизненных ситуациях.

Обучение «больше чем», «меньше чем» и «равно»

• Поставщики услуг по уходу за детьми знают, что дети понимают понятия «больше чем», «меньше чем» и «равно», когда они дают детям крекеры, и Джимми говорит, что у Дэнни больше крекеров, чем у него.Забрать крекеры у Дэнни и отдать их Джимми может не понравиться Дэнни, но если он понимает концепции «больше чем», «меньше чем», «равно» или «то же самое», это решение будет сочтено справедливым.
• Вы также можете использовать числовую линию, чтобы показать эти концепции и попросить детей следить за ними. Например, вы можете попросить их указать пальцем на число 3 и показать им, что если число стоит перед 3, оно меньше, а если оно идет после 3, то больше. Вы также можете научить маленьких детей сложению и вычитанию.
• Как показывает пример в сопровождающем видео, вы также можете обучать детей, давая им числа и прося их показать вам «больше 4» или «равно 2» и т. Д. Если дети физически передвигают небольшие манипуляторы или блоки, могут помочь закрепить то, что они делают, и сделать это более практичным и увлекательным.

Видео-пример обучения математике дошкольников

Чтобы увидеть пример обучения этой математической концепции детей дошкольного возраста, посмотрите следующий видеоролик eXtension Alliance for Better Child Care:

Для получения дополнительной информации

Чтобы узнать больше об обучении математике в сфере ухода за детьми, ознакомьтесь со следующими статьями eXtension Alliance for Better Child Care:

Детский сад Урок «Больше, меньше и равно»

В этой части урока я использую доску SMARTBoard.Если у вас есть доска SMARTBoard, элементы «Больше», «Меньше» и «Равно» можно легко загрузить и открыть. Если у вас есть интерактивная доска другого типа, вы все равно можете использовать этот урок, открыв файл в Smart Notebook Express. Нажмите здесь, чтобы загрузить. Также есть PDF-файл, чтобы вы могли воссоздать эту часть урока.

Я собираю учеников перед Smartboard. У меня есть карточки с именами каждого ученика. Эти карточки используются для выбора тех, кто будет подходить к Smartboard.

Я открываю первый слайд (слайд SMARTBoard Slide 1) с целью урока, написанной «дружественными для учащихся» терминами.Есть цель содержания и цель языка, чтобы помочь сосредоточить внимание на расширении словарного запаса для моих изучающих английский язык (EL), чтобы соответствовать методам обучения SIOP. Я зачитываю эти цели своим ученикам.

Content Objective
Я могу сравнить количество объектов в двух группах.

Языковая цель
Когда я разговариваю с другом, я могу использовать слова больше, меньше или равно, чтобы сравнивать объекты в двух группах

Затем я провожу своих студентов по следующим слайдам.

Слайд 2: Я вызываю группы студентов по 5-6 человек за раз. Задайте студентам вопросы, например: – Есть ли еще мальчики или девочки? Задав вопрос, я повторяю предложение: «Мальчиков больше, чем девочек». Сделайте это несколько раз, чтобы дать учащимся возможность познакомиться с лексикой большего, меньшего и равного.

Slide 3: Когда мы используем слово «больше», это означает, что количество объектов больше или больше.
Я предлагаю студентам разделить лягушек и рыбок на группы, чтобы упростить встречу.Я прошу их помочь мне определить, есть ли еще лягушки или рыба. Лягушек больше, чем рыб.

Slide 4: Когда мы используем слово «меньше», это означает, что количество объектов меньше или меньше.
Снова предложите студенту помочь разбиться на группы, чтобы помочь в подсчете. Подсчитайте, чтобы определить, меньше ли рыбы, чем лягушек. Рыбы меньше, чем лягушек.

Slide 5: Есть еще собаки или кошки? Напомните учащимся, что они могут переставлять картинки в группы, чтобы облегчить сравнение.Попросите учеников ответить на правильный ответ справа. Верно. Собак больше, чем кошек. Я всегда помещаю ответ в законченное предложение, чтобы студенты могли практиковать свой академический язык. Количество собак больше или больше, чем количество кошек.

Slide 6: Есть еще бананы или яблоки? Напомните учащимся, что они могут переставлять картинки в группы, чтобы облегчить сравнение. Попросите учеников ответить на правильный ответ справа.Продолжайте обсуждать, почему это правильный ответ.

Slide 7: Я говорю студентам, что теперь мы собираемся сосредоточиться на меньшем. Машин или велосипедов меньше? Попросите учеников ответить на правильный ответ справа. Верно. Мы знаем, что велосипедов меньше, чем автомобилей, потому что количество велосипедов меньше количества автомобилей.

Slide 8: Стулья и столы меньше? Студент должен снова обвести ответ справа.

Slide 9: Рубашек и брюк стало меньше? Это хитрый ответ для студентов, так как числа равны. Мы обсудим это далее на следующем слайде.

Slide 10: Количество штанов и рубашек было одинаковым. Когда это происходит, мы говорим, что они равны. Студенты иногда борются со словарём «равный». Они понимают слово «одинаковый», но «равный» не так привычно для слова. Я часто привожу несколько примеров …. подняв пальцы вверх…. звонить мальчикам и девочкам … и т. д. просто чтобы дать им возможность использовать это слово.

Slide 11: Что вы можете сказать о количестве сердечек и звездочек? Я даю всем ученикам время сосчитать и сравнить две группы. Группы одинаковые, так что мы о них говорим? Правильно … равный!

Slide 12: Теперь время поворота и разговора. Студенты получают возможность практиковать свой академический язык. Я прошу их взяться за руки с назначенным для них поворотом и собеседником и поднять руку в воздух, чтобы я знал, что у каждого есть партнер.Я говорю: А теперь повернись к другу и скажи им, есть ли больше или меньше мячей, чем скакалок. Я даю им время поговорить со своим партнером, затем прошу их сказать на счет три, больше или меньше. Мы вместе говорим: мячей больше, чем скакалок.

После того, как мы закончим этот слайд, я предлагаю студентам вернуться на свои места для практики с гидом. Не закрывайте урок SMARTBoard. Это нужно для следующей части инструкции.

Обучение большему или меньшему, чем сравнение количеств

Этот урок знакомит детей со сравнением количеств с помощью слов больше, меньше и равно.

При обучении сопоставлению количеств ребенку в первую очередь важно хорошо понимать порядок чисел, и этому можно научить с помощью числовой линии.

Как только порядок чисел может быть визуализирован в последовательности, мы можем переходить к практике подсчета объектов.

Ниже наш первый пример.

Мы посчитаем количество моих шариков и подсчитаем количество шариков моего друга.

У меня есть 1 шарик.

У моего друга 4 шарика.

Мы знаем, что 4 больше, чем 1, потому что мы знаем последовательность чисел и знаем, что 4 идет после 1.

Однако это может помочь усилить сравнительный размер каждого числа с помощью числовой прямой.

Больше значит больше.

Поскольку количество шариков, которое есть у моего друга, на больше числа на , чем количество шариков у меня, мы говорим, что:

У моего друга больше чем меня.

Противоположность больше – меньше

У меня меньше дружище.

Вот еще один пример:

Сравним количество шариков путем подсчета.

У меня есть 3 шарика, а у моего друга 2 шарика.

3 стоит после 2, поэтому это большее число.

Мы видим, что 3 дальше по числовой прямой, чем 2.

У меня больше шариков, чем у моего друга.

У меня на больше, чем у моего друга, на шариков.

У моего друга на мраморных шариков меньше, чем у моего друга.

Вот еще один пример обучения больше или меньше.

Один из способов научить чему-то большему или меньшему – это расположить предметы рядом друг с другом.

Считая количество моих медведей, у меня их 5.

У моего друга 3 медведя.

Мы можем научить концепции большего, чем просто объединяя по одному каждому объекту за раз.

Мы видим, что после того, как я соединил всех трех медведей моего друга, некоторые из них остались.

У меня больше, чем у моего друга.

Мы видим, что у меня на 2 больше, чем у моего друга.

В этом новом примере ниже моему другу подарили еще несколько плюшевых мишек.

У кого сейчас больше всего?

У меня все еще столько же плюшевых игрушек.

У меня 5 плюшевых мишек.

У моего друга теперь тоже 5 медведей.

У нас столько же медведей.

Равно – это слово, которое мы используем для обозначения одинаковых чисел.

Мы можем видеть, что количество медведей равно , если их объединить в пары.

Мы можем научить этому, сгруппировав каждую пару в коробку, как указано выше, или физически держа два предмета в каждой руке, когда вы их поднимаете. Вы можете попросить ребенка взять по одной из каждой группы в каждую руку, пока вы их считаете.

В следующих примерах мы сравним более двух групп элементов, используя следующие определения:

Если что-то больше всего , значит, это больше, чем все остальное.Больше ничего нет.

минимум означает, что это на меньше, чем все остальное. Нет ничего меньшего, чем это.

В этом примере у трех человек есть шарики.

У Тома 3 шарика.

У Сары 2 шарика.

У Чарли 5 шариков.

У Сары наименьшее количество шариков, меньше, чем у Тома и Чарли. У Сары минимум .

У Чарли больше всего шариков, больше, чем у Тома и Сары.У Чарли больше всего .

Вот еще один пример сравнения количества яблок.

У Джона есть 1 яблоко.

У Клэр 1 яблоко.

У Криса 3 яблока.

У Криса самое большое количество яблок и яблок, больше всего .

У Джона и Клэр одинаковое количество яблок.

Слово для этого равно .

У Джона и Клэр одинаковых яблок – штук.

В этом примере у Джона и Клэр меньше .

В приведенном ниже примере нам предлагается заполнить поля, относящиеся к количеству шариков.

У Джеймса 6 шариков.

У Оскара и Изабеллы 2 шарика.

У Джеймса есть наибольшее количество шариков , потому что у него больше, чем у всех остальных.

Поскольку у Оскара и Изабеллы одинаковое количество шариков, мы говорим, что у них одинаковое количество шариков.

Вот еще один пример сравнения количеств.

У Лили есть 1 плюшевый мишка.

У Макса 4 плюшевых мишки.

У Гарриет 2 плюшевых мишки.

Сравнивая плюшевых мишек Макс с плюшевыми мишками Харриет, у Макс на больше, чем на , чем у Харриет.

У Лили меньше, чем у Макса, и меньше, чем у Харриет.

У Лили минимум .

Больше, чем аллигаторов

Некоторые математические понятия усвоить детям труднее, чем другие.Это, безусловно, верно для символов больше и меньше!

К счастью, эти практичные аллигаторы помогают разобраться в сложных математических знаках и мотивируют детей тренироваться снова и снова. Они являются прекрасным дополнением к нашим популярным рекламным материалам, которые можно приобрести в магазине или на сайте Teachers Pay Teachers!

Готовимся

Чтобы подготовить упражнение, я просто напечатал символы «больше», «меньше» и «равно» печеньям и аллигаторам на карточках и вырезал их по серым линиям, чтобы разделить их.

Чтобы работа длилась из года в год, я пропустил детали через ламинатор. Затем я поместил печенье в одну стопку, а символы – в другую.

Я был готов!

Больше и меньше аллигаторов

Моим первоклассникам понравилось это занятие! Чтобы поиграть, я собрал своих учеников на ковре и просмотрел символы больше, меньше и равно, напоминая им, что это помогает думать о знаках больше и меньше как о голодных аллигаторах, которые хотят съесть наибольшее число.

Я показал своим ученикам манипуляционный коврик и зачетный лист и проработал пример.

Я положил первое печенье в стопку в коробку с надписью «1-й номер», а второе печенье справа, закрывая поле с пометкой «2-й номер».

Мы читали каждое число и говорили о том, что побольше.

«Если бы голодный аллигатор пришел перекусить, какое печенье он хотел бы съесть: 17 или 58?» Я спросил.

Класс единогласно согласился, что большее число пойдет первым.

Мы просмотрели наши символы и нашли картинку, на которой голова аллигатора обращена вправо. Доброволец поместил символ в центре доски, чтобы завершить наше числовое предложение.

«17 меньше 58» читаем вместе.

Мы с классом потренировались еще на нескольких примерах. Затем я убрал мультяшные символы аллигатора и вытащил более традиционные.

Для них это был плавный переход.

Когда дети были готовы, я попросил их сделать еще один шаг в обучении, записав свои сравнения в зачетный лист.

Это был отличный способ бросить вызов некоторым из моих детишек!

Возьмите копию

Готовы играть? Нажмите синюю кнопку ниже, чтобы загрузить бесплатную копию, а затем прыгайте и покупайте наши рекламные материалы в магазине или на сайте Teachers Pay Teachers!

Как обучать детей с аутизмом большему и меньшему количеству концепций

Обучение детей большему и меньшему количеству концепций важно для сравнения количества предметов и определения того, какие из них больше или меньше.Детей с аутизмом можно научить большему и меньшему понятию с помощью игрушек, привлекательных предметов, фруктов, овощей и т. Д., А не только с помощью слов. Исследования подтверждают тот факт, что дети с аутизмом лучше учатся с помощью визуальной структуры, то есть добавления объекта к задаче, который помогает ребенку эффективно учиться и выполнять задачу.

Предпосылки для изучения большего и меньшего понятия:

• Допуск сидения
• Зрительный контакт
• Внимание, концентрация
• Идентификация номера
• Порядок номеров
• Подсчет объектов
• Навыки сопоставления – чтобы количество соответствовало количеству

Есть много техник или методов для обучения этой концепции, давайте рассмотрим один из них шаг за шагом.

В этой методике мы стремимся научить ребенка сначала концепции БОЛЬШЕ , а затем – меньшей концепции.

ШАГ 1:

• Давайте возьмем две чаши и наполним одну чашу 10 шариками, а другую – всего двумя шариками.
• Теперь объясните ребенку, что эта чаша (чаша с 10 шариками) содержит на шариков больше, чем другая (чаша с 2 шариками).

(Примечание: используйте какое-нибудь выражение лица, произнося слово more и сделайте ударение на этом слове.)

• Затем спросите ребенка, в какой чаше еще еще шариков. Ребенок должен уметь правильно отвечать.
• Повторите это упражнение с разными предметами и попросите ребенка определить, в какой чаше находится еще предметов.
• Как только ребенок поймет еще концепцию, то есть значение слова еще , мы можем перейти к шагу 2.
  

ШАГ 2:

• Здесь давайте используйте полоску с числами, написанными на них, как показано ниже:

• Научите ребенка, что 1 – больше , чем 0, 2 – больше , чем 1, 3 – больше , чем 2, 6 на больше , чем на 3 и т. д.
• Повторяйте и задавайте вопросы ребенку, пока ребенок не поймет.
  

ШАГ 3:

• Возьмем две пластины разного цвета, например, зеленого и красного.
• Заполните зеленую тарелку 7 помпонами, а красную тарелку 3 помпонами.
• Попросите ребенка сосчитать помпоны на зеленой тарелке и поставить соответствующий номер под тарелкой.

• Таким же образом попросите ребенка сосчитать помпоны на красной тарелке и поставить соответствующий номер под тарелкой.

• Теперь спросите ребенка, обратившись к полосе из шага 2, какой номер на больше , чем другой.

Здесь, в данном случае, 7 – это больше , чем 3.

• Повторяйте действие, пока ребенок не овладеет им.
  

Вышеупомянутый метод повторяется для обучения концепции LESS .

ШАГ 1:

• Давайте возьмем две чаши и наполним одну чашу 9 бусинками, а другую – всего 2 бусинками.
• Теперь объясните ребенку, что эта чаша (чаша с 2 бусинами) содержит на меньше бусинок , чем другая (чаша с 9 бусинами)

(Примечание: используйте выражение лица, произнося слово меньше и подчеркните это слово.)

• Затем спросите ребенка, в какой чаше минус бусинок. Ребенок должен уметь правильно отвечать.
• Повторите это упражнение с разными предметами и попросите ребенка определить, в какой чаше минус предметов.
• Как только ребенок поймет концепцию минус , то есть значение слова минус , можно обучить шагу 2.
  

ШАГ 2:

• Та же полоса снова используется для обучения концепции минус .

• Теперь научите ребенка, что 2 равно меньше , чем 3, 3 равно меньше , чем 4, 6 равно меньше , чем 9, 5 равно меньше , чем 8 и так на.
• Повторяйте и задавайте вопросы ребенку, пока ребенок не поймет.
  

ШАГ 3:

• Возьмите две пластины разного цвета, например желтого и синего.
• Заполните желтую тарелку 8 помпонами, а синюю тарелку 2 помпонами.
• Попросите ребенка сосчитать помпоны на желтой тарелке и поставить соответствующий номер под тарелкой.

• Снова попросите ребенка сосчитать помпоны на синей тарелке и поставить соответствующий номер под тарелкой.

• Теперь спросите ребенка, обратившись к полосе из шага 2, какой номер на меньше , чем другой.

Здесь, в этом случае, 2 – это меньше , чем 8.

• Повторяйте действие, пока ребенок не овладеет им.

Эту технику можно практиковать с использованием разных предметов в зависимости от интересов ребенка.

Есть много интересных способов научить этой концепции, и рабочие листы доступны в Интернете для загрузки и практики.

Счастливого обучения.

Что дети знают и что им нужно узнать о счете

Переход к письменной символьной математике

Контекст и обзор
Формальная символьная математика может дать детям более мощные инструменты и идеи, чем те, которые даются через их повседневную неформальную математику. Формальная математика (и использование в ней символов) развивалась в нескольких культурах и теперь стала практически универсальной. Детям нужно этому учиться.

Повседневное происхождение и формальная математика
Дети сталкиваются с математическими символами в повседневной жизни: номера лифтов, номера автобусов, телеканалы и уличные знаки – среди многих других.Часто родители, телевидение и программное обеспечение вводят простую символическую математику, такую ​​как чтение записанных чисел на экране телевизора или игральных карт.

Школы, безусловно, должны преподавать формальную математику. Но сделать это непросто. Даже если они компетентны в повседневной математике, у детей могут возникнуть проблемы с осмыслением и связью своих неформальных знаний с тем, чему их учат в школе. Учителя часто не обучают символизму эффективно. Если дети встают не на ту символическую ногу, результатом может быть неприятное падение с учебной лестницы.Таким образом, цель учителей – помочь детям, даже начиная с дошкольного возраста, понять, почему используются символы, и использовать их осмысленно, чтобы связать уже известную неформальную математику с формальной символической математикой. Учителю необходимо «математизировать» повседневную личную математику детей; то есть помочь детям связать их неформальную систему с формальной математикой, преподаваемой в школе. Не является опрометчивым или неуместным с точки зрения развития ребенка знакомить детей с символами, если это мотивирующее и значимое занятие.Напротив, очень важно, чтобы обучение символам начиналось на ранней стадии, но опять же, если и только если это делается осмысленным образом.

Вот ключевые вопросы, связанные с введением формальной математики маленьким детям:

Детям младшего возраста сложно соединять цифры и арифметические символы (+ и -) со своей повседневной математикой
Они могут хорошо складывать, но их сбивает с толку выражение 3 + 2. альтернативные реальности: повседневный мир и «академический» (в уничижительном смысле) мир.Повседневный мир имеет смысл, а мир школы – нет. Вы думаете о себе в первом и делаете то, что вам говорят во втором.

Знак равенства (=) – сложная задача
Учитель намеревается научить знак равенства как «эквивалент» и думает, что у него это есть, но ребенок усваивает его как «делает» (например, 3 + 2 дает 5). Это рассказ о том, как детский эгоцентризм встречается с эгоцентризмом учителя, но ни один из них не разговаривает друг с другом.

Решение
Нам не следует избегать обучения символам, мы должны вводить их осмысленно.Это означает учет того, что дети уже знают, и соотнесение введения символов с этим предварительным знанием. Это также означает мотивацию использования символов. Таким образом, если вы хотите сказать другу, сколько кукол у вас дома, вам нужно посчитать их числовыми словами (символами), а затем использовать произнесенные слова («У меня пять кукол»), письменные слова («У меня пять кукол» », Написанные на листе бумаги или экране компьютера), или письменные символы (5), чтобы сообщить результат.

Манипуляторы могут помочь
Использование манипуляторов может быть эффективным при обучении символизму и формальной математике, но они часто используются плохо.Цель состоит не в том, чтобы ребенок играл с конкретными предметами, а в том, чтобы использовать эти предметы, чтобы помочь ребенку усвоить абстрактные идеи. Цель манипуляторов – избавиться от них, вложив их в голову ребенка, чтобы использовать их в мыслях. Например, предположим, что ребенок учится представлять десятки и единицы с помощью десятичных блоков.